A New Simple Chaotic System with One Nonlinear Term

Abstract

In this research article, a simple four-dimensional (4D) chaotic dynamic system with uncomplicated structure and only one nonlinear term is introduced. The features of the proposed design have been conducted with some standard nonlinear dynamic analysis and mathematical tools which show the chaotic nature. One of the most important indicators for detecting complexity of the chaotic systems is the Kaplan-York dimension of the system. Moreover, one of the main criteria of chaotic systems is its simplicity due to the reduction of operating costs. Therefore, it seems necessary to design a system as simple as possible and with high complexity. In this research, a comparison has been made between the proposed system and similar chaotic systems, which has given noticeable results. For the practical implementation of the proposed design, the circuit analysis using Multisim software has been employed. The proposed scheme has been used in the application of image encryption to show the efficiency of the proposed chaotic system and standard encryption tests have been performed. The rest of the numerical results have been conducted using MATLAB/Simulink software.

1. Introduction

Lorenz’s simplified system, which is based on atmospheric convection, was designed and discovered by Lorenz in 1963 [1]. This dynamic system, which is considered the world’s first chaotic attractor, has become a basis for research on nonlinear dynamic systems [2,3]. After this discovery, the research in the field of chaotic dynamic systems using differential equations was expanded and used in many physical and dynamic structures [4,5,6,7,8]. Many hidden attractors can be found in these types of systems, and chaotic systems can be used in different structures based on the type of attractors [9,10]. Due to the complexities of n^th nonlinear chaotic dynamic systems, including the sensitivity of these types of systems to parameters, initial conditions and being unpredictable, this type of nonlinear systems can be used in biomedical engineering [11], laser applications [12], secure communications [13], wireless sensor networks [14] and image encryption/decryption [15].

Three main criteria for designing and building a chaotic dynamic system were proposed in 2012 [16]. One of these three mentioned criteria is that the newly designed dynamic system should be simple in comparison with other dynamic systems [17,18,19,20]. Therefore, the system should have dynamic simplicity while being chaotic. In this regard, researchers of chaotic dynamic nonlinear systems have conducted extensive research to achieve the mentioned goals [21,22,23,24]. For example, in [25], a nonlinear chaotic dynamic system with only two nonlinear terms and strange attractors was proposed. In the following, the dynamic characteristics of the novel nonlinear dynamic system, the analysis, and the practical circuit of the novel 4D dynamic system has been implemented. It is shown that the novel 4D nonlinear dynamic system can implement good encryption. In [26], an autonomous 4D nonlinear chaotic system with three nonlinear terms has been implemented with a simple mathematical model and chaotic attractors. This system has only two unstable equilibrium points and the electronic circuit of the nonlinear system has been designed. In [27], a 4D chaotic dynamic system without an equilibrium point with rich dynamics with three nonlinear terms and one fixed term is presented. The dynamic properties of the new system have been shown using nonlinear analysis, including: 2D and 3D chaotic attractors, bifurcation diagrams, and equilibrium points. In [28], using Lorenz equations, a 4D dynamic system with two nonlinear terms and three equilibria is introduced. Standard dynamic analyses, bifurcation diagrams and coexisting behaviors have been analyzed. To prove the effectiveness of the dynamic system, image encryption and standard tests have been performed. In [29], a 4D dynamic system with nonlinear attractors has been introduced, considering the parameters of the system with two nonlinear terms. The exact nonlinear dynamic characteristics of standard chaos have been analyzed and the attractors have been investigated by fixing the initial conditions and parameters of the new nonlinear system. In addition, the practical electronic circuit corresponding to the new dynamic system has also been proposed. For the effectiveness of the chaotic dynamic system, image encryption has been performed using security analysis. In [30], various types of coexisting attractors in the 4D autonomous chaotic systems are presented. In this system, the coexisting attractions are existed, and the system has four unstable equilibria. The results show that the introduced system has many hidden attractors compared to the change of initial conditions and parameters. The bifurcation diagrams show the coexistence attractors and the chaotic attractors have been confirmed with the Lyapunov exponents. In the end, an electronic circuit has been designed and used to understand the dynamic behavior experimentally. In [31], a 4D nonlinear system is proposed in which the hyperbolic cosine nonlinear function is used. The above research has been implemented using a pair of semiconductor-based circuits. After studying the bifurcation diagrams, the Lyapunov exponent and phase portrait, special behaviors of the new system such as periodicity and chaos have been discovered. In this article, the coexistence of hidden attractions and multi-stability phenomenon are analyzed. At the end, the design of the analog circuit is created by PSpice simulations and the practical feasibility is proven with hyperbolic cosine nonlinearity. In [32], a 4D chaotic system is built based on the Sprott-B system. The designed system has two saddle foci. By changing the initial conditions, the system has multiple attractors, which are confirmed by bifurcation diagrams. In the end, a passive controller is used to control the chaos.

Therefore, according to the mentioned contents, the design of a simple chaotic dynamic system with high complexity is worthy of literature. The proposed system in this research article is simple and has only one nonlinear term. The important contributions of this research article can include the following:

• We introduce a novel and attractive 4D nonlinear chaotic system with only one nonlinear term.
• We analyze the nonlinear dynamic behavior, mathematical model and chaotic behaviors of the proposed dynamic system.
• We design and implement the operational model of chaotic dynamic system.
• We use a chaotic dynamic system in color image encryption and perform standard analyses.

The organization of the rest of this research article is as follows: Section 2 is assigned to introducing the mathematical model of the dynamic system and nonlinear analysis. Section 3 is assigned to system theory analysis. In Section 4, the practical circuit and circuit characteristics of the nonlinear dynamic system are designed. Section 5 is assigned to the engineering applications of chaotic dynamic system in the field of color image encryption/decryption. Finally, in Section 6, the results are introduced.

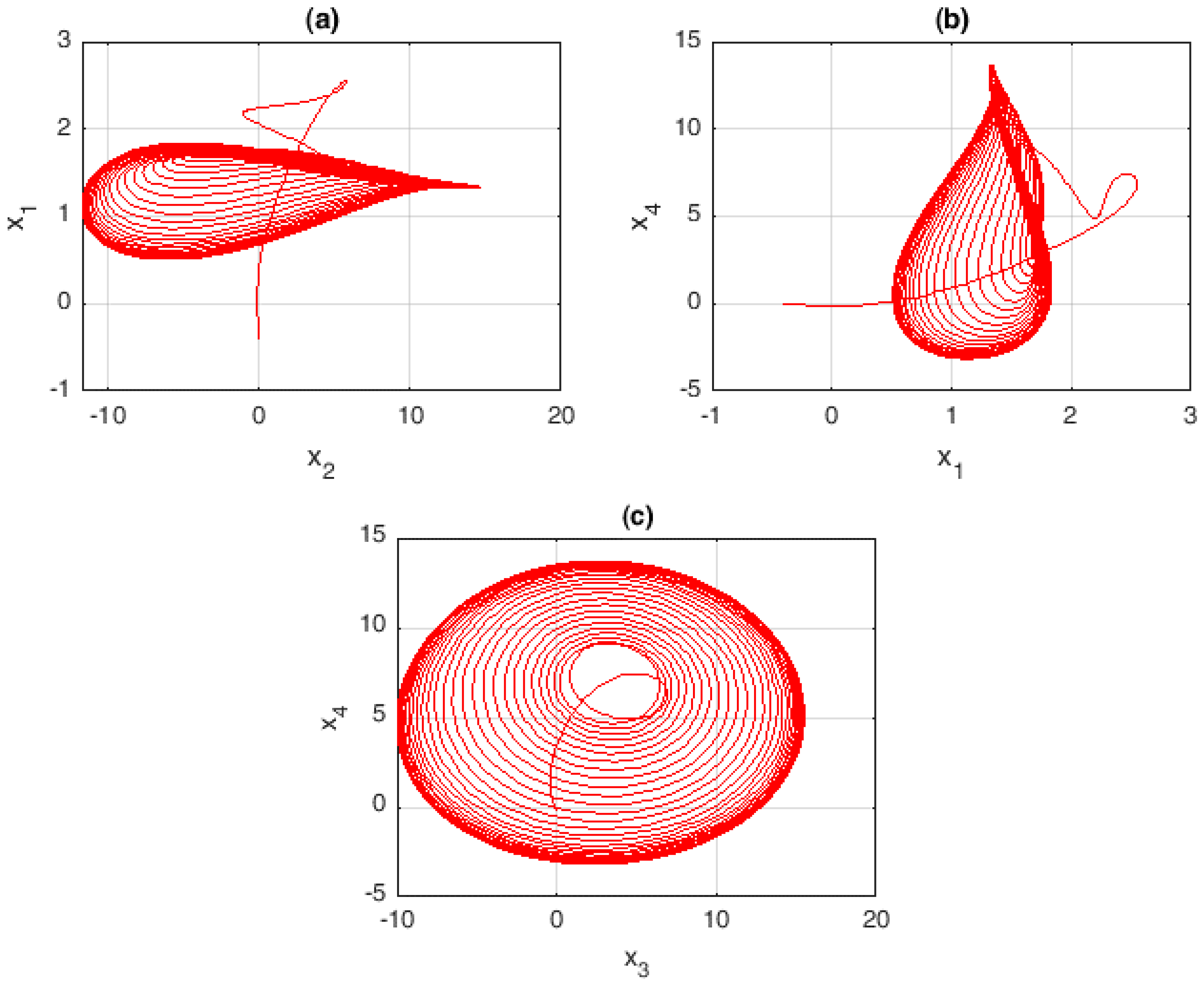
2. Mathematical Model of the Chaotic System

In the search for nonlinear chaotic systems, we describe the mathematical model of the 4D nonlinear chaotic system:

$$\begin{array}{c}\dot{x}=a_1+a_{2}y+a_{3}x\left(0.1+0.01w^2\right)\hfill \\ \dot{y}=a_{4}x+a_{5}y+a_{6}z+a_{7}w\hfill \\ \dot{z}=a_{8}y\hfill \\ \dot{w}=a_{9}x+a_{10}z\hfill \end{array}$$

(1)

where $x$, $y$, $z$ and $w$ signify the state variables, and $\left[a_1,a_2,\cdots ,a_{10}\right]$ are the constant parameters.

The equilibrium points of the chaotic system (1) are achieved as

$$\begin{array}{c}{a}_1+a_{2}y+a_{3}x\left(0.1+0.01w^2\right)=0\hfill \\ a_{4}x+a_{5}y+a_{6}z+a_{7}w=0\hfill \\ y=w\hfill \\ z=-\frac{a_9}{a_{10}}x\hfill \end{array}$$

(2)

Considering many combinations of parameters, a comprehensive computer search of a₁, …, a₁₀ and initial conditions is performed. With this method, the constant parameters of the nonlinear system are chosen as

$$\begin{array}{c}{a}_1=7,a_2=1.3,a_3=-9,a_4=7.8,a_5=-1.5,\hfill \\ a_6=-8.5,a_7=2.7,a_8=7.8,a_9=11.6,a_{10}=-5.7.\hfill \end{array}$$

(3)

For this system, the initial conditions are set as: (−0.4, −0.03, −0.004, −0.001), then the Lyapunov exponents are found as 1.71, 0, −1.08 and −3.42. Therefore, for the parameters (3), the system (1) has a chaotic behavior according to the definitions of the chaos theory; the designed system has a positive Lyapunov exponent. The Kaplan-York dimension is as follows [33]:

$$D_{KY}=\lambda +\frac{{{\displaystyle \sum }}_{\lambda =1}^{n}L{E}_{\lambda }}{\left|L{E}_{{\lambda }_n}\right|}=3+\frac{1.71+0-1.08}{\left|-3.42\right|}=3.184$$

(4)

It specifies that the designed nonlinear dynamic system (1) has a fractal dimension. One of the most important indicators for diagnosing the complexity of chaotic and hyperchaotic systems is the high Kaplan–York dimensions of the system [34]. As mentioned in Section 1, one of the main criteria of chaotic systems is its simplicity due to the reduction of operational costs. Therefore, it seems necessary to design a system that is as simple as possible and has high complexity.

Table 1. Comparison between the topology of the proposed system and similar 4D simple chaotic systems.

No.	System	Total No. of Terms	No. of Nonlinear Terms	Maximum Kaplan–York
1	Gong et al. [25]	7	2	3.1481
2	Lai et al. [26]	7	3	3.0157
3	Natiq et al. [28]	10	2	3.152
4	Singh and Roy [35]	8	1	3.0695
5	Zhang and Li [27]	8	3	3.171
6	Singning and Kengne [31]	8	1	3.098
7	Sahin et al. [36]	7	1	2.579
8	Singh and Roy [37]	8	1	3.0860
9	System (1)	11	1	3.184

is a comparison between the topology of the proposed system and 4D simple chaotic systems.

As it is known, compared to similar systems, the chaotic system (1) is simpler than the above-mentioned systems and has higher Kaplan–York dimension.

The phase portrait and spectrums of the Lyapunov exponents of a typical nonlinear chaotic attractor of mentioned system are illustrated in Figure 1 and Figure 2, correspondingly.

Substituting the constant parameters into dynamical model (2), one obtains

$$\begin{array}{c}{y}^{*}=0\hfill \\ w^{*}{}^3+10w^{*}=273.612\hfill \\ x^{*}=\frac{7.7778}{1+0.1w^{*}{}^2}\hfill \\ z^{*}=2.0351x^{*}\hfill \end{array}$$

(5)

where it is easy to calculate the equation $w^{*}{}^3+10w^{*}=273.612$, with the roots 5.9797 and $-2.9898\pm 6.0678j$. Hence, this chaotic system has one real equilibrium point $E_1\left(x^{*},y^{*},z^{*},w^{*}\right)=\left[1.6998,0,3.4593,5.9797\right]$ and two complex equilibrium points as $E_{2,3}\left(x^{*},y^{*},z^{*},w^{*}\right)=\left[-0.8499\pm 1.7248j,0,-1.7297\pm 3.5102j,-2.9898\pm 6.0678j\right]$.

To analyze the state trajectories of the nonlinear dynamic system (1) in the vicinity of the equilibrium points, the Jacobian matrix is found as:

$$J=\left[\begin{array}{cccc}0.1a_3\left(1+0.1w^{*}{}^2\right)& a_2& 0& 0.02a_3{x}^{*}{w}^{*}\\ a_4& a_5& a_6& a_7\\ 0& a_8& 0& 0\\ a_9& 0& a_{10}& 0\end{array}\right],$$

(6)

where substituting the constant parameters (3) into (6), we have

$$J=\left[\begin{array}{cccc}-0.9\left(1+0.1w^{*}{}^2\right)& 1.3& 0& -0.18x^{*}{w}^{*}\\ 7.8& -1.5& -8.5& 2.7\\ 0& 7.8& 0& 0\\ 11.6& 0& -5.7& 0\end{array}\right].$$

(7)

For equilibrium point $E_1={[1.6998,0,3.4593,5.9797]}^T$, the Jacobian matrix is defined as

$$J_1=\left[\begin{array}{cccc}-4.1181& 1.3& 0& -1.8296\\ 7.8& -1.5& -8.5& 2.7\\ 0& 7.8& 0& 0\\ 11.6& 0& -5.7& 0\end{array}\right].$$

(8)

Hence, the eigenvalues of the linearized system are achieved as

$$\begin{array}{c}\left|\lambda I-J_1\right|=\left|\begin{array}{cccc}\lambda +4.1181& -1.3& 0& 1.8296\\ -7.8& \lambda +1.5& 8.5& -2.7\\ 0& -7.8& \lambda & 0\\ -11.6& 0& 5.7& \lambda \end{array}\right|\hfill \\ \hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=({(\lambda -0.1408)}^2+66.0156)({(\lambda +2.9499)}^2+10.4846)=0\hfill \\ \Rightarrow {\lambda }_1=-a,{\lambda }_{2,3}=\frac{-1\pm j\sqrt{3}}{2}.\hfill \end{array}$$

(9)

Since real parts of two eigenvalues are positive, the equilibrium point E₁ is an unstable focus. This system displays strange attractors.

On the other hand, for the equilibrium points $E_{2,3}=\left[-0.8499\pm 1.7248j,0,-1.7297\pm 3.5102j,-2.9898\pm 6.0678j\right]$, the Jacobian matrices are calculated as

$$J_{2,3}=\left[\begin{array}{cccc}1.6091\pm 3.2655j& 1.3& 0& 1.4264\pm 1.8565j\\ 7.8& -1.5& -8.5& 2.7\\ 0& 7.8& 0& 0\\ 11.6& 0& -5.7& 0\end{array}\right].$$

(10)

Therefore, the eigenvalues of the linearized system are obtained as

$$\left|\lambda I-J_{2,3}\right|=\left|\begin{array}{cccc}\lambda -1.6091\mp 3.2655j& -1.3& 0& -1.4264\mp 1.8565j\\ -7.8& \lambda +1.5& 8.5& -2.7\\ 0& -7.8& \lambda & 0\\ -11.6& 0& 5.7& \lambda \end{array}\right|=0$$

(11)

For the equilibrium point $E_2$, the eigenvalues of the linearized system are λ₁ = 5.0608 + 4.8336j, λ₂ = −0.5963 + 6.7291j, λ₃ = −3.8945 − 0.7331j, λ₄ = −0.4608 − 7.5641j, and for the equilibrium point $E_3$, the calculated eigenvalues are λ₁ = 5.0608 − 4.8336j, λ₂ = −0.5963 − 6.7291j, λ₃ = −3.8945 + 0.7331j, λ₄ = −0.4608 + 7.5641j. Since real part of one eigenvalue is positive (for both cases), the equilibrium points E₂ and E₃ are unstable focus.

3. Theoretical Analysis of Dynamic System Characteristics

In this section, to investigate the dynamic behaviors of the nonlinear dynamic system (1), we increase the value of parameter a₂ of dynamic system (1) from 0.85 to 4.4. The bifurcation diagram shown in Figure 3 for the first Lyapunov exponent has three different values with respect to zero. All the numerical simulations related to the chaotic system (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) have been performed via MATLAB/Simulink toolbox, with step size of 1 ms and by the ode45 solver.

If $0.85\le a_2<2.66$, the nonlinear dynamic system (1) is in quasi periodic state. In this case, the phase portrait of the system is shown in Figure 4.

If $2.66\le a_2<3.19$, the dynamic system (1) is in periodic state. In this case, the phase portrait of the system is shown in Figure 5.

If $3.19\le a_2\le 4.4$, the dynamic system (1) is in chaotic state. In this case, the phase portrait of the system is shown in Figure 6.

4. Circuit Implementation

One of the alternative approaches to explore the modeling of chaotic systems is the realization of digital electronic circuits which model the designed systems. The designed circuits are usually simulated by various electronic software in different references [38]. In this section, we simulated the circuit implementation of dynamic system (1) with electronic components in Multisim software. The used electronic components include capacitors, resistors multipliers and operational amplifiers which are proposed based on Kirchhoff’s circuit laws. The circuit design of the proposed chaotic system is implemented as follows:

$$\begin{array}{cc}\hfill \dot{X}& =\frac{1}{C_1}\left[-\frac{1}{R_1}{V}_1-\frac{1}{R_2}\left(\frac{R_{14}}{R_{13}}\right)Y+\frac{1}{R_3}X+\frac{1}{10R_4}X{W}^2\right]\hfill \\ \hfill \dot{Y}& =\frac{1}{C_2}\left[-\frac{1}{R_5}\left(\frac{R_{16}}{R_{15}}\right)X+\frac{1}{R_6}Y+\frac{1}{R_7}Z-\frac{1}{R_8}\left(\frac{R_{18}}{R_{17}}\right)W\right]\hfill \\ \hfill \dot{Z}& =\frac{1}{C_3}\left[-\frac{1}{R_9}\left(\frac{R_{14}}{R_{13}}\right)Y+\frac{1}{R_{10}}X\right]\hfill \\ \hfill \dot{W}& =\frac{1}{C_4}\left[-\frac{1}{R_{11}}\left(\frac{R_{16}}{R_{15}}\right)X+\frac{1}{R_{12}}Z\right]\hfill \end{array}$$

(12)

where the element values are selected as follows:

$$\begin{array}{c}{C}_1=C_2=C_3=C_4=1nF,V_1=-1mV\hfill \\ R_1=0.05K\Omega ,R_2=307.69K\Omega ,R_3=R_4=444.44K\Omega \hfill \\ R_5=R_9=R_{10}=51.282K\Omega ,R_6=266.67K\Omega ,R_7=47.059K\Omega \hfill \\ R_8=148.148K\Omega ,R_{11}=34.483K\Omega ,R_{12}=70.175K\Omega \hfill \\ R_{13}=R_{14}=R_{15}=R_{16}=R_{17}=R_{18}=100K\Omega ,\hfill \end{array}$$

(13)

Figure 7 shows the circuit diagram of the designed nonlinear chaotic system (1).

In the proposed circuit design shown in Figure 7, two AD633AN is used as the multiplier, five TL082CD A-type as the operational amplifier and ±15 Volts power supply is applied to the system. The 2D phase portrait diagrams of the nonlinear dynamic system (1) using the proposed circuit design are shown in Figure 4.

From the comparison between Figure 1 and Figure 8, the realization of the proposed design is determined.

5. Engineering Applications

5.1. Image Encryption

In this section, we will use a 4D nonlinear chaotic system designed to implement an image encryption system. We use an 8-bit RGB color image with ${\rm M}\times {\rm M}$ dimensions as the main cryptographic image. The details and steps of encryption include the following:

• Equation (3) and (x₀, y₀, z₀, w₀) = (−0.4, −0.03, −0.004, −0.001), are considered as the parameters and initial conditions for the implementation of cryptography in the cryptographic system. From 4D Rung-Kutta algorithm, chaotic signals $\left[x_s\left(i\right),y_s\left(i\right),z_s\left(i\right),w_s\left(i\right)\right]$, $i=\left(1,2,\dots ,M/2\right)$ are generated numerically with an accuracy of 15 decimal places. It should be noted that 15 decimal places of each number in the chaotic sequence are converted to a 64-bit number and 32 low-value bits, but with high accuracy, are selected as $\left(rn{g}_{4s}\left(i\right), rn{g}_{2s}\left(i\right), rn{g}_{3s}\left(i\right), rn{g}_{1s}\left(i\right)\right)$. Using a sequence of defined random bits, we will have:

  $$rng\left(i\right)=bitxor\left(rn{g}_{4s}\left(i\right), rn{g}_{2s}\left(i\right), rn{g}_{3s}\left(i\right), rn{g}_{1s}\left(i\right)\right)$$

  (14)
• Using the chaotic vector sequences $x_{js}\left(i\right),j=1,2,3,4 and i=1,2,\dots ,M/2$, permutations $p_x,p_y$ are constructed as follows:

  $$\begin{array}{c}{P}_x=sort\left\{\left[x_{1s};x_{2s}\right]\right\}\hfill \\ P_y=sort\left\{\left[x_{3s};x_{4s}\right]\right\}\hfill \end{array}$$

  (15)
  The vector Sort is an ascending vector and an indicator for chaotic sequences.
• Color image I is decomposed into components R, G, B, and then components R, G, and B are transformed into three main matrices. The two substitution vectors $p_x$ and $p_y$ are used to replace the row and column indices of these principal matrices, respectively. Assuming the matrix is the original image $R_{M\times M}^{\left(0\right)}$, we have:

  $$R_{M\times M}^{\left(0\right)}=\left[{\Re }_1^T,{\Re }_2^T,\dots ,{\Re }_M^T\right]$$

  (16)

  where ${\Re }_1^T,{\Re }_2^T,\dots ,{\Re }_M^T$ are linear vectors. After permitting the row by $P_x$, we will have:

  $$R_{M\times M}^{\left(1\right)}=\left[{\Re }_{P_x\left(1\right)}^T,{\Re }_{P_x\left(2\right)}^T,\dots ,{\Re }_{P_x\left(M\right)}^T\right]=\left[{\hslash }_1,{\hslash }_2,\dots ,{\hslash }_M\right]$$

  (17)

Similarly, the columns are replaced by the vector $P_y$, and the corresponding chaotic image matrix is transformed as follows after both row and column spatial displacement:

$$R_{M\times M}^{\left(2\right)}=\left[{\hslash }_{P_y\left(1\right)},{\hslash }_{P_y\left(2\right)},\dots ,{\hslash }_{P_y\left(M\right)}\right]=\left[{ƛ}_1^T,{ƛ}_2^T,\dots ,{ƛ}_M^T\right]$$

(18)

The above steps also apply to the G and B matrices. Finally, we can get the encrypted image. To increase the security of the transmitted data, the pixel values are also changed. At this point, the chaotic image matrix $R_{M\times M}^{\left(2\right)}$ is converted to the vector $V_{M\times M}$ and decrypted by the random numbers $rng$ of Equation (14) and the XOR operation:

$$E_R=V_{M\times M}\left(i\right)\oplus rng\left(i\right),i=M^2$$

(19)

The above steps apply to the R, G, B matrices. Finally, we can get the encrypted image.

5.2. Image Decryption

To decode the image, we will consider the chaotic keys as $\left[x_{1m}\left(i\right),x_{2m}\left(i\right),x_{3m}\left(i\right),x_{4m}\left(i\right)\right]$ and reverse the encryption operation. When the synchronization goal is met, the decoding chaotic keys $x_m\left(i\right),y_m\left(i\right),z_m\left(i\right),w_m\left(i\right) and i=1,2,\dots ,M/2$ are synchronized with the chaotic keys $x_s\left(i\right),y_s\left(i\right),z_s\left(i\right),w_s\left(i\right) and i=1,2,\dots ,M/2$, and the first original image can be recovered according to the above algorithm using an inverse operation.

5.3. Main Results

In this section, the usefulness and efficiency of the designed method for color image encryption/decryption using numerical simulations is investigated. “Lena” and “patient” images in JPG color image format are used for encryption/decryption in this simulation as the main data (see Figure 9a,d). Cryptographic keys are generated by the cryptographer’s nonlinear chaotic system. Using the encryption method introduced in the previous section and chaotic keys, we encrypt the original color image. Figure 9b,e shows the encrypted color images in the encryption/decryption process. In decoding, the novel dynamic nonlinear system (1) is used to generate decryption keys in the encryption/decryption process. The encrypted image of “Lena” and “patient” can be obtained after the decoding process (see Figure 9c,f). According to the encryption/decryption process and the obtained images, it can be seen that the images obtained in the encryption/decryption process are similar to noise and have a uniform distribution. The proposed method has been shown to have good cryptographic performance in terms of visual impact.

Then, to show the high security of the chaotic cryptography and to show the efficiency of the proposed design, histogram analysis, correlation test, an entropy test and an NIST test were performed.

5.3.1. Histogram Analysis

It is very useful to prevent disclosure and lack of access to image information by unknown sources if the encrypted image in the encryption/decryption process has no statistical similarity with the original color image or is very small. The relationship between the distribution of the color intensity level measurement and the graphical display of pixel elements is expressed by the histogram diagram. The analysis of this diagram shows the uniformity of coding and the distribution of pixel values in the image. When this graph becomes uniform, we have security cryptography. Figure 10 shows the R (red), G (green), and B (blue) channel diagrams of the original “Lena” encrypted images.

Due to the equal and appropriate distribution of pixels in Figure 10d–f, the original color image in Figure 10a will be very difficult and impossible to decode.

5.3.2. Correlation Test

The statistical study of the correlation between adjacent pixels in color images includes horizontal, vertical, and diagonal correlations of other main and standard indicators in the encryption/decryption process. Figure 11 shows this standard which contains 5000 pixels.

The difference between the scatter of the pixels in the original image (Figure 11a–c) and the cryptography in (Figure 11d–f) is clear. According to Figure 11, the horizontal, vertical, and diagonal correlation values of the original image are approximately close to one, indicating a high correlation between the pixels. In addition, this figure shows that there is no relationship between the horizontal, vertical, and diagonal correlation values of the channels and it is close to zero.

5.3.3. Entropy Test

Another standard index in the process of encryption/decryption color images is the entropy index, which shows the information and numerical value of a random variable. To be more precise, the entropy of a random variable is the average value (mathematical expectation) of the amount of information obtained from observing it. In other words, more entropy of a random variable means more ambiguity about it, so the more information we get by looking at the definitive result of that random variable. The information entropy test for a color image is defined as follows:

$$IE\left(\varphi \right)={\displaystyle \sum }_{i=1}^{255}\hslash \left({\varphi }_i\right)log(\frac{1}{\hslash \left({\varphi }_i\right)})$$

(20)

where $\hslash \left({\varphi }_i\right)$ indicates the probability of ${\varphi }_i$. The maximum entropy value for a truly random source is 8, and the closer the entropy of the encrypted image is to 8, the better the cryptographic quality. In the proposed method, the entropy value is equal to 7.9604.

5.3.4. NIST Test

To use a sequence of random bits (Equation (14)) in cryptography, these sequences of bits must have the appropriate random property. The NIST 800-22 test is a set of internationally accepted and commonly used tests in cryptography that determines the randomness of a sequence of random bits using a variety of different tests. The results of NIST 800-22 test for random bit sequences are shown in

Table 2. NIST 800-22 test results.

NIST Statistical Tests	p-Value	Results
Cumulative-Sums Test	0.04821	passed
Block-Frequency Test	0.0501	passed
Frequency (Mono bit) Test	0.3031	passed
Binary Matrix Rank Test	0.1602	passed
Maurer’s Universal Statistical Test	0.5271	passed
Runs Test	0.2638	passed
Longest-Run Test	0.9722	passed
Linear-Complexity Test	0.7505	passed
Discrete Fourier Transform Test	0.1325	passed
Overlapping Templates Test	0.6311	passed
Serial Test-1	0.5893	passed
Serial Test-2	0.1964	passed
Overlapping Templates Test	0.6197	passed
Random-Excursions Variant Test (x = −4)	0.7288	passed
Random-Excursions Test (x = −4)	0.8831	passed

. As is clear, it is observed that the random numbers generated in Equation (15), pass all the tests.

6. Conclusions

This article provides a novel 4D dynamic chaotic system with simple structure and only one nonlinear term. Dynamical features of this nonlinear chaotic system are demonstrated by the Kaplan–York dimension, Lyapunov exponents, bifurcation diagram, and phase portraits. The designed nonlinear dynamic system has three unstable focus equilibrium points. In the continuation of the practical implementation of the proposed dynamic system, with Multisim software its circuit analysis was conducted. At the end, to show the effectiveness of the proposed 4D dynamic system, color image encryption/decryption was performed and chaotic encryption standards were implemented on the new chaotic dynamic system.