MHD Mixed Convection of Hybrid Ferrofluid Flow over an Exponentially Stretching/Shrinking Surface with Heat Source/Sink and Velocity Slip
Abstract
1. Introduction
2. Mathematical Formulation
3. Stability Analysis
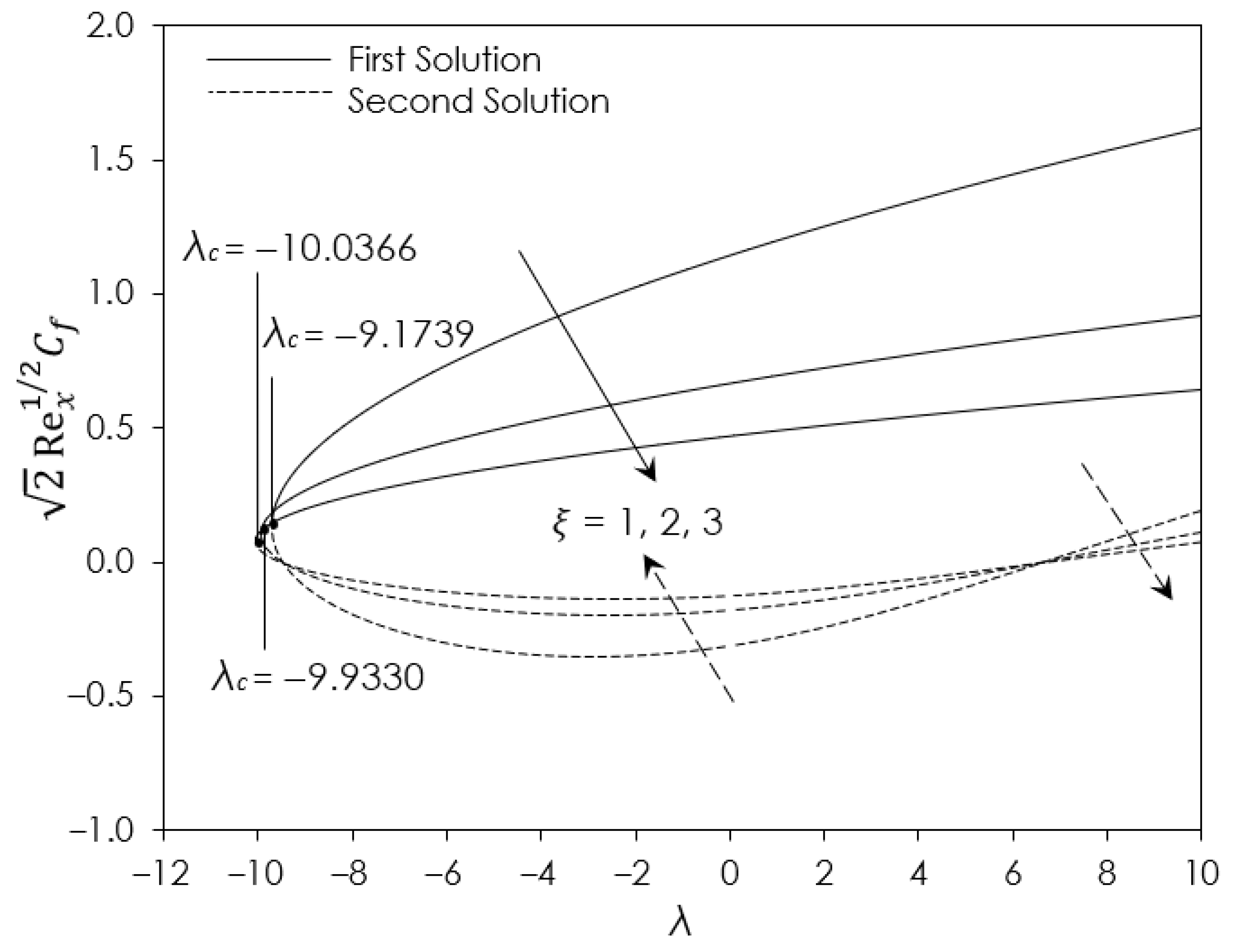
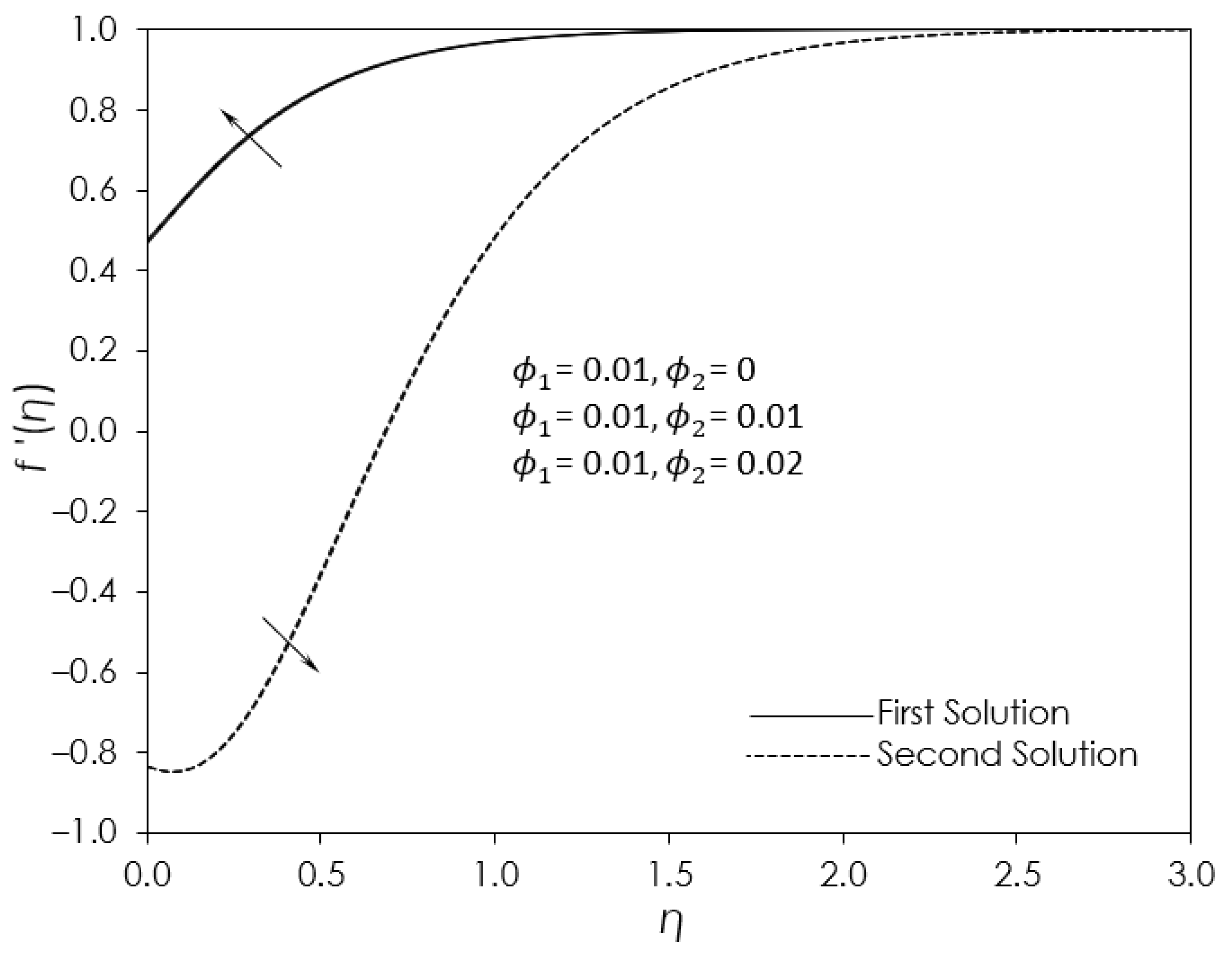
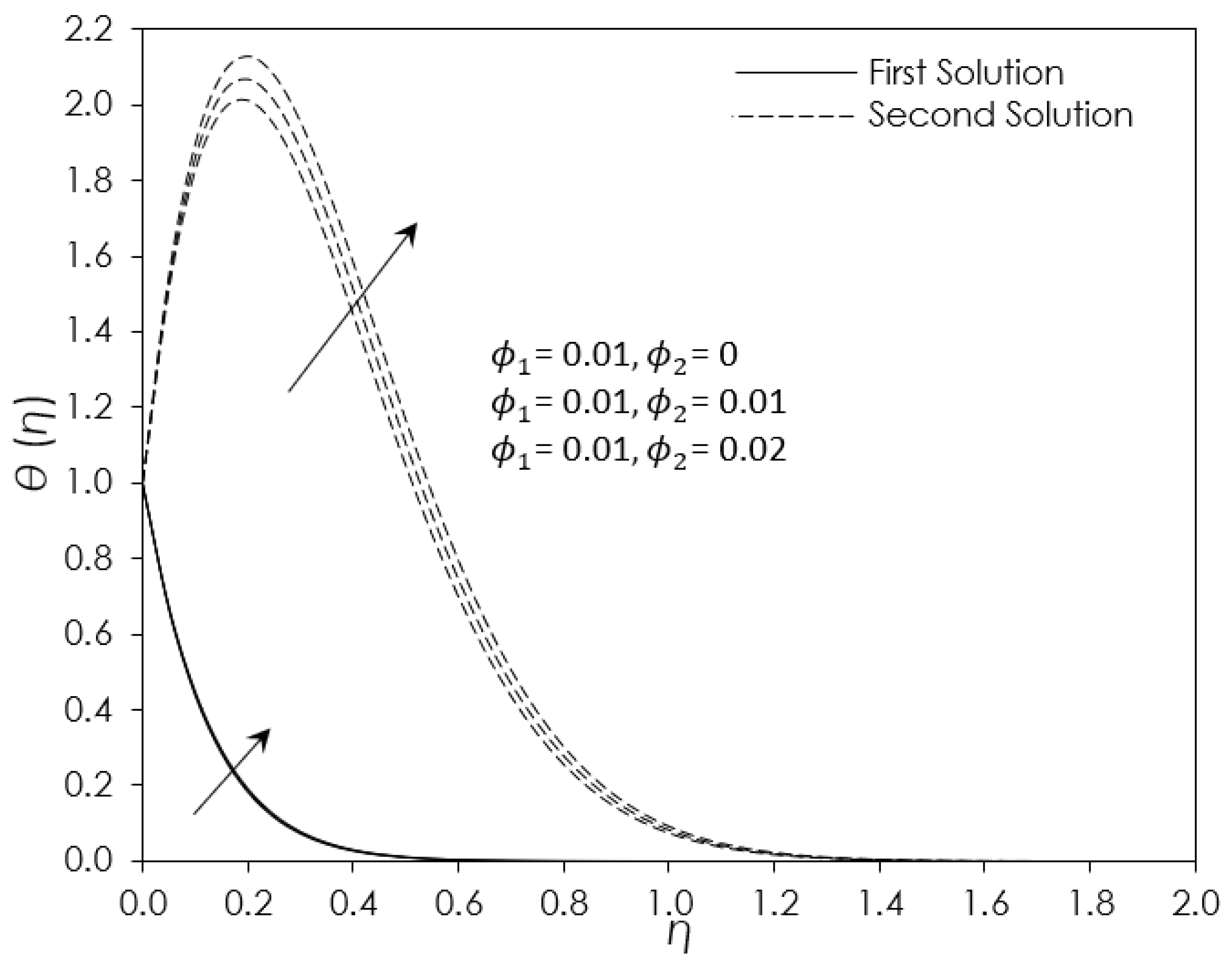
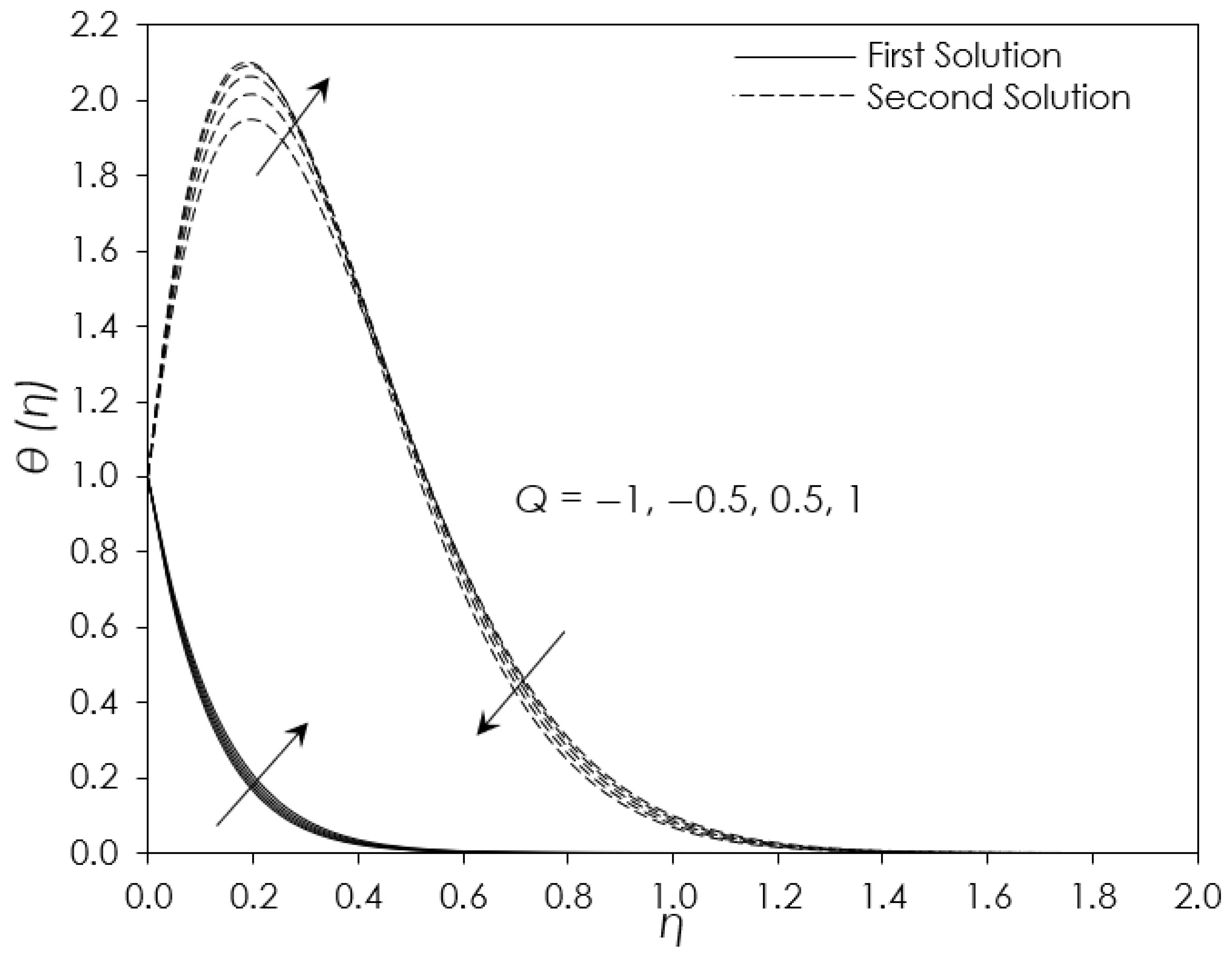
4. Results and Discussion
5. Conclusion
- The appearance of a non-unique solution or dual solution for a certain governing parameter in both assisting flow and opposing flow. The bifurcation point occurs at the opposing flow region.
- The stability analysis results show a stable first solution and an unstable second solution.
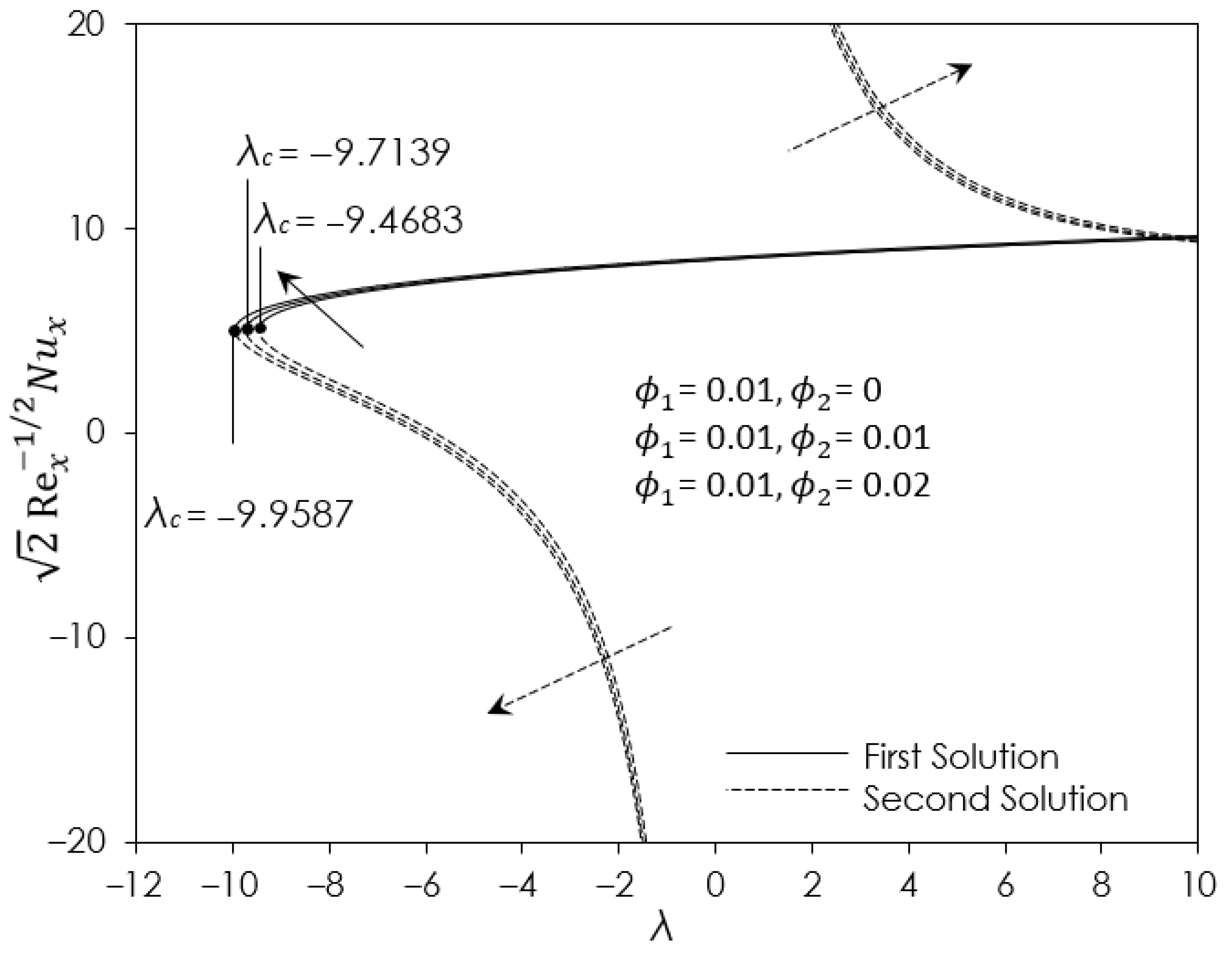
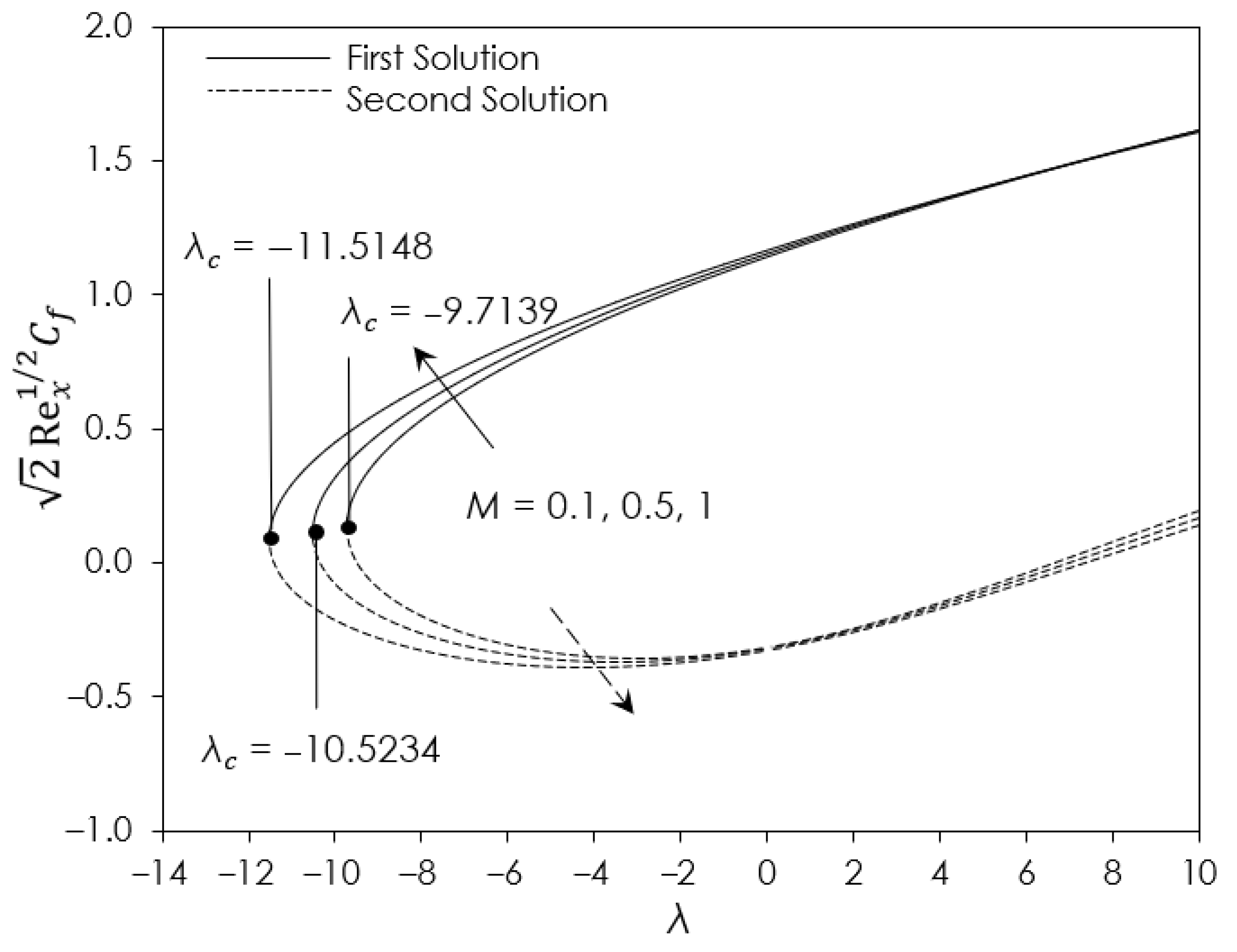
- The increment of nanoparticle volume fraction () increases heat transfer and skin friction.
- The addition of nanoparticle to hybrid ferrofluid -/water enhances the heat transfer rate better than ferrofluid /water due to the collision between two nanoparticles enhancing the synergistic effects.
- The influence of the magnetic field enhanced the fluid flow velocity due to the presence of Lorentz forces in flow and slowing down the boundary layer separation.
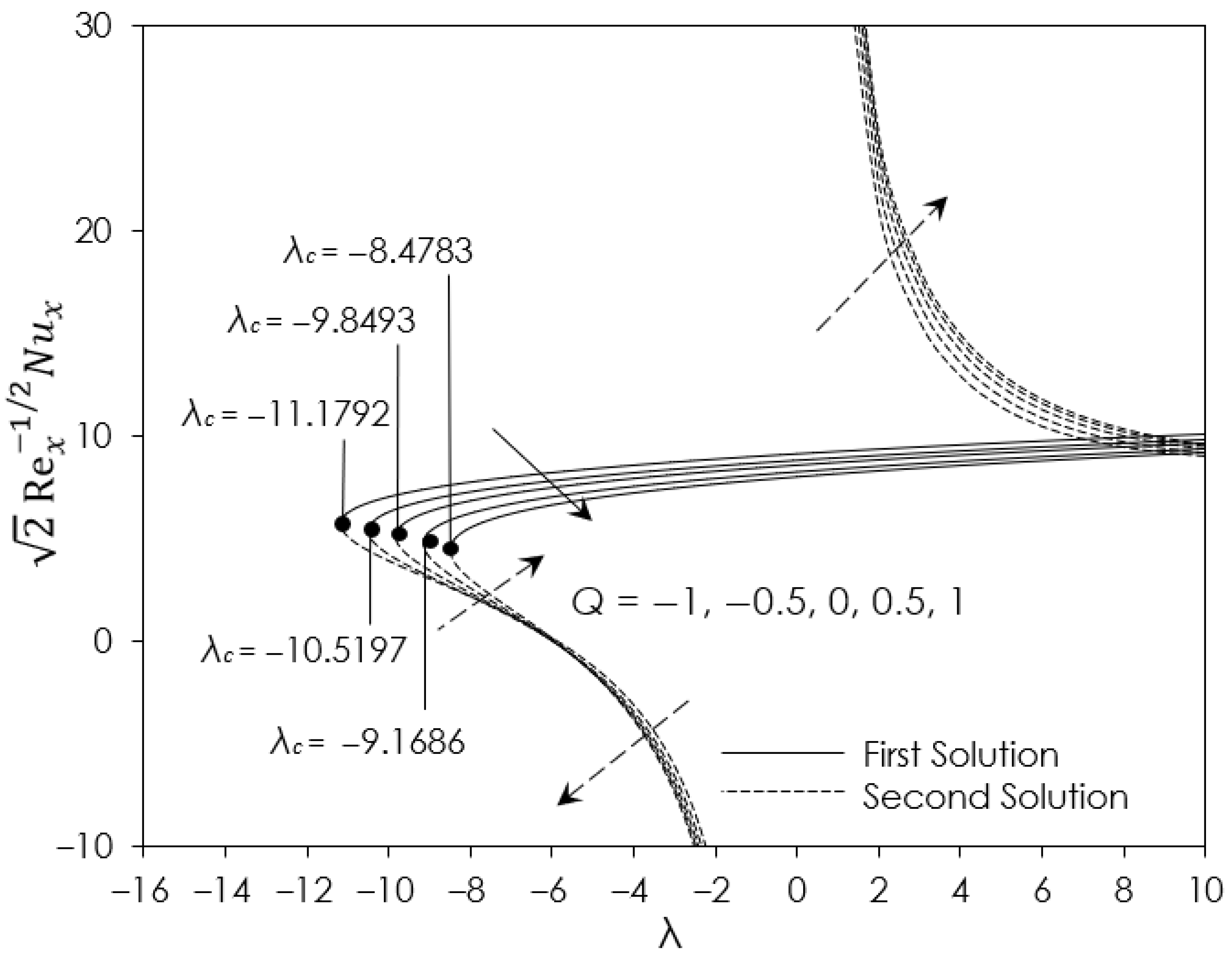
- The increased strength of the heat source reduced the heat transfer efficiency because of the larger thermal boundary layer thickness due to the additional external heat sources. Meanwhile, the increased strength of the heat sink yields the reverse result, which in turn reduced thermal boundary layer thickness due to the heat loss for the heat sink.
- The presence of velocity slip reduced the flow velocity and delayed the boundary layer separation.
- The increment of stretching parameter reduced the skin friction value, which slows down the fluid flow velocity. Meanwhile, the increment of shrinking parameter increases the skin friction value, which accelerates the fluid flow velocity.
- In terms of heat transfer, the increment of stretching parameter gives a better value of the Nusselt number, while the increment of shrinking parameter gives a reverse result.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. ASME Publ. Fed. 1995, 231, 99–106. [Google Scholar]
- Saidur, R.; Leong, K.Y.; Mohammed, H.A. A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 1646–1668. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Jamil, M.M.; Japar, W.M.A.A.; Adamu, I.M. A review on preparation methods, stability and applications of hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 80, 1112–1122. [Google Scholar] [CrossRef]
- Zulkifli, S.N.; Sarif, N.M.; Salleh, M.Z. Numerical solution of boundary layer flow over a moving plate in a nanofluid with viscous dissipation: A revised model. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 287–295. [Google Scholar]
- Al-Rashed, A.A.; Sheikhzadeh, G.A.; Aghaei, A.; Monfared, F.; Shahsavar, A.; Afrand, M. Effect of a porous medium on flow and mixed convection heat transfer of nanofluids with variable properties in a trapezoidal enclosure. J. Therm. Anal. Calorim. 2020, 139, 741–754. [Google Scholar] [CrossRef]
- Ferdows, M.; Shamshuddin, M.D.; Salawu, S.O.; Zaimi, K. Numerical simulation for the steady nanofluid boundary layer flow over a moving plate with suction and heat generation. SN Appl. Sci. 2021, 3, 1–11. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Nanofluid flow on a shrinking cylinder with Al2O3 nanoparticles. Mathematics 2021, 9, 1612. [Google Scholar] [CrossRef]
- Rosenweig, R.E. Magnetic fluids. Annu. Rev. Fluid Mech. 1987, 19, 437–463. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Pîslaru-Danescu, L.; Morega, A.M.; Morega, M.; Stoica, V.; Marinica, O.M.; Nouras, F.; Paduraru, N.; Borbath, I.; Borbath, T. Prototyping a ferrofluid-cooled transformer. IEEE Trans. Ind. Appl. 2013, 49, 1289–1298. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Yu, Y.; Zhao, Y. Flexible ferrofluids: Design and applications. Adv. Mater. 2019, 31, 1903497. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.K.A.; Abas, F.N.; Salleh, M.Z. MHD boundary layer flow over a permeable flat plate in a ferrofluid with thermal radiation effect. J. Phys. Conf. Ser. 2019, 1366, 012014. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; El-Zahar, E.R.; Modather, M.; Gorla, R.S.R.; Rashad, A.M. Unsteady MHD slip flow of a ferrofluid over an impulsively stretched vertical surface. AIP Adv. 2019, 9, 045112. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. Thermal radiation and MHD effects in the mixed convection flow of Fe3O4-water ferrofluid towards a nonlinearly moving surface. Processes 2020, 8, 95. [Google Scholar] [CrossRef]
- Mehrez, Z.; El Cafsi, A. Heat exchange enhancement of ferrofluid flow into rectangular channel in the presence of a magnetic field. Appl. Math. Comput. 2021, 391, 125634. [Google Scholar] [CrossRef]
- Hamid, R.A.; Nazar, R.; Naganthran, K.; Pop, I. Effects of Magnetic Fields, Coupled Stefan Blowing and Thermodiffusion on Ferrofluid Transport Phenomena. Mathematics 2022, 10, 1646. [Google Scholar] [CrossRef]
- Kumar, K.A.; Sandeep, N.; Sugunamma, V.; Animasaun, I.L. Effect of irregular heat source/sink on the radiative thin film flow of MHD hybrid ferrofluid. J. Therm. Anal. Calorim. 2020, 139, 2145–2153. [Google Scholar] [CrossRef]
- Tlili, I.; Mustafa, M.T.; Kumar, K.A.; Sandeep, N. Effect of asymmetrical heat rise/fall on the film flow of magnetohydrodynamic hybrid ferrofluid. Sci. Rep. 2020, 10, 6677. [Google Scholar] [CrossRef]
- Manh, T.D.; Khan, A.R.; Shafee, A.; Nam, N.D.; Tlili, I.; Nguyen-Thoi, T.; Li, Z. Hybrid nanoparticles migration due to MHD free convection considering radiation effect. Phys. A Stat. Mech. Its Appl. 2020, 551, 124042. [Google Scholar] [CrossRef]
- Giwa, S.O.; Sharifpur, M.; Meyer, J.P. Effects of uniform magnetic induction on heat transfer performance of aqueous hybrid ferrofluid in a rectangular cavity. Appl. Therm. Eng. 2020, 170, 115004. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Influence of MHD Hybrid Ferrofluid Flow on Exponentially Stretching/Shrinking Surface with Heat Source/Sink under Stagnation Point Region. Mathematics 2021, 9, 2932. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Eichhorn, R.; Gregg, J.L. Combined forced and free convection in a boundary layer flow. Phys. Fluids 1959, 2, 319–328. [Google Scholar] [CrossRef]
- Ramachandran, N.; Chen, T.S.; Armaly, B.F. Mixed convection in stagnation flows adjacent to vertical surfaces. ASME J. Heat Mass Transf. 1988, 110, 373–377. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Yashkun, U.; Zaimi, K.; Ishak, A.; Pop, I.; Sidaoui, R. Hybrid nanofluid flow through an exponentially stretching/shrinking sheet with mixed convection and Joule heating. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1930–1950. [Google Scholar] [CrossRef]
- Lund, L.A.; Lashin, M.; Yashkun, U.; Guedri, K.; Khan, S.U.; Khan, M.I.; Kumam, P. Thermal stable properties of solid hybrid nanoparticles for mixed convection flow with slip features. Sci. Rep. 2022, 12, 16447. [Google Scholar] [CrossRef]
- Hayat, T.; Fetecau, C.; Sajid, M. Analytic solution for MHD transient rotating flow of a second grade fluid in a porous space. Nonlinear Anal. Real World Appl. 2008, 9, 1619–1627. [Google Scholar] [CrossRef]
- Khan, A.Q.; Rasheed, A. Mixed convection magnetohydrodynamics flow of a nanofluid with heat transfer: A numerical study. Math. Probl. Eng. 2019, 2019, 8129564. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. MHD mixed convection flow of a hybrid nanofluid past a permeable vertical flat plate with thermal radiation effect. Alex. Eng. J. 2022, 61, 3323–3333. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Niranjan, H.; Bhuvaneswari, M. Chemical reaction, radiation and slip effects on MHD mixed convection stagnation-point flow in a porous medium with convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 454–470. [Google Scholar] [CrossRef]
- Patil, P.M.; Kulkarni, M. Analysis of MHD mixed convection in a Ag-TiO2 hybrid nanofluid flow past a slender cylinder. Chin. J. Phys. 2021, 73, 406–419. [Google Scholar] [CrossRef]
- Lone, S.A.; Alyami, M.A.; Saeed, A.; Dawar, A.; Kumam, P.; Kumam, W. MHD micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal radiation. Sci. Rep. 2022, 12, 17283. [Google Scholar] [CrossRef] [PubMed]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD mixed convection stagnation point flow of a hybrid nanofluid past a vertical flat plate with convective boundary condition. Chin. J. Phys. 2020, 66, 630–644. [Google Scholar] [CrossRef]
- Sharma, P.R.; Sinha, S.; Yadav, R.S.; Filippov, A.N. MHD mixed convective stagnation point flow along a vertical stretching sheet with heat source/sink. Int. J. Heat Mass Transf. 2018, 117, 780–786. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Jamaludin, A.; Naganthran, K.; Nazar, R.; Pop, I. MHD mixed convection stagnation-point flow of Cu-Al2O3/water hybrid nanofluid over a permeable stretching/shrinking surface with heat source/sink. Eur. J. Mech. B Fluids 2020, 84, 71–80. [Google Scholar] [CrossRef]
- Armaghani, T.; Sadeghi, M.S.; Rashad, A.M.; Mansour, M.A.; Chamkha, A.J.; Dogonchi, A.S.; Nabwey, H.A. MHD mixed convection of localized heat source/sink in an Al2O3-Cu/water hybrid nanofluid in L-shaped cavity. Alex. Eng. J. 2021, 60, 2947–2962. [Google Scholar] [CrossRef]
- Zainal, N.A.; Naganthran, K.; Nazar, R. Unsteady MHD Rear Stagnation-Point Flow of a Hybrid Nanofluid with Heat Generation/Absorption Effect. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 87, 41–51. [Google Scholar] [CrossRef]
- Agrawal, P.; Dadheech, P.K.; Jat, R.N.; Baleanu, D.; Purohit, S.D. Radiative MHD hybrid-nanofluids flow over a permeable stretching surface with heat source/sink embedded in porous medium. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2818–2840. [Google Scholar] [CrossRef]
- Yaseen, M.; Kumar, M.; Rawat, S.K. Assisting and opposing flow of a MHD hybrid nanofluid flow past a permeable moving surface with heat source/sink and thermal radiation. Part. Differ. Equ. Appl. Math. 2021, 4, 100168. [Google Scholar] [CrossRef]
- Sneha, K.N.; Mahabaleshwar, U.S.; Bhattacharyya, S. An effect of thermal radiation on inclined MHD flow in hybrid nanofluids over a stretching/shrinking sheet. J. Therm. Anal. Calorim. 2022. [Google Scholar] [CrossRef]
- Karwe, M.V.; Jaluria, Y. Numerical simulation of thermal transport associated with a continuously moving flat sheet in materials processing. J. Heat Transf. 1991, 113, 612–619. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer Equations for two-dimensional and axisymmetric flow. AICHE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Für Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over an exponentially stretching continuous surface with suction. Arch. Mech. 2001, 53, 643–651. [Google Scholar]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. Effect of suction/injection on stagnation point flow of hybrid nanofluid over an exponentially shrinking sheet with stability analysis. CFD Lett. 2019, 11, 21–33. [Google Scholar]
- Patil, P.M.; Latha, D.N.; Chamkha, A.J. Non-similar Solutions of MHD Mixed Convection over an Exponentially Stretching Surface: Influence of Non-uniform Heat Source or Sink. J. Appl. Comput. Mech. 2021, 7, 1334–1347. [Google Scholar]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on an exponentially stretching/shrinking vertical sheet with buoyancy effects. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 216–235. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Viscous dissipation and MHD hybrid nanofluid flow towards an exponentially stretching/shrinking surface. Neural Comput. Appl. 2021, 33, 11285–11295. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Naganthran, K.; Pop, I. Mixed convection hybrid nanofluid flow over an exponentially accelerating surface in a porous media. Neural Comput. Appl. 2021, 33, 15719–15729. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. Slip mechanisms in complex fluid flows. Soft Matter. 2015, 11, 7851–7856. [Google Scholar] [CrossRef] [PubMed]
- Khader, M.M.; Megahed, A.M. Numerical solution for boundary layer flow due to a nonlinearly stretching sheet with variable thickness and slip velocity. Eur. Phys. J. Plus 2013, 128, 100. [Google Scholar] [CrossRef]
- Hafidzuddin, E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Effects of anisotropic slip on three-dimensional stagnation-point flow past a permeable moving surface. Eur. J. Mech. B Fluids 2017, 65, 515–521. [Google Scholar] [CrossRef]
- Navier, C.L. Memorie sur les lois du lois du mouvement des fluides. Mem. Acad. Sci. Inst. Fr. 1827, 6, 298–440. [Google Scholar]
- Maxwell, J.C., III. On stresses in rarefied gases arising from inequalities of temperature. Proc. R. Soc. Lond. 1878, 27, 304–308. [Google Scholar]
- Rao, I.J.; Rajagopal, K.R. The effect of the slip boundary condition on the flow of fluids in a channel. Acta Mech. 1999, 135, 113–126. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. Mixed Convection Flow and Heat Transfer of Carbon Nanotubes Over an Exponentially Stretching/Shrinking Sheet with Suction and Slip Effect. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 59, 232–242. [Google Scholar]
- Ghosh, S.; Mukhopadhyay, S. Stability analysis for model-based study of nanofluid flow over an exponentially shrinking permeable sheet in presence of slip. Neural Comput. Appl. 2020, 32, 7201–7211. [Google Scholar] [CrossRef]
- Yan, L.; Dero, S.; Khan, I.; Mari, I.A.; Baleanu, D.; Nisar, K.S.; Sherif, E.-S.M.; Abdo, H.S. Dual solutions and stability analysis of magnetized hybrid nanofluid with joule heating and multiple slip conditions. Processes 2020, 8, 332. [Google Scholar] [CrossRef]
- Abu Bakar, S.; Md Arifin, N.; Khashi’ie, N.S.; Bachok, N. Hybrid Nanofluid Flow over a Permeable Shrinking Sheet Embedded in a Porous Medium with Radiation and Slip Impacts. Mathematics 2021, 9, 878. [Google Scholar] [CrossRef]
- Yatsyshin, P.; Kalliadasis, S. Coupled Mathematical Models for Physical and Biological Nanoscale Systems and Their Applications; Springer: Basel, Switzerland, 2018; pp. 171–185. [Google Scholar]
- Ha, S.N. A nonlinear shooting method for two-point boundary value problems. Comput. Math. Appl. 2001, 42, 1411–1420. [Google Scholar] [CrossRef]
- Shampine, L.F.; Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with Matlab; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.; Turner, M.R. Stagnation-point flows with stretching surfaces: A unified formulation and new results. Eur. J. Mech. B Fluids 2017, 61, 144–153. [Google Scholar] [CrossRef]
- Pang, C.; Jung, J.Y.; Kang, Y.T. Aggregation based model for heat conduction mechanism in nanofluids. Int. J. Heat Mass Transf. 2014, 72, 392–399. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int. J. Heat Mass Transf. 2012, 55, 8122–8128. [Google Scholar] [CrossRef]
- Rehman, F.U.; Nadeem, S.; Rehman, H.U.; Haq, R.U. Thermophysical analysis for three-dimensional MHD stagnation-point flow of nano-material influenced by an exponential stretching surface. Results Phys. 2018, 8, 316–323. [Google Scholar] [CrossRef]
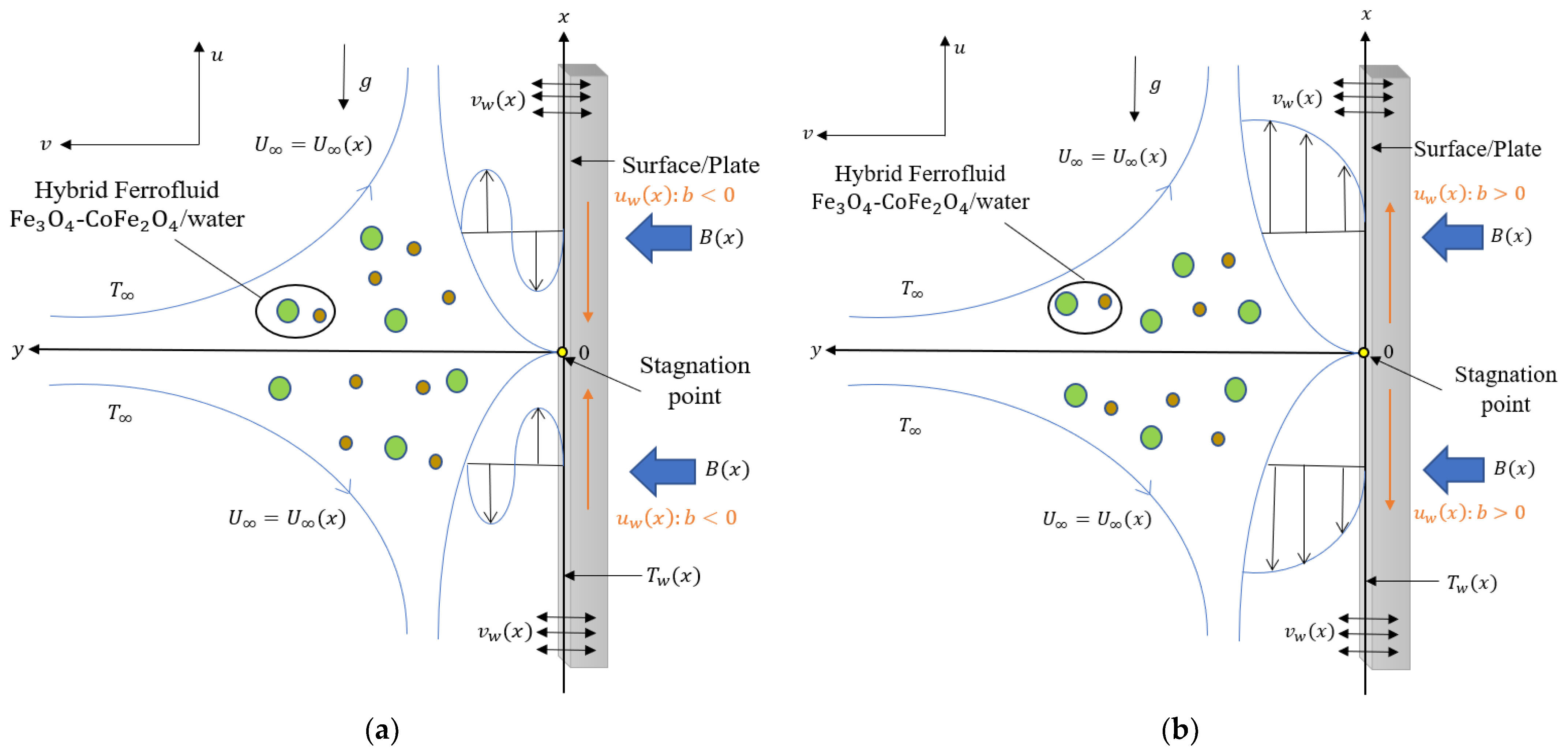


| Properties | Ferrofluid | Hybrid Ferrofluids |
|---|---|---|
| Viscosity | ||
| Density | ||
| Electrical Conductivity | where | |
| Thermal Diffusivity | ||
| Thermal Expansion Coefficient | ||
| Heat Capacity |
| Thermophysical Properties | |||
| 670 | 700 | 4179 | |
| 5180 | 4907 | 997.1 | |
| 9.7 | 3.7 | 0.613 | |
| 1.3 | 1.3 | 21 | |
| c | Rehman et al. [72] | Waini et al. [50] | Present Results | Waini et al. [50] | Present Results | ||
|---|---|---|---|---|---|---|---|
| −0.5 | 0 | 2.1182 | 2.1182 | 2.118169 | 0.0588 | 0.058787 | |
| 0.1 | 2.7531 | 2.7531 | 2.753091 | 0.4439 | 0.443904 | ||
| 0.2 | 3.5372 | 3.5372 | 3.537175 | 0.7636 | 0.763593 | ||
| 0 | 0 | 1.6872 | 1.68720 | 1.6872 | 1.687218 | 2.5066 | 2.506625 |
| 0.1 | 2.1929 | 2.19293 | 2.1930 | 2.192963 | 2.9655 | 2.965516 | |
| 0.2 | 2.8174 | 2.81750 | 2.8175 | 2.817522 | 3.4292 | 3.429219 | |
| 0.5 | 0 | 0.9604 | 0.96040 | 0.9604 | 0.960416 | 4.0816 | 4.081573 |
| 0.1 | 1.2483 | 1.24829 | 1.2483 | 1.248302 | 4.6637 | 4.663651 | |
| 0.2 | 1.6039 | 1.60399 | 1.6038 | 1.603819 | 5.2726 | 5.272615 | |
| λ | c | |||||
|---|---|---|---|---|---|---|
| −1.5 | −1.0 | −0.5 | 0.5 | 1.0 | 1.5 | |
| 5 | 2.168550 | 1.784748 | 1.397650 | 0.614603 | 0.219096 | −0.178813 |
| 4 | 2.115534 | 1.734606 | 1.350040 | 0.571247 | 0.177546 | −0.218730 |
| 3 | 2.060326 | 1.682616 | 1.300853 | 0.526709 | 0.134958 | −0.259564 |
| 2 | 2.002605 | 1.628538 | 1.249907 | 0.480876 | 0.091243 | −0.301388 |
| 1 | 1.941959 | 1.572076 | 1.196980 | 0.433617 | 0.046297 | −0.344285 |
| 0 | 1.877853 | 1.512850 | 1.141798 | 0.384778 | 0.000000 | −0.388351 |
| −1 | 1.809554 | 1.450369 | 1.084017 | 0.334170 | −0.047792 | −0.433696 |
| −2 | 1.736025 | 1.383972 | 1.023190 | 0.281566 | −0.097249 | −0.480452 |
| −3 | 1.655703 | 1.312731 | 0.958725 | 0.226683 | −0.148578 | −0.528774 |
| −4 | 1.566017 | 1.235271 | 0.889801 | 0.169164 | −0.202032 | −0.578847 |
| −5 | 1.462139 | 1.149388 | 0.815224 | 0.108540 | −0.257932 | −0.630900 |
| λ | c | |||||
|---|---|---|---|---|---|---|
| −1.5 | −1.0 | −0.5 | 0.5 | 1.0 | 1.5 | |
| 5 | 8.570820 | 8.855438 | 9.123041 | 9.615376 | 9.843333 | 10.060869 |
| 4 | 8.441423 | 8.738077 | 9.015792 | 9.524113 | 9.758478 | 9.981619 |
| 3 | 8.303596 | 8.613944 | 8.903014 | 9.429008 | 9.670365 | 9.899579 |
| 2 | 8.155904 | 8.482027 | 8.783971 | 9.329647 | 9.578673 | 9.814497 |
| 1 | 7.996487 | 8.341045 | 8.657756 | 9.225537 | 9.483029 | 9.726082 |
| 0 | 7.822852 | 8.189350 | 8.523232 | 9.116087 | 9.382989 | 9.633998 |
| −1 | 7.631547 | 8.024754 | 8.378948 | 9.000581 | 9.278027 | 9.537849 |
| −2 | 7.417554 | 7.844264 | 8.222997 | 8.878132 | 9.167509 | 9.437166 |
| −3 | 7.173119 | 7.643590 | ..052800 | 8.747629 | 9.050654 | 9.331386 |
| −4 | 6.885144 | 7.416234 | 7.864719 | 8.607640 | 8.926494 | 9.219827 |
| −5 | 6.528230 | 7.151525 | 7.653359 | 8.456280 | 8.793795 | 9.101644 |
| 0.1 | 0 | −6 −9.1 −9.43 | 3.6558 1.2011 0.4997 | −3.3488 −1.2430 −0.5765 |
| 0.1 | 0.5 | −9.4 −10.4 −10.52 | 2.0449 0.6352 0.0656 | −2.0046 −0.7137 −0.1580 |
| 0.1 | 1.0 | −9 −10.4 −11.44 | 3.1228 2.0376 0.4799 | −2.8976 −1.9977 −0.5702 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zainodin, S.; Jamaludin, A.; Nazar, R.; Pop, I. MHD Mixed Convection of Hybrid Ferrofluid Flow over an Exponentially Stretching/Shrinking Surface with Heat Source/Sink and Velocity Slip. Mathematics 2022, 10, 4400. https://doi.org/10.3390/math10234400
Zainodin S, Jamaludin A, Nazar R, Pop I. MHD Mixed Convection of Hybrid Ferrofluid Flow over an Exponentially Stretching/Shrinking Surface with Heat Source/Sink and Velocity Slip. Mathematics. 2022; 10(23):4400. https://doi.org/10.3390/math10234400
Chicago/Turabian StyleZainodin, Syafiq, Anuar Jamaludin, Roslinda Nazar, and Ioan Pop. 2022. "MHD Mixed Convection of Hybrid Ferrofluid Flow over an Exponentially Stretching/Shrinking Surface with Heat Source/Sink and Velocity Slip" Mathematics 10, no. 23: 4400. https://doi.org/10.3390/math10234400
APA StyleZainodin, S., Jamaludin, A., Nazar, R., & Pop, I. (2022). MHD Mixed Convection of Hybrid Ferrofluid Flow over an Exponentially Stretching/Shrinking Surface with Heat Source/Sink and Velocity Slip. Mathematics, 10(23), 4400. https://doi.org/10.3390/math10234400






