Ergodicity Bounds and Limiting Characteristics for a Modified Prendiville Model
Abstract
1. Introduction
- In the first approach, we examine the standard way to eliminate the state with the minimum number and then apply the diagonal transformation. Previously, this type of transformation (using a triangular matrix) was considered in [17]. This approach allows one to obtain exhaustive estimates of the rate of convergence to the limiting mode in the space .
- Using the second approach, we pass from the forward Kolmogorov system to a system of the form for (see [18]). This method was previously applied to the study of one class of supercomputer systems in [3] (for nonstationary models, simple methods for solving the forward Kolmogorov system do not give good results).
- We also briefly review some issues related to proportional intensities and perturbation bounds.
- Numerical examples are considered, in which estimates of the rate of convergence to the limit mode are obtained and the limit characteristics themselves are constructed.
2. Model Description and Basic Notions
- with intensity function for ,
- with intensity function for ,
- with intensity function for ,
- with intensity function for ,
- with intensity function .
3. First Approach
4. Second Approach
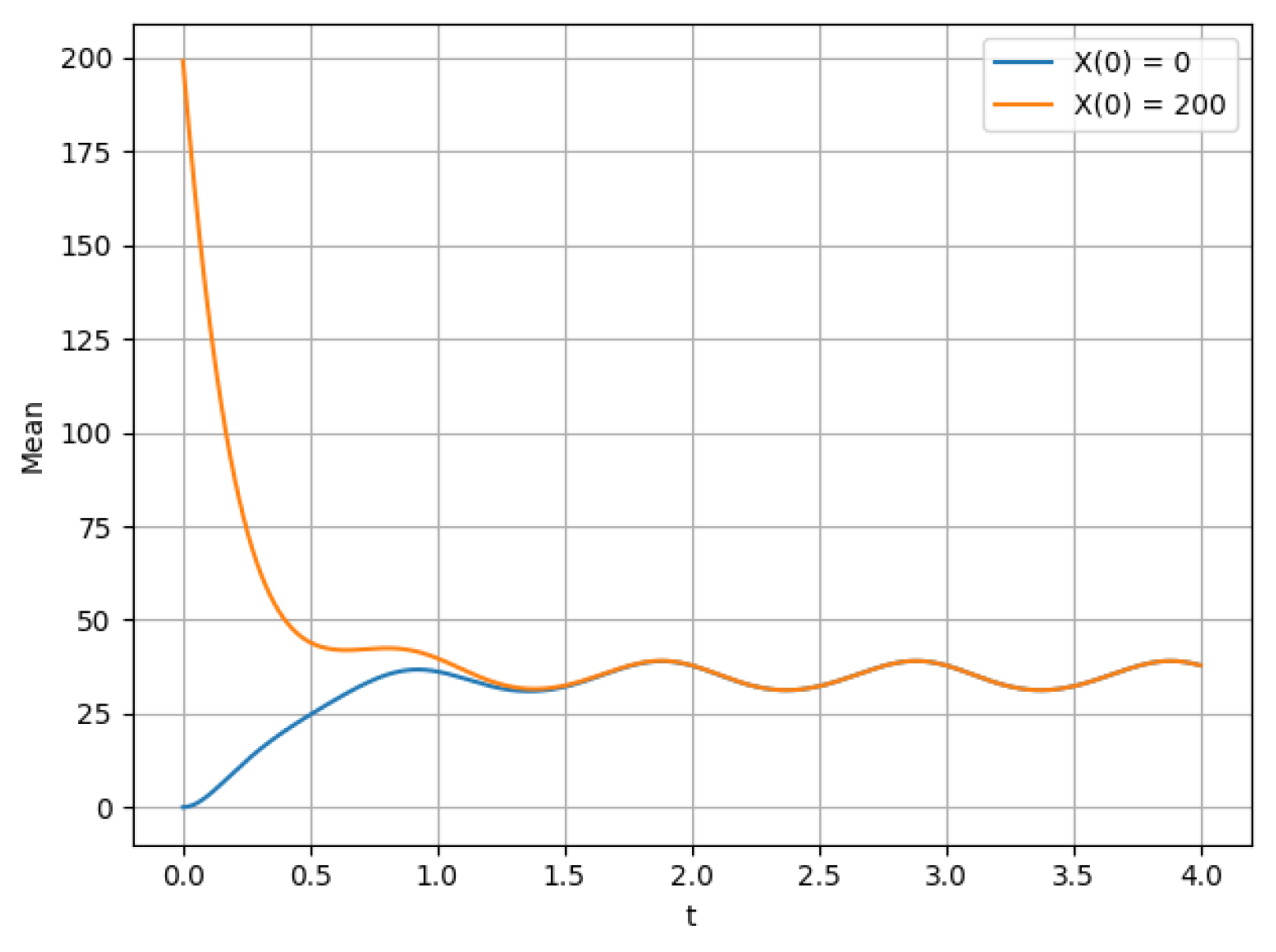
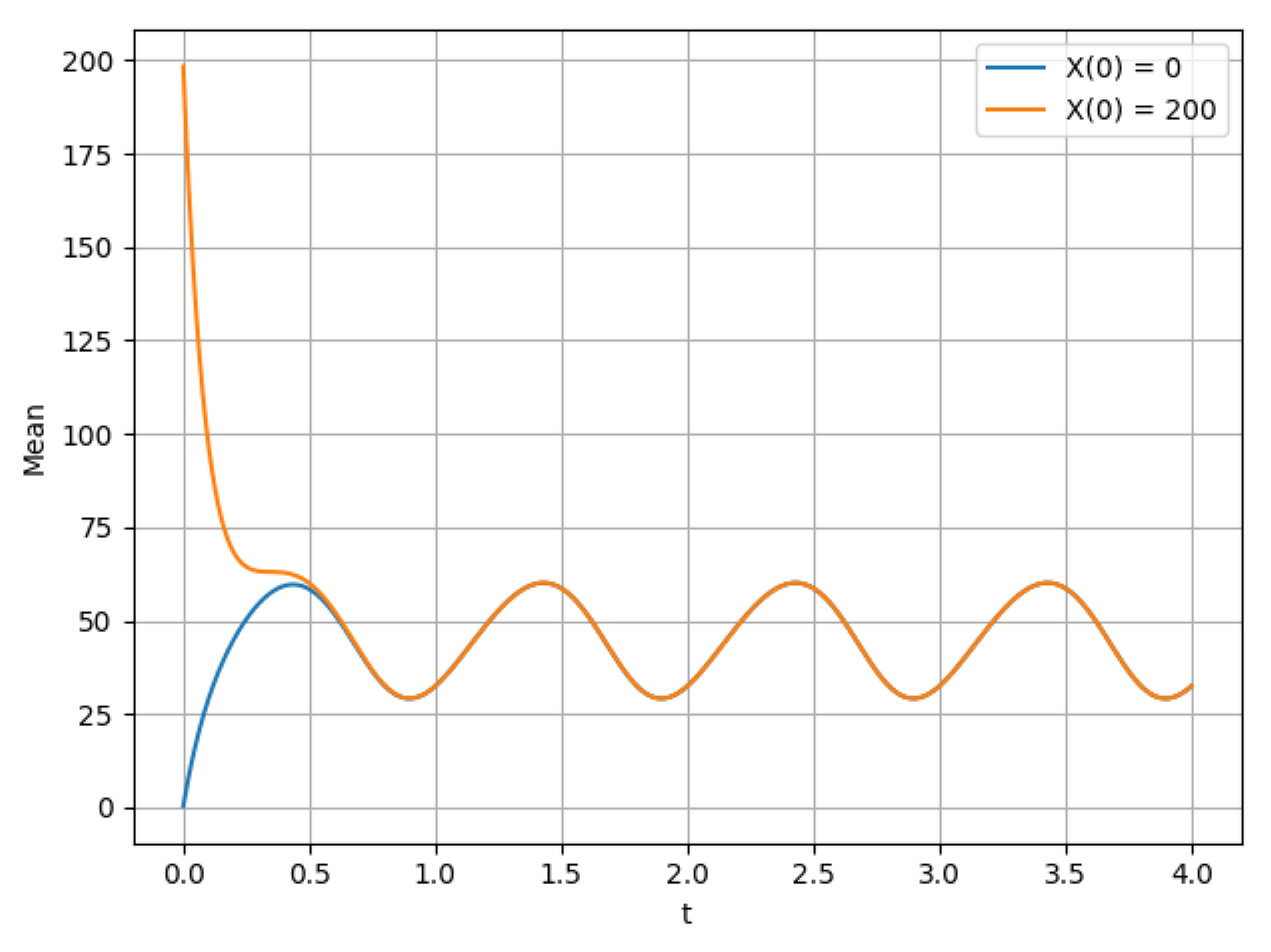
- The mathematical expectation of the number of customers in the system for and different initial conditions and .
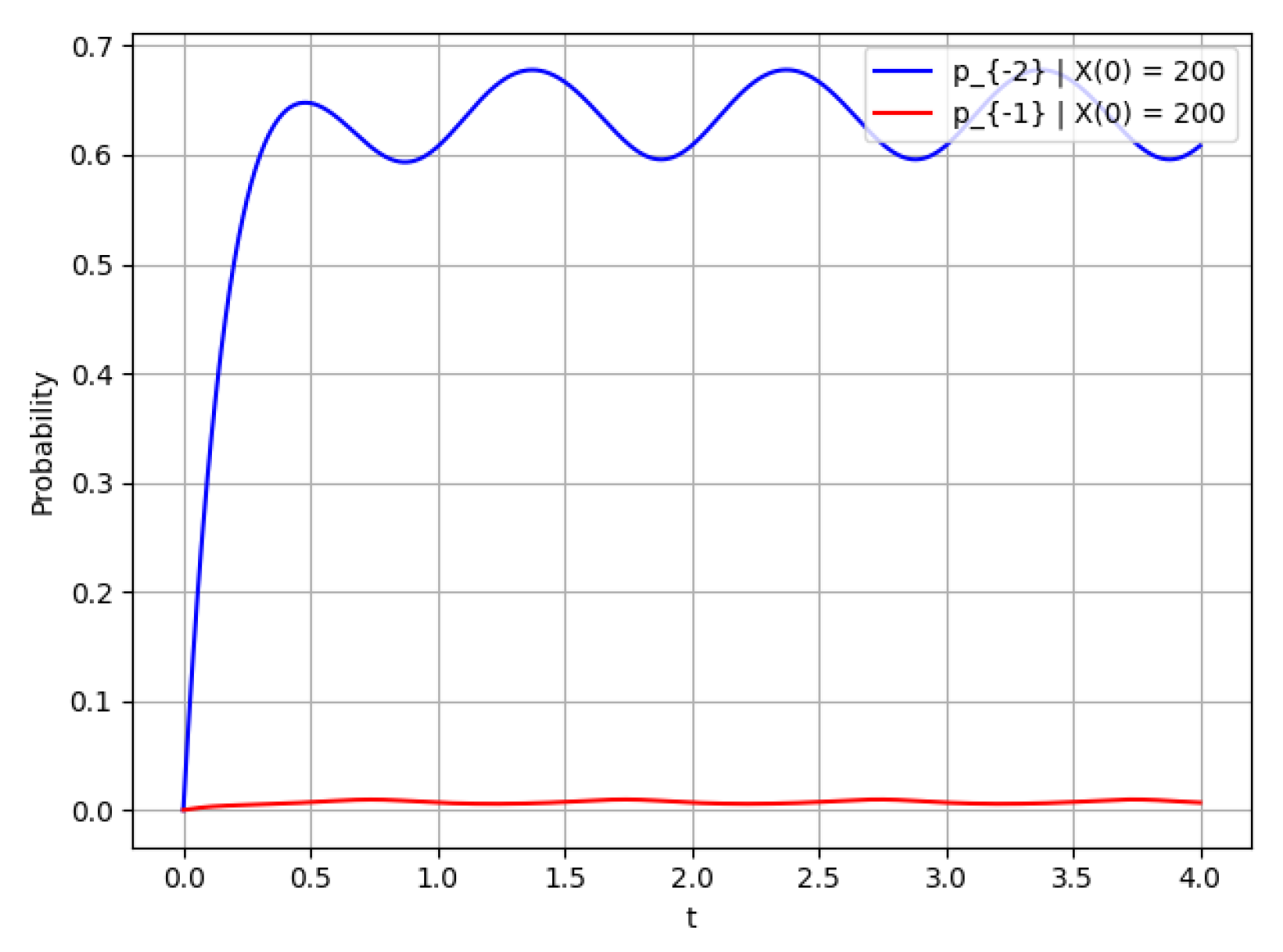
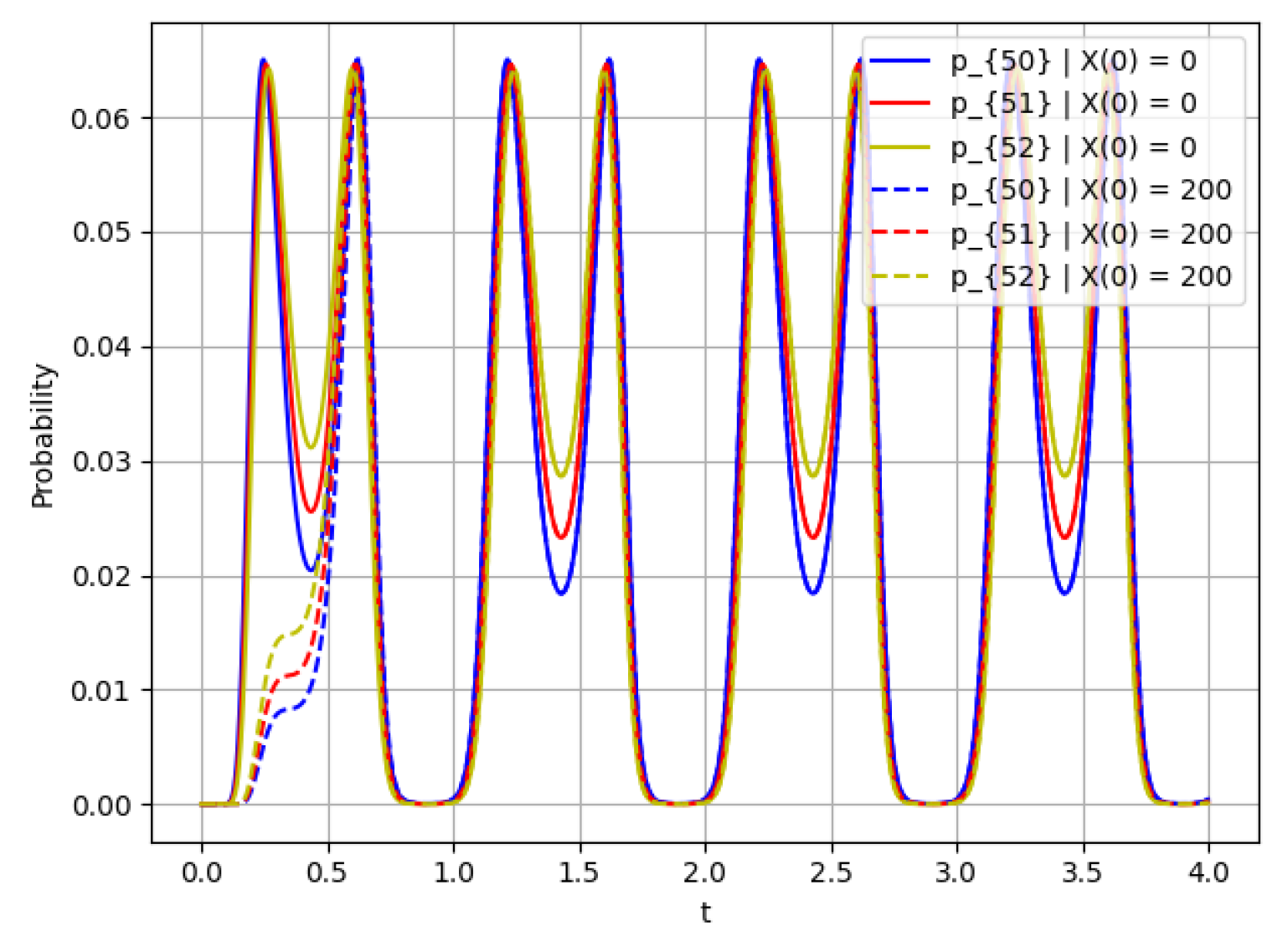
- The probability of states for and .
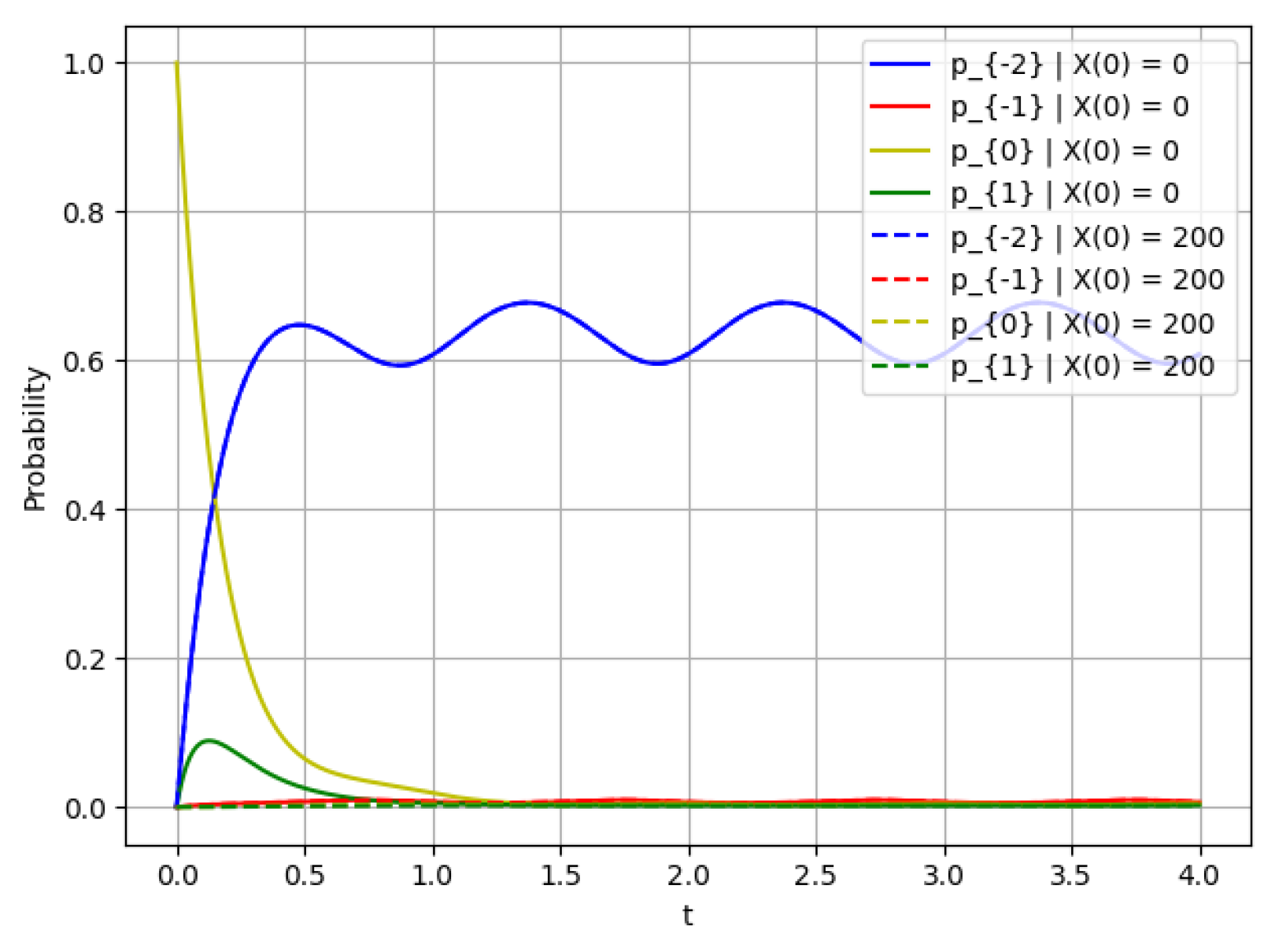
- The probability and several operating states , at and different initial conditions (solid lines) and (dashed lines).
- The mathematical expectation of the number of customers in the system for and different initial conditions and .
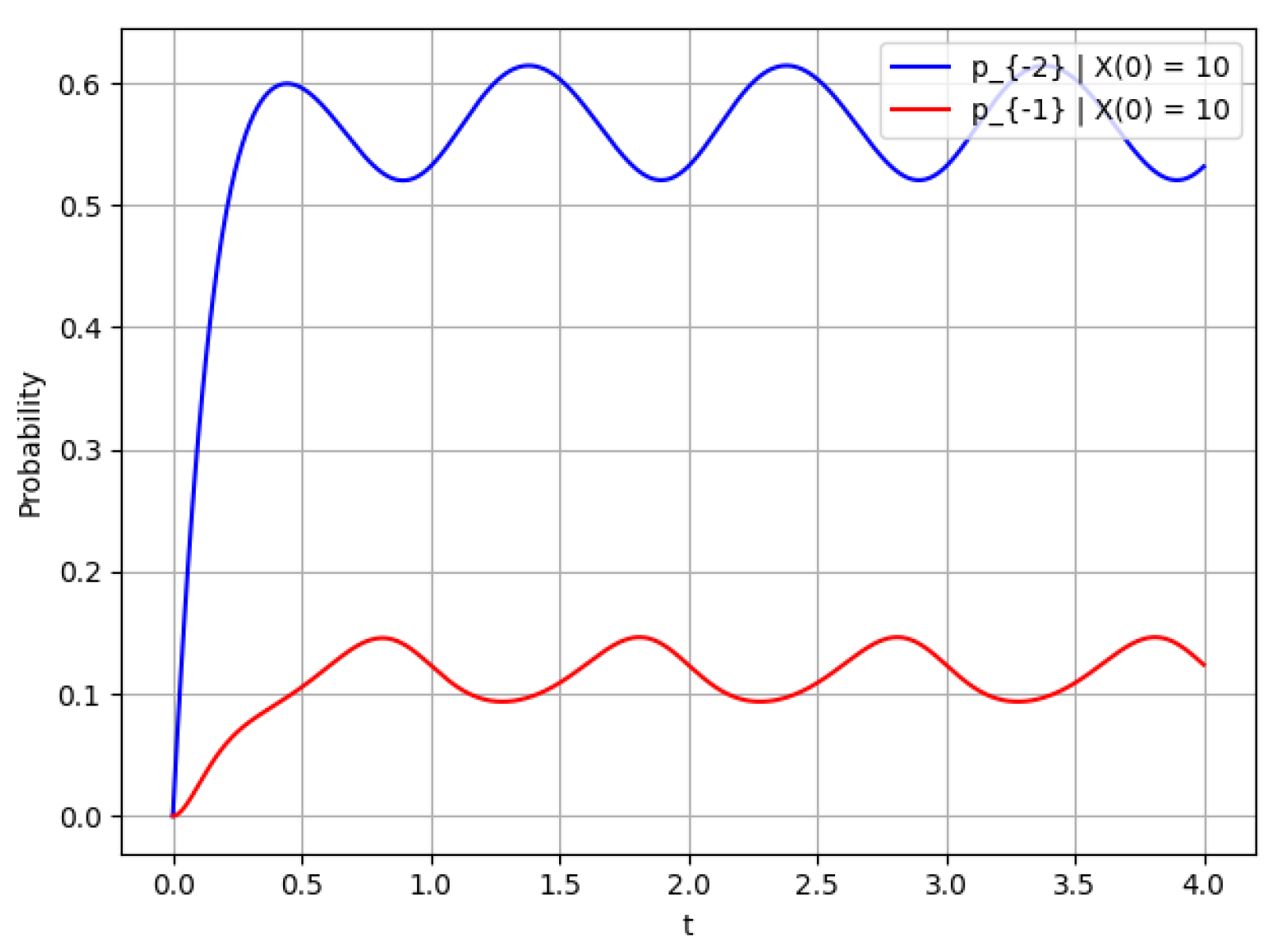
- The probability of states for and .
- The probability and several operating states , at and different initial conditions (solid lines) and (dashed lines).
- (a)
- The mathematical expectation of the number of customers in the system for and different initial conditions and .
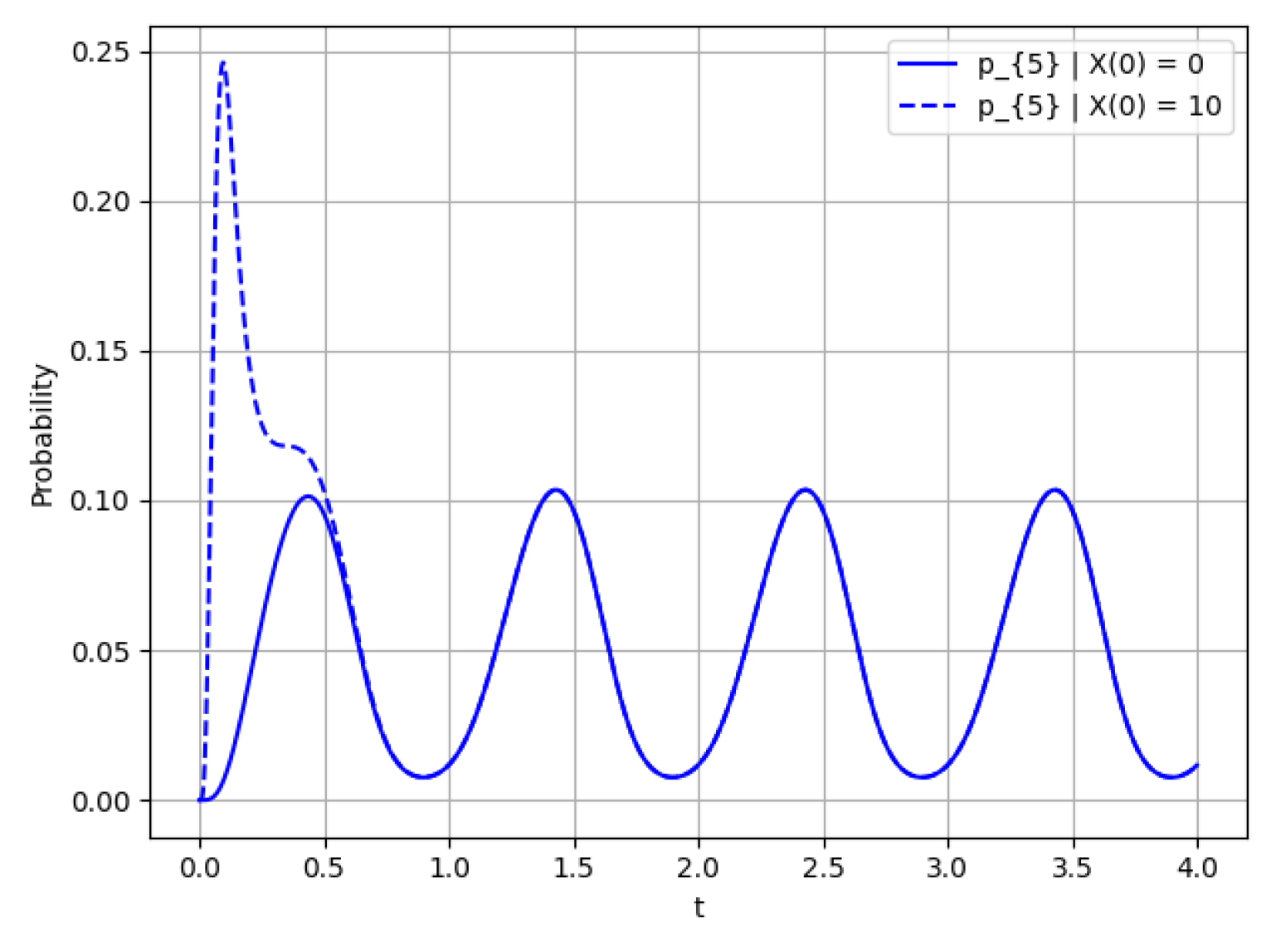
- The probability for and different initial conditions (solid line) and (dashed line).
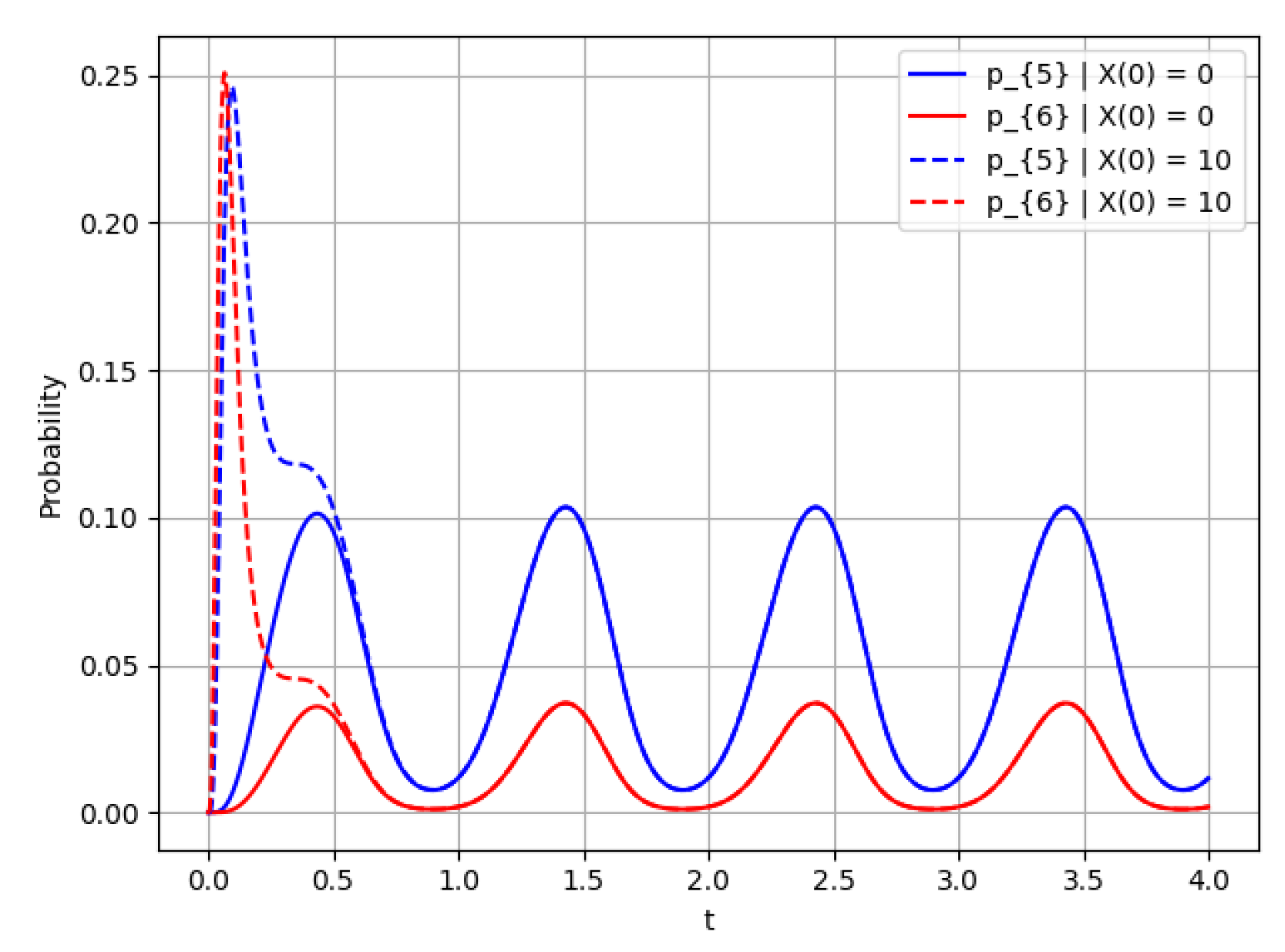
- The probability for and different initial conditions (solid lines) and (dashed lines).
- The probability for and different initial conditions (solid lines) and (dashed lines).
- (b)
- The mathematical expectation of the number of customers in the system for and different initial conditions and .
- The probability for and different initial conditions (solid line) and (dashed line).
- The probability for and different initial conditions (solid lines) and (dashed lines).
- The probability for and different initial conditions (solid lines) and (dashed lines).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ricciardi, L.M. Stochastic Population Theory: Birth and Death Processes. In Mathematical Ecology. Biomathematics; Hallam, T.G., Levin, S.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; Volume 17, pp. 155–190. [Google Scholar] [CrossRef]
- Zeifman, A.; Satin, Y.; Kovalev, I.; Razumchik, R.; Korolev, V. Facilitating Numerical Solutions of Inhomogeneous Continuous Time Markov Chains Using Ergodicity Bounds Obtained with Logarithmic Norm Method. Mathematics. 2021, 9, 42. [Google Scholar] [CrossRef]
- Razumchik, R.; Rumyantsev, A. Some ergodicity and truncation bounds for a small scale Markovian supercomputer model. In Proceedings of the 36th ECMS International Conference on Modelling and Simulation ECMS 2022, Norway, Alesund, 30 May–3 June 2022. [Google Scholar] [CrossRef]
- Gnedenko, B.V.; Makarov, I.P. Properties of a problem with losses in the case of periodic intensities. Diff. Equs. 1971, 7, 1696–1698. [Google Scholar]
- Prendiville, B.J. Discussion Symposium on stochastic processes. J. R. Statist. Soc. B 1949, 11, 273. [Google Scholar]
- Takashima, M. Note on evolutionary processes. Bull. Math. Stat. 1956, 7, 18–24. [Google Scholar] [CrossRef]
- Giorno, V.; Negri, C.; Nobile, A.G. A solvable model for a finite capacity queueing system. Appl. Prob. 1985, 22, 903–911. [Google Scholar] [CrossRef]
- Karlin, S.; McGregor, J. Ehrenfest Urn Model. J. Appl. Prob. 1965, 2, 352–376. [Google Scholar] [CrossRef]
- Flegg, M.B.; Pollett, P.K.; Gramotnev, D.K. Ehrenfest model for condensation and evaporation processes in degrading aggregates with multiple bonds. Phys. Rev. 2008, 78, 031117. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q. Note on the non-homogeneous Prendiville process. Math. Biosci. 1998, 148, 1–5. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G. Bell Polynomial Approach for Time-Inhomogeneous Linear Birth–Death Process with Immigration. Mathematics 2020, 8, 1123. [Google Scholar] [CrossRef]
- Mitrophanov, A.Y. Stability and exponential convergence of continuous-time Markov chains. J. Appl. Prob. 2003, 40, 970–979. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G.; Spina, S. Some remarks on the prendiville model in the presence of jumps. In International Conference on Computer Aided Systems Theory, Proceedings of the 17th International Conference, Las Palmas de Gran Canaria, Spain, 17–22 February 2019; Springer: Cham, Switzerland, 2019; pp. 150–157. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G. A Time-Inhomogeneous Prendiville Model with Failures and Repairs. Mathematics 2022, 10, 251. [Google Scholar] [CrossRef]
- Matis, J.H.; Kiffe, T.R. Stochastic Compartment models with Prendiville growth rates. Math. Biosci. 1996, 138, 31–43. [Google Scholar] [CrossRef]
- Parthasarathy, P.R.; Krishna Kumar, B. Stochastic Compartmental models with Prendiville growth mechanisms. Math. Biosci. 1995, 125, 51–60. [Google Scholar] [CrossRef]
- Zeifman, A.; Leorato, S.; Orsingher, E.; Satin, Y.; Shilova, G. Some universal limits for nonhomogeneous birth and death processes. Queueing Syst. 2006, 52, 139–151. [Google Scholar] [CrossRef]
- Satin, Y.A. On the bounds of the rate of convergence for Mt/Mt/1 model with two different requests. Syst. Means Inform. 2021, 31, 17–27. [Google Scholar] [CrossRef]
- Zeifman, A.I.; Satin, Y.A.; Korolev, V. Two Approaches to the Construction of Perturbation Bounds for Continuous-Time Markov Chains. Mathematics 2020, 8, 253. [Google Scholar] [CrossRef]
- Zeifman, A.I. Quasi-ergodicity for non-homogeneous continuous-time Markov chains. J. Appl. Probab. 1989, 26, 643–648. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usov, I.; Satin, Y.; Zeifman, A.; Korolev, V. Ergodicity Bounds and Limiting Characteristics for a Modified Prendiville Model. Mathematics 2022, 10, 4401. https://doi.org/10.3390/math10234401
Usov I, Satin Y, Zeifman A, Korolev V. Ergodicity Bounds and Limiting Characteristics for a Modified Prendiville Model. Mathematics. 2022; 10(23):4401. https://doi.org/10.3390/math10234401
Chicago/Turabian StyleUsov, Ilya, Yacov Satin, Alexander Zeifman, and Victor Korolev. 2022. "Ergodicity Bounds and Limiting Characteristics for a Modified Prendiville Model" Mathematics 10, no. 23: 4401. https://doi.org/10.3390/math10234401
APA StyleUsov, I., Satin, Y., Zeifman, A., & Korolev, V. (2022). Ergodicity Bounds and Limiting Characteristics for a Modified Prendiville Model. Mathematics, 10(23), 4401. https://doi.org/10.3390/math10234401







