Adaptive Continuous-Variable Quantum Key Distribution with Discrete Modulation Regulative in Free Space

Abstract

The finite sampling bandwidth of an analog-to-digital converter has a negative effect on the continuous-variable quantum key distribution (CVQKD), which leaves a potential loophole for an eavesdropper and weakens the practical security of the system. To compensate for the loss in free space, we deploy an adaptive optics (AO) unit in the detector of the CVQKD system with discrete modulations. Since the closed-loop control bandwidth of the embedded AO unit can be optimized with the sampling frequency, the practical security of the system can be enhanced in terms of the secret key rate. The security analysis is demonstrated on the basis of the derived secret key rate with numerical simulations, providing a feasible implementation of CVQKD in realistic free-space environments.

1. Introduction

Quantum key distribution (QKD) [1,2,3,4], which randomly generates secret keys for legal participants, can be composed of discrete-variable (DV) QKD [1,2] and continuous-variable (CV) QKD [3,4]. The former encodes information of key bits in the polarization states of a single photon, whereas the latter encodes information with the momentum and position quadratures ($\widehat{x}$ and $\widehat{p}$) of an optical field that involves Gaussian modulation. The security has been proven in both finite-size regimes and asymptotic limits [5]. The traditional CVQKD can be implemented with Gaussian modulations (GM). However, it is difficult to break the limitation of a low signal-to-noise ratio (SNR), which results in a decline in reconciliation efficiency. As a result, a discretely modulated (DM) CVQKD has been proposed to address such limitations and the security has been demonstrated in the asymptotic regime [6]. Unfortunately, it is still vulnerable to insecure loopholes, which have an effect on practical security when performing potential attack strategies, such as local oscillator (LO) fluctuation attacks [7], LO calibration attacks [8], wavelength attacks [9], saturation attacks [10], finite sampling bandwidth effects [11], blinding attacks on the detector [12], jitter in clock synchronization [13], polarization attacks [14], side-channel attacks [15,16], and so on. In consequence, a large number of countermeasures have been proposed [17]. A measurement-device-measurement (MDI) scheme has been used for defending attacks in detectors [18,19]. However, it remains vulnerable because of imperfect equipment that contains concealed loopholes in practical systems.

When being implemented in free-space (FS) channels, the transmission coefficient fluctuates because of turbulent atmospheric effects. As coherent detection can be distorted by atmospheric turbulence, the performance of the system will be degraded. Fortunately, suitable adaptive optics (AO) can be used to mitigate turbulence-induced wavefront aberrations of the received quantum states. In this paper, we demonstrate the effects of a finite sampling bandwidth on the practical security of CVQKD regulative in free space. An AO-enabled approach is used for performance improvement in terms of the secret key rate.

This paper is organized as follows: In Section 2, we propose an AO-embedded detector for a free-space CVQKD system with discrete modulations. In Section 3, we demonstrate the effect of the finite sampling bandwidth on the practical security of the AO-enabled CVQKD system when considering collective attacks. We evaluate the secret key rate with numerical simulations using a linear model by taking the effects of the finite sampling bandwidth into account. Finally, conclusions are drawn in Section 4.

2. AO-Enabled CVQKD with Discrete Modulations

In the prepare-and-measure scheme, there are usually N coherent states denoted as $|{\alpha }_k^N⟩=|\alpha e^{i2k\pi /N}⟩$ with modulation variance $V_M=2{\alpha }^2$ for $k\in Z_N=\{0,1,\cdots ,N-1\}$ [20]. Each coherent state $|{\alpha }_k^N⟩$ can be represented using the amplitude quadrature ($\widehat{x}$) and the phase quadrature ($\widehat{x}$). Alice prepares N coherent states and sends one of the coherent states at random to the receiver Bob in free space, which can be characterized using the transmission T and the excess noise $ϵ$. Upon receiving the coherent states, Bob performs either a homodyne detector or a heterodyne detector to measure one of the two quadratures $\widehat{x}$ or $\widehat{p}$ or both the quadratures.

To simplify the description of the proposed CVQKD system, we consider an equivalent entanglement-based scheme with discrete modulations. As shown in Figure 1, Alice prepares for N coherent states given by

$$\begin{array}{c}\hfill |{\mathrm{\Psi }}_N⟩=\frac{1}{4}\sum _{k=0}^{N-1}|{\psi }_k⟩|{\beta }_k⟩,\end{array}$$

(1)

where the states $|{\psi }_k⟩$ for $k\in Z_N$ can be described as

$$\begin{array}{c}\hfill |{\psi }_k⟩=\frac{1}{2}\sum _{m=0}^{N-1}{e}^{i(\frac{N}{2}k+1)m\pi /4}|{\varphi }_k⟩.\end{array}$$

(2)

Figure 1. Scheme diagram of the AO-enabled CVQKD with discrete modulations. HD and HE denote homodyne detection or heterodyne detection, Att denotes attenuation, QM denotes quantum memory, and EPR is a two-mode squeezed vacuum (EPR) state.

Moreover, the state $|{\varphi }_k⟩$ for $k\in Z_N$ can be described as

$$\begin{array}{c}\hfill |{\varphi }_k⟩=\frac{e^{-\frac{{\alpha }^2}{2}}}{\sqrt{{\lambda }_k}}\sum _{n=0}^{\infty }{(-1)}^n{e}^{\frac{{\alpha }^{(Nn+k)}}{\sqrt{(Nn+k)!}}}|(Nn+k)⟩.\end{array}$$

(3)

In Figure 1, we present a schematic diagram of the AO-based DM CVQKD in free space. Alice prepares for the bipartite state $|{\mathrm{\Psi }}_N⟩$, as described in Equation (1), with modulation variance $V=1+V_M$. She measures the coherent states projected on mode A, while projecting another state to mode B that is transmitted in free space. Afterwards, Bob can perform either homodyne detection (HD) or heterodyne detection (HE) to measure the received mode $B_2$.

At the receiver, we consider the influence of the finite sampling bandwidth on the estimated secret key rate of the CVQKD system. The AO-embedded detector can realize the real-time detection of a distorted wavefront and then correct the distorted wavefront, which can be used for potential loss compensation in free space.

2.1. Finite Sampling Frequency

As is well-known in traditional optical signal processing, frequency aliasing usually leads to the distinct spectrum of discrete Fourier transformation (DFT), and, thus, an analog-to-digital converter with decreased finite sampling frequency will fail to restore the initial signals at the receiver. Taking into account $f_s\in \{50,100,200\}$ Hz as an example, the spectrum may overlap with the decreasing sampling frequency. According to the optical signal processing, we can find the signal distortion, though the restored signal shapes can be produced like a Gaussian-distribution sampled at the above-mentioned frequency $f_s$.

While performing the DFT operation, we find that the low sampling frequency leads to frequency aliasing in the frequency domain. With increasing sampling frequency, the restored signals approach the original Gaussian-distribution signals. The reason is that fewer sampling points may result in unavoidable information loss in terms of signal-restored processing. Only when the sampling frequency is twice the signal frequency can the sample value approach the maximal value of the output signals. Therefore, we focus on the influence of the finite sampling frequency in the frequency domain. To offset the loophole, a suitable sampling frequency for state preparation is recommended for attenuation (Att), resulting in less electrical noise.

2.2. AO-Embedded Detector

As shown in Figure 1, an AO unit, which includes a wavefront corrector, a wavefront controller and a wavefront sensor, can be embedded in the detector to compensate for the loss in free space. The AO-embedded detector can be used for performance improvement of the CVQKD system in free space.

When Bob performs optical coherent detection to estimate the excess noise, he needs a combination of the received optical signals and other signals derived from local oscillation (LO). We assume that the LO laser turns to plane waves and the intensity of the optical signal passing through the AO unit is uniform. The efficiency introduced by the AO unit outweighs the AO-added noise. The total noise that includes the channel-added, the AO-added and the detection-added noise decreases due to the effect of the AO unit on the detector. Since the AO unit achieves real-time detection of the distorted wavefront and then controls it immediately, the quality of the transformed optical signal is improved [21,22].

3. Security Analysis

3.1. Derivation of the Secret Key Rate

Since CVQKD can be implemented with a pulsed signal light, the received signals, which can be described as the secret bit rate $R=f_{s}K$, depend on the sampling repetition rate $f_s$ and the secret key rate K, thereby contributing to performance improvement. The secret key rate is an important parameter that can be used to assess the performance of the proposed system. To obtain the secret key rate, the covariance matrix should be derived. The secret key rate, in the case of an asymptotic framework, can be given by

$$\begin{array}{c}\hfill K=\beta I_{AB}-{\chi }_{BE}\end{array},$$

(4)

where $\beta$ is the reconciliation efficiency, $I_{AB}$ refers to the mutual information shared by both Alice and Bob, and ${\chi }_{BE}$ represents the Holevo bound between Bob and Eve.

In what follows, the secret key rate is determined based on the reverse reconciliation $({\chi }_E={\chi }_{BE})$, where the Holevo bound ${\chi }_{BE}$ can be calculated as follows,

$$\begin{array}{c}\hfill {\chi }_{BE}=\sum _{i=1}^{2}G(\frac{({\lambda }_i-1)}{2})-\sum _{i=3}^{5}G(\frac{({\lambda }_i-1)}{2})\end{array},$$

(5)

where $G\left(x\right)=(x+1)log(x+1)-xlog\left(x\right)$. Taking the notation $T_{nf}=⟨T^2⟩$, the symplectic eigenvalues ${\lambda }_{1,2}$ can be described as

$$\begin{array}{c}\hfill {\lambda }_{1,2}^2=\frac{1}{2}[A\pm \sqrt{A^2-4B}]\end{array}$$

(6)

with the denotations

$$\begin{array}{cc}\hfill A& =V^2(1-2T)+2t{T}_{nf}{T}^2{(V+{\chi }_{line})}^2,\hfill \\ \hfill B& =T_{nf}^2{(V{\chi }_{line}+1)}^2.\hfill \end{array}$$

(7)

The remaining symplectic eigenvalues ${\lambda }_{3,4,5}$ of the covariance matrix are calculated based on the above elements. Therefore, the eigenvalues ${\lambda }_{3,4}$ can be rewritten as

$$\begin{array}{c}\hfill {\lambda }_{3,4}^2=\frac{1}{2}[C+\sqrt{C^2-4D}]\end{array},$$

(8)

where

$$\begin{array}{cc}\hfill C& =\frac{A({\chi }_w+{\chi }_h)+V\sqrt{B}+T_{nf}(V+{\chi }_{line})}{T_{nf}(V+{\chi }_{tot})},\hfill \\ \hfill D& =\frac{\sqrt{B}+B({\chi }_w+{\chi }_h)}{T_{nf}(V+{\chi }_{tot})},\hfill \end{array}$$

(9)

where ${\chi }_{tot}={\chi }_{line}+({\chi }_w+{\chi }_h)/T_{nf}$ is the total noise, and ${\chi }_{line}$ is the total channel-added noise introduced by atmospheric turbulence given by

$${\chi }_{line}=V_T(V-1+\xi )+{⟨T^2⟩}^{-1}-1,$$

(10)

with notation $V_T=⟨T⟩-{⟨\sqrt{T}⟩}^2$. In addition, the symplectic eigenvalue is ${\lambda }_5=1$. Let ${\xi }_{nf}=V_T(V-1+\xi )$, and then the above-derived noise can be rewritten as ${\chi }_{line}=1/T_{nf}-1+{\xi }_{nf}$, which is characterized by the parameter transmission (T). Then the mutual information $I_{AB}$ can be achieved as follows,

$$\begin{array}{c}\hfill I_{AB}=\frac{1}{2}log(\frac{V_A}{V_{A|B}})=\frac{1}{2}log(\frac{V+{\chi }_{tot}}{1+{\chi }_{tot}})\end{array},$$

(11)

where ${\chi }_w$ is the AO-added noise, and ${\chi }_h$ is the detection-added noise. In this way, the secret key rate, which is based on the covariance matrix in the asymptotic framework, can be obtained.

3.2. Tunable Parameter Optimization

To optimize the performance of the system, we take into account the modulation variance $V_M$ for coherence state preparation. According to the derived secret key rate K in Equation (5), this depends on the parameter of modulation variance $V_M$ in the source preparation. Numerical simulations demonstrate the optimal interval where the minimal secret key rate is bound to be over ${10}^{-6}$ for the given maximal transmission distance $d\in \{60\mathrm{km},80\mathrm{km},100\mathrm{km}\}$, as shown in Figure 2, where the different transmission distances are represented with lines using respective colors. We find that the increasing transmission distance narrows down this interval $[0.02,0.16]$. In the meantime, there is a decline in the secret key rate. Narrow though each optimal interval is, every curve involves the common optimal interval, where the secret key rate reaches a peak for $V_M=0.1$. As a result, we have an optimal modulation variance $V_M=0.1$ in CVQKD according to the numerical simulations of the secret key rate for the variable modulated variance $V_M$ in the range $[0,0.2]$.

Figure 2. The secret key rate as a function of the modulated variance $V_M$ for the given transmission distance $d\in \{60,80,100\}$ km of (a) eight-state DM DVQKD and (b) four-state DM CVQKD.

The sampling frequency also plays a role in the performance improvement, as shown in Figure 3, where the different frequencies $f_s\in \{2\mathrm{GHz},4\mathrm{GHz},\infty \mathrm{GHz}\}$ are represented with lines using respective colors. We find that the increasing sampling frequency narrows down this interval $[0.01,0.19]$. For the given variance $V_M$, the large sampling frequency results in an increased secret key rate. Similar to the above analysis, there is also a decline in the secret key rate for the modulated variance $V_M$$\in [0,0.2]$. Moreover, as the sampling frequency reaches 4 GHz, the secret key rate approaches the optimal value. Consequently, we can select the values $f_s=4$ GHz and $V_M=0.1$ in numerical simulations.

Figure 3. The secret key rate as a function of the modulated variance with sampling frequency $f_s\in \{2,4,\infty \}$ GHz of (a) eight-state DM DVQKD and (b) four-state DM DVQKD.

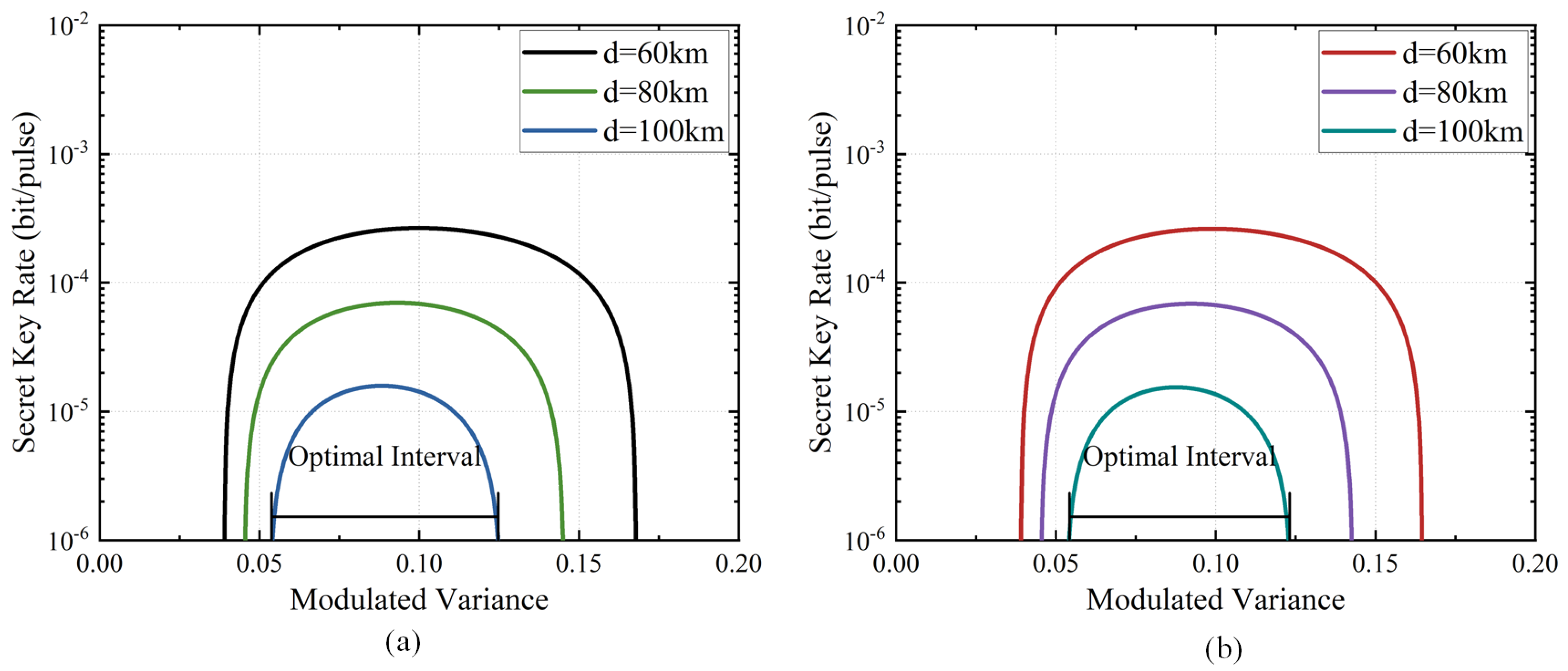
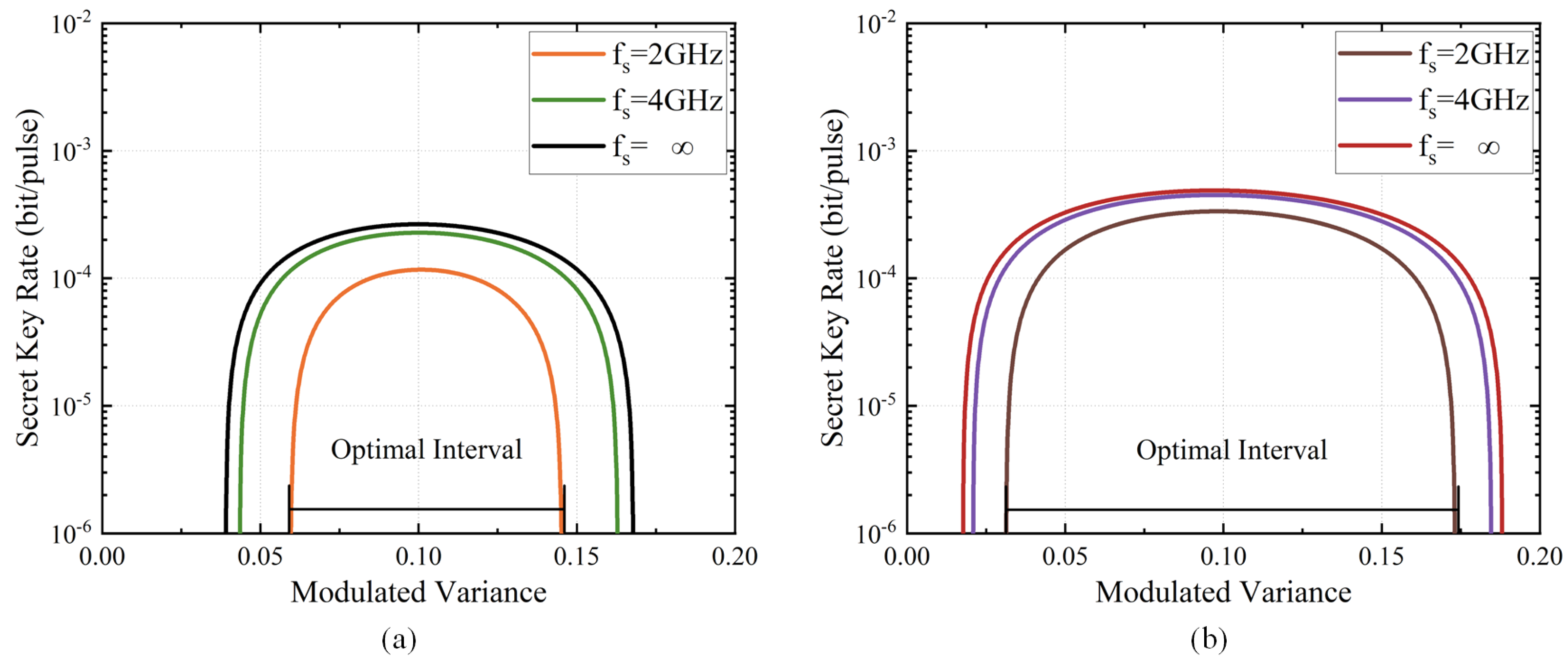
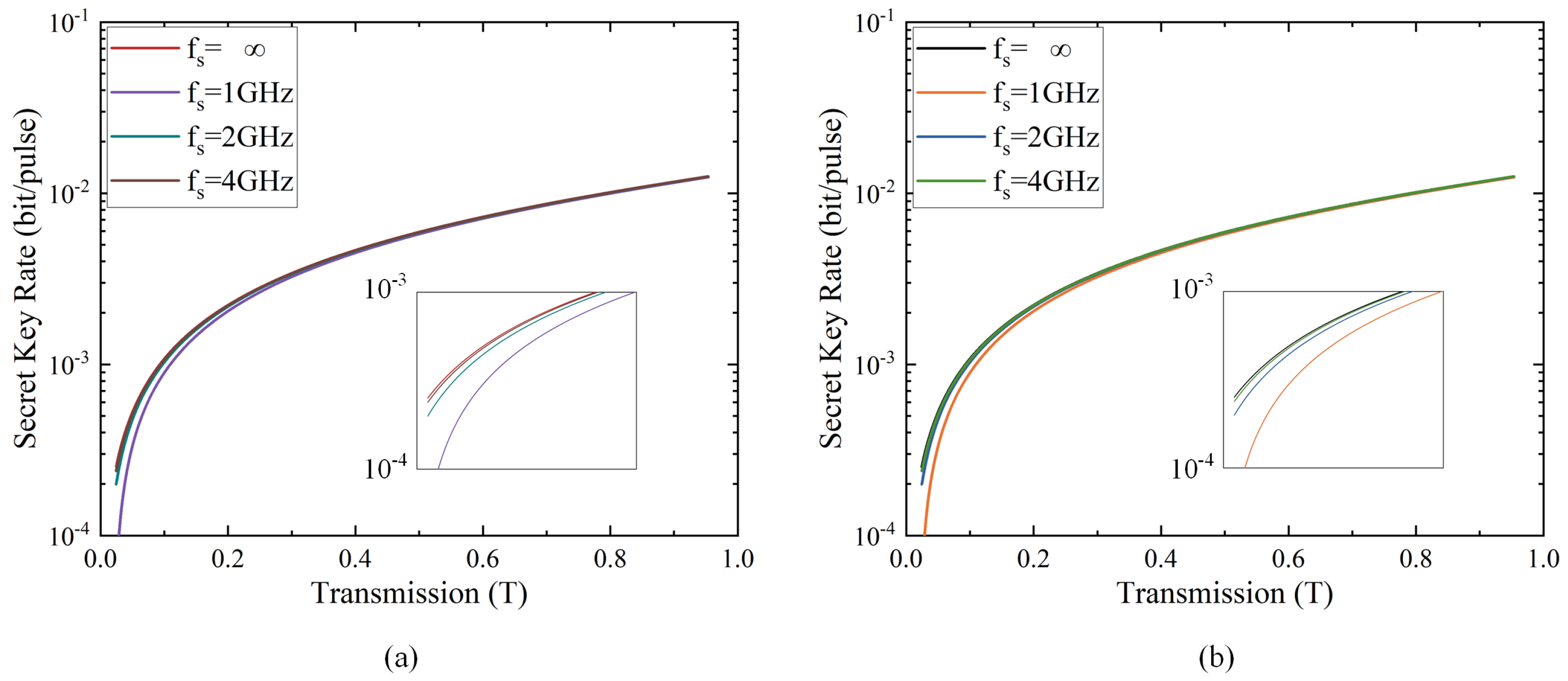
3.3. Simulation Results

In Figure 4, we demonstrate the secret key rate of the AO-enabled DM CVQKD system for both (a) the four-state scheme and (b) the eight-state scheme, which is a function of the transmission (T$\in [0,1]$), while illustrating the effect of the sampling frequency $f_s$ on performance. In numerical simulations, we achieve a secret key rate for the given sampling frequency $f_s\in \{1\mathrm{GHz},2\mathrm{GHz},4\mathrm{GHz},\infty \mathrm{GHz}\}$. The higher sampling frequency results in a higher secret key rate. It is observed that there is a decline in the secret key rate with decreasing sampling frequency. The high-rate sampling frequency generates a high-rate CVQKD system due to the effect of the AO unit on the detector of the receiver, which can be regarded as compensation for the suffering it has been caused. Since the previously mentioned loophole can be solved at the AO-involved receiver, the eavesdropper has no access to the unsolved loophole. Given the finite sampling frequencies of ADC, for example $f_s=4$ GHz, it can be used to apply a suitable ADC to achieve a practical high-rate CVQKD system.

Figure 4. The secret key rate of the DM CVQKD system as a function of the transmission with $f_s\in \{1,2,4,\infty \}$ GHz by applying homodyne detection of (a) a four-state scheme and (b) an eight-state scheme. The lines from the top down denote the secret key rates of the system with frequencies ∞ GHz, 4 GHz, 2 GHz and 1 GHz, respectively. The higher sampling frequency means a higher secret key rate.

In Figure 5, we compare the secret key rate of the AO-enabled DM CVQKD system with the traditional system without embedding the AO unit, where the lines from the top down denote the secret key rates of the AO-enabled system and the traditional system, while considering the four-state scheme for modulations. We observe that the embedded AO unit in the receiver improves the performance of the system. Combined with Figure 4, the eight-state scheme performs only a little better than the four-state scheme in terms of the secret key rate when considering the effects of the AO unit on the secret key rate. However, as for the DM scheme for modulations, the AO unit cannot always be more advantaged compared with the traditional CVQKD system with Gaussian modulation.

Figure 5. The performance of the AO-enabled DM CVQKD system for the four-state scheme.

4. Conclusions

We have proposed an AO-enabled DM CVQKD over an atmospheric turbulent channel and demonstrated the influence of the finite sampling frequency on performance improvement. We found that an increased sampling frequency may have a positive effect on performance. We illustrated the performance of the AO-enabled DM CVQKD over an atmospheric turbulent channel in the asymptotic regime, which resulted in an increased secret key rate. The proposal represents an elegant approach to performance improvement of a practical CVQKD system in FS-involved environments. With respect to other approaches to performance improvement, we can make use of non-Gaussian operations for source preparation or signal detection, which will be investigated in future work.