Kinematic Modeling and Stiffness Analysis of a 3-DOF 3SPS + 3PRS Parallel Manipulator
Abstract
:1. Introduction
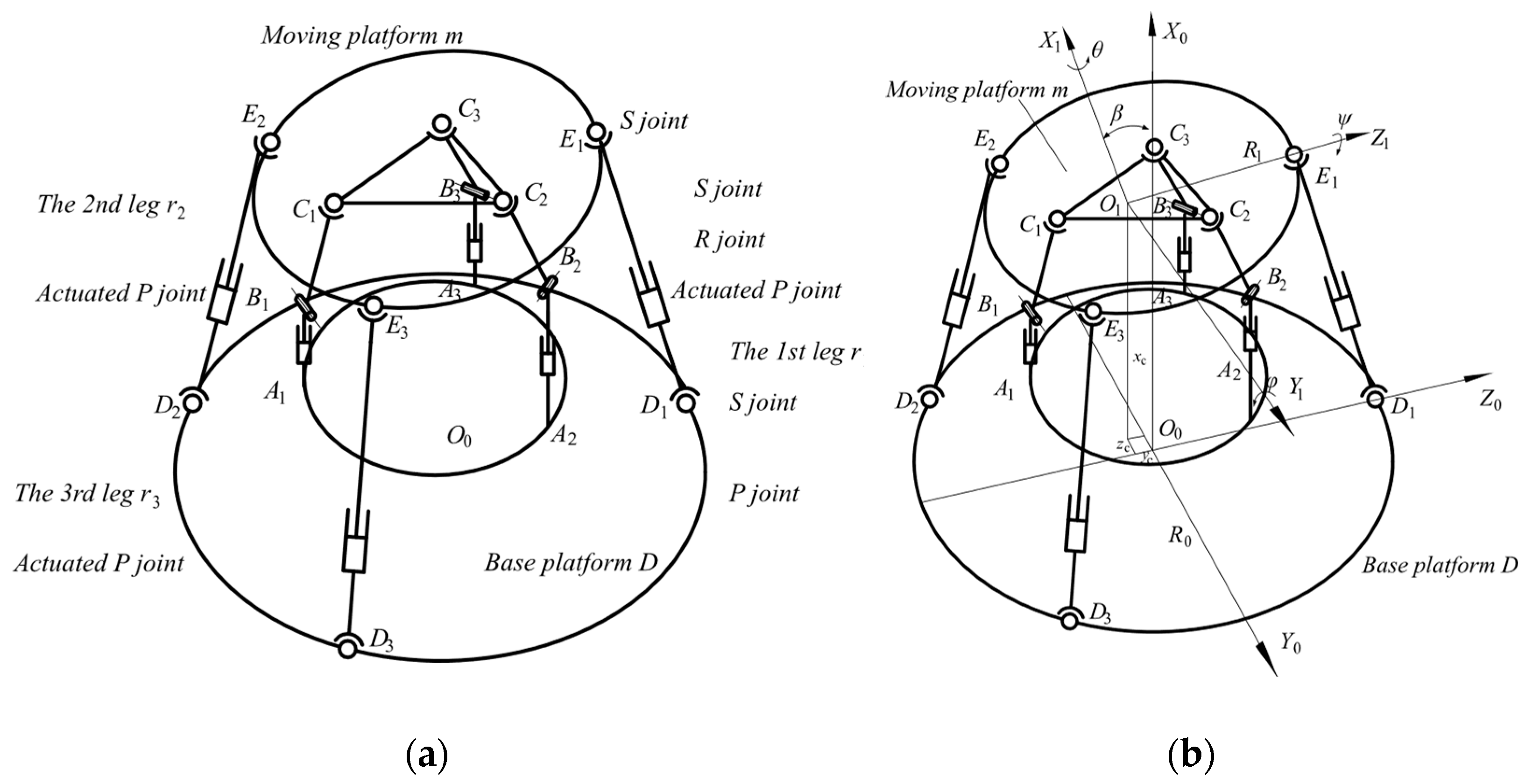
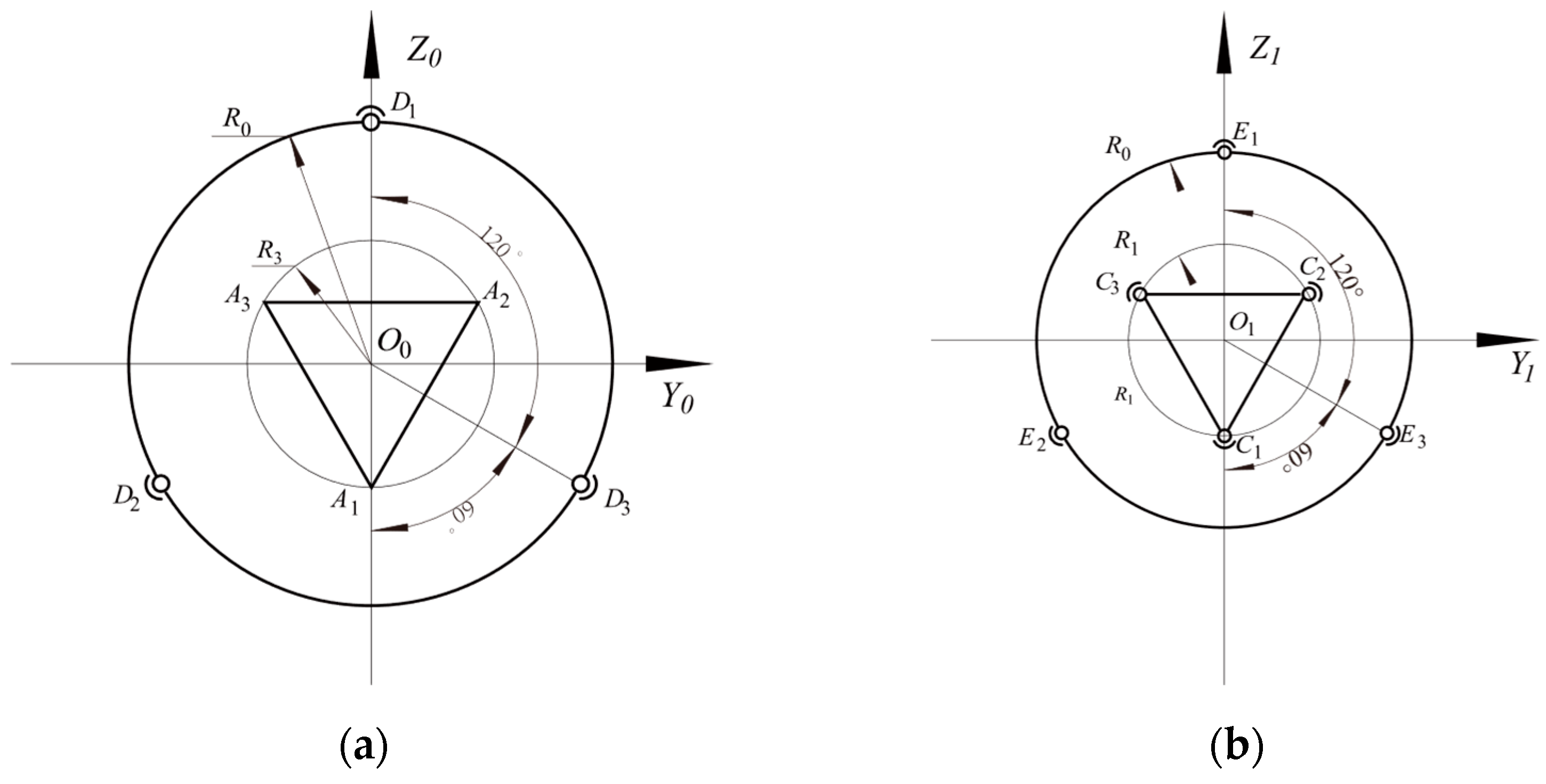
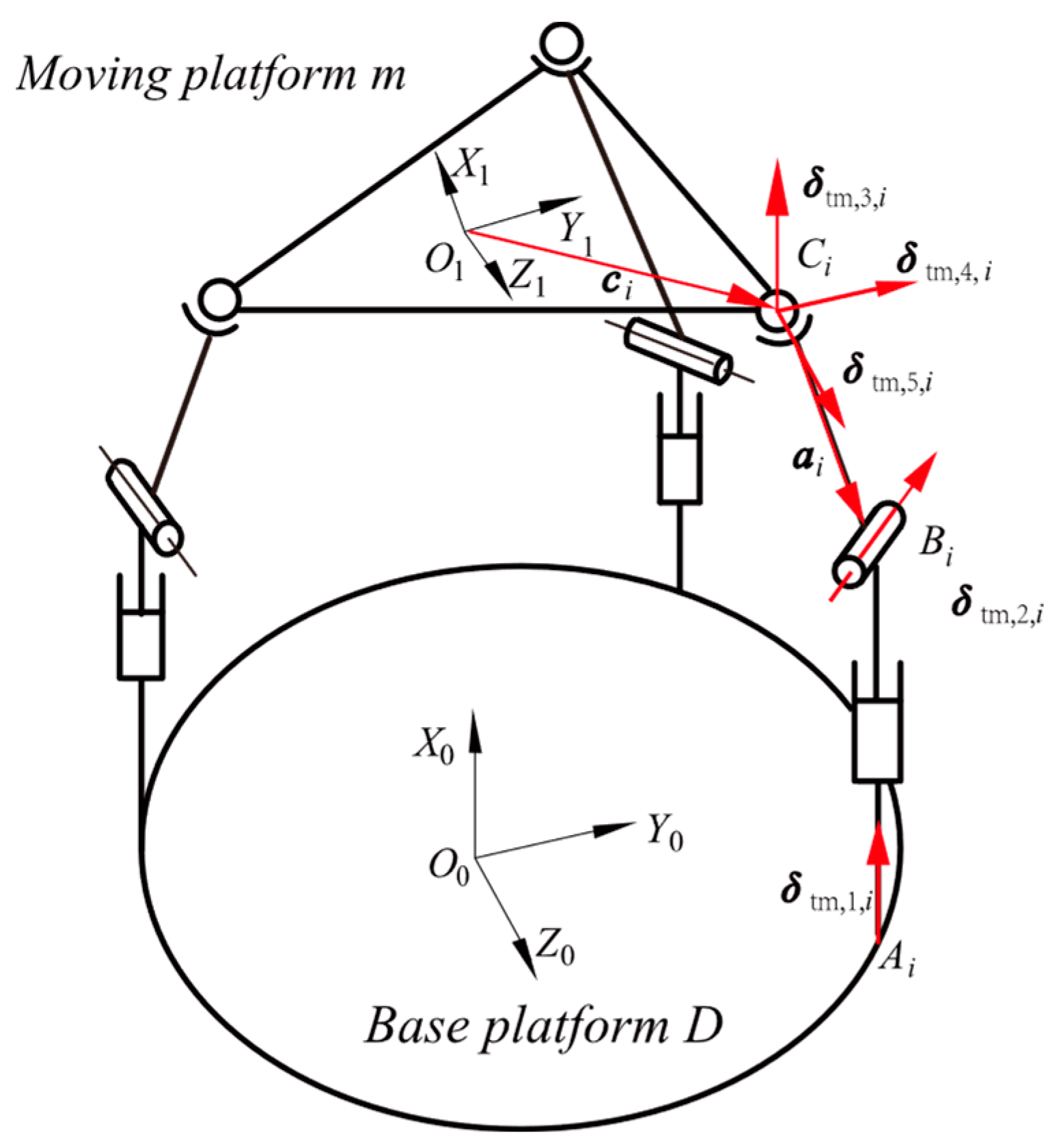
1.1. Mechanism Architecture
1.2. Calculation of the Degree of Freedom
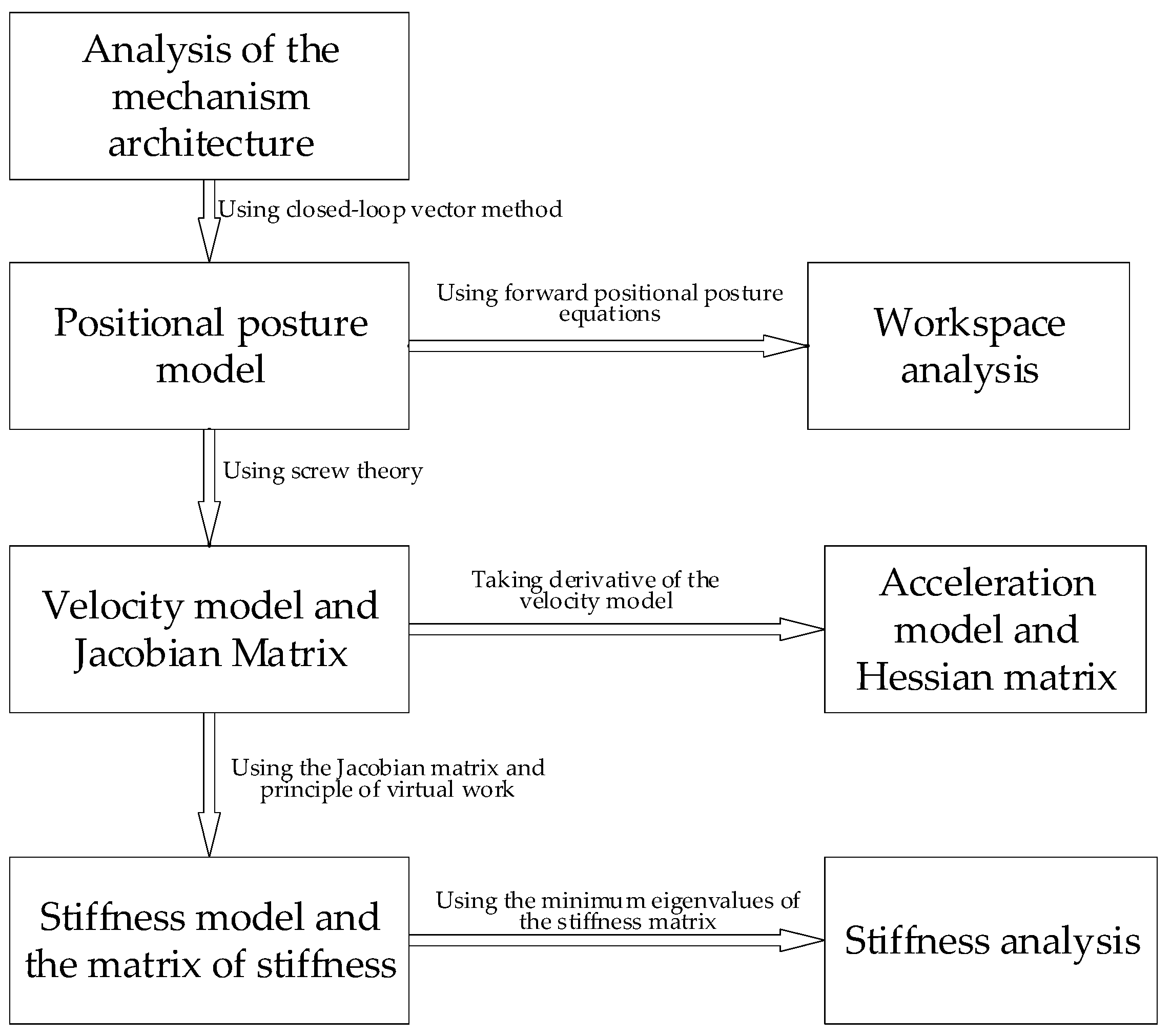
2. Kinematic Modeling of the 3SPS + 3PRS PM
2.1. Positional Posture Model
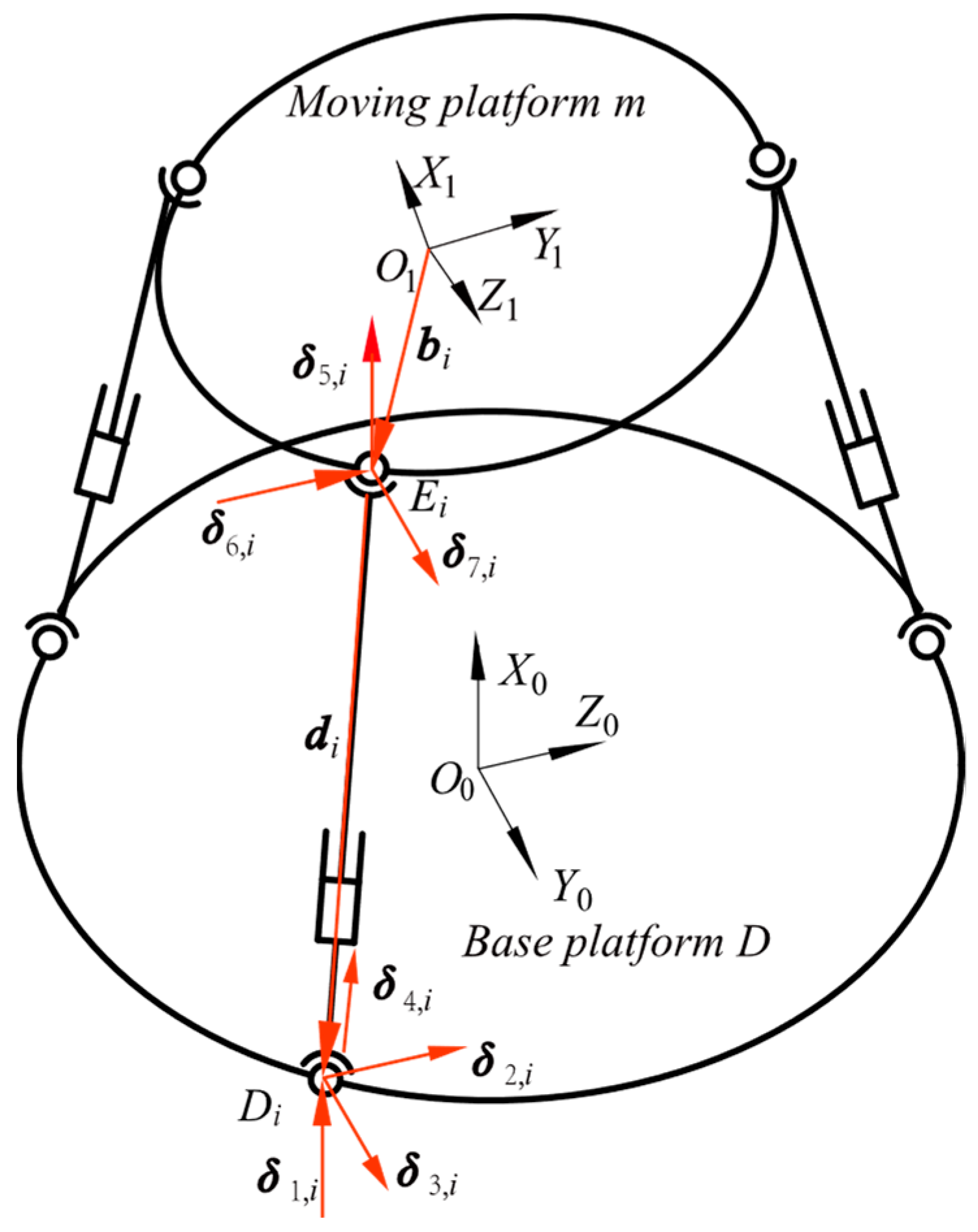
2.2. Velocity Model
- (1)
- The SPS limbs
- (2)
- The PRS limbs
2.3. Acceleration Model
3. Stiffness Modeling of the 3SPS + 3PRS PM
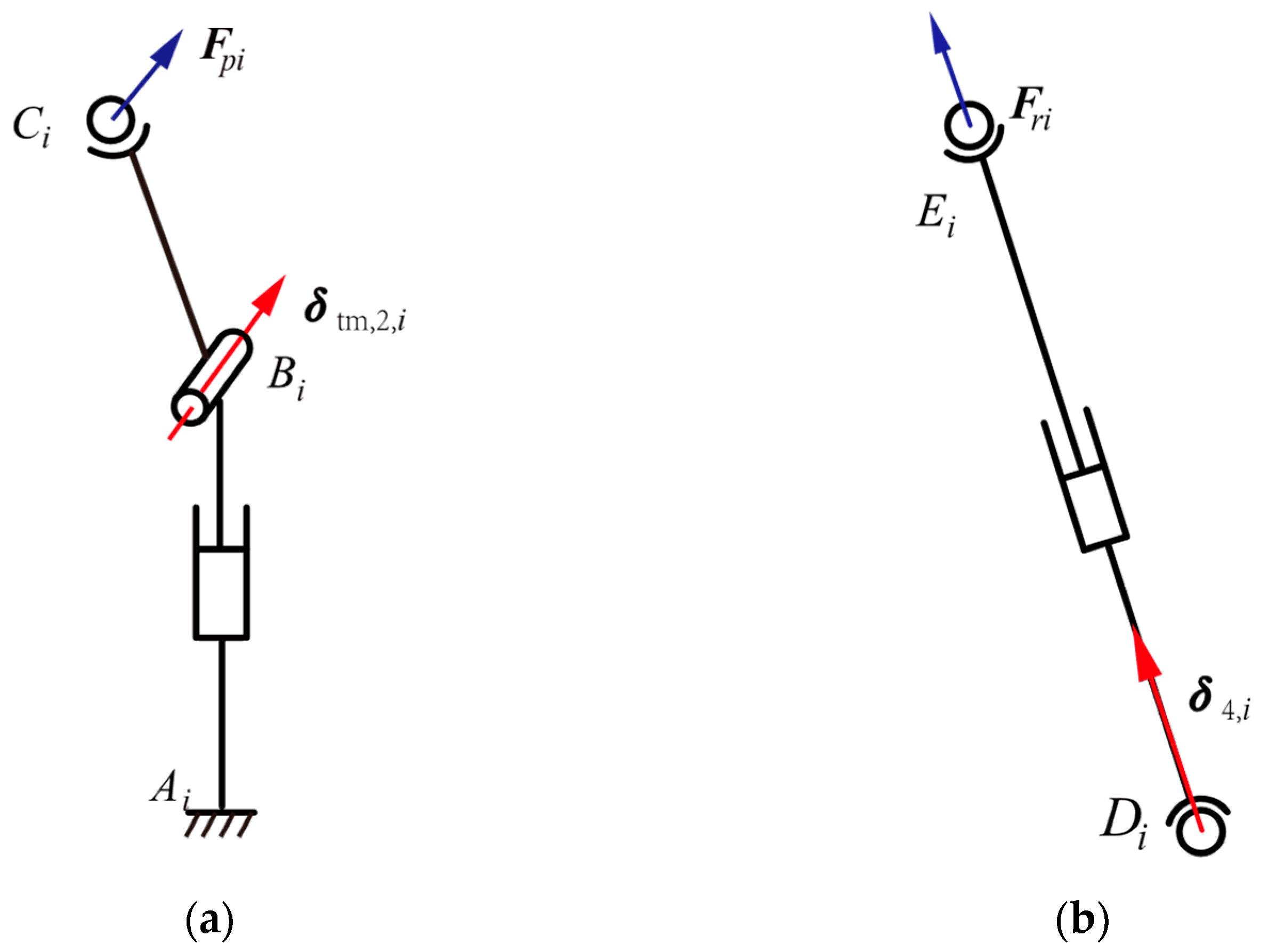
3.1. Stiffness Model
3.2. Calculation of the Stiffness Coefficient
- (1)
- The SPS limbs
- (2)
- The PRS limbs
4. Numerical Examples
4.1. Positional Posture Numerical Example
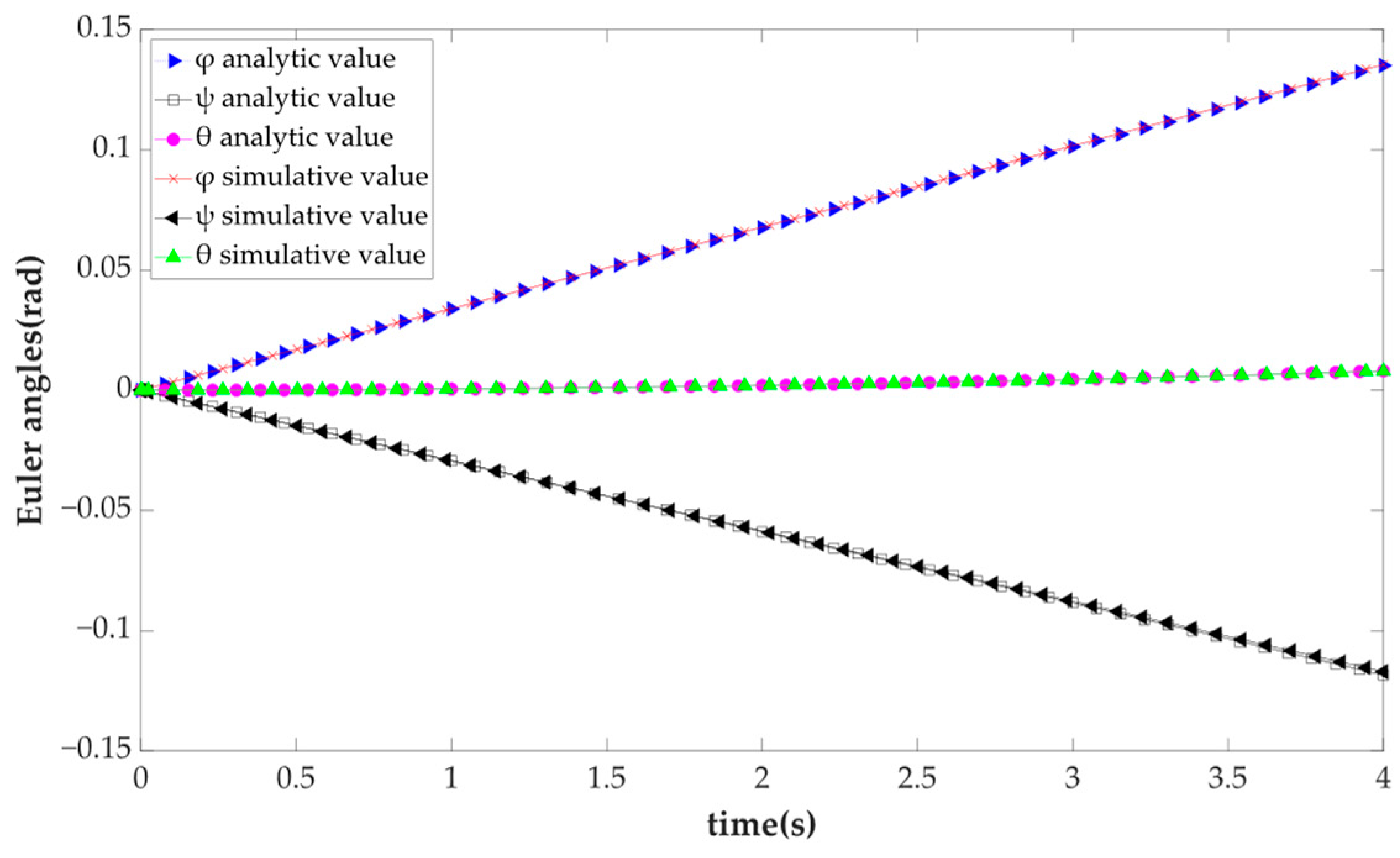
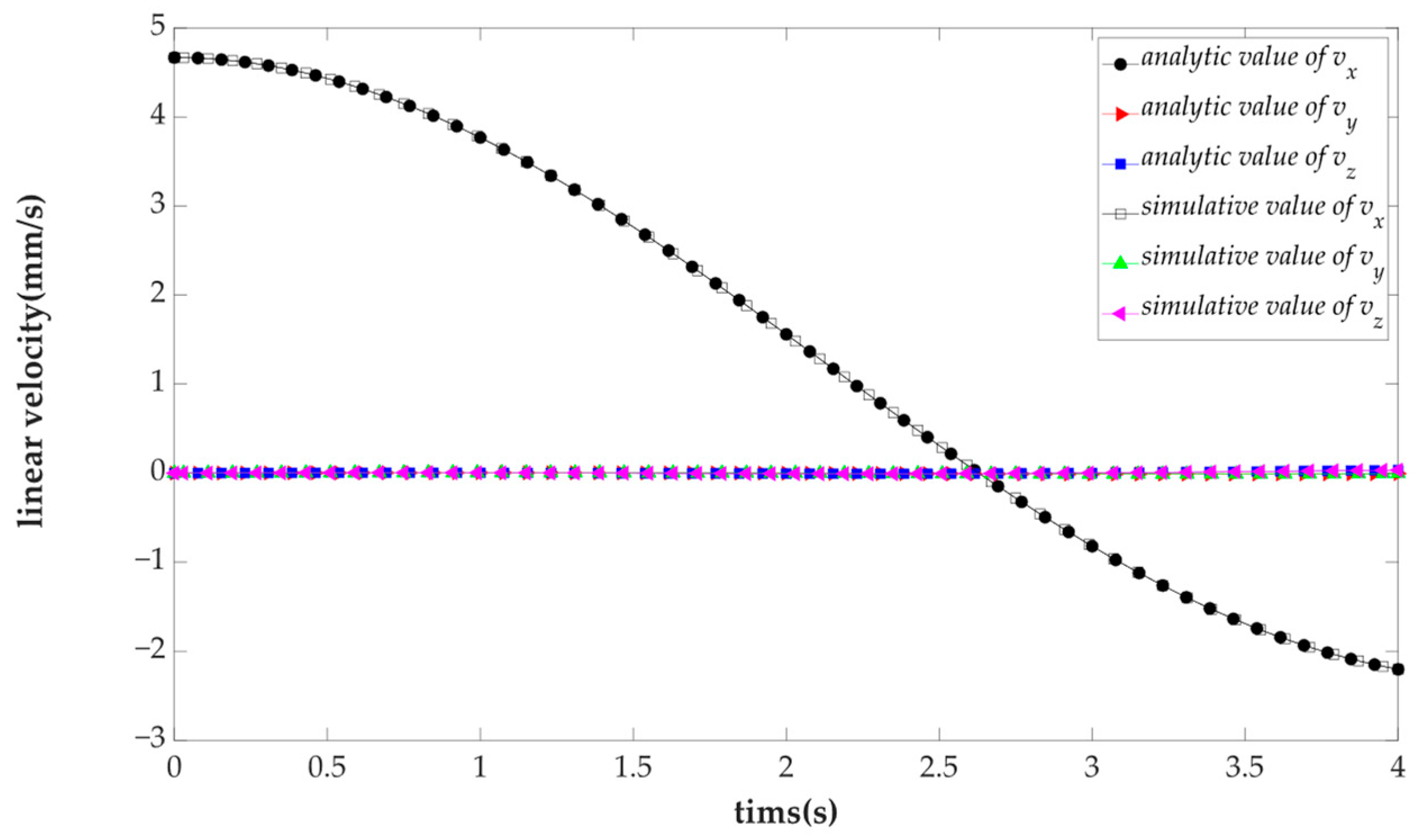
4.2. Kinematic Numerical Example
4.3. Workspace Analysis
4.4. Stiffness Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A complete analytical solution for the dimensional synthesis of 3-DOF delta parallel robot for a prescribed workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Wang, L.; Xu, H.; Guan, L.; Zhi, Y. A novel 3-PUU parallel mechanism and its kinematic issues. Robot. Comput.-Integr. Manuf. 2016, 42, 86–102. [Google Scholar]
- Wang, L.; Xu, H.; Guan, L. Optimal design of a 3-PUU parallel mechanism with 2R1T DOFs. Robot. Mech. Mach. Theory 2017, 114, 190–203. [Google Scholar] [CrossRef]
- Ruiz-Hidalgo, N.C.; Blanco-Ortega, A.; Abúndez-Pliego, A.; Colín-Ocampo, J.; Arias-Montiel, M. Design and Control of a Novel 3-DOF Parallel Robot. In Proceedings of the IEEE International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 22–25 November 2016; pp. 66–71. [Google Scholar]
- Zou, Q.; Zhang, D.; Zhang, S.; Luo, X. Kinematic and dynamic analysis of a 3-DOF parallel mechanism. Int. J. Mech. Mater. Des. 2021, 17, 587–599. [Google Scholar] [CrossRef]
- Xu, Y.; Li, B.; Zhao, X. Influence upon Kinematics Performance of a Family of 3-PRS Parallel Mechanisms Affected by Kinematic Chain Layout. In Proceedings of the International Conference on Mechatronics and Industrial Informatics (ICMII), Guangzhou, China, 13–14 March 2013; pp. 37–41. [Google Scholar]
- Hu, X.; Li, F.; Tang, G. Kinematics Analysis of 3UPU_UP Coupling Parallel Platform in the Marine Environment. IEEE Access. 2020, 8, 158142–158151. [Google Scholar] [CrossRef]
- Hu, B.; Huang, Z. Kinetostatic model of overconstrained lower mobility parallel manipulators. Nonlinear Dyn. 2016, 8, 309–322. [Google Scholar] [CrossRef]
- Qin, Y.; Shirinzadeh, B.; Zhang, D.; Tian, Y. Design and kinematics modeling of a novel 3-DOF monolithic manipulator featuring improved Scott-Russell mechanisms. J. Mech. Des. 2013, 135, 101004. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J.; Rodriguez-Castro, R. A new parallel manipulator with multiple operation modes. J. Mech. Robot. 2018, 10, 051012. [Google Scholar] [CrossRef]
- Aghajari, M.; Fathollahi Dehkordi, S.; Korayem, M.H. Nonlinear dynamic analysis of the extended telescopic joints manipulator with flexible links. Arab. J. Sci. Eng. 2021, 46, 7909–7928. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F.; Mojarradi, M.; Monfared, P. Analytical and experimental investigation of the dynamic behavior of a revolute-prismatic manipulator with N flexible links and hubs. Int. J. Adv. Manuf. Technol. 2019, 103, 2235–2256. [Google Scholar] [CrossRef]
- Korayem, M.H.; Shafei, A.M. Motion equation of nonholonomic wheeled mobile robotic manipulator with revolute–prismatic joints using recursive Gibbs–Appell formulation. Appl. Math. Model. 2015, 39, 1701–1716. [Google Scholar] [CrossRef]
- Gosselin, C. Stiffness mapping for parallel manipulators. IEEE Trans. Robot. Autom. 1990, 6, 377–382. [Google Scholar] [CrossRef]
- Gonçalves, R.S.; Carvalho, J.C.M. Stiffness Analysis of Parallel Manipulator Using Matrix Structural Analysis. In Proceedings of the 2nd European Conference on Mechanism Science, Cassino, Italy, 17–20 September 2008; pp. 255–262. [Google Scholar]
- Lu, Y.; Hu, B.; Yu, J. Analyses of the stiffness and elastic deformation of a 2 (3-SPR) serial—Parallel manipulator. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 2009, 223, 189–198. [Google Scholar] [CrossRef]
- Shankar Ganesh, S.; Koteswara Rao, A.B. Stiffness of a 3-degree of freedom translational parallel kinematic machine. Front. Mech. Eng. 2014, 9, 233–241. [Google Scholar] [CrossRef]
- Zhang, N. Stiffness Analysis of a 3-DOF 2SPR+RPS Parallel Manipulator. In Proceedings of the 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 24–25 August 2019; pp. 76–79. [Google Scholar]
- Ceccarelli, M.; Carbone, G.A. Stiffness analysis for CaPaMan (Cassino parallel manipulator). Mech. Mach. Theory 2002, 37, 427–439. [Google Scholar] [CrossRef]
- Ye, N.; Hu, B. Kinematic and Stiffness Modeling of a Novel 3-DOF RPU+UPU+SPU Parallel Manipulator. IEEE Access 2022, 10, 6304–6318. [Google Scholar] [CrossRef]
- Zeng, Q.; Ehmann, K.F.; Cao, J. Tri-pyramid Robot: Stiffness modeling of a 3-DOF translational parallel manipulator. Robotica 2016, 34, 383–402. [Google Scholar] [CrossRef]
- Rezaei, A.; Akbarzadeh, A. Position and stiffness analysis of a new asymmetric 2 PRR–PPR parallel CNC machine. Adv. Robot. 2013, 27, 133–145. [Google Scholar] [CrossRef]
- Wu, J.; Li, T.; Wang, J.; Wang, L. Stiffness and natural frequency of a 3-DOF parallel manipulator with consideration of additional leg candidates. Robot. Auton. Syst. 2013, 61, 868–875. [Google Scholar] [CrossRef]
- Yu, G.; Wang, L.; Wu, J.; Wang, D.; Hu, C. Stiffness modeling approach for a 3-DOF parallel manipulator with consideration of nonlinear joint stiffness. Mech. Mach. Theory 2018, 123, 137–152. [Google Scholar] [CrossRef]
- Wu, G. Stiffness analysis and optimization of a co-axial spherical parallel manipulator. Model. Identif. Control 2014, 35, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Tang, J.; Yan, C.; Cui, G.; Zhang, M.; Yao, Y.A. Stiffness analysis of a 3-DOF parallel mechanism for engineering special machining. Mech. Sci. 2022, 13, 635–645. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: London, UK, 2005; pp. 25–30. [Google Scholar]


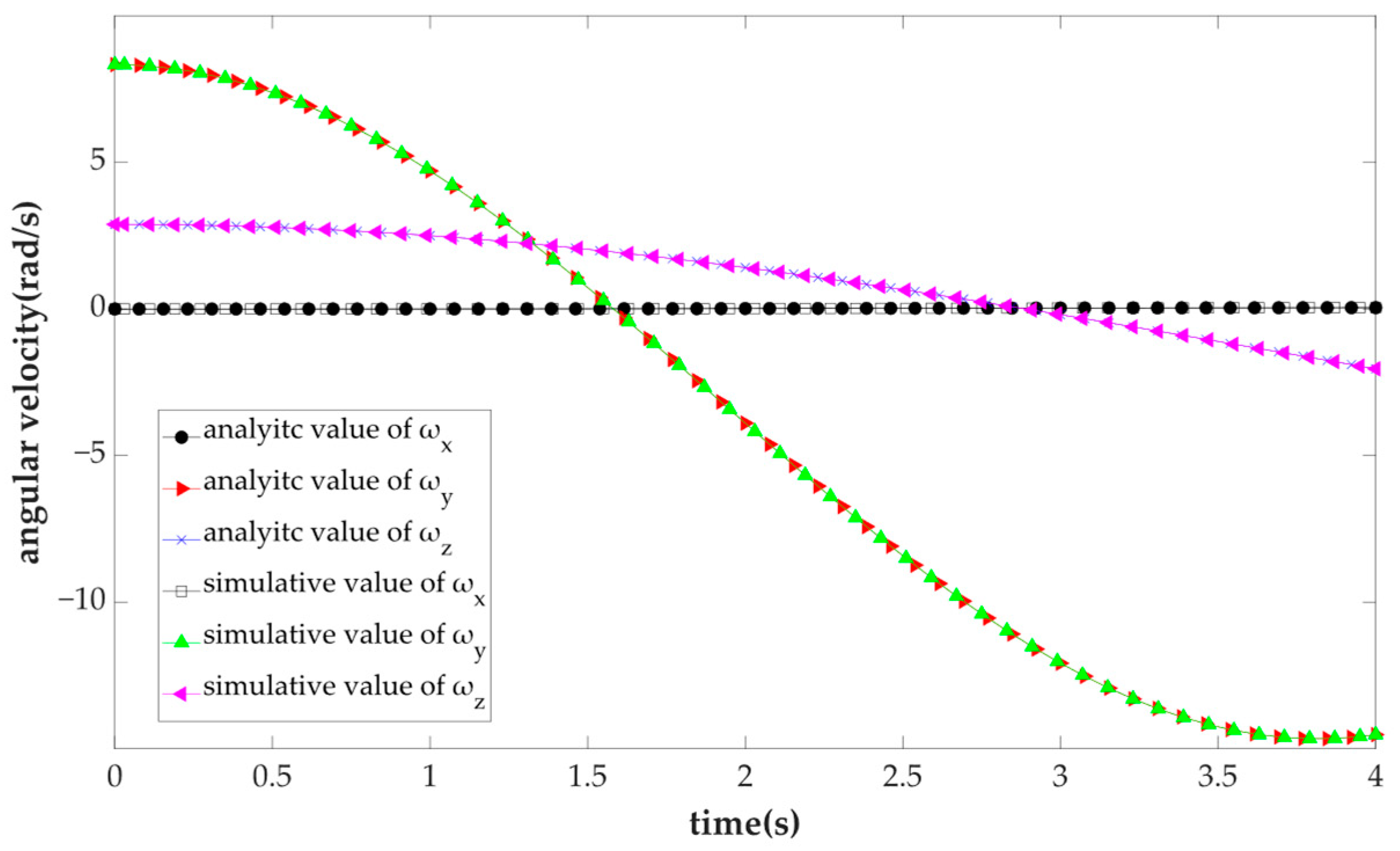
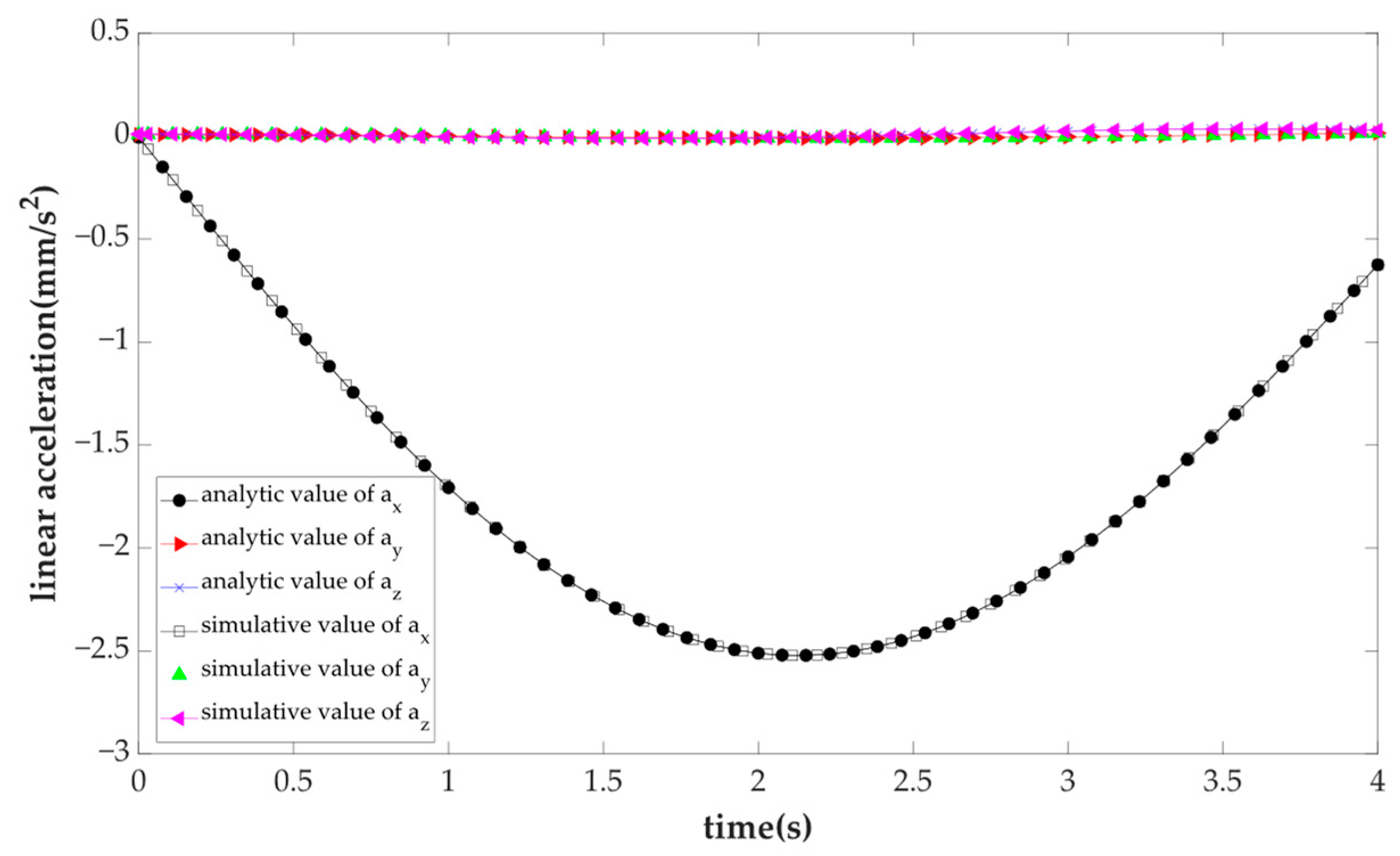
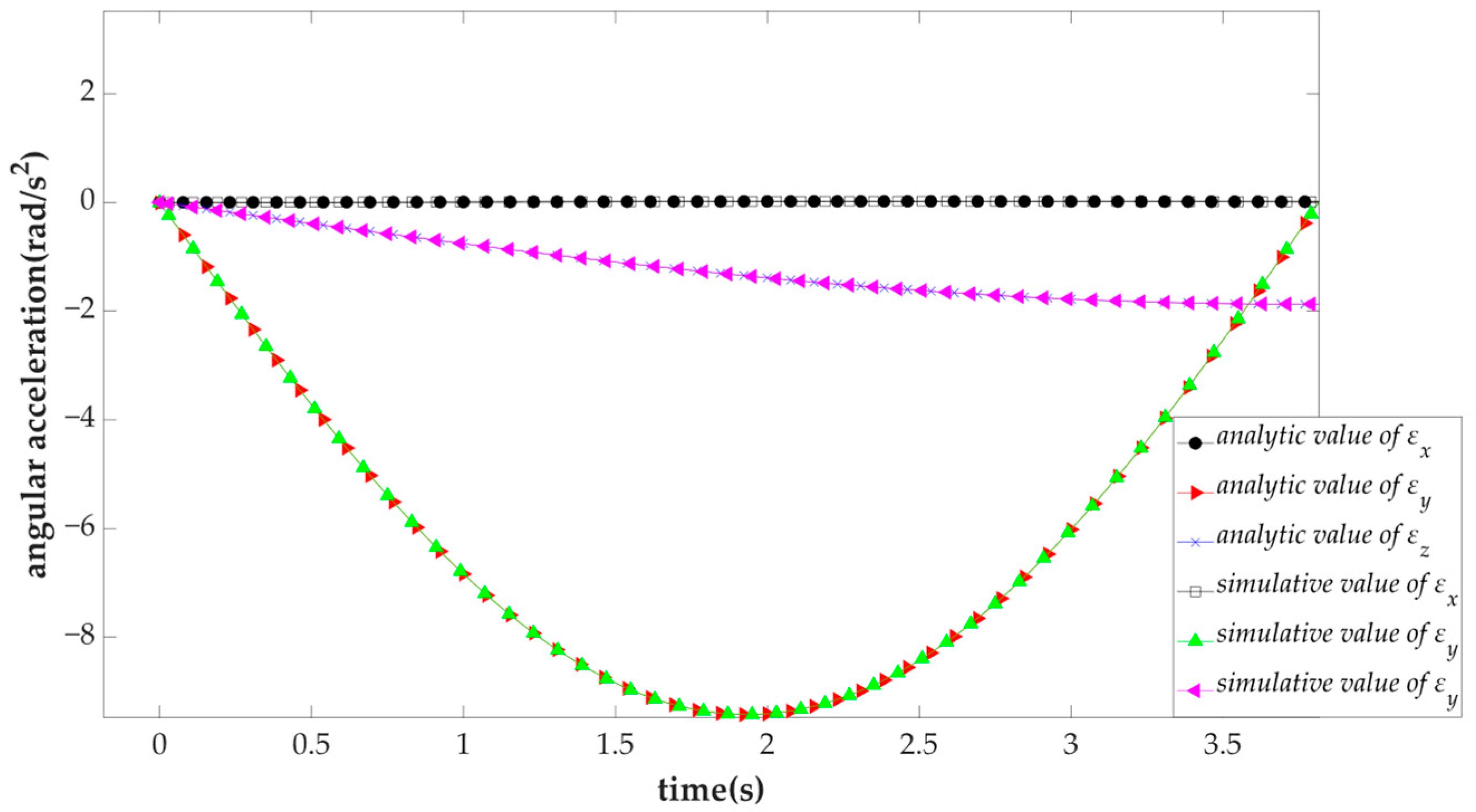
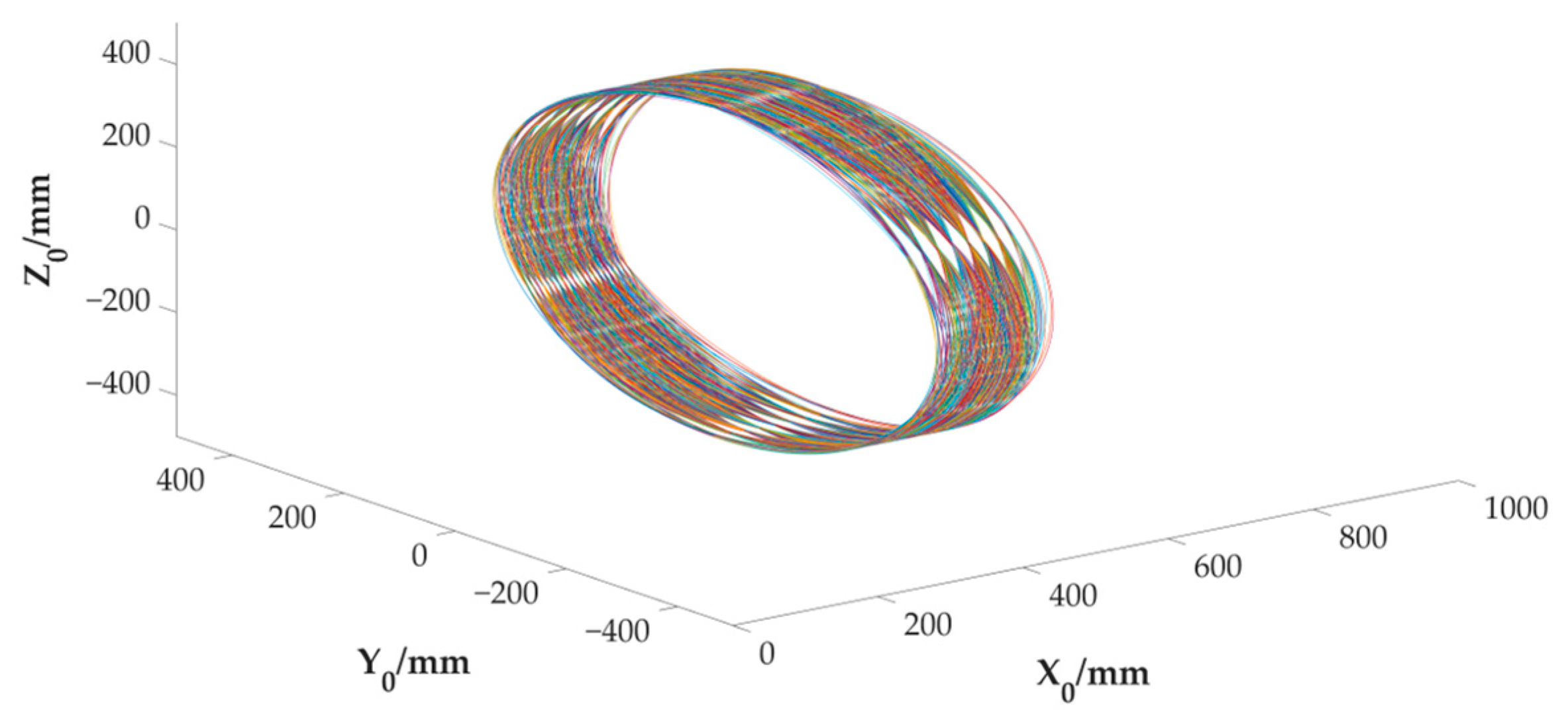


| (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|
| 470 | 400 | 300 | 350 |
| No. | Initial (mm) | Parameters | Analytic Value (mm) | Simulative Value (mm) | Parameters | Analytic Value (mm) | Simulative Value (mm) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 40 | 390.5 | 390.5 | 0.0002 | 0.0002 | |||
| 30 | 0.0373 | 0.0373 | 0.0254 | 0.0254 | ||||
| 20 | 0.0214 | 0.0294 | 0.0147 | 0.0147 | ||||
| 2 | 100 | 461.4046 | 461.1046 | 0 | 0 | |||
| 120 | 0.0005 | 0.0004 | 0 | 0 | ||||
| 80 | 0.1707 | 0.1951 | 0.0584 | 0.0584 | ||||
| Initial | Acceleration | ||||
|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm/ ) | (mm/ ) | (mm/ ) |
| 366.7424 | 366.7424 | 366.7424 | |||
| Kinematic | t = 1s | t = 2s | t = 3s | |||
|---|---|---|---|---|---|---|
| Parameters | Analytic | Simulative | Analytic | Simulative | Analytic | Simulative |
| 3.7683 | 3.835 | 1.5589 | 1.659 | −0.8208 | −0.7382 | |
| 0.0046 | 0.0047 | −0.0011 | −0.0008 | −0.0049 | −0.0096 | |
| 0.0040 | 0.0040 | −0.0055 | −0.0051 | 0.0012 | 0.0011 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.0047 | 0.0049 | −0.0039 | −0.0035 | −0.0121 | −0.0118 | |
| 0.0025 | 0.0025 | 0.0014 | 0.0014 | 0 | 0 | |
| −1.7067 | −1.593 | −2.5107 | −2.491 | −2.0427 | −2.214 | |
| 0 | 0 | 0 | 0 | −0.0040 | −0.0047 | |
| −0.0046 | −0.0039 | −0.0079 | −0.0083 | 0.0238 | 0.0230 | |
| 0 | 0 | 0 | 0 | 0 | 0 | |
| −0.0068 | −0.0064 | −0.0094 | −0.0094 | −0.0060 | −0.0064 | |
| 0 | 0.0001 | −0.0014 | −0.0013 | −0.0018 | −0.0018 | |
| (rad) | (rad) | |
|---|---|---|
| 400, 480, 560 | [−, ] | [−, ] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Gao, H.; Xu, C.; Jia, Z.; Lin, J.; Han, Q.; Luo, Z. Kinematic Modeling and Stiffness Analysis of a 3-DOF 3SPS + 3PRS Parallel Manipulator. Mathematics 2022, 10, 4465. https://doi.org/10.3390/math10234465
Zhou S, Gao H, Xu C, Jia Z, Lin J, Han Q, Luo Z. Kinematic Modeling and Stiffness Analysis of a 3-DOF 3SPS + 3PRS Parallel Manipulator. Mathematics. 2022; 10(23):4465. https://doi.org/10.3390/math10234465
Chicago/Turabian StyleZhou, Shenghao, Houkun Gao, Chunyang Xu, Zhichao Jia, Junzhe Lin, Qingkai Han, and Zhong Luo. 2022. "Kinematic Modeling and Stiffness Analysis of a 3-DOF 3SPS + 3PRS Parallel Manipulator" Mathematics 10, no. 23: 4465. https://doi.org/10.3390/math10234465
APA StyleZhou, S., Gao, H., Xu, C., Jia, Z., Lin, J., Han, Q., & Luo, Z. (2022). Kinematic Modeling and Stiffness Analysis of a 3-DOF 3SPS + 3PRS Parallel Manipulator. Mathematics, 10(23), 4465. https://doi.org/10.3390/math10234465





