Abstract
Trajectory prediction technology uses the trajectory data of historical ships to predict future ship trajectory, which has significant application value in the field of ship driving and ship management. With the popularization of Automatic Identification System (AIS) equipment in-stalled on ships, many ship trajectory data are collected and stored, providing a data basis for ship trajectory prediction. Currently, most of the ship trajectory prediction methods do not fully consider the influence of ship density in different sea areas, leading to a large difference in the prediction effect in different sea areas. This paper proposes a hybrid trajectory prediction model based on K-Nearest Neighbor (KNN) and Long Short-Term Memory (LSTM) methods. In this model, different methods are used to predict trajectory based on trajectory density. For offshore waters with a high density of trajectory, an optimized K-Nearest Neighbor algorithm is used for prediction. For open sea waters with low density of trajectory, the Long Short-Term Memory model is used for prediction. To further improve the prediction effect, the spatio-temporal characteristics of the trajectory are fully considered in the prediction process of the model. The experimental results for the dataset of historical data show that the mean square error of the proposed method is less than 2.92 × 10−9. Compared to the prediction methods based on the Kalman filter, the mean square error decreases by two orders of magnitude. Compared to the prediction methods based on recurrent neural network, the mean square error decreases by 82%. The advantage of the proposed model is that it can always obtain a better prediction result under different conditions of trajectory density available for different sea areas.
Keywords:
LSTM neural network; KNN; trajectory prediction; automatic recognition system; sea area division MSC:
68T01
1. Introduction
To help maritime supervisors track ships and ensure navigation safety, the Interna-tional Maritime Organization (IMO) requires that ships with a gross tonnage of more than 300, or ships with a cargo capacity of more than 500 gross tons and non-international voyage cargo ships to be equipped with automatic identification system (AIS) [1,2]. Meanwhile, with the increase of the AIS data scale and the continuous development of artificial intelligence technology in recent years [3,4], ships’ intelligence and behavioral autonomy have been significantly improved [5,6]. However, the level of intelligence of the existing AISs is far from meeting the maritime management requirements. The ship trajectory prediction is vital to the intelligence of an AIS, and the higher the accuracy of ship trajectory prediction using AIS data, the more sufficient the response space and time to avoid accidents of ship collision [7,8].
This paper focuses on the ship trajectory prediction problem. In the past, ship path prediction relied on mathematical models such as the one proposed by Sutulo [9], the structure of the generic maneuvering mathematical model leads naturally to two basic approaches based on dynamic and purely kinematic prediction models. An analytical scheme for the short-term kinematic prediction accounting for current values of accelerations is proposed. However, the mathematical model requires a large amount of input parameters, such as ship shape, current, wind direction, maneuvering, etc. It is difficult to obtain all the input parameters data needed. On the other hand, the inference-based trajectory prediction methods, such as Markov Chain [10], based on the hidden Markov model (HMM), a spatio-temporal predictor, and a next-place predictor are proposed. Living habits are analyzed in terms of entropy, upon which users are clustered into distinct groups. They are subjected to unbiased statistics, resulting in poor scalability. Recently, neural network technologies, such as Recurrent Neural Network (RNN) [11] and Long Short-Term Memory Networks [12], based on the route data, a prediction algorithm such as LSTM (Long Short-Term Memory) recurrent neural network used to realize the prediction of the ship’s navigation trajectory showed good performance in trajectory prediction in cases where sufficient samples are available. However, most of these techniques focus only on the optimization of the methods, the density of ships and the density of ship routes are not considered. According to the distribution of real-time ship trajectory data, not only there is a great difference in ship density between offshore areas with high vessel density and open sea with low ship density [13], the human factors also increased the complexity of the ship trajectory prediction, especially in offshore areas. The traditional machine learning algorithm can be used to predict the ship’s navigation trajectory. However, there are limitations in both accuracy and flexibility, as ship trajectory prediction is quite different in the offshore sea and open seas.
This paper proposed a new ship trajectory prediction method based on a neural network. The main innovation is to embed the optimized algorithm into the discriminant learning method, which combined the optimized KNN algorithm with neural network and LSTM neural network (Long Short-Term Memory network) to predict the ship trajectory in the open sea area when ship density is low. However, in offshore areas where ship density is high, current methods based on distance-trajectory similarity do not fully consider the speed characteristics of ship trajectories. Existing methods do not measure distance for the spherical characteristics of the nautical domain, resulting in less accurate measurement results, this paper used a new similarity distance formula in the KNN algorithm to predict ship tracks. As a result, the influence caused by different characteristics of trajectory data in trajectory prediction can be eliminated effectively.
The main contributions of this paper are as follows: (1) In view of the poor performance of the traditional KNN algorithm in low-density areas, the sea areas where the ships travel are divided according to the density of ships, and different trajectory prediction methods are adopted in sea areas with different vessel densities to avoid the influence of different trajectory data characteristics on prediction accuracy as far as possible. (2) The similarity distance formula in the traditional KNN algorithm is optimized to solve the problem that the effect of the KNN algorithm is not good because the Euclidean distance is not applicable to the similarity measurement between ship tracks, and further improves the prediction results in the sea area with large ship density. (3) The improved KNN algorithm and LSTM neural network are used to predict different ship density areas, respectively, to solve the problem of LSTM’s reduced prediction effect caused by insufficient data.
2. Related Works
The study of the transportation system model has been classical research content, and the method of big data analysis has the advantages of good experimental effect and portability compared with the transport system model, but it cannot make accurate estimation of the influence produced by the intervention of infrastructures and transport services [14]. This paper predicts the trajectory of ships sailing at sea, and the ships are rarely interfered with by infrastructure and traffic service during the long voyage, so the method of big data analysis is more suitable for the trajectory prediction of ships at sea. Moreover, for the ship trajectory prediction, the most commonly used prediction methods in previous literature predict the ship movement using historical trajectory information of the ship to predict the future ship trajectory accurately and efficiently. In the discussion of related works, the mainstream of the existing work was classified, according to the implementation mechanism of ship trajectory prediction methods into three categories: methods based on the physical (mathematical) models, methods based on the learning models, and methods using a mixture of multiple models.
2.1. Methods Based on the Physical (Mathematical) Models
This kind of method attempts to explicitly consider all influencing factors in the modeling process. Abdelaal et al. [15] took impact force and yaw moment into consideration to build a prediction model and applied it to the anti-collision system. However, the use scenarios are limited since detailed ship information is required by this method. Vijverberg et al. [16] used a linear extrapolation model to predict the future position of the ships. This method did not consider environmental factors, which affect the prediction accuracy. Zhang et al. [17] used pneumatic parameters to design a set of maneuvering modes using aerodynamic parameters, and realized trajectory prediction using Markov chain Monte Carlo and Bayesian decision theory. Compared with the traditional extrapolation theory, the accuracy was higher, but it needed more comprehensive maneuvering modes, which were difficult to obtain in reality. Virjonen et al. [18] used the KNN algorithm to predict ship trajectories, and the performance of the method as well as the hyperparameters of the proposed model was optimized using a nested leave-one-out crossvalidation approach. Based on the traditional Kalman filter theory, Liang et al. [19] constructs a polynomial Kalman filter to fit a non-linear system and predict the ship’s trajectory based on latitude and longitude information. The results show that the method is simple to implement and converges quickly, and can effectively solve the problem of predicting ship trajectories in practical processes, meeting basic timeliness and accuracy. Xie et al. [20] proposed a short-term trajectory prediction method based on a movement model and a long-distance trajectory prediction method based on maneuvering intention, and applied two interacting multiple models for trajectory prediction. The dynamic model prediction in this method achieves better real-time performance, but it needed to establish a more accurate dynamic model for the target, and this is difficult to achieve in real situations. Therefore, this method often leads to serious prediction errors.
2.2. Methods Based on the Machine Learning Model
The ship movement is often modeled using a learning model in this type of method, which learns the movement characteristics from the historical movement data to implicitly integrate all possible influencing factors. According to the existing research results in this field, Burger et al. [21] compared DKF (Discrete Kalman Filter) and LRM (Linear Regression Model) under the learning model based on statistics. When these two methods were used to predict linear trajectories, DKF was much higher than LRM in parameter complexity, but the results showed no significant improvement in performance. Moreover, the error distribution of DKF was more dispersed than that of LRM, which was unfavorable for the observation of outliers. Hexeberg et al. [22] proposed a data-driven Single Point Neighbor Search (SPNS) method based on AIS ship trajectory prediction. This method recursively used historical AIS data to predict the next position and time near the predicted location, but the time accuracy of this algorithm was within 30 min, and it could not deal with the sea branch conditions. In addition, for the model based on machine learning, Liu et al. proposed an online multiple outputs Least Squares Support Vector Machine (LS-SVM) based on a selection mechanism. The LS-SVM model [23] was used for ship trajectory prediction. Murray et al. [24] evaluated a data-driven method, which used historical data to predict ship track within the time range of 5–30 min, and proposed a single point neighbor search based on clustering. The method of trajectory extraction was used to evaluate the predicted ship route. The disadvantage is that the speed is constant, which reduces the result of prediction iteration. Bao [25] proposes a high-precision ship track prediction model based on a combination of a multi-head attention mechanism, and bidirectional gate recurrent unit (MHA-BiGRU). Last et al. [26] proposed a new method for ship movement prediction based on movement data. By compressing AIS data, a background trajectory model was proposed, but it can only predict local clustering for a given region. Volkova [27] uses a neural network of the previous coordinates of the vessel’s trajectory to predict the estimated next coordinates of the vessel during river navigation. Wang et al. [28] proposed a sequence-to-sequence Deep Long Short-Term Memory network (SS-DLSTM) for trajectory prediction, which increased the prediction accuracy and robustness. However, it was only applied to the Terminal Airspace. The trajectories in Terminal Airspace were relatively stable. In the case of complex trajectories, the prediction accuracy would be greatly reduced. Han et al. [29] used a gated recurrent unit (GRU) to predict flight trajectory, selected the optimal GRU network by comparing the number of network layers and neuron number, and compared it with the BP network. The prediction error was reduced, but it needed too much data in the offline training process. Liu et al. [30] proposed an end-to-end Convolutional Neural Network (CNN) to predict the trajectory, which used an encoder to encode flight information as a hidden state variable and a decoder to learn the temporal and spatial relevance of historical tracks. However, when the trajectory changed dramatically, the prediction error will grow large. The above research showed that the machine learning methods are easy to implement and can achieve high accuracy in the case of sufficient data, but the training process requires too much data and have strong data dependence.
2.3. Methods Based on the Hybrid Model
The main goal of a hybrid model approach is to combine the advantages of its constituent models, which either explicitly consider some of the influencing factors and train with historical movement data, or combine different learning methods to form a model to achieve better performance. Lin et al. [31] proposed a prediction method in which the Hidden Markov Model (HMM) was used to model the flight movement trend based on the historical trajectory and the Gaussian Mixture Model was used to predict the aircraft speed vector, but the prediction error was large in the case of high-speed maneuvering. Yang et al. [32] proposed a high-precision trajectory prediction model under multi-dimensional factors. In this algorithm, the Douglas–Peucker algorithm is used to compress track data, the DBSCAN algorithm is used to perform track clustering, and trajectory is predicted by LRCN (Long-term Recurrent Convolutional Networks) prediction model. Wang et al. [33] proposed a gray dynamic filtering method for trajectory prediction. Compared with the traditional KALMAN FILTER and the original gray method, the prediction accuracy was greatly improved. However, it used Minimum Variance Estimation to replace the actual value and introduced differential equations, therefore parameters could not be accurately estimated. Inaccurate parameters would reduce the accuracy of prediction. Qiao et al. [34] proposed a trajectory prediction method based on the Hidden Markov Model (HMM), in which adaptive parameters were added to the Hidden Markov process to improve the prediction efficiency and the trajectory prediction length could be adjusted adaptively, but the prediction accuracy must be enhanced. Ma et al. [35] designed an integrated model for the simultaneous prediction of multiple trajectories using the proposed features and employed the Long Short-Term Memory-based neural network and Recurrent Neural Network to pursue this time series task. Wang X et al. [36] designed a trajectory prediction framework on the spark platform based on the second-order Hidden Markov Model. Compared with the hidden Markov model, the robustness of the algorithm was higher, but the prediction accuracy of the algorithm needed to be improved. The above methods showed that the hybrid theory method is widely applied, but the algorithm is too complex, and the prediction accuracy and real-time prediction performance are not outstanding.
Through the study of relevant literature, it can be seen that AIS data are very important for ship trajectory prediction results. However, the density of ships in the offshore and far-sea areas is very different. The density of ships in offshore waters is high, and the trajectories of ships are easily affected by other ships or human influences. The density of ships in the open seas is relatively low, the ship trajectories are mostly single-vessel trajectories, and are less influenced by the trajectory data of other ships around. At the same time, the trajectory of the ship to be predicted cannot be filled with the future trajectory of the surrounding similar ships, Therefore, it is necessary to adopt different targeted trajectory prediction methods for sea areas with different ship densities. This paper proposes a new prediction method based on neural network. Its core idea is to embed the optimization algorithm into the discriminant learning method, analyze the characteristics of data existing in different ship density regions, and adopt targeted prediction methods for different ship density regions.
3. The Proposed Method
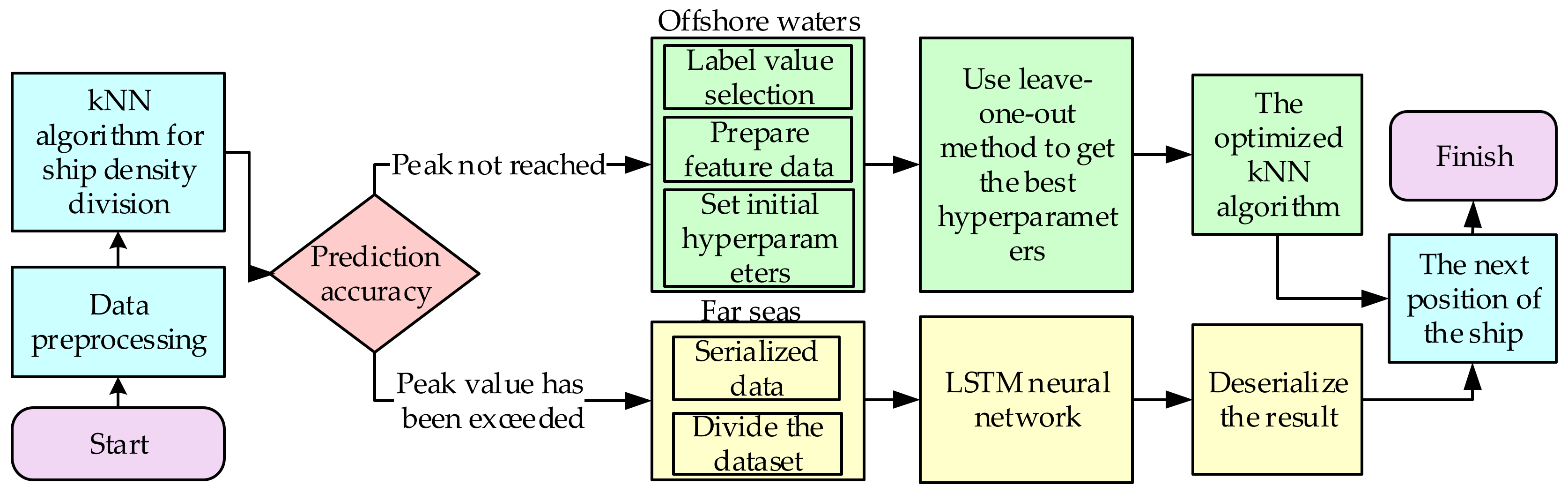
The model’s architecture in this paper is divided into two layers according to various ship densities, ship trajectory prediction in the offshore area, and ship trajectory prediction in the open sea area. From the observations of the offshore area, the data on single ships are small in size, but the overall number of ships is high. Furthermore, the ships influence each other in their trajectories. Thus, the classification method can be used for this prediction. When the ship enters the open sea, due to the change in the density of ships in the sea and the density of routes, the previous forecasting methods can no longer achieve the desired results all the time. Therefore, a new trajectory prediction method is proposed.
The overall structure of the model in this paper is shown in Figure 1. The first step is to preprocess AIS data to remove null values inside, and divide the data according to the sea areas [37]. Then, the optimized KNN algorithm is used to separate sea areas into offshore sea areas, and distant sea area by ship density, the details of the sea area division are described in Section 3.2. After selecting the label and characteristic data, the final optimal hyperparameters are obtained by the retention method. The KNN algorithms obtain the classification of ships, the KNN algorithm is described in detail in Section 3.2. For far seas, it is necessary to serialize the preprocessed data and divide the dataset first, before training and predicting the LSTM neural network. The LSTM neural network is described in detail in Section 3.3.
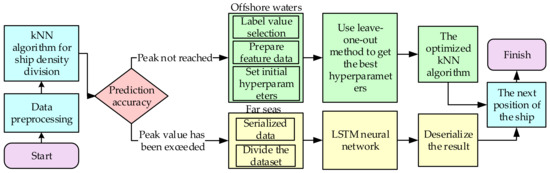
Figure 1.
The ship trajectory prediction method flow chart.
3.1. Trajectory Prediction Method for the Offshore Areas
Due to the high concentration of ships in an offshore area, the classification approach is to classify ships using their characteristics, predicting the ship’s following positions according to the ships’ positions of the same type. While the traditional KNN algorithm is to classify the trajectory points of the ship, this paper uses the KNN algorithm to classify the characteristics of ships, which can reduce the influence of other factors on the ship’s navigation trajectory.
The main idea of the KNN algorithm is that if most K closest samples in the feature space belong to a certain category, the samples also belong to that category, and have the same characteristics as samples in this category [38,39,40]. The KNN method mainly depends on the surrounding limited adjacent samples to determine the category, rather than the method of discriminating the class domain. Therefore, the KNN method is more suitable than the other methods for classifying sample sets with overlapping class domains.
The KNN algorithm that predicts the ship trajectory uses Euclidean distance as sim-ilarity distance and classification standard. However, many features were included dur-ing the classification of ship trajectory, such as latitude and longitude, velocity to earth, etc. Since the calculation of the ship distance is not the calculation of the straight-line distance on the plane, but the calculation of the spherical distance, the calculation of the Euclidean distance is prone to overfitting, so Euclidean distance, Frechet distance, Manhattan distance, etc., are no longer applicable. Therefore, the similarity distance in the KNN algorithm needs to be optimized, the relationships between ship position and speed are integrated, and the dynamic weights are allocated, so that the optimized KNN algorithm can be better applied to the ship trajectory classification.
Based on the above ideas, the KNN algorithm is obtained and the input training data set is given as the Formula (1).
The instance eigenvector of n dimension as the Formula (2).
This formula is the category of instances, where i = 1, 2, 3 … n, prediction instance x.
Output category Y to which prediction instance X belongs.
Distance equation: The Euclidean distance adopted by the KNN algorithm cannot measure the similarity between ship tracks and the actual movement of ships, its earth-moving velocity has a great influence on ship tracks, and Euclidean distance does not involve this factor.
The distance measurement adopted in this paper is as the Formula (3)
In Formula (3), a is the weight value. In the new similarity distance, a is used as the hyperparameter value and the new similarity distance uses the idea of weighted voting, so a more reasonable weight value can lead to better prediction results.
Assume that the latitude of point A is lat1, and the longitude is lon1. The latitude of point B is lat2, the longitude is lon2, and the radius of the Earth is R. Before finding this angle, first convert the coordinates to a point in the Cartesian space coordinate system, and let the center of the Earth be the coordinate center point, The coordinates of points A and B after the transformation are shown in Formulas (4) and (5).
Then, calculate the angle and use the vector angle calculation method to find the cosine value of the angle, let A be (x1,y1,z1), B (x2,y2,z2), and the formula is as the Formula (6).
Substitute the latitude and longitude coordinates as the Formula (7)
Let be the actual distance between two ships, and further find the arc length (distance between ships), the formula is as the Formulas (8) and (9).
the specific calculation formula is as the Formula (10).
Let be the difference in ground speed between two ships, which is computed as the Formula (11).
The parameter description is shown in Table 1.

Table 1.
Information of KNN algorithm parameters.
The steps of the method to predict the ship trajectory based on the KNN algorithm are as follows.
Step 1: prepare and preprocess data;
Step 2: calculate the similarity distance between the test sample point and every other sample point;
Step 3: sort all distances and select k points with the smallest similarity distance;
Step 4: compare the categories in which K track points belong, and classify the test sample points into the category with the highest proportion among k points according to classification decision rules;
Step 5: replace the next position of the ship to be predicted with the track point of a similar ship;
3.2. Division of the Sea Areas
In a traditional trajectory prediction model, for the coastal area with a high density of ships, the trajectory of one ship is affected by other ships. For example, the mutual blocking and collision avoidance between ships will affect the trajectory of the ship’s navigation. Therefore, the trajectory prediction error can be large if only the ship is considered. Furthermore, in offshore waters, the initial amount of ship data (such as latitude and longitude information, etc.) may also be insufficient to support the training part of the neural network model. Therefore, in offshore waters, using the LSTM neural network method for prediction may not achieve good results.
Due to the limitation of the number of relevant samples in the classification, the prediction accuracy will decrease as the ship density decreases. In addition, the ship track with low ship density is less affected by other ships. In open sea area with low ship density, the continuous use of the offshore area trajectory prediction method for ship track domain measurement will lead to poor classification effects. Therefore, according to the density of ship distribution, the method in this paper needs to choose the KNN algorithm to predict the peak time as the point at which the sea borders ship prior to this point in time, defined as the offshore waters, is optimized by KNN algorithm.
The steps of the method to predict the ship trajectory based on the KNN algorithm are as follows.
Step 1: Prepare and preprocess data;
Step 2: Select the trajectory data of the ship sailing from offshore to offshore in the experimental data set, and get the trajectory data of the surrounding ships in different time intervals corresponding to the trajectory.
Step 3: Experiment with the data of different time intervals obtained in the first step separately using the KNN algorithm, and optimize them using the leave-one-out method, and finally obtain the classification accuracy.
Step 4: analyze the results obtained in the second step and select the peak point of KNN classification accuracy as the dividing point of offshore and distant sea areas.
According to the actual environment and ship type factors in the offshore area, the reference data of a single ship is rich, which is suitable for trajectory prediction based on the machine learning classification method. For a ship in the open sea, its track can be regarded as the single ship track in the region. There is little that can be predicted on the influences among the trajectories of other ships, As the other ships have little influence on the predicted ship’s trajectory, the accuracy of the trajectory prediction method in the offshore area decreases. Moreover, the amount of track data of a single ship in the open sea is large, and the fluctuation of the ship’s track is small. Thus, it is suitable for adopting deep learning methods to predict the position based on historical track data.
3.3. Trajectory Prediction Method for the Open Sea Area
It can be regarded that the track of a ship in the open sea will not be affected by the track of other ships. The neural network method can implicitly consider the weather and sea area influence factors of the ship track in the open sea area. On the other hand, the ship track strongly correlates with time.
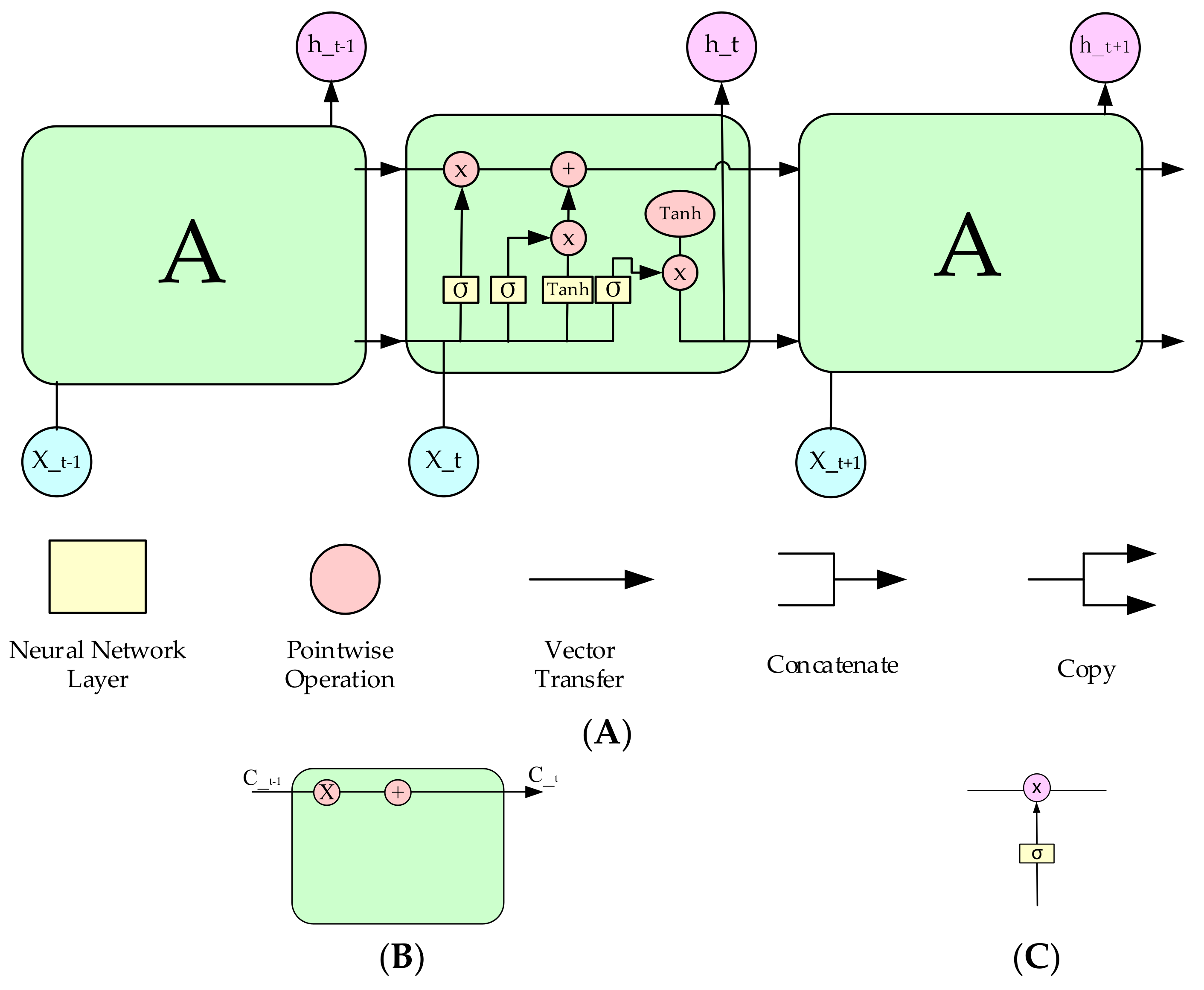
LSTM is usually suitable for dealing with issues sensitive to time series [41]. LSTM can learn long-term dependence and has the form of a repeat module chain of a neural network, but it has a different structure in Recurrent Neural Network from other neural networks [42,43]. LSTM has a four-layer structure in which the layers uniquely interact with each other, and its selective memory-forget mechanism design makes it a powerful tool for sequence generation and prediction [44]. As shown in Figure 2, the key to LSTM is the cell state, the line running horizontally through the top of Figure 2B represents the cell state.
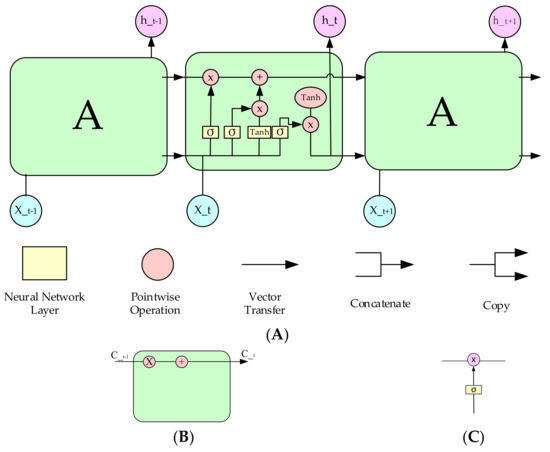
Figure 2.
LSTM neural network structure diagram. (A) Repeated modules in LSTM contain four layers of interactive neural network. (B) Cell status. (C) Repeated modules in LSTM contain four layers.
The LSTM can delete and add information to the cell state, which is enabled by a structure called a gate. As shown in Figure 2C, a gate is an optional way to let information through. It consists of a sigmoid neural network layer and a dot multiplication operation.
The ship trajectory prediction method for the open sea area based on LSTM performs the following steps.
Step 1: determine what information should be discarded from the cell state, which is implemented by the Sigmoid layer called “forget gate” (). It looks at (the previous output) and (the current input), and outputs the number between 0 and 1 for each number in the cell state Ct−1 (the previous state) as Formula (12). Here, 1 represents complete retention and 0 represents complete deletion.
where .
Step 2: decide what information is to be stored in the cell state. The Sigmoid layer, called the Input Gate layer , determines which values will be updated. The TANH layer then creates candidate vector Ct, which will be added to the state of the cell as the Formulas (13) and (14).
where .
Step 3: update the previous state value, Ct−1, and update it to Ct. Multiply the previous state value to express the part expected to be forgotten. All these values are then added to to create new candidate values as the Formula (15).
Step 4: run a Sigmoid layer that determines which parts of the cell state to output. The cell state is then passed through tanh (normalizing the value to between −1 and 1) and multiplied by the output of the Sigmoid gate as the Formula (16).
where .
The tunable elements of the LSTM model can be divided into two broad categories, parameters, and hyperparameters. Although parameters are model elements learned directly from training data, there is no available analysis formula to calculate appropriate values, therefore, it is not possible to estimate the hyperparameters directly from training data, and they are usually specified manually based on heuristic methods [45].
The main hyperparameters that affect the performance of neural networks are the number of hidden layer layers, the number of nodes in each layer, the Activation Function in each layer, the Batch size, and the Dropout rate in each layer. Dropout rates apply to deep artificial neural networks by randomly deleting nodes (and their connections) from nodes to reduce model over-fitting during training. Dropout rates control for the likelihood of such a random effect occurring at each node.
These layers control the depth of the neural network. Increasing the depth of the network will increase its ability to learn features at different levels of abstraction. Excessive increasing depth will lead to over-fitting of the model. The number of nodes in each layer controls its width. Increasing the width will increase its memory capacity, and if the propagation depth is excessively increased, the gradient amplitude will be sharply reduced, which will lead to slow weight update of shallow neurons, and result in gradient dispersion.
Given a neural network with input layer X, a hidden layer of with M nodes and a regressor of the output layer composed of a single node, the form of each node is as the Formulas (17) and (18).
where Z = (Z1, Z2......, Zm), σ(*) is the activation function, and g(*) is the optional output function. The sigmoID, TANH, or Relu functions are the main activation functions.
The batch size specifies the number of training instances entered into the model before updating the model parameters. Larger batches reduce the computational cost required, which may result in local optimality.
To sum up, when it comes to the trajectory prediction of ships in the open sea, it is necessary to preprocess the trajectory data of ships first, screen the data sensitive to time series as characteristic values, then convert these characteristic values into time series, and train the model by adjusting the hyperparameters of the neural network. The prediction of ship trajectory can then be realized after the training.
3.3.1. Parameter Settings
Hyperparameter selection of KNN algorithm: the value of weight a is 0.7, 0.8, 0.9, and the value range of k is [11,24], parameters are mainly used for tuning hyperparameters using grid search methods, parameter settings are shown in Table 2.

Table 2.
Information of KNN parameters.
LSTM network parameters are set as follows: the neural network layer is set to 3 layers, the LSTM network width of layer 1 is set to 64, the Dropout rate is set to 0.3, and the activation function is set to ReLU. The LSTM network width of layer 2 is set to 128, the Dropout rate is set to 0.3, and the activation function is set to ReLU. The width of the output gate is set to 2, the activation function is set to ReLU, the Optimizer of the neural network is set to Adam, and the number of samples contained in each batch in gradient Descent is 64. The epoch value of training model iteration times was 100 when training terminated. The structure of the LSTM neural network is shown in Table 3.

Table 3.
Information of neural network parameters.
3.3.2. Evaluation Criteria
In this paper, three evaluation criteria are used to evaluate the effect of the method on ship trajectory prediction: accuracy, mean square error, and coefficient of determination. Accuracy ACC refers to the degree to which the average value measured several times is consistent with the actual value under certain experimental conditions. It is expressed by error and used to indicate the size of systematic error.
Mean-square error (MSE) can be used to evaluate the degree of data change. The smaller the MSE value is, the better accuracy the prediction model has in describing experimental data. The real value-predicted value is adopted, and then the square is followed by the sum and average. The calculation formula is as the Formula (19).
The R2 coefficient, also known as the coefficient of determination, measures the overall fitting degree of the regression equation and expresses the overall relationship between the dependent variable and all independent variables. The closer R2_score is to 1, the better the regression fitting effect is. Its calculation formula is as the Formula (20).
4. Experiment and Verification
4.1. Preparation for Experiment
4.1.1. Dataset
In the sea area division experiment, the data used in this experiment are from the AIS data of the sea area near Xiamen Port, Fujian Province, China [46], The dataset covers the period from 1 January 2018, to 3 January 2019, The latitude range covered by the dataset is 24.16° N to 24.61° N, and the longitude range covered by the dataset is 117.84° E to 118.63° E. The data used in the experiments are parsed AIS data and do not require the use of a GIS tool.
The data used in this experiment is a random sample of 30 ships in the dataset and divided into 8 time periods. The 30 ships contain a total of 2,915,683 trajectory data. A total of 200 track points were selected for each ship in each time period, and a total of 48,000 data samples were used for the KNN algorithm experiment. The time span was from 12:52:54 on 25 November 2018, to 14:40:25 on 21 December 2018. The latitude and longitude were selected from 118.02–118.15° and 24.33–24.5°.
In the experiment of trajectory prediction in offshore waters, 30 ships near Xiamen port were randomly selected with their corresponding 200 trajectory point data, and a total of 6000 pieces of data samples were selected for the KNN algorithm experiment. The time span was from 11:46:46 on 21 December 2018, to 12:05:54 on 21 December 2018. Its latitude and longitude were 118° ± 1° and 24° ± 1°, respectively.
In the open sea area trajectory prediction experiment, the track data of a ship near Xiamen port were selected, and the MMSI value of the ship was 41,369 ****, a total of 9571 data samples were used for the experiment. The time span was from 11:46 min 41 s on 21 December 2018 to 7:30 min 22 s on 3 January 2019, with latitude and longitude of 118.06–118.07° and 24.483–24.484°.
The data fields are shown as in Table 4.

Table 4.
Data field description.
4.1.2. Experimental Environment
The experimental hardware environment in this paper is Intel(R) Core(TM) i7-8700 octa-core CPU (3.20 GHz), 8 GB RAM; the software experimental environment is Windows10 (Microsoft, Redmond, Washington, DC, USA), Pycharm2020 (JetBrains, Prague, Czech Republic), Python3.8, Scikit-learn 0.20 and TensorFlow2.0.
4.2. Sea Area Division Experiment
Aiming at the problem of how to divide sea areas, the AIS data in different time stamps (Unix Timestamp) were used for the experimental test of the optimized KNN algorithm. The experimental results showed that the Timestamp of 1,545,371,999 (Unix Timestamp) should be selected for the threshold of division between offshore sea area and open sea area. The data of ships with a time stamp less than 1,545,371,999 is regarded as data in the offshore sea, and data of ships with a timestamp greater than 1,545,371,999 is regarded as data in the open sea. According to the nuclear density graph, the density of ships decreases with the increase of time stamps.
The Unix timestamp, which was defined as the total number of seconds from 00:00:00, 01, 01, 1970 GMT to the present, was added to the original AIS data, and the timestamp node was selected to conduct an experiment every 200 data pieces.
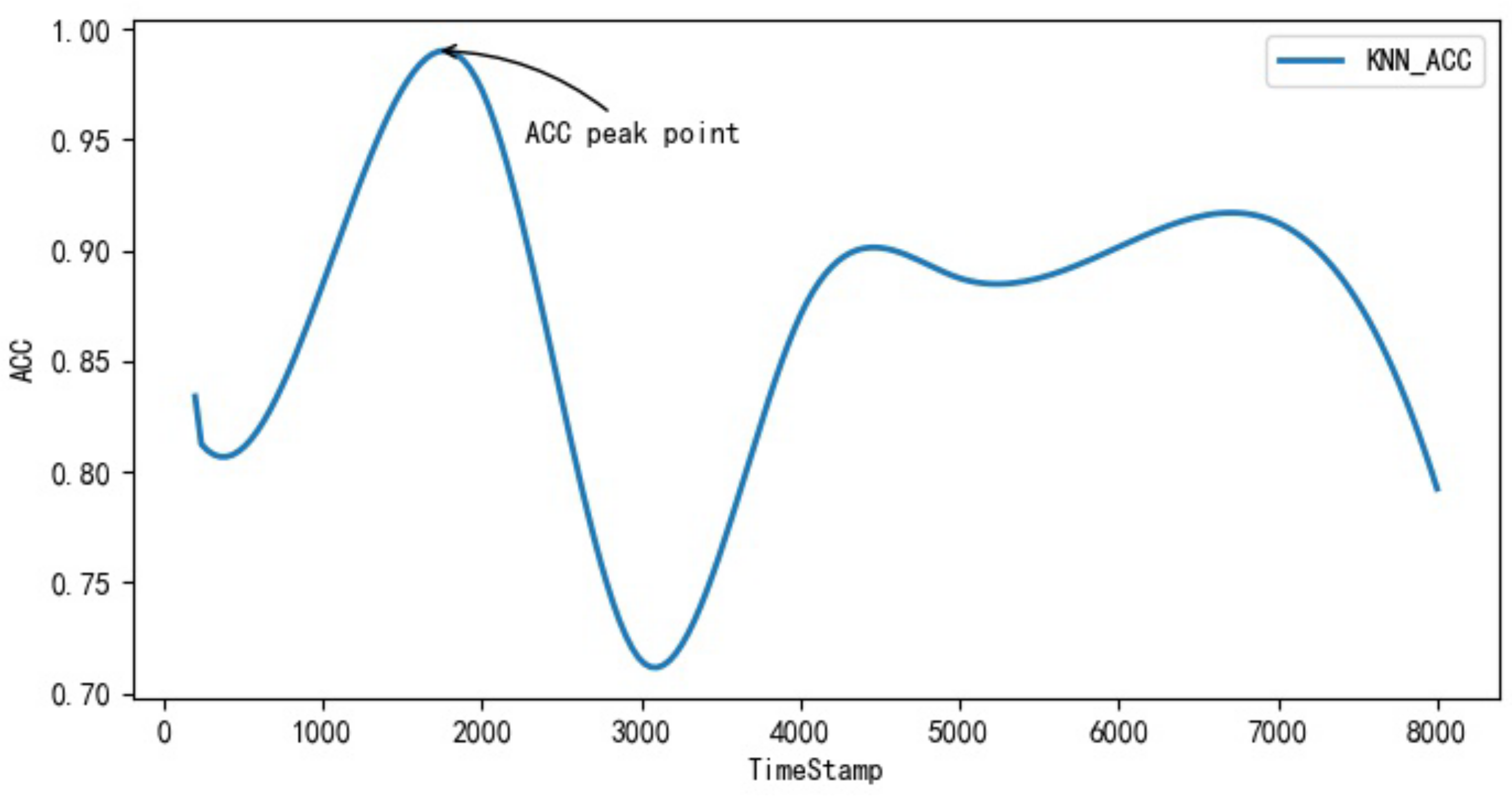
Experimental results show that when the optimized KNN algorithm is used for ship trajectory prediction, the timestamp reaches 154,537,199 (Unix timestamp), and the prediction accuracy of the KNN algorithm reaches the peak of 99.1%, after which, the accuracy of the KNN algorithm in trajectory prediction begins to decline. Experimental results are shown in Figure 3.
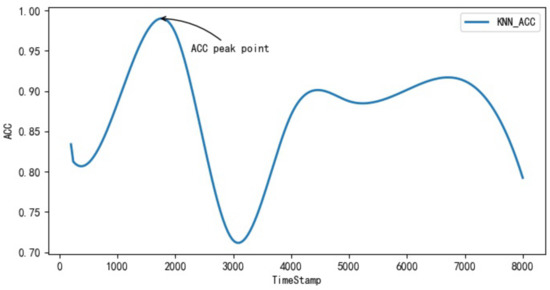
Figure 3.
KNN_ACC prediction accuracy diagram.
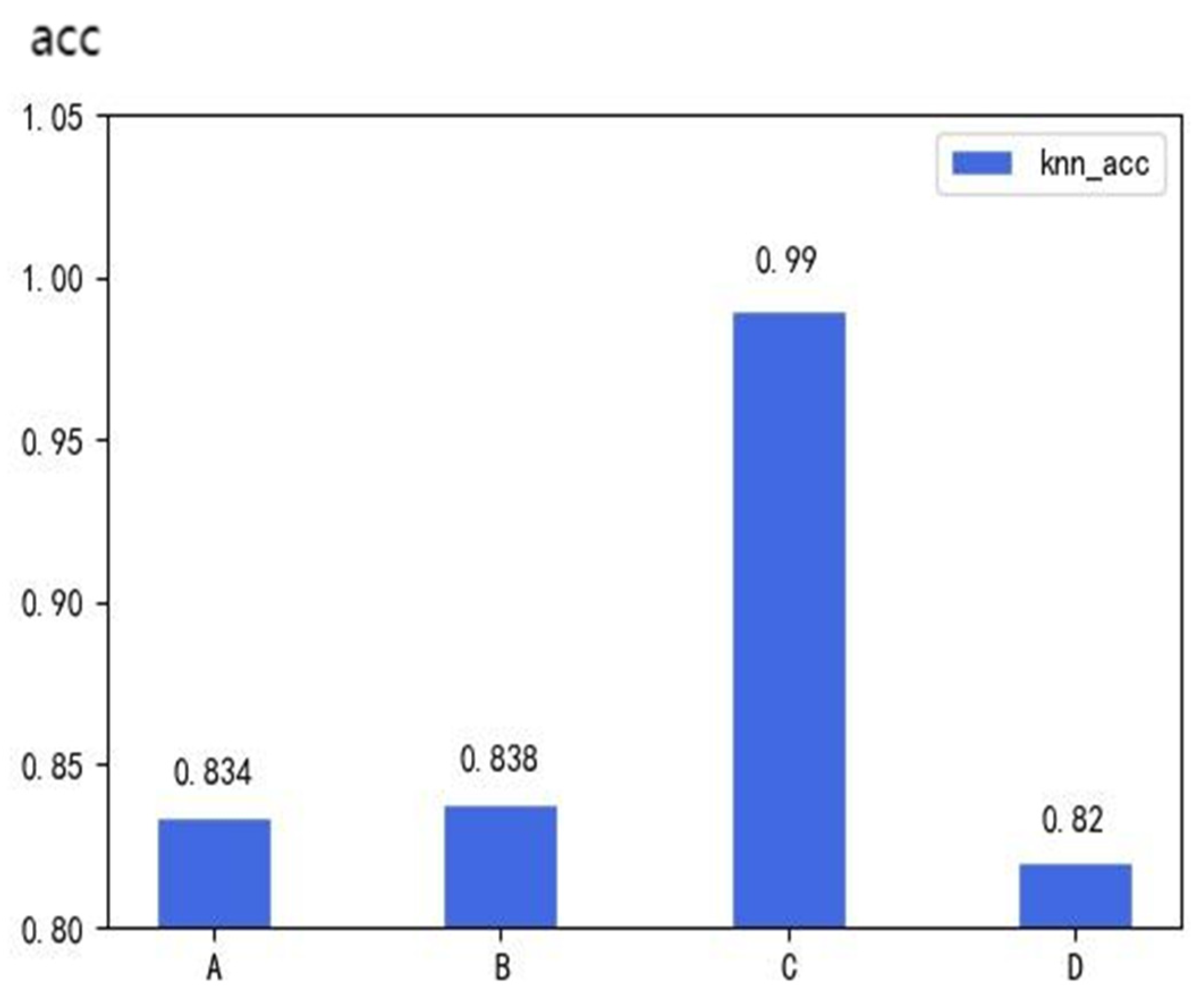
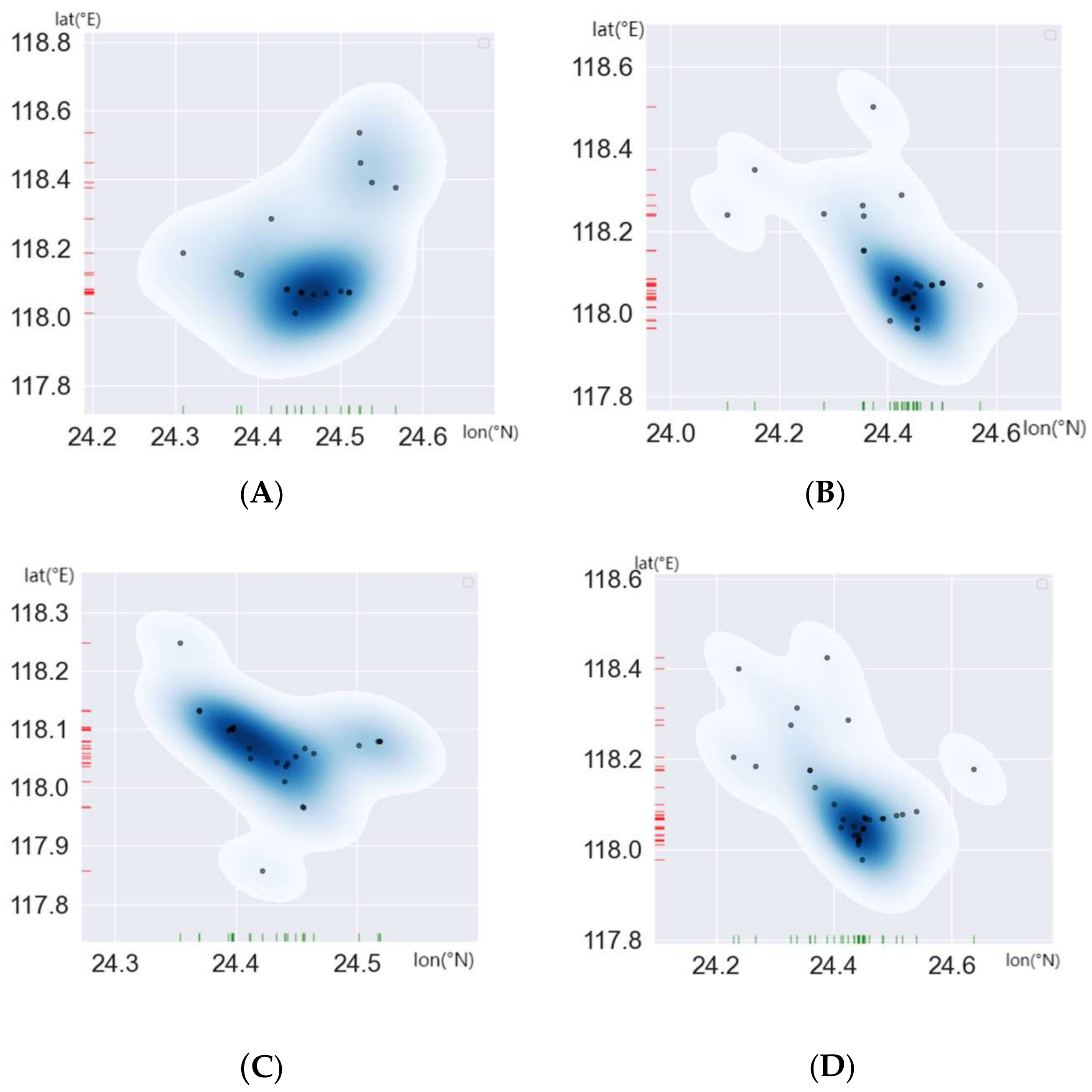
Shown in Figure 4 and Figure 5 A–D are the four moments during the voyage of the ship, the Maritime Mobile Service Identify (MMSI) number of the ship is 15,453 ****, Figure 4 shows the prediction accuracy of the KNN algorithm at four different times, The horizontal and vertical coordinates in Figure 5 represent the latitude and longitude, and the change in color depth represents the change in the density of ships. The darker the color in Figure 5, the higher the density of the ships. As can be seen from Figure 4 and Figure 5, as the ship density increases, the prediction accuracy of the KNN algorithm also increases, both the prediction accuracy and the ship density peaked at time c, but as the ship density decreases, the accuracy of the KNN algorithm’s prediction also decreases.
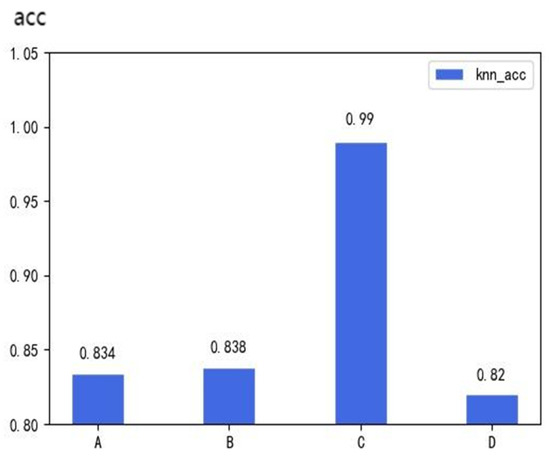
Figure 4.
The prediction accuracy of KNN in each density diagram.
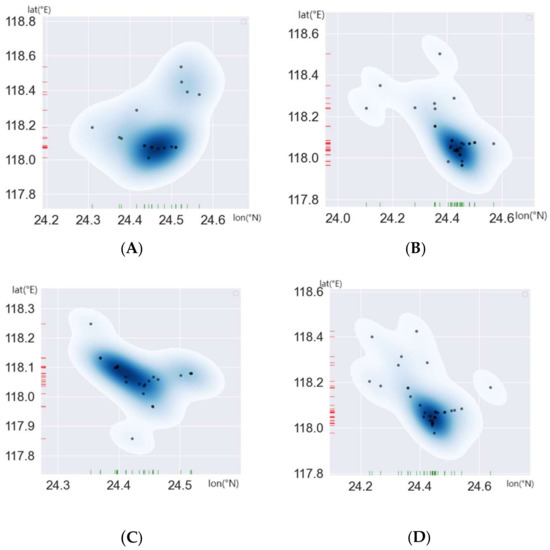
Figure 5.
The ship density distribution diagram. (A) Schematic of ship density at moment A, (B) Schematic of ship density at moment B, (C) Schematic of ship density at moment C, (D) Schematic of ship density at moment D.
4.3. Trajectory Prediction in the Offshore Sea
4.3.1. Experiment Content and Results
Due to the small amount of trajectory data of a single ship in the offshore area, there is insufficient training data for neural network training. The KNN algorithm is used to classify ship trajectories, and ship trajectories belonging to the same class are regarded as the same trajectory. That is, according to the trajectory data within a certain time interval, the longitude and latitude values of ships of the same category at the next moment are regarded as the ones of ships to be predicted.
After optimizing the similarity distance formula of the KNN algorithm, adding longitude and latitude and ground speed (SOG) as parameters, and setting weights as hyperparameters, AIS data were allocated into training sets and test sets in a ratio of 8:2 for the experiments. The Leave-One-Out (LOO) method was used to obtain the best hyperparameter values. The optimal hyperparameter is substituted into the KNN algorithm to verify its classification results.
The first 10 predicted results (MMSI values) are shown as examples: [‘41,369 ****’, ‘41,245 ****’, ‘41,370 ****’, ‘41,275 ****’, ‘41,370 ****’, ‘22,180 ****’, ‘41,275 ****’, ‘41,233 ****’, ‘41,370 ****’, ‘11,133 ****’].
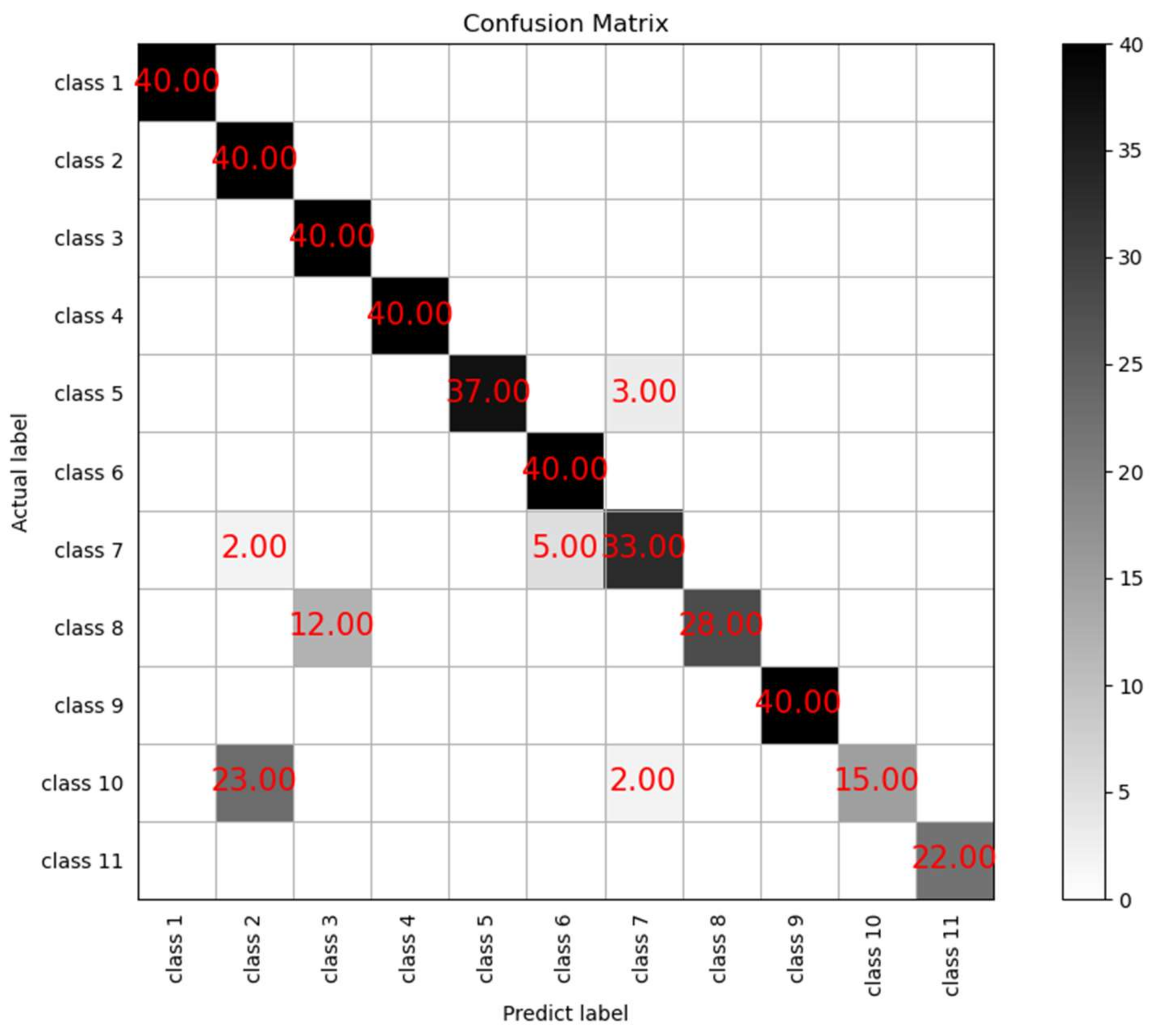
Experimental results show that the optimal hyperparameter of the algorithm is K = 22. A = 0.9. The experimental accuracy was 0.947. To verify the accuracy of the prediction of the KNN algorithm. The confusion matrix of the classification results of the KNN algorithm is plotted. The total number of experimental samples is 440 data, which are divided into 11 classes, and the horizontal coordinates are the predicted values and the vertical coordinates are the actual values, the diagonal line in the figure is TP (True Position), and the test results are shown in Figure 6.
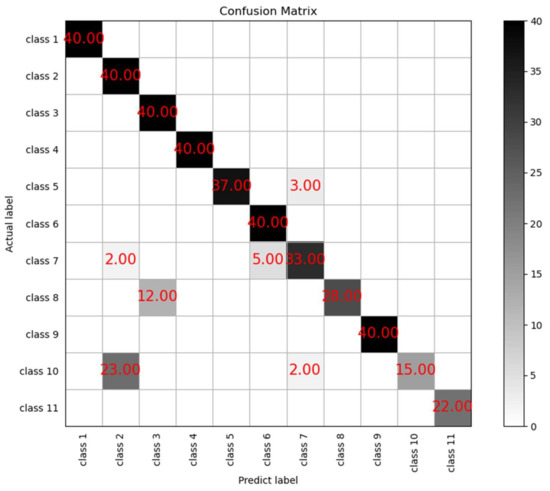
Figure 6.
Confusion matrix plot of the KNN algorithm.
4.3.2. Experiment Comparison
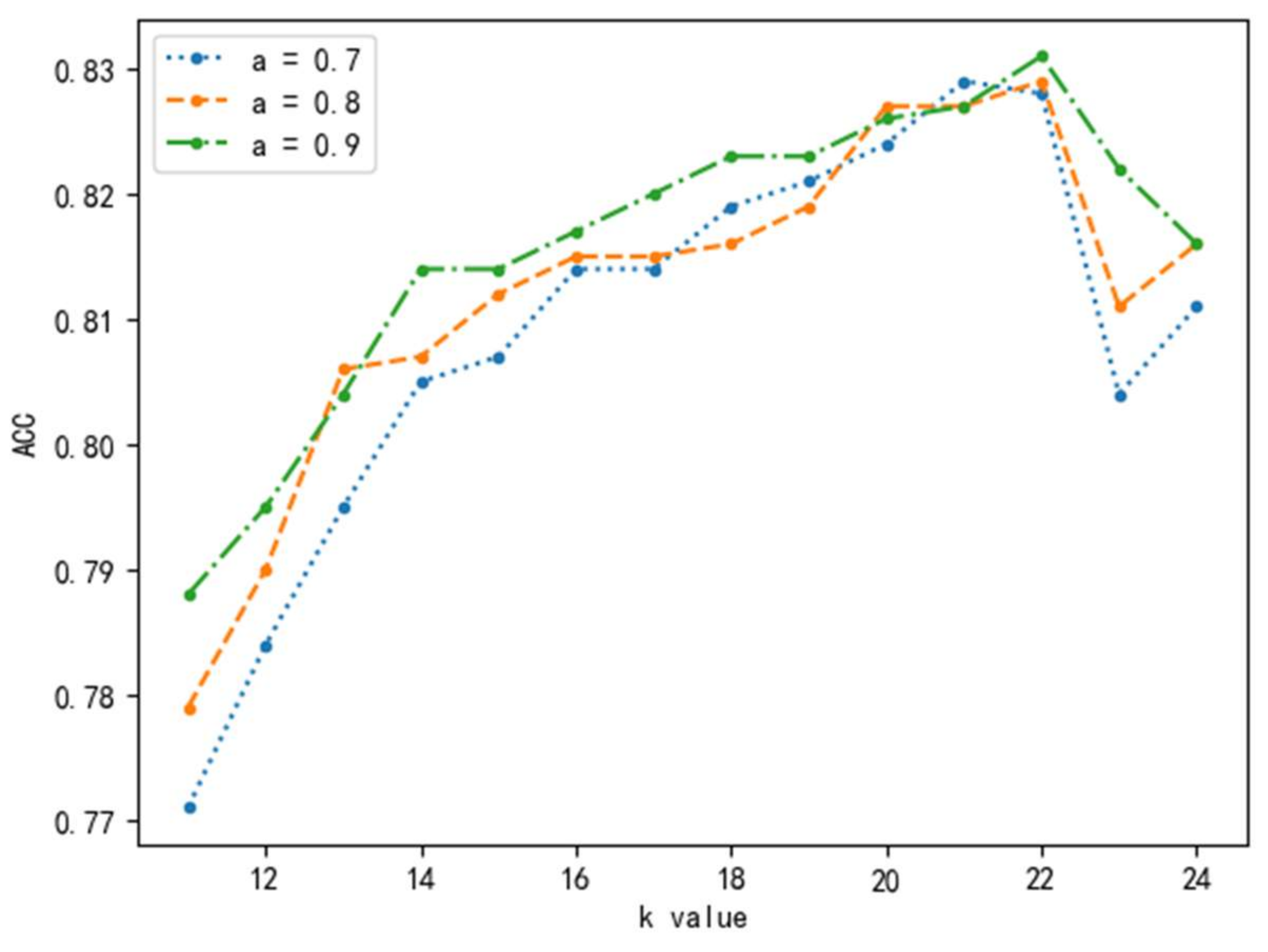
The Leave-One-Out (LOO) method is to divide a large dataset into K small datasets, among which K-1 is used as the training set and the remaining one as the test set, and then select the next one as the test set and the remaining K-1 as the training set. The accuracy of classification is adopted as the evaluation standard. Experimental results show that, when the hyperparameter K is 22 and a is 0.9, the algorithm achieves the best effect and the accuracy is 83.1% in the test set. The comparison effect is shown in Figure 7.
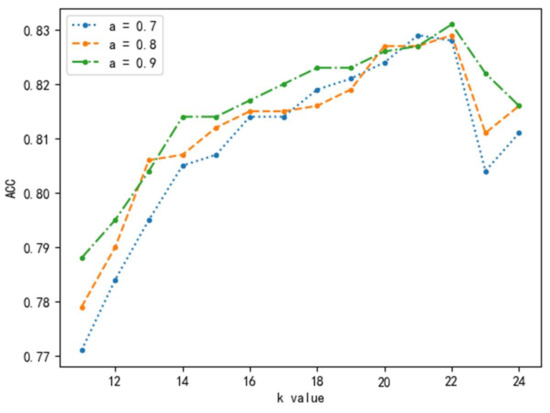
Figure 7.
Comparison of KNN prediction results under different parameters.
The comparison results are shown in Table 5.

Table 5.
Experimental results of leaving-one method.
4.4. Trajectory Prediction in the Open Sea
Experiment Content and Results
Since AIS initial data cannot be put directly into the LSTM model for training, it needs to be processed as the serialized data first, turning it into temporal data as the input of the neural network and deleting AIS null values in the original data, the neural network input for the first 15 timestamp vessel position information, outputting the ship position information for the next time stamp, and then normalizing the data. The experiment divided the data into three parts according to the ratio of 8:1:1 for the train, validation, and test sets. The training set is used for neural network training, and the verification set is used to verify the loss value in neural network training and display the model’s performance on the verification set. Finally, the model completed by training is predicted on the test set.
The LSTM network uses a 5-layer network structure and dropout layer to prevent overfitting in the network structure except for the output input layer, with a dropout rate of 0.3. The Relu function is used as the activation function of the neural network, the optimizer is Adam, and the MSE is used to measure the training loss of the neural network. 100 iterations are used to train the neural network. The experimental results show that the neural network Loss values tend to be smooth after 40–50 epochs.
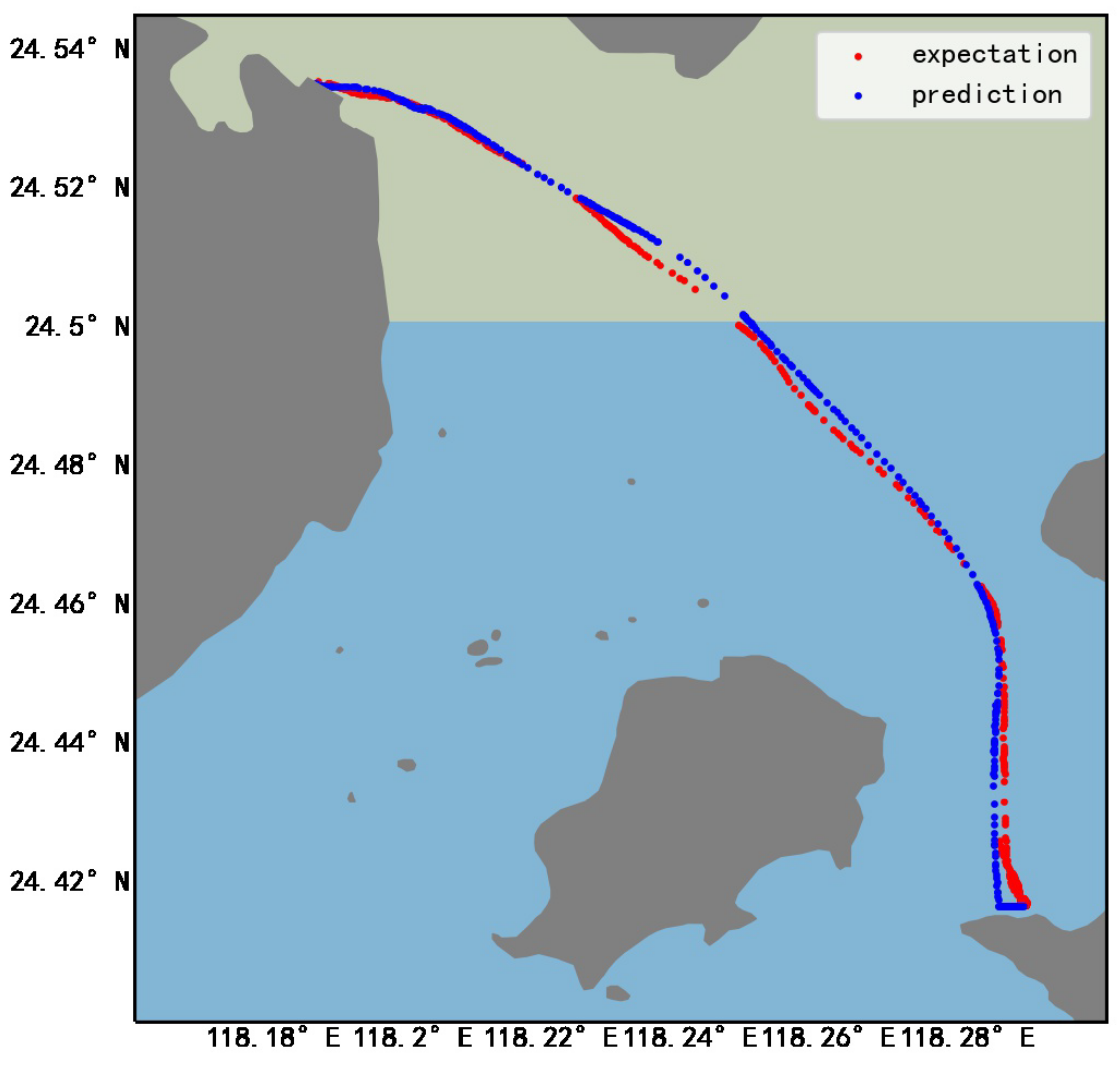
Experimental results show that the R2 value of longitude and latitude prediction by this method is 99% and the mean square error is only . The ship trajectory prediction results are shown in Figure 8.
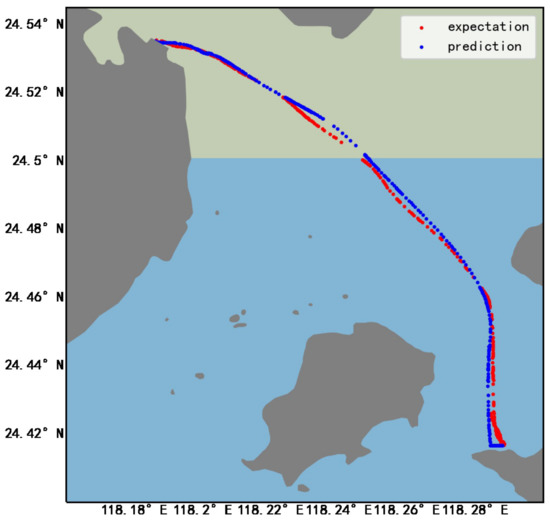
Figure 8.
AIS trajectory prediction effect diagram.
To achieve better prediction of ship trajectories using neural networks, the longitude and latitude values predicted by the different number of previous timestamps were compared, the experiment was conducted five times in total with the results averaged. The results show that the neural network achieved better prediction results when the number of previous timestamps using prediction was greater than 10. The results were compared from five aspects: loss value, accuracy, running time, mean square error, and R2 value, after the number of predicted timestamps reaches 10, the loss values and the accuracy of the predictions achieve better results, as shown in Table 6.

Table 6.
Comparison of prediction effects with the different number of timestamps.
4.5. Verification of Experimental Results
4.5.1. The Experimental Results
Methods proposed in top papers in recent years are selected, and the experimental methods in these papers were reproduced. Nine trajectory prediction methods are selected, which are HMM, Seq2Seq-single, Seq2Seq-multi, BP(back propagation), Kalman filtering model, Linear kernel function SVM, Polynomial kernel function SVM, Recurrent Neural Network (RNN), and Gated Recurrent Unit (GRU), the same AIS data used for this paper are used in the experiment, and mean square error (MSE) is used to evaluate the prediction effect. The experimental methods in these papers were reproduced and the experimental results are shown in Table 7.

Table 7.
Experimental results.
From the experimental results, the MSE of the KNN-LSTM hybrid method proposed in this paper is far lower than other methods and has better performance in ship trajectory prediction.
In order to reflect the difference of the prediction accuracy before and after the division of the sea area, the error value of the prediction of the offshore sea area and the open sea area was counted, and good prediction results were achieved in both the offshore sea area and the open sea area by this method, and the experimental results are shown in Table 8.

Table 8.
Comparison of predicted results for offshore area and open sea area.
4.5.2. Comparison of Experimental Results
The BP neural network method proposed by Zhang Z et al. [47] and the Kalman filtering algorithm mentioned by Jiang et al. [19] were selected to reproduce AIS data using the same method as in this paper, and mean square error was selected as the evaluation standard. The experimental results show that the MSE value of the BP neural network is 7.482, while the MSE value of the Kalman filter algorithm is 2.25 × 10−6.
From the experimental results, the MSE of the KNN-LSTM hybrid method proposed in this paper is far lower than other methods and has better performance in ship trajectory prediction. The model prediction time is controlled within 0.86 s and meets the needs of ship position prediction for a long time interval. The experimental results are shown in Table 9.

Table 9.
Results contrast.
5. Conclusions
This paper proposed a new vessel trajectory prediction method based on the trajecto-ry prediction of different ship densities in different sea areas. In the offshore sea area, the accuracy of the improved KNN algorithm for ship category judgment reaches 94.7%, which makes up for the poor prediction effect of the neural network due to the lack of training data. Our future work is mainly to cluster ship trajectories, and the result of ship clustering is used as the label value to predict the trajectory of the offshore sea. In the open sea area, the R2 value of the LSTM neural network for ship trajectory prediction reaches about 99%, and the mean square error value is in the order of 10−9. According to the ex-perimental comparison results, this method’s effectiveness is significantly superior to other methods. The next research step is to predict the ship’s trajectory based on weather factors and sea conditions.
Author Contributions
Conceptualization, L.Z. and Y.Z.; methodology, L.Z.; software, L.Z., J.S. and W.L.; validation, L.Z., J.S. and W.L.; formal analysis, W.L., J.L. and Y.Y.; investigation, L.Z., J.S. and W.L.; resources, Y.Z., W.L. and Y.Y.; data curation, L.Z. and J.S.; writing—original draft preparation, L.Z. and J.S.; writing—review and editing, L.Z., J.S. and W.L.; visualization, J.S. and J.L.; supervision, Y.Z., W.L. and Y.Y.; project administration, Y.Z., W.L. and Y.Y.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key Research and Development Program of China, grant number 2020YFB1712201 and 2021YFC2802503; Key Research and Development Program of Shaanxi Province, grant number 2021ZDLGY05-05.
Data Availability Statement
The data presented in this study are available from https://www.vtexplorer.com (accessed on 10 December 2018).
Acknowledgments
We would like to thank the reviewers for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, C.; Wang, J.; Liu, A.; Cai, Y.; Ai, B. An Asynchronous Trajectory Matching Method Based on Piecewise Space-Time Constraints. IEEE Access 2020, 8, 224712–224728. [Google Scholar] [CrossRef]
- Iphar, C.; Napoli, A.; Ray, C. Detection of false AIS messages for the improvement of maritime situational awareness. In Proceedings of the OCEANS 2015—MTS/IEEE, Washington, DC, USA, 19–22 October 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Gasparin, A.; Lukovic, S.; Alippi, C. Deep learning for time series forecasting: The electric load case. CAAI Trans. Intell. Technol. 2022, 7, 1–25. [Google Scholar] [CrossRef]
- Mukherjee, S.; Sadhukhan, B.; Sarkar, N.; Roy, D.; De, S. Stock market prediction using deep learning algorithms. CAAI Trans. Intell. Technol. 2021, 8–31. [Google Scholar] [CrossRef]
- Yang, C.-H.; Lin, G.-C.; Wu, C.-H.; Liu, Y.-H.; Wang, Y.-C.; Chen, K.-C. Deep Learning for Vessel Trajectory Prediction Using Clustered AIS Data. Mathematics 2022, 10, 2936. [Google Scholar] [CrossRef]
- Graser, A.; Dragaschnig, M.; Widhalm, P.; Koller, H.; Brändle, N. Exploratory Trajectory Analysis for Massive Historical AIS Datasets. In Proceedings of the 2020 21st IEEE International Conference on Mobile Data Management (MDM), Versailles, France, 30 June 2020–3 July 2020; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Cui, H.; Zhang, F.; Li, M.; Cui, Y.; Wang, R. A Novel Driving-Strategy Generating Method of Collision Avoidance for Unmanned Ships Based on Extensive-Form Game Model with Fuzzy Credibility Numbers. Mathematics 2022, 10, 3316. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, D.; Zhang, J.; Zhang, M.; Soares, C.G. A novel real-time collision risk awareness method based on velocity obstacle considering uncertainties in ship dynamics. Ocean. Eng. 2020, 220, 108436. [Google Scholar] [CrossRef]
- Sutulo, S.; Moreira, L.; Soares, C.G. Mathematical models for ship path prediction in manoeuvring simulation systems. Ocean. Eng. 2002, 29, 1–19. [Google Scholar] [CrossRef]
- Lv, Q.; Qiao, Y.; Ansari, N.; Liu, J.; Yang, J. Big Data Driven Hidden Markov Model Based Individual Mobility Prediction at Points of Interest. IEEE Trans. Veh. Technol. 2017, 66, 5204–5216. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Zhang, C.; Sun, F.; Meng, F.; Guo, A.; Jin, D. DeepMove: Predicting Human Mobility with Attentional Recurrent Networks. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018. [Google Scholar]
- Zhang, Z.; Ni, G.; Xu, Y. Ship Trajectory Prediction based on LSTM Neural Network. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Available online: https://ais.msa.gov.cn/ (accessed on 1 May 2020).
- Birgillito, G.; Rindone, C.; Vitetta, A. Passenger mobility in a discontinuous space: Modelling Access/Egress to maritime barrier in a case study. J. Adv. Transp. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Abdelaal, M.; Fränzle, M.; Hahn, A. Nonlinear Model Predictive Control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean. Eng. 2018, 160, 168–180. [Google Scholar] [CrossRef]
- Vijverberg, K. Radboud University Object Localization and Path Prediction Using Radar and Other Sources Towards Autonomous Shipping. Radboud Univ. 2018. [Google Scholar]
- Zhang, K.; Xiong, J.J.; Li, F.; Fu, T.T. Bayesian Trajectory Prediction for a Hypersonic Gliding Reentry Vehicle Based on Intent Inference. Yuhang Xuebao/J. Astronaut. 2018, 39, 1258–1265. [Google Scholar]
- Virjonen, P.; Nevalainen, P.; Pahikkala, T.; Heikkonen, J. Ship Movement Prediction Using k-NN Method. In Proceedings of the 2022 8th International Conference on Energy Efficiency and Agricultural Engineering (EE&AE), Olsztyn, Poland, 21–23 June 2018; pp. 304–309. [Google Scholar]
- Jiang, B.; Guan, J.; Zhou, W.; Chen, X. Vessel Trajectory Prediction Algorithm Based on Polynomial Fitting Kalman Filtering. J. Signal Process. 2019, 5, 74I–746. [Google Scholar] [CrossRef]
- Xie, G.; Gao, H.; Qian, L.; Huang, B.; Li, K.; Wang, J. Vehicle Trajectory Prediction by Integrating Physics- and Maneuver-Based Approaches Using Interactive Multiple Models. IEEE Trans. Ind. Electron. 2017, 65, 5999–6008. [Google Scholar] [CrossRef]
- Burger, C.N.; Grobler, T.L.; Kleynhans, W. Discrete Kalman Filter and Linear Regression Comparison for Vessel Coordinate Prediction. In Proceedings of the 2020 21st IEEE International Conference on Mobile Data Management (MDM), Versailles, France, 30 June 2020–3 July 2020; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Hexeberg, S.; Flåten, A.L.; Eriksen, B.H.; Brekke, E.F. AIS-based vessel trajectory prediction. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, J.; Shi, G.; Zhu, K. Online multiple outputs least-squares support vector regression model of ship trajectory prediction based on automatic information system data and selection mechanism. IEEE Access 2020, 8, 154727–154745. [Google Scholar] [CrossRef]
- Murray, B.; Perera, L.P. A Data-Driven Approach to Vessel Trajectory Prediction for Safe Autonomous Ship Operations. In Proceedings of the the 13th International Conference on Digital Information Management (ICDIM 2018), Berlin, Germany, 24–26 September 2018. [Google Scholar]
- Bao, K.; Bi, J.; Gao, M.; Sun, Y.; Zhang, X.; Zhang, W. An Improved Ship Trajectory Prediction Based on AIS Data Using MHA-BiGRU. J. Mar. Sci. Eng. 2022, 10, 804. [Google Scholar] [CrossRef]
- Last, P.; Hering-Bertram, M.; Linsen, L. Interactive history-based vessel movement prediction. IEEE Intell. Syst. 2019, 34, 3–13. [Google Scholar] [CrossRef]
- Volkova, T.A.; Balykina, Y.E.; Bespalov, A. Predicting Ship Trajectory Based on Neural Networks Using AIS Data. J. Mar. Sci. Eng. 2021, 9, 254. [Google Scholar] [CrossRef]
- Zeng, W.; Quan, Z.; Zhao, Z.; Xie, C.; Lu, X. A Deep Learning Approach for Aircraft Trajectory Prediction in Terminal Airspace. IEEE Access 2020, 8, 151250–151266. [Google Scholar] [CrossRef]
- Han, P.; Wang, W.; Shi, Q.; Yang, J. Real-time Short-Term Trajectory Prediction Based on GRU Neural Network. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–8. [Google Scholar]
- Liu, Y.; Hansen, M. Predicting Aircraft Trajectories: A Deep Generative Convolutional Recurrent Neural Networks Approach. arXiv 2018, arXiv:1812.11670. [Google Scholar]
- Lin, Y.; Zhang, J.W.; Liu, H. An algorithm for trajectory prediction of flight plan based on relative motion between positions. Front. Inf. Technol. Electron. Eng. 2018, 19, 95–106. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, Q.; Hu, Q.; Wen, X. High-precision intelligent track prediction under multi-dimensional conditions. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020. [Google Scholar]
- Wang, Q.; Zhang, Z.; Wang, Z.; Wang, Y.; Zhou, W. The trajectory prediction of spacecraft by grey method. Meas. Sci. Technol. 2016, 27, 085011. [Google Scholar] [CrossRef]
- Qiao, S.; Shen, D.; Wang, X.; Han, N.; Zhu, W. A Self-Adaptive Parameter Selection Trajectory Prediction Approach via Hidden Markov Models. IEEE Trans. Intell. Transp. Syst. 2015, 16, 284–296. [Google Scholar] [CrossRef]
- Ma, H.; Zuo, Y.; Li, T. Vessel Navigation Behavior Analysis and Multiple-Trajectory Prediction Model Based on AIS Data. J. Adv. Transp. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, X.; Wu, Y.; Lin, M. A Second-Order HMM Trajectory Prediction Method based on the Spark Platform. J. Inf. Hiding Multim. Signal Process 2019, 10, 346–358. [Google Scholar]
- Zhang, L.; Zhu, Y.; Lu, W.; Wen, J.; Cui, J. A detection and restoration approach for vessel trajectory anomalies based on AIS. J. Northwestern Polytech. Univ. 2021, 39, 119–125. [Google Scholar] [CrossRef]
- Wang, L.; Khan, L.; Thuraisingham, B. An Effective Evidence Theory Based K-Nearest Neighbor (KNN) Classification. In Proceedings of the 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, Sydney, Australia, 9–12 December 2008; Volume 1, pp. 797–801. [Google Scholar]
- Xiang, Y.; Cao, Z.; Yao, S.; He, J. CW-KNN: An efficient KNN-based model for imbalanced dataset classification. In Proceedings of the ICCIP ‘18: The 4th International Conference on Communication and Information Processing, Qingdao, China, 2–4 November 2018. [Google Scholar]
- Altman, N. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Lecun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-Series. In The Handbook of Brain Theory and Neural Networks; The MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Xu, X. Context-based Trajectory Prediction with LSTM Networks. In Proceedings of the 2020 the 3rd International Conference on Computational Intelligence and Intelligent Systems, Tokyo, Japan, 13–15 November 2020. [Google Scholar]
- Xue, H.; Huynh, D.; Reynolds, M. PoPPL: Pedestrian Trajectory Prediction by LSTM with Automatic Route Class Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 77–90. [Google Scholar] [CrossRef]
- Xue, P.; Liu, J.; Chen, S.; Zhou, Z.; Huo, Y.; Zheng, N. Crossing-Road Pedestrian Trajectory Prediction via Encoder-Decoder LSTM. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2027–2033. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I. A novel, data-driven heuristic framework for vessel weather routing. Ocean. Eng. 2020, 197, 106887. [Google Scholar] [CrossRef]
- Historical AIS Data Services [DB/OL]. Available online: http://www.vtexplorer.com/ (accessed on 10 December 2018).
- Zhang, Z.; Ni, G.; Xu, Y. Trajectory prediction based on AIS and BP neural network. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 601–605. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).