Abstract
Video monitoring has a wide range of applications in a variety of scenarios, especially in smart parks. How to improve the efficiency of video data processing and reduce resource consumption have become of increasing concern. The high complexity of traditional computation offloading algorithms makes it difficult to apply them to real-time decision-making scenarios. Thus, we propose a multi-agent deep reinforcement learning algorithm with credit assignment (MACA) for computation offloading in smart park monitoring. By making online decisions after offline training, the agent can give consideration to both decision time and accuracy in effectively solving the problem of the curse of dimensionality. Via simulation, we compare the performance of MACA with traditional deep Q-network reinforcement learning algorithm and other methods. Our results show that MACA performs better in scenarios where there are a higher number of agents and can minimize request delay and reduce task energy consumption. In addition, we also provide results from a generalization capability verified experiment and ablation study, which demonstrate the contribution of MACA algorithm to each component.
Keywords:
computation offloading; deep reinforcement learning; credit assignment; multi-agent; video monitoring MSC:
68T42
1. Introduction
Video monitoring systems represent the momentous application of the Internet of Things while also playing an important role in urban security, traffic management, building security, and other fields [1]. According to data statistics, the number of global Internet video monitoring system has multiplied several fold in recent years [2], and the masses of data are bringing new challenges to video data processing. With the rise of mobile internet, it has become a new trend to offload computing tasks to the cloud center or the edge computing node of the network. Mobile edge computing (MEC) technology [3] is a distributed computing architecture and an intermediate layer connecting a traditional cloud center and devices. It was deployed as close as possible to the users and only sends necessary results to the cloud data center, which greatly reduces the time delay of the data transmission process. MEC technology aims at offloading computing tasks to mobile edge servers, which are always connected to the user device. Thus, computing intensive and delay critical tasks can be well supported because of the short distance between user devices and the mobile edge server.
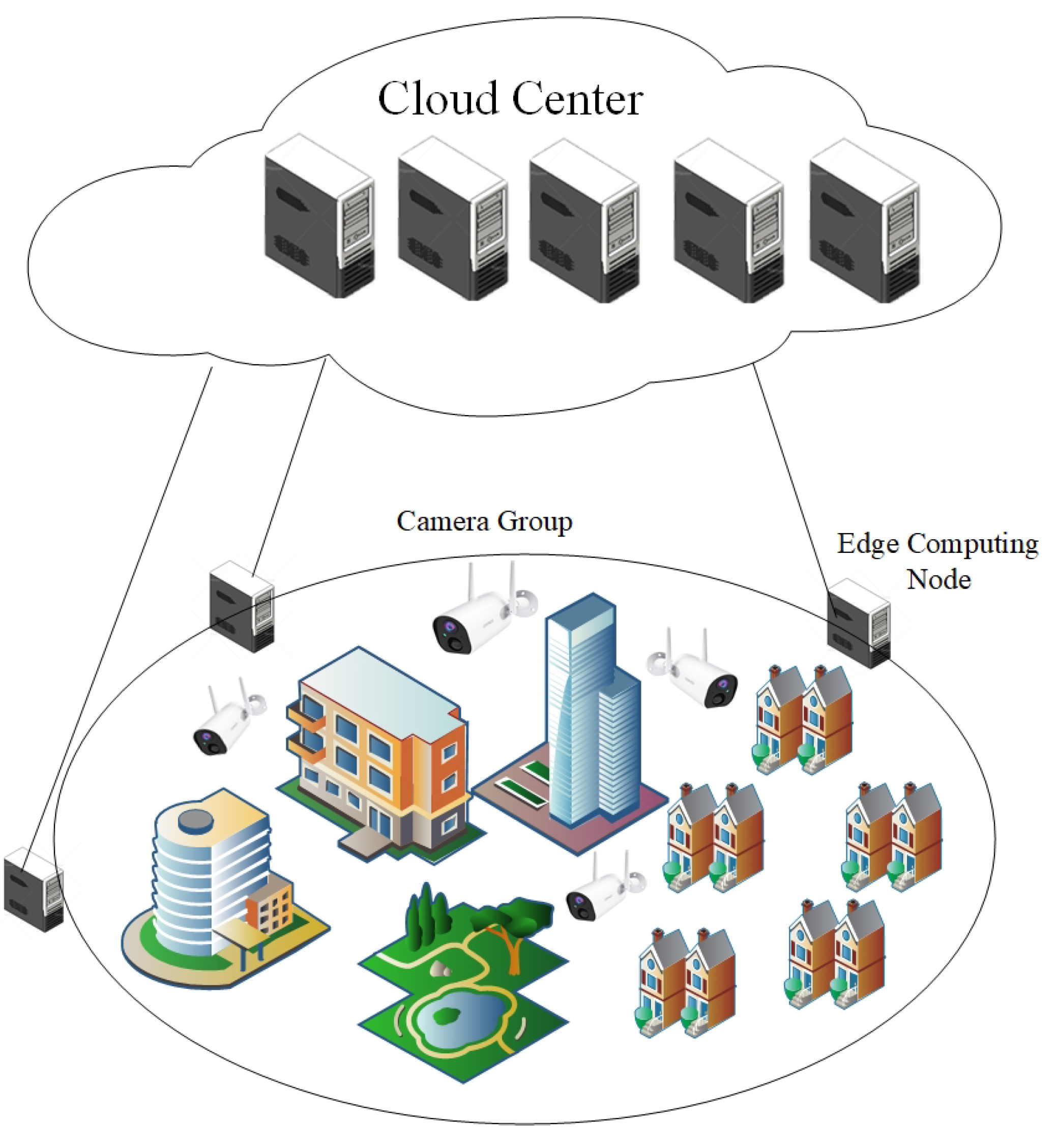
This paper will focus on the computation offloading approach in smart park monitoring. In Figure 1, the video analysis data are first collected by the camera sensor and then transmitted to the MEC server for further computation. For high complexity and delay critical image processing tasks, the bottleneck to solve the delay problem is the limitation of computing capability and communication resources between the channels. The existing MEC based on video data analysis computation offloading task approaches usually tends to allocate all computing tasks to local video devices or mobile edge servers. However, both of the approaches have their own inherent problems [4]. Due to the unacceptable level of energy consumption, it is impractical to allocate sufficient computation resources to the local video device to satisfy the video analysis task. On the other extreme, offloading the entire task to the MEC consumes excessive bandwidth resources for transmitting the raw video data, which is also unrealistic because of the limitation of bandwidth resources. In order to resolve the abovementioned problems, an MEC based on computation offloading approach is proposed, in which assignment of the computing task is balanced between the local device and MEC server. However, the NP hard problem gives rise to a new issue, namely that traditional approaches often fail to provide the allocation scheme of computational offloading in time [5]. At the same time, the transmission order of multiple local devices and the time-varying communication channel raise new challenges for the computation offloading strategy.

Figure 1.
Computation offloading scenario comprising multiple video monitoring devices, multiple edge computing nodes, and a cloud data center. The video analysis data can be offloaded from local monitoring devices to an edge computing node and thereafter to the cloud data center.
In this paper, we aim to establish a computation offloading approach to minimize the request delay while reducing the task energy consumption. We model the computation offloading task as a cooperative multi-agent reinforcement learning (MARL) problem. We proposed a multi-agent deep reinforcement learning algorithm with credit assignment (MACA) and introduce a centralized training with decentralized execution framework. In addition, we focus on the online decision-making ability speed and the accuracy after offline training. The contributions of this paper are as follows:
- (1)
- In order to solve the video monitoring analysis task in smart parks, the edge computing node and cloud data center are introduced to satisfy the computation offloading requirements. The system model includes multiple devices and multiple edge computing nodes, taking into account the dynamically changing communication channel states and task characteristics. We introduce reinforcement learning to overcome the ultra-high computation time of traditional methods through offline training and online decision-making, which makes the computation offloading utilizable in real-time scenes.
- (2)
- To deal with the curse of dimensionality caused by the expansion of the decision feasible region, we introduce a credit assignment method into value-based reinforcement learning, which is converted from being a single-agent scenario to a multi-agent scenario. The credit assignment method decomposes the global Q-value to each individual Q-value , which enforces the monotonous constraint between global and individual Q-values. Meanwhile, the centralized training and decentralized execution framework makes use of the global statue information when training agents, which makes agents work more cooperatively and accelerates the training process.
- (3)
- In addition, we introduce a double Q-network, dueling Q-network, and priority experience replay method into our proposed multi-agent reinforcement learning algorithm and analyze the contribution of each component via an ablation study. Through numerical simulation, we demonstrate that our proposed MACA algorithm can achieve better performance compared with traditional DQN algorithms and other approaches, especially when the number of agents increases. Furthermore, we also verify the generalization capability of our proposed MACA algorithm.
The rest of this paper is organized as follows: In Section 2, we introduce relevant research results of computation offloading and deep reinforcement learning algorithms. In Section 3, we introduce the system model of the computation offloading scenario and our proposed MACA multi-agent reinforcement learning algorithm, in which credit assignment is applied in the training process. Section 4 introduces the simulation experiment. Finally, Section 5 concludes this article.
2. Related Works
2.1. Computation Offloading Task
Edge computation offloading, which deploys multiple edge devices with computational capability as nodes of providing services [6], extends the concept of cloud computing. It can reduce the request delay, but the timing-vary bandwidth and resources required for users give rise to a crucial problem regarding to which server node the computational task can be offloaded such that the requirements of computational resource and delay are satisfactory. Computation offloading is one of the important research directions of edge computing. Computation offloading generally includes two aspects: one is the offload decision, which mainly concerns determining whether a computation offloading process is required and the selection of computation offloading nodes; the second is resource allocation, which aims to solve how to allocate resources for global nodes, or how to allocate communication resources in the process of offloading and transmission. The application of edge computation multi-level offloading technology in real-time video monitoring networks has important research significance. Real-time video monitoring networks need to satisfy the characteristics of low delay requirement. At the same time, due to the wide application of video monitoring networks, it is also necessary to consider reducing energy consumption in resource-constrained scenarios.
2.2. Reinforcement Learning
Reinforcement learning [7] can be seen as the process of interaction between agents and the environment in addition to the constant exploration of strategies for learning to obtain the maximum cumulative reward in experiments. In reinforce learning [8], the agent performs actions in the environment, and the environment is transformed to a new state while the agent can obtain a certain reward. The interaction process can be described as follows: at time t, the agent executes action according to the probability distribution of strategy , and at the next time , the state of the environment changes from to , and propagates the agent with a certain reward . The Markov process can be described as follows: at the next time , the state of the environment is only related to , and has nothing to do with the time of the past environment. Reinforcement learning is usually described using five tuples , where P is the action to environment mapping and is the discount factor.
The reinforcement learning algorithm can be classified into different categories: according to the algorithm update mechanism, where it can be divided into a round update Monte Carlo algorithm and one-step update temporary difference algorithm; according to the consistency of policy execution and policy evaluation, where it is divided into an on-policy and an off-policy algorithm; according to whether to build a model, where it is divided into model-free algorithm and model-based algorithm; according to the way of action selection, where reinforcement learning is divided into value-based, policy-based, and actor–critic reinforcement learning algorithms. Using deep reinforcement learning, end-to-end learning from perception to decision-making is realized.
Among the value-based reinforcement learning algorithms, the traditional reinforcement learning algorithms include the Q-learning and SARSA [9] algorithm. The deep Q-network [10] algorithm is based on experience replay and estimation of the value function of the target network and surpasses human players in Atari games. Since then, there has been various variants of the DQN algorithm [11], which effectively solves the overfitting problem in the DQN algorithm and has higher learning efficiency, value function evaluation, and search ability [12].
In the model-based reinforcement learning algorithm, the strategy parameters are updated by directly searching the best strategy to maximize the return. The classic REINFORCE [13] algorithm uses the Monte Carlo method to estimate the gradient strategy. In the estimation process, the information of the whole trajectory is considered, and it has a large strategy gradient variance. By introducing the value baseline, it can effectively reduce the variance. In order to improve the stability and convergence speed of the algorithm, avoid excessive update step size, and obtain returns monotonically and incrementally to continuously obtain the optimal policy, there are trust region policy optimization algorithms (TRPO) [14], proximate policy optimization algorithms (PPO) [15] and distributed proximate policy optimization algorithms (DPPO) [16].
In the reinforcement learning algorithm based on combined value strategy, strategy and value are learned at the same time. The actor–critic algorithm [17] is used as the benchmark of the strategy gradient. The actor network trains the strategy according to the value function fed back by critic network, and the critic network trains the value function, and uses the time series difference method for one-step update. The actor–critic algorithm has the characteristics of small variance of value function estimation, high sample utilization, and fast training speed. Subsequently, a series of reinforcement learning algorithms that are improvements of the actor–critical algorithm have appeared, such as deep deterministic policy gradient algorithm (DDPG) [18], asynchronous advanced actor–critical algorithm (A3C) [19], twin delayed deep deterministic policy gradient algorithm (TD3) [20], and soft actor–critical algorithm (SAC) [21].
At present, there are many excellent algorithms to complete the control of a single agent, among which DDPG, PPO, and other deep reinforcement learning algorithms are the most effective. Strategically, a multi-agent system composed of multiple independent agents lacks flexibility, due to the complexity and dynamic characteristics of the environment. The MADDPG [22] algorithm proposed in an article published by OpenAI on nips in 2017 is an extension of the DDPG [18] algorithm, which enables an actor to learn decision-making ability through interaction with complex environments and provides a good idea for multi-agent collaborative control.
Based on reinforcement learning algorithm to solve computation offloading problem, Lee et al. [23] proposed a reinforcement learning method based on an auction mechanism to solve the problem of computation offloading using the real secondary price auction as the baseline, in which the requirements of personal rationality and incentive compatibility are met. The experimental simulation showed that the proposed method can meet the above characteristics and increase the overall income of the seller. Pradhan et al. [24] used reinforcement learning to solve the problem of computation offloading of IOT applications in multiple input and output cloud wireless access networks. A computation offloading algorithm was proposed to minimize the total transmission power of the Internet of Things, and a low complexity supervised deep learning method was used to solve the problem. The effectiveness of the method was demonstrated using comparative experiments. Zhang et al. [25] proposed a method to alleviate the heavy burden of equipment through mobile edge computing and adopted a reinforcement learning method to design different states of multiple different edge servers and offloading modes of various vehicles. The experiments show that the proposed computation offloading scheme has great advantages in optimizing system utility and improving offloading reliability. Ren et al. [26] solved the problem of fog computing access node in the industrial Internet of Things through deep reinforcement learning. The created environment has multiple IIOT devices and multiple access nodes. The multi-agent reinforcement learning method was compared with a greedy algorithm and genetic algorithm. It was shown that the proposed algorithm can overcome the dimensional curse caused by the increase of access nodes and is competitive among the many algorithms in use. Yu et al. [27] proposed a new deep simulation learning-driven MEC network edge cloud computing offload framework. By optimizing behavior cloning to minimize the offloading cost in time-varying networks, the direction and advantages of applying the deep learning method to multiple MEC research fields are discussed, including edge data analysis, dynamic resource allocation, security, and privacy.
3. The Proposed Approach
In this section, we will first establish the task model, delay model, energy consumption model, and transmission model in computation offloading and determine the goal of computation offloading tasks, namely minimizing calculation delay and energy consumption, which will play an important role in subsequent simulation experiments. The main notation in our model is listed in Abbreviations. We will then introduce the multi-agent reinforce learning framework and our proposed MACA algorithm.
3.1. Problem Definition
We consider a computation offloading scenario where a large number of video monitoring cameras are set up in the smart park, and multiple cameras transmit monitoring video data to a relay node, which can complete some computational tasks. The camera that transfers computational tasks to the same node is called a camera group. There are N camera groups that generate computationally intensive tasks. In this paper, a camera group denotes the minimum unit device for computation task offloading. We assume that the decision-making time is slotted as , which is called a computation offloading cycle. In a computation offloading cycle, each device generates only one computationally intensive task (if a device generates multiple tasks, the device can be decomposed into multiple devices). The task characteristics are , where denotes the amount of data that needs to be uploaded to complete the task, and denotes the number of CPU cycles for computing tasks (in this paper, it is assumed that the number of CPU cycles required to complete a task is unchanged no matter where the task is executed). Above the relay node, multiple edge computing access nodes are deployed in the smart park to process the computing tasks offloaded by the camera group. If the edge computing node remains busy, it can choose to further offload the computing task to the cloud data center for executing. In a computation offloading cycle, the relay node can select to execute computing task locally or offload the task to the edge computing node, the edge computing node can directly calculate the task or further offload the task to the cloud computing service center. In this way, a three-level cloud-edge-segment computation offloading scenario from camera groups to edge computing nodes to a cloud computing center is built.
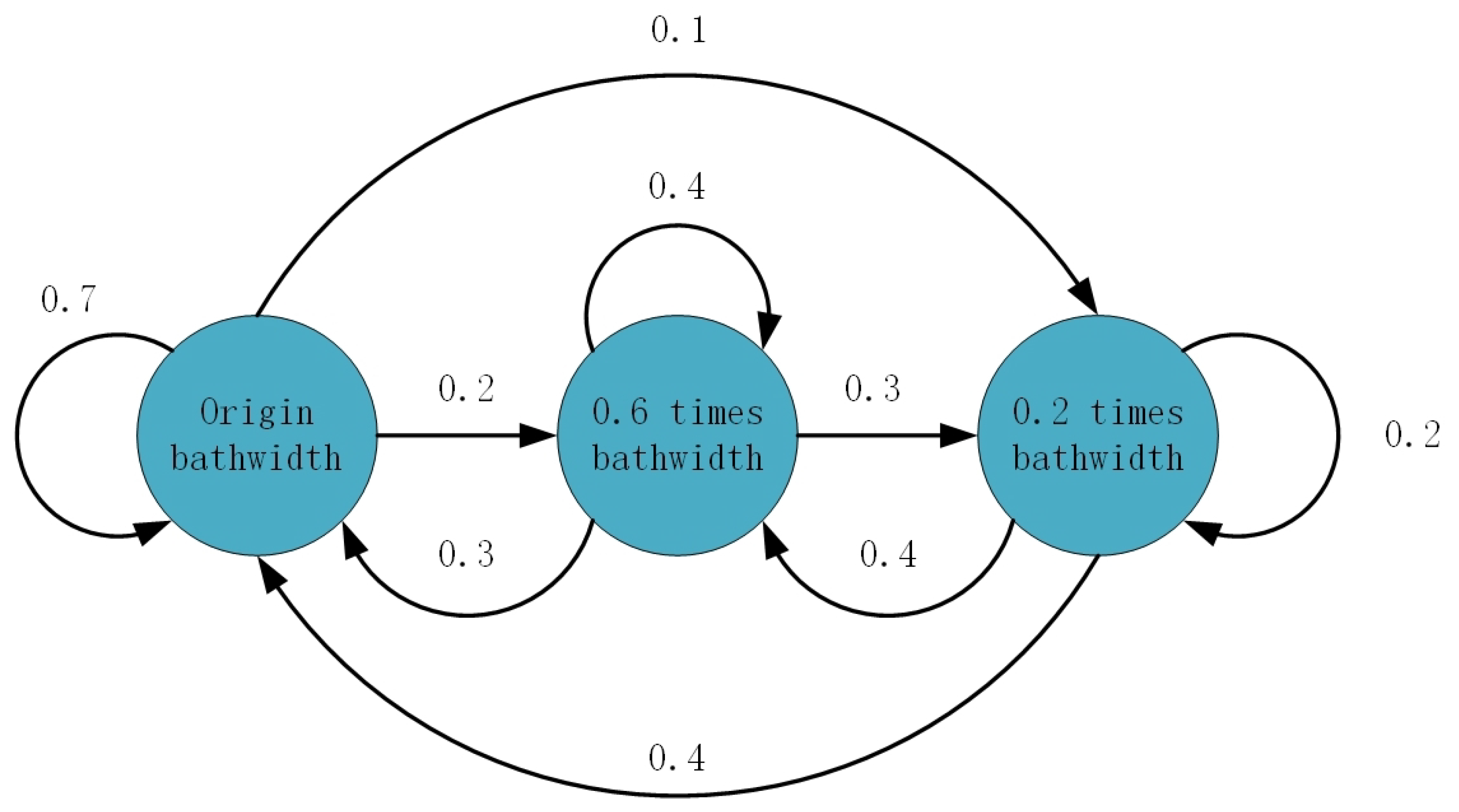
Due to the limited number of edge computing nodes, it may not be enough to meet the needs of computing all tasks at the same time in one computation offloading cycle. We define the channel bandwidth between the device n and the edge computing node f as . Since the available bandwidth resources between device and edge computing node is time-varying, we assume that the bandwidth variation conforms to a Markov process. There are three states of original bandwidth, 0.6 times bandwidth and 0.2 times bandwidth. The transition probability between each state is shown in Figure 2.
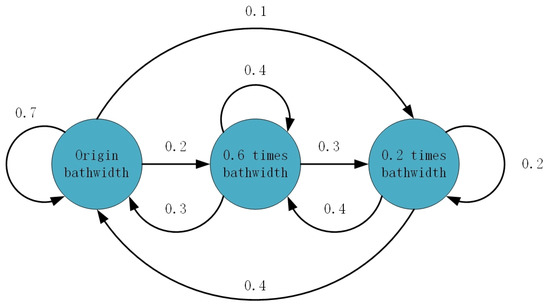
Figure 2.
The transition probability between three bandwidth status, where the origin state remains unchanged with a probability of 0.7, transitions to the 0.6 times bandwidth status state with a probability of 0.2, then transitions to the 0.2 times bandwidth status with a probability of 0.1. The 0.6 times bandwidth state remains unchanged with a probability of 0.4, transitions to the 0.2 times bandwidth status state with a probability of 0.3, and then transitions to the origin bandwidth status with a probability of 0.3. The 0.2 times bandwidth state remains unchanged with a probability of 0.2, and then transitions to the 0.6 times bandwidth status state with a probability of 0.4, and then transitions to the origin bandwidth status with a probability of 0.4.
If multiple devices simultaneously select one edge computing node to offload the task, the channel bandwidth will be equally allocated to all devices to offload data. Therefore, the data offload rate of the device can be expressed as Formula (1):
where N denotes the number of devices offloading tasks at the same time, P denotes the offload power of the computation offloading task, h denotes the gain of the communication channel when the task is transmitted, and is the variance of the complex Gaussian white channel noise. Next, we will introduce the time delay and energy consumption model of local computation.
If device n determines that the computing task should be executed locally, we define the local request time delay as . The local computing request delay only includes the CPU processing delay during the local computing of tasks. The computing capacity (CPU cycles per second) of each relay node may be different, which is expressed in . Then, the time delay of the local calculation can be defined as Formula (2):
We define the energy consumption of tasks as , which can be expressed as Formula (3):
where denotes the number of CPU cycles required by the task, denotes the calculation factor, set as , and denotes the computing capacity of the local relay node.
If device n chooses to offload task in the computation process, the task needs to go through three stages: task data uploading, task calculation, and result data downloading. Due to the fact that, when computing tasks are uploaded, there is often a large amount of raw data, the data can be ignored when the results are being downloaded in contrast to when they are being uploaded, and the downlink communication capability is often strong, the delay when the task results are downloaded is not considered in this paper. Moreover, since the edge computing nodes can choose whether to further offload tasks to the cloud center via the greedy algorithm, we integrate the computing capabilities of the cloud computing center into the edge computing nodes and then only consider the computation offloading process from the device to the edge computing node.
According to the above analysis, the delay of task uploading can be expressed as:
where denotes the data upload rate when device n is connected to the edge access node through the communication channel. Similarly, the calculation delay in the task calculation can be expressed as:
where denotes the computing capacity of the edge computing node (CPU cycles per second). A requirement is that the sum of computing resources allocated to each task does not exceed the overall computing capacity of the current node .
The calculation delay in the whole computation offloading process can be expressed as:
Correspondingly, the energy consumption in the offloading process is calculated as:
where denotes the energy gain in the transmission process, and the energy consumption in the calculation task can be expressed as:
Then, the energy consumption after offloading can be expressed as:
3.2. Multi-Agent Reinforcement Learning Scenario
In this subsection, we first provide some necessary background on reinforcement learning as a basis for deriving our proposed algorithm. Then, we model computation offloading scenario as a multi-agent reinforcement learning process and introduce the four key elements in reinforcement learning: action, state, observation, and reward.
Differently from the reinforcement learning algorithm of a single agent, the multi-agent cooperative algorithm can be described as , where denotes a stochastic Markov decision process. denotes the global state at time step t, and the action of each agent u is , which generate the joint action . The mapping of action change state of the environment is . Since the problem is modeled as a cooperative task, all agents share a global reward function . In addition, O denotes the global observation of agents. N denotes the number of agent participate in the game. In particular, Z denotes a partial observation in which each agent draws individual observations according to the observation function .
The reward discount function is , which denotes the total return as . An agent trains its own policy to maximize the expected reward. There are three standard definitions to describe a joint action policy, the state-action value function , the state value function , and the advantage function :
All the agents work together to maximize the total reward and generate a joint policy as:
Next, we will introduce four key elements of reinforcement learning settings in the computation offloading experiment.
Action: In the video monitoring computation offloading scenario of the smart parks, each device (camera group) is set as an agent with its own individual environment observation. In each computation offloading cycle, agents make action decisions by observing the partial state of the environment. Agents can choose local computing or to offload tasks to an edge computing node.
Suppose there are N devices, each of which acts as an agent. After receiving the offloading request from a device, the agent n observes the local status . Then, the offloading decision is generated by back-propagation of the Q-network reward. In this process, due to the limitation of computing capability, we set the maximum number of CPU cycles that each edge computing node can allocate. The maximum allocatable task number that the agent can assign on each edge computing node is , and agent n executes operation , which can be expressed as:
where means that the agent chooses to offload the task, and means the agent chooses to complete the task locally.
State and Observation: When making offloading decisions, the agent’s local observation of the environment can be defined as:
where denotes the channel gain state between device n and edge computing nodes, denotes the number of bits required for the task to upload, and denotes the CPU cycle required for the task to complete the calculation. The global observation is composed of all agents’ partial observations, which can be expressed as:
After the agent makes a decision to offload, it propagates the action to the environment and gains rewards , and it then enters the next stage , so as to constantly interact with the environment. Next, the obtained information is placed in the experience buffer D.
Reward: In this paper, the task of computation offloading process is set to minimize request delay and energy consumption. It is obvious that the request delay of computation offloading process is lower than the local computing because of the higher computing capability of edge computing nodes. Thus, we can define relative increments of request delay as:
The smaller the value of , the larger the reward value, which is consistent with our target. In the same way, we can define the relative increments of energy consumption as:
Combined with the above time delay and energy consumption formula, the reward can be expressed as:
where and denote the proportion weight of request delay and energy consumption in the computation offloading task , which needs to meet the constraints of , , and . The proportion weight may change with different task scenarios. After estimation, we take as remaining unchanged during the entire computation offloading process in this paper.
3.3. MACA Algorithm Design for Computation Offloading
In the real computation offloading scene, monitoring devices’ cooperation in making decisions in a decentralized manner. However, in the experimental environment, we can train the agents using a centralized function [28]. Thus, there is a question of how to represent and use the action-value function defined in Formula (10). On the one hand, some approaches forgo the use of centralized information and estimate the of each agent, which cannot explicitly reflect the communication between a cooperative agent and the confounded contribution of each agent in the total reward. At the other extreme, having a training processing that is fully centralized makes it impractical to train agents with mass information, and it becomes impossible to support the global observation hypothesis in some application scenarios [29].
Thus, the multi-agent reinforcement learning algorithm with credit assignment (MACA) for computation offloading is proposed by us, in which we introduce centralized training and decentralized execution thinking. We assume that the agents jointly interact with the environment and receive a global reward, denoted as . Each agent holds an individual Q function , and the global reward can be decomposed into individual rewards for each agent. The relationship between and is much more than simple factorization and involves a complex nonlinear combination in which a neural network, called a mixing network, is implemented and can distinguish the contribution between each agent with credit assignment process.
We focus on the consistency of partial reward and global reward, namely the monotonicity constraint of and . Therefore, we rule that the weight of the mixing network must be non-negative; that is, there is a requirement to satisfy the relationship between the individual reward and the global reward:
We add global observation information S to the mixing network while imposing the limitation that the weight of the mixing network must remain non-negative. The addition of global information allows the mixing network to more explicitly determine the contribution of each agent. In addition, when building the Q-network, we introduced some existing tricks for Q-networks, such as the double Q-network and dueling Q-network, which can improve the training effect. The double Q-network requires the construction of two action-value functions, one for estimating the action and one for estimating the value of that action. In the application of the MACA algorithm, the evaluation network is used to determine the action, and the target network is used to determine the action value. This double Q-network architecture can effectively solve the overestimation problem generated by the Q-network.
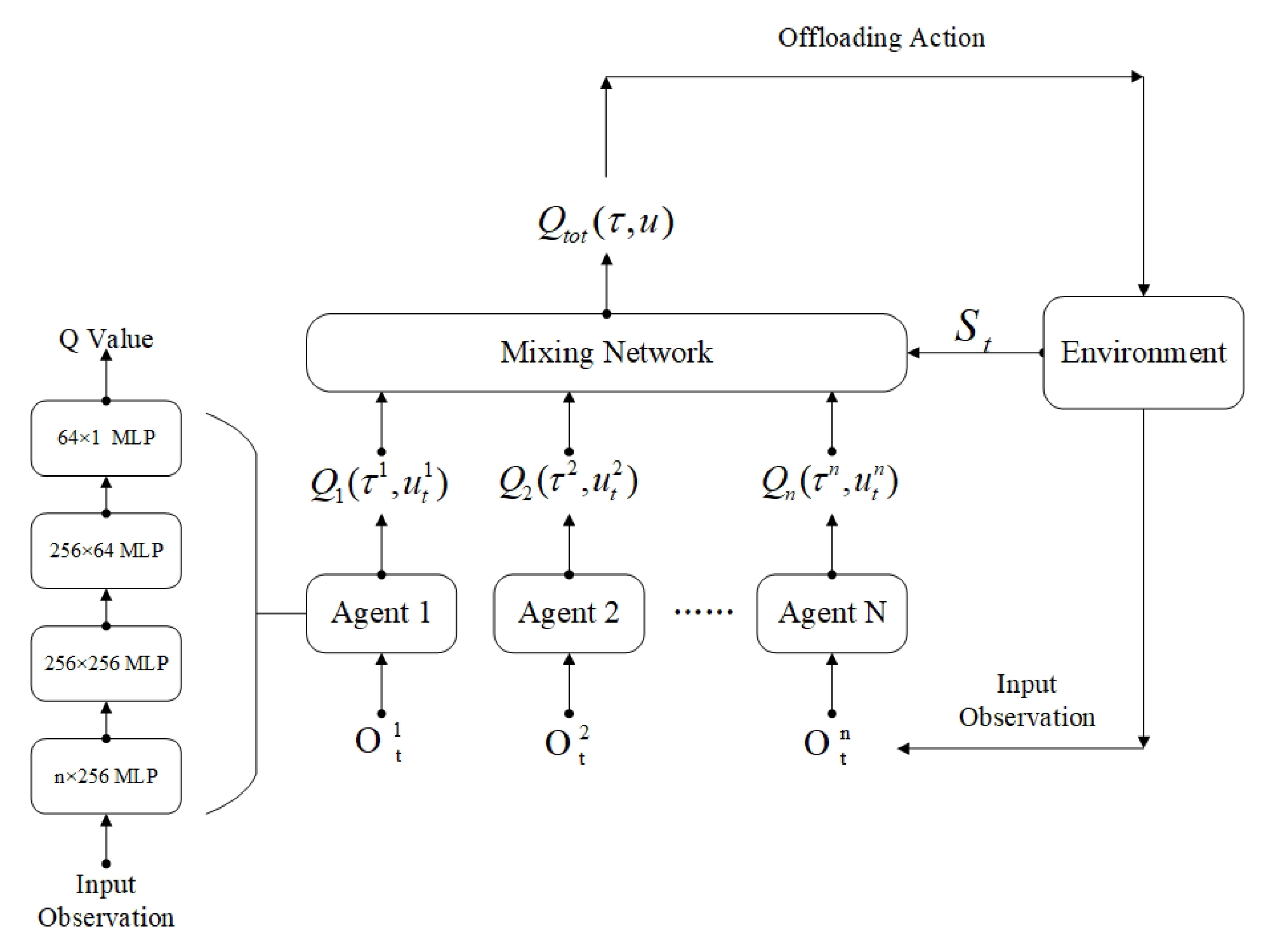
Similarly, considering that the reward obtained from the computation offloading scenario is less related to the environment state but more related to the joint action selected by the agent, we introduce the dueling Q-network architecture during training. Dueling Q-network changes the output value to two branches, which are the scalar state value V of the state and the advantage value A of each action. The advantage value A is a vector of the same dimension as the action space. Under this framework, Q-network is more inclined to change each advantage value A of each action instead of changing the state value V, and this architecture can better distinguish the pros and cons of each action of the agent, speeding up training. The overall architecture of our proposed MACA algorithm is shown in Figure 3.

Figure 3.
Schematic diagram of MACA network architecture. The Q-network of each agent contains [256, 256, 64] hidden layers, introducing a double Q-network and dueling Q-network. The global state information is added to the mixing network, and the global reward is monotonically decomposed into the local reward of each agent.
At the beginning of each offloading decision cycle, each agent n obtains part of the current environment state through interaction with the environment, that is, the observation of the agent is used as the input of the Q-network. The Q-network generates the estimated Q value for further rewards. The Q value generated by multiple agent networks is jointly input to the credit assignment mixing network. All weight items in the network are non-negative, so the output result is positively related to the Q value generated by the agent Q-network. The credit assignment network back-propagates the action space to generate and select the maximum reward actions that react to the environment. Then, the environment changes from to state. Before the next round of computing offloading decisions, the experience storage enters the buffer. After interactions with the environment, the agent takes a small batch of experience values from the buffer to learn and update the Q-network and the mixing network. The loss function is defined as follows:
where b is the batch size of experience sampled form the replay buffer, and represents the real future reward. represents the parameters for the Q-network. Then, we can obtain the corresponding agent’s policy of maximizing the Q value through the following formula traversal enumeration, naturally avoiding the curse of dimensionality. The whole process of MACA algorithm can be represented by Algorithm 1.
| Algorithm 1: Multi-Agent Deep Reinforcement Learning Algorithm with Credit Assignment. |
 |
4. Experiment
In this section, we will first outline the simulation experiment settings. Then, we will compare our proposed MACA algorithm with other traditional algorithms through discussion and analysis.
4.1. Simulation Settings
In the simulation experiment, we simulate smart park video monitoring computation offloading of video data processing tasks by considering scenarios consisting of multiple edge computing nodes and multiple camera groups where tasks are to be assigned to devices. The simulation process goes through a total of five computation offloading cycles. During this process, the communication transmission channels of all tasks are shared and time-varying. The computational capacity of each local relay node is Hz per second.
For actual computation offloading scenarios, the size of task data and the number of required CPU cycles will not be fixed. Therefore, we assume that a task model within the scope is randomly generated during the offloading process. In addition, considering the cumulative cost of computing delay and energy consumption in each computation offloading cycle, the discounter factor is set to 1. In addition, other parameters are summarized as follows in Table 1.

Table 1.
Main parameters.
4.2. Simulation Results
In this subsection, we will introduce the simulation results of the MACA algorithm experiment from the aspects of the training process, agent number comparison experiment, and ablation experiment. Through comparison with numerous existing algorithms, we demonstrate the superiority of our proposed MACA algorithm.
4.2.1. Training Process
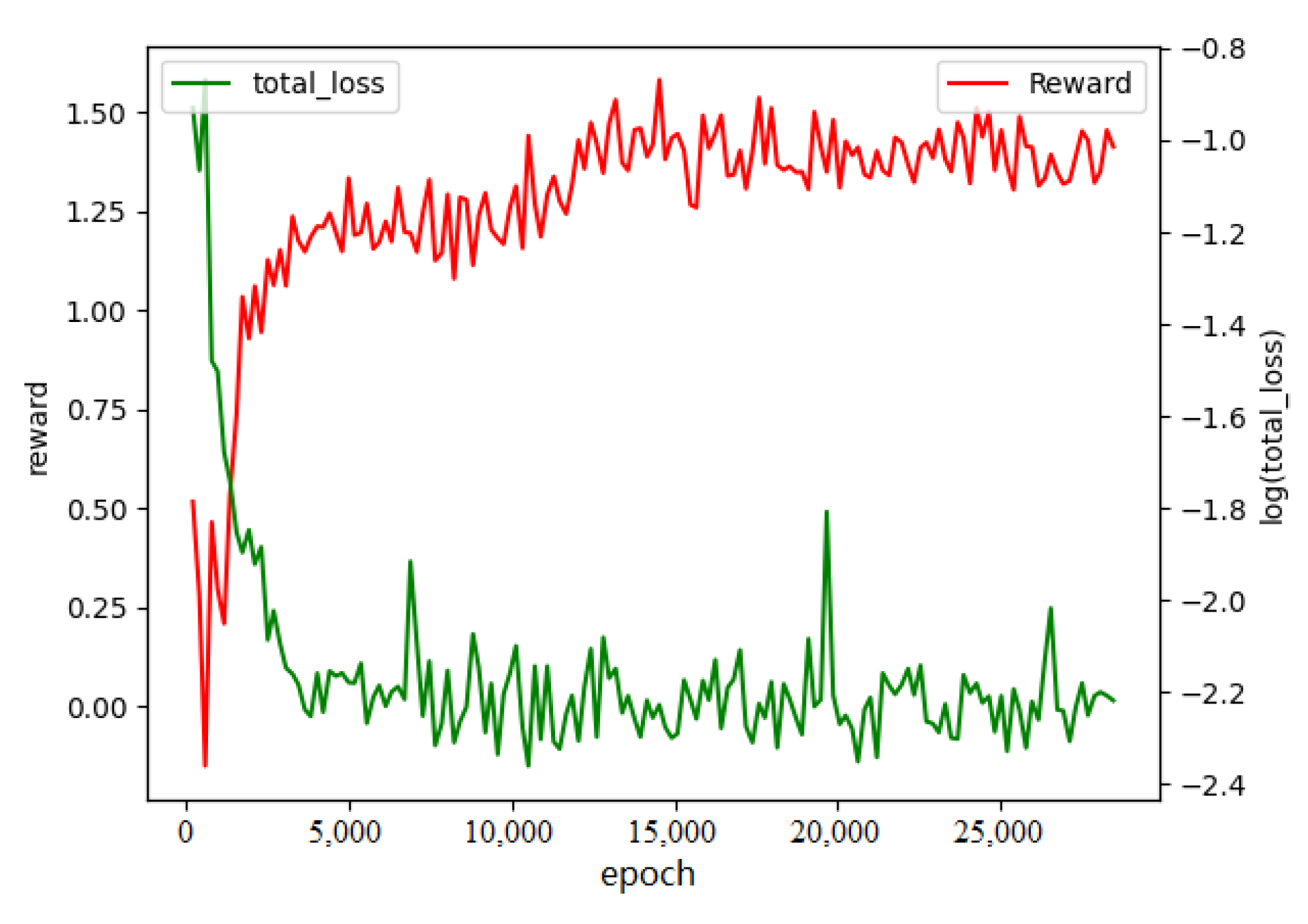
In the process of the computation offloading experiment, we set up seven agents to conduct computation offloading decisions. Tasks can be offloaded to three edge computing nodes or executed locally by agents. In the experiment, the observation space of each agent is , 5 in total. The action space is 4, meaning there are three edge computing nodes and one local device. Every ten generations of data are collected, and the agent loads the data with a batch size of 128 from the buffer for learning. The learning rate is , and the size of the hidden layer of the neural network is . Since computation offloading is a continuous process, we set the discounted factor as 1. At the same time, in order to encourage agents to explore more actions, we adopted the - method, with decaying from 1 to during the training process. We gave the iteration curve of Q-loss value and reward value in the training process, as shown in Figure 4.
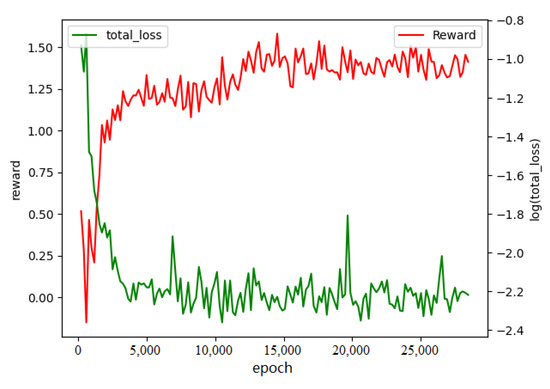
Figure 4.
Iteration curve of loss value and reward value. The data are smoothed for five generations. In order to better observe the trend of data changes, the data are logarithmically processed. Each evaluation of the agent goes through five interactions with the environment, and the final reward is stable at around 1.5, which is equivalent to an average reward value of 0.3 per interaction with the environment. That is, after the computation offloading plan, the current consumption is only 0.7 times of the local computation.
It can be seen from Figure 4 that the network loss value has been declining and finally approaches zero near the th generation. The reward function has a significant improvement in this process and tends to be stable around in the th generation. This shows that the agent is increasingly accurate in estimating the environment Q-value in the continuous interaction of the environment and has learned the method to improve the target reward value.
In order to more clearly illustrate the results of agent training, we select 10,000 and 30,000 generations of agent training models to evaluate in one round of computing offloading scenarios. The results are shown in Figure 5 and Figure 6.

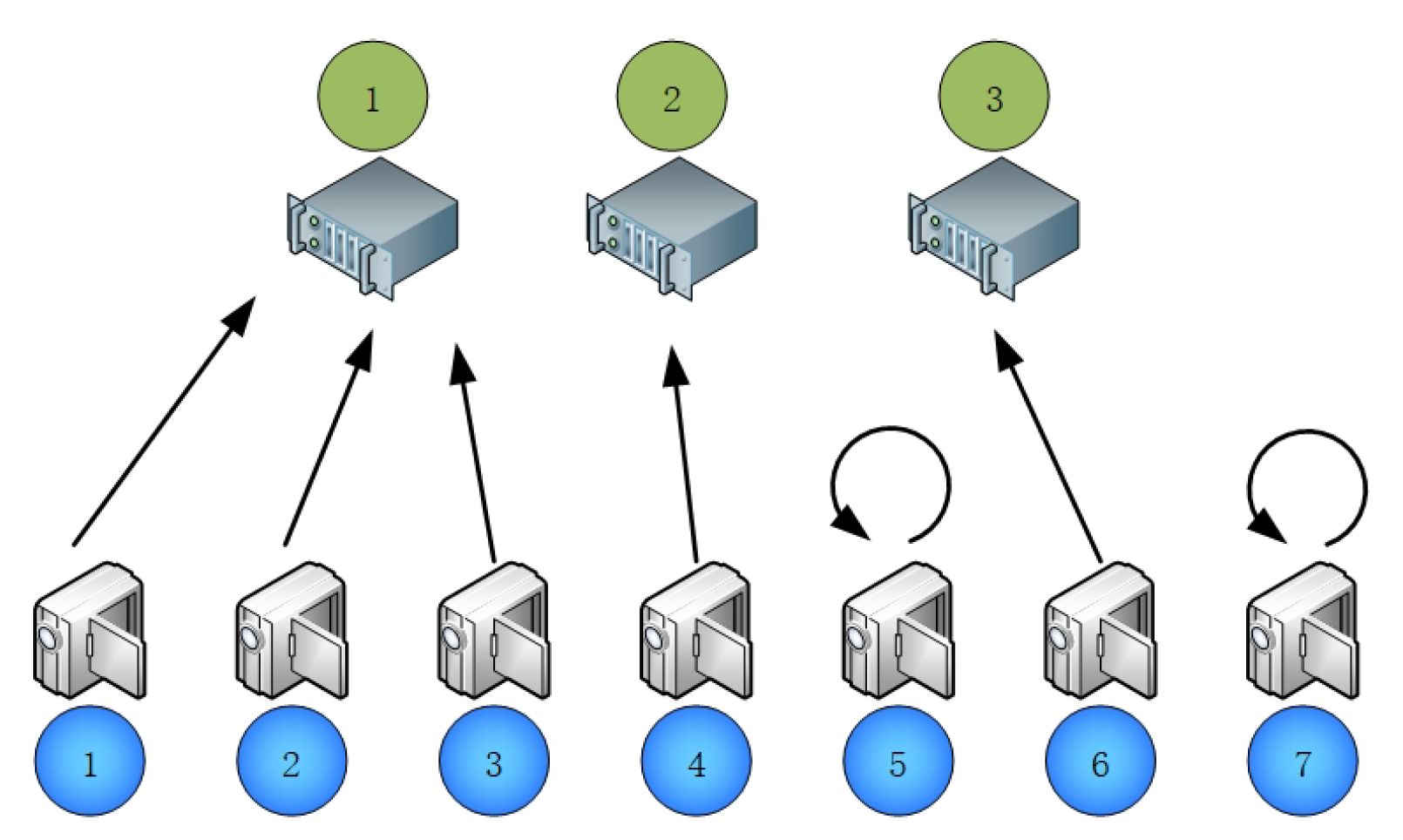
Figure 5.
Agent joint-action of 10,000 epoch training. In the above experimental settings, an optimal situation for two devices would be to select an edge computing node for computation offloading at the same time. In this scenario, three devices simultaneously select an edge node for offloading, which will cause channel congestion and increase the request delay. Nodes 2 and 3 are selected by only one device in computation offloading, which will lead to a waste of resources, while one device is chosen for local computation. The desired optimal effect was obviously not achieved in this action situation.
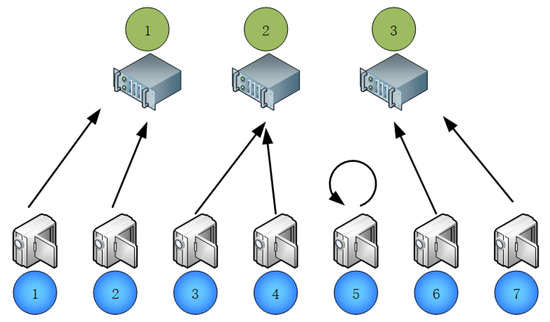
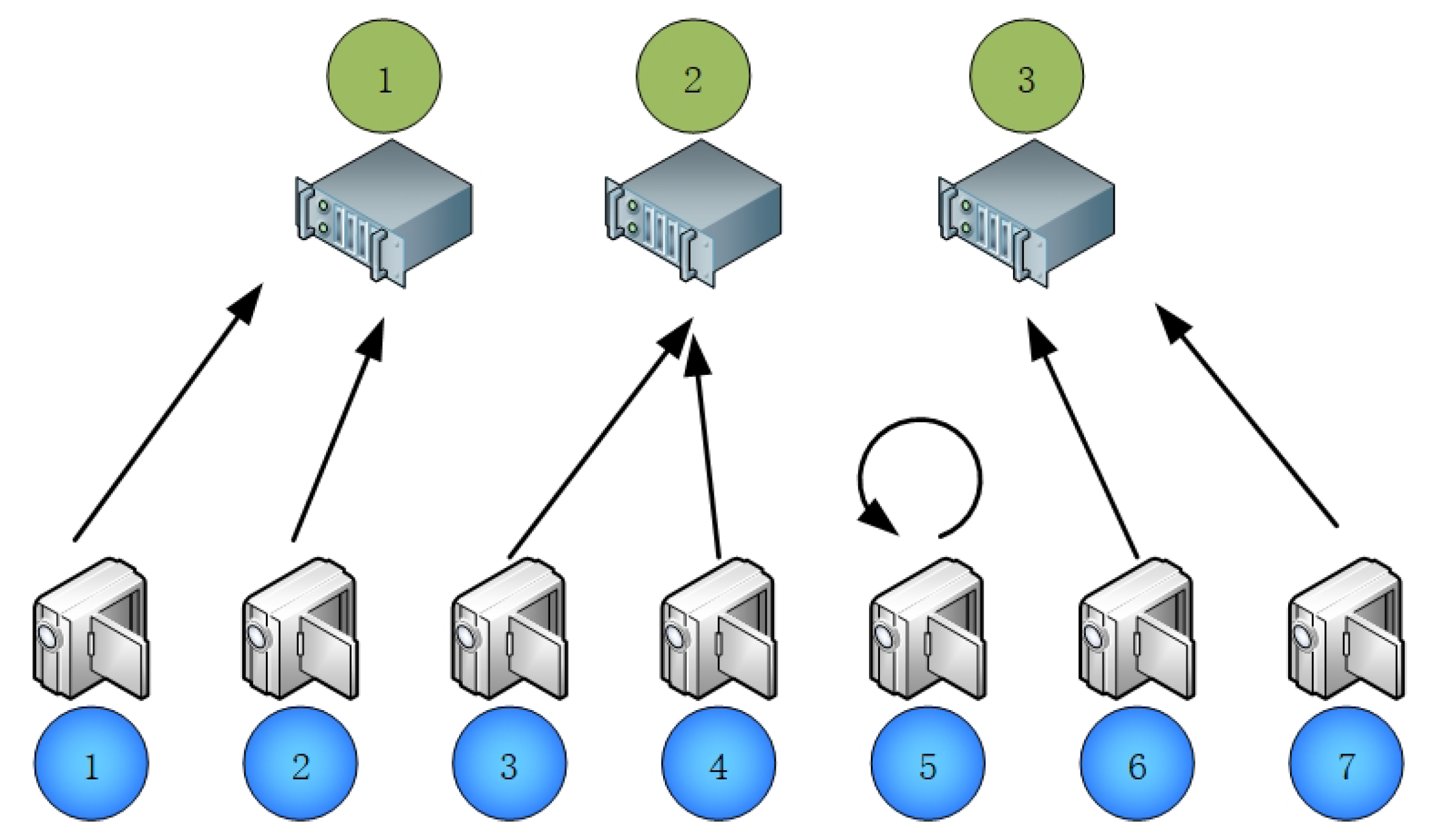
Figure 6.
Agent joint-action of 30,000 epoch training. In this scenario, each edge computing node is selected by two devices for computation offload, which achieves the best utilization of resources. At the same time, the device No. 5, with the worst channel state, is selected for local computing. It can be seen that, after 30,000 generations of training, the agent has learned how to make optimal decisions.
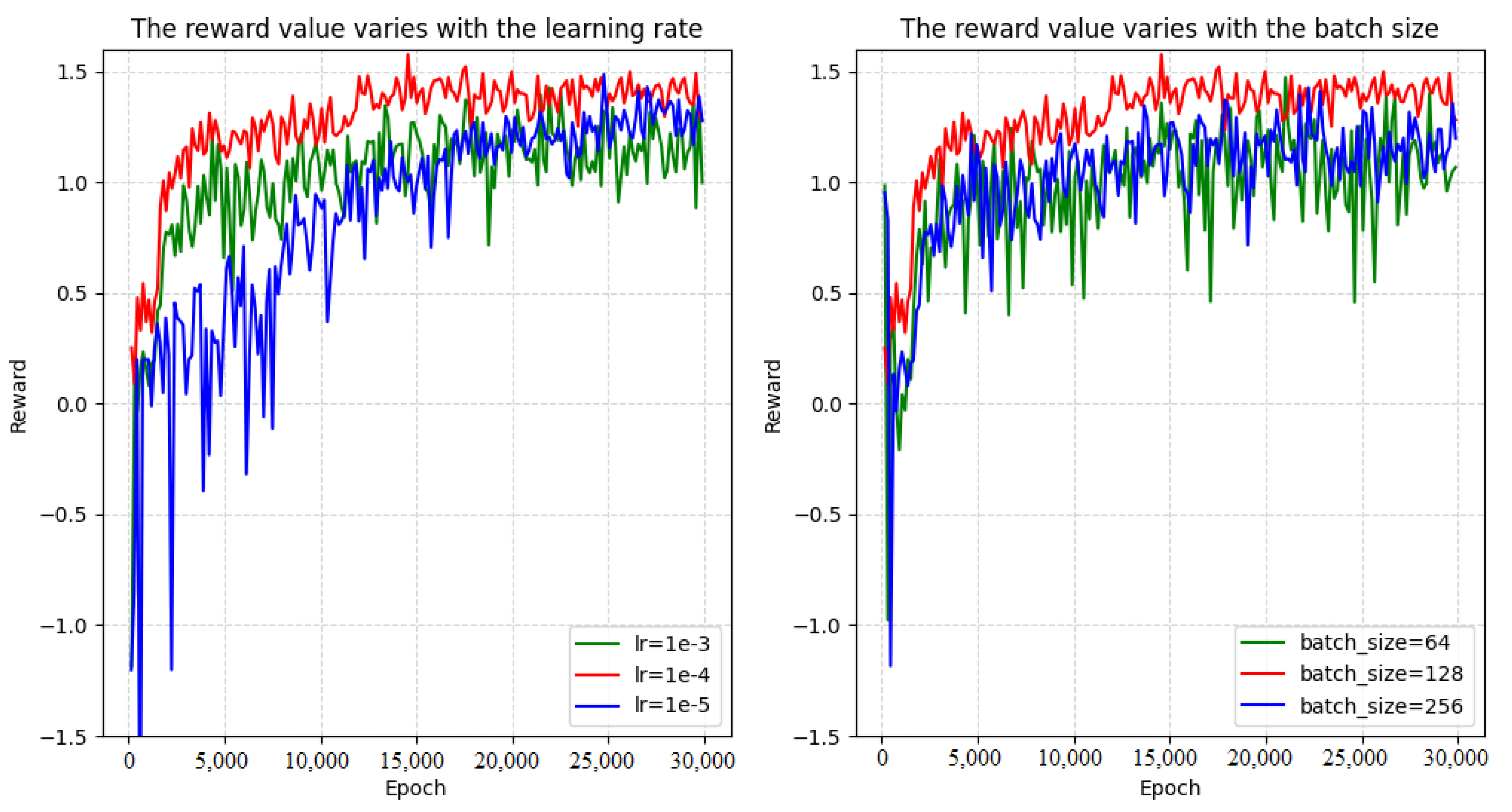
In addition, to demonstrate the rationality of our parameter selection, we conduct experiments comparing learning rate and . The result is shown as Figure 7.
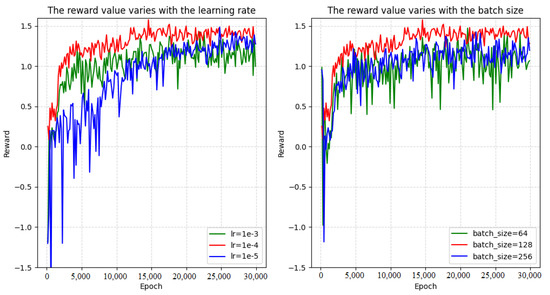
Figure 7.
Reward curse change with learning rate and batch size.
It can be seen that, when a higher learning rate is selected, the learning effect is not good, and the reward function cannot converge due to oscillation back and forth. When a lower learning rate is selected, the reward value function converges slowly and cannot reach the optimal value. Similarly, when a large batch size is selected, convergence of the reward value function is difficult, and it is difficult to reach the optimal value. When a small batch size is selected, it is difficult for the agent to effectively learn knowledge, resulting in non-convergence of the training curve.
4.2.2. Agent Number Comparison Experiment
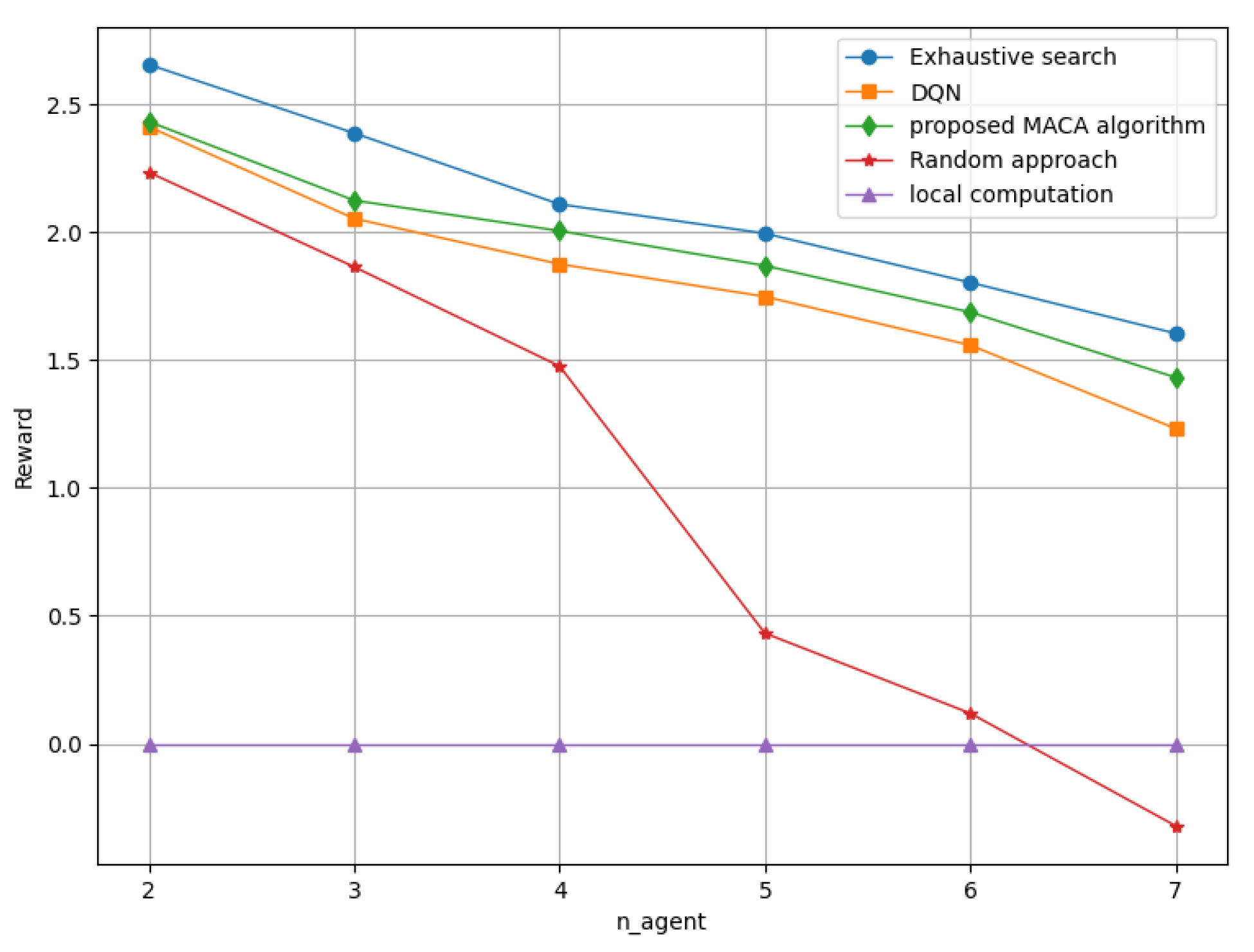
In order to demonstrate that our proposed MACA algorithm is superior to traditional methods, we compare the performance of the MACA algorithm with a deep Q-learning algorithm, random offloading approach, and local computation approach. To ensure fairness in comparison, we use the same training trick of double Q-network and dueling Q-network in DQN. It can be seen that the reinforcement learning algorithm is more effective than the random approach and local computation approach. Moreover, when the number of devices as independent agents increases, the performance of DQN decreases significantly, while the performance of our proposed algorithm remains relatively stable. This is obvious because, as the number of agents increases, the action space of the DQN algorithm will increase in geometric multiples, while the multi-agent algorithm will combine the rewards of each agent into an overall reward, which only increases the action space linearly, thus allowing it to easily avoid this problem, and the specific results are shown in Figure 8.
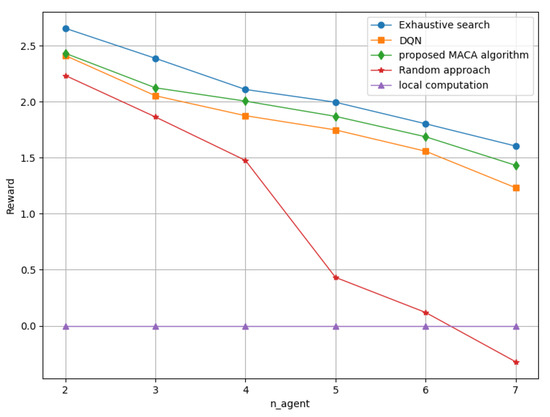
Figure 8.
Algorithm performance varies with the number of agents.
As the number of agents increases, the reward value obtained by interacting with the environment is increasingly diminished because the computing resources available to edge computing nodes also continually decrease, and so to does the reduced value relative to local computing. It can be seen that the performance of our proposed MACA algorithm is more stable and higher than the corresponding DQN algorithm, and this phenomenon is especially obvious when the number of agents increases. However, when the number of agents is 7, the effect of random assignment approach is even worse than that of local computation, which further illustrates the importance of planning computing offloading. More results are shown in Table 2.

Table 2.
The reward value varies with devices and computing nodes.
We also evaluate the time taken to solve the computation offloading schedule for different methods. Solving a problem of the same size and parameters on the same computer configuration, the DQN method takes 0.902 s, our proposed MACA method takes 0.971 s, and the method using exhaustive search takes 184.985 s. It can be seen that our method reduces the computation time to about 1/200 of the original.
4.2.3. Ablation Experiment
In this subsection, we ablate each component in the MACA algorithm and compare the contribution of each component in the algorithm.
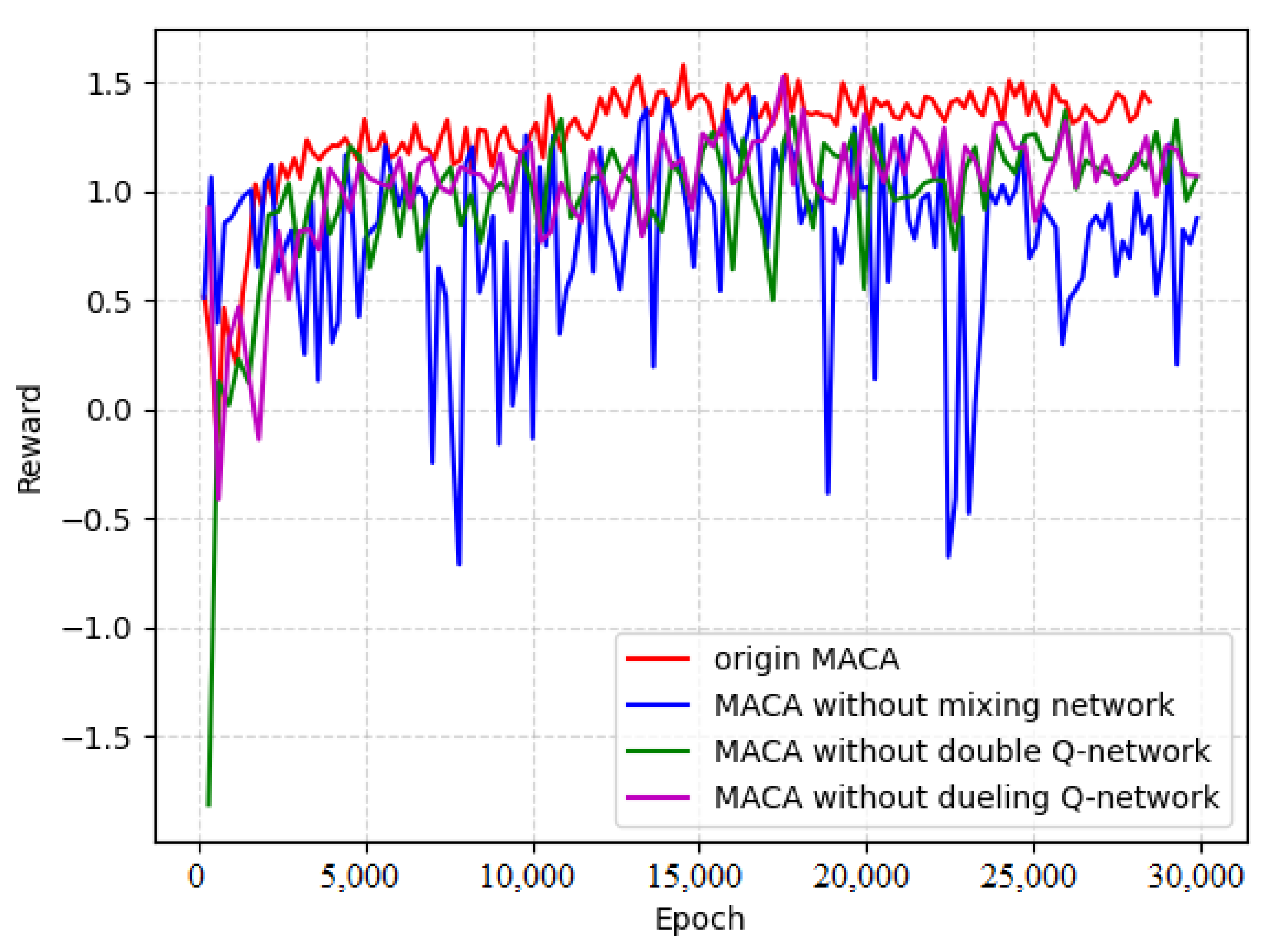
We compared the original MACA algorithm, the MACA algorithm without a mixing network, the MACA algorithm without a double Q-network, and the MACA algorithm without dueling Q-network, corresponding to a total of four curves. In the ablation experiment, seven local device and three edge computing nodes are set. In addition, all experiments were carried out under the optimal experimental conditions selected above. The results of the ablation experiment are shown as Figure 9.
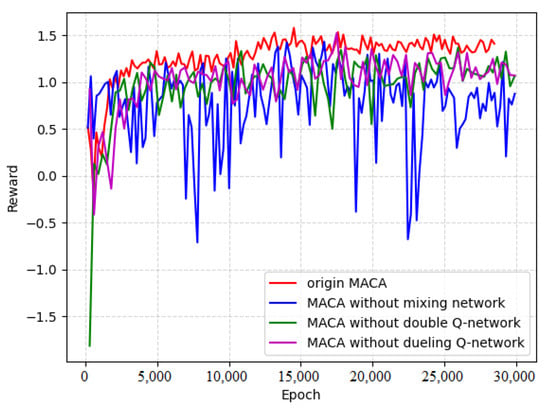
Figure 9.
Ablation experiment results.
As can be seen in Figure 9, compared with the original MACA algorithm, if the mixing network is removed, the training curve will fluctuate greatly, which results in difficulties for achieving convergence, and it is difficult to obtain the optimal effect. Removing the double Q-network or dueling Q-network will lead to slower training and worse final results. The results of the ablation experiments show that our proposed value decomposition method based on credit assignment can avoid the problem of the dimensional curse and allow the agent to more effectively learn the cooperative strategy. At the same time, the addition of the double Q-network and dueling Q-network to the architecture can effectively alleviate the overestimation of the Q network and help the agent reduce the interference caused by the dynamic environment, effectively promoting the learning process of the agent.
4.3. Discussion
In this paper, a multi-agent reinforcement learning algorithm is proposed for computation offloading in smart park monitoring. By training the agent offline and making decisions online, the reinforcement learning method solves the shortcomings of high computing delay in the traditional method and can effectively reduce the delay and energy consumption in the process of computation offloading. In the experimental part, we demonstrated the effectiveness of our proposed algorithm by presenting the training process and training results of the MACA algorithm. Then, through generalization experiments on the number of agents and devices, we show that, compared with the DQN algorithm, random allocation, and local computation approaches, our proposed MACA algorithm achieves the highest performance in most cases. Finally, the contribution of each component of the MACA algorithm to the overall algorithm is verified through the ablation experiment for the Q-network architecture.
Although, to a certain extent, some progress has been made in our research in terms of performance, there are still some limitations. First, more complex challenges are often faced in real computation offloading environments. On the one hand, the impact of edge computing node deployment location on offloading efficiency should be considered and, on the other hand, the queuing theory model between tasks should be considered. Second, the performance comparison between our proposed value-based multi-agent reinforcement learning method and some existing policy-based reinforcement learning methods remains to be conducted. Finally, the safety and interpretability of artificial intelligence algorithms, such as reinforcement learning, have always been an issue, and further work on the interpretation of models needs to be conducted.
5. Conclusions
This paper studies the problem of computation offloading for multiple video monitoring in smart parks and introduces deep reinforcement learning as a solution, in which offline training and online decision-making are introduced to resolve unbearable computational delays, which represent the problem of traditional methods. Credit assignment is used to extend the single-agent scenario to a multi-agent scenario and solve the problem of cooperation between agents. As an agent, each device chooses to deal with computing-intensive tasks locally or through computation offloading. We evaluated the algorithm effect with different numbers of devices and edge computing nodes, thus demonstrating that our proposed MACA algorithm is more stable than many existing algorithms and can more effectively identify the computation offloading scheme in the search space with geometric multiple growth. On this basis, the random arrival of tasks and time-varying bandwidth channel is simulated, and offline training and online decision-making are carried out according to the task size and CPU cycles within a certain range to better formulate resource allocation strategies. With the introduction of the Q-network tricks, agents can optimize themselves more clearly based on the double Q-network and dueling Q-network. A large number of simulation experiments and ablation experiments were used to verify the validity of the model. This model can meet the requirements of the real-time offloading of computing-intensive tasks and reduce the request delays and computing energy consumption of tasks.
Author Contributions
Methodology, L.S.; Investigation, J.W. and Y.B.; Data curation, L.S.; Writing — original draft, L.S. and Y.B.; Writing — review and editing, J.W.; Supervision, J.W. and Y.Z.; Funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 72274058).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Notation | Definition |
| N | The set of camera device group |
| f | Edge computing node |
| T | The computation offloading cycle |
| The amount of data that needs to be uploaded to complete the task | |
| The number of CPU cycles required for computing tasks | |
| The channel bandwidth between the device n and the edge computing node f | |
| P | The power of the computational offloading task |
| h | The gain of the communication channel when the task is transmitted |
| The variance of the complex Gaussian white channel noise | |
| Time delay of execute task locally | |
| Local computational capability | |
| Edge computing node computational capability | |
| Energy consumption for executing task locally | |
| Time delay of transmission when executing task with edge node | |
| Time delay of computation when executing task with edge node | |
| Energy consumption of transmission when executing task with edge node | |
| Energy consumption of computation when executing task with edge node | |
| The cost of computation offloading process |
References
- Kim, J.B.; Kim, H.J. Efficient region-based motion segmentation for a video monitoring system. Pattern Recognit. Lett. 2003, 24, 113–128. [Google Scholar] [CrossRef]
- Li, C.; Pourtaherian, A.; van Onzenoort, L.; a Ten, W.T.; de With, P. Infant facial expression analysis: Towards a real-time video monitoring system using R-CNN and HMM. IEEE J. Biomed. Health Inform. 2020, 25, 1429–1440. [Google Scholar] [CrossRef] [PubMed]
- Kekki, S.; Featherstone, W.; Fang, Y.; Kuure, P.; Li, A.; Ranjan, A.; Purkayastha, D.; Jiangping, F.; Frydman, D.; Verin, G.; et al. Mec in 5G networks. ETSI White Pap. 2018, 28, 1–28. [Google Scholar]
- Zeng, F.; Tang, J.; Liu, C.; Deng, X.; Li, W. Task-offloading strategy based on performance prediction in vehicular edge computing. Mathematics 2022, 10, 1010. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile edge computing: A survey on architecture and computation offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Lin, L.; Liao, X.; Jin, H.; Li, P. Computation offloading toward edge computing. Proc. IEEE 2019, 107, 1584–1607. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep reinforcement learning that matters. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Nosratabadi, S.; Mosavi, A.; Duan, P.; Ghamisi, P.; Filip, F.; Band, S.S.; Reuter, U.; Gama, J.; Gandomi, A.H. Data science in economics: Comprehensive review of advanced machine learning and deep learning methods. Mathematics 2020, 8, 1799. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An introduction to deep reinforcement learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, L.; Wei, Q.; Xu, X.; Chen, C. A novel DDPG method with prioritized experience replay. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 316–321. [Google Scholar]
- Thomas, P.S.; Brunskill, E. Policy gradient methods for reinforcement learning with function approximation and action-dependent baselines. arXiv 2017, arXiv:1706.06643. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Heess, N.; TB, D.; Sriram, S.; Lemmon, J.; Merel, J.; Wayne, G.; Tassa, Y.; Erez, T.; Wang, Z.; Eslami, S.; et al. Emergence of locomotion behaviours in rich environments. arXiv 2017, arXiv:1707.02286. [Google Scholar]
- Konda, V.; Tsitsiklis, J. Actor-critic algorithms. Adv. Neural Inf. Process. Syst. 1999, 12, 1008–1014. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30, 6382–6393. [Google Scholar]
- Lee, H.; Park, S.; Kim, J.; Kim, J. Auction-based deep learning computation offloading for truthful edge computing: A myerson auction approach. In Proceedings of the 2021 International Conference on Information Networking (ICOIN), Jeju Island, Republic of Korea, 13–16 January 2021; pp. 457–459. [Google Scholar]
- Pradhan, C.; Li, A.; She, C.; Li, Y.; Vucetic, B. Computation offloading for iot in C-RAN: Optimization and deep learning. IEEE Trans. Commun. 2020, 68, 4565–4579. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, Y.; Leng, S.; He, Y.; Maharjan, S.; Zhang, Y. Deep learning empowered task offloading for mobile edge computing in urban informatics. IEEE Internet Things J. 2019, 6, 7635–7647. [Google Scholar] [CrossRef]
- Ren, Y.; Sun, Y.; Peng, M. Deep reinforcement learning based computation offloading in fog enabled industrial internet of things. IEEE Trans. Ind. Inform. 2020, 17, 4978–4987. [Google Scholar] [CrossRef]
- Yu, S.; Chen, X.; Yang, L.; Wu, D.; Bennis, M.; Zhang, J. Intelligent edge: Leveraging deep imitation learning for mobile edge computation offloading. IEEE Wirel. Commun. 2020, 27, 92–99. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4295–4304. [Google Scholar]
- Bušoniu, L.; Babuxsxka, R.; Schutter, B.D. Multi-agent reinforcement learning: An overview. In Innovations in Multi-Agent Systems and Applications—1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 183–221. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).