The Effect of Adhesion on Indentation Behavior of Various Smart Materials
Abstract
:1. Introduction
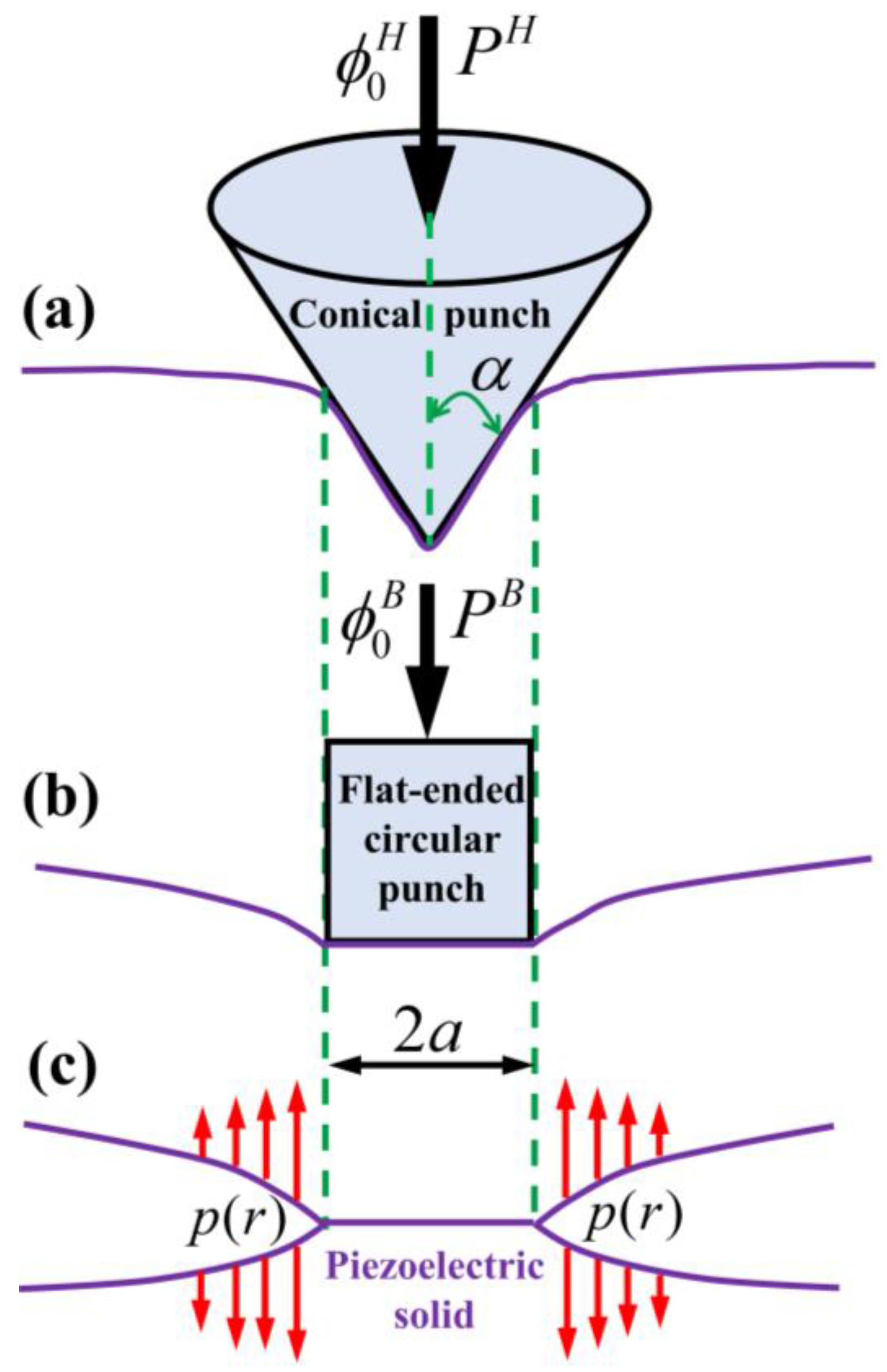
2. Problem Description and Formulation
2.1. Problem Description
2.2. Governing Equations
2.3. General Solutions
3. The Solution of the JKR Model
3.1. Boundary Conditions for the JKR Model
3.2. The Solution of Case I: Electrically Conducting Punch
4. The Solution of M-D Model
4.1. Boundary Conditions for the M-D Model
4.2. The Solution of Case I: Electrically Conducting Punch
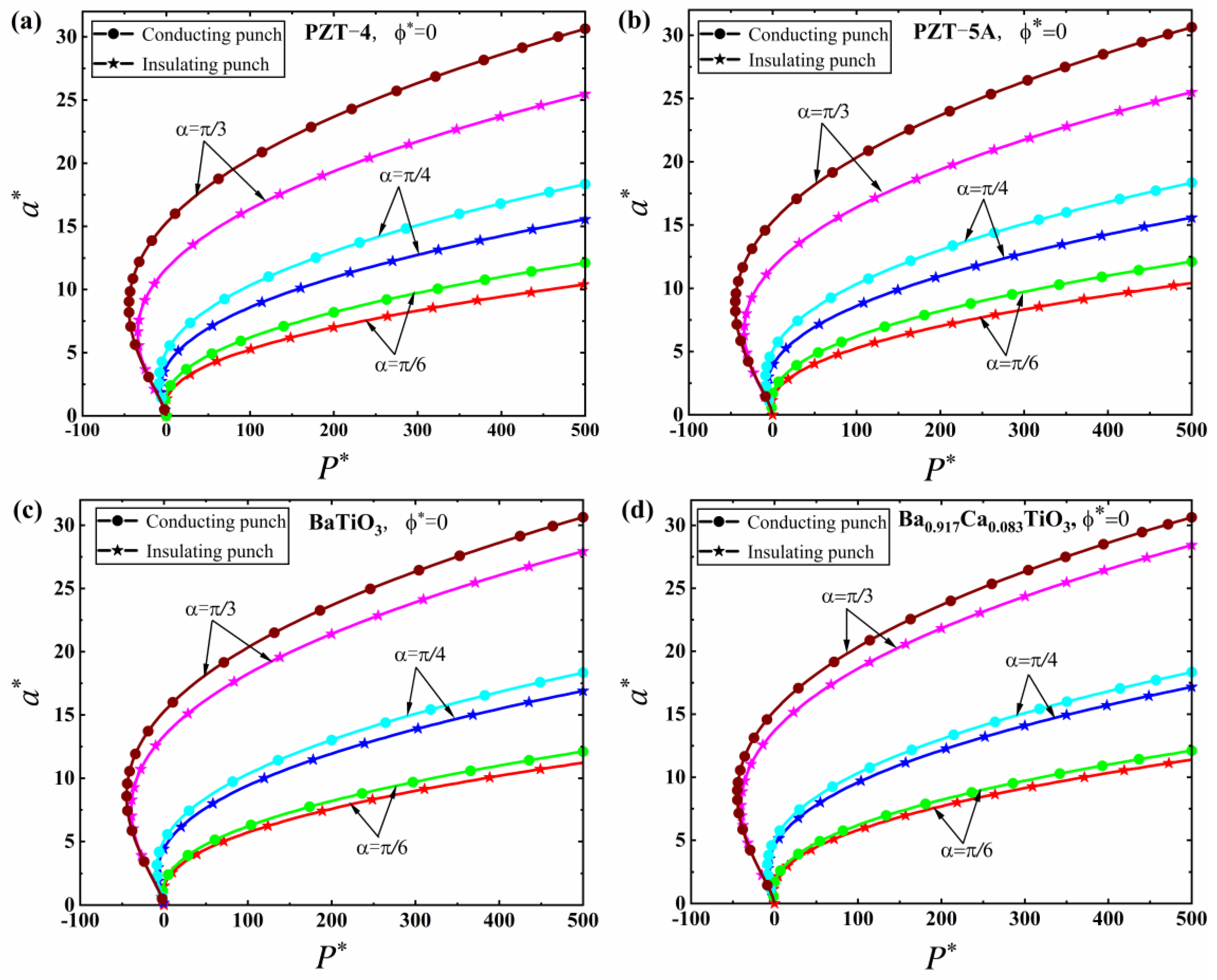
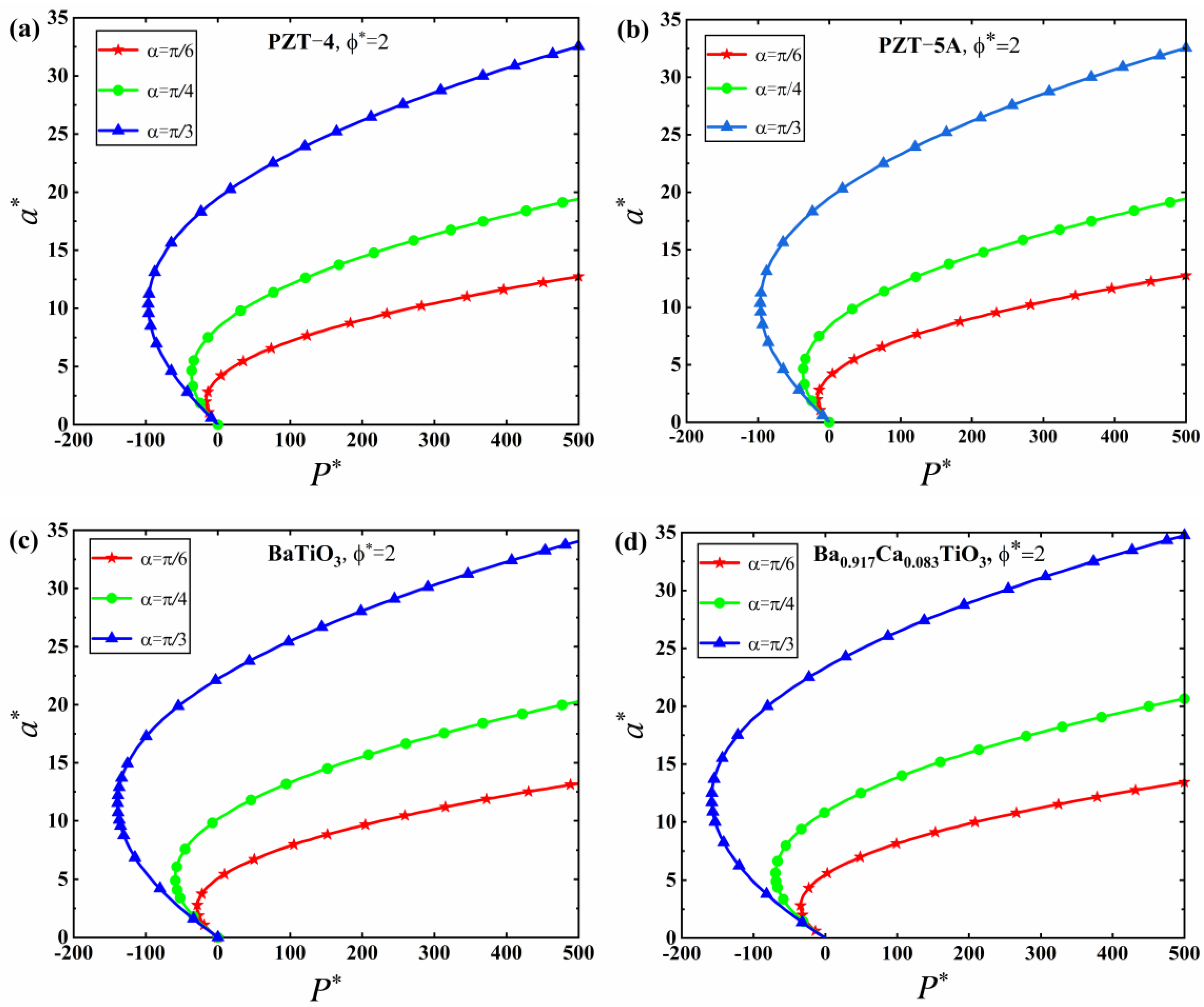
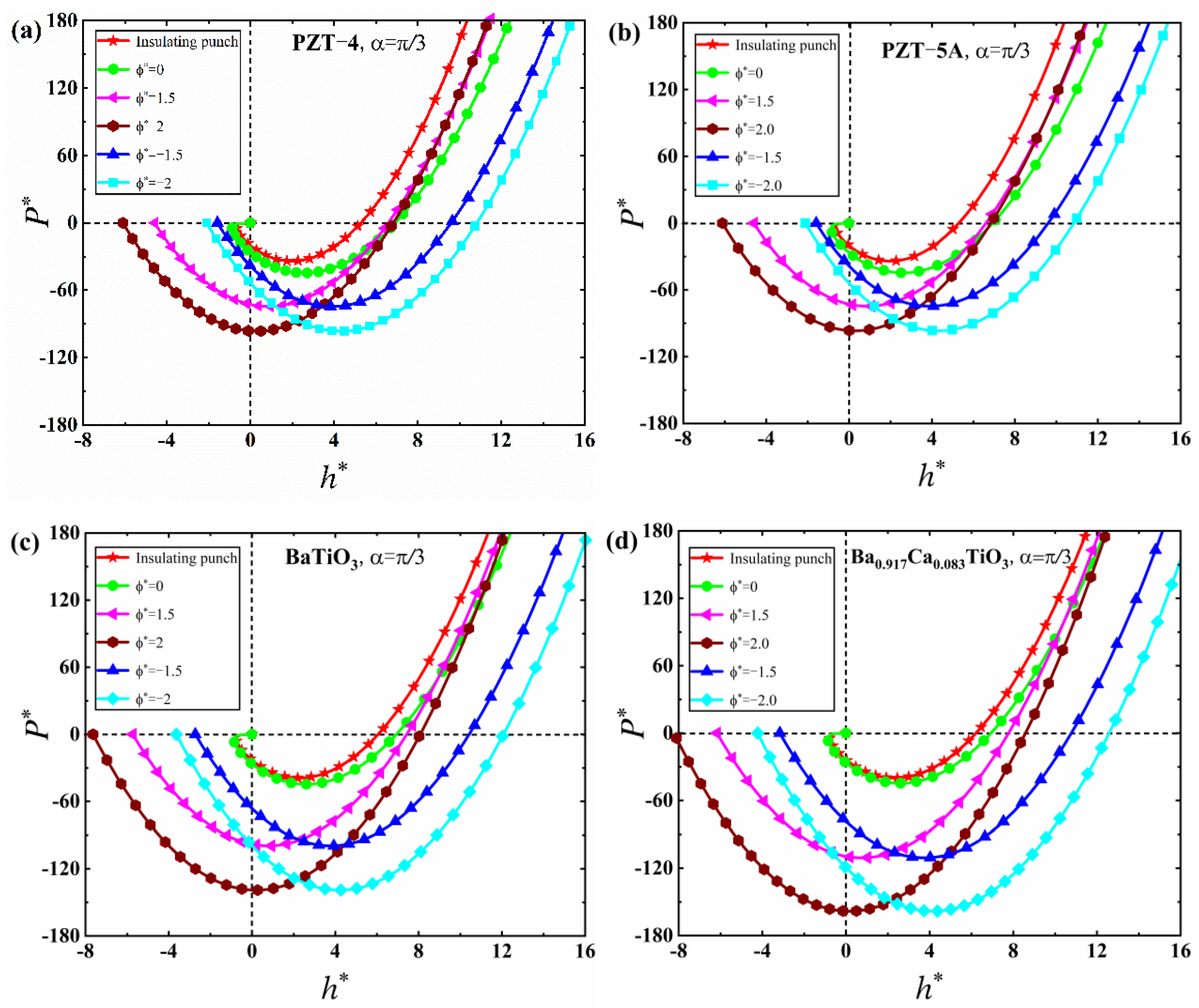
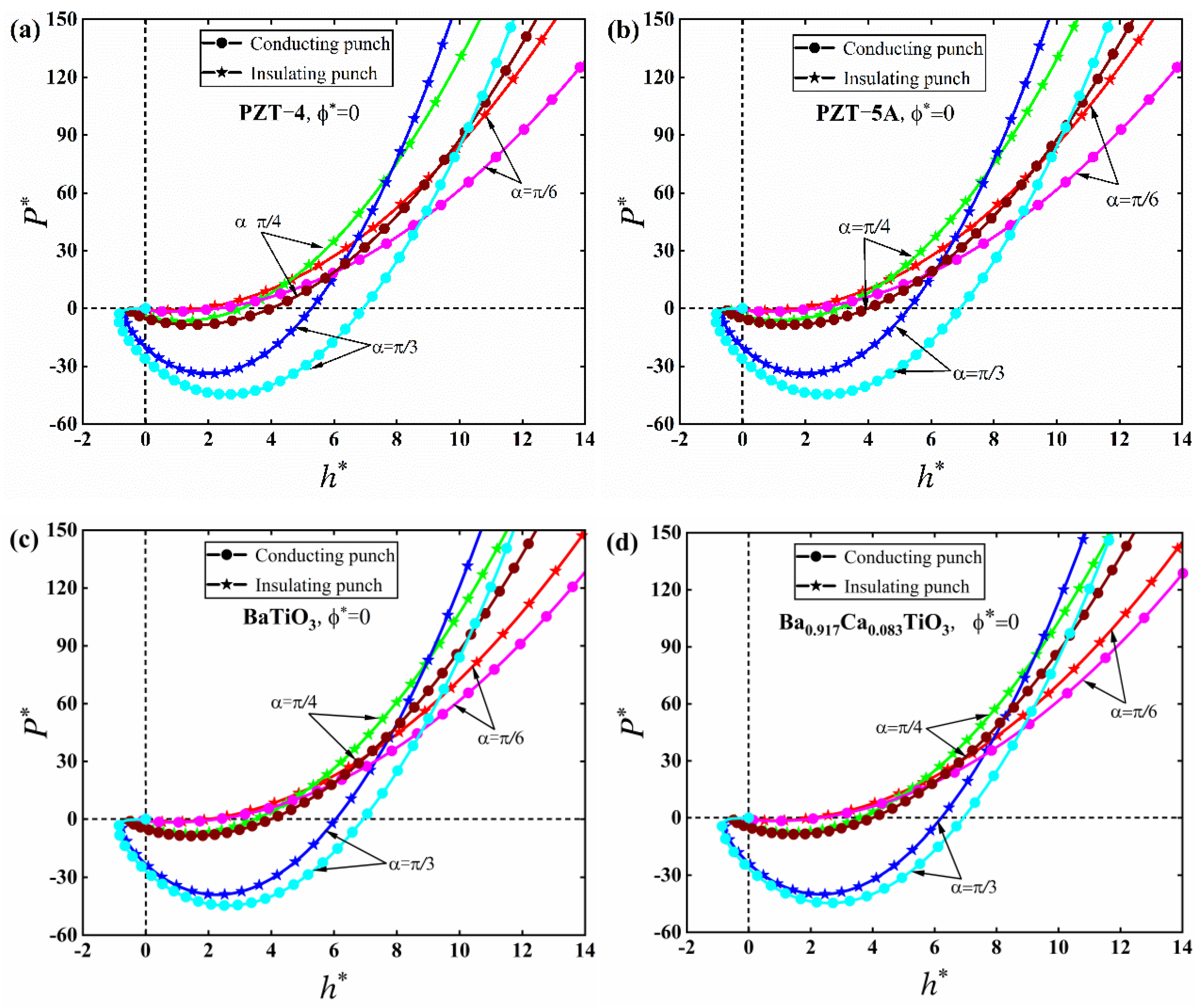
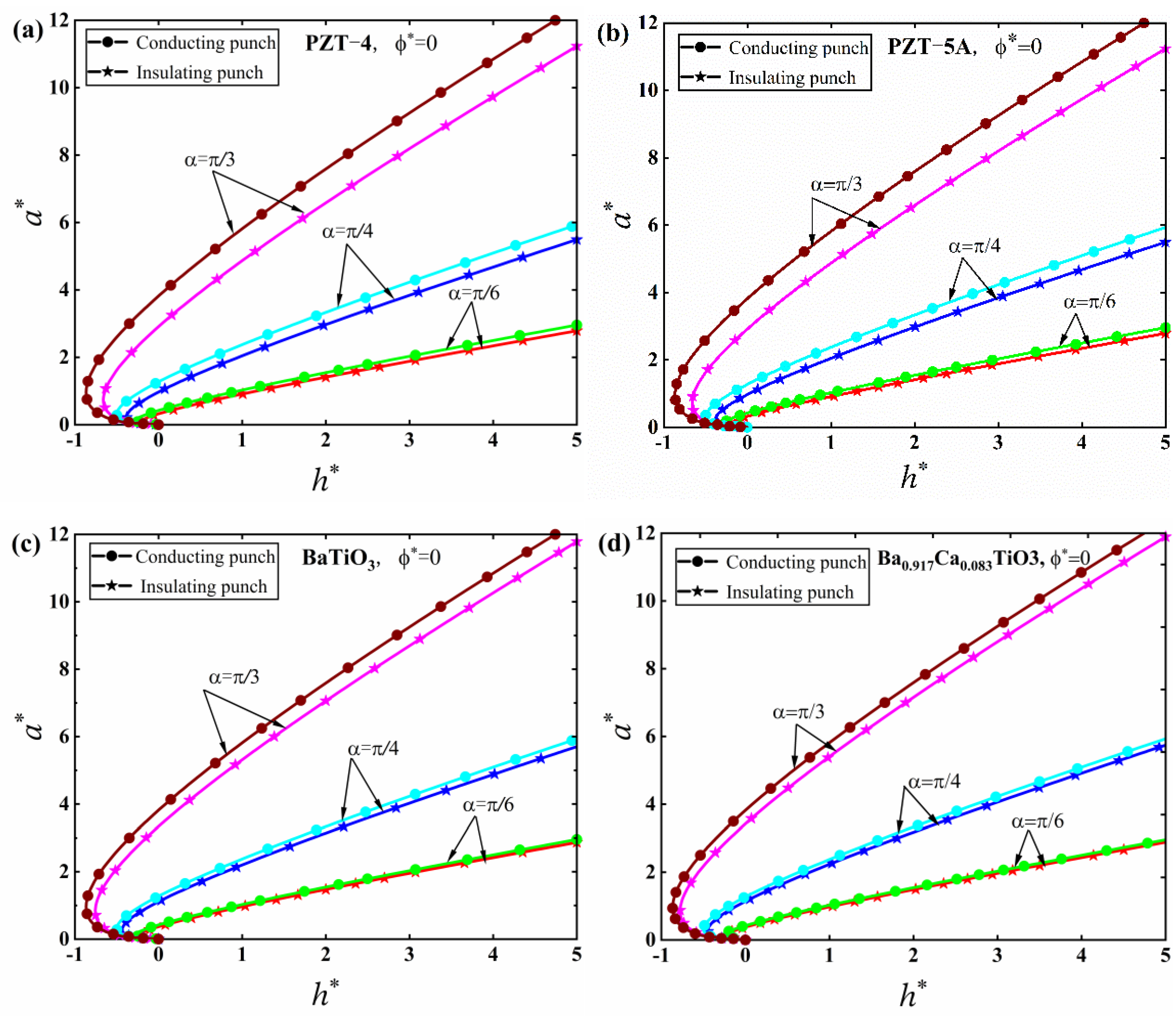
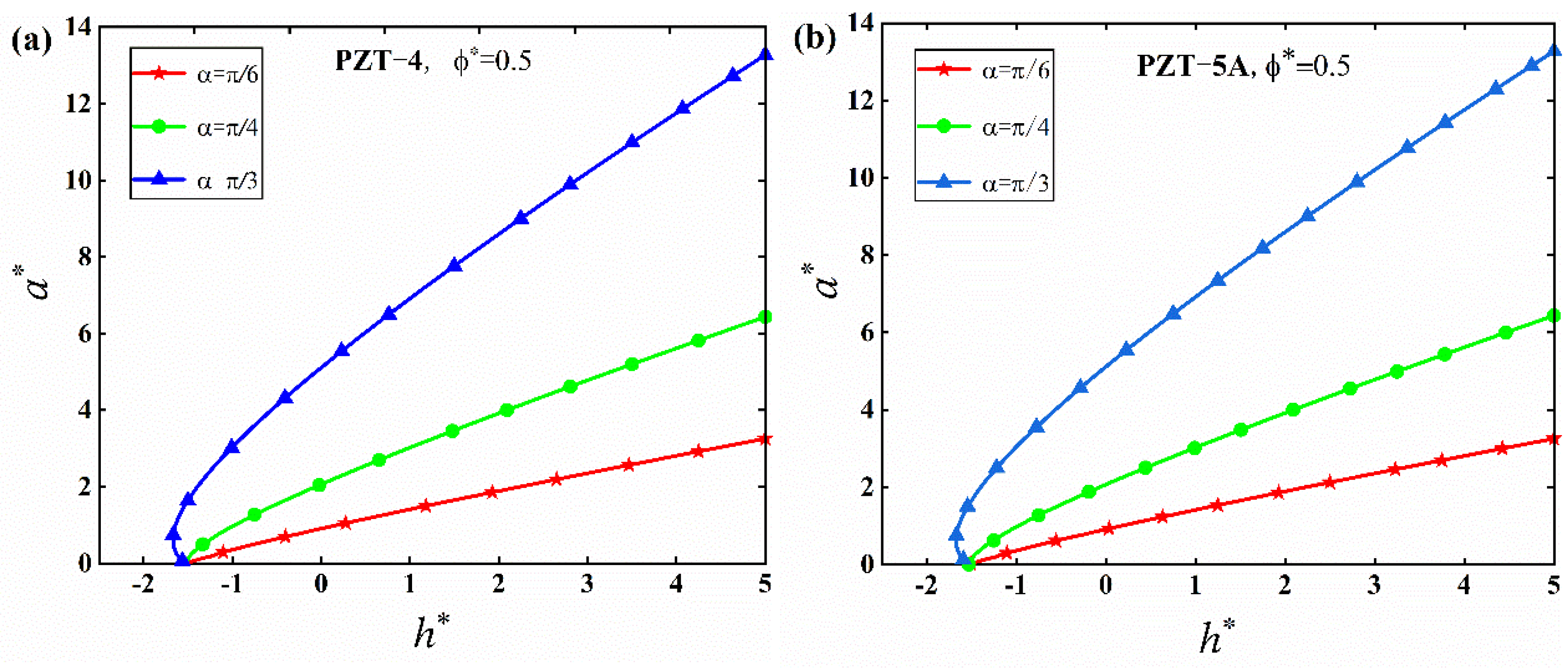
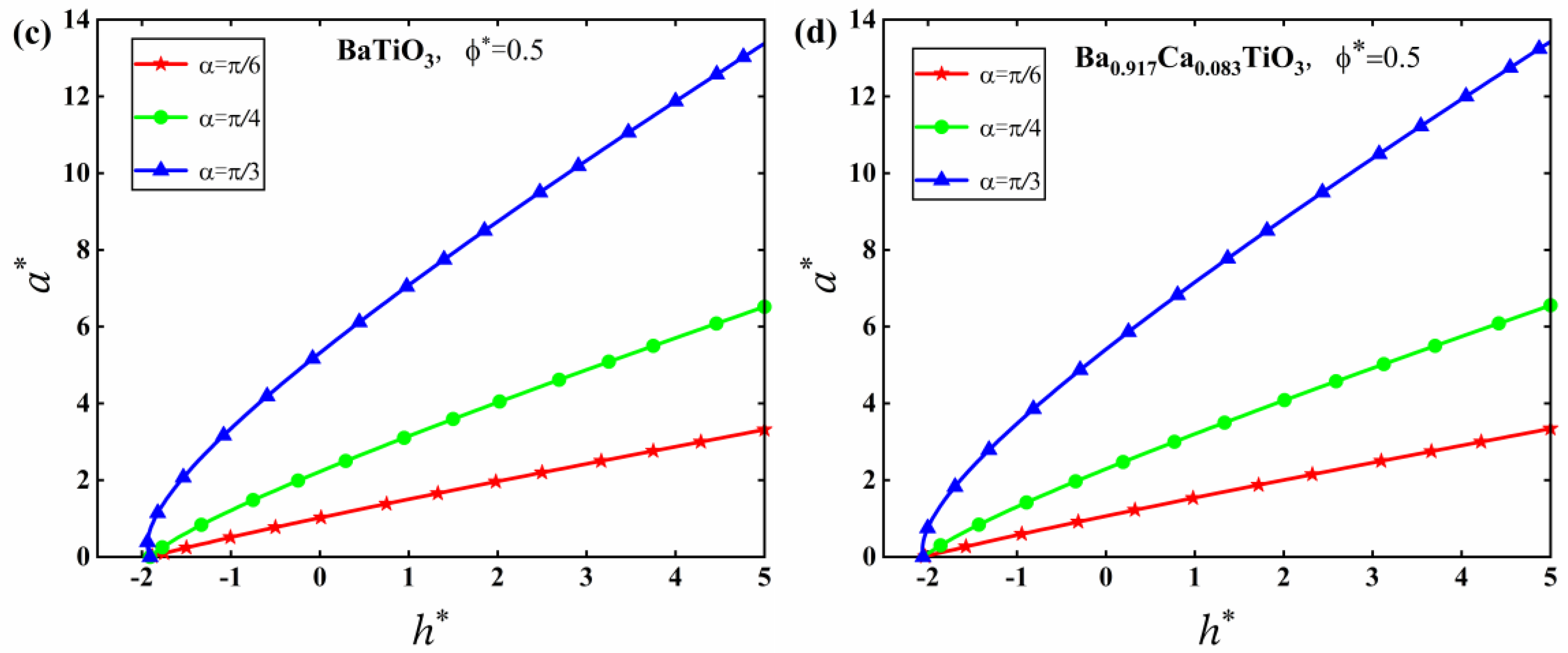
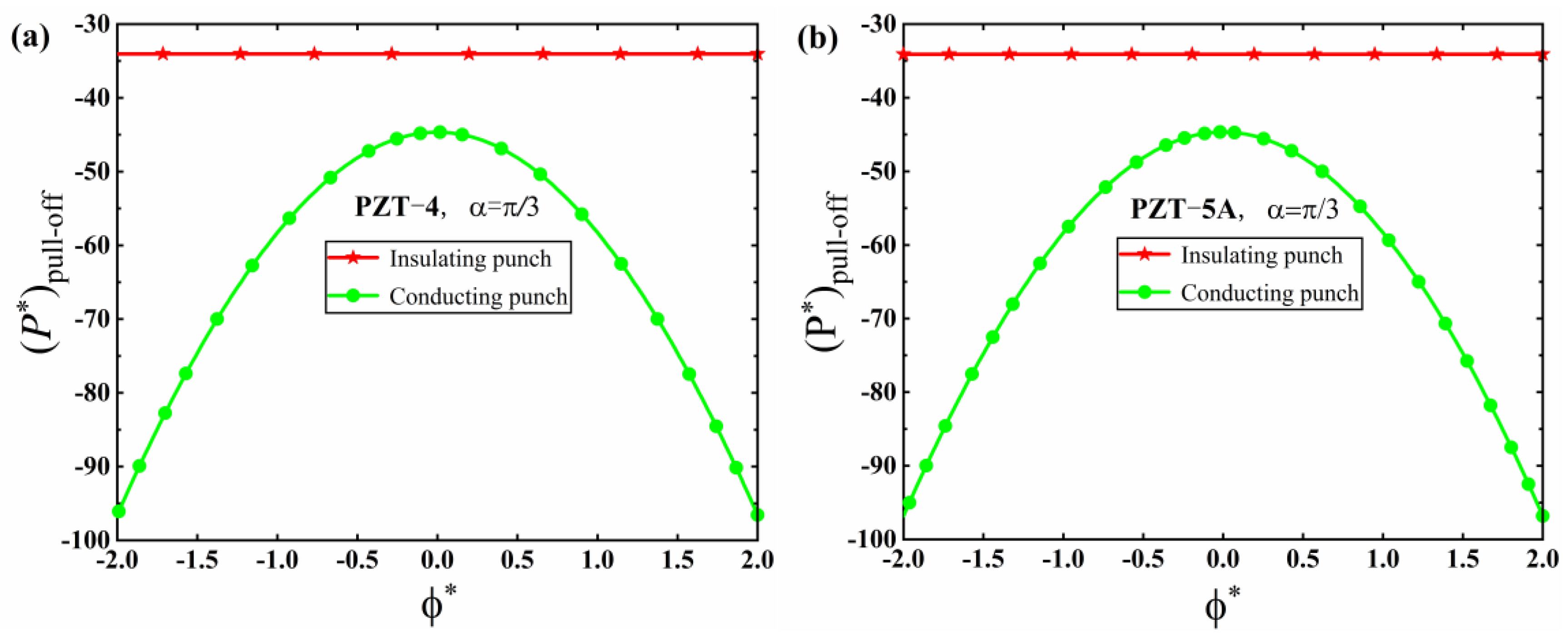
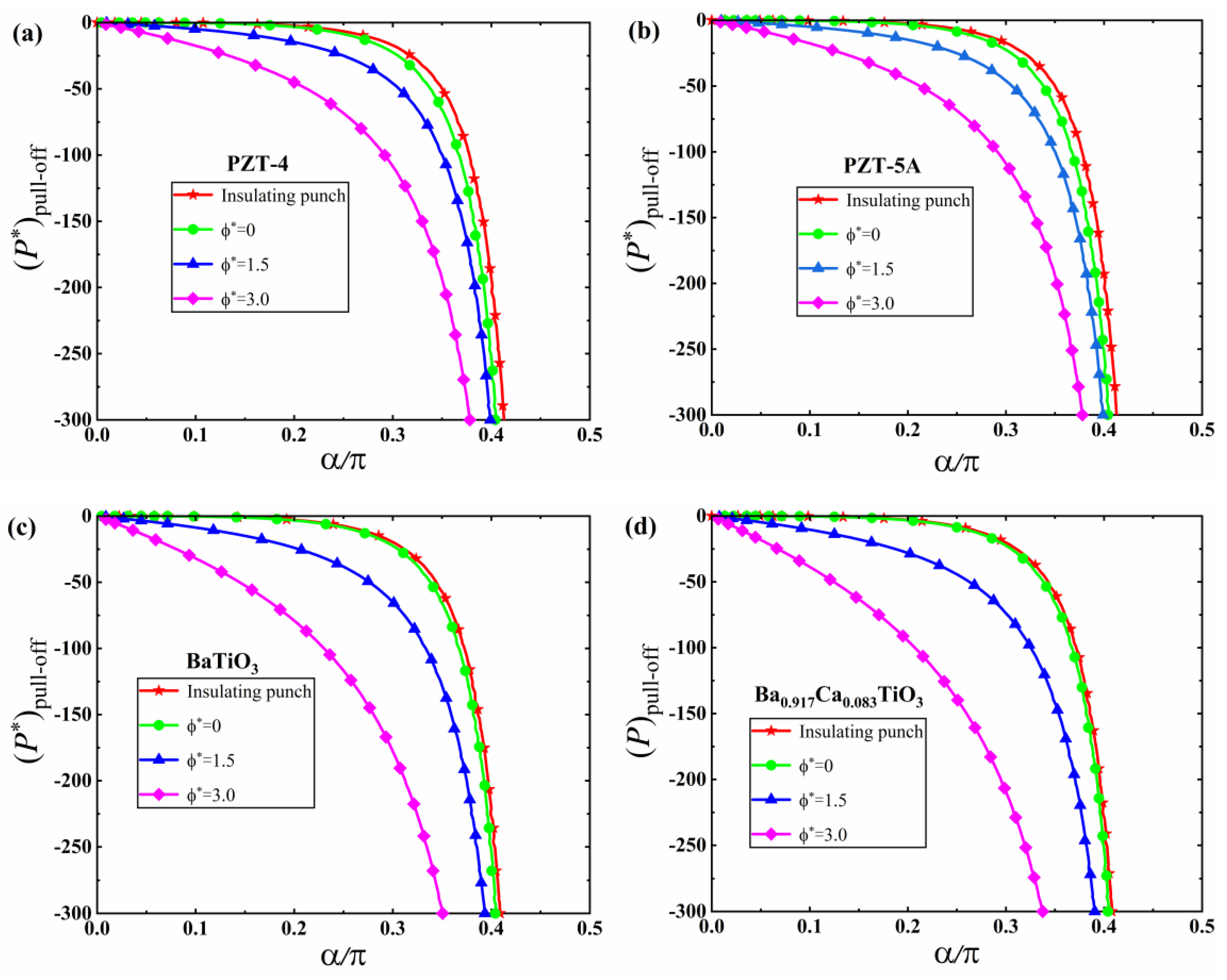
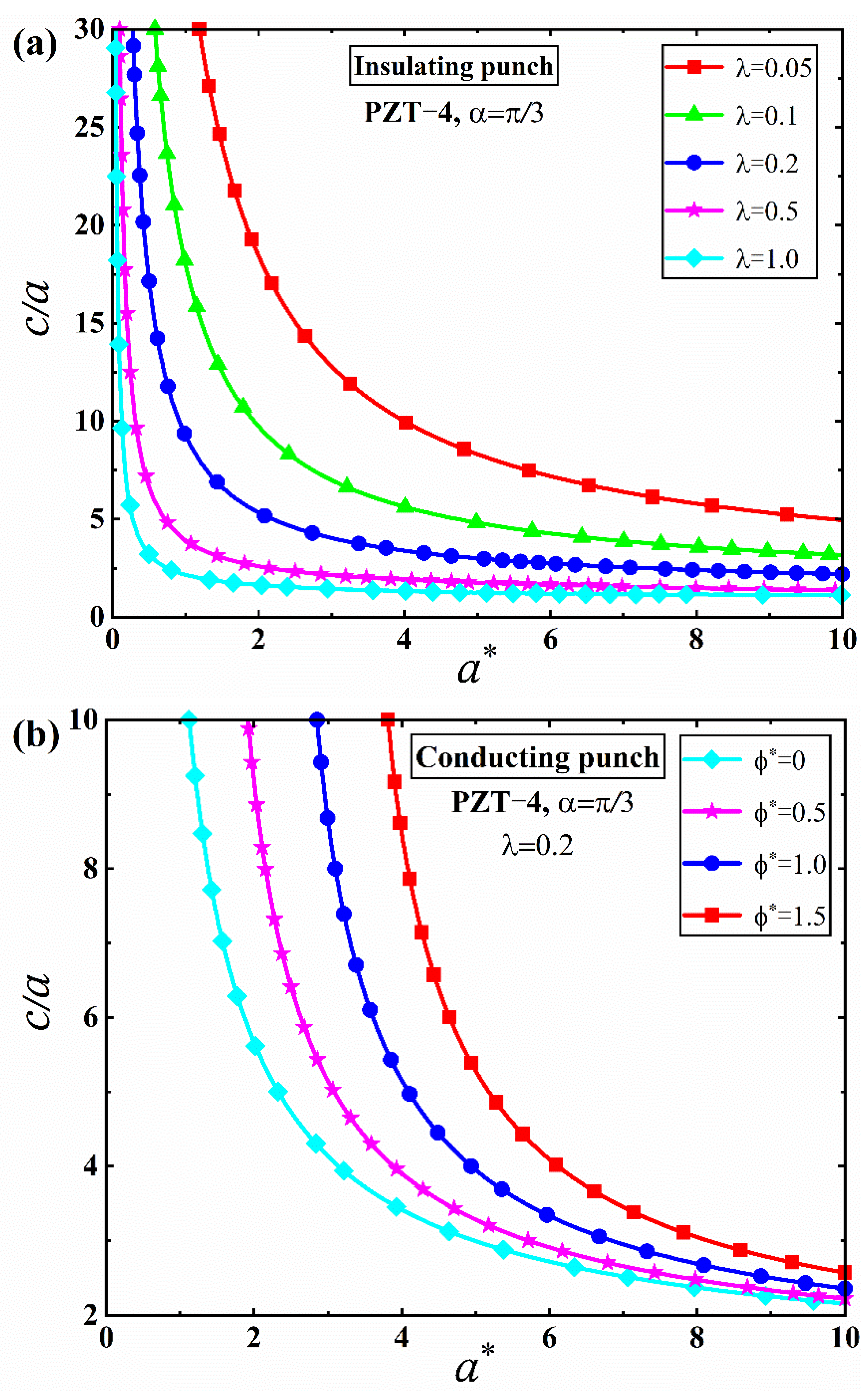
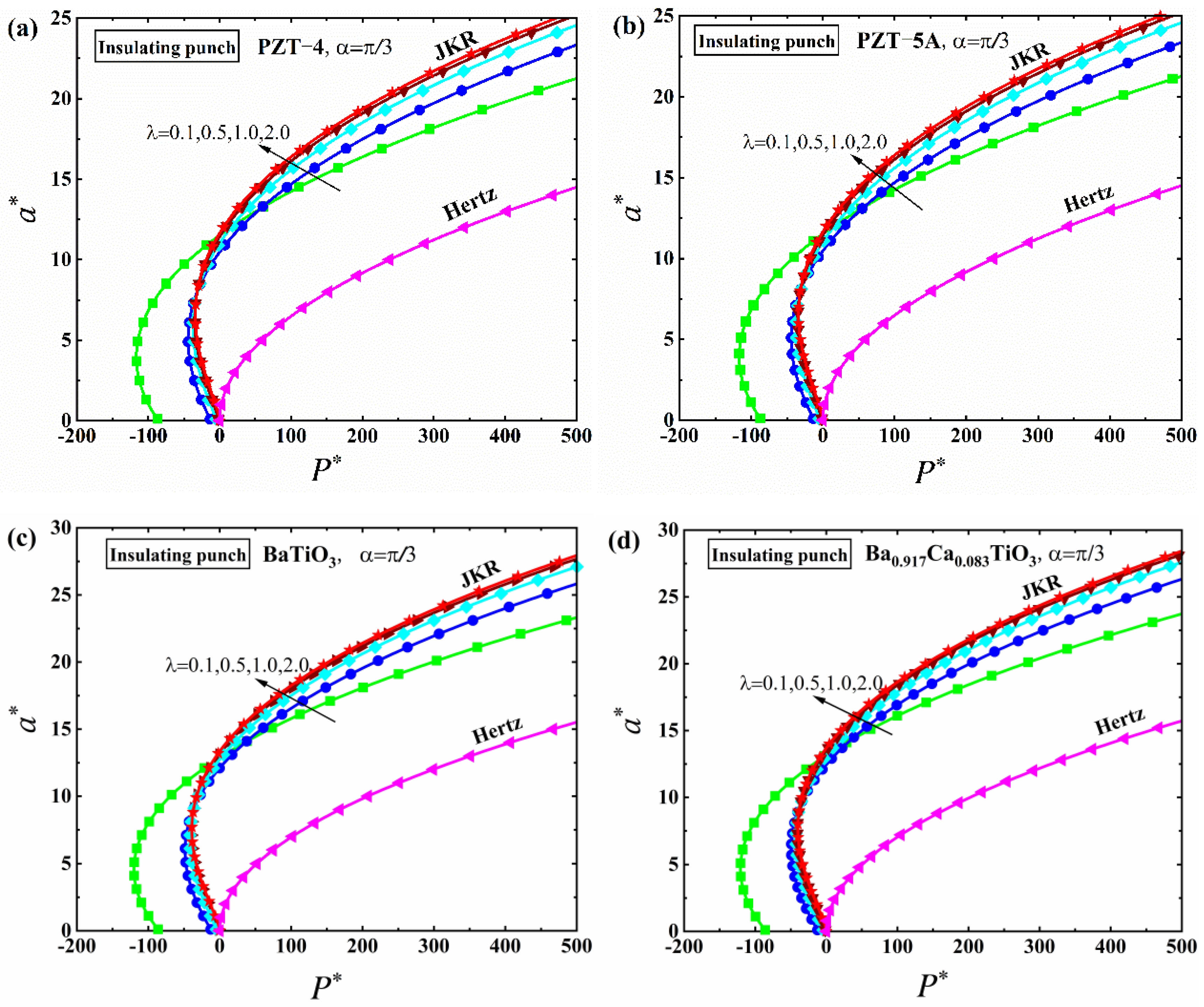
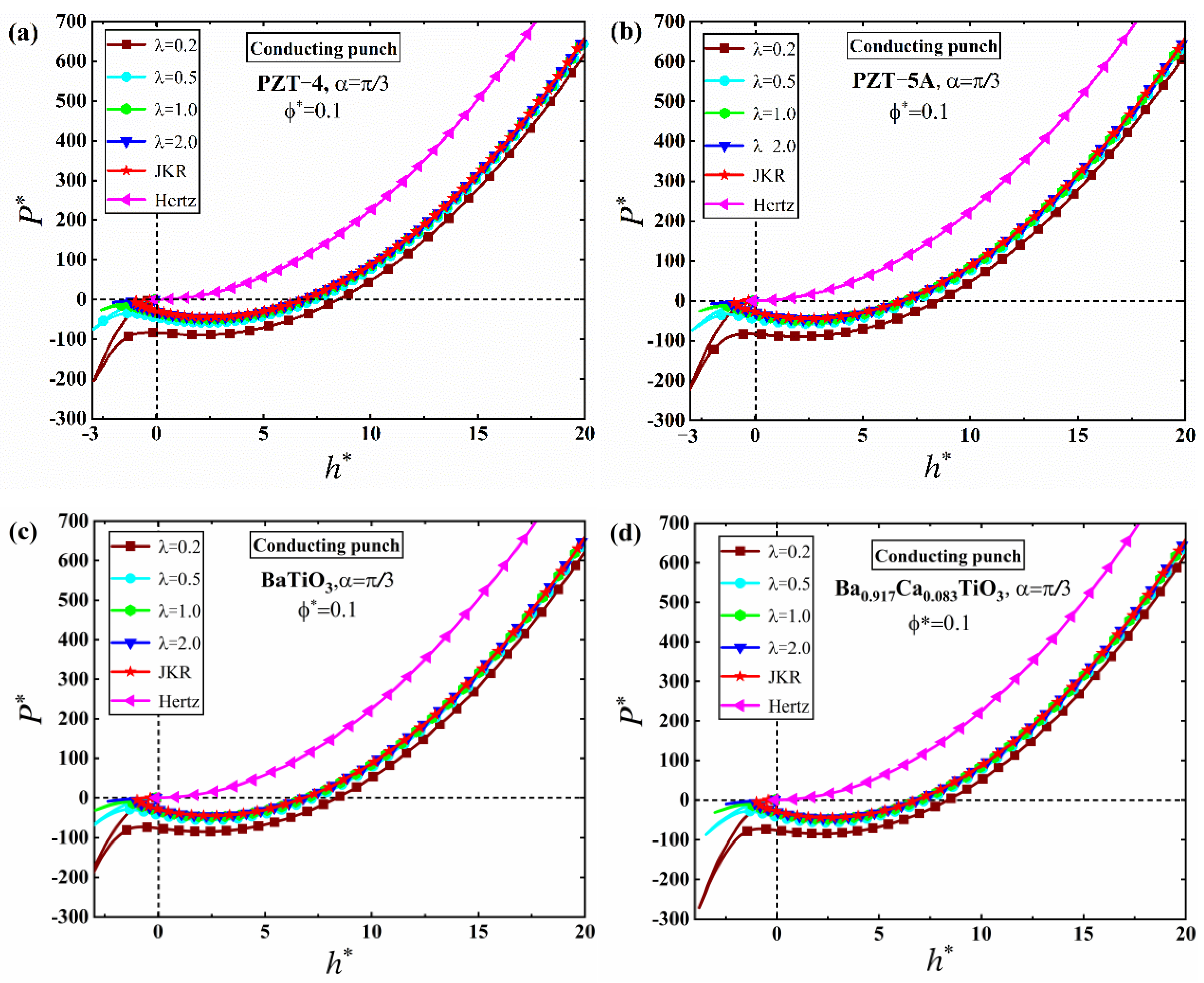
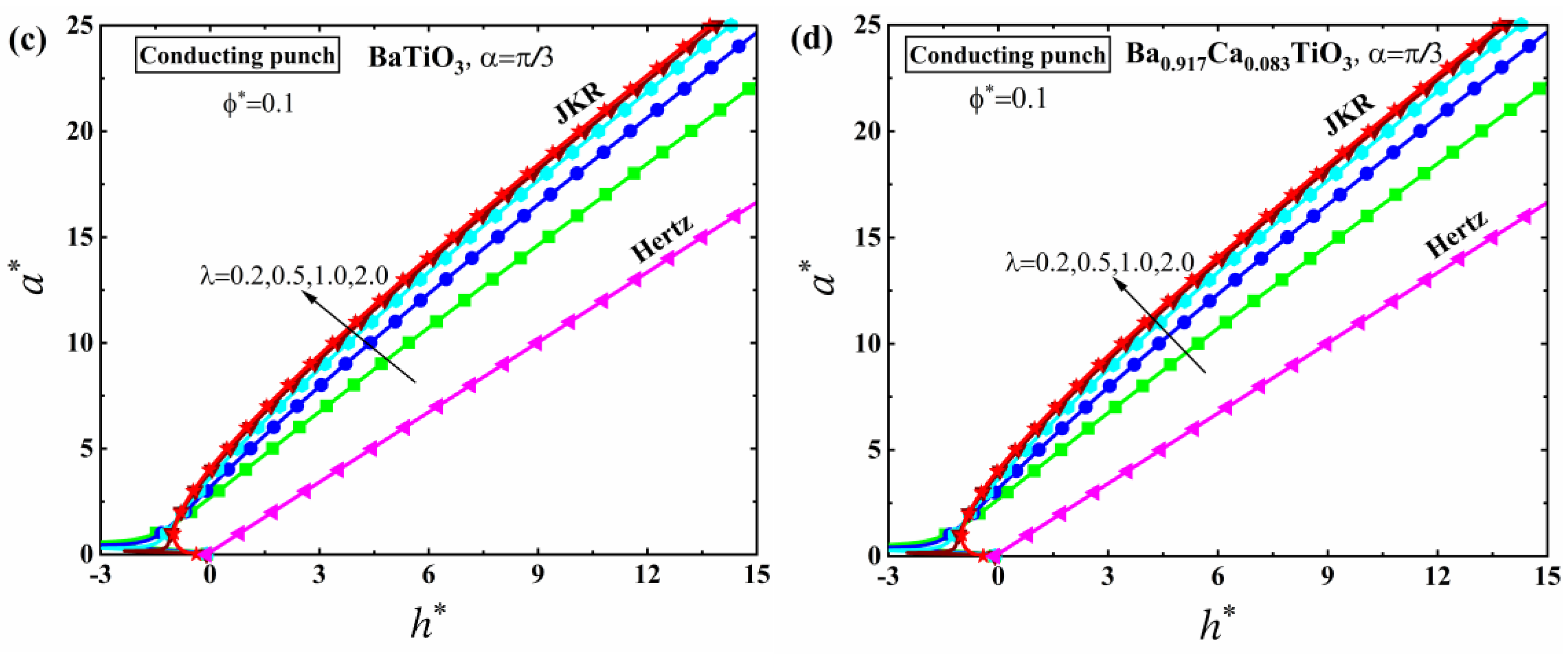
5. Numerical Results and Discussion
5.1. JKR Solutions
5.2. M-D Solutions
6. Conclusions
- (1)
- The adhesion effect between the tip of the conical punch and the piezoelectric solid can be enhanced by increasing the electric potential and the half cone angle of the punch, which suggests that a conical punch with a small half cone angle should be adopted in nanoindentation tests in order to reduce the effect of adhesion and improve the accuracy of characterization results.
- (2)
- The effect of electric potential on adhesion behaviors is sensitive to different material properties, while the effect of the half cone angle of the conical punch on adhesion behaviors is insensitive to different material properties. These conclusions were made for the first time in this work.
- (3)
- The load-displacement curves under the conical punch with different half cone angles have very different slopes, which indicates that the half cone angle of the conical punch can significantly affect the characterization of mechanical properties of piezoelectric solids in nanoindentation tests.
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Hertz Contact Solution
Appendix B. The Boussinesq Contact Solution
Appendix C. The Solutions of the JKR Model for Case II
Appendix D. The Solutions of the M-D Model for Case II
Appendix E. External Circular Crack Problem

Appendix F. Verification of the Results in Section 4.2
References
- Zhao, C.; Knisely, K.E.; Colesa, D.J.; Pfingst, B.E.; Raphael, Y.; Grosh, K. Voltage readout from a piezoelectric intracochlear acoustic transducer implanted in a living guinea pig. Sci. Rep. 2019, 9, 3711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ejeian, F.; Azadi, S.; Razmjou, A.; Orooji, Y.; Kottapalli, A.; Warkiani, M.E.; Asadnia, M. Design and applications of MEMS flow sensors: A review. Sens. Actuators A Phys. 2019, 295, 483–502. [Google Scholar] [CrossRef]
- Murray, C.; McCoul, D.; Sollier, E.; Ruggiero, T.; Niu, X.; Pei, Q.; Di Carlo, D. Electro-adaptive microfluidics for active tuning of channel geometry using polymer actuators. Microfluid. Nanofluidics 2012, 14, 345–358. [Google Scholar] [CrossRef]
- Deng, W.; Zhou, Y.; Libanori, A.; Chen, G.; Yang, W.; Chen, J. Piezoelectric nanogenerators for personalized healthcare. Chem. Soc. Rev. 2022, 51, 3380–3435. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-G.; Priya, S.; Kanno, I. Piezoelectric MEMS for energy harvesting. MRS Bull. 2012, 37, 1039–1050. [Google Scholar] [CrossRef] [Green Version]
- Awada, A.; Younes, R.; Ilinca, A. Optimized Active Control of a Smart Cantilever Beam Using Genetic Algorithm. Designs 2022, 6, 36. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, X.; Zhang, S.; Bai, J.; Li, J.; Yu, G. Optimal Shape Control of Piezoelectric Intelligent Structure Based on Genetic Algorithm. Adv. Mater. Sci. Eng. 2017, 2017, 6702183. [Google Scholar] [CrossRef] [Green Version]
- Mangaiyarkarasi, P.; Lakshmi, P. Numerical and experimental analysis of piezoelectric vibration energy harvester in IoT based F-SEPS application using optimization techniques. Microsyst. Technol. 2021, 27, 2955–2979. [Google Scholar] [CrossRef]
- Fountas, N.A.; Vaxevanidis, N.M. Optimization of abrasive flow nano-finishing processes by adopting artificial viral intelligence. J. Manuf. Mater. Process. 2021, 5, 22. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Frequency Tuning and Efficiency Improvement of Piezoelectric MEMS Vibration Energy Harvesters. J. Microelectromech. Syst. 2018, 28, 77–87. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Inman, D.J. Active vibration control of flexible cantilever plates using piezoelectric materials and artificial neural networks. J. Sound Vib. 2016, 363, 33–53. [Google Scholar] [CrossRef]
- Abolhasani, M.M.; Shirvanimoghaddam, K.; Khayyam, H.; Moosavi, S.M.; Zohdi, N.; Naebe, M. Towards predicting the piezoelectricity and physiochemical properties of the electrospun P(VDF-TrFE) nanogenrators using an artificial neural network. Polym. Test. 2018, 66, 178–188. [Google Scholar] [CrossRef]
- Kachanov, M.; Kalinin, S. Nanoelectromechanics of piezoelectric indentation and applications to scanning probe microscopies of ferroelectric materials. Philos. Mag. 2005, 85, 1017–1051. [Google Scholar]
- Carrillo, F.; Gupta, S.; Balooch, M.; Marshall, S.J.; Marshall, G.W.; Pruitt, L.; Puttlitz, C.M. Nanoindentation of polydimethylsiloxane elastomers: Effect of crosslinking, work of adhesion, and fluid environment on elastic modulus. J. Mater. Res. 2011, 20, 2820–2830. [Google Scholar] [CrossRef]
- Lin, Z.; Yu, Z.; Wei, Y. Measurement of nanoindentation properties of polymers considering adhesion effects between AFM sharp indenter and material. J. Adhes. Sci. Technol. 2020, 34, 1591–1608. [Google Scholar] [CrossRef]
- Kohn, J.C.; Ebenstein, D. Eliminating adhesion errors in nanoindentation of compliant polymers and hydrogels. J. Mech. Behav. Biomed. Mater. 2013, 20, 316–326. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Wang, L.S.; Yu, T.X. Mechanics of adhesion in MEMS—A review. J. Adhes. Sci. Technol. 2003, 17, 519–546. [Google Scholar] [CrossRef]
- Zhou, S.A. On forces in microelectromechanical systems. Int. J. Eng. Sci. 2003, 41, 313–335. [Google Scholar] [CrossRef]
- Lim, A.E.; Lam, Y.C. Vertical Squeezing Route Taylor Flow with Angled Microchannel Junctions. Ind. Eng. Chem. Res. 2021, 60, 14307–14317. [Google Scholar] [CrossRef]
- Yang, F.Q. Effect of adhesion energy on the contact stiffness in nanoindentation. J. Mater. Res. 2006, 21, 2683–2688. [Google Scholar] [CrossRef]
- Chen, W.-Q.; Shioya, T.; Ding, H.-J. The Elasto-Electric Field for a Rigid Conical Punch on a Transversely Isotropic Piezoelectric Half-Space. J. Appl. Mech. 1999, 66, 764–771. [Google Scholar] [CrossRef]
- Giannakopoulos, A.; Suresh, S. Theory of indentation of piezoelectric materials. Acta Mater. 1999, 47, 2153–2164. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, S.; Giannakopoulos, A.E.; Suresh, S. Mechanical and electrical responses of piezoelectric solids to conical indentation. J. Appl. Phys. 2000, 87, 8451–8456. [Google Scholar] [CrossRef]
- Makagon, A.; Kachanov, M.; Kalinin, S.V.; Karapetian, E. Indentation of spherical and conical punches into piezoelectric half-space with frictional sliding: Applications to scanning probe microscopy. Phys. Rev. B 2007, 76, 064115. [Google Scholar] [CrossRef]
- Wang, J.H.; Chen, C.Q.; Lu, T.J. Indentation responses of piezoelectric films. J. Mech. Phys. Solids 2008, 56, 3331–3351. [Google Scholar] [CrossRef]
- Yang, F. Analysis of the axisymmetric indentation of a semi-infinite piezoelectric material: The evaluation of the contact stiffness and the effective piezoelectric constant. J. Appl. Phys. 2008, 103, 074115. [Google Scholar] [CrossRef]
- Kamble, S.N.; Kubair, D.V.; Ramamurty, U. Indentation strength of a piezoelectric ceramic: Experiments and simulations. J. Mater. Res. 2009, 24, 926–935. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Yang, F.Q. Orientation effect on the Boussinesq indentation of a transversely isotropic piezoelectric material. Int. J. Solids Struct. 2013, 50, 2542–2547. [Google Scholar] [CrossRef] [Green Version]
- Berndt, E.A.; Sevostianov, I. Action of a smooth flat charged punch on the piezoelectric half-space possessing symmetry of class 6. Int. J. Eng. Sci. 2016, 103, 77–96. [Google Scholar] [CrossRef]
- Rodríguez-Tembleque, L.; Sáez, A.; Aliabadi, M. Indentation response of piezoelectric films under frictional contact. Int. J. Eng. Sci. 2016, 107, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Hou, P.F.; Zhang, W.H. 3D Axisymmetric exact solutions of the piezo-coating sensors for coating/substrate system under charged conical contact. Int. J. Solids Struct. 2019, 185–186, 342–364. [Google Scholar] [CrossRef]
- Guillermo, R.; Paul, H. Frictionless contact in a layered piezoelectric half-space. Smart Mater. Struct. 2003, 12, 612–625. [Google Scholar]
- Hao, T.H. Exact solution of a flat smooth punch on a piezoelectric half plane. Mech. Res. Commun. 2003, 30, 455–461. [Google Scholar]
- Guillermo, R. Frictionless contact in a layered piezoelectric medium characterized by complex eigenvalues. Smart Mater. Struct. 2006, 15, 1287–1295. [Google Scholar]
- Wang, B.L.; Han, J.C.; Du, S.Y.; Zhang, H.Y.; Sun, Y.G. Electromechanical behaviour of a finite piezoelectric layer under a flat punch. Int. J. Solids Struct. 2008, 45, 6384–6398. [Google Scholar] [CrossRef]
- Zhou, Y.T.; Lee, K.Y. New, real fundamental solutions to the transient thermal contact problem in a piezoelectric strip under the coupling actions of a rigid punch and a convective heat supply. Int. J. Solids Struct. 2011, 48, 2706–2717. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.-T.; Lee, K.Y. Theory of moving contact of anisotropic piezoelectric materials via real fundamental solutions approach. Eur. J. Mech. A Solids 2012, 35, 22–36. [Google Scholar] [CrossRef]
- Zhou, Y.-T.; Zhong, Z. Application of dual series equations to wavy contact between piezoelectric materials and an elastic solid. Int. J. Appl. Mech. 2014, 6, 1450046. [Google Scholar] [CrossRef]
- Zhou, Y.-T.; Zhong, Z. The interaction of two rigid semi-cylinders over anisotropic piezoelectric materials by the generalized Almansi theorem. Smart Mater. Struct. 2015, 24, 085011. [Google Scholar] [CrossRef]
- Çömez, İ.; Güler, M.A.; El-Borgi, S. Continuous and discontinuous contact problems of a homogeneous piezoelectric layer pressed by a conducting rigid flat punch. Acta Mech. 2019, 231, 957–976. [Google Scholar] [CrossRef]
- Su, J.; Ke, L.-L.; Wang, Y.-S. Elastohydrodynamic lubrication line contact of piezoelectric materials. Int. J. Mech. Sci. 2019, 163, 105145. [Google Scholar] [CrossRef]
- Fan, H.; Sze, K.-Y.; Yang, W. Two-dimensional contact on a piezoelectric half-space. Int. J. Solids Struct. 1996, 33, 1305–1315. [Google Scholar] [CrossRef]
- Zhou, Y.T.; Lee, K.Y. Thermo-electro-mechanical contact behavior of a finite piezoelectric layer under a sliding punch with frictional heat generation. J. Mech. Phys. Solids 2011, 59, 1037–1061. [Google Scholar] [CrossRef]
- Zhou, Y.T.; Lee, K.Y. Exact solutions of the 2-D frictional sliding contact problem of electrically insulated triangular and cylindrical punches on piezoelectric materials. Zamm-Z. Angew. Math. Phys. 2013, 93, 217–232. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.-T.; Zhong, Z. On the analytical solution for sliding contact of piezoelectric materials subjected to a flat or parabolic indenter. Z. Angew. Math. Phys. 2014, 66, 473–495. [Google Scholar] [CrossRef]
- Ma, J.; Ke, L.-L.; Wang, Y.-S. Electro-mechanical sliding frictional contact of a piezoelectric half-plane under a rigid conducting punch. Appl. Math. Model. 2014, 38, 5471–5489. [Google Scholar] [CrossRef]
- Zhou, Y.-T.; Lee, K.Y. Investigation of frictional sliding contact problems of triangular and cylindrical punches on monoclinic piezoelectric materials. Mech. Mater. 2014, 69, 237–250. [Google Scholar] [CrossRef]
- Su, J.; Ke, L.-L.; Wang, Y.-S. Two-dimensional fretting contact analysis of piezoelectric materials. Int. J. Solids Struct. 2015, 73-74, 41–54. [Google Scholar] [CrossRef]
- Su, J.; Ke, L.-L.; Wang, Y.-S. Two-dimensional fretting contact of piezoelectric materials under a rigid conducting cylindrical punch. J. Mech. Mater. Struct. 2016, 11, 535–558. [Google Scholar] [CrossRef]
- Shu, Y.-J.; Ke, L.-L.; Su, J.; Wang, Y.-S. Experimental Investigation on Fretting Wear Behavior of Piezoceramics under Sphere-on-Flat Contact. Tribol. Trans. 2020, 63, 971–985. [Google Scholar] [CrossRef]
- Lv, X.; Ke, L.-L.; Su, J.; Tian, J.-Y. Axisymmetric contact vibration analysis of a rigid spherical punch on a piezoelectric half-space. Int. J. Solids Struct. 2020, 210–211, 224–236. [Google Scholar] [CrossRef]
- Lv, X.; Su, J.; Tian, J.-Y.; Ke, L.-L. Dynamic contact response of an elastic sphere on a piezoelectric half-space. Appl. Math. Model. 2021, 100, 16–32. [Google Scholar] [CrossRef]
- Ding, H.-J.; Hou, P.-F.; Guo, F.-L. The elastic and electric fields for three-dimensional contact for transversely isotropic piezoelectric materials. Int. J. Solids Struct. 2000, 37, 3201–3229. [Google Scholar] [CrossRef]
- Wu, Y.F.; Yu, H.Y.; Chen, W.Q. Mechanics of indentation for piezoelectric thin films on elastic substrate. Int. J. Solids Struct. 2012, 49, 95–110. [Google Scholar] [CrossRef]
- Chen, Z.-R.; Yu, S.-W. Micro-scale adhesive contact of a spherical rigid punch on a piezoelectric half-space. Compos. Sci. Technol. 2005, 65, 1372–1381. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–313. [Google Scholar]
- Maugis, D. Adhesion of spheres: The JKR-DMT transition using a Dugdale model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Rogowski, B.; Kaliński, W. The adhesive contact problem for a piezoelectric half-space. Int. J. Press. Vessel. Pip. 2007, 84, 502–511. [Google Scholar] [CrossRef]
- Guo, X.; Jin, F. A generalized JKR-model for two-dimensional adhesive contact of transversely isotropic piezoelectric half-space. Int. J. Solids Struct. 2009, 46, 3607–3619. [Google Scholar] [CrossRef] [Green Version]
- Jin, F.; Yan, S.P.; Guo, X.; Wang, X.Y. On the contact and adhesion of a piezoelectric half-space under a rigid punch with an axisymmetric power-law profile. Mech. Mater. 2018, 129, 189–197. [Google Scholar] [CrossRef]
- Kanda, K.; Hirai, S.; Fujita, T.; Maenaka, K. Piezoelectric MEMS with multilayered Pb(Zr,Ti)O3 thin films for energy harvesting. Sens. Actuators A Phys. 2018, 281, 229–235. [Google Scholar] [CrossRef]
- Zhou, Y.-T.; Luo, Q.-H. Asymmetric non-slipping adhesion behavior of layered piezoelectric structures. Int. J. Mech. Sci. 2022, 224, 107330. [Google Scholar] [CrossRef]
- Luo, Q.-H.; Zhou, Y.-T. Adhesive contact behavior between piezoelectric and elastic materials with a mismatch strain. Acta Mech. 2022, 233, 617–639. [Google Scholar] [CrossRef]
- Luo, Q.-H.; Zhou, Y.-T. Adhesive behavior of transversely isotropic piezoelectric bimaterials. Int. J. Solids Struct. 2021, 236–237, 111360. [Google Scholar] [CrossRef]
- Shirbani, M.M.; Shishesaz, M.; Hajnayeb, A.; Sedighi, H.M. Coupled magneto-electro-mechanical lumped parameter model for a novel vibration-based magneto-electro-elastic energy harvesting systems. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 90, 158–169. [Google Scholar] [CrossRef]
- Shishesaz, M.; Shirbani, M.M.; Sedighi, H.M.; Hajnayeb, A. Design and analytical modeling of magneto-electro-mechanical characteristics of a novel magneto-electro-elastic vibration-based energy harvesting system. J. Sound Vib. 2018, 425, 149–169. [Google Scholar] [CrossRef]
- Skrzypacz, P.; Ellis, G.; He, J.H.; He, C.H. Dynamic pull-in and oscillations of current-carrying filaments in magnetic micro-electro-mechanical system. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106350. [Google Scholar] [CrossRef]
- Wu, F.; Li, X.-Y.; Zheng, R.-F.; Kang, G.-Z. Theory of adhesive contact on multi-ferroic composite materials: Spherical indenter. Int. J. Eng. Sci. 2018, 134, 77–116. [Google Scholar] [CrossRef]
- Wu, F.; Li, C. Theory of adhesive contact on multi-ferroic composite materials: Conical indenter. Int. J. Solids Struct. 2021, 233, 111217. [Google Scholar] [CrossRef]
- Rar, A.; Pharr, G.M.; Oliver, W.C.; Karapetian, E.; Kalinin, S.V. Piezoelectric nanoindentation. J. Mater. Res. 2006, 21, 552–556. [Google Scholar] [CrossRef]
- Pan, K.; Liu, Y.Y.; Xie, S.H.; Liu, Y.M.; Li, J.Y. The electromechanics of piezoresponse force microscopy for a transversely isotropic piezoelectric medium. Acta Mater. 2013, 61, 7020–7033. [Google Scholar] [CrossRef]
- Broitman, E.; Soomro, M.Y.; Lu, J.; Willander, M.; Hultman, L. Nanoscale piezoelectric response of ZnO nanowires measured using a nanoindentation technique. Phys. Chem. Chem. Phys. 2013, 15, 11113–11118. [Google Scholar] [CrossRef] [Green Version]
- Derjaguin, B.; Muller, V.; Toporov, Y. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Johnson, K.L. An alternative to the Maugis model of adhesion between elastic spheres. J. Phys. D Appl. Phys. 1998, 31, 3279–3290. [Google Scholar] [CrossRef]
- Tabor, D. Surface forces and surface interactions. J. Colloid Interface Sci. 1977, 58, 3–14. [Google Scholar] [CrossRef]
- Ganser, C.; Czibula, C.; Tscharnuter, D.; Schoberl, T.; Teichert, C.; Hirn, U. Combining adhesive contact mechanics with a viscoelastic material model to probe local material properties by AFM. Soft Matter 2017, 14, 140–150. [Google Scholar] [CrossRef] [Green Version]
- Argatov, I.; Mishuris, G. Cylindrical lateral depth-sensing indentation of anisotropic elastic tissues: Effects of adhesion and incompressibility. J. Adhes. 2017, 94, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Vallet, D.; Barquins, M. Adhesive contact and kinetics of adherence of a rigid conical punch on an elastic half-space (natural rubber). Int. J. Adhes. Adhes. 2002, 22, 41–46. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of stress sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Suo, Z.G.; Kuo, C.M.; Barnett, D.M.; Willis, J.R. Fracture mechanics for piezoelectric ceramics. J. Mech. Phys. Solids 1992, 40, 739–765. [Google Scholar] [CrossRef]
- Maugis, D. Contact, Adhesion and Rupture of Elastic Solids; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Cacucciolo, V.; Shea, H.; Carbone, G. Peeling in electroadhesion soft grippers. Extreme Mech. Lett. 2021, 50, 101529. [Google Scholar] [CrossRef]
- Lowengrub, M.; Sneddon, I.N. The distribution of stress in the vicinity of an external crack in an infinite elastic solid. Int. J. Eng. Sci. 1965, 3, 451–460. [Google Scholar] [CrossRef]
- Sneddon, I.N. The elementary solution of dual integral equation. Glasg. Math. J. 1960, 4, 108–110. [Google Scholar] [CrossRef]







| PZT-4 | PZT-5A | BaTiO3 | (Ba0.917Ca0.083)TiO3 | |
| Elastic coefficients (GPa) | ||||
| 139.00 | 121.00 | 150.00 | 158.00 | |
| 115.00 | 111.00 | 146.00 | 150.00 | |
| 25.60 | 21.10 | 44.00 | 45.00 | |
| 77.80 | 75.40 | 66.00 | 69.00 | |
| 74.30 | 75.20 | 66.00 | 67.50 | |
| Piezoelectric coefficients (C/m2) | ||||
| −5.200 | −5.400 | −4.350 | −3.100 | |
| 15.10 | 15.80 | 17.50 | 13.50 | |
| 12.70 | 12.30 | 11.40 | 10.90 | |
| Dielectric constants (10−9 F/m) | ||||
| 6.461 | 8.107 | 9.868 | 8.850 | |
| 5.620 | 7.346 | 11.151 | 8.054 | |
| Material coefficients | ||||
| (GPa) | 56.41 | 47.88 | 70.68 | 71.48 |
| (109 V/m) | 1.246 | 1.0196 | 0.8645 | 0.8787 |
| (10−10 m/V) | 2.501 | 3.035 | 1.668 | 1.312 |
| (GPa) | 43.00 | 36.56 | 61.77 | 64.09 |
| (C/m2) | 10.756 | 11.097 | 10.302 | 8.411 |
| (10−10 m/V) | 8.027 | 9.807 | 11.567 | 11.381 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Zhou, Y.; Wang, L.; Ding, S. The Effect of Adhesion on Indentation Behavior of Various Smart Materials. Mathematics 2022, 10, 4511. https://doi.org/10.3390/math10234511
Luo Q, Zhou Y, Wang L, Ding S. The Effect of Adhesion on Indentation Behavior of Various Smart Materials. Mathematics. 2022; 10(23):4511. https://doi.org/10.3390/math10234511
Chicago/Turabian StyleLuo, Qinghui, Yueting Zhou, Lihua Wang, and Shenghu Ding. 2022. "The Effect of Adhesion on Indentation Behavior of Various Smart Materials" Mathematics 10, no. 23: 4511. https://doi.org/10.3390/math10234511
APA StyleLuo, Q., Zhou, Y., Wang, L., & Ding, S. (2022). The Effect of Adhesion on Indentation Behavior of Various Smart Materials. Mathematics, 10(23), 4511. https://doi.org/10.3390/math10234511







