Performance of a Vector-Controlled PMSM Drive without Using Current Sensors

Abstract

The current sensorless vector-controlled permanent-magnet synchronous motor (PMSM) drive using a single sensor (i.e., speed sensor) is presented in this work. The current sensors are removed, and the estimated currents are used to close the current loop to minimize the drive cost and make it fault-tolerant against current sensor failure. A classical vector-control PMSM drive requires at least three sensors, i.e., two current sensors and one speed/position sensor. This paper presents a new current estimation technique that is free from inverter switching states, an integrator, and differentiator terms. The drive is suitable for retrofit applications, as it does not require any additional hardware. The reference voltages ($v_{ds} \mathrm{and} v_{qs}$) are used to estimate the rotor reference frame currents (i.e., $i_{qs}\mathrm{and}{i}_{ds}$). The presented algorithm depends on the stator resistance (${Ɍ}_{\mathrm{s}}$). The online ${Ɍ}_{\mathrm{s}}$ estimation algorithm is used for compensation to overcome the effect of the ${Ɍ}_{\mathrm{s}}$ on the estimated currents. The sensitivity analysis for the currents against the speed is verified and presented. The speed loop is closed with actual speed information, which will try to maintain the reference speed under any circumstances. The proposed current sensorless PMSM drive was validated using MATLAB/Simulink and also verified on a hardware prototype. The presented technique was verified for various operation conditions, and some of the extensive results are presented.

1. Introduction

PMSMs (permanent-magnet synchronous machines) have been gaining a strong interest over the past decades. Its unique characteristics meet the electric vehicle drive operation criteria, with a higher torque/inertia ratio and minimum copper losses with high efficiency, and the PMSM operates successfully at the required speed and load [1]. A PMSM is smaller in size compared to other machines [1]. Vector-control drive has an excellent dynamic performance [2]. The speed/position data are accessed from a sensor attached to the machine shaft for controlling the drive. In general, a three-phase PMSM requires at least two phase currents and rotor position information to compute the rotating reference frame currents [1,2].

Torque ripple in the drive operation can be caused by sensor parameters, such as gain errors, drift, and offset, resulting in poorer performance [3]. The failure of the sensor occurs under heavily loaded conditions and high ambient temperature, which results in drive instability. The decrease in the sensors in the drive will lower the failure rate, increase the reliability, and reduce the cost of the drive.

This paper mainly concerns the reduction of the sensor’s dependability (i.e., current sensors), increasing the drive reliability, and making it fault-tolerant. In the literature, current sensor reduction/elimination is discussed. This section starts with a brief overview of the various current estimating techniques for current sensor reduction, and then it is carried out with the proposed estimation technique.

In the literature, there are a few single-current sensor-based drive approaches. Based on the placement of the current sensor in the inverter, the reconstruction of three-phase currents is divided into a DC-link current measurement, measuring multiple branch current measurements with a single current sensor, and a single-phase current measurement [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Three-phase currents are reconstructed based on the DC-link current, voltage, and inverter switching information [8,10,19,20,21,22]. Although DC-link current measurement is a common strategy, it has certain drawbacks: low modulation index, active-switching states at the sector boundary/short duration, and phase variation in the estimated currents, which are all factors to consider. A few solutions for enhancing the phase current accuracy in the reconstruction in all four-quadrant regions have been given in the literature. Under the zero-voltage vector sampling zone, an isolated current sensor technique is used to detect phase currents matching the DC-link current [4]. The measurement vector insertion approach was adopted to overcome the difficulty of switching states in a short period [23]. In [16], it shows how to measure phase currents in a low-modulation index or a near-sector boundary region. These approaches rely on the DC-link current and inverter switching states to reconstruct the phase currents and require an extremely complicated analysis.

A current sensor is used to measure the current passing through multiple branches [4,5,6,9,10,12]. The three-phase currents are reconstructed using the advantage of switching states and the sum of the branch currents. In this method, a current sensor is employed to measure more than the rated current [12], which increases the current sensor’s cost.

The estimation of the current without using a DC-link current sensor is presented in [21,24,25,26,27,28,29,30,31]. These methods use either a speed encoder/voltage sensor/single-phase current measurement and an accurate machine model to estimate the currents. The current sensor detects the single-phase current, and using an observer design approach, the remaining phase currents are estimated [32]. The PMSM drive current sensorless procedure makes the drive more robust, cost effective, and reliable. References [25,33] present a PMSM drive prediction approach based on a current sensorless extended Kalman-filtered operation. This approach is mostly machine-dependent and involves both the initial conditions and filters.

A new technique is presented for current estimation with a low precession speed/position sensor for a PMSM drive. In the $d \mathrm{and}q\mathrm{axes}$ frame, the current estimation was constructed on machine formulae. The dead-time was employed to make the delay caused by the machine and inverter in real time. This process was simulated in MATLAB/Simulink and verified for various conditions and verified for a four-quadrant operation.

To overcome the drawbacks in the existing methods, the paper presents a new method for a current sensorless approach. The proposed method has several advantages. As it does not require any additional sensors or hardware, it makes the drive suitable for retrofit applications. The current estimation technique can be used to monitor the status of current sensors by implementing them in the existing PMSM drive. A speed sensor was employed to perform the drive operation, and the current estimation technique reduces the drive cost and complexity. The reliability and immunity to signal noise are increased, as a single sensor is used, i.e., speed/position sensor. The proposed drive is independent of the switching states, an integrator, and differentiator terms.

➢

A current sensorless algorithm for a PMSM drive;

➢

An algorithm that is independent of an integrator and differentiator terms;

➢

The algorithm can be applied with a low-resolution speed sensor;

➢

The overall drive cost can be reduced for low-precession applications;

➢

Has a reduced current sensor dependency;

➢

The proposed current estimation method can be used to make the existing PMSM drives (which use all of the current sensors) fault-tolerant against failure of the current sensors.

The following is a summary of the structure of the paper. In Section 2, the modeling of the PMSM is discussed. Section 3 explains the mathematical model of the current estimating scheme. In Section 4, a sensitivity analysis is performed and presented. In Section 5, the proposed drive is validated using the MATLAB/Simulink platform, and the results are provided to show the performance under various conditions. On the dSPACE 1104-based laboratory prototype, the current sensorless PMSM drive is validated, and the results are presented in Section 6. Finally, in Section 7, this work is concluded.

2. Modeling of PMSM

Reference [1] was used to model the PMSM machine. The stator currents (i.e., “$d$” and “$q$”$\mathrm{axes}$) in the rotor-reference frame for the PMSM are shown in (1).

$$\left[\begin{array}{c}{Þ\mathrm{i}}_{\mathrm{ds}}\\ {Þ\mathrm{i}}_{\mathrm{qs}}\end{array}\right]=\left[\begin{array}{cc}\frac{-{Ɍ}_{\mathrm{s}}}{{\mathrm{L}}_{\mathrm{d}}}& \frac{{\mathsf{\omega }}_{\mathrm{s}}{\mathrm{L}}_{\mathrm{q}}}{{\mathrm{L}}_{\mathrm{d}}}\\ \frac{-{\mathsf{\omega }}_{\mathrm{s}}{\mathrm{L}}_{\mathrm{d}}}{{\mathrm{L}}_{\mathrm{q}}}& \frac{-{Ɍ}_{\mathrm{s}}}{{\mathrm{L}}_{\mathrm{q}}}\end{array}\right]\left(\begin{array}{c}{\mathrm{i}}_{\mathrm{ds}}\\ {\mathrm{i}}_{\mathrm{qs}}\end{array}\right)+\left[\begin{array}{cc}\frac{1}{{\mathrm{L}}_{\mathrm{d}}}& 0\\ 0& \frac{1}{{\mathrm{L}}_{\mathrm{q}}}\end{array}\right]\left(\begin{array}{c}{\mathrm{v}}_{\mathrm{ds}}\\ {\mathrm{v}}_{\mathrm{qs}}\end{array}\right)+\left[\begin{array}{c}0\\ \frac{-{\mathsf{\omega }}_{\mathrm{s}}{\mathsf{\lambda }}_{\mathrm{af}}}{{\mathrm{L}}_{\mathrm{q}}}\end{array}\right]$$

(1)

$${\mathrm{T}}_e=\left(\frac{3}{2}\right)\mathrm{P}\left( i_{qs} {\lambda }_{af}+\left( L_d-L_q\right) i_{ds} i_{qs}\right)$$

(2)

$${\mathrm{T}}_e-{\mathrm{T}}_L=J \frac{d{\omega }_r}{dt}+B {\omega }_r$$

(3)

The electromagnetic torque is expressed as shown in (2). The electromechanical dynamics equation is shown in (3). $Þ=\mathrm{derivative}-\mathrm{term}$ ($\mathrm{d}/\mathrm{dt});{\mathsf{\omega }}_{\mathrm{s}}=\mathrm{P}{\mathsf{\omega }}_{\mathrm{r}};$ and the machine was a nonsaliency type with a sinusoidal back—EMF waveform, where ${\mathrm{T}}_{\mathrm{e}}$ and ${\mathrm{T}}_{\mathrm{L}}$ are the electric-torque and load-torque, respectively.

Table 1. Machine parameters.

“Nominal shaft power” ($P_N$)	3 KW
“Pole pair” ($P$)	2
“Nominal speed” (${\mathsf{\omega }}_n$)	157 rad/s.
“$d-\mathrm{axis}$ inductance” ($L_d$)	0.0107637 H
“$q-\mathrm{axis}$ inductance” ($L_q$)	0.0553733 H
${ƛ}_{af}$ (“Mutual flux linkage between rotor and stator due to the permanent magnet”)	0.553161 Wb/m2
“Stator resistance” (${Ɍ}_{\mathrm{s}}$)	0.78 Ω
Rated current	5.9 A
Rated voltage	415 V
Rated torque	16 N·m

shows the PMSM machine’s parameters.

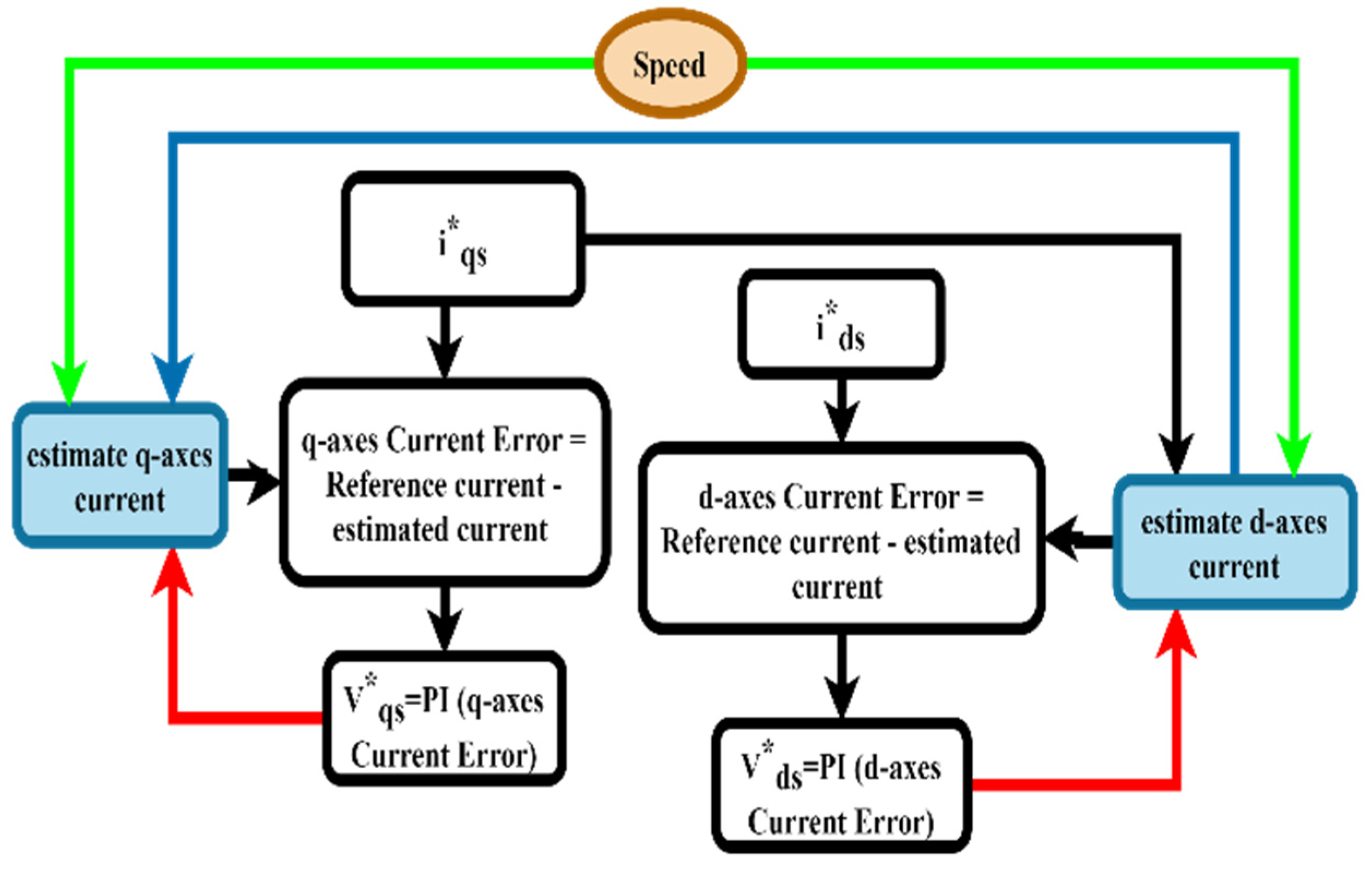
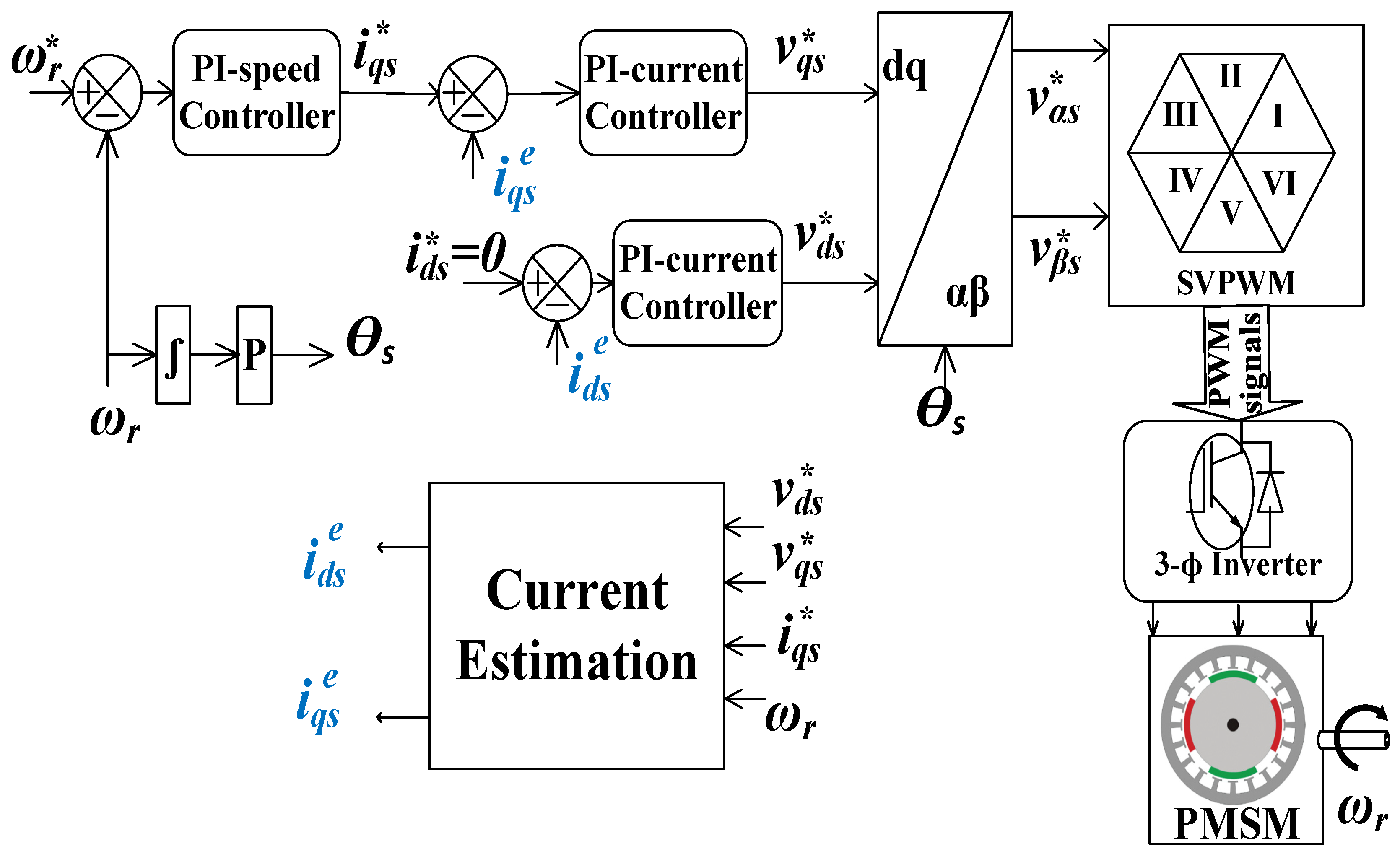
3. Current Sensorless Methodology

In the “$d$” and “$q$”$\mathrm{axes}$ frame, the proposed method estimates the currents using the machine modeling in Equation (1). In the rotor reference frame, the stator voltages were defined as in (4) and (5), where $i_{ds} \mathrm{and} i_{qs}$ show the actual $d \mathrm{and} q \mathrm{axes}\mathrm{stator}\mathrm{currents}$; $i_{ds}^e \mathrm{and} i_{qs}^e$ show the estimated $d \mathrm{and} q \mathrm{axes}\mathrm{stator}\mathrm{currents}$; and $i_{ds}^{*} \mathrm{and} i_{qs}^{*}$ represent the $d \mathrm{and} q \mathrm{axes}$ reference currents.

$$V_{ds}={Ɍ}_s{i}_{ds}+L_d\frac{d{i}_{ds}}{dt}-{\omega }_s L_q i_{qs}$$

(4)

$$V_{qs}={Ɍ}_s i_{qs}+L_q\frac{d{i}_{qs}}{dt}+{\omega }_s L_{d }{i}_{ds}+{\omega }_s {\mathsf{\lambda }}_{af}$$

(5)

Under a steady-state operation, the differential terms are considered as zero.

$$V_{ds}={Ɍ}_s{i}_{ds}-{\omega }_s L_q i_{qs}$$

(6)

$$V_{qs}={Ɍ}_s i_{qs}+{\omega }_s L_d i_{ds}+{\mathsf{\omega }}_s{\mathsf{\lambda }}_{\mathrm{af}}$$

(7)

taking $i_{qs}$ from $i_{qs}^{*}$ in $i_{ds}^e$ for (6) and $i_{ds}^e$ in $i_{ds}$ for (7). The currents on the $d\mathrm{and}q\mathrm{axes}$ are calculated and presented as $i_{ds}^e\mathrm{and}{i}_{qs}^e$.

$$i_{ds}^e=\left[V_{ds}^{*}+{\omega }_s L_q i_{qs}^{*}\right]\frac{1}{R_s}$$

(8)

$$i_{qs}^e=\left[V_{qs}^{*}-{\omega }_s {\lambda }_{af}-{\omega }_s L_d{i}_{ds}^e\right]\frac{1}{R_s}$$

(9)

Figure 1 shows a flow chart for the proposed current estimation method. From Figure 1, the outer speed loop from the motor speed sensor maintains the voltage gains to maintain the estimated currents in a closed loop.

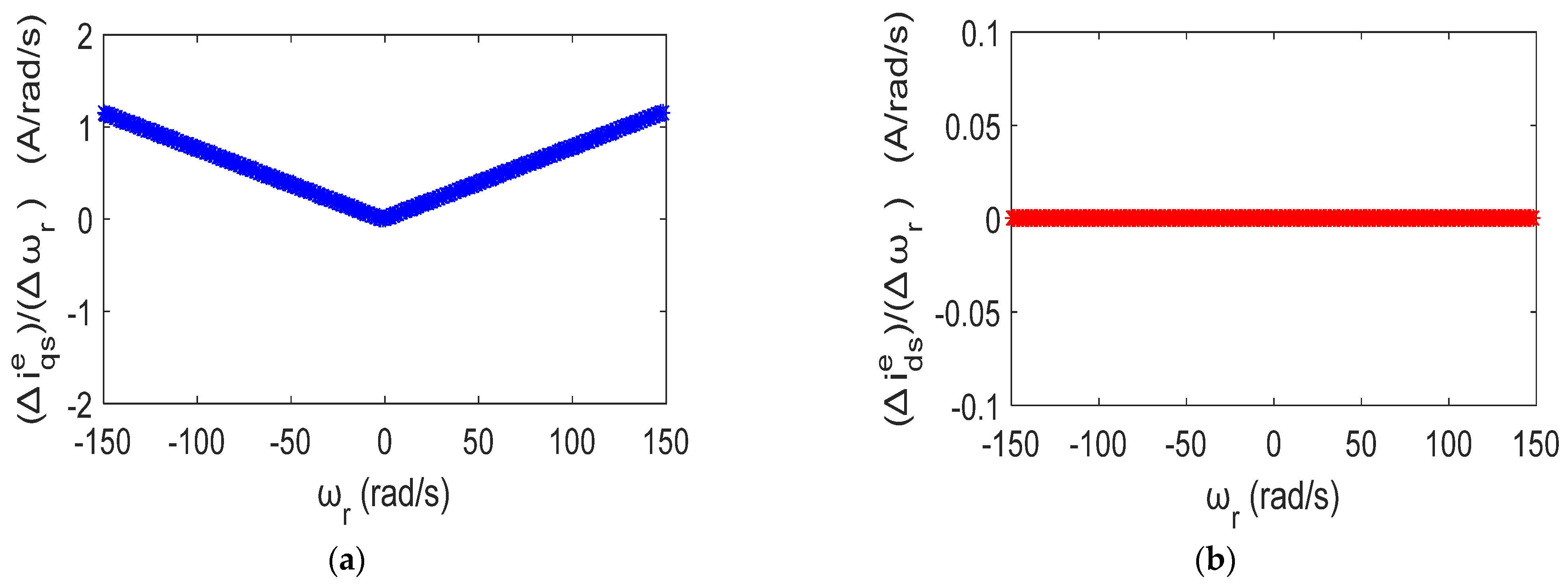
4. Sensitivity Analysis

In this secession, the sensitivity [34] of the estimated currents against ${\omega }_r$ variation was performed. The $\frac{\Delta i_{ds}^e}{\Delta {\omega }_r}$ and $\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}$ are considered as the sensitivity indicators, and $\frac{\Delta i_{ds}^e}{\Delta {\omega }_r}$ and $\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}$ are plotted against the speed variation.

$$\mathrm{Let},r_1=\frac{s{k}_{p1}+k_{i1}}{s}, r_2=\frac{s{k}_{p2}+k_{i2}}{s}, r_3=\frac{s{k}_{p3}+k_{i3}}{s}$$

(10)

These $r_{n \left(n = 1,2,3\&4\right)}$ are the transfer functions of the PI controllers of the speed loop and the q axes and d axes current loops.

$i_{qs}^{*}$, $v_{ds}^{*}$, and $v_{qs}^{*}$ are stated in (11), (15), and (21), which are taken from Figure 2 and (10).

$\Delta i_{qs}^{*}$ is expressed as

$$i_{qs}^{*}=r_1\left({\omega }_r^{*}-{\omega }_r\right)$$

(11)

$$\Delta i_{qs}^{*}=\Delta r_1\left({\omega }_r^{*}-{\omega }_r\right)$$

(12)

$$\Delta i_{qs}^{*}=r_1\left(0-\Delta {\omega }_r\right)$$

(13)

$$\Delta i_{qs}^{*}=-r_1\Delta {\omega }_r$$

(14)

$\Delta v_{ds}^{*}$ is expressed as

$$V_{ds}^{*}=r_3\left(i_{ds}^{*}-i_{ds}^e\right)$$

(15)

$$\Delta V_{ds}^{*}=\Delta r_3\left(i_{ds}^{*}-i_{ds}^e\right)$$

(16)

$$\Delta V_{ds}^{*}=r_3\left(\Delta i_{ds}^{*}-\Delta i_{ds}^e\right)$$

(17)

$$\mathrm{As}{i}_{ds}^{*}=0$$

(18)

From (17) and (18)

$$\Delta V_{ds}^{*}=r_3\left(0-\Delta i_{ds}^e\right)$$

(19)

$$\Delta V_{ds}^{*}=-r_3\Delta i_{ds}^e$$

(20)

$\Delta v_{qs}^{*}$ is expressed as

$$V_{qs}^{*}=r_2\left(i_{qs}^{*}-i_{qs}^e\right)$$

(21)

$$\Delta V_{qs}^{*}=\Delta r_2\left(i_{qs}^{*}-i_{qs}^e\right)$$

(22)

$$\Delta V_{qs}^{*}=r_2\left(\Delta i_{qs}^{*}-\Delta i_{qs}^e\right)$$

(23)

$$\Delta V_{qs}^{*}=r_2\left(-r_1\Delta {\omega }_r-\Delta i_{qs}^e\right)$$

(24)

$$\Delta V_{qs}^{*}=-r_2\left(r_1\Delta {\omega }_r+\Delta i_{qs}^e\right)$$

(25)

Using a small-signal analysis, the expressions for $\Delta i_{ds}^e$ and $\Delta i_{qs}^e$ become:

$\Delta i_{ds}^e$ is expressed as

$$i_{ds}^e=\left[V_{ds}^{*}+{\omega }_s L_q i_{qs}^{*}\right]\frac{1}{R_s}$$

(26)

$$\Delta i_{ds}^e=\Delta \left[V_{ds}^{*}+{\omega }_s L_q i_{qs}^{*}\right]\frac{1}{R_s}$$

(27)

$$\Delta i_{ds}^e=\left[\Delta V_{ds}^{*}+\Delta \left({\omega }_s L_q i_{qs}^{*}\right)\right]\frac{1}{R_s}$$

(28)

$$\Delta i_{ds}^e=\left[\Delta V_{ds}^{*}+{\omega }_s L_q \Delta i_{qs}^{*}+L_q i_{qs}^{*}\Delta {\omega }_s\right]\frac{1}{R_s}$$

(29)

$$\Delta i_{ds}^e=\left[\Delta V_{ds}^{*}+{\omega }_s L_q\left(-r_1\Delta {\omega }_r\right)+L_q i_{qs}^{*}\Delta {\omega }_s\right]\frac{1}{R_s}$$

(30)

$$\Delta i_{ds}^e=\left[-r_3\Delta i_{ds}^e-r_1{\omega }_s L_q\Delta {\omega }_r+L_q i_{qs}^{*}\Delta {\omega }_s\right]\frac{1}{R_s}$$

(31)

$$R_s\Delta i_{ds}^e=-r_3\Delta i_{ds}^e-r_1{\omega }_s L_q\Delta {\omega }_r+L_q i_{qs}^{*}\Delta {\omega }_s$$

(32)

$$R_s\Delta i_{ds}^e+r_3\Delta i_{ds}^e=-r_1{\omega }_s L_q\Delta {\omega }_r+L_q i_{qs}^{*}\Delta {\omega }_s$$

(33)

where

$${\omega }_s=P{\omega }_r$$

(34)

$$\left(R_s+r_3\right)\Delta i_{ds}^e=-r_1{\omega }_s L_q\Delta {\omega }_r+L_q i_{qs}^{*}P\Delta {\omega }_r$$

(35)

$$\left(R_s+r_3\right)\Delta i_{ds}^e=\left(-r_1{\omega }_s L_q+L_q i_{qs}^{*}P\right)\Delta {\omega }_r$$

(36)

$$\frac{\Delta i_{ds}^e}{\Delta {\omega }_r}=\frac{-r_1{\omega }_s L_q+L_q i_{qs}^{*}P}{R_s+r_3}$$

(37)

$\Delta i_{qs}^e$ is expressed as

$$i_{qs}^e=\left[V_{qs}^{*}-{\omega }_s {\lambda }_{af}-{\omega }_s L_d{i}_{ds}^e\right]\frac{1}{R_s}$$

(38)

$$\Delta i_{qs}^e=\Delta \left[V_{qs}^{*}-{\omega }_s {\lambda }_{af}-{\omega }_s L_d{i}_{ds}^e\right]\frac{1}{R_s}$$

(39)

$$\Delta i_{qs}^e=\left[\Delta V_{qs}^{*}-\Delta ({\omega }_s {\lambda }_{af})-\Delta ({\omega }_s L_d{i}_{ds}^e)\right]\frac{1}{R_s}$$

(40)

$$\Delta i_{qs}^e=\left[\Delta V_{qs}^{*}-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e\right]\frac{1}{R_s}$$

(41)

$$R_s\Delta i_{qs}^e=\left[\Delta V_{qs}^{*}-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e\right]$$

(42)

$$R_s\Delta i_{qs}^e=\left[-r_2\left(r_1\Delta {\omega }_r+\Delta i_{qs}^e\right)-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e\right]$$

(43)

$$R_s\Delta i_{qs}^e=-r_2{r}_1\Delta {\omega }_r-r_2\Delta i_{qs}^e-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e$$

(44)

$$R_s\Delta i_{qs}^e+r_2\Delta i_{qs}^e=-r_2{r}_1\Delta {\omega }_r-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e$$

(45)

$$\left(R_s+r_2\right)\Delta i_{qs}^e=-r_2{r}_1\Delta {\omega }_r-{\lambda }_{af}\Delta {\omega }_s-L_d{i}_{ds}^e\Delta {\omega }_s-{\omega }_s L_d\Delta i_{ds}^e$$

(46)

$$\left(R_s+r_2\right)\Delta i_{qs}^e=-r_2{r}_1\Delta {\omega }_r-P{\lambda }_{af}\Delta {\omega }_r-L_d{i}_{ds}^{e}P\Delta {\omega }_r-{\omega }_s L_d\Delta i_{ds}^e$$

(47)

$$\left(R_s+r_2\right)\Delta i_{qs}^e=\left(-r_2{r}_1-P{\lambda }_{af}-L_d{i}_{ds}^{e}P\right)\Delta {\omega }_r-{\omega }_s L_d\Delta i_{ds}^e$$

(48)

$$\left(R_s+r_2\right)\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}=-(\frac{r_2{r}_1}{P}+\left({\lambda }_{af}+L_d{i}_{ds}^e\right)P-{\omega }_s L_d\frac{\Delta i_{ds}^e}{\Delta {\omega }_r}$$

(49)

$$\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}=\frac{\left(-r_2{r}_1-P{\lambda }_{af}-L_d{i}_{ds}^e\mathrm{P}\right)}{\left(R_s+r_2\right)}-\frac{{\omega }_s L_d}{\left(R_s+r_2\right)} \frac{\Delta i_{ds}^e}{\Delta {\omega }_r}$$

(50)

$$\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}=\frac{\left(-r_2{r}_1-P{\lambda }_{af}-L_d{i}_{ds}^e\mathrm{P}\right)}{\left(R_s+r_2\right)}-\frac{{\omega }_s L_d}{\left(R_s+r_2\right)} \frac{\left(-r_1{\omega }_s L_q+L_q i_{qs}^{*}\mathrm{P}\right)}{\left(R_s+r_3\right)}$$

(51)

The sensitivity plot for the estimated currents is shown in Figure 3 for the ${\mathsf{\omega }}_r$ variation. Figure 3a presents $\frac{\Delta i_{qs}^e}{\Delta {\omega }_r}$ with respect to the ${\omega }_r$ variation. Figure 3b presents $\frac{\Delta i_{ds}^e}{\Delta {\omega }_r}$ with respect to the ${\omega }_r$ variation. The performance of the estimated current is presented with the speed (${\omega }_r$). The sensitivity is shown for the motoring and regenerating mode operation range with a 10 N·m load. The outer loop was closed with the actual speed information from the sensor; thus, the drive stabilized itself to maintain the shaft speed at the reference speed.

5. Simulation Results

This work presents a position or speed sensor-based vector-controlled PMSM drive for the current sensorless scheme. A schematic diagram is shown in Figure 2. References [1,2] present the switching sequence, vector-control, and mathematical model for the PMSM drive. Under various operating speeds/loads, the PMSM drive with the current sensorless algorithm was modeled and tested in MATLAB/Simulink, and some of the results are demonstrated to show the performance of the PMSM drive. The speed loop was closed using data acquired from the speed sensor, while the currents were closed with the estimated quantities. Table 1 shows the machine’s parameter obtained from a laboratory prototype of the PMSM machine.

The actual currents $dq \mathrm{axes}$ and the estimated currents $dq \mathrm{axes}$ are shown in the rotor-reference frames. $i_{ds}=0$ denotes a successful vector-control operation, whereas $i_{qs}$ denotes the torque-producing current component. The simulation plots the shaft speed ($w_r$) against the reference speed ($w_r^{*}$), and the position is displayed.

The drive performance is presented for the various reference speed commands, and the simulation results confirmed the performance of the proposed method. The drive was verified for the ramp speed command, step speed command, and four-quadrant operation. To check the accuracy of the estimated values, the actual currents, reference currents, and estimated currents are shown on the same graph in the simulation results.

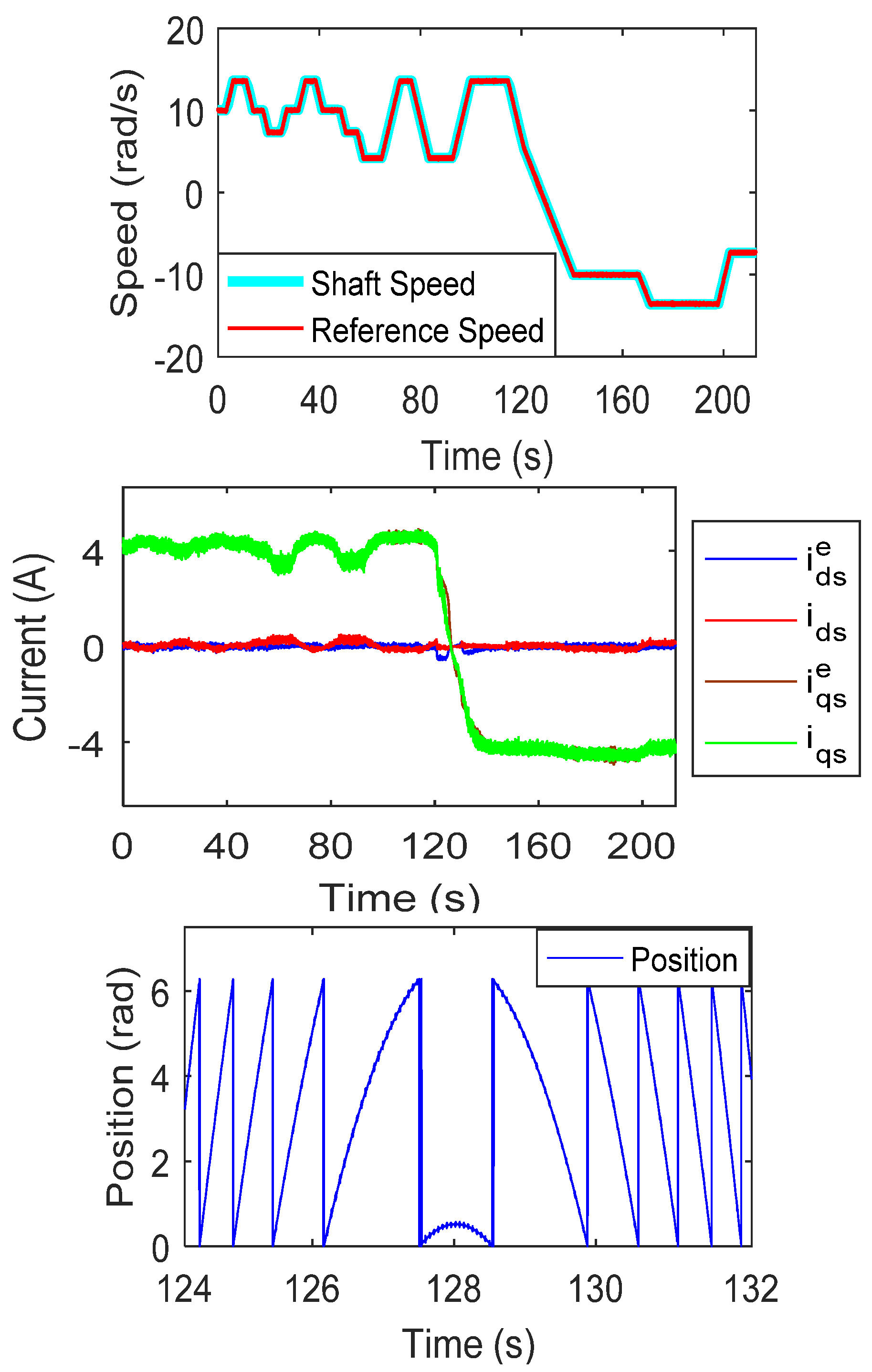
5.1. Various Speed Operations

The current sensorless PMSM drive was evaluated for various speed operations, and the simulation results are presented in Figure 4. The current sensors were used to observe the actual currents and verify the estimation technique performance. The estimated current followed the actual currents observed from the simulation results presented in Figure 2. To demonstrate the accuracy of the current estimation technique, the $q \mathrm{and} d \mathrm{axes}$ estimated and the actual currents are plotted on the same scale in Figure 4.

5.2. Drive Performance for the Ramp Speed Command

The drive was verified and tested for the ramp command, and the results are shown in Figure 5 under varied load and speed circumstances. The tracking performance was tested for the ramp-type speed (i.e., slow zero crossings). The reference speed was changed in a slow ramp command with +10 to −10 rad/s. The PMSM was connected with the DC generator-type load (i.e., $K{\omega }_r$ load). The $i_{ds}$ was maintained at zero, reflects the q-axes vector-control operation. The estimated and actual $i_{qs}$ torque-producing stator current components are presented on the same scale. The current estimation technique’s performance is shown in Figure 5 for the ramp speed command and slow zero crossings.

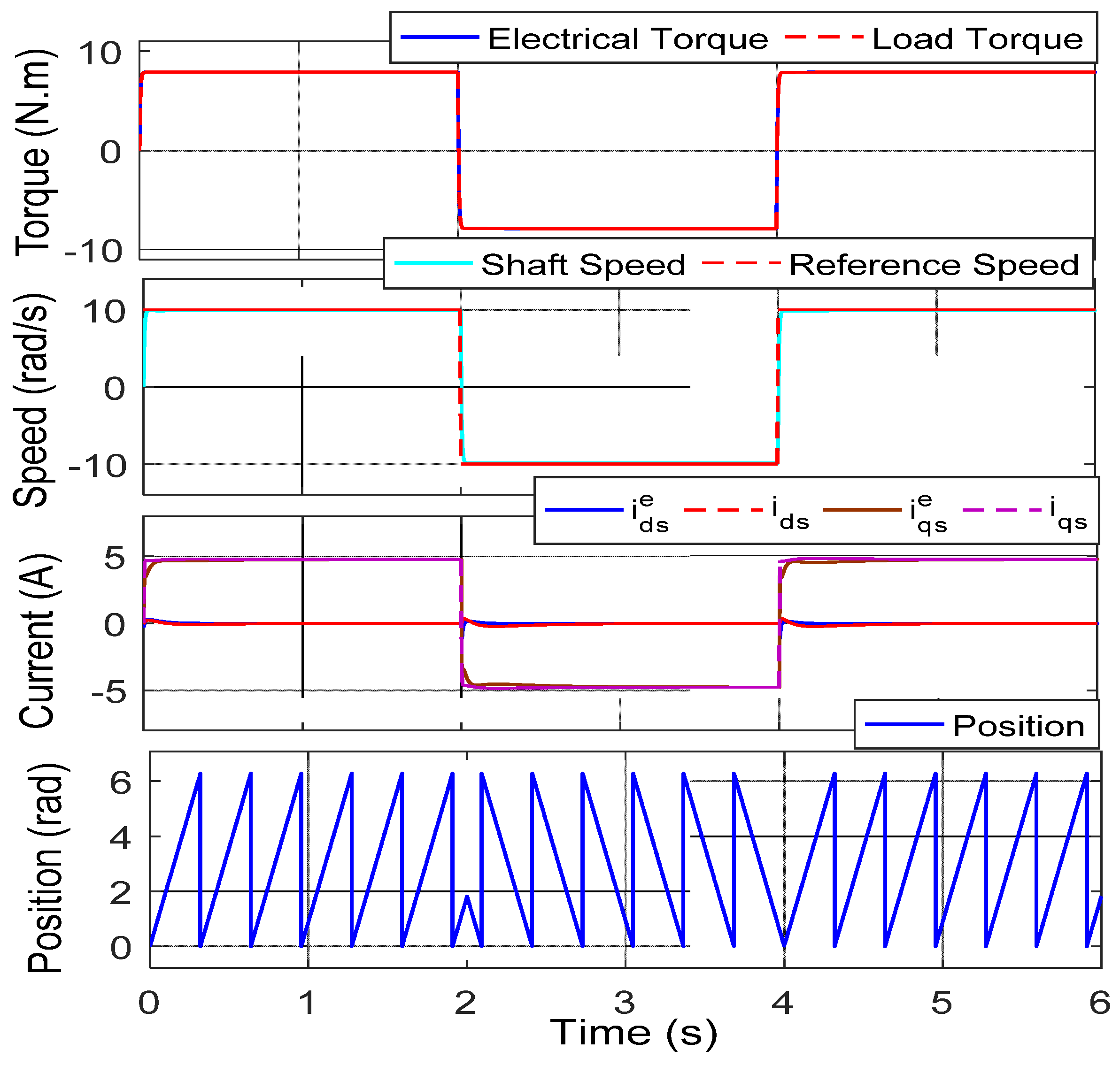
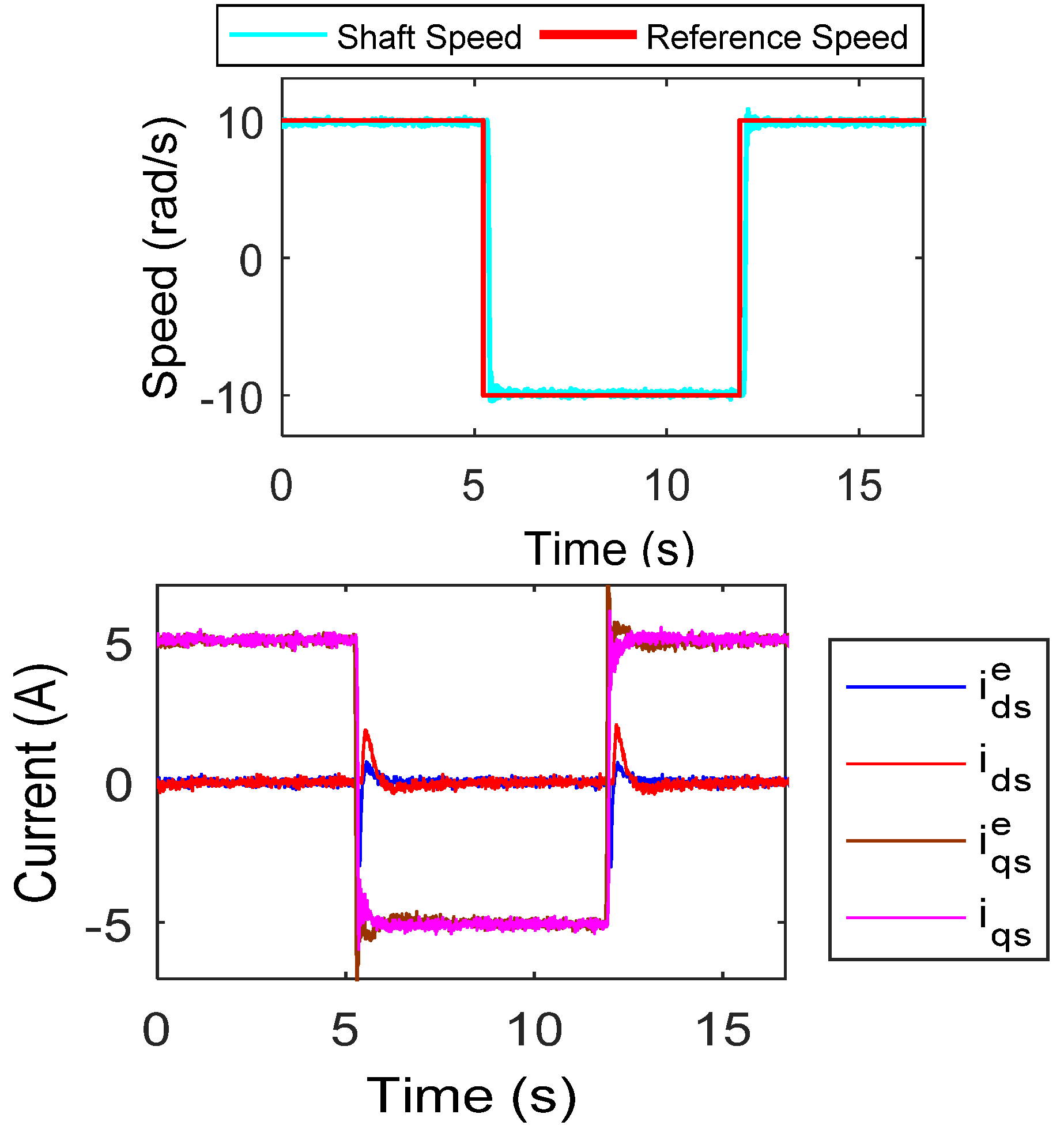
5.3. Drive performance for Step Speed Command

The simulation results for the proposed technique for the step speed command are illustrated in Figure 6. Initially, the reference speed was set at ten rad/s, and the speed was altered between ±10 rad/s. The DC generator-type load (i.e., $K{\omega }_r$ load) was acting on the PMSM. It was observed that the estimated and actual $dq \mathrm{axes}$ stator currents were comparably similar. The estimated currents and actual currents are shown on the same scale to demonstrate the accuracy of the proposed current estimation technique.

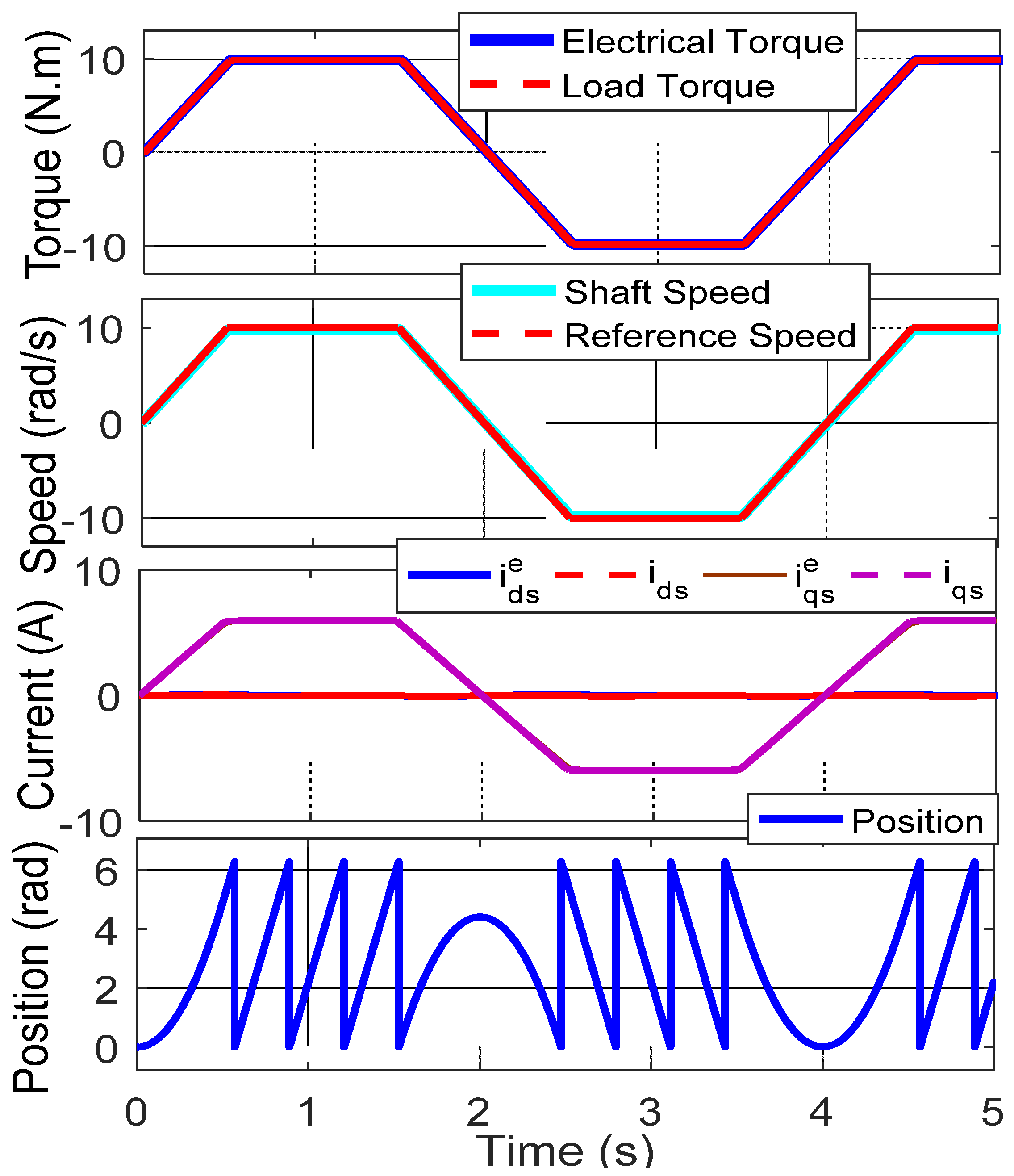
5.4. Drive Performance for the Four-Quadrant Operation

Figure 7 shows a four-quadrant operation. The machine was initially set to +10 rad/s and 8 N·m. The reference speed was changed from +10 to 0, −10, and +10 rad/s at t = 2, 3, and 6 s. The load was changed within ±8 N·m at t = 4 and 7 s.

The PMSM was coupled with a DC motor, and for the first two seconds, the torque and speed were both positive, resulting in the first quadrant operation. The DC motor produced the torque in the same direction as the PMSM. In the simulation results, a zero-speed operation with a positive load was demonstrated.

From t = 2 to 3 s, the DC motor pushed the PMSM machine and acted as a generator until the speed was negative and the torque was positive. From t = 4 s to t = 6 s, the torque was negative, and the speed was negative, resulting in the third quadrant reverse motoring action. From t = 6 s to t = 7 s, the torque was negative, and the speed was positive, resulting in a second quadrant operation. The DC motor pushed the PMSM machine, which acted as a generator. The position information provides the accuracy of the presented algorithm for a zero-speed and four-quadrant operation.

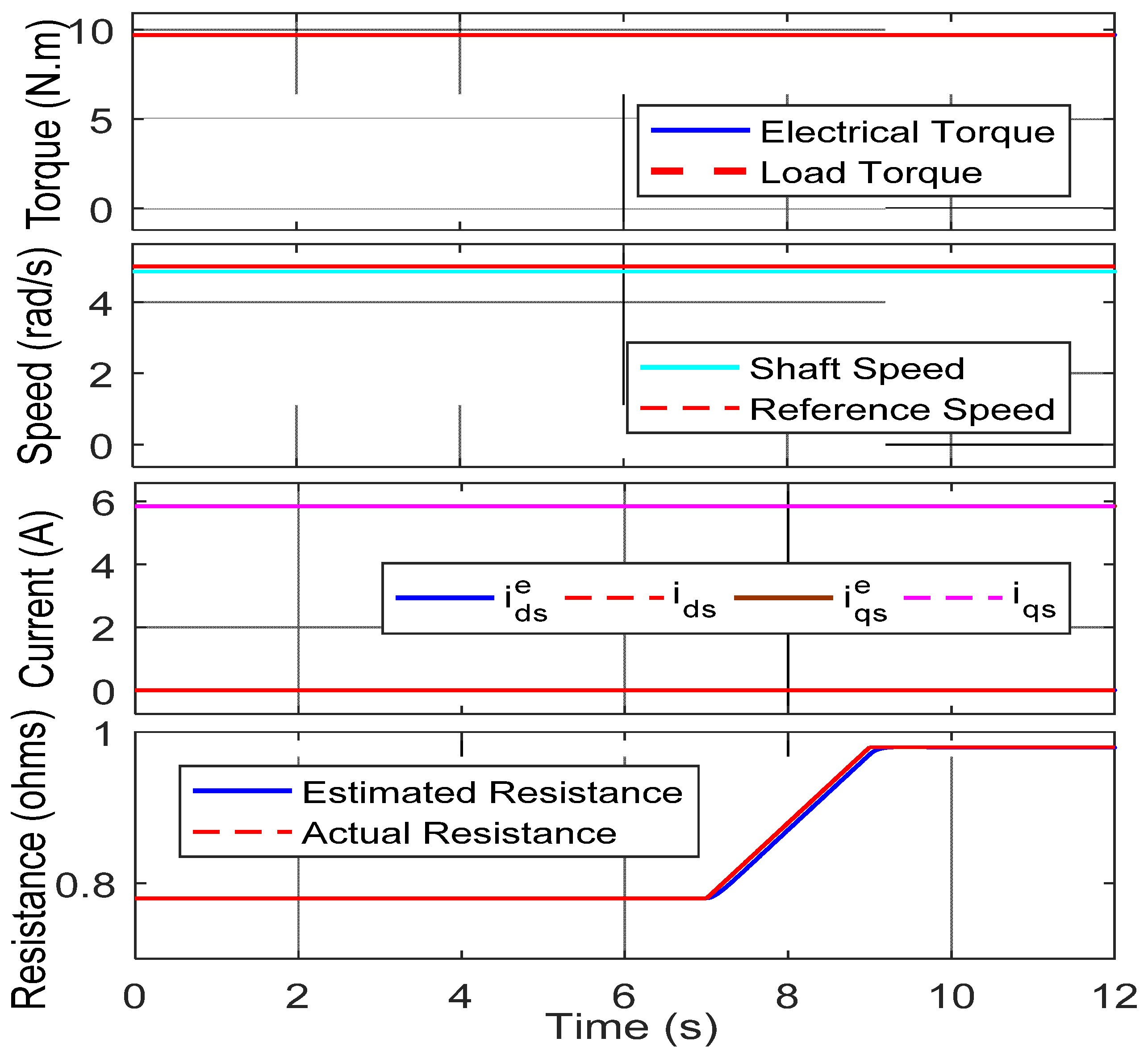
5.5. Effect of the Stator Resistance (${Ɍ}_s$)

The method was tested for the parameter change, and the simulation results are displayed in Figure 8. The current loop was closed with the estimated d and q axes current quantities. The machine resistance was varied with +0.2 ohms from t =10 s to t = 12 s. The effect of the parameter variation was observed on the vector-control (as $i_{ds} \ne 0$), and the simulation results are given in Figure 8. The estimated and the actual currents were affected from t = 10 s, with the ${Ɍ}_{\mathrm{s}}$ variation effect. Therefore, the drive requires the estimation algorithm with ${Ɍ}_{\mathrm{s}}$ compensation to avoid the impact of the machine’s parameters.

5.6. Stator Resistance Compensation

The procedure was verified for the ${Ɍ}_{\mathrm{s}}$ variation with online estimation [34] and compensation. The algorithm failed to estimate the actual $dq\text{-}axes$ currents under ${Ɍ}_{\mathrm{s}}$ variation. The online ${Ɍ}_{\mathrm{s}}$ estimation algorithm was used to estimate and compensate for the current estimation algorithm. The machine was loaded with the $k{w}_r$ load. The speed command was changed in a ramp form and maintained constant at five rad/s. The ${Ɍ}_{\mathrm{s}}$ was estimated and compensated in the current estimation algorithm at t = 5 s. At t = 10 s, the ${Ɍ}_{\mathrm{s}}$ was changed in a ramp form with 0.22 ohms, and the simulation results are given in Figure 9. Figure 9 confirms the satisfactory results for the ${Ɍ}_{\mathrm{s}}$ estimation and compensation to the current estimation algorithm.

6. Hardware Validation

The presented method was validated experimentally on a laboratory prototype using dSPACE 1104 (shown in Figure 10). The drive consisted of the DC generator, PMSM, inverter, driver and protection circuit, and dSPACE 1104. The current sensorless PMSM drive was verified for various conditions; some are presented to show the performance of the proposed algorithm. The experimental results show the shaft speed (${\omega }_r$), reference speed (${\omega }_{ref}$), actual $d \mathrm{and}q \mathrm{axes}\mathrm{stator}\mathrm{currents}$ ($i_{ds} \mathrm{and} i_{qs}$), and estimated $d \mathrm{and} q \mathrm{axes}\mathrm{stator}\mathrm{currents}$ ($i_{ds}^e \mathrm{and} i_{qs}^e$), $d \mathrm{and} q \mathrm{axes}$ reference currents ($i_{ds}^{*} \mathrm{and} i_{qs}^{*}$), and the position.

The dSPACE-based laboratory interface is more flexible for verifying the algorithms and advantageous for testing in various applications, such as robotics and electric drives. The dSPACE 1104 is more suitable for a laboratory interface with a cost-effective, real-time processor with an I/O interface. The dSPACE is user friendly with MATLAB/Simulink (the Realtime Interface provides Simulink with blocks for the I/O configuration). Using the DS1104, the Simulink block was interfaced with the I/O graphically, and the code was generated for the Realtime Interface (RTI). The model was compiled and built into the DS1104 controller board connected with the PC.

The I/O signals were accessed via an adapter cable from the CP1104 (connector panel) to the DS1104 controller board. The CP1104 had eight ADCs and eight DACs, a digital I/O, a slave I/O PWM, two incremental encoders, and serial communication: RS232 and RS485. For the IPMSM drive, two ADCs were used: one for speed information and the other for the current sensor information. The controller board computed the control algorithm, and three-pulse width modulation (PWM) signals with 5 V were generated on the CP1104 (slave I/O PWM). Three PWM pulses were sent to the driver circuit board from the dSPACE-1104 PWM I/O board. Six PWM pulses of 15 V (three inverting and three noninverting PWMs) were generated using three PWM pulses. The pulses were generated with a dead band of 2 µsec to the SKYPER 32 R (SEMIKRON) driver circuit in the inverter. The Semikron driver circuit could control the IGBT (SKM75GB12T4) switching in the inverter.

6.1. Variable Speed Operations

This section shows the experimental results for the current sensorless PMSM drive under various speed commands and slowly zero crossings. The current sensors were used to observe the actual currents and to verify the estimation technique’s performance. The estimated current followed the actual currents that can be observed in Figure 11. The actual currents and estimated currents were plotted on the same graph to see the accuracy of the estimated quantities.

6.2. Forward and Reverse Motoring Operations in a Ramp Speed Command

Figure 12 shows the experimental results for the ramp speed command. The speed command changed between 15 and −15 rad/s in a ramp form. The machine was loaded with a DC generator-type load. The machine was started from a standstill position to 15 rad/s in a ramp form. The drive performance confirmed the ramp speed change with zero crossing also.

6.3. Drive Operation for the Step Speed Command

Figure 13 shows the experimental results for the step speed change. The machine was loaded with a DC generator-type load. The speed command was altered up to ±10 rad/s in a step form. The drive was verified for the step command, and the results confirmed the performance of the presented algorithm.

6.4. Drive Operation with Online Rotor Resistance Estimation and Compensation

The dive performance was verified for the ${Ɍ}_{\mathrm{s}}$ variation, with online estimation and compensation. Figure 14 shows the actual shaft speed and reference speed command, which was maintained at 5 rad/s. The machine was loaded with a constant load (DC generator load). The ${Ɍ}_{\mathrm{s}}$ was estimated using [34] and compensated to the current estimation technique. The drive performance confirmed the current sensorless algorithm under stator resistance variation.

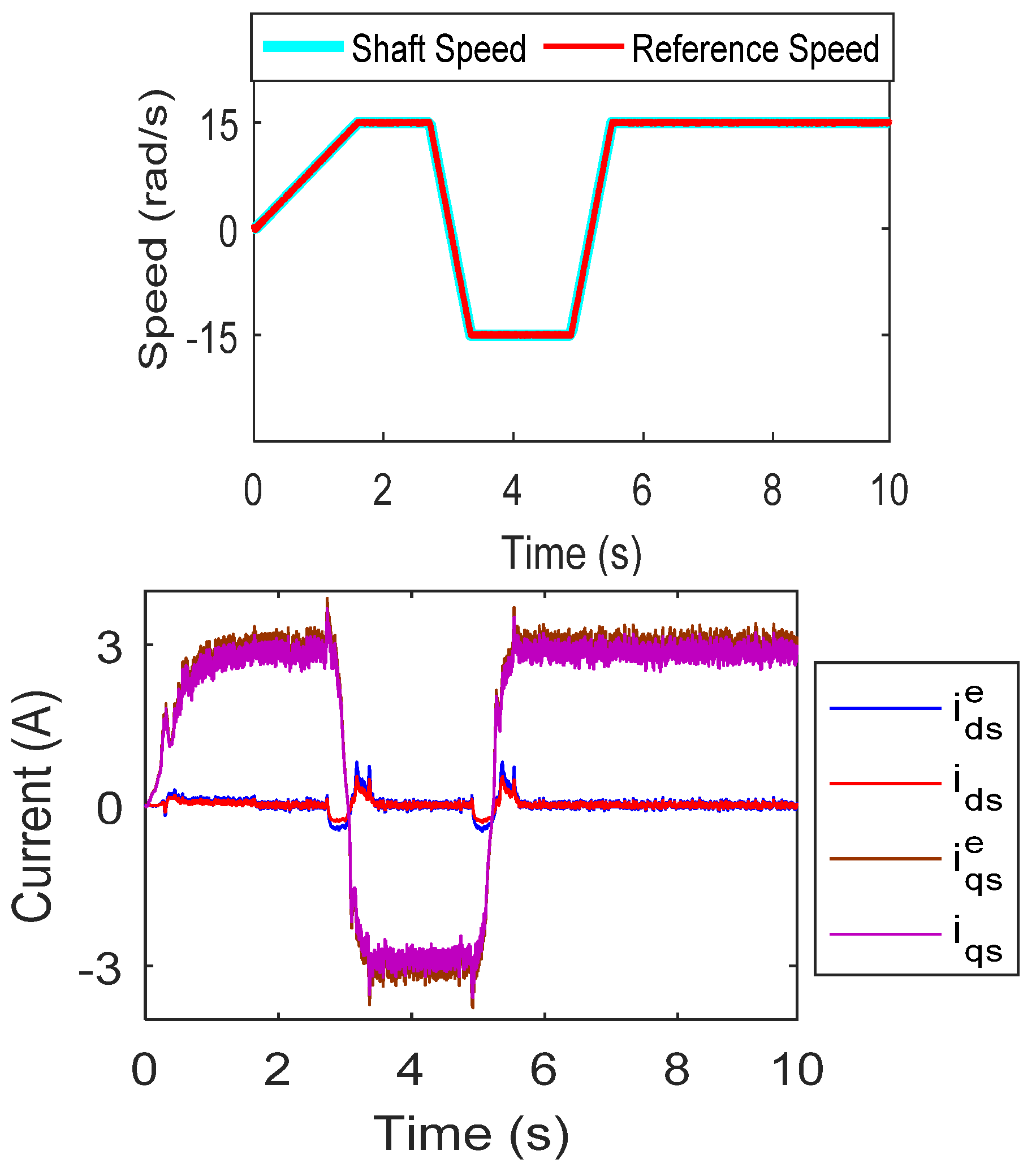
6.5. Drive Operation for the High-Speed Command

Figure 15 shows the experimental results for the high-speed reference command. The machine was connected with a DC generator-type load (i.e., $k{\omega }_r$-type load). The machine was initially at the rest position. The reference speed was changed from 0 to 150 rad/s in a ramp form. At 13 s, the load on the machine was varied by changing the load resistance connected to the DC motor. The estimated and actual currents were plotted on the same scale to show the accuracy of the proposed technique.

7. Conclusions

In this paper, a current sensorless PMSM motor with a position/speed sensor was presented. The currents were estimated from the reference voltages. In the d and q axes rotating reference frame, the stator currents were calculated and closed in the loop to perform an all four-quadrant operation. No additional sensors or hardware is required to implement the proposed method, which makes the drive suitable for retrofitting applications. The current sensorless algorithm can be applied to various PMSM motor types. The current estimation technique can be used to monitor the status of the current sensors by implementing them in the existing PMSM drive. A speed sensor is employed to perform the drive operation with the current estimation technique, which reduces the drive cost and complexity. The reliability and immunity to signal noise is reduced by using a single sensor, i.e., speed or position sensor. The proposed drive is independent of the switching states, integrator, and differentiator terms. The sensitivity of the estimated currents is also performed with speed information. The algorithm was tested on the MATLAB/Simulink platform and also verified on a laboratory prototype. Finally, the current sensorless for PMSM was experimentally validated, and the system’s good performance at a variety of speeds and loading circumstances was confirmed.