Componentwise Perturbation Analysis of the QR Decomposition of a Matrix

Abstract

The paper presents a rigorous perturbation analysis of the QR decomposition $A=QR$ of an $n\times m$ matrix A using the method of splitting operators. New asymptotic componentwise perturbation bounds are derived for the elements of Q and R and the subspaces spanned by the first $p\le m$ columns of A. The new bounds are less conservative than the known bounds and are significantly better than the normwise bounds. An iterative scheme is proposed to determine global componentwise bounds in the case of perturbations for which such bounds are valid. Several numerical results are given that illustrate the analysis and the quality of the bounds obtained.

1. Introduction

The QR decomposition of a matrix $A\in {\mathbb{R}}^{n\times m}$ with $n\ge m$ as the factorization

$$A:=Q\left[\begin{array}{c}R\\ 0\end{array}\right],$$

(1)

where $Q\in {\mathbb{R}}^{n\times n}$ is an orthogonal matrix and $R\in {\mathbb{R}}^{m\times m}$ is the upper triangular matrix. The matrices Q and R are referred to as the Q-factor and the R-factor, respectively. Further on, we shall assume that the matrix A has rank m, i.e., it has full column rank. In such a case, the matrix R is nonsingular, and the matrix Q can be represented as

$$Q=[Q_1,Q_2],Q_1\in {\mathbb{R}}^{n\times m},Q_2\in {\mathbb{R}}^{n\times (n-m)},$$

where $\mathcal{R}\left(Q_1\right)=\mathcal{R}\left(A\right)$ and the columns of $Q_2$ form an orthonormal basis for the complementary subspace $\mathcal{R}{\left(A\right)}^{\perp }$ ([1], Ch. 1). Thus,

$$A=Q_{1}R.$$

(2)

The representation (2) is frequently called QR factorization of A, and it is unique up to the signs of the diagonal elements of R. The matrix $Q_2$ is not unique but has to obey the orthogonality condition

$$Q^{T}Q=\left[\begin{array}{cc}{Q}_1^T{Q}_1& Q_1^T{Q}_2\\ Q_2^T{Q}_1& Q_2^T{Q}_2\end{array}\right]=\left[\begin{array}{cc}{I}_m& 0\\ 0& I_{n-m}\end{array}\right].$$

(3)

In practice, the matrix A is subject to perturbations of different kinds (model inconsistencies, measurement and rounding errors), which leads to the necessity of investigating the sensitivity of the different elements of the QR decomposition to perturbations in the data, i.e., to perform a perturbation analysis of the decomposition [2]. Further on, we assume that the matrix A is subject to an additive perturbation $\delta A\in {\mathbb{R}}^{n\times m}$ and that there exist another pair of matrix $\tilde{Q}$ and upper triangular matrix $\tilde{R}$ such that

$$\tilde{A}=\tilde{Q}\left[\begin{array}{c}\tilde{R}\\ 0\end{array}\right],\tilde{A}=A+\delta A.$$

(4)

The purpose of the perturbation analysis of the QR decomposition is to find bounds on the sizes of $\delta Q=\tilde{Q}-Q$ and $\delta R=\tilde{R}-R$ as functions of the size of $\delta A$ for sufficiently small perturbations of A [3,4]. Due to the non-uniqueness of the matrix $Q_2$, its perturbation is also non-unique. Thus, in the perturbation analysis, one usually considers only the perturbations of the matrix $Q_1$, which are uniquely defined by the perturbations of A. However, in the analysis, we shall need to use an arbitrary matrix $Q_2$ that satisfies the orthogonality condition (3).

The sizes of the perturbations $\delta A$, $\delta Q_1$ and $\delta R$ in the QR factorization are measured by using some of the matrix norms, and, in this case, we call the respective analysis normwise perturbation analysis. Sometimes, however, we are interested in the size of perturbations in individual elements of $\delta Q_1$ and $\delta R$, and, in such a case, the analysis is called componentwise perturbation analysis [5]. In the cases when the estimated vector or matrix has components that differ greatly in size, the normwise estimate does not produce reliable results, and it is preferable to use the componentwise perturbation analysis.

The perturbation analysis of the QR decomposition was performed for the first time by Stewart [6], and improved results were presented by Sun [7] and Stewart [8]. Using a different approach, Chang, Paige and Stewart [9] gave new asymptotic perturbation bounds for the R-factor. Additional improvements of the normwise perturbation bounds of the QR-decomposition were proposed by Chang and Stehlé [10] and Li and Wei [11]. Different componentwise estimates of the perturbations of the Q-factor and the R-factor were derived by Sun [12], Zha [13], Chang and Paige [14] and Chang [15].

A general approach, based on the use of the so-called splitting operators, which can be used in the perturbation analysis of several unitary decompositions, was proposed in [16]; for details, see [17]. The method of the splitting operators can be used to determine normwise as well as componentwise perturbation bounds of different unitary decompositions; see [18,19,20,21,22]. This method was implemented by Sun [23], who obtained improved normwise perturbation bounds of the QR decomposition.

This paper presents a rigorous componentwise perturbation analysis of the QR decomposition based on the method of splitting operators. The analysis presented aims at finding normwise and componentwise perturbation bounds for infinitely small perturbations (asymptotic bounds) as well as for finite perturbations (global bounds). The main result is the obtaining of new asymptotic componentwise perturbation bounds that produce less conservative estimates of the QR decomposition perturbations. A particular case of these bounds is the asymptotic normwise bounds of the QR decomposition derived previously.

This is demonstrated by an example that the new componentwise perturbation bounds of the R factor can be several orders of magnitude smaller than the normwise perturbation bound of this factor. An iterative scheme is proposed to determine global componentwise bounds in the case of perturbations for which such bounds exist. The analysis conducted in this paper is unified with the perturbation analysis of the Schur decomposition presented in [20] and can be easily extended to the case of complex matrices.

In Section 2, we introduce the basic scheme of the perturbation analysis. Section 3 is devoted to determining normwise and componentwise perturbation bounds of the matrix $Q_1$. In Section 4, we present estimates for the perturbations of the column subspaces of A, and, in Section 5, we derive bounds of the elements of R. An iterative scheme for finding global componentwise perturbation bounds of the QR decomposition is proposed in Section 6. A comparison with some of the known methods for perturbation analysis of the QR decomposition is performed in Section 7, and our conclusions are made in Section 8.

The numerical results presented in the paper were obtained with MATLAB^® R2020b [24] using IEEE double precision arithmetic with roundoff unit $\mathbf{u}\approx 1.11\times {10}^{-16}$.

2. Bounding the Basic Perturbation Parameters

Let

$$Q:=[q_1,q_2,\dots ,q_n],q_j\in {\mathbb{R}}^n$$

and the unperturbed and perturbed matrices of the orthogonal factor of the QR decomposition be

$$\begin{array}{ccc}\hfill Q& :=& [q_1,q_2,\dots ,q_n],\hfill \\ \hfill \tilde{Q}& :=& [{\tilde{q}}_1,{\tilde{q}}_2,\dots ,{\tilde{q}}_n],\hfill \\ \hfill {\tilde{q}}_j& :=& q_j+\delta q_j,j=1,2,\dots n,\hfill \end{array}$$

respectively. Define the perturbation matrix

$$\delta Q_1:=[\delta q_1,\delta q_2,\dots ,\delta q_m],\delta q_j\in {\mathbb{R}}^n.$$

It follows from (1) and (4) that

$$\delta q_i^T{a}_j=-{\tilde{q}}_i^T\delta a_j=0,1\le j\le m,j<i\le n.$$

(5)

The column $a_j$ can be obtained from the QR factorization (2) as

$$a_j=\sum _{k=1}^j{r}_{kj}{q}_k,1\le j\le m.$$

(6)

Substituting (6) in (5) yields

$$\sum _{k=1}^j{r}_{kj}\delta q_i^T{q}_k=-{\tilde{q}}_i^T\delta a_j.$$

(7)

Since ${\tilde{Q}}^T\tilde{Q}=I_n$, it follows that

$$Q^T\delta Q=-\delta Q^{T}Q-\delta Q^T\delta Q$$

and

$$\delta q_i^T{q}_j=-q_i^T\delta q_j-\delta q_i^T\delta q_j,1\le j\le m,j<i\le n.$$

(8)

Using (8), Equation (7) can be written as

$$\sum _{k=1}^j{r}_{kj}{q}_i^T\delta q_k+\sum _{k=1}^j{r}_{kj}\delta q_i^T\delta q_k={\tilde{q}}_i^T\delta a_j.$$

(9)

Equation (9) represents a system of

$$\nu =n(n-1)/2-m(m-1)/2=m(2n-m-1)/2$$

nonlinear algebraic equations for the $\nu$ unknown quantities

$$x_{\ell }:=q_i^T\delta q_j,\ell =i+(j-1)n-\frac{j(j+1)}{2},1\le j\le m,j<i\le n.$$

These quantities, which we call basic perturbation parameters, are elements of the strict lower part of the matrix $\delta W=Q^T\delta Q_1$. More precisely, one has that

$$x=\mathrm{vec}\left(\mathrm{Low}\right(\delta W\left)\right),$$

or, equivalently,

$$x=\mathsf{\Omega }\mathrm{vec}\left(\delta W\right),$$

where

$$\begin{array}{ccc}\hfill \mathsf{\Omega }& :=& \left[\mathrm{diag}({\omega }_1,{\omega }_2,\dots ,{\omega }_m)\right]\in {\mathbb{R}}^{\nu \times nm},\hfill \\ \hfill {\omega }_k& :=& \left[0_{(n-k)\times k},I_{n-k}\right]\in {\mathbb{R}}^{(n-k)\times n},k=1,2,\dots ,m,\hfill \\ & & {\mathsf{\Omega }}^T\mathsf{\Omega }=I_{\nu },{\parallel \mathsf{\Omega }\parallel }_2=1.\hfill \end{array}$$

Define the lower triangular matrix

$$M:=\mathsf{\Omega }(R^T\otimes I_m){\mathsf{\Omega }}^T\in {\mathbb{R}}^{\nu \times \nu }$$

whose elements are determined entirely from the elements of R. It can be shown that

$$\sum _{k=i}^n{t}_{ik}{q}_k^T\delta q_j=Mx.$$

The matrix M has the form

$$M=\left[\begin{array}{cccccccccc}{r}_{11}& 0& \dots & 0& 0& 0& \dots & 0& \dots & 0\\ 0& r_{11}& \dots & 0& 0& 0& \dots & 0& \dots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \dots & r_{11}& 0& 0& \dots & 0& \dots & 0\\ 0& r_{12}& \dots & 0& r_{22}& 0& \dots & 0& \dots & 0\\ 0& 0& \dots & 0& 0& r_{22}& \dots & 0& \dots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& \dots & r_{12}& 0& 0& \dots & r_{22}& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & r_{1,m}& 0& 0& \dots & r_{2,m}& \dots & r_{mm}\end{array}\right],$$

which shows that this matrix is nonsingular if the diagonal elements of R are nonzero. The matrix M is called the perturbation operator matrix.

From (9), we obtain that

$$Mx=f-{\mathsf{\Delta }}^x$$

(10)

where

$$f=\mathrm{vec}\left(\mathrm{Low}\left(F\right)\right)=\mathsf{\Omega }\mathrm{vec}\left(F\right)\in {\mathbb{R}}^{\nu },F={\tilde{Q}}^T\delta A$$

and the vector ${\mathsf{\Delta }}^x\in {\mathbb{R}}^{\nu }$ has components

$$\begin{array}{ccc}\hfill {\mathsf{\Delta }}_{\ell }^x& ={\sum }_{k=1}^j{r}_{kj}\delta q_i^T\delta q_k,& \ell =i+(j-1)n-\frac{j(j+1)}{2},\hfill \\ & & 1\le j\le m,j<i\le n.\hfill \end{array}$$

(11)

containing second-order terms in the perturbations $\delta q_i,i=1,2,\dots ,n$.

An asymptotic (linear) approximation of x is obtained from (10) neglecting the second-order term ${\mathsf{\Delta }}^x$,

$$x=M^{-1}f.$$

(12)

The norm of this approximation obeys

$${\parallel x\parallel }_2\le \parallel M^{-1}{\parallel }_2{\parallel f\parallel }_2,$$

which shows that the size of the linear bound of ${\parallel x\parallel }_2$ depends on $1/{\sigma }_{min}\left(M\right)={\parallel M^{-1}\parallel }_2$. As shown by Sun [23],

$$\parallel M^{-1}{\parallel }_2\le {\parallel A^{†}\parallel }_2.$$

Since

$${\parallel f\parallel }_2\le {\parallel \delta A\parallel }_F,$$

one obtains the asymptotic normwise bound

$${\parallel x\parallel }_2\le \parallel M^{-1}{\parallel }_2{\parallel \delta A\parallel }_F.$$

Since the matrix M is lower triangular, it is usually inverted with high precision. Using (12), one can obtain asymptotic componentwise bounds on the perturbation vector x. Since

$$x_{\ell }=M_{\ell ,1:\nu }^{-1}f,\ell =1,2,\dots \nu ,$$

(13)

it follows that

$$|x_{\ell }|\le \parallel M_{\ell ,1:\nu }^{-1}{\parallel }_2{\parallel f\parallel }_2,\ell =1,2,\dots ,\nu$$

and using the inequality ${\parallel f\parallel }_2\le {\parallel \delta A\parallel }_F$, one obtains the asymptotic bound

$$|x_{\ell }|\le x_{\ell }^{lin}:=\parallel M_{\ell ,1:\nu }^{-1}{\parallel }_2{\parallel \delta A\parallel }_F.$$

(14)

The quantity $\mathrm{cond}\left(x_{\ell }\right)={\parallel M_{\ell ,1:\nu }^{-1}\parallel }_2$ can be considered as a componentwise condition number [25] of the element $x_{\ell }$.

Example 1.

Consider the $4\times 3$ matrix

$$A=\left[\begin{array}{ccc}\hfill 18& \hfill -6& \hfill -18\\ \hfill 6& \hfill -2& \hfill -8\\ \hfill -9& \hfill 3.001& \hfill 7\\ \hfill 9& \hfill -3& \hfill -10\end{array}\right]$$

and assume that it is perturbed by

$$\begin{array}{ccc}\hfill \delta A& =& c·{10}^{-k}·A_0,\hfill \\ \hfill A_0& =& \left[\begin{array}{ccc}\hfill 7& \hfill -4& \hfill 1\\ \hfill -4& \hfill 2& \hfill -9\\ \hfill 1& \hfill 6& \hfill -5\\ \hfill -8& \hfill -4& \hfill 3\end{array}\right],\hfill \end{array}$$

where c and k are varying parameters. The QR decompositions of matrices A and $A+\delta A$ are computed by the function qr of MATLAB^®. In the given case, the perturbation operator matrix M is of order $\nu =6$ and $\parallel M^{-1}{\parallel }_2=1.71871\times {10}^3$.

The exact absolute values of the elements of the vector x and their linear approximations computed according to (12) for three perturbations $\delta A={10}^{-11}{A}_0,5\times {10}^{-9}{A}_0$, and $3\times {10}^{-6}$ of different size, are given to five decimal digits in the third and fourth columns of

Table 1. Exact basic perturbation parameters and their linear and nonlinear estimates.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	${\mathit{x}}_{\mathit{\ell }}={\mathit{q}}_{\mathit{i}}^{\mathit{T}}\mathit{\delta }{\mathit{q}}_{\mathit{j}}$	$|{\mathit{x}}_{\mathit{\ell }}|$	${\mathit{x}}_{\mathit{\ell }}^{\mathit{lin}}$	${\mathit{x}}_{\mathit{\ell }}^{\mathit{nonl}}$
1	2	3	4	5
$1.78326\times {10}^{-10}$	$x_1=q_2^T\delta q_1$	$6.48563\times {10}^{-13}$	$7.80510\times {10}^{-12}$	$7.80510\times {10}^{-12}$
	$x_2=q_3^T\delta q_1$	$3.81408\times {10}^{-12}$	$7.80510\times {10}^{-12}$	$7.80510\times {10}^{-12}$
	$x_3=q_4^T\delta q_1$	$3.12632\times {10}^{-12}$	$7.80510\times {10}^{-12}$	$7.80510\times {10}^{-12}$
	$x_4=q_3^T\delta q_2$	$6.73721\times {10}^{-9}$	$2.04508\times {10}^{-7}$	$2.04508\times {10}^{-7}$
	$x_5=q_4^T\delta q_2$	$6.00990\times {10}^{-8}$	$2.04508\times {10}^{-7}$	$2.04508\times {10}^{-7}$
	$x_6=q_4^T\delta q_3$	$6.70820\times {10}^{-8}$	$2.28281\times {10}^{-7}$	$2.28281\times {10}^{-7}$
$8.91628\times {10}^{-8}$	$x_1=q_2^T\delta q_1$	$3.24302\times {10}^{-10}$	$3.90255\times {10}^{-9}$	$3.90335\times {10}^{-9}$
	$x_2=q_3^T\delta q_1$	$1.90707\times {10}^{-9}$	$3.90255\times {10}^{-9}$	$3.90340\times {10}^{-9}$
	$x_3=q_4^T\delta q_1$	$1.56317\times {10}^{-9}$	$3.90255\times {10}^{-9}$	$3.90340\times {10}^{-9}$
	$x_4=q_3^T\delta q_2$	$3.36826\times {10}^{-6}$	$1.02254\times {10}^{-4}$	$1.02280\times {10}^{-4}$
	$x_5=q_4^T\delta q_2$	$3.00486\times {10}^{-5}$	$1.02254\times {10}^{-4}$	$1.02280\times {10}^{-4}$
	$x_6=q_4^T\delta q_3$	$3.35398\times {10}^{-5}$	$1.14140\times {10}^{-4}$	$1.14193\times {10}^{-4}$
$5.34977\times {10}^{-5}$	$x_1=q_2^T\delta q_1$	$1.94581\times {10}^{-7}$	$2.34153\times {10}^{-6}$	$2.75590\times {10}^{-6}$
	$x_2=q_3^T\delta q_1$	$1.14424\times {10}^{-6}$	$2.34153\times {10}^{-6}$	$2.82650\times {10}^{-6}$
	$x_3=q_4^T\delta q_1$	$9.37903\times {10}^{-7}$	$2.34153\times {10}^{-6}$	$2.81974\times {10}^{-6}$
	$x_4=q_3^T\delta q_2$	$1.99332\times {10}^{-3}$	$6.13524\times {10}^{-2}$	$7.59140\times {10}^{-2}$
	$x_5=q_4^T\delta q_2$	$1.77825\times {10}^{-2}$	$6.13524\times {10}^{-2}$	$7.65532\times {10}^{-2}$
	$x_6=q_4^T\delta q_3$	$1.97618\times {10}^{-2}$	$6.84843\times {10}^{-2}$	$9.92798\times {10}^{-2}$

, respectively. It is seen that the elements of the linear estimate $x_{lin}$ closely follow the corresponding elements of the exact perturbation vector $\left|x\right|$.

3. Bounding the Perturbations of the Matrix $Q_1$

Consider the matrix

$$\delta W=Q^T\delta Q_1:=[\delta w_1,\delta w_2,\dots ,\delta w_m],\delta w_j\in {\mathbb{R}}^n.$$

The strictly lower part of this matrix contains elements of the form

$$q_i^T\delta q_j,1\le j\le m,j<i\le n,$$

which can be substituted by the corresponding elements $x_{\ell },\ell =i+(j-1)n-\frac{j(j+1)}{2}$ of the vector x. The elements of the strictly upper part of $\delta W$ are of the form

$$q_i^T\delta q_j,1\le i<j\le m,$$

which, according to the orthogonality condition (8), can be represented as

$$q_i^T\delta q_j=-q_j^T\delta q_i-\delta q_i^T\delta q_j.$$

(15)

In this way, the matrix $\delta W$ can be written as

$$\delta W=\delta V+\delta D-\delta Y,$$

(16)

where the matrix

$$\begin{array}{ccc}\hfill \delta V& =& \left[\begin{array}{ccccc}0& -x_1& -x_2& \dots & -x_{m-1}\\ x_1& 0& -x_n& \dots & -x_{n+m-3}\\ x_2& x_n& 0& \dots & -x_{2n+m-6}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{m-1}& x_{n+m-3}& x_{2n+m-6}& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n-1}& x_{2n-3}& x_{3n-6}& \dots & x_{\nu }\end{array}\right]\hfill \\ & :=& [\delta v_1,\delta v_2,\dots ,\delta v_m],v_j\in {\mathbb{R}}^n\hfill \end{array}$$

has elements depending only on the basic perturbation parameters,

$$\delta D=\left[\begin{array}{cccc}{q}_1^T\delta q_1& 0& \dots & 0\\ 0& q_2^T\delta q_2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & q_m^T\delta q_m\\ 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & 0\end{array}\right]\in {\mathbb{R}}^{n\times m},$$

and the matrix

$$\delta Y=\left[\begin{array}{ccccc}0& \delta q_1^T\delta q_2& \delta q_1^T\delta q_3& \dots & \delta q_1^T\delta q_m\\ 0& 0& \delta q_2^T\delta q_3& \dots & \delta q_2^T\delta q_m\\ 0& 0& 0& \dots & \delta q_3^T\delta q_m\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & \delta q_{m-1}^T\delta q_m\\ 0& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \dots & 0\end{array}\right]\in {\mathbb{R}}^{n\times m},$$

contains second-order terms in $\delta q_j,j=1,2,\dots ,m$.

Consider how to determine the diagonal elements of the matrix W (the nontrivial elements of D) from the elements of x. Denote that ${\alpha }_j=\delta q_j^T{q}_j$. According to (8), one has that

$$2\delta q_j^T{q}_j=-\delta q_j^T\delta q_j,1\le j\le m,$$

or

$$2{\alpha }_j=-{\parallel \delta q_j\parallel }^2.$$

The above expression shows that $\alpha$ is always nonnegative.

On the other hand, we have that

$$\delta w_j=\delta v_j+\left[\begin{array}{c}0\\ ⋮\\ {\alpha }_j\\ ⋮\\ 0\end{array}\right]\begin{array}{c}\\ \leftarrow j,\\ \end{array}j=1,2,\dots ,m$$

so that

$$\parallel \delta w_j{\parallel }_2^2={\parallel \delta v_j\parallel }_2^2+{\alpha }_j^2.$$

(17)

From

$$\delta w_j=Q^T\delta q_j,$$

it follows that

$$\parallel \delta w_j{\parallel }_2={\parallel \delta q_j\parallel }_2=-2{\alpha }_j.$$

(18)

From (17) and (18), we obtain the quadratic equation

$${\alpha }_j^2+2{\alpha }_j+{\parallel \delta v_j\parallel }_2^2=0.$$

(19)

The negative solution of this equation is

$${\alpha }_j^{nonl}=-{\parallel \delta v_j\parallel }_2^2/(1+\sqrt{1-\parallel \delta v_j{\parallel }_2^2}),j=1,2,\dots ,m.$$

(20)

For a small perturbation $\delta A$ (small values of $\parallel \delta v_j{\parallel }_2$), one has the estimate

$${\alpha }_j^{lin}=-{\parallel \delta v_j\parallel }_2^2/2.$$

Thus, for small perturbations, the quantities $|{\alpha }_j^{lin}|,j=1,2,\dots ,m$ depend quadratically on ${\parallel \delta A\parallel }_F$.

In

Table 2. Approximation of the diagonal elements of matrix W.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	$1.78325\times {10}^{-10}$	$8.91627\times {10}^{-8}$	$5.34976\times {10}^{-5}$
$|{\alpha }_1|$	$1.67646\times {10}^{-16}$	$1.74935\times {10}^{-16}$	$1.11378\times {10}^{-12}$
$|{\alpha }_2|$	$1.98416\times {10}^{-15}$	$4.57132\times {10}^{-10}$	$1.60108\times {10}^{-4}$
$|{\alpha }_3|$	$2.33940\times {10}^{-15}$	$5.68134\times {10}^{-10}$	$1.98034\times {10}^{-4}$
$|{\alpha }_1^{lin}|$	$1.23709\times {10}^{-23}$	$3.09280\times {10}^{-18}$	$1.11341\times {10}^{-12}$
$|{\alpha }_2^{lin}|$	$1.82864\times {10}^{-15}$	$4.57132\times {10}^{-10}$	$1.60095\times {10}^{-4}$
$|{\alpha }_3^{lin}|$	$2.27269\times {10}^{-15}$	$5.68131\times {10}^{-10}$	$1.97252\times {10}^{-4}$
$|{\alpha }_1^{nonl}|$	$1.23709\times {10}^{-23}$	$3.09280\times {10}^{-18}$	$1.11341\times {10}^{-12}$
$|{\alpha }_2^{nonl}|$	$1.82864\times {10}^{-15}$	$4.57132\times {10}^{-10}$	$1.60108\times {10}^{-4}$
$|{\alpha }_3^{nonl}|$	$2.27269\times {10}^{-15}$	$5.68131\times {10}^{-10}$	$1.97271\times {10}^{-4}$

, for the same matrix and perturbations that are given in Example 1, we give the exact values of ${\alpha }_j$ and their linear ${\alpha }_j^{lin}$ and nonlinear ${\alpha }_j^{nonl}$ estimates computed using the exact vectors x.

    Thus, having the linear approximations of the elements of x, one can compute the linear approximations of the matrices $\delta V$ and $\delta D$. According to (16), the sum $\delta V+\delta D$ is the linear approximation of $\delta W$, and $\delta Y$ contains second-order terms in ${\parallel \delta A\parallel }_F$ that can be neglected in the asymptotic analysis. As shown below, the determining of an estimate of $\delta W$ allows one to find a bound on $\delta Q_1$.

3.1. Normwise Bounds

The estimate of $\parallel x^{lin}{\parallel }_2$ can be used to find an asymptotic normwise bound of $\parallel \delta Q_1{\parallel }_F$. In determining condition numbers, one assumes ${\parallel \delta A\parallel }_F\to 0$, so that ${\parallel \delta W\parallel }_F\approx {\parallel \delta V\parallel }_F$. From Equation (16), it follows that the Frobenius norm of the strictly upper triangular part $\mathrm{Up}\left(\delta V\right)$ of the matrix $\delta V$ is less than (if $m<n$) or equal (if $m=n$) to the norm of the strictly lower part $\mathrm{Low}\left(\delta V\right)$. Since ${\parallel \mathrm{Low}\left(\delta V\right)\parallel }_F={\parallel x^{lin}\parallel }_2$, we have that ${\parallel \delta W\parallel }_F\le \sqrt{2}{\parallel x^{lin}\parallel }_2$, and the change of the matrix $Q_1$ obeys

$$\parallel \delta Q_1{\parallel }_F=\parallel Q^T\delta Q_1{\parallel }_F\le \sqrt{2}\parallel x^{lin}{\parallel }_2\le c_Q{\parallel \delta A\parallel }_F,$$

(21)

where $c_Q{\parallel \delta A\parallel }_F$ is an asymptotic normwise bound on $\parallel \delta Q_1{\parallel }_F$ and

$$c_Q:=\sqrt{2}{\parallel M^{-1}\parallel }_2$$

can be considered as a normwise condition number of the matrix $Q_1$ with respect to the perturbations of A.

Since, in first-order approximation, it is fulfilled that

$$\delta R=\delta Q^{T}A+Q^T\delta A,$$

considering (21), one obtains that

$${\parallel \delta R\parallel }_F\le c_R{\parallel \delta A\parallel }_F,$$

(22)

where  

$$c_R=1+2\sqrt{2}\parallel M^{-1}{\parallel }_2{\parallel A\parallel }_F$$

is the normwise condition number of the matrix R with respect to the perturbation $\delta A$.

The asymptotic normwise estimates of $\delta Q$ and $\delta R$ thus obtained coincide with the corresponding estimates derived in [17,23].

3.2. Componentwise Bounds

The componentwise bounds of the elements of the matrix $\delta Q_1$ can be found by using the componentwise estimates of the elements of x. An asymptotic bound on the matrix $|\delta W=Q^T\delta Q_1|$ is given by

$$|\delta W^{lin}|=|\delta V|=\left[\begin{array}{ccccc}|{\alpha }_1^{lin}|& |x_1^{lin}|& |x_2^{lin}|& \dots & |x_{m-1}^{lin}|\\ |x_1^{lin}|& |{\alpha }_2^{lin}|& |x_n^{lin}|& \dots & |x_{n+m-3}^{lin}|\\ |x_2^{lin}|& |x_n^{lin}|& |{\alpha }_3^{lin}|& \dots & |x_{2n+m-6}^{lin}|\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ |x_{m-1}^{lin}|& |x_{n+m-3}^{lin}|& |x_{2n+m-6}^{lin}|& \dots & |{\alpha }_m^{lin}|\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ |x_{n-1}^{lin}|& |x_{2n-3}^{lin}|& |x_{3n-6}^{lin}|& \dots & |x_{\nu }^{lin}|\end{array}\right]\in {\mathbb{R}}^{n\times m}.$$

Considering that $\delta Q_1=Q\delta W$ and using (16), a linear approximation of the perturbation $|\delta Q_1|$ is determined as

$$|\delta Q_1|⪯\delta Q_1^{lin}=\left|Q\right||\delta W^{lin}|.$$

(23)

This equation gives asymptotic bounds of the perturbations in the individual elements $q_{ij}$, i.e., componentwise perturbation bounds of the matrix $Q_1$. Since ${\parallel \left|Q\right|\parallel }_F$ = ${\parallel Q\parallel }_F=\sqrt{n}$, we have that

$$\parallel \delta Q_1^{lin}{\parallel }_F\le \sqrt{n}{\parallel \delta W^{lin}\parallel }_F,$$

i.e., the obtaining of the asymptotic componentwise estimate $\delta Q_1^{lin}$ through (23) may increase the bounds on $|\delta q_{ij}|$ at most $\sqrt{n}$ times.

In

Table 3. Exact perturbations of the elements of the matrix $Q_1$ and their linear and nonlinear estimates, $\delta A=3\times {10}^{-6}{A}_0,{\parallel \delta A\parallel }_F=5.34977\times {10}^{-5}$, $B\left(\delta Q^{lin}\right)=c_Q{\parallel \delta A\parallel }_F=0.13003$, and $B\left(\delta Q^{nonl}\right)=0.14519$.

${\mathit{q}}_{\mathit{ij}}$	$|\mathit{\delta }{\mathit{q}}_{\mathit{ij}}|$	$\mathit{\delta }{\mathit{q}}_{\mathit{ij}}^{\mathit{lin}}$	$\mathit{\delta }{\mathit{q}}_{\mathit{ij}}^{\mathit{nonl}}$
$q_{11}$	$8.24060\times {10}^{-7}$	$2.46313\times {10}^{-6}$	$2.94752\times {10}^{-6}$
$q_{21}$	$5.56921\times {10}^{-7}$	$3.27407\times {10}^{-6}$	$3.94135\times {10}^{-6}$
$q_{31}$	$1.78849\times {10}^{-7}$	$2.15221\times {10}^{-6}$	$2.53307\times {10}^{-6}$
$q_{41}$	$1.09799\times {10}^{-6}$	$3.07134\times {10}^{-6}$	$3.68975\times {10}^{-6}$
$q_{12}$	$5.88076\times {10}^{-3}$	$4.50959\times {10}^{-2}$	$5.63774\times {10}^{-2}$
$q_{22}$	$5.89442\times {10}^{-3}$	$7.93060\times {10}^{-2}$	$9.85345\times {10}^{-2}$
$q_{32}$	$1.47078\times {10}^{-4}$	$3.46070\times {10}^{-3}$	$5.35863\times {10}^{-3}$
$q_{42}$	$1.58388\times {10}^{-2}$	$7.07534\times {10}^{-2}$	$8.82920\times {10}^{-2}$
$q_{13}$	$4.76877\times {10}^{-3}$	$4.20957\times {10}^{-2}$	$5.95634\times {10}^{-2}$
$q_{23}$	$8.37491\times {10}^{-3}$	$3.98794\times {10}^{-2}$	$5.85481\times {10}^{-2}$
$q_{33}$	$2.15468\times {10}^{-3}$	$5.63927\times {10}^{-2}$	$7.57743\times {10}^{-2}$
$q_{43}$	$1.72784\times {10}^{-2}$	$7.02671\times {10}^{-2}$	$1.01256\times {10}^{-1}$

, we give, for the same QR decomposition as the one presented in Example  1, the exact values of $|\delta q_{ij}|$ and their linear approximations $\delta q_{ij}^{lin}$ for $\delta A=3\times {10}^{-6}{A}_0$. The comparison of the componentwise bounds with the normwise linear bound $B\left(\delta Q^{lin}\right)=c_Q{\parallel \delta A\parallel }_F$ shows that the bounds on the individual elements of $\delta Q_1$ are smaller than $B\left(\delta Q^{lin}\right)$ for all $j\le m,j<i\le n$. The difference between the componentwise and normwise bounds is particularly significant for the elements in the first column of $\delta Q_1$ whose absolute values are of order ${10}^{-7}$, while the normwise bound is of order ${10}^{-1}$.

4. Estimating Column Subspace Sensitivity

The determination of bounds on the elements of the matrix $\delta Q_1$ makes it possible to estimate the sensitivity of the column subspaces ${\mathcal{X}}_p=\mathcal{R}\left([a_1,a_2,\dots ,a_p]\right),p=1,2,\dots ,m$. (Note that, for $p=m$, the corresponding column subspace ${\mathcal{X}}_m$ coincides with the range $\mathcal{R}\left(A\right)$ of A.) Since we assume that R is of full rank, we have that $\mathcal{R}\left([a_1,a_2,\dots ,a_p]\right)=\mathcal{R}\left([q_1,q_2,\dots ,q_p]\right),p=1,2,\dots ,m$, i.e., the first $p\le m$ columns of Q form an orthonormal basis for the subspace ${\mathcal{X}}_p$.

As is known [26], the sensitivity of a subspace of dimension p is measured by the p angles between the perturbed and unperturbed subspace. Let $Q_X$ and ${\tilde{Q}}_X$ be the orthonormal bases for ${\mathcal{X}}_p$ and its perturbed counterpart ${\tilde{\mathcal{X}}}_p$, respectively. Then, the maximum angle $\delta \mathsf{\Theta }{max}_p:=\delta \mathsf{\Theta }max({\tilde{\mathcal{X}}}_p,{\mathcal{X}}_p)$ between ${\tilde{\mathcal{X}}}_p$ and ${\mathcal{X}}_p$ is determined from [26]

$$sin\left(\delta \mathsf{\Theta }{max}_p\right)={\parallel {Q_X^{\perp }}^T{\tilde{Q}}_X\parallel }_2,$$

(24)

where $Q_X^{\perp }$ is the orthogonal complement of $Q_X$, ${Q_X^{\perp }}^T{Q}_X=0$. Since

$${\tilde{Q}}_X=Q_X+\delta Q_X,$$

one has that

$$sin\left(\delta \mathsf{\Theta }{max}_p\right)={\parallel {Q_X^{\perp }}^T\delta Q_X\parallel }_2.$$

(25)

    Equation (25) shows that the sensitivity of the column subspace ${\mathcal{X}}_p$ is related to the values of the basic perturbation parameters $x_{\ell }=q_i^T\delta q_j,\ell =i+(j-1)n-\frac{j(j+1)}{2},i>p,j=1,2,\dots ,p$. In particular, for $p=1$, the sensitivity of the first column of A is determined as

$$sin(\delta \mathsf{\Theta }max(\widetilde{{\mathcal{X}}_1},{\mathcal{X}}_1))={\parallel \delta W_{2:n,1}\parallel }_2,$$

for $p=2$, one has

$$sin(\delta \mathsf{\Theta }max(\widetilde{{\mathcal{X}}_2},{\mathcal{X}}_2))={\parallel \delta W_{3:n,1:2}\parallel }_2$$

and so on (see Figure 1).

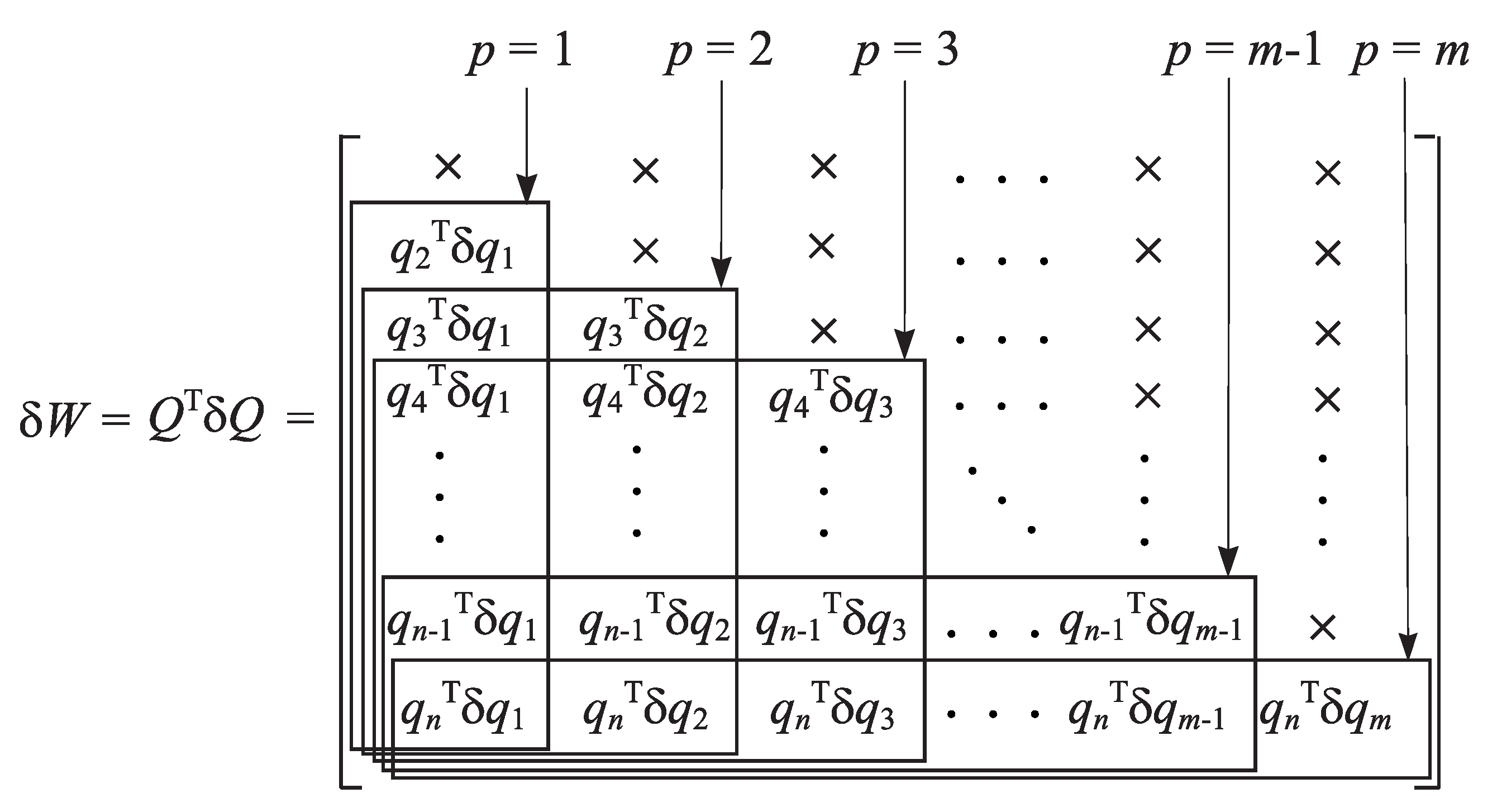
In this way, if the basic perturbation parameters are known, it is possible to find the sensitivity estimates of all column subspaces with dimension $p=1,2,\dots ,m$. More specifically, let  

$$\delta W=\left[\begin{array}{ccccc}\times & \times & \times & \dots & \times \\ x_1& \times & \times & \dots & \times \\ x_2& x_n& \times & \dots & \times \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{m-1}& x_{n+m-3}& x_{2n+m-6}& \dots & \times \\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n-1}& x_{2n-3}& x_{3n-6}& \dots & x_{\nu }\end{array}\right]\in {\mathbb{R}}^{n\times m}.$$

Then, we have that the maximum angle between the perturbed and unperturbed column subspace of dimension p is

$$\delta \mathsf{\Theta }{max}_p=arcsin(\parallel \delta W_{p+1:n,1:p}{\parallel }_2).$$

(26)

In particular, for the sensitivity of $\mathcal{R}\left(A\right)$, we obtain that

$$sin(\delta \mathsf{\Theta }max({\tilde{\mathcal{X}}}_m,{\mathcal{X}}_m))={\parallel \delta W_{m+1:n,1:m}\parallel }_2.$$

An asymptotic estimate of the maximum angle can be obtained, if, in the expression for the matrix $\delta W$, the elements $x_{\ell },\ell =1,2,\dots ,\nu$ are replaced by their linear approximations (12). Representing the matrix $M^{-1}$ as

$$M^{-1}=\left[\begin{array}{c}{M}_{1,1:\nu }^{-1}\\ M_{2,1:\nu }^{-1}\\ M_{3,1:\nu }^{-1}\\ ⋮\\ M_{\nu ,1:\nu }^{-1}\end{array}\right],$$

the matrix $\delta W$ can be written as

$$\delta W=\left[\begin{array}{ccccc}\times & \times & \times & \dots & \times \\ & & & & \\ \overline{)M_{1,1:\nu }^{-1}}f& \times & \times & \dots & \times \\ \overline{)M_{2,1:\nu }^{-1}}f& \overline{)M_{n,1:\nu }^{-1}}f& \times & \dots & \times \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \overline{)M_{n-1,1:\nu }^{-1}}f& \overline{)M_{2n-3,1:\nu }^{-1}}f& \overline{)M_{3n-6,1:\nu }^{-1}}f& \dots & \times \end{array}\right]=L(I_n\otimes f),$$

where the rows of $M^{-1}$ are highlighted in boxes,

$$L=\left[\begin{array}{ccccc}\times & \times & \times & \dots & \times \\ \overline{)M_{1,1:\nu }^{-1}}& \times & \times & \dots & \times \\ & & & & \\ \overline{)M_{2,1:\nu }^{-1}}& \overline{)M_{n,1:\nu }^{-1}}& \times & \dots & \times \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \overline{)M_{n-1,1:\nu }^{-1}}& \overline{)M_{2n-3,1:\nu }^{-1}}& \overline{)M_{3n-6,1:\nu }^{-1}}& \dots & \times \end{array}\right]\in {\mathbb{R}}^{n\times n\nu }$$

and

$$I_n\otimes f=\left[\begin{array}{cccc}f& & & \\ & f& & \\ & & \ddots & \\ & & & f\end{array}\right]\in {\mathbb{R}}^{n\nu \times n}.$$

Using the fact that

$$\parallel I_n{\otimes f\parallel }_2={\parallel f\parallel }_2,$$

we obtain the following asymptotic estimate,

$$\begin{array}{ccc}\hfill |\delta \mathsf{\Theta }{max}_p|& \le & arcsin(\parallel L_{p+1:n,1:p\nu }{\parallel }_2\parallel f{\parallel }_2)\hfill \\ & \le & arcsin(\parallel L_{p+1:n,1:p\nu }{\parallel }_2\parallel \delta A{\parallel }_F),\hfill \\ & & p=1,2,\dots ,m.\hfill \end{array}$$

(27)

Thus, an asymptotic bound of $\delta \mathsf{\Theta }max({\tilde{\mathcal{X}}}_p,{\mathcal{X}}_p)$ is determined as

$$|\delta \mathsf{\Theta }{max}_p|\le \delta \mathsf{\Theta }{max}_p^{lin}:=\mathrm{cond}\left(\mathsf{\Theta }{max}_p\right){\parallel \delta A\parallel }_F,$$

(28)

where the quantity

$$\mathrm{cond}\left(\mathsf{\Theta }{max}_p\right):={\parallel L_{p+1:n,1:p\nu }\parallel }_2$$

can be considered as a condition number of the column subspace ${\mathcal{X}}_p$. The derivation of $\mathrm{cond}\left(\mathsf{\Theta }{max}_p\right)$ is performed such that to find its possible minimum value.

In

Table 4. Exact perturbations of the maximum subspace angles and their linear and nonlinear  estimates.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34977\times {10}^{-5}$
$|\delta \mathsf{\Theta }{max}_1|$	$4.97410\times {10}^{-12}$	$2.48709\times {10}^{-9}$	$1.49225\times {10}^{-6}$
$|\delta \mathsf{\Theta }{max}_2|$	$6.04754\times {10}^{-8}$	$3.02368\times {10}^{-5}$	$1.78948\times {10}^{-2}$
$|\delta \mathsf{\Theta }{max}_3|$	$9.00660\times {10}^{-8}$	$4.50315\times {10}^{-5}$	$2.65878\times {10}^{-2}$
$\delta \mathsf{\Theta }{max}_1^{lin}$	$7.80510\times {10}^{-12}$	$3.90255\times {10}^{-9}$	$2.34153\times {10}^{-6}$
$\delta \mathsf{\Theta }{max}_2^{lin}$	$2.04508\times {10}^{-7}$	$1.02254\times {10}^{-4}$	$6.13524\times {10}^{-2}$
$\delta \mathsf{\Theta }{max}_3^{lin}$	$3.06490\times {10}^{-7}$	$1.53245\times {10}^{-4}$	$9.19468\times {10}^{-2}$
$\delta \mathsf{\Theta }{max}_1^{nonl}$	$1.35188\times {10}^{-11}$	$6.76085\times {10}^{-9}$	$4.85129\times {10}^{-6}$
$\delta \mathsf{\Theta }{max}_2^{nonl}$	$2.89218\times {10}^{-7}$	$1.44645\times {10}^{-4}$	$1.08022\times {10}^{-1}$
$\delta \mathsf{\Theta }{max}_3^{nonl}$	$3.06490\times {10}^{-7}$	$1.53301\times {10}^{-4}$	$1.25698\times {10}^{-1}$

, we give the exact values of maximum angle $|\delta \mathsf{\Theta }{max}_p|$ and its asymptotic bound $\delta \mathsf{\Theta }{max}_p^{lin}$ for the perturbation problem considered in Example 1. In all cases, the size of the estimate matches correctly the size of the actual maximum angle between the perturbed and unperturbed subspace.

5. Perturbation Bounds of the Elements of R

It is convenient to first consider the sensitivity of the nontrivial elements of the upper triangular matrix R for the case of the diagonal elements. Due to the nonsingularity of R, these elements are nonzero.

5.1. Sensitivity Estimates of the Diagonal Elements of R

The changes in the elements of the perturbed matrix R satisfy

$$\delta r_{ij}={\tilde{r}}_{ij}-r_{ij}={\tilde{q}}_i^T(a_j+\delta a_j),1\le i\le j\le m.$$

The above equation can be rewritten as

$$\delta r_{ij}=\delta q_i^T{a}_j+{\tilde{q}}_i^T\delta a_j.$$

(29)

Using Equations (7) and (8), one obtains for the perturbations of the diagonal ($i=j$) elements of R, the expressions

$$\delta r_{ii}=-\sum _{k=1}^i{r}_{ki}{q}_i^T\delta q_k-\sum _{k=1}^i{r}_{ki}\delta q_i^T\delta q_k+{\tilde{q}}_i^T\delta a_i,i=1,2,\dots ,m.$$

(30)

Further on, we shall use the following quantities:

• The diagonal elements of the matrix ${\tilde{Q}}^T\delta A$,

  $$g={\left[{\tilde{q}}_1^T\delta a_1,{\tilde{q}}_2^T\delta a_2,\dots ,{\tilde{q}}_m^T\delta a_m\right]}^T\in {\mathbb{R}}^m.$$
• The changes of the diagonal elements of R,

  $$\delta r_{diag}={\left[\delta r_{11},\delta r_{22},\dots ,\delta r_{mm}\right]}^T\in {\mathbb{R}}^m.$$
• The diagonal elements of W,

  $$\alpha ={\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\right]}^T\in {\mathbb{R}}^m.$$
• The quadratic terms in (30),

  $${\mathsf{\Delta }}^d={\left[{\mathsf{\Delta }}_1^d,{\mathsf{\Delta }}_2^d,\dots ,{\mathsf{\Delta }}_m^d\right]}^T\in {\mathbb{R}}^m,$$

  where

  $${\mathsf{\Delta }}_i^d=-\sum _{k=1}^i{r}_{ki}\delta q_i^T\delta q_k,i=1,2,\dots ,m.$$

Denote the columns of $I_n$ as $e_j,j=1,2,\dots ,n$ and the columns of $I_m$ as ${\eta }_j,j=1,2,\dots ,m$. Then, the system of Equation (30) can be represented as

$$\delta r_{diag}=N_{1}x+N_2\alpha +g+{\mathsf{\Delta }}^d,$$

(31)

where

$$N_1=-\mathsf{\Pi }(R^T\otimes I_n){\mathsf{\Omega }}^T\in {\mathbb{R}}^{m\times \nu },N_2=-\mathrm{diag}(r_{11},r_{22},\dots ,r_{mm})\in {\mathbb{R}}^{m\times m},$$

$$\mathsf{\Pi }=\left[{\eta }_1{e}_1^T,{\eta }_2{e}_2^T,\dots ,{\eta }_m{e}_m^T\right]\in {\mathbb{R}}^{m\times n·m},$$

and the matrix $\mathsf{\Omega }$ was defined earlier. Neglecting the quadratic terms in (31), one obtains the linear estimate

$$\delta r_{diag}=N_1{M}^{-1}f+g.$$

(32)

Equation (32) can be represented in the compact form

$$\delta r_{diag}=[N_1{M}^{-1},I_m]\left[\begin{array}{c}f\\ g\end{array}\right].$$

(33)

Using (33), one can derive condition numbers of the diagonal elements of R. Let

$$Z=[N_1{M}^{-1},I_m]\in {\mathbb{R}}^{m\times (\nu +m)}.$$

Since

$${∥\left[\begin{array}{c}f\\ g\end{array}\right]∥}_2\le {\parallel \delta A\parallel }_F,$$

it follows from (33) that the asymptotic perturbation $\delta r_{ii}$ satisfies

$$|\delta r_{ii}|\le \delta r_{ii}^{lin}:=\mathrm{cond}\left(r_{ii}\right){\parallel \delta A\parallel }_F,i=1,2,\dots ,m,$$

(34)

where

$$\mathrm{cond}\left(r_{ii}\right)={\parallel Z_{i,1:\nu +m}\parallel }_2$$

(35)

is considered as a condition number of $r_{ii}$. The derivation of (35) is performed to find the minimum possible value of $\mathrm{cond}\left(r_{ii}\right)$.

In

Table 5. Exact perturbations of the diagonal elements of R and their linear and nonlinear bounds.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34977\times {10}^{-5}$
$|\delta r_{11}|$	$9.19442\times {10}^{-12}$	$4.59573\times {10}^{-9}$	$2.75746\times {10}^{-6}$
$|\delta r_{22}|$	$4.20811\times {10}^{-11}$	$2.10408\times {10}^{-8}$	$1.27735\times {10}^{-5}$
$|\delta r_{33}|$	$1.51994\times {10}^{-8}$	$7.60002\times {10}^{-6}$	$4.88606\times {10}^{-3}$
$\delta r_{11}^{lin}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34977\times {10}^{-5}$
$\delta r_{22}^{lin}$	$1.87973\times {10}^{-10}$	$9.39863\times {10}^{-8}$	$5.63918\times {10}^{-5}$
$\delta r_{33}^{lin}$	$4.56562\times {10}^{-7}$	$2.28281\times {10}^{-4}$	$1.36969\times {10}^{-1}$
$\delta r_{11}^{nonl}$	$1.78618\times {10}^{-10}$	$1.62255\times {10}^{-7}$	$4.80568\times {10}^{-2}$
$\delta r_{22}^{nonl}$	$1.88265\times {10}^{-10}$	$1.67069\times {10}^{-7}$	$4.80543\times {10}^{-2}$
$\delta r_{33}^{nonl}$	$4.56562\times {10}^{-7}$	$2.28330\times {10}^{-4}$	$1.69291\times {10}^{-1}$
$B\left(\delta R^{lin}\right)$	$1.44561\times {10}^{-5}$	$7.22804\times {10}^{-3}$	$4.33683\times {10}^0$
$B\left(\delta R^{nonl}\right)$	$1.44561\times {10}^{-5}$	$7.22915\times {10}^{-3}$	$4.84251\times {10}^0$

, for the matrix A and the perturbations given in Example 1, we present the exact perturbations $|\delta r_{ii}|$ of the diagonal elements of R and their linear and nonlinear estimates. The normwise quantities $B\left(\delta R^{lin}\right)$ and $B\left(\delta R^{nonl}\right)$ are the normwise linear and nonlinear bounds, derived in [17,23]. These bounds are more pessimistic than the bounds $\delta r_{ii}^{lin}$ and $\delta r_{ii}^{nonl}$.

5.2. Sensitivity Estimates of the Super Diagonal Elements of R

According to (29), the perturbations of the super diagonal elements of the matrix R can be determined as

$$\begin{array}{ccc}\hfill \delta r_{ij}={\tilde{r}}_{ij}-r_{ij}& =& -\sum _{k=1}^j{r}_{kj}{q}_i^T\delta q_k-\sum _{k=1}^j{r}_{kj}\delta q_i^T\delta q_k+{\tilde{q}}_i^T\delta a_j,\hfill \\ & & 1\le i<j\le m.\hfill \end{array}$$

(36)

Let us define the vectors (the elements of the corresponding matrices are taken row-wise),

$$\begin{array}{ccc}\hfill \delta r_{supd}& :=& \mathrm{vec}\left({\left(\mathrm{Up}\left(\delta R\right)\right)}^T\right)={\mathsf{\Omega }}_2\mathrm{vec}\left(\delta R^T\right)\in {\mathbb{R}}^{{\nu }_2},{\nu }_2=m(m-1)/2,\hfill \\ & & {\left(\delta r_{supd}\right)}_{{\ell }_2}=\delta r_{ij},{\ell }_2=j+(i-1)m-\frac{i(i+1)}{2},1\le i<j\le m,\hfill \\ \hfill y& :=& \mathrm{vec}\left({\left(\mathrm{Up}\left(Q_1^T\delta Q_1\right)\right)}^T\right)={\mathsf{\Omega }}_2\mathrm{vec}\left({\left(Q_1^T\delta Q_1\right)}^T\right)\in {\mathbb{R}}^{{\nu }_2},\hfill \\ & & y_{{\ell }_2}=q_i^T\delta q_j,\hfill \\ \hfill h& :=& \mathrm{vec}\left({\left(\mathrm{Up}\left({\tilde{Q}}_1^T\delta A\right)\right)}^T\right)={\mathsf{\Omega }}_2\mathrm{vec}{\left(\left({\tilde{Q}}_1^T\delta A\right)\right)}^T)\in {\mathbb{R}}^{{\nu }_2},\hfill \\ & & h_{{\ell }_2}={\tilde{q}}_i^T\delta a_j,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\mathsf{\Delta }}^r& =& \left[\begin{array}{c}{\mathsf{\Delta }}_1^r\\ {\mathsf{\Delta }}_2^r\\ ⋮\\ {\mathsf{\Delta }}_{{\nu }_2}^r\end{array}\right],\begin{array}{ccc}\hfill {\mathsf{\Delta }}_{{\ell }_2}^r& =& -\sum _{k=1}^j{r}_{kj}\delta q_i^T\delta q_k,\hfill \\ & & {\ell }_2=j+(i-1)m-\frac{i(i+1)}{2},1\le i<j\le m,\hfill \end{array}\hfill \end{array}$$

(37)

where

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_2& :=& \left[\mathrm{diag}({\omega }_1,{\omega }_2,\dots ,{\omega }_{m-1}),0_{{\nu }_2\times m}\right]\in {\mathbb{R}}^{{\nu }_2\times m^2},\hfill \\ \hfill {\omega }_k& :=& \left[0_{(m-k)\times k},I_{m-k}\right]\in {\mathbb{R}}^{(m-k)\times m},k=1,2,\dots ,m-1,\hfill \\ & & {\mathsf{\Omega }}_2^T{\mathsf{\Omega }}_2=I_{m^2},{\parallel {\mathsf{\Omega }}_2\parallel }_2=1.\hfill \end{array}$$

Then, Equation (36) may be represented as the system of ${\nu }_2$ nonlinear algebraic equations

$$\delta r_{supd}=M_{1}y+M_{2}x+M_3\alpha +h+{\mathsf{\Delta }}^r,1\le i<j\le m,$$

(38)

where $M_1,M_2$ and $M_3$ are matrices whose elements are functions of the elements of R. These matrices are determined from

$$M_1=-{\mathsf{\Omega }}_2{P}_{vec}(R^T\otimes I_m)P_{vec}{\mathsf{\Omega }}_2^T\in {\mathbb{R}}^{{\nu }_2\times {\nu }_2},$$

$$M_2=-{\mathsf{\Omega }}_2{P}_{vec}(R^T\otimes I_m){\mathsf{\Omega }}_3^T\in {\mathbb{R}}^{{\nu }_2\times \nu },$$

$$M_3=-{\mathsf{\Omega }}_2(I_m\otimes R^T){\mathsf{\Pi }}^T\in {\mathbb{R}}^{{\nu }_2\times m},$$

where

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_3& :=& \left[\begin{array}{c}\mathrm{diag}({\omega }_1,{\omega }_2,\dots ,{\omega }_{m-1}),0_{(\nu -q)\times m}\\ 0_{q\times m^2}\end{array}\right]\in {\mathbb{R}}^{\nu \times m^2},q=2(n-m),\hfill \\ \hfill {\omega }_k& :=& \left[0_{(m-k)\times k},I_{m-k}\right]\in {\mathbb{R}}^{(m-k)\times m},k=1,2,\dots ,m-1,\hfill \\ & & {\mathsf{\Omega }}_3^T{\mathsf{\Omega }}_3=I_{m^2},{\parallel {\mathsf{\Omega }}_3\parallel }_2=1,\hfill \end{array}$$

and $P_{vec}$ is the vec-permutation matrix as determined from ([27], Ch. 4)

$$\mathrm{vec}\left(A^T\right)=P_{vec}\mathrm{vec}\left(A\right).$$

According to (15), the components of the vector y satisfy

$$\begin{array}{ccc}\hfill y_{{\ell }_2}=-x_{\ell }-\delta q_i^T\delta q_j,& & \ell =j+(i-1)n-\frac{i(i+1)}{2},\hfill \\ & & {\ell }_2=j+(i-1)m-\frac{i(i+1)}{2},\hfill \\ & & 1\le i<j\le m.\hfill \end{array}$$

(39)

In a linear approximation, one has

$$y_{{\ell }_2}=-x_{\ell },$$

and it is possible to show that

$$y={\mathsf{\Omega }}_{4}x,$$

where

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}_4& :=& \left[\mathrm{diag}({\omega }_1,{\omega }_2,\dots ,{\omega }_{m-1}),0_{{\nu }_2\times (n-m)}\right]\in {\mathbb{R}}^{{\nu }_2\times \nu },\hfill \\ \hfill {\omega }_k& :=& \left[I_{m-k},0_{(m-k)\times (n-m)}\right]\in {\mathbb{R}}^{(m-k)\times (n-k)},k=1,2,\dots ,m-1,\hfill \\ & & {\mathsf{\Omega }}_4^T{\mathsf{\Omega }}_4=I_{\nu },{\parallel {\mathsf{\Omega }}_4\parallel }_2=1.\hfill \end{array}$$

Neglecting the second-order terms in Equation (38) and using the linear estimate $x=M^{-1}f$, one obtains the asymptotic estimate

$$\delta r_{supd}=-M_1{\mathsf{\Omega }}_{4}x+M_{2}x+h=-M_1{\mathsf{\Omega }}_4{M}^{-1}f+M_2{M}^{-1}f+h,1\le i<j\le m.$$

Let us denote

$$Z=\left[|M_1{\mathsf{\Omega }}_4{M}^{-1}|+|M_2{M}^{-1}|,I_{{\nu }_2}\right]\in {\mathbb{R}}^{{\nu }_2\times (\nu +{\nu }_2)}.$$

Since

$${∥\left[\begin{array}{c}f\\ h\end{array}\right]∥}_2\le {\parallel \delta A\parallel }_F,$$

one concludes that, in a first-order approximation, the super diagonal elements of $\left|\delta R\right|$ fulfill

$$|\delta r_{ij}|⪯\delta r_{ij}^{lin}=\mathrm{cond}\left(r_{ij}\right){\parallel \delta A\parallel }_F,1\le i<j\le m,$$

(40)

where

$$\begin{array}{ccc}\hfill \mathrm{cond}\left(r_{ij}\right)={\parallel Z_{{\ell }_2,1:\nu +{\nu }_2}\parallel }_2,& & {\ell }_2=j+(i-1)m-\frac{i(i+1)}{2},\hfill \\ & & 1\le i<j\le m.\hfill \end{array}$$

(41)

Equation (40) gives asymptotic componentwise perturbation bounds for the super diagonal part of R. The quantity $\mathrm{cond}\left(r_{ij}\right)$ represents the condition number of $r_{ij}$ with respect to the perturbations in A.

In

Table 6. Exact perturbations of the super diagonal elements of R and their linear and nonlinear bounds.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34977\times {10}^{-5}$
$|\delta r_{12}|$	$6.56506\times {10}^{-11}$	$3.28263\times {10}^{-8}$	$1.96958\times {10}^{-5}$
$|\delta r_{13}|$	$2.19309\times {10}^{-11}$	$1.09686\times {10}^{-8}$	$6.58120\times {10}^{-6}$
$|\delta r_{23}|$	$1.34417\times {10}^{-8}$	$6.72117\times {10}^{-6}$	$4.33437\times {10}^{-3}$
$\delta r_{12}^{lin}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34977\times {10}^{-5}$
$\delta r_{13}^{lin}$	$1.79853\times {10}^{-10}$	$8.99267\times {10}^{-8}$	$5.39560\times {10}^{-5}$
$\delta r_{23}^{lin}$	$4.09016\times {10}^{-7}$	$2.04508\times {10}^{-4}$	$1.22705\times {10}^{-1}$
$\delta r_{12}^{nonl}$	$1.78326\times {10}^{-10}$	$8.91628\times {10}^{-8}$	$5.34981\times {10}^{-5}$
$\delta r_{13}^{nonl}$	$1.79853\times {10}^{-10}$	$8.99301\times {10}^{-8}$	$5.58512\times {10}^{-5}$
$\delta r_{23}^{nonl}$	$4.09016\times {10}^{-7}$	$2.04555\times {10}^{-4}$	$1.48774\times {10}^{-1}$
$B\left(\delta R^{lin}\right)$	$1.44561\times {10}^{-5}$	$7.22804\times {10}^{-3}$	$4.33683\times {10}^0$
$B\left(\delta R^{nonl}\right)$	$1.44561\times {10}^{-5}$	$7.22915\times {10}^{-3}$	$4.84251\times {10}^0$

, for the matrix A and the perturbations given in Example 1, we give the exact perturbations of the super diagonal elements of R and their linear estimates. As in the case of the diagonal elements, the normwise linear and nonlinear bounds $B\left(\delta R^{lin}\right)$ and $B\left(\delta R^{nonl}\right)$ give worse estimates than $\delta r_{ij}^{lin}$.

Hence, the full asymptotic componentwise perturbation analysis of the QR decomposition can be conducted using Equations (12), (23), (28), (34) and (40).

6. Determining Global Perturbation Bounds

Based on the analysis presented above, it is possible to derive an iterative scheme for finding global perturbation bounds of the QR decomposition. The main task of such a scheme is to find a nonlinear estimate of the vector x of the basic perturbation parameters. For this aim, it is necessary to estimate the quadratic term ${\mathsf{\Delta }}^x$ in (10). The analysis of the expression (10) shows that ${\mathsf{\Delta }}^x$ contains terms involving the perturbations $\delta q_i$ for $m<i\le n$, which are not estimates up to the moment since they are columns of the matrix $\delta Q_2={\tilde{Q}}_2-Q_2$. As mentioned previously, the matrix $Q_2$ is not unique, and consequently its perturbation $\delta Q_2$ is also non-unique. However, the problem with finding $\delta Q_2$ of the minimum norm for a fixed $Q_2$ has a unique solution, and our first task in this section is to find an approximation of this perturbation.

6.1. Perturbation Bounds of the Columns of $Q_2$

According to (3), the perturbation $\delta Q_2$ should satisfy the conditions:

$$\begin{array}{ccc}\hfill {(Q_1+\delta Q_1)}^T(Q_2+\delta Q_2)& =& 0,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill {(Q_2+\delta Q_2)}^T(Q_2+\delta Q_2)& =& I_{n-m}.\hfill \end{array}$$

(43)

Equations (42) and (43) can be represented as

$$\begin{array}{ccc}\hfill Q_1^T\delta Q_2+\delta Q_1^T{Q}_2& =& -\delta Q_1^T\delta Q_2,\hfill \\ \hfill Q_2^T\delta Q_2+\delta Q_2^T{Q}_2& =& -\delta Q_2^T\delta Q_2.\hfill \end{array}$$

Setting $X_1=Q_1^T\delta Q_2,X_2=Q_2^T\delta Q_2$, we obtain that

$$\begin{array}{ccc}\hfill ort{h}_1(X_1,X_2)& :=& (I_m+W_1^T)X_1+W_2^T{X}_2+W_2^T=0,\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill ort{h}_2(X_1,X_2)& :=& X_2+X_2^T+X_1^T{X}_1+X_2^T{X}_2=0,\hfill \end{array}$$

(45)

where $W_1=Q_1^T\delta Q_1,W_2=Q_2^T\delta Q_1$. (Note that $\delta W={\left[W_1^T{W}_2^T\right]}^T$ is already estimated). For sufficiently small perturbations $\delta Q_1$, the matrix $I_m+W_1^T$ is nonsingular, and we have that

$$\begin{array}{ccc}\hfill X_1& =& -{(I_m+W_1^T)}^{-1}{W}_2^T(I_{n-m}+X_2),\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill X_2+X_2^T& =& -X_1^T{X}_1-X_2^T{X}_2.\hfill \end{array}$$

(47)

In the first-order analysis of (47), the term $X_2^T{X}_2$ can be neglected, and we have the approximation

$$X_2+X_2^T\approx -X_1^T{X}_1.$$

(48)

As shown in Appendix A, the minimum norm solution of the matrix Equation (48) with respect to $X_2$ is

$$X_2^{appr}=-X_1^T{X}_1/2.$$

(49)

The expression (49) shows that the size of the minimum norm matrix $X_2^{appr}$ is of second order regarding to the size of $X_1$, and hence $X_2$ can be neglected in the asymptotic analysis of (46). Thus, we obtain the first-order approximations

$$\begin{array}{c}\hfill X_1^{appr}=-{(I_m+W_1^T)}^{-1}{W}_2^T,\end{array}$$

(50)

$$\begin{array}{c}\hfill X_2^{appr}=-X_1^T{X}_1/2.\end{array}$$

(51)

In this way, the matrix

$$X=\left[\begin{array}{c}{X}_1\\ X_2\end{array}\right]=Q^T\delta Q_2$$

is approximated as

$$X^{appr}=\left[\begin{array}{c}{X}_1^{appr}\\ X_2^{appr}\end{array}\right],$$

and an approximation of $\delta Q_2$ is obtained as

$$\delta Q_2^{appr}=Q{X}^{appr}.$$

(52)

In

Table 7. Quantities related to the approximation of $\delta Q_2$.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	$1.7832554500\times {10}^{-10}$	$8.9162772500\times {10}^{-8}$	$5.3497663500\times {10}^{-5}$
$\parallel X_1{\parallel }_F$	$9.0065954775\times {10}^{-8}$	$4.5031489846\times {10}^{-5}$	$2.6584712300\times {10}^{-2}$
$\parallel X_2{\parallel }_F$	$4.1725109797\times {10}^{-15}$	$1.0139176039\times {10}^{-9}$	$3.5343592252\times {10}^{-4}$
$er{r}_1$	$1.0034590138\times {10}^{-16}$	$1.2139643751\times {10}^{-16}$	$1.0775666870\times {10}^{-16}$
$er{r}_2$	$2.3314574995\times {10}^{-16}$	$1.2904023661\times {10}^{-16}$	$5.7370600309\times {10}^{-19}$
$\parallel X_1^T{X}_1{\parallel }_F$	$8.1118762095\times {10}^{-15}$	$2.0278350777\times {10}^{-9}$	$7.0674692808\times {10}^{-4}$
$\parallel X_2^T{X}_2{\parallel }_F$	$1.7409847876\times {10}^{-29}$	$1.0280289075\times {10}^{-18}$	$1.2491695133\times {10}^{-7}$
$\parallel X_1^{appr}{\parallel }_F$	$9.0065954782\times {10}^{-8}$	$4.5031489891\times {10}^{-5}$	$2.6594111615\times {10}^{-2}$
$\parallel X_2^{appr}{\parallel }_F$	$4.0559381054\times {10}^{-15}$	$1.0139175409\times {10}^{-9}$	$3.5362338628\times {10}^{-4}$
$er{r}_3$	$3.7480684521\times {10}^{-22}$	$4.5658214975\times {10}^{-14}$	$9.4009759870\times {10}^{-6}$
$er{r}_4$	$1.6450633915\times {10}^{-29}$	$1.0280287798\times {10}^{-18}$	$1.2504949933\times {10}^{-7}$
$\parallel \delta Q_2{\parallel }_F$	$9.0065954775\times {10}^{-8}$	$4.5031489857\times {10}^{-5}$	$2.6587061610\times {10}^{-2}$
$\parallel \delta Q_2^{appr}{\parallel }_F$	$9.0065954782\times {10}^{-8}$	$4.5031489903\times {10}^{-5}$	$2.6596462586\times {10}^{-2}$
$er{r}_5$	$3.1278945183\times {10}^{-16}$	$7.5350125919\times {10}^{-16}$	$7.8338852224\times {10}^{-16}$
$er{r}_6$	$3.4777636565\times {10}^{-16}$	$6.4524550180\times {10}^{-14}$	$1.3295575820\times {10}^{-5}$
$er{r}_1={\parallel ort{h}_1(X_1,X_2)\parallel }_F$,		$er{r}_2={\parallel ort{h}_2(X_1,X_2)\parallel }_F$,
$er{r}_3={\parallel ort{h}_1(X_1^{appr},X_2^{appr})\parallel }_F$,		$er{r}_4={\parallel ort{h}_2(X_1^{appr},X_2^{appr})\parallel }_F$,
$er{r}_5={\parallel ort{h}_3\left(\tilde{Q}\right)\parallel }_F$,		$er{r}_6={\parallel ort{h}_3\left({\tilde{Q}}^{appr}\right)\parallel }_F$

, for the perturbation problem presented in Example 1, we show the quantities related to the approximation of $\delta Q_2$ and the norms of the matrices

$$\begin{array}{ccc}\hfill ort{h}_3\left(\tilde{Q}\right)& =& I_n-{\tilde{Q}}^T\tilde{Q},\hfill \\ \hfill ort{h}_3\left({\tilde{Q}}^{appr}\right)& =& I_n-{\left({\tilde{Q}}^{appr}\right)}^T{\tilde{Q}}^{appr},\hfill \end{array}$$

characterizing the errors in the orthogonal matrices $\tilde{Q}$ and ${\tilde{Q}}^{appr}$, respectively. The approximation of the perturbed orthogonal factor ${\tilde{Q}}^{appr}$ is obtained as  

$${\tilde{Q}}^{appr}=[Q_1+\delta Q_1,Q_2+\delta Q_2^{appr}],$$

where $\delta Q_1$ is the exact perturbation of $Q_1$. These quantities are computed for the three perturbations $\delta A={10}^{-11}{A}_0,5\times {10}^{-9}{A}_0$ and $3\times {10}^{-6}{A}_0$. The results given in the table confirm the assumptions from the perturbation analysis of $Q_2$.

For the same example used previously, in

Table 8. Approximated perturbations of the elements of $Q_2$ and their approximations.

${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	${\mathit{q}}_{\mathit{ij}}$	$|\mathit{\delta }{\mathit{q}}_{\mathit{ij}}|$	$|\mathit{\delta }{\mathit{q}}_{\mathit{ij}}^{\mathit{appr}}|$
$1.7832554500\times {10}^{-10}$	$q_{14}$	$4.9044000886\times {10}^{-8}$	$4.9044000819\times {10}^{-8}$
	$q_{24}$	$5.0733955344\times {10}^{-8}$	$5.0733955468\times {10}^{-8}$
	$q_{34}$	$5.5238446041\times {10}^{-8}$	$5.5238446008\times {10}^{-8}$
	$q_{44}$	$9.0189822446\times {10}^{-9}$	$9.0189821929\times {10}^{-8}$
$8.9162772501\times {10}^{-8}$	$q_{14}$	$2.4521479462\times {10}^{-5}$	$2.4521479487\times {10}^{-5}$
	$q_{24}$	$2.5365705574\times {10}^{-5}$	$2.5365705600\times {10}^{-5}$
	$q_{34}$	$2.7618311270\times {10}^{-5}$	$2.7618311298\times {10}^{-5}$
	$q_{44}$	$4.5102092035\times {10}^{-6}$	$4.5102092081\times {10}^{-5}$
$5.3497663500\times {10}^{-5}$	$q_{14}$	$1.4577251477\times {10}^{-2}$	$1.4582423281\times {10}^{-2}$
	$q_{24}$	$1.4823481491\times {10}^{-2}$	$1.4828695707\times {10}^{-2}$
	$q_{34}$	$1.6304869299\times {10}^{-2}$	$1.6310634063\times {10}^{-2}$
	$q_{44}$	$2.9649988293\times {10}^{-3}$	$2.9661007106\times {10}^{-3}$

, we give the exact values of the elements of $\delta Q_2$ and their approximations using (52). The exact minimum norm perturbation $\delta Q_2$ is found numerically by solving the minimization problem

$$\delta Q_2=\underset{U}{min}{\parallel U\parallel }_F$$

under the constraint ${\tilde{Q}}^T\tilde{Q}=I_n,\tilde{Q}=[Q_1+\delta Q_1,Q_2+U]$. The minimization is performed by the MATLAB^® function fmincon. The results show that, in all cases, $|\delta q_{ij}^{appr}|$ is close to $|\delta q_{ij}|$.

6.2. Iterative Procedure for Finding Global Bounds of the Elements of x

Since one has linear estimates of the basic perturbation terms $x_{\ell }=q_i^T\delta q_j$, it is appropriate to substitute the terms containing the perturbations $\delta q_j$ in Equation (16) by the perturbations

$$\delta w_j=Q^T\delta q_j,j=1,2,\dots ,m,$$

which are of the same size as $\delta q_j$. Since  

$$\delta q_i^T\delta q_j=\delta q_i^{T}Q{Q}^T\delta q_j=\delta w_i^T\delta w_j,$$

the absolute value of the matrix $\delta W$ (16) can be bounded as

$$\begin{array}{ccc}\hfill \left|\delta W\right|& =& |Q^T\delta Q_1|:=[|\delta w_1|,|\delta w_2|,\dots ,|\delta w_m\left|\right],\hfill \\ & ⪯& \delta W^{nonl}=\left|\delta V\right|+\left|\delta D\right|+\left|\delta Y\right|,\hfill \end{array}$$

(53)

where

$$\left|\delta V\right|=\left[\begin{array}{ccccc}0& |x_1|& |x_2|& \dots & |x_{m-1}|\\ |x_1|& 0& |x_n|& \dots & |x_{n+m-3}|\\ |x_2|& |x_n|& 0& \dots & |x_{2n+m-6}|\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ |x_{m-1}|& |x_{n+m-3}|& |x_{2n+m-6}|& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ |x_{n-1}|& |x_{2n-3}|& |x_{3n-6}|& \dots & |x_{\nu }|\end{array}\right]\in {\mathbb{R}}^{n\times m},$$

$$\left|\delta D\right|=\left[\begin{array}{ccccc}|{\alpha }_1|& 0& 0& \dots & 0\\ 0& |{\alpha }_2|& 0& \dots & 0\\ 0& 0& |{\alpha }_3|& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & |{\alpha }_m|\\ 0& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \dots & 0\end{array}\right]\in {\mathbb{R}}^{n\times m},$$

$$\left|\delta Y\right|=\left[\begin{array}{ccccc}0& |\delta w_1^T\left|\right|\delta w_2|& |\delta w_1^T\left|\right|\delta w_3|& \dots & |\delta w_1^T\left|\right|\delta w_m|\\ 0& 0& |\delta w_2^T\left|\right|\delta w_3|& \dots & |\delta w_2^T\left|\right|\delta w_m|\\ 0& 0& 0& \dots & |\delta w_3^T\left|\right|\delta w_m|\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & |\delta w_{m-1}^T\left|\right|\delta w_m|\\ 0& 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \dots & 0\end{array}\right]\in {\mathbb{R}}^{n\times m}.$$

Since the unknown column estimates $|\delta w_j|$ participate in both sides of (53), it is possible to obtain $|\delta w_j|$ recursively as follows.

Let

$$|\delta w_1|=|\delta v_1|+|\delta d_1|,$$

where $|\delta v_1|$ and $|\delta d_1|$ are the first columns of $\left|\delta V\right|$ and $\left|\delta D\right|$, respectively. Then, the next column estimates $|\delta w_j|,j=2,3,\dots m$ can be determined as

$$|\delta w_j|⪯|S_j{|}^{-1}|\delta w_{j-1}|=|S_j{|}^{-1}\left(\right|\delta v_{j-1}|+|\delta d_{j-1}\left|\right),$$

(54)

where

$$\left|S_j\right|=\left[\begin{array}{c}{e}_1^T-\left|\delta w_1^T\right|\\ e_2^T-\left|\delta w_2^T\right|\\ ⋮\\ e_{j-1}^T-\left|\delta w_{j-1}^T\right|\\ e_j^T\\ ⋮\\ e_n^T\end{array}\right]\in {\mathbb{R}}^{n\times n}.$$

If $\left|\right|\delta w_k{\left|\right|}_2<1,k=1,2,\dots ,j-1$, the matrix $|S_j|$ is strictly diagonally dominant and nonsingular ([28], p. 352) and if $\left|\right|\delta w_k{\left|\right|}_2$ are small, then the condition number of $S_j$ is close to 1.

The matrix $\delta W^{nonl}$ only gives estimates of the first m columns of $|Q^T\delta Q|$. Using the representation

$$\delta W^{nonl}=\left[\begin{array}{c}{W}_1\\ W_2\end{array}\right],W_1\in {\mathbb{R}}^{m\times m},W_2\in {\mathbb{R}}^{(n-m)\times m},$$

one can find an approximation $X^{appr}$ of the matrix $Q^T{Q}_2$ using the Equations (50) and (51). Thus, an approximation of $|Q^T\delta Q|$ is obtained as

$$Z=\left[\delta W^{nonl},\left|X^{appr}\right|\right].$$

After determining estimates of $|\delta w_j|,j=1,2,\dots ,m$, it is possible to bound the absolute values of the quadratic terms ${\mathsf{\Delta }}_{\ell }^x$, given in (11), as

$$\begin{array}{ccc}\hfill |{\mathsf{\Delta }}_{\ell }^x|& ={\sum }_{k=1}^j\left|r_{kj}\right|z_i^T{z}_k,& \ell =i+(j-1)n-\frac{j(j-1)}{2},\hfill \\ & & 1\le j\le m,j<i\le n.\hfill \end{array}$$

(55)

The column $z_j,1\le j\le n$ represents an estimate of $|Q^T\delta q_j|$ such that $|\delta q_i^T\delta q_k|\le |\delta q_i^{T}Q\left|\right|Q^T\delta q_k|=z_i^T{z}_k$.

In this way, one obtains an iterative scheme involving Equations (11) and (53)–(55). At each step s, the value of the nonlinear estimate of x is determined from

$$x_s^{nonl}=x^{lin}+|M^{-1}\left|\right|{\mathsf{\Delta }}_s^x|,s=0,1,\dots$$

with initial condition $x_0^{nonl}=eps{[1,1,\dots ,1]}^T$, where $eps$ is the MATLAB^® function eps, $eps=2^{-52}=2\mathbf{u}$. The stopping criterion is taken as

$$er{r}_s=\parallel x_s^{nonl}-x_{s-1}^{nonl}{\parallel }_2/{\parallel x_{s-1}^{nonl}\parallel }_2<tol=10eps.$$

This scheme converges for perturbations of restricted size. As shown in ([17], Ch. 4), the size of the maximum allowable perturbation for which the nonlinear normwise estimate of x is valid is given by

$${\parallel \delta A\parallel }_F\le {\delta }^0:=\frac{1}{\parallel M^{-1}{\parallel }_2(2{\mu }_{\nu }+\sqrt{2+8{\mu }_{\nu }^2})},$$

(56)

where ${\mu }_{\nu }=\sqrt{(\nu -1)/\left(2\nu \right)}$.

In

Table 9. Convergence of the global bounds.

k	${\parallel \mathit{\delta }\mathit{A}\parallel }_{\mathit{F}}$	${\parallel \mathit{x}\parallel }_2$	Number of Iterations	$\parallel {\mathit{x}}^{\mathit{nonl}}{\parallel }_2$
$-11$	$1.78326\times {10}^{-10}$	$9.03176\times {10}^{-8}$	4	$3.68455\times {10}^{-7}$
$-10$	$1.78326\times {10}^{-9}$	$9.03170\times {10}^{-7}$	4	$3.68458\times {10}^{-6}$
$-9$	$1.78326\times {10}^{-8}$	$9.03165\times {10}^{-6}$	5	$3.68480\times {10}^{-5}$
$-8$	$1.78326\times {10}^{-7}$	$9.03122\times {10}^{-5}$	6	$3.68699\times {10}^{-4}$
$-7$	$1.78326\times {10}^{-6}$	$9.02688\times {10}^{-4}$	9	$3.70916\times {10}^{-3}$
$-6$	$1.78326\times {10}^{-5}$	$8.98346\times {10}^{-3}$	17	$3.96070\times {10}^{-2}$
$-5$	$1.78326\times {10}^{-4}$	$8.54366\times {10}^{-2}$	No convergence	-

, we present the number of iterations necessary to find the nonlinear estimate $x^{nonl}$ for the perturbation problem considered in Example 1, along with ${\parallel x\parallel }_2$ and $\parallel x^{nonl}{\parallel }_2$. The components of $x^{nonl}$ are shown for three different perturbations in the fifth column of Table 1 along with the vectors $\left|x\right|$ and $x^{lin}$.

    In Figure 2, we show the convergence of the relative error $er{r}_s$ as a function of s for different perturbations $\delta A={10}^{-k}{A}_0$. As is seen from the figure, with the increasing perturbation size, the convergence worsens, and, for $k=-5$$(\parallel \delta A{\parallel }_F=1.78326\times {10}^{-4})$, the iterations do not converge since the global bound does not exist. The convergence of the iterations is linear, and this can be improved by using appropriate optimization techniques.

6.3. Global Perturbation Bounds of $Q_1$, Column Subspaces and R

Implementing the obtained nonlinear estimate of x, one may find nonlocal bounds on the perturbations of the column subspaces, diagonal and super diagonal elements of R using Equations (26), (31) and (38).

After determining the nonlinear bounds of x and $\left|\delta W\right|$, it is possible to find nonlinear bounds on the perturbations of the elements of $Q_1$ according to the relationship

$$\delta Q_1^{nonl}=\left|Q\right||\delta W^{nonl}|.$$

(57)

The nonlinear bounds $\delta q_{ij}^{nonl}$ of the elements of $Q_1$ for the QR decomposition given in Example 1 and a perturbation $\delta A=3\times {10}^{-6}{A}_0$ are shown in the last column of Table 3 along with $|\delta q_{ij}|$ and $\delta q_{ij}^{lin}$.

A global estimate of the maximum angle between the perturbed and unperturbed column subspace of dimension p is obtained from (26). The values of $\delta \mathsf{\Theta }{max}_p^{nonl}$ for the matrix A from Example 1 and three different perturbations are given in the last rows of Table 4.

Nonlinear bounds on the diagonal elements of R can be obtained by using the expressions

$$\begin{array}{ccc}\hfill \delta r_{diag}^{nonl}& =& \delta r_{diag}^{lin}+\left|{\mathsf{\Delta }}^d\right|,\hfill \\ \hfill |{\mathsf{\Delta }}_i^d|& =& \sum _{k=1}^i\left|r_{ki}\right||\delta w_i^T\left|\right|\delta w_k|,\hfill \\ & & i=1,2,\dots ,m,\hfill \end{array}$$

(58)

and global bounds of the perturbations of the super diagonal elements of R can be found from  

$$\begin{array}{ccc}\hfill \delta r_{supd}^{nonl}& =& \delta r_{supd}^{lin}+|M_3|\alpha +|{\mathsf{\Delta }}^r|,\hfill \\ \hfill \alpha & =& \left[\right|{\alpha }_1|,|{\alpha }_2|,\dots ,|{\alpha }_m{\left|\right]}^T,\hfill \\ \hfill |{\alpha }_j|& =& \parallel \delta w_j{\parallel }_2^2/(1+\sqrt{1-\parallel \delta w_j{\parallel }_2^2}),j=1,2,\dots ,m,\hfill \\ \hfill |{\mathsf{\Delta }}_{{\ell }_2}^r|& =& \sum _{k=1}^j|r_{kj}\left|\right|\delta w_i^T\left|\right|\delta w_k|,\hfill \\ & & {\ell }_2=j+(i-1)m-\frac{i(i+1)}{2},1\le i<j\le m.\hfill \end{array}$$

(59)

The nonlinear perturbation bounds $\delta r_{ii}^{nonl}$ of the diagonal elements of R for the matrix A from Example 1 and for three perturbations $\delta A$ are given in Table 5, and the nonlinear bounds $\delta r_{ij}^{nonl}$ of the super diagonal elements are presented in Table 6. We note that the global perturbation estimates are slightly larger than the corresponding asymptotic estimates but give guaranteed bounds on the perturbations whenever these estimate exist.

7. Comparison with Other Bounds

In this section, we consider two examples in which we compare the perturbation bounds of the QR decomposition obtained in this paper with the bounds that were previously proposed.

Example 2.

Consider the fifth-order matrix [12],

$$A=\left[\begin{array}{ccccc}\hfill 1& \hfill -1& \hfill -1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 1& \hfill -1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right].$$

The matrix A is nonsingular, and its QR factors are $Q=I_5$ and $R=A$. The perturbation matrix is the $5\times 5$ random matrix

$${\delta }_A={10}^{-3}\left[\begin{array}{ccccc}\hfill 0.2742& \hfill 0.2944& \hfill -0.3245& \hfill 0.1483& \hfill 0.9386\\ \hfill 0.1186& \hfill -0.1669& \hfill 0.9198& \hfill -0.2358& \hfill 0.9445\\ \hfill 0.6810& \hfill 0.1577& \hfill 0.1804& \hfill 0.1979& \hfill -0.1045\\ \hfill 0.8284& \hfill -0.9223& \hfill 0.3286& \hfill 0.7425& \hfill -0.2188\\ \hfill 0.2091& \hfill -0.4420& \hfill -0.2410& \hfill 0.8721& \hfill 0.2947\end{array}\right].$$

Using the function qr of MATLAB^®, we obtain (to four decimal digits) that

$$\left|\delta Q\right|=\left[\begin{array}{ccccc}6.0357\times {10}^{-7}& 1.1901\times {10}^{-4}& 6.8154\times {10}^{-4}& 8.2758\times {10}^{-4}& 2.0877\times {10}^{-4}\\ 1.1857\times {10}^{-4}& 3.9005\times {10}^{-7}& 8.3831\times {10}^{-4}& 9.5401\times {10}^{-5}& 2.3275\times {10}^{-4}\\ 6.8081\times {10}^{-4}& 8.3827\times {10}^{-4}& 1.1808\times {10}^{-6}& 1.0608\times {10}^{-3}& 2.6485\times {10}^{-4}\\ 8.2817\times {10}^{-4}& 9.4474\times {10}^{-5}& 1.0605\times {10}^{-3}& 1.0795\times {10}^{-6}& 5.8280\times {10}^{-4}\\ 2.0904\times {10}^{-4}& 2.3305\times {10}^{-4}& 2.6418\times {10}^{-4}& 5.8289\times {10}^{-4}& 2.5378\times {10}^{-7}\end{array}\right].$$

The nonlinear bound of the perturbation of Q, obtained after 16 iterations, is

$$\delta Q^{nonl}=\left[\begin{array}{ccccc}1.4500\times {10}^{-5}& 2.7027\times {10}^{-3}& 2.7360\times {10}^{-3}& 2.7719\times {10}^{-3}& 2.7723\times {10}^{-3}\\ 2.6710\times {10}^{-3}& 2.6773\times {10}^{-5}& 3.9544\times {10}^{-3}& 4.0418\times {10}^{-3}& 4.0428\times {10}^{-3}\\ 2.6876\times {10}^{-3}& 3.8918\times {10}^{-3}& 6.0542\times {10}^{-5}& 7.1420\times {10}^{-3}& 7.1444\times {10}^{-3}\\ 2.7056\times {10}^{-3}& 3.9535\times {10}^{-3}& 7.0244\times {10}^{-3}& 1.2828\times {10}^{-4}& 1.3645\times {10}^{-2}\\ 2.7058\times {10}^{-3}& 3.9541\times {10}^{-3}& 7.0263\times {10}^{-3}& 1.3574\times {10}^{-2}& 1.2829\times {10}^{-4}\end{array}\right].$$

The maximum element of the global estimate $B_{qr,w}$ of $\delta Q$, obtained in [12], is $3.59687\times {10}^{-2}$, while the maximum element of $\delta Q^{nonl}$ is $1.3645\times {10}^{-2}$. Furthermore, $\parallel B_{qr,w}{\parallel }_F=0.0648$, while $\parallel \delta Q^{nonl}{\parallel }_F=0.02693$.

Example 3.

Consider a $20\times 15$ matrix A, taken as

$$A=P_0\left[\begin{array}{c}{S}_0\\ 0\end{array}\right],$$

where $S_0$ is an upper triangular matrix with unit diagonal and super diagonal elements equal to 3, and the matrix $P_0$ is constructed as proposed in [29],

$$\begin{array}{ccc}\hfill P_0& =& H_2\mathsf{\Sigma }{H}_1,\hfill \\ \hfill H_1& =& I_n-2u{u}^T/n,H_2=I_n-2v{v}^T/n,\hfill \\ \hfill u& =& {[1,1,1,\dots ,1]}^T,v={[1,-1,1,\dots ,{(-1)}^{n-1}]}^T,\hfill \\ \hfill \mathsf{\Sigma }& =& \mathrm{diag}(1,\sigma ,{\sigma }^2,\dots ,{\sigma }^{n-1}),\hfill \end{array}$$

where $H_1$ and $H_2$ are elementary reflections that are orthogonal and symmetric matrices [30]. The condition number of $P_0$ with respect to the inversion is controlled by the variable σ and is equal to ${\sigma }^{n-1}$. In the given case, σ is taken equal to $1.2$, and $\mathrm{cond}\left(P_0\right)=31.9480$. The minimum singular value of the matrix M satisfies

$$1/{\sigma }_{min\left(M\right)}=2784.9,$$

which means that the perturbations of Q and R can be several orders of magnitude larger than the perturbations of A. The perturbation of A is chosen as $\delta A={10}^{-c}·A_0$, where c is a positive number and $A_0$ is a matrix with random entries generated by the MATLAB^® function rand.

Several results related to the perturbation problem under consideration for 30 values of c between 13 and 5 are given in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. In Figure 3, we display the perturbations of the particular entry $Q_{15,10}$, which is an element of the matrix $Q_1$. The quantities $B\left(\delta Q^{lin}\right)$ and $B\left(\delta Q^{nonl}\right)$ are the normwise linear and nonlinear bounds derived in [17,23].

These bounds are more than 12-times larger than the norms of the linear $\delta Q^{lin}$ and nonlinear $\delta Q^{nonl}$ componentwise bounds obtained in Section 3. The nonlinear bound is close to the linear one for perturbations of different sizes and increases gradually in the vicinity of the quantity ${\parallel \delta A\parallel }_F\le 6.20078\times {10}^{-7}$. For perturbations of a larger size, the iterations for $x^{nonl}$ do not converge. In Figure 4, we compare the exact perturbation $\delta Q_{15,16}$ of the entry $Q_{15,16}$ (which is also the element ${\left(\delta Q_2\right)}_{15,1}$ of $\delta Q_2$) with the linear approximation $\delta Q_{15,16}^{appr}$. Both quantities are close for all perturbations. This is confirmed by the values of the errors

$$\parallel ort{h}_1(X_1^{appr},X_2^{appr}){\parallel }_F,\parallel ort{h}_2(X_1^{appr},X_2^{appr}){\parallel }_F,{\parallel ort{h}_3\left({\tilde{Q}}^{appr}\right)\parallel }_F,$$

shown in Figure 5, which are much smaller than the value of ${\parallel \delta Q\parallel }_F$ for all perturbations.

The bounds of the quantity $\delta \mathsf{\Theta }{max}_{15}$ (the maximum angle between the perturbed and unperturbed range of A), shown in Figure 6, are close to the exact value of this angle, with the nonlinear bound being slightly greater than the linear one. The normwise linear $B\left(\delta R^{lin}\right)$ and the nonlinear $B\left(\delta R^{nonl}\right)$ bounds obtained in [17,23], are more than 75,000-times greater than the linear $\delta R_{55}^{lin}$ and the nonlinear $\delta R_{55}^{nonl}$ bounds of the diagonal element $R_{55}$, shown in Figure 7. Similarly, the normwise bounds $B\left(\delta R^{lin}\right)$ and $B\left(\delta R^{nonl}\right)$ are more than 13,000-times greater than the bounds $\delta R_{2,10}^{lin}$ and $\delta R_{2,10}^{nonl}$ as shown in Figure 8. This large difference between the sizes of the actual component perturbations of R and the normwise bounds is explained by the large condition number of the computed R—equal to $1.5353\times {10}^6$. (Note that $\mathrm{cond}\left(R\right)=\mathrm{cond}\left(A\right)$).

Note that, while the normwise estimates are valid for perturbations with sizes up to ${\delta }^0=9.31420\times {10}^{-5}$, the iterations to find $x^{nonl}$ converge for perturbations ${\parallel \delta A\parallel }_F\le 6.20078\times {10}^{-7}$.

The results obtained show that the asymptotic bounds are valid for much larger perturbations then the global bounds.

8. Conclusions

The method presented in the paper allows us to find, in a unified manner, componentwise asymptotic and global perturbation bounds for all elements of the QR decomposition, thus, providing a complete perturbation analysis of this important matrix factorization. The bounds obtained in the paper are smaller than some known bounds and can be significantly better than the normwise bounds.