Schur Complement-Based Infinity Norm Bound for the Inverse of Dashnic-Zusmanovich Type Matrices

Abstract

It is necessary to explore more accurate estimates of the infinity norm of the inverse of a matrix in both theoretical analysis and practical applications. This paper focuses on obtaining a tighter upper bound on the infinite norm of the inverse of Dashnic–Zusmanovich-type (DZT) matrices. The realization of this goal benefits from constructing the scaling matrix of DZT matrices and the diagonal dominant degrees of Schur complements of DZT matrices. The effectiveness and superiority of the obtained bounds are demonstrated through several numerical examples involving random variables. Moreover, a lower bound for the smallest singular value is given by using the proposed bound.

1. Introduction

A matrix $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ is referred to as a nonsingular H-matrix [1] if its comparison matrix $\mu \left(A\right)=\left({\mu }_{ij}\right)$ defined by

$$\begin{array}{c}\hfill {\mu }_{ij}:=\left\{\begin{array}{c}|a_{ij}|,j=i,\\ -|a_{ij}|,j\ne i,\end{array}\right.\end{array}$$

is a nonsingular M-matrix. In other words, ${\left[\mu \left(A\right)\right]}^{-1}\ge 0$. H-matrices have significant applications in many fields, such as numerical analysis [2], control theory [3], mathematical programming [4], parallel algorithms in computer science [5], partial differential equations [6] and so on. One intriguing problem is to determine upper bounds for the infinity norm of the inverse of H-matrices. This is because such bounds can be utilized to analyze the convergence of matrix splitting and matrix multi-splitting iterative methods for solving large-scale linear systems [7] as well as linear complementarity problems [4]. Moreover, due to the importance of the matrix condition number $\kappa \left(A\right)$, where $\kappa \left(A\right)=∥A^{-1}∥·∥A∥$, estimating the infinity norm of the inverse matrices is a potential issue.

A traditional approach to finding upper bounds for the infinity norm of the inverse of nonsingular matrices involves utilizing the definition and properties of a given matrix class. For further details, please refer to [8,9,10,11,12,13]. This work has its origins in 1975 when Varah [14] proposed a straightforward and refined upper bound for the infinity norm of the inverse of the strictly diagonally dominant (SDD) matrices class, which is one of the most vital subclasses of H-matrices. A matrix $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ is defined as an SDD matrix if, for each $i\in N:=\{1,2,\cdots ,n\}$,

$$\left|a_{ii}\right|>R_i\left(A\right):=\sum _{j\in N\backslash \left\{i\right\}}\left|a_{ij}\right|.$$

Theorem 1

([14,15]). If $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ is an SDD matrix, then

$$\begin{array}{c}\hfill ∥A^{-1}∥\le \underset{i\in N}{max}\frac{1}{|a_{ii}| -R_i\left(A\right)}.\end{array}$$

(1)

Bound (1) is commonly referred to as Varah’s bound and is applicable only to SDD matrices. Consequently, many researchers have investigated the infinite norm bound for the inverse matrix of broader of H-matrices. For example, Liu et al. [16] obtained the following upper bound on doubly strictly diagonally dominant (DSDD) matrices, which extend SDD matrices on H-matrices.

Theorem 2

([16]). Let $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$, $n\ge 2$, be a DSDD matrix. Then

$$\begin{array}{c}\hfill ∥A^{-1}∥\le \underset{i,j\in N,i\ne j}{max}\frac{|a_{jj}|+R_i\left(A\right)}{|a_{ii}\left|\right|a_{jj}| -R_i\left(A\right)R_j\left(A\right)}.\end{array}$$

(2)

In addition, there are other types of matrices such as S-strictly diagonally dominant (S-SDD) matrices [17,18] and Nekrasov matrices [8,12], among others [9,19,20].

Recently, a meaningful subclass of H-matrices, called Dashnic–Zusmanovich-type (DZT) matrices, has been proposed by Zhao et al. [21]. It is defined as follows:

Definition 1.

A matrix $A=\left[a_{ij}\right]\in {\mathbb{C}}^{n\times n}$ is called a DZT matrix if, for any $i\in N$, the set

$${\gamma }_i\left(A\right):=\left\{j\in N\backslash \left\{i\right\}:\left(\right|a_{ii}| -R_i^{N\backslash \left\{j\right\}}\left(A\right)\left)\right|a_{jj}|>|a_{ij}|R_j\left(A\right)\right\}$$

(3)

is nonempty, where $R_i^S\left(A\right)$ represents the sum of the absolute values of the off-diagonal elements in the i-th row of A corresponding to the set S, i.e.,

$$\begin{array}{c}\hfill R_i^S\left(A\right):=\sum _{j\in S,j\ne i}\left|a_{ij}\right|,\end{array}$$

when $S=N$, we omit S for convenience.

Later, Li et al. proposed the following infinite norm bound for the inverse matrix of DZT matrices.

Theorem 3

([10]). Let $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ be a DZT matrix. Then

$$\begin{array}{c}\hfill \parallel A^{-1}{\parallel }_{\infty }\le \underset{i\in N}{max}\underset{j\in {\gamma }_i\left(A\right)}{min}\frac{|a_{jj}|+|a_{ij}|}{\left(\right|a_{ii}| -R_i^{N\backslash \left\{j\right\}}\left(A\right)\left)\right|a_{jj}| - |a_{ij}|R_j\left(A\right)}.\end{array}$$

(4)

From an application standpoint, obtaining a tight upper bound for $\parallel A^{-1}{\parallel }_{\infty }$ is crucial. When the denominator of the upper bound given by (4) is tiny, the upper bound obtained by Theorem 3 may be too large. Hence, it is of great theoretical and practical significance to explore a better bound on $\parallel A^{-1}{\parallel }_{\infty }$ with a DZT matrix A.

It is well established that for any given H-matrix A, a positive diagonal matrix exists that can scale A (by multiplying it from the right) into an SDD matrix. While Zhao et al. [21] demonstrated that a DZT matrix is indeed an H-matrix, they did not provide the corresponding scaling matrix. In this work, we derive the scaling matrix for DZT matrices to address this gap.

This paper presents a method for constructing scaling matrices for DZT matrices and uses their special structure to establish a sufficient condition for the Schur complement of a DZT matrix to be an SDD matrix. This, in turn, allows us to derive new upper bounds for the infinity norm of the inverse of a DZT matrix based on the Schur complement. The validity and superiority of the obtained bounds are illustrated by some numerical examples with random variables. Finally, we propose a lower bound for the smallest singular value using the proposed bound.

2. Schur Complement-Based Infinity Bounds for the Inverse of DZT Matrices

Let us begin by reviewing the concept of the Schur complement. Given nonempty index sets $\alpha ,\beta \subseteq N$, we use ${\alpha }^c$ to represent the complement of $\alpha$ with respect to N. The submatrix of $A\in {\mathbb{C}}^{n\times n}$ that lies in the rows indexed by $\alpha$ and the columns indexed by $\beta$ is denoted by $A(\alpha ,\beta )$. We use $A(\alpha ,\alpha )$ as shorthand for $A(\alpha ,\alpha )$. If $A\left(\alpha \right)$ is invertible, the Schur complement of A with respect to $A\left(\alpha \right)$ is denoted by $A/A\left(\alpha \right)$ or simply $A/\alpha$, and it is equal to

$$\begin{array}{c}\hfill A\left({\alpha }^c\right)-A({\alpha }^c,\alpha )A{\left(\alpha \right)}^{-1}A(\alpha ,{\alpha }^c).\end{array}$$

For a given nonempty subset $\alpha \subset N$, there exists a permutation matrix P such that

$$\begin{array}{c}\hfill P^{T}AP=\left[\begin{array}{cc}A\left(\alpha \right)& A\left(\alpha ,{\alpha }^c\right)\\ A\left({\alpha }^c,\alpha \right)& A\left({\alpha }^c\right)\end{array}\right].\end{array}$$

Since the inverse of a permutation is also a permutation matrix, the infinity norm of the inverse of a permutation matrix is equal to 1. Therefore, for a nonsingular matrix A, we have

$${∥A^{-1}∥}_{\infty }={∥P{\left(P^{T}AP\right)}^{-1}{P}^T∥}_{\infty }\le {∥{\left(P^{T}AP\right)}^{-1}∥}_{\infty }.$$

So we just need to focus on ${∥{\left(P^{T}AP\right)}^{-1}∥}_{\infty }$. Let $\alpha =\{i_1,i_2,\cdots ,i_k\}$ be a given nonempty subset of N; note that

$$P^{T}AP=\left(\begin{array}{cc}{I}_k& 0\\ A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}& I_{n-k}\end{array}\right)\left(\begin{array}{cc}A\left(\alpha \right)& 0\\ 0& A/\alpha \end{array}\right)\left(\begin{array}{cc}{I}_k& A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)\\ 0& I_{n-k}\end{array}\right),$$

hence

$$P^T{A}^{-1}P=\left(\begin{array}{cc}{I}_k& -A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)\\ 0& I_{n-k}\end{array}\right)\left(\begin{array}{cc}A{\left(\alpha \right)}^{-1}& 0\\ 0& {(A/\alpha )}^{-1}\end{array}\right)\left(\begin{array}{cc}{I}_k& 0\\ -A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}& I_{n-k}\end{array}\right).$$

Then, combining Lemma 2 of [11], the upper bound for ${∥A^{-1}∥}_{\infty }$ is measured by

$$\begin{array}{c}\hfill {∥A^{-1}∥}_{\infty }\le {∥L∥}_{\infty }{∥U∥}_{\infty }max\left\{{∥A{\left(\alpha \right)}^{-1}∥}_{\infty },{∥{(A/\alpha )}^{-1}∥}_{\infty }\right\},\end{array}$$

(5)

where

$${\parallel L\parallel }_{\infty }={∥\left(\begin{array}{cc}{I}_k& 0\\ -A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}& I_{n-k}\end{array}\right)∥}_{\infty }=1+{∥A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}∥}_{\infty },$$

(6)

$${\parallel U\parallel }_{\infty }={∥\left(\begin{array}{cc}{I}_k& -A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)\\ 0& I_{n-k}\end{array}\right)∥}_{\infty }=1+{∥A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)∥}_{\infty }.$$

(7)

Therefore, the problem is transformed into estimating the upper bounds of ${∥A{\left(\alpha \right)}^{-1}∥}_{\infty }$, ${∥{(A/\alpha )}^{-1}∥}_{\infty }$, ${∥A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}∥}_{\infty }$ and ${∥A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)∥}_{\infty }$. More generally, to simplify notation, the problem is transformed into estimating the upper bounds of ${∥A{\left(\alpha \right)}^{-1}∥}_{\infty }$, ${∥{(A/\alpha )}^{-1}∥}_{\infty }$, ${∥B{A}^{-1}∥}_{\infty }$ and ${∥A^{-1}C∥}_{\infty }$, where ${∥A{\left(\alpha \right)}^{-1}∥}_{\infty }$ can apply the results associated with $\parallel A^{-1}\parallel$. Next, we will give the upper bounds for ${∥B{A}^{-1}∥}_{\infty }$ and ${∥A^{-1}C∥}_{\infty }$, when A is an SDD matrix. We need to use the following lemma.

Lemma 1

([1]). Suppose $A=\left(a_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is an H-matrix, then

$$|A^{-1}{|\le \left\{\mu \left(A\right)\right\}}^{-1}.$$

We are now ready to present upper bounds for ${∥B{A}^{-1}∥}_{\infty }$ and ${∥A^{-1}C∥}_{\infty }$ when A is an SDD matrix.

Lemma 2.

Let $A=\left(a_{ij}\right)\in {\mathbb{R}}^{n\times n}$, $n\ge 2$, be an SDD matrix, $B=\left(b_{ij}\right)\in {\mathbb{R}}^{m\times n}$, $C=\left(c_{ij}\right)\in {\mathbb{R}}^{n\times m}$. Then

$$\begin{array}{c}\hfill {∥B{A}^{-1}∥}_{\infty }\le \underset{j\in M}{max}\sum _{i\in N}\frac{|b_{ji}|(1+\varphi R_i\left(A\right))}{|a_{ii}|},\end{array}$$

(8)

$$\begin{array}{c}\hfill {∥A^{-1}C∥}_{\infty }\le \underset{i,j\in N,i\ne j}{max}\frac{|a_{jj}|{\displaystyle \sum _{k\in M}}|c_{ik}|+R_i\left(A\right){\displaystyle \sum _{k\in M}}\left|c_{jk}\right|}{|a_{ii}\left|\right|a_{jj}| -R_i\left(A\right)R_j\left(A\right)},\end{array}$$

(9)

where $M=\{1,2,\cdots ,m\}$ and $\varphi =\underset{i,j\in N,i\ne j}{max}\frac{|a_{jj}|+R_i\left(A\right)}{|a_{ii}\left|\right|a_{jj}|-R_i\left(A\right)R_i\left(A\right)}$.

Proof. 

Since A is an SDD matrix, by Lemma 1, we have

$$|A^{-1}{|\le \left\{\mu \left(A\right)\right\}}^{-1}.$$

Let $y={\left\{\mu \left(A\right)\right\}}^{-1}{e}_n$ and $y_u=\underset{i\in N}{max}{y}_i$, where $e_n={(1,\cdots ,1)}^T\in {\mathbb{R}}^n$, then $\mu \left(A\right)y=e_n$. From (2), we have

$$\begin{array}{c}\hfill y_u={∥{\left\{\mu \left(A\right)\right\}}^{-1}{e}_n∥}_{\infty }={∥{\left\{\mu \left(A\right)\right\}}^{-1}∥}_{\infty }\le \underset{i,j\in N,i\ne j}{max}\frac{|a_{jj}|+R_i\left(A\right)}{|a_{ii}\left|\right|a_{jj}| -R_i\left(A\right)R_i\left(A\right)}:=\varphi .\end{array}$$

(10)

Considering the i-th equation of the system of linear equations $\mu \left(A\right)y=e_n$, we obtain

$$\begin{array}{c}\hfill 1=|a_{ii}|y_i-\sum _{j\in N\backslash \left\{i\right\}}|a_{ij}|y_j\ge |a_{ii}|y_i-\sum _{j\in N\backslash \left\{i\right\}}|a_{ij}|y_u\ge \left|a_{ii}\right|y_i-\varphi R_i\left(A\right),\end{array}$$

(11)

which implies

$$\begin{array}{c}\hfill y_i\le \frac{1+\varphi R_i\left(A\right)}{|a_{ii}|},i\in N.\end{array}$$

Let $x=|B{A}^{-1}|e_n={(x_1,x_2,\cdots ,x_m)}^T$. Hence, by the following equation:

$$\begin{array}{c}\hfill x=|B{A}^{-1}|e_n\le \left|B\right||A^{-1}|e_n\le {\left|B\right|\left\{\mu \left(A\right)\right\}}^{-1}{e}_n=\left|B\right|y,\end{array}$$

one immediately obtains:

$$\begin{array}{c}\hfill {∥B{A}^{-1}∥}_{\infty }=\underset{j\in M}{max}{x}_j\le \underset{j\in M}{max}\sum _{i\in N}|b_{ji}|y_i\le \underset{j\in M}{max}\sum _{i\in N}\left|b_{ji}\right|\frac{1+\varphi R_i\left(A\right)}{|a_{ii}|}.\end{array}$$

While for $∥A^{-1}C∥$, similarly to the proof of Theorem 4.1 in [16], we can easily obtain that

$$\begin{array}{c}\hfill {∥A^{-1}C∥}_{\infty }\le \underset{i,j\in N,i\ne j}{max}\frac{|a_{jj}|{\displaystyle \sum _{k\in M}}|c_{ik}|+R_i\left(A\right){\displaystyle \sum _{k\in M}}\left|c_{jk}\right|}{|a_{ii}\left|\right|a_{jj}| -R_i\left(A\right)R_j\left(A\right)},\end{array}$$

The proof is completed. □

Next, we will discuss $∥{(A/\alpha )}^{-1}∥$ for a DZT matrix A.

It is well known that for a given H-matrix A, there exists a positive diagonal matrix that scales A (by multiplying it from the right) to produce an SDD matrix. Although Zhao et al. [21] have proved that a DZT matrix must be an H-matrix, they do not give the scaling matrix. Next, we will give the scaling matrix for a DZT matrix to complete this point. Moreover, our procedure for proving the conclusion that each DZT matrix is an H-matrix is much simpler.

Given a matrix $A=\left(a_{ij}\right)\in {\mathbb{R}}^{n\times n}$, denote

$$\mathcal{N}\left(A\right):=\left\{i\in N:|a_{ii}|\le R_i\left(A\right)\right\},$$

$$\mathcal{J}\left(A\right):=\left\{i\in N:|a_{ii}|>R_i\left(A\right)\right\},$$

$$\mathcal{S}\left(A\right):=\bigcup _{i\in \mathcal{N}}{\gamma }_i\left(A\right),$$

where ${\gamma }_i\left(A\right)$ is defined as (3). If there is no confusion, $\mathcal{N}$, $\mathcal{J}$ and $\mathcal{S}$ stand for $\mathcal{N}\left(A\right)$, $\mathcal{J}\left(A\right)$ and $\mathcal{S}\left(A\right)$, respectively. Obviously, $\mathcal{S}\subseteq \mathcal{J}$. Let $\left|\mathcal{S}\right|$ denote the cardinality of $\mathcal{S}$.

Theorem 4.

If $A=\left(a_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is a DZT matrix, then the matrix $D=diag(d_1,\cdots ,d_n)$ with

$$\begin{array}{c}\hfill d_i=\left\{\begin{array}{c}1,i\in N\backslash \mathcal{S},\\ \frac{R_i\left(A\right)+\epsilon }{|a_{ii}|},i\in \mathcal{S},\end{array}\right.\end{array}$$

(12)

is a positive diagonal matrix such that $AD$ is an SDD matrix, where ε only needs to satisfy

$$\begin{array}{c}\hfill 0<\epsilon \le \underset{i\in \Gamma }{min}\underset{j\in {\gamma }_i\left(A\right)}{min}\frac{\left(\right|a_{ii}| -R_i^{N\backslash \left\{j\right\}}\left(A\right)\left)\right|a_{jj}| - |a_{ij}|R_j\left(A\right)}{|a_{ij}|}.\end{array}$$

(13)

Furthermore, A is an H-matrix.

Proof. 

It suffices to prove that $B:=AD=\left(b_{ij}\right)$ is an SDD matrix. Note that $0<d_i\le 1$ for any $i\in N$.

• For any $i\in N\backslash \mathcal{S}$, according to Definition 1, there exists some $j_0$ such that

$$\left(\right|a_{ii}| -R_i^{N\backslash \left\{j_0\right\}}\left(A\right)\left)\right|a_{j_0{j}_0}| - |a_{i{j}_0}|R_{j_0}\left(A\right)>0.$$

Since $\epsilon$ satisfies (13), we have

$$\left(\right|a_{ii}|-R_i^{N\backslash \left\{j_0\right\}}\left(A\right)\left)\right|a_{j_0{j}_0}| - |a_{i{j}_0}|(R_{j_0}\left(A\right)+\epsilon )>0.$$

Therefore, through calculation, we can obtain that

$$\begin{array}{cc}\hfill |b_{ii}| -R_i\left(B\right)& = | a_{ii}|-\sum _{j\in N\backslash \left\{i\right\}}\left|a_{ij}\right|d_j\hfill \\ \hfill & \ge |a_{ii}|-R_i^{N\backslash \left\{j_0\right\}}\left(A\right)-\left|a_{i{j}_0}\right|\frac{R_{j_0}\left(A\right)+\epsilon }{|a_{j_0{j}_0}|}\hfill \\ \hfill & >0.\hfill \end{array}$$

• For any $i\in \mathcal{S}$, we have

  $$\begin{array}{c}\hfill |b_{ii}| -R_i\left(B\right)= |a_{ii}|\times \frac{R_i\left(A\right)+\epsilon }{|a_{ii}|}-\sum _{j\in N\backslash \left\{i\right\}}|a_{ij}|d_j\ge R_i\left(A\right)+\epsilon -\sum _{j\in N\backslash \left\{i\right\}}\left|a_{ij}\right|=\epsilon >0.\end{array}$$

Hence, $B=AD$ is an SDD matrix, so A is an H-matrix. □

Based on the scaling matrix of the DZT matrix obtained by Theorem 4, we give a result about the Schur complement of the DZT matrix.

Theorem 5.

Suppose $A=\left(a_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is a DZT matrix and α is a nonempty proper subset of N. If α satisfies $\mathcal{S}\subseteq \alpha$, then $A/\alpha$ is an SDD matrix. Denote $A/\alpha =\left(a_{ts}^{\prime }\right)$ and ${\alpha }^c=\{j_1,j_2,\cdots ,j_l\}$, then for $t=1,\cdots ,l,$

$$\begin{array}{c}\hfill |a_{tt}|-R_t(A/\alpha )\ge |a_{j_t{j}_t}|-R_{j_t}^{{\alpha }^c}\left(A\right)+\sum _{h\in \alpha }\left|a_{j_{t}h}\right|\frac{R_h\left(A\right)}{|a_{hh}|},\end{array}$$

(14)

Furthermore,

$$\begin{array}{c}\hfill ∥{(A/\alpha )}^{-1}∥\le \underset{1\le t\le l}{max}\frac{1}{|a_{j_t{j}_t}|-R_{j_t}^{{\alpha }^c}\left(A\right)+{\displaystyle \sum _{h\in \alpha }}\left|a_{j_{t}h}\right|\frac{R_h\left(A\right)}{|a_{hh}|}}.\end{array}$$

(15)

Proof. 

For the DZT matrix A, we can construct its scaling matrix D according to Theorem 4, such that $C:=AD=\left(c_{ij}\right)$ is an SDD matrix. Observe that

$$\begin{array}{cc}\hfill C/\alpha =\left(AD\right)/\alpha & =\left(AD\right)\left({\alpha }^c\right)-\left(AD\right)({\alpha }^c,\alpha ){\left[\left(AD\right)\left(\alpha \right)\right]}^{-1}\left(AD\right)(\alpha ,{\alpha }^c)\hfill \\ \hfill & =A\left({\alpha }^c\right)D\left({\alpha }^c\right)-A({\alpha }^c,\alpha )D\left(\alpha \right){\left[A\left(\alpha \right)D\left(\alpha \right)\right]}^{-1}A(\alpha ,{\alpha }^c)D\left({\alpha }^c\right)\hfill \\ \hfill & =\{A\left({\alpha }^c\right)-A({\alpha }^c,\alpha ){\left[A\left(\alpha \right)\right]}^{-1}A(\alpha ,{\alpha }^c)\}D\left({\alpha }^c\right)\hfill \\ \hfill & =(A/\alpha )D\left({\alpha }^c\right).\hfill \end{array}$$

Since $\mathcal{S}\subseteq \alpha$, then $D\left({\alpha }^c\right)=I$. So, we obtain $C/\alpha =A/\alpha$. It is a well-established fact that the Schur complement of an SDD matrix is also an SDD matrix [22]. Hence, $A/\alpha$ is an SDD matrix. By Theorem 1 of [23], for $t=1,\cdots ,l$, we obtain

$$\begin{array}{cc}\hfill |a_{tt}|-R_t(A/\alpha )\ge & |a_{j_t{j}_t}|-R_{j_t}\left(A\right)+\sum _{h\in \alpha }\left|a_{j_{t}h}\right|\frac{|a_{hh}| -R_h\left(A\right)}{|a_{hh}|}\hfill \\ \hfill =& |a_{j_t{j}_t}|-R_{j_t}^{{\alpha }^c}\left(A\right)+\sum _{h\in \alpha }\left|a_{j_{t}h}\right|\frac{R_h\left(A\right)}{|a_{hh}|}.\hfill \end{array}$$

By the fact that $A/\alpha$ is an SDD matrix and (1), it follows that

$$\begin{array}{c}\hfill ∥{(A/\alpha )}^{-1}∥\le \underset{1\le t\le l}{max}\frac{1}{|a_{j_t{j}_t}| -R_{j_t}^{{\alpha }^c}\left(A\right)+{\displaystyle \sum _{h\in \alpha }}\left|a_{j_{t}h}\right|\frac{R_h\left(A\right)}{|a_{hh}|}}.\end{array}$$

□

Next, by utilizing the relation between the original matrix and the Schur complement and Theorem 5, we obtain a new upper bound for $∥A^{-1}∥$ as follows.

Theorem 6.

Let $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ be a DZT matrix with $\left|\mathcal{S}\right|\ge 2$. Then

$$\begin{array}{cc}\hfill {∥A^{-1}∥}_{\infty }\le & \underset{\mathcal{S}\subseteq \alpha \subseteq \mathcal{J}}{max}\left(1+\underset{j\in {\alpha }^c}{max}\sum _{i\in \alpha }\frac{|a_{ji}|(1+\varphi R_i^{\alpha }\left(A\right))}{|a_{ii}|}\right)·\left(1+\underset{i,j\in \alpha ,i\ne j}{max}\frac{|a_{jj}|R_i^{{\alpha }^c}\left(A\right)+R_i^{\alpha }\left(A\right)R_j^{{\alpha }^c}\left(A\right)}{|a_{ii}\left|\right|a_{jj}|-R_i^{\alpha }\left(A\right)R_j^{\alpha }\left(A\right)}\right)\hfill \\ & ·max\left\{\varphi ,\underset{j\in {\alpha }^c}{max}\frac{1}{|a_{jj}|-R_j^{{\alpha }^c}\left(A\right)+{\displaystyle \sum _{i\in \alpha }}\left|a_{ji}\right|\frac{R_i\left(A\right)}{|a_{ii}|}}\right\},\hfill \end{array}$$

(16)

where $\varphi =\underset{i,j\in \alpha ,i\ne j}{max}\frac{|a_{jj}|+R_i^{\alpha }\left(A\right)}{|a_{ii}\left|\right|a_{jj}|-R_i^{\alpha }\left(A\right)R_j^{\alpha }\left(A\right)}$.

Proof. 

If A is an SDD matrix, then $\mathcal{S}=\mathcal{J}=N$. This implies that $\alpha$ in (16) can only be set $\alpha =N$, and then ${\alpha }^c=\varnothing .$ In this case, (16) can be reduced to the bound (2). The conclusion is valid.

Next, we discuss the case when A is not an SDD matrix.

From (5), it follows that

$$\begin{array}{c}\hfill {∥A^{-1}∥}_{\infty }\le {∥L∥}_{\infty }{∥U∥}_{\infty }max\left\{{∥A{\left(\alpha \right)}^{-1}∥}_{\infty },{∥{(A/\alpha )}^{-1}∥}_{\infty }\right\},\end{array}$$

(17)

where

$${\parallel L\parallel }_{\infty }=1+{∥A\left({\alpha }^c,\alpha \right)A{\left(\alpha \right)}^{-1}∥}_{\infty },$$

$${\parallel U\parallel }_{\infty }=1+{∥A{\left(\alpha \right)}^{-1}A\left(\alpha ,{\alpha }^c\right)∥}_{\infty }.$$

Since A is a DZT matrix and not an SDD matrix, then $\mathcal{S}$ is a nonempty proper subset of N. Choose $\alpha$ to satisfy $\mathcal{S}\subseteq \alpha \subset J$, then $A\left(\alpha \right)$ is an SDD matrix. By Theorem 2,

$$\begin{array}{c}\hfill ∥A{\left(\alpha \right)}^{-1}∥\le \underset{i,j\in \alpha ,i\ne j}{max}\frac{|a_{jj}|+R_i^{\alpha }\left(A\right)}{|a_{ii}\left|\right|a_{jj}| -R_i^{\alpha }\left(A\right)R_j^{\alpha }\left(A\right)}:=\varphi \end{array}$$

(18)

follows in virtue of (1). By Theorem 5, we obtain that

$$\begin{array}{c}\hfill ∥{(A/\alpha )}^{-1}∥\le \underset{j\in {\alpha }^c}{max}\frac{1}{|a_{jj}| -R_j^{{\alpha }^c}\left(A\right)+{\displaystyle \sum _{i\in \alpha }}\left|a_{ji}\right|\frac{R_i\left(A\right)}{|a_{ii}|}}.\end{array}$$

(19)

By Lemma 2, we have

$$\begin{array}{c}\hfill {∥L∥}_{\infty }\le 1+\underset{j\in {\alpha }^c}{max}\sum _{i\in \alpha }\frac{|a_{ji}|(1+\varphi R_i^{\alpha }\left(A\right))}{|a_{ii}|},\end{array}$$

(20)

and

$$\begin{array}{c}\hfill {∥U∥}_{\infty }\le 1+\underset{i,j\in \alpha ,i\ne j}{max}\frac{|a_{jj}|R_i^{{\alpha }^c}\left(A\right)+R_i^{\alpha }\left(A\right)R_j^{{\alpha }^c}\left(A\right)}{|a_{ii}\left|\right|a_{jj}| -R_i^{\alpha }\left(A\right)R_j^{\alpha }\left(A\right)}.\end{array}$$

(21)

To sum up the above inequalities, the conclusion (16) follows. □

In practice, $\mathcal{J}$ is very easy to solve. In particular, by setting $\alpha =\mathcal{J}$ in Theorem 6, we obtain a result with greater applicability as follows.

Theorem 7.

Let $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ be a DZT matrix $\left|\mathcal{S}\right|\ge 2$. Then

$$\begin{array}{cc}\hfill {∥A^{-1}∥}_{\infty }\le & \left(1+\underset{j\in \mathcal{N}}{max}\sum _{i\in \mathcal{J}}\frac{|a_{ji}|(1+\varphi R_i^{\mathcal{J}}\left(A\right))}{|a_{ii}|}\right)·\left(1+\underset{i,j\in \mathcal{J},i\ne j}{max}\frac{|a_{jj}|R_i^{\mathcal{N}}\left(A\right)+R_i^{\mathcal{J}}\left(A\right)R_j^{\mathcal{N}}\left(A\right)}{|a_{ii}\left|\right|a_{jj}|-R_i^{\mathcal{J}}\left(A\right)R_j^{\mathcal{J}}\left(A\right)}\right)\hfill \\ & ·max\left\{\varphi ,\underset{j\in \mathcal{N}}{max}\frac{1}{|a_{jj}|-R_j^{\mathcal{N}}\left(A\right)+{\displaystyle \sum _{i\in \mathcal{J}}}\left|a_{ji}\right|\frac{R_i\left(A\right)}{|a_{ii}|}}\right\}:=\mathrm{\Lambda }\left(A\right),\hfill \end{array}$$

(22)

where $\varphi =\underset{i,j\in \mathcal{J},i\ne j}{max}\frac{|a_{jj}|+R_i^{\mathcal{J}}\left(A\right)}{|a_{ii}\left|\right|a_{jj}|-R_i^{\mathcal{J}}\left(A\right)R_j^{\mathcal{J}}\left(A\right)}$.

3. Numerical Examples

In this section, we will show the validity and superiority of Theorem 7 through some examples.

Example 1.

Consider the matrix from [10,21]:

$$A=\left(\begin{array}{cccc}36& -6& 2& 3\\ 3& 16& 9& -8\\ 9& -9& 19& 4\\ -1& 6& 2& 21\end{array}\right).$$

As shown in [10], by Theorem 3, it follows that $\parallel A^{-1}{\parallel }_{\infty }\le 2.4167$. Obviously, $\mathcal{J}=\{1,4\}$ and $\mathcal{S}=\{2,3\}$. If we apply Theorem 7, we obtain that

$$\parallel A^{-1}{\parallel }_{\infty }\le 0.7847.$$

Let us now consider an example of a complex matrix.

Example 2.

Consider the complex matrix:

$$A=\left(\begin{array}{cccccc}19+19i& i& 1+2i& 2i& 3& 1+2i\\ 2+i& 28+12i& 5& 3i& 0& -1+i\\ 1+3i& 2i+1& 19+17i& 3+i& 1+2i& 1+3i\\ -2i& 2+4i& 3i& -9+10i& 5+i& 1+i\\ 1& 2+i& 2i& 6+i& 8+11i& 3i\\ 3+i& 1+2i& 3i& 3+2i& 2+i& 10+8i\end{array}\right),$$

where i is the imaginary unit.

Through calculation, we obtain that ${\gamma }_1\left(A\right)=\{2,3,4,5,6\}$, ${\gamma }_2\left(A\right)=\{1,3,4,5,6\}$, ${\gamma }_3\left(A\right)=\{1,2,4,5,6\}$, ${\gamma }_4\left(A\right)=\left\{2\right\}$, ${\gamma }_5\left(A\right)=\{2,3\}$, ${\gamma }_6\left(A\right)=\left\{1\right\}$, $\mathcal{J}=\{1,2,3\}$ and $\mathcal{S}=\{4,5,6\}$. Thus, A is a DZT matrix. By applying Theorem 3, it follows that $\parallel A^{-1}{\parallel }_{\infty }\le 16.9163$. However, if we apply Theorem 7, we obtain

$$\parallel A^{-1}{\parallel }_{\infty }\le 0.9281.$$

In fact, $\parallel A^{-1}{\parallel }_{\infty }\le 0.0567.$ Therefore, Theorem 7 is more tighter than Theorem 3 in this example.

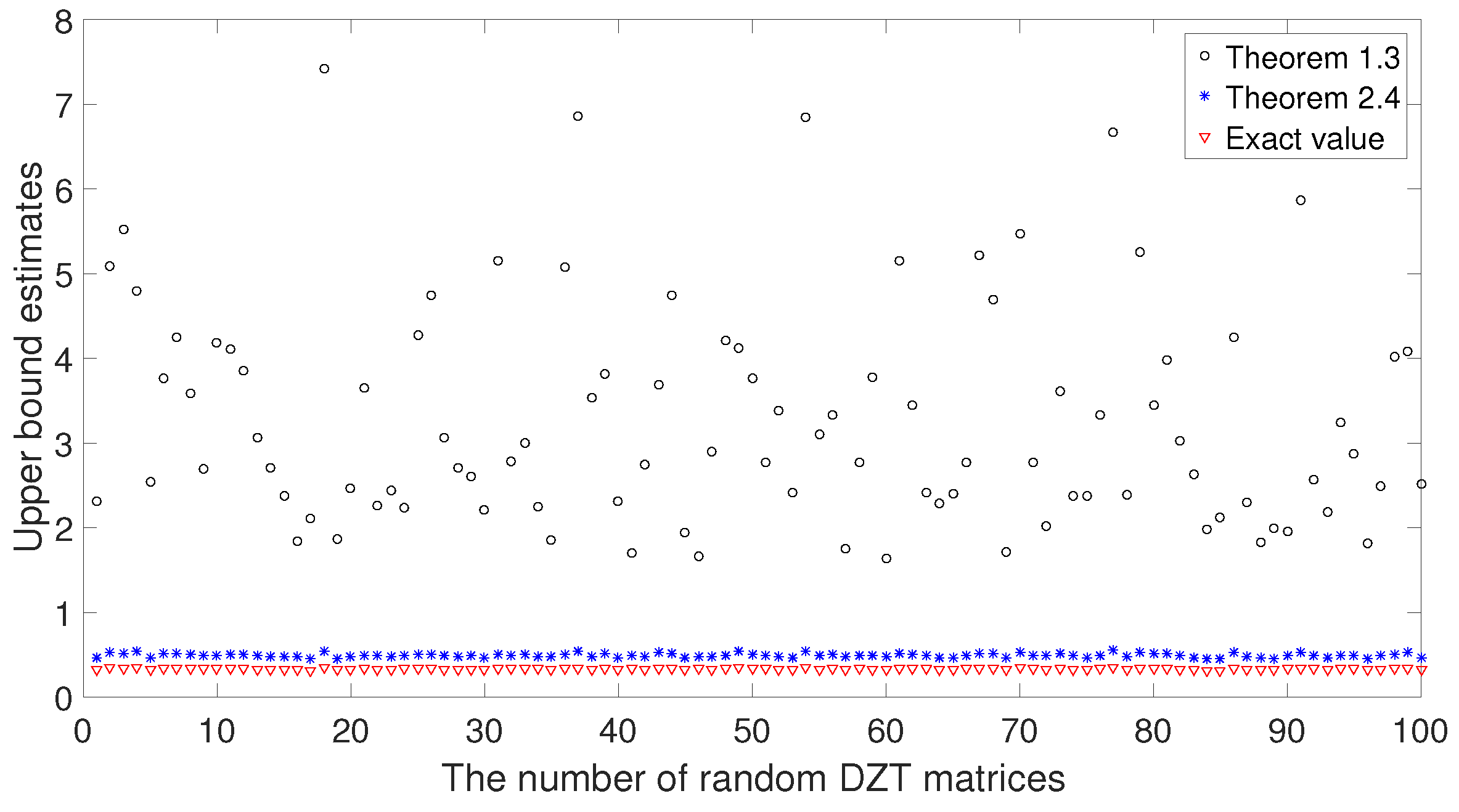
Example 3.

Consider the first 100 DZT matrices generated by the following form:

$$A^{\left(k\right)}=\left(\begin{array}{ccccc}31& -4& 1& -2& -2x_1\\ -3& 36& -1& 3x_2& 2\\ -1& -x_3& -26& 2& 1\\ -2-x_4& 1& -2& 7& 3\\ -2& 1+x_5& 2& -4& -9\end{array}\right),k=1,\cdots ,100,$$

where $x_i(i=1,\cdots ,5,)$ independently obeys a uniform distribution from 0 to 1. We then compare the infinite norm bound between Theorems 3 and 7.

As shown in Figure 1, the infinite norm bound in Theorem 7 is better than that in Theorem 3.

Figure 1. Upper bounds for ${\parallel \left[A^{\left(k\right)}\right]}^{-1}{\parallel }_{\infty }$ of the first 100 DZT matrices generated randomly.

To assess the stability of the upper bounds as the matrix dimension increases, we test the following example.

Example 4.

Consider the following family of matrices of increasing order: $A_n,n=6,7,\cdots ,100,$ where

$$A_n=\left(\begin{array}{ccccccc}n-1.5-0.01x_1& 1& 1& 1& 1& 1& 1\\ 1& n-1.5-0.01x_2& 1& 1& 1& 1& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ 1& 1& 1& n-1.5-0.01x_{\left[\frac{n}{2}\right]}& 1& 1& 1\\ 1& 1& 1& 1& 2n+\frac{n}{4}{x}_{\left[\frac{n}{2}\right]+1}& 1& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& 1& 1& 1& 1& 1& 2n+\frac{n}{4}{x}_n\end{array}\right),$$

$\left[\frac{n}{2}\right]$ is the largest integer not exceeding $\frac{n}{2}$, and all $x_i$ independently obey a uniform distribution from 0 to 1.

As shown in Figure 2, as n increases, the upper bound given by Theorem 3 tends to increase, while the bound given by Theorem 7 decreases and approaches the exact value. The effectiveness and superiority of Theorem 7 are illustrated.

Figure 2. Upper bounds of $\parallel {A_n}^{-1}{\parallel }_{\infty }$ as matrix order n increases.

4. Applications to the Smallest Singular Value for DZT Matrix

The infinite norm bound of the inverse matrix can be used to bound the smallest singular value. The singular values of A are denoted by

$${\sigma }_1\left(A\right)\ge {\sigma }_2\left(A\right)\ge \cdots \ge {\sigma }_n\left(A\right).$$

The smallest singular value represents important properties of matrices. For a square matrix, A indicates its nonsingularity and distance from singular matrices. Additionally, ${\sigma }_n\left(A\right)$ is a key component in the spectral condition number ${\sigma }_1\left(A\right)/{\sigma }_n\left(A\right)$, which is crucial in assessing numerical calculations involving A. Thus, estimating the smallest singular value is meaningful.

Varah [14] presented the following lower bound for ${\sigma }_n\left(A\right)$ with an SDD matrix A.

Theorem 8.

If $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ and its transpose $A^T$ are both SDD matrices, then

$$\begin{array}{c}\hfill {\sigma }_n\left(A\right)\ge \sqrt{\underset{i\in N}{min}\left\{|a_{ii}|-R_i\left(A\right)\right\}·\underset{i\in N}{min}\left\{|a_{ii}|-R_i\left(A^T\right)\right\}}.\end{array}$$

(23)

In addition, many researchers obtained other results for the smallest singular value; see [11,13,24] and references therein. Based on Theorem 7, a new lower bound for ${\sigma }_n\left(A\right)$ is obtained.

Theorem 9.

If $A=\left(a_{ij}\right)\in {\mathbb{C}}^{n\times n}$ and its transpose $A^T$ are both DZT matrices, then

$$\begin{array}{c}\hfill {\sigma }_n\left(A\right)\ge \sqrt{\frac{1}{\mathrm{\Lambda }\left(A^T\right)·\mathrm{\Lambda }\left(A\right)}},\end{array}$$

(24)

where $\mathrm{\Lambda }\left(A\right)$ is defined as in Theorem 7.

Proof. 

Since $A^T$ is a DZT matrix, it follows from Theorem 7 that

$$\begin{array}{c}\hfill \parallel A^{-1}{\parallel }_1= \parallel {\left(A^{-1}\right)}^T{\parallel }_{\infty }={\parallel {\left(A^T\right)}^{-1}\parallel }_{\infty }\le \mathrm{\Lambda }\left(A^T\right).\end{array}$$

By the following noted inequality [24]:

$$\begin{array}{c}\hfill \parallel A^{-1}{\parallel }_2^2 \le \parallel A^{-1}{\parallel }_1{\parallel A^{-1}\parallel }_{\infty },\end{array}$$

we have

$$\begin{array}{c}\hfill \parallel A^{-1}{\parallel }_2^2 \le \mathrm{\Lambda }\left(A^T\right)·\mathrm{\Lambda }\left(A\right),\end{array}$$

which implies that

$$\begin{array}{c}\hfill \parallel A^{-1}{\parallel }_2^{-1}\ge \sqrt{\frac{1}{\mathrm{\Lambda }\left(A^T\right)·\mathrm{\Lambda }\left(A\right)}}.\end{array}$$

From $\parallel A^{-1}{\parallel }_2^{-1}={\sigma }_n\left(A\right)$, the conclusion follows. □

5. Discussion

The primary objective of this study is to obtain a tighter upper bound on the infinity norm of the inverse of DZT matrices. The numerical results are consistent with the expected results. The upper bound is obtained using a method based on Schur’s complement. In this process, we obtain a construction method for the positive diagonal matrix of a DZT matrix after right-multiplying by a positive diagonal matrix to become a strictly diagonal dominant matrix. This is rare and makes up for the shortcomings of existing research on DZT matrices. Furthermore, we provide a sufficient condition that the Schur complement of a DZT matrix is an SDD matrix (see Theorem 5), which includes the condition of Theorem 3.4 in Reference [1]. Therefore, Theorem 5 can be regarded as an improvement of Theorem 3.4 in Reference [25] to some extent. Although Reference [1] discusses that DZT matrices are subclasses of a certain class of H-matrices under two conditions, it is not perfect. The conclusions of this paper are expected to provide reference for further improving the closure of the Schur complement of DZT matrices. In fact, exploring the upper bound of the infinity norm of the inverse matrix not only helps to estimate the lower bound of the minimum singular value but also can be applied to linear complementarity problems and the pseudospectra localization of eigenvalues, which can be found in References [10,26,27] and their corresponding references. This is also one of our future research works.

6. Conclusions

In this paper, we present a method for constructing scaling matrices of DZT matrices. Based on the structure of the scaling matrices, we explore a sufficient condition for the Schur complements of specific subsets to be strictly diagonally dominant matrices and obtain the corresponding diagonal dominant degrees. We then use a method based on Schur complements to explore a new upper bound for the infinity norm of the inverse of DZT matrices. Numerical experiments with randomly generated matrices show that the new upper bound proposed in this paper is superior to existing results. In addition, we provide a lower bound for the smallest singular value based on the new upper bound.