Latin Matchings and Ordered Designs OD(n−1, n, 2n−1) ^†

Abstract

This paper revisits a combinatorial structure called the large set of ordered design ($LOD$). Among others, we introduce a novel structure called Latin matching and prove that a Latin matching of order n leads to an $LOD(n-1, n, 2n-1)$; thus, we obtain constructions for $LOD(1, 2, 3)$, $LOD(2, 3, 5)$, and $LOD(4, 5, 9)$. Moreover, we show that constructing a Latin matching of order n is at least as hard as constructing a Steiner system $S(n-2, n-1, 2n-2)$; therefore, the order of a Latin matching must be prime. We also show some applications in multiagent systems.

1. Introduction

Combinatorial designs have found applications in various fields, including experiment design, cryptography, and computer science. Some examples include the random pattern testing of VLSI chips, authentication code design, and the derandomization of algorithms [1,2,3]. Motivated by these applications, the theory of combinatorial designs has drawn much attention and has been rapidly developing for many years [4,5,6]. On the other hand, the study of combinatorial designs promotes the study of geometry, group theory, coding theory, and other related fields of mathematics. In this paper, we revisit a combinatorial structure called ordered design, and we provide new such designs and their new applications.

An ordered design with parameters $t, n, v$, written as $OD(t, n, v)$, is an $n\times \left(\genfrac{}{}{0pt}{}{v}{t}\right)t!$ array with v entries, such that each column has n distinct entries, and any t rows contain each column tuple of t distinct entries exactly once [7,8,9]. A large set of ordered design $OD(t, n, v)$, written as $LOD(t, n, v)$, is a collection of $OD(t, n, v)$, such that any n-permutation of $\left[v\right]$ appears in exactly one OD (as one of its column) [7,10]. Throughout, $\left[v\right]=\{1, \dots , v\}$.

This paper mainly focuses on $OD(t, n, v)$ and $LOD(t, n, v)$ where $t=n-1$, and we abbreviate $OD(n-1, n, v)$ and $LOD(n-1, n, v)$ as $OD(n, v)$ and $LOD(n, v)$, respectively.

Example 1. 

An $OD(3, 5)$ is as follows.

1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5

2 3 4 5 1 3 4 5 1 2 4 5 1 2 3 5 1 2 3 4

3 5 2 4 4 1 5 3 5 4 1 2 3 5 2 1 2 1 4 3

The main agenda of this paper is investigating the existence of $OD(n, 2n-1)$. Teirlinck [10] proved the existence of $LOD(n-1, 2n-2)$ and hence $OD(n-1, 2n-2)$ for prime n (see Section 3 for an introduction). However, the existence of $OD(n-1, 2n-2)$ is necessary but insufficient for the existence of $OD(n, 2n-1)$ (Lemma 1).

A closely related problem is the existence of perpendicular array $PA(n, 2n-1)$ (see a definition in Section 2), which was settled affirmatively as early as the 1990s [7]. Recently, Jin [11] reported two explicit constructions of $PA(n, 2n-1)$ by utilizing the well-known lexicographic matching and modular matching between $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$ and $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n}\right)$, i.e., the set of $(n-1)$-element subsets of $[2n-1]$ and the set of n-element subsets of $[2n-1]$.

The main contribution of this paper is as follows. First, we introduce a novel and interesting notion called Latin matching. The Latin matching of order n is a perfect matching between $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$ and $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n}\right)$ with several remarkable properties; see its definition in Section 2. We construct Latin matchings of orders $2, 3, 5$. Case $n=5$ is the most nontrivial for which we apply the Hamming code $\mathsf{Hamming}(8, 4, 4)$ or, equivalently, the Steiner system $S(3, 4, 8)$. We then show that a Latin matching of order n leads to an $LOD(n, 2n-1)$; thus, we obtain $LOD(2, 3), LOD(3, 5), LOD(5, 9)$. In particular, $LOD(5, 9)$ has not been reported in literature. In addition, we show that constructing a Latin matching of order n is at least as hard as constructing a Steiner system $S(n-2, n-1, 2n-2)$ (a notoriously difficult problem); as one corollary, the order of a Latin matching must be prime.

A byproduct of our work is a set of 4 mutually orthogonal Latin squares (MOLS) of order 5 (built from our $LOD(3, 5)$). The existence of 4 MOLS of order 5 is known [8](p. 163), but our construction might be simpler (Remark 5). Another byproduct is an $LO{D}_6(3, 9, 9)$ (built from our $LOD(5, 9)$; see Section 7.2). An $O{D}_{\lambda }(t, n, v)$ is an $n\times (\lambda \left(\genfrac{}{}{0pt}{}{v}{t}\right)t!)$ array with v entries such each column has n distinct entries and any t rows contain each column tuple of t distinct entries exactly $\lambda$ times [7,8]. An $LO{D}_{\lambda }(t, n, v)$, is a collection of $O{D}_{\lambda }(t, n, v)$, such that any n-permutation of $\left[v\right]$ appears in exactly one OD (as one of its column) [7,10].

Applications of Latin matchings and related designs in multiagent systems (e.g., hat guessing games, scheduling tournaments, secret sharing schemes) are discussed in Section 7.

The Latin matching of order 5 is highly symmetric (e.g., cyclic and flipping-invariant; see Figure 1) and deserves more attention in the filed of combinatorial design in the future.

2. Preliminaries

Let $G(n, v)$ be the graph whose vertices are the n-permutations of $\left[v\right]$, and two vertices are connected if their Hamming distance is 1. The Hamming distance of $(a_1, \dots , a_n)$ and $(b_1, \dots , b_n)$ is the number of i, such that $a_i\ne b_i$.

We assume that the reader is familiar with the maximal independent (vertex) set (MIS). $\alpha \left(G\right)$ denotes the size of MIS of G. The following propositions are trivial (proof omitted).

Proposition 1. 

The columns of an $OD(n, v)$ constitute an independent set of $G(n, v)$.

Proposition 2. 

$\alpha \left(G(n, v)\right)\le \left(\genfrac{}{}{0pt}{}{v}{t}\right)t!$.

Proposition 3. 

$\alpha \left(G(n, v)\right)=\left(\genfrac{}{}{0pt}{}{v}{t}\right)t!$ if and only if there exists an $OD(n, v)$. If the equality holds, an MIS of $G(n, v)$ corresponds to an $OD(n, v)$.

As $G(n, v)$ has $\left(\genfrac{}{}{0pt}{}{v}{n}\right)n!=\left(\genfrac{}{}{0pt}{}{v}{t}\right)t!(v-n+1)$ vertices, an $LOD(n, v)$ is a collection of $v-n+1$ disjoint $OD(n, v)$ where two $OD(n, v)$ are disjoint if they do not share a common column.

Proposition 4. 

An $LOD(n, v)$ is a vertex coloring of $G(n, v)$ using $v-n+1$ colors.

We now introduce a notion called Latin function that interprets OD from another angle. A Latin function (LF) with parameters $n, v$, written as $LF(n, v)$, maps each $(n-1)$-permutation $(a_1, \dots , a_{n-1})$ of $\left[v\right]$ to a number $f(a_1, \dots , a_{n-1})\in \left[v\right]\backslash \{a_1, \dots , a_{n-1}\}$, admitting the following property: If two $(n-1)$-permutations have Hamming distance 1, their images under f are distinct. This property is referred to as the Latin property.

Clearly, an $OD(n, v)$ is equivalent to an $LF(n, v)$; given an $OD(n, v)$ A, we can choose any row of A to be the output and the remaining $n-1$ rows as the input, and define a Latin function $LF(n, v)$; given a $LF(n, v)$ f, we can reversely obtain an $OD(n, v)$.

A symmetric Latin function (SLF) with parameters $n, v$, written as $SLF(n, v)$, refers to an $LF(n, v)$ admitting the following symmetric property: if $(a_1, \dots , a_{n-1})$ is a permutation of $(b_1, \dots , b_{n-1})$, then $f(a_1, \dots , a_{n-1})=f(b_1, \dots , b_{n-1})$.

A Latin matching (LM) with parameters $n, v$, written as $LM(n, v)$, refers to an $SLF(n, v)$ admitting the following injective property: if $\{a_1, \dots , a_{n-1}\}\ne \{b_1, \dots , b_{n-1}\}$, it holds that $\{a_1, \dots , a_{n-1}, f(a_1, \dots , a_{n-1})\}\ne \{b_1, \dots , b_{n-1}, f(b_1, \dots , b_{n-1})\}$. In particular, for $v=2n-1$, the Latin matching $LM(n, v)=LM(n, 2n-1)$ is called a Latin matching of order n. Due to the injective property, $F:\{a_1, \dots , a_{n-1}\}\to \{a_1, \dots , a_{n-1}, f(a_1, \dots , a_{n-1})\}$ is a perfect matching from $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$ to $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n}\right)$. This suggests the name “Latin matching”.

For $1\le t<n<v$, a perpendicular array with parameters $\lambda ;t, n, v$, denoted by $P{A}_{\lambda }(t, n, v)$ or $PA(t, n, v)$ when $\lambda =1$, is an n by $\lambda \left(\genfrac{}{}{0pt}{}{v}{t}\right)$ matrix over $\left[v\right]$ such that: (I) all entries in any specific column are distinct, and (II) each set of t rows contain each t-element subset of $\left[v\right]$ as a column exactly $\lambda$ times [7,8]. A large set of perpendicular array $P{A}_{\lambda }(t, n, v)$, written as $LP{A}_{\lambda }(t, n, v)$ or $LPA(t, n, v)$ when $\lambda =1$, is a collection of $P{A}_{\lambda }(t, n, v)$ such that any n-permutation of $\left[v\right]$ appears in exactly one PA (as one of its column) [7].

Lemma 1. 

An $OD(t, n, v)$ implies an $OD(t-1, n-1, v-1)$.

Proof. 

Select those columns in which the last row is v, and delete the last row.    □

3. Related Work

Some important known results about ODs are summarized in the following.

• Teirlinck,1988 [10] If $v=p_1^{{\alpha }_l}\dots {p_s}^{{\alpha }_s}$, where, $p_1, \dots , p_s$ are distinct primes, satisfying ${\alpha }_i(p_i-1)>t$ for all i, there is an $LOD(t, t+1, t+v)$. As a corollary, there are infinitely many $LOD(n, v)$ for all n, and there is an $LOD(n-1, 2n-2)$ for all prime n.
• Teirlinck and Lindner, 1988 [12] For $v\ge 3, v\notin \{6, 14, 62\}$, there is an $LOD(2, 3, v)$. There is an $OD(2, 3, 6)$, but no $LOD(2, 3, 6)$ exists (this is the 36-generals problem).
• Teirlinck, 1990 [13] For odd $v\ge 4, v\ne 7$, there is an $OD(3, 4, v)$.
• Teirlinck, 1992 [7] (this is a survey)

  (a)

  There is no $OD(3, 4, 7)$ (page 569). We verified this result.

  (b)

  An $OD(2, n, n)$ exists if and only if an affine plane of order n exists (page 575).

  (c)

  An $LOD(t, n, v)$ implies an $LOD(t-1, n-1, v-1)$ (page 570).

  (d)

  An $O{D}_{\lambda }(t, v, v)$ implies an $LO{D}_{\lambda }(t, v, v)$ (page 571).

  (e)

  An $LOD(2, n, q)$ exists for every prime power $q\ge n$; an $LOD(3, n, q+1)$ exists for every prime power $q\ge n-1$; an $LOD(4, n, 11)$ exists for $4\le n\le 11$; and an $LOD(5, n, 12)$ exists for $5\le n\le 12$ (page 578).

• Ray-Chaudhuri and Zhu, 1997 [14] If an $LO{D}_{\lambda }(t, t+1, v)$ and an $LO{D}_{{\lambda }^{\prime }}(t, t+1, v^{\prime })$ exists, such that $(v-t)/\lambda =(v^{\prime }-t)/{\lambda }^{\prime }$, then an $LO{D}_{\lambda +{\lambda }^{\prime }}(t, t+1, v+v^{\prime }-t)$ exists. In particular, if an $LO{D}_{\lambda }(t, t+1, t+v)$ exists, then an $LO{D}_{s\lambda }(t, t+1, t+sv)$ exists for all positive s. Moreover, for any $n, v$, there is an $LO{D}_{\lambda }(n, v)$ for some finite $\lambda$.

Ordered design (OD) is closely related to the perpendicular array (PA) and orthogonal array (OA). In fact, in the seminal work of Rao [9], OD and PA are called OA Types I and II, respectively. Moreover, it is a trivial fact that every OD is a PA. OA has been studied even more extensively than OD and PA; the definition and an exposition of this structure can be found in [4]. Many connections between OA and OD are shown in [7,9,14]. Some important known results about PA, especially $PA(t, t+1, v)$, are introduced in the following. Among others, there exist $P{A}_3(3, 9, 9)$ [15], and $PA(3, 5, 5)$, $PA(3, 8, 8)$, $PA(3, 32, 32)$, $P{A}_2(4, 5, 5)$, $P{A}_4(4, 9, 9)$, $P{A}_2(4, 5, 11)$ [16]. The authors in Ref. [17] showed that, for an even v, there exists a $PA(3, 4, v)$ if and only if $v\ne 0(mod6)$. Moreover, there exist $PA(3, 4, v)$ for $v\in \{5, 7, 11, 13, 17, 23, 25, 29, 49, 53, 65, 85, 89, 97\}$, and there is a $P{A}_3(3, 4, v)$ if and only if $v\ge 4$. In Ref. [11], the authors showed two explicit constructions of $PA(t, t+1, 2t+1)$. The survey in [7] showed that a $P{A}_{\lambda }(t, k, k)$ implies an $LP{A}_{\lambda }(t, k, k)$ (page 571), and there exist (1) $LPA(3, k, 8)$ for $3\le k\le 8$; $LPA(5, k, 8)$ for $5\le k\le 8$; (2) $LPA(3, k, 32)$ for $3\le k\le 32$; $LPA(29, k, 32)$ for $29\le k\le 32$; and (3) $LPA(t, t+1, t+(t+1)/d)$ for all d dividing $t+1$.

Another combinatorial design closely related to OD/LOD is the Steiner system (SS). A Steiner system (SS) with parameters $t, n, v$, written as $S(t, n, v)$, is a v-element set S together with a set of n-element subsets of S, called blocks, with the property that each t-element subset of S is contained in exactly one block [5,8,18]. Many connections between OD/LOD and SS are shown in [7]; indeed, an OD is called an ordered Steiner system by Teirlinck [10]. Important existing results of SS are introduced in Section 6. Here, we mention an astonishing result on this topic: Keevash [6] showed that, for a fixed $t, n$, there exist $S(t, n, v)$ for a large enough v satisfying certain necessary conditions.

4. Major Findings

This section presents two major findings of this paper. First, there exist Latin matchings of order 2, 3,5. Second, an $LOD(n, 2n-1)$ can be constructed from an $LM(n, 2n-1)$.

We first show how to construct $LM(5, 9)$ from $\mathsf{Hamming}(8, 4, 4)$.

A Latin function f is cyclic if

$$f\left(\{i_1+1, \dots , i_{n-1}+1\}\right)\equiv f\left(\{i_1, \dots , i_{n-1}\}\right)+1,$$

(1)

where the numbers are taken modulo by $(2n-1)$.

We constructed an $LM(5, 9)$ f that was cyclic. Since cyclic, the function can be indicated by $\left(\genfrac{}{}{0pt}{}{9}{4}\right)/9=14$ values. We used 14 pictures to illustrate these values, as shown in Figure 1. Each picture contains 9 small circles labelled with 1 to 9 lying in clockwise order, four of which are solid (black) and four of which are hollow (white) except for the ninth small circle, which is special. If the four solid circles are labeled by $i_1, i_2, i_3, i_4$, this picture indicates that $f\left(\{i_1, i_2, i_3, i_4\}\right)=9$. For example, the first picture indicates that $f\left(\right\{3, 4, 5, 6\left\}\right)=9$.

Each picture can be represented by a binary word $a_1{a}_2\dots a_8$ (e.g., 00111100 and 01011010 for the first two pictures) – if $a_i=1$, the small circle labelled as i is solid; otherwise, it is hollow. The key part of this construction lies in selecting these binary words. We use the 14 codewords of $\mathsf{Hamming}(8, 4, 4)$ defined in the following equation that are not all zeros and not all ones.

$$\left\{\begin{array}{ccccccc}\hfill a_5& =\hfill & \hfill a_1\oplus a_2\oplus a_3, & \hfill & \hfill a_6& =\hfill & \hfill a_1\oplus a_2\oplus a_4, \\ \hfill a_7& =\hfill & \hfill a_1\oplus a_3\oplus a_4, & \hfill & \hfill a_8& =\hfill & \hfill a_2\oplus a_3\oplus a_4.\end{array}\right.$$

(2)

Proposition 5. 

For each 4-permutation $(a_1, \dots , a_4)$ of $\left[9\right]=\{1, \dots , 9\}$, the value of $f(a_1, \dots , a_4)$ is well-defined by the above figure and belongs to $\left[9\right]\backslash \{a_1, \dots , a_4\}$.

Proof. 

For each 4-element subset $\{i_1, i_2, i_3, i_4\}\in \left(\genfrac{}{}{0pt}{}{\left[9\right]}{4}\right)$, we prove that $f\left(\{i_1, i_2, i_3, i_4\}\right)$ is indicated by one of the above pictures. These 4-element subsets can be partitioned into $\left(\genfrac{}{}{0pt}{}{9}{4}\right)/9=14$ groups. Those subsets that are equivalent under cyclic rotation are in the same group (so, a group is $\{i_1+j, i_2+j, i_3+j, i_4+j\}\mid 1\le j\le 9$).

On the other hand, the positions of the solid circles among the 14 pictures are distinct under cyclic-rotating; see Figure 1. So, each group is taken care by exactly one picture.    □

Lemma 2. 

Function f defined above is indeed an $LM(5, 9)$.

Proof. 

A well-known property of $\mathsf{Hamming}(8, 4, 4)$ is that the Hamming distance between the codewords is at least 4. This property is useful in proving the Latin property of f:

Suppose to the opposite that f is not Latin. There should be two 4-element subsets $A, B$ of $\left[9\right]$ with exactly three common elements such that they are both mapped to 9 under f. If we translate A and B into w length 8 binary codes a and b, we know that $\mathsf{d}(a, b)\ge 4$ according to the well-known property of $\mathsf{Hamming}(8, 4, 4)$ mentioned above, where $\mathsf{d}(a, b)$ denotes the Hamming distance between a and b. On the other hand, $\mathsf{d}(a, b)=2$ since sets $A, B$ are of size 4 and they share exactly three common elements, which is contradictory.

The symmetric property is naturally admitted by f according to the construction of f. The positions of four hollow circles in the 14 pictures are distinct under cyclic rotation (see Figure 1), which implies the injective property of f. Altogether, f is a Latin matching.    □

Remark 1. 

The Hamming code given by (2) is not the original Hamming code – the 8 bits are rearranged here, and it admits a symmetric property that is not admitted by the original one:

if$a_1\dots a_8$is a codeword, its reverse$a_8\dots a_1$is also a codeword.

We do not know whether this variant of Hamming code has been found in literature.

Remark 2. 

In addition to the Latin, symmetric, injective, and cyclic properties, the following properties of f are also noteworthy. Recall bijection $F:\{a_1, \dots , a_4\}\to \{a_1, \dots , a_4, f(a_1, \dots , a_4)\}$ from $\left(\genfrac{}{}{0pt}{}{\left[9\right]}{4}\right)$ to $\left(\genfrac{}{}{0pt}{}{\left[9\right]}{5}\right)$. Suppose F maps A to B. We claim that

(1) F maps $\left[9\right]/B$ to $\left[9\right]/A$, and

(2) F maps $\{9-a\mid a\in A\}$ to $\{9-b\mid b\in B\}$.

The first claim follows from the (trivial) fact that

if $a_1\dots a_8$ is a codeword, its flip $\overline{a_1}\dots \overline{a_8}$ is also a codeword,

where $\overline{x}=1-x$. The second claim follows from the reverse property in Remark 1.

The Hamming code $\mathsf{Hamming}(8, 4, 4)$ is equivalent to the Steiner system $S(3, 4, 8)$. For constructing Latin matchings of higher orders, it is actually more appropriate to use Steiner systems than Hamming codes. We show the reasons in Section 6.

Two more constructions of $LM(5, 9)$. The $LM(5, 9)$ shown in Figure 1 is not the unique $LM(5, 9)$. Two other cyclic Latin matchings of order 5 are drawn in Figure 2, which are found by using computer programs. These two matchings can also be constructed from codewords of different $\mathsf{Hamming}(8, 4, 4)$s.

Constructions of an $LM(2, 3)$ and an $LM(3, 5)$.

An $LM(2, 3)$f is easy to find. For example,

$$f\left(\right\{1\left\}\right)=2, f\left(\right\{2\left\}\right)=3, f\left(\right\{3\left\}\right)=1.$$

(3)

This LM is also cyclic.

Next, we give a cyclic $LM(3, 5)$. We use two binary codes of length 4 in this case, one is 0110 and the other is 1001, which means that $f\left(\right\{2, 3\left\}\right)=5$ and $f\left(\right\{1, 4\left\}\right)=5$. We leave it as an easy exercise for the reader to verify that f is indeed an $LM(3, 5)$.

As a summary of this subsection, we showed that

Theorem 1. 

There exist (cyclic) Latin matchings of orders $2, 3, 5$.

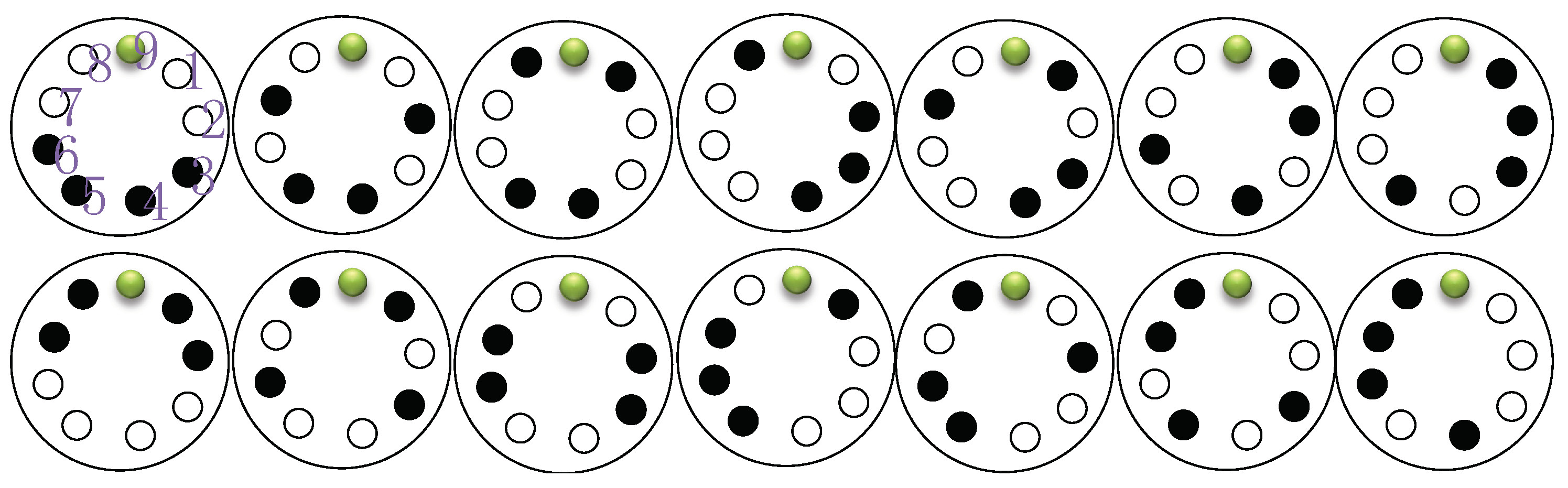
4.1. Construction of LOD from LM

Lemma 3. 

A Latin matching of order n implies an $LOD(n, 2n-1)$.

Proof. 

Let f be a Latin matching of order n (i.e., f is a $LM(n, 2n-1)$). Define

$$\begin{array}{c}{I}_1=\left\{(f\left(\{i_1, \dots , i_{n-1}\}\right), i_1, i_2, \dots , i_{n-1})\mid \{i_1, \dots , i_{n-1}\}\in \left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)\right\}, \\ I_2=\left\{(i_1, f\left(\{i_1, \dots , i_{n-1}\}\right), i_2, \dots , i_{n-1})\mid \{i_1, \dots , i_{n-1}\}\in \left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)\right\}, \\ \dots \\ I_n=\left\{(i_1, i_2, \dots , i_{n-1}, f\left(\{i_1, \dots , i_{n-1}\}\right))\mid \{i_1, \dots , i_{n-1}\}\in \left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)\right\}.\end{array}$$

(4)

$I_j$ contains a set of vertices of $G(n, 2n-1)$. The following facts imply an n-coloring of $G(n, 2n-1)$, which further implies an $LOD(n, 2n-1)$ by Proposition 4.

• $I_1, \dots , I_n$ are independent sets of $G(n, 2n-1)$.
• $I_1, \dots , I_n$ are disjoint and they contain all the vertices of $G(n, 2n-1)$.

We prove the two facts in the following.

Fact 1 follows immediately from the Latin property of f.

To prove Fact 2, we only need to prove the disjointness part. If $I_1, \dots , I_n$ are disjoint, we can compute that $I_1\cup \dots \cup I_n$ has the same amount of vertices as $G(n, 2n-1)$.

Now, suppose that $I_j$ and $I_k$ share a vertex $(u_1, \dots , u_n)$.

Denote $J=\{u_1, \dots , u_n\}\backslash u_j$ and $K=\{u_1, \dots , u_n\}\backslash u_k$. Clearly, $J\ne K$.

As $(u_1, \dots , u_n)\in I_j$, we know $u_j=f\left(J\right)$. As $(u_1, \dots , u_n)\in I_k$, we know $u_k=f\left(K\right)$.

Recall the matching $F:\{a_1, \dots , a_{n-1}\}\to \{a_1, \dots , a_{n-1}, f(a_1, \dots , a_{n-1})\}$ in the definition of LM. We see $F\left(J\right)=J\cup f\left(J\right)=J\cup u_j=\{u_1, \dots , u_n\}=K\cup u_k=K\cup f\left(K\right)=F\left(K\right)$. Therefore, F is not a perfect matching; the injective property is violated, which is contradictory.    □

The coloring of $G(n, v)$ in the above proof can be summarized as follows. For any vertex $(u_1, \dots , u_n)$ of $G(n, 2n-1)$ (according to the bijective property), there must be a unique $i\in \left[n\right]$, such that $F(\{u_1, \dots , u_n\}\backslash u_i)=\{u_1, \dots , u_n\}$, and we color the vertex by i.

Corollary 1. 

There exist $LOD(2, 3), LOD(3, 5), LOD(5, 9)$.

Remark 3. 

The approach for constructing LODs from LMs only works for the case $v=2n-1$. When $v\ge 2n$, an $LM(n, v)$ does not imply an $LOD(n, v)$. When $v\le 2n-2$, there is actually no $LM(n, v)$. (As $\left(\genfrac{}{}{0pt}{}{v}{n-1}\right)>\left(\genfrac{}{}{0pt}{}{v}{n}\right)$, no SLF can satisfy the injective property.)

Remark 4. 

Graph $G(n, 2n-1)$ can be reformulated as an incomplete n-dimensional hypercube, and coloring this graph by n colors is a variant of a high-dimensional Latin square problem [1,19].

We build the incomplete hypercube as follows. Initially, this hypercube has side length $2n-1$ and consists of ${(2n-1)}^n$ unit cells, each of which is denoted by a coordinate $(a_1, \dots , a_n)$ where $a_1, \dots , a_n\in [2n-1]$. Then, we remove cells for which $a_1, \dots , a_n$ are not distinct. Clearly, the vertices of $G(n, v)$ correspond to the remaining cells, and two vertices are connected if their corresponding cells are in the same orthogonal line (lines that are parallel to one of the n axes).

Finding an n-coloring of $G(n, v)$ is equivalent to coloring the cells of the incomplete hypercube such that the colors of cells in any orthogonal line are a permutation of all n colors.

Unlike the complete hypercube case, the above incomplete case does not always has a solution.

5. An Orthogonal Property of the $\mathit{OD}(\mathit{n}, \mathbf{2}\mathit{n}-\mathbf{1})$’s Obtained from $\mathit{LM}(\mathit{n}, \mathbf{2}\mathit{n}-\mathbf{1})$

Recall $I_1, \dots , I_n$ in the proof of Lemma 3, which are independent sets of $G(n, 2n-1)$. We saw that $I_1, \dots , I_n$ constitute an $LOD(n, 2n-1)$. So, each $I_j(1\le j\le n)$ gives an $OD(n, 2n-1)$, denoted by $A_j$ (each element in $I_j$ serves as a column of $A_j$). We state that

Theorem 2. 

n ODs $A_1, \dots , A_n$ are pairwise orthogonal to each other.

See Definition 1 for the concept of “orthogonal” between $OD(n, 2n-1)$’s.

Definition 1. 

An $OD(n, 2n-1)$ is canonical if its columns are sorted in lexicographical order; see Example 1. As the first $n-1$ rows are fixed (after sorting), a canonical $OD(n, 2n-1)$ A can be indicated by its last row (i.e., the n-th row) $A_{n,1}, \dots , A_{n,c}$, where $c=(2n-1)!/n!$.

Two canonical $OD(n, 2n-1)$s $A, B$ are orthogonal if for every pair $(x, y)$ such that $x\ne y, x\in [2n-1], y\in [2n-1]$, the size of $\{i\mid A_{n,i}=x, B_{n,i}=y\}$ is a constant $\frac{c}{(2n-1)(2n-2)}$.

Moreover, two $OD(n, 2n-1)$s are orthogonal if their canonical forms are orthogonal.

Proof of Theorem 2 

First, we introduce two matrices, X and Y. We use X to represent the submatrix with the first $n-1$ rows of any canonical $OD(n, 2n-1)$. For ease of discussion, assume that $A_1, \dots , A_n$ are already in canonical form. Therefore, $A_1, \dots , A_n$ share the same first $n-1$ rows, that is X. We choose the last row of $A_i(1\le i\le n)$ to be the i-th row of Y. Denote by $S_k$ the set of numbers in the k-th column of X; formally, $S_k=\{X_{1, k}, \dots , X_{n-1, k}\}$. □

Claim 1. The k-th column of Y is a permutation of $[2n-1]\backslash S_k$. Thus, every column of $\left[\begin{array}{c}X\\ Y\end{array}\right]$ is a permutation of $[2n-1]$. (Example: for $n=5$, the first column is ${(1, 2, 3, 4, 6, 9, 5, 8, 7)}^T$.)

Proof. 

Abbreviate $X_{1,k}, \dots , X_{n-1,k}, Y_{1,k}, \dots , Y_{n,k}$ as $x_1, \dots , x_{n-1}, y_1, \dots , y_n$, respectively.

Clearly, $y_1, \dots , y_n$ belong to $[2n-1]\backslash S_k$. It remains to show that $y_i\ne y_j(i<j)$.

Due to the construction of Y and (4),

$$\begin{array}{ccc}\hfill x_i& =& f(x_1, \dots , x_{i-1}, y_i, x_{i+1}, \dots , x_{n-1})(i<n)\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill y_n& =& f(x_1, x_2, \dots , x_{n-1}).\hfill \end{array}$$

(6)

Case 1: $i<j<n$. We prove it by contradiction. Suppose $y_i=y_j=e$. Applying (5), we obtain $x_i=f(S_k\cup \left\{e\right\}\backslash \left\{x_i\right\})$ and $x_j=f(S_k\cup \left\{e\right\}\backslash \left\{x_j\right\})$, which means $S_k\cup \left\{e\right\}\backslash \left\{x_i\right\}$ and $S_k\cup \left\{e\right\}\backslash \left\{x_j\right\}$ are both mapped to $S_k\cup \left\{e\right\}$ under $F:\{a_1, \dots , a_{n-1}\}\to \{a_1, \dots , a_{n-1}, f(a_1, \dots , a_{n-1})\},$ violating the injective property of f.

Case 2: $i<j=n$. The proof is similar to Case 1. Suppose $y_i=y_n=e(i<n)$. Applying (5) and (6), we obtain $x_i=f(S_k\cup \left\{e\right\}\backslash \left\{x_i\right\})$ and $e=f\left(S_k\right)$, which means both $S_k$ and $S_k\cup \left\{e\right\}\backslash \left\{x_i\right\}$ are mapped to $S_k\cup \left\{e\right\}$, violating the injective property of f.    □

Claim 2. All columns of $Y^{\prime }$ are distinct, where $Y^{\prime }$ is the submatrix of Y without the last row.

Proof. 

Fix any set $S=\{x_1, \dots , x_{n-1}\}\in \left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$ and denote $z=f(x_1, \dots , x_{n-1})$. According to the definition of X, exactly one column of X equals ${(x_{{\pi }_1}, \dots , x_{{\pi }_{n-1}})}^T$ for each permutation $({\pi }_1, \dots , {\pi }_{n-1})$ of $[n-1]$. Let $Y_{{\pi }_1, \dots , {\pi }_{n-1}}$ denote the column of Y for which this column of X equals ${(x_{{\pi }_1}, \dots , x_{{\pi }_{n-1}})}^T$. A simple connection between $Y_{1, \dots , n-1}$ and $Y_{{\pi }_1, \dots , {\pi }_{n-1}}$ is as follows.

$$\mathrm{If}{Y}_{1, \dots , n-1}={(y_1, \dots , y_{n-1}, z)}^T, \mathrm{then}{Y}_{{\pi }_1, \dots , {\pi }_{n-1}}={(y_{{\pi }_1}, \dots , y_{{\pi }_{n-1}}, z)}^T.$$

(7)

We prove this connection in the following. Because $Y_{1, \dots , n-1}={(y_1, \dots , y_{n-1}, z)}^T$, by the definition of X and Y, we have $x_i=f(S\cup \left\{y_i\right\}\backslash \left\{x_i\right\})(1\le i\le n-1)$. This implies that $x_{{\pi }_i}=f(S\cup \left\{y_{{\pi }_i}\right\}\backslash \left\{x_{{\pi }_i}\right\})(1\le i\le n-1)$, which means $Y_{{\pi }_1, \dots , {\pi }_{n-1}}={(y_{{\pi }_1}, \dots , y_{{\pi }_{n-1}}, z)}^T$.

Let $S^{\prime }=[2n-1]\backslash (S\cup \left\{z\right\})$. By the injective property of f, if S is taken over $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$, set $S\cup \left\{z\right\}$ is taken over by $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n}\right)$ and thereby $S^{\prime }$ would be taken over by $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$. On the other hand, due to the connection in (7), for any fixed $S^{\prime }$, each permutation of $S^{\prime }$ appears as a column of $Y^{\prime }$. Together, each $(n-1)$-permutation of $[2n-1]$ appears once in $Y^{\prime }$. This further implies Claim 2, by counting the number of $(n-1)$-permutations of $[2n-1]$.    □

Claim 3.Y is an $OD(n, 2n-1)$.

Proof. 

It suffices to show that the Hamming distance between two distinct columns of Y is at least 2. Following Claim 2, the distance is at least 1. We prove that the distance is not 1. Suppose that Y has two columns $Y_j, Y_k$ with Hamming distance 1.

Case 1: $Y_{i, j}\ne Y_{i, k}$ for some $i<n$ (i.e., the difference is not at the last row).

Denote the j-th and k-th column of Y by ${(y_1, \dots , y_n)}^T$ and ${(y_1, \dots , y_{i-1}, y_i^{\prime }, y_{i+1}, \dots , y_n)}^T$, respectively. Let $S=[2n-1]\backslash \{y_1, \dots , y_n\}$. Via Claim 1, the set of elements in the j-th column of X is S, and that in the k-th column of X is $S\cup \left\{y_i\right\}\backslash \left\{y_i^{\prime }\right\}$. Following the definition of X and Y, we obtain $f\left(S\right)=y_n=f(S\cup \left\{y_i\right\}\backslash \left\{y_i^{\prime }\right\})$, violating the Latin property of f.

Case 2: $Y_{n, j}\ne Y_{n, k}$ (i.e., the difference is at the last row).

Denote the j-th and k-th column of Y by ${(y_1, \dots , y_n)}^T$ and ${(y_1, \dots , y_{n-1}, y_n^{\prime })}^T$, respectively. Let $S=[2n-1]\backslash \{y_1, \dots , y_{n-1}\}$. By Claim 1, the set of elements in the j-th column of X is $S\backslash \left\{y_n\right\}$, and that in the k-th column of X is $S\backslash \left\{y_n^{\prime }\right\}$. Following the definition of X and Y, we obtain $f(S\backslash \left\{y_n\right\})=y_n$ and $f(S\backslash \left\{y_n^{\prime }\right\})=y_n^{\prime }$, violating the injective property of f.

As a consequence of Claim 3, $A_1, \dots , A_n$ are pairwise orthogonal to each other.    □

Remark 5. 

For $n=3$, each of the independent sets $I_1, I_2, I_3$ (constructed from the $LM(3, 5)$ f introduced above Theorem 1) represents a Latin square of order 5. To this end, the diagonal should be filled with $1, \dots , 5$ in these squares; see Figure 3 for an illustration. As a corollary of Theorem 2, these three Latin squares are mutually orthogonal Latin squares (MOLS) of order 5.

Moreover, if we define another Latin square M to be $M_{i, j}=(j-i+5)mod5+1$, it can be verified that M together with the three Latin squares above are a set of 4 MOLS of order 5. Although a set of 4 MOLS of order 5 is known [8](p. 163), our construction might be easier to remember: it is simply built upon the Latin matching that is described by the two codewords of 0110 and 1001.

Remark 6. 

In the proof of Theorem 2, we showed that matrix Y is an $OD(n, 2n-1)$, where the i-th row of Y is the last row of $A_i(1\le i\le n)$. We can further prove that Y is actually the same OD as $A_n$ when the underlying Latin matching f admits the “flip property” defined below. (Because this equivalence between Y and $A_n$ is trivial, we leave the easy proof as an exercise to the readers.)

Recall Remark 2. Recall $F:\{a_1, \dots , a_{n-1}\}\to \{a_1, \dots , a_{n-1}, f(a_1, \dots , a_{n-1})\}$ from $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n-1}\right)$ to $\left(\genfrac{}{}{0pt}{}{[2n-1]}{n}\right)$. f has the flip property if: $F\left(A\right)=B$ implies $F\left(\right[2n-1]\backslash B)=[2n-1]\backslash A$. Equivalently, f has the flip property if: $f\left(S\right)=z$ implies $f\left(\right[2n-1]\backslash (S\cup \left\{z\right\}\left)\right)=z$.

Our $LM(2, 3)$ does not admit the flip property.

6. Connections between SLF and SS with Implications

SLFs are special LFs, whereas LFs are equivalent to ODs. This section provides some necessary conditions for the existence of $SLF(n, 2n-1)$ and $SLF(n, v)$.

First, we show a lemma that sandwiches an SLF between two Steiner systems.

In this paper, we mainly focus on $S(n-1, n, v)$ and it as $S(n, v)$.

Example 2. 

The 14 codewords used in drawing Figure 1 constitute an $S(4, 8)$. A proof is as follows. Consider the 3-element subsets of $\left[8\right]$. We prove that each subset is contained as a subset of exactly one block (a block is corresponding to a codeword here). First, applying the fact that the Hamming distance of the codewords is at least 4, each subset is contained in at most one block. Therefore, the 14 blocks cover $14\times 4$ = 56 different 3-element subsets of $\left[8\right]$. Further, since the number of 3-elements of $\left[8\right]$ is $\left(\genfrac{}{}{0pt}{}{8}{3}\right)=56$, each 3-element subset of $\left[8\right]$ is contained in exactly one block.

Lemma 4. 

An $S(n, v)$ implies an $SLF(n, v)$, and an $SLF(n, v)$ implies an $S(n-1, v-1)$.

Proof. 

First, given an $S(n, v)$, denoted by $S$, we construct an $SLF(n, v)$. For each block $B=\{a_1, \dots , a_n\}$ in $S$ and each $i\in \left[n\right]$, define $f(B\backslash \left\{a_i\right\})=a_i$. Check that the image of every $(n-1)$-element subset of $\left[v\right]$ is determined, since $S$ is an $S(n, v)$. We now prove by contradiction that f is Latin and hence an $SLF(n, v)$. Suppose that f is not Latin. This implies that there exist $\{b_1, \dots , b_{n-2}, c\}$ and $\{b_1, \dots , b_{n-2}, d\}$ that are mapped to the same element a, which means that we have two blocks $\{b_1, \dots , b_{n-2}, c, a\}$ and $\{b_1, \dots , b_{n-2}, d, a\}$ in $S$. It follows that $\{b_1, \dots , b_{n-2}, a\}$ is contained by two blocks, which is contradictory.

Next, given an $SLF(n, v)$, denoted by f, we construct an $S(n-1, v-1)$. Because f is an $LF(n, v)$ and an $LF(n, v)$ is equivalent to an $OD(n, v)$, function f is equally likely to take any value among $1, \dots , v$. So, the number of $(n-1)$-element subsets of $\left[v\right]$ that are mapped to value v is $\left(\genfrac{}{}{0pt}{}{v}{n-1}\right)/v$. Denote $m=\left(\genfrac{}{}{0pt}{}{v}{n-1}\right)/v$. Each such subset mapped to v can be described by a binary string of length $v-1$ that contains $(n-1)$ 1’s. Let $S$ be the set of these m strings (each called a block). We claim that $S$ is an $S(n-1, v-1)$. The proof is as follows. Because f is Latin, each $(n-2)$-element subset of $[v-1]$ is contained in at most one block. This further implies that the blocks in $S$ cover $m(n-1)=\left(\genfrac{}{}{0pt}{}{v}{n-1}\right)(n-1)/v=\left(\genfrac{}{}{0pt}{}{v-1}{n-2}\right)$ different $(n-2)$-element subsets of $[v-1]$. However, the number of $(n-2)$-element subsets of $[v-1]$ is $\left(\genfrac{}{}{0pt}{}{v-1}{n-2}\right)$. Therefore, each $(n-2)$-element subset is contained in exactly one block.    □

Applying Lemma 4, we can rapidly derive a few results about SLF from the studies of SS, which are shown below. Designing SSs is notoriously difficult. Very little is known about the existence of SS, especially for $t>5$.

Proposition 6.

A necessary condition for the existence of $SLF(n, 2n-1)$ is that n is a prime.

As a corollary, the order of a Latin matching must be a prime.

Proof. 

If an $SLF(n, 2n-1)$ exists, there must be an $S(n-1, 2n-2)$ according to Lemma 4. Moreover, it is known that if $S(t+1, v)$ exists, $gcd(v-t, lcm(1, \dots , t+1\left)\right)=1$ [7]. In particular, if $S(n-1, 2n-2)$ exists, $gcd(n, lcm(1, \dots , n-1\left)\right)=1$, i.e., n is a prime.    □

Proposition 7.

1. There is an $SLF(6, 12)$.

2. There is no $SLF(11, 21)$. Therefore, a Latin matching of order 11 does not exist.

3. There is no $SLF(13, 25)$. Therefore, a Latin matching of order 13 does not exist.

Proof. 

Applying Lemma 4 with the existence of $S(6, 12)$ [18], we obtain Part 1.

Since there is no $S(5, 15)$ [20], there is no $S(5+5, 15+5)=S(10, 20)$.

Since there is no $S(5, 17)$ [21], there is no $S(5+7, 17+7)=S(12, 24)$.

Applying these with Lemma 4, we obtain Parts 2 and 3, respectively.    □

Proposition 8. 

An $SLF(n, 2n)$ exists if and only if $S(n, 2n)$ exists.

Proof. 

Use Lemma 4 with the interesting fact that $S(n, 2n)$ exists if and only if $S(n-1, 2n-1)$ exists [22].    □

We were most curious about the existence of $SLF(n, 2n-1)$ (for prime n). Using Lemma 4, one might be tempted to design an $S(n, 2n-1)$, in order to find an $SLF(n, 2n-1)$. However, there is no $S(n, 2n-1)$ according to the division condition $gcd(v-t, lcm(1, \dots , t+1\left)\right)=1$ (here, $v-t=t+1=n$). So, we have to approach $SLF(n, 2n-1)$ in other ways.

Further Investigation on the Existence or Nonexistence of $SLF(n, 2n-1)$ for Prime n

We saw that $SLF(n, 2n-1)$ exists for $n=2, 3, 5$, but not for $n\in \{11, 13\}$ Proposition 7) or composite n (Proposition 6). We consider $n=7$ and $n=17$ below.

Theorem 3. 

There is no $SLF(7, 13)$. So, there is no Latin matching of order 7.

Proof. 

Suppose f is an $SLF(7, 13)$. Recall the proof of Lemma 4, which indicates that f is equally likely to be any value among $1, \dots , 13$, and that all those 6-element subsets of $\left[13\right]$ mapped to 13 constitute an $S(6, 12)$ (each such subset forms a block, and the set of these blocks form an $S(6, 12)$.) In fact, for each $i\in \left[13\right]$, those 6-element subsets of $\left[13\right]$ mapped to i constitute an $S(6, 12)$, denoted by $S_i$. Clearly, f is fixed as long as $S_1, \dots , S_{13}$ are given. On the other hand, it is widely known that an $S(6, 12)$ exists and is unique up to isomorphism (this combinatorial design is also known as the small Witt design $W_{12}$) [18].

We can use a computer program to test all possible choices of $(S_1, \dots , S_{13})$. First, generate all the $S(6, 12)$s (the number of $S(6, 12)$ is 5040) from the unique one up to isomorphism. Then, choose an $S(6, 12)$ for each $i\in \left[13\right]$ and check if $S_1, \dots , S_{13}$ constitute an $SLF(7, 13)$. The rough complexity of this exhaustive searching program would be ${5040}^{13}$. Nevertheless, the program can be optimized by some trivial pruning (we omitted the details) and can be rendered very fast. The searching result denies an $SLF(7, 13)$; see Appendix A.    □

We now quickly discuss the situation of $n=17$ for which the answer is unknown. According to Lemma 4, a necessary condition is the existence of $S(16, 32)$. Unfortunately, it is not known whether $S(16, 32)$ exists. In fact, it is not known whether $S(5, 21)$ exists [23], let alone $S(5+11, 21+11)$. However, it is known that $S(4, 20)$ exists [8,23].

For prime $n\ge 17$, a key subproblem is the existence of $S(n-1, 2n-2)$. To the best of our knowledge, the existence of $S(n-1, 2n-2)$ for prime $n\ge 17$ has not been settled.

Remark 7. 

A constant weight code with parameters $n, d, w$ is a set of codewords (vectors) of length n and weight w, and with a Hamming distance at least d between codewords [24,25,26]. The maximal possible number of codewords in a constant weight code is usually denoted by $A(n, d, w)$.

An $S(n-1, 2n-2)$ exists if $A(2n-2, 4, n-1)$ equals its trivial upper bound. However, the study of constant weight code so far does not imply or deny the existence of $S(n-1, 2n-2)$.

Table 1. On the existence of $LF(n, 2n-1)$ and Latin matchings.

ordern	$2, 3, 5$	$7, 11, 13$	prime ≥ 17	4	composite ≥ 6
Latin matching	Yes	No	Unknown	No	No
$LF(n, 2n-1)$	Yes	Unknown	Unknown	No [7] (p. 569)	Unknown

summarizes our knowledge on Latin matchings and $LF(n, 2n-1)$s.

There exist $LF(n, 2n-1)$s that are not SLFs. For example, we can construct some $LF(3, 5)$s from the $OD(3, 5)$ shown in Example 1, and none of them is an SLF.

An $LF(n, 2n-1)$ exists only if there exists an $LF(n-1, 2n-2)$ (Lemma 1). Teirlinck gave an $OD(n-1, 2n-2)$ (and hence an $LF(n-1, 2n-2)$) for any prime n [10].

7. Applications

7.1. Cooperation via Ordered Designs in Hat Guessing Games

Hat guessing games have drawn much attention among mathematicians, computer scientists, coding theorists, and even the press due to their relations to graph theory, circuit complexity, network coding, and auctions [27,28,29,30,31,32]. Some versions of hat guessing games are used in derandomizing protocols in circuit complexity and derandomizing auctions in auction mechanism design due to the innate similarities between these games, and the number-on-forehead models in complexity [33,34] and the bid-independent auctions [35]. Moreover, these games are attractive because their optimal solutions have many unexpected connections to coding theory [33,34]. In this paper, we consider a variant of such games called unique-supply hat guessing game, defined below, which is a special case of the finite-supply hat guessing game studied in [29,31].

• Assume there are nplayers and vhats with different colors $1, \dots , v$. (the supply for hats of any specific color is unique; in other words, each hat is unique). A dealer randomly places one hat to each of the n players (according to uniform distribution).
• Each player can observe the colors of the hats of other players, but cannot see and has to guess the color they receive. All players must guess simultaneously.
• The n players act as a team, and the team wins if all players are right. The question is how to design the best cooperative strategy to obtain the maximal winning probability.
• Parameters $(n, v)$ are known to the players. No communication is allowed between players after the game starts; communication via wait used in some hat puzzles is also forbidden. However, it is permissible for them to discuss a strategy beforehand.

Example 3. 

For $n=2$, the following strategy is optimal: Player 1 guesses $(B-1)modv$ after observing color B of their teammate, whereas Player 2 guesses $(A+1)modv$ after observing color A of their teammate. Clearly, the players both simultaneously guess right or both fail.

A placement of the v hats to n players can be represented by an n-permutation $(a_1, \dots , a_n)$ of $\left[v\right]$, which is a vertex in $G(n, v)$; vice versa. The winning placements of a strategy s refer to those placements for which a team wins when they adopt strategy s. $\alpha \left(G\right)$ is the cardinality of the maximal independent (vertex) set of graph G.

Lemma 5. 

The winning placements of any strategy form an independent set of $G(n, v)$. Moreover, given an independent set I of $G(n, v)$, the winning placements of some strategy contains I. As a corollary, finding the optimal strategy is equivalent to finding the MIS of $G(n, v)$; the maximal winning probability of the team is given by $\alpha \left(G\right(n, v\left)\right)$ divided by the number of vertices of $G(n, v)$.

Proof. 

A strategy s cannot win two adjacent vertices (i.e., placements). Why? Suppose $(a_1, \dots , a_n)$ and $(a_1, \dots , a_{i-1}, a_i^{\prime }, a_{i+1}, \dots a_n)$ are winning placements of s that are adjacent. The i-th player cannot distinguish the placements, as their observation is invariant. So their guess should be consistent in two cases, which is wrong in one case.

Given an independent set I of $G(n, v)$, the following strategy wins all placements in I. For each player, there is at most one vertex $(a_1, \dots , a_n)$ in I that is consistent with their observation (since all such placements are clearly adjacent yet I is independent). The player guesses according to the mentioned vertex if it exists, or arbitrarily otherwise.    □

Combining Lemma 5 with Proposition 3, we obtain

Corollary 2. 

The maximal winning probability equals $\frac{1}{v-n+1}$ if and only if there is an $OD(n, v)$.

Recall the MIS $I_c(1\le c\le n)$ of $G(n, 2n-1)$ introduced in (4). An optimal strategy wins all the vertices in $I_C$ as analyzed above. In the following, we give an explicit description of this optimal strategy using underlying Latin function f instead of set $I_c$.

Explicit description for the strategy that wins all the placements in $I_c$: Given a placement $\mathbf{a}=(a_1, \dots , a_n)$, denote $A_i=\{a_1, \dots , a_n\}\backslash \left\{a_i\right\}$ for each $i\in \left[n\right]$, which is the set of colors observed by player i. Player c guesses $g_c=f\left(A_c\right)$. Player $i(i\ne c)$ guesses $g_i$, where $g_i$ denotes the unique number $g\notin A_i\backslash \left\{a_c\right\}$ such that $f(A_i\backslash \left\{a_c\right\}\cup \left\{g\right\})=a_c$ (note that $a_c$ is known by player i and the uniqueness of g follows from the Latin property).

When $\mathbf{a}\in I_c$, every player guesses right, i.e., $g_i=a_i(1\le i\le n)$. The trivial proof is omitted.

Remark 8.

(1) In the strategy corresponding to $I_c$, player c can be regarded as the leader of the team. This does not mean that they would answer earlier than the others. Instead, everybody figures out what the leader would do and searches for the unique answer that is consistent with the leader.

(2) For making the decision, each player only checks the set of colors of other players and the color of the leader (if they are not the leader). Therefore, the $n-1$ members other than the leader c can be indistinguishable if the above strategy is applied.

To sum up, we show how to use our combinatorial design called Latin matching to solve a variant of hat guessing games. This application of the Latin matching has the same favor as the application of the Hamming code in the original hat guessing game [29,31]. Unfortunately, the Latin matching does not always exist just as the Hamming code.

7.2. Apply Known $LOD(n, 2n-1)$ to Construct Other Ordered Designs

Recall matrices X and Y in the proof of Theorem 2, which are constructed from $I_1, \dots , I_n$ (who form $LOD(n, 2n-1)$). Let $Z=\left[\begin{array}{c}X\\ Y\end{array}\right]$, which has $2n-1$ rows. We claim that

(1)

for $n=3$, matrix Z is an $OD(2, 5, 5)$;

(2)

for $n=5$, matrix Z is an $O{D}_6(3, 9, 9)$ (note: Z is not an $OD(4, 9, 9)$).

Claim (1) easily follows from Theorem 2. Claim (2) does not immediately follow from Theorem 2. We used a computer program to prove this claim; see Appendix B. We can further obtain $LOD(2, 5, 5)$ and $LO{D}_6(3, 9, 9)$ applying Point 4-(d) in Section 3.

7.3. Applications of Ordered Designs or Large Set of Ordered Designs in Experimental Designs, Error-Correcting Codes, Secret-Sharing Scheme, Tournament Scheduling, etc.

Applications of combinatorial design theory in experimental design have a long history; see a textbook written in the 1980s [3] . Specifically, the connections between ordered designs and experimental design (such as factorial experiments) can be found in [9,36] and the references within. Some other applications of perpendicular arrays in [9,36] are also applications of ordered designs because ordered designs are perpendicular arrays.

An $LOD(n, v)$, which is equivalent to a $(v-n+1)$-coloring of $G(n, v)$, can be used in error-correcting code. Let $\mathbf{a}=(a_1, \dots , a_n)$ denote a vertex in $G(n, v)$. The color of $\mathbf{a}$ is $c\left(\mathbf{a}\right)$. Because $c\left(\mathbf{a}\right)$ changes whenever exactly one of $a_1, \dots , a_n$ changes, this value can serve as the one-error detecting bit when we send message $a_1, \dots , a_n$.

An $LOD(n, v)$ is also useful in secret-sharing schemes. Suppose n persons want to hold a secret $s\in [v-n+1]$. Assign each person i a number $a_i$ in $\left[v\right]$, so that $\mathbf{a}=(a_1, \dots , a_n)$ is a vertex in $G(n, v)$ with color s (in the given LOD). It can be easily observed that (1) n persons together can obtain the secret, and (2) every $n-1$ persons cannot obtain any information about the secret.

Ordered designs have connections to Latin squares and MOLS (see Remark 5 and [9]), orthogonal arrays, and Steiner systems. In fact, ordered designs are called orthogonal arrays of type I by Rao [9] or ordered Steiner systems by Teirlinck [10]. All these mentioned combinatorial designs have found a variety of applications, and ordered designs may find similar applications. In particular, the Latin squares can be used for sampling [37,38] cryptography [39], and for scheduling tournaments and processors of parallel computer [40,41,42]. The n-coloring of $G(n, 2n-1)$ shown in Section 4.1 is essentially a Latin hypercube (see Remark 4) that has analogous applications. We do not dwell on applications of Steiner systems and orthogonal arrays, and we refer the reader to [1,2,4].

8. Concluding Remarks

We proposed a new combinatorial structure called Latin matchings and showed that a Latin matching of order n leads to an $LOD(n, 2n-1)$, thus obtaining an $LOD(5, 9)$, among others. Latin matchings and the more general structures called symmetric Latin functions have strong connections to Steiner systems, as shown in Lemma 4. Due to these connections, designing Latin matchings is at least as difficult as designing Steiner systems.

The Latin matching of order 5 given in Figure 1 derived from $\mathsf{Hamming}(8, 4, 4)$ is a perfect matching between $\left(\genfrac{}{}{0pt}{}{\left[9\right]}{4}\right)$ and $\left(\genfrac{}{}{0pt}{}{\left[9\right]}{5}\right)$ with several remarkable properties (see Remarks 1 and 2). The existence of such an interesting matching is surprising and might have more applications. We end this paper by pointing out several unsolved problems.

• Does an $OD(4, 9, 9)$ exist?
• Does an $LF(6, 11)$ exist? Does an $LF(n, 2n-1)$ exist for a composite n?
• Does an $LF(7, 13)$ exist? Moreover, does an $LOD(7, 13)$ exist?
• Does an $SLF(17, 33)$ exist? Does an $S(16, 32)$ exist?
• Is it true that every $SLF(n, 2n-1)$ is a Latin matching? (we verified that this holds for $n=2, 3, 5$, and we conjecture that this holds for all n.)
• Is it true that every Latin matching is isomorphic to a cyclic Latin matching?