Geometric Brownian Motion (GBM) of Stock Indexes and Financial Market Uncertainty in the Context of Non-Crisis and Financial Crisis Scenarios

Abstract

The present article proposes a methodology for modeling the evolution of stock market indexes for 2020 using geometric Brownian motion (GBM), but in which drift and diffusion are determined considering two states of economic conjunctures (states of the economy), i.e., non-crisis and financial crisis. Based on this approach, we have found that the GBM proved to be a suitable model for making forecasts of stock market index values, as it describes quite well their future evolution. However, the model proposed by us, modified geometric Brownian motion (mGBM), brings some contributions that better describe the future evolution of stock indexes. Evidence in this regard was provided by analyzing the DAX, S&P 500, and SHANGHAI Composite stock indexes. Throughout the research, it was also found that the entropy of these markets, analyzed in the periods of non-crisis and financial crisis, does not differ significantly for DAX—German Stock Exchange (EU) and S&P 500—New York Stock Exchange (US), and insignificant differences for SHANGHAI Composite—Shanghai Stock Exchange (Asia). Given the fact that there is a direct link between market efficiency and their entropy (high entropy—high efficiency; low entropy—low efficiency), it can be deduced that the analyzed markets are information-efficient in both economic conjunctures, and, in this case, the use of GBM for forecasting is justified, as the prices have a random evolution (random walk).

1. Introduction

In this paper we aim to make forecasts, at different moments of time (3, 6, 9, and 12 months), of DAX, S&P 500, and SHANGHAI Composite stock indexes values for 2020, using geometric Brownian motion (GBM), but in which drift and diffusion are determined by considering two states of the economic situation weighted with their probabilities of occurrence. We chose to make the forecasts for 2020, as this year was characterized by the onset of the health crisis (COVID-19 pandemic) but also by a probability of a financial crisis. In addition, the real data of the indices from 2020 allowed us to test the forecast models: GBM and modified geometric Brownian motion (mGBM) at different time intervals of 3, 6, 9, and 12 months. In fact, if investors would not consider the occurrence of a possible financial crisis, the data used to build the differential equation (GBM) is limited in practice to the year 2019. This period does not contain a financial crisis in the data, as no such event took place during this period and, as a result, although GBM may well capture the future evolution of stock indexes, some nuanced aspects may have been lost sight of in a closer analysis of these evolutions (we found that year 2019 is the same year when many of the stock indexes on the markets examined were historically high, in line with Flitter [1], Wearden [2], and Carlson [3]). Therefore, if we consider several economic conjunctures, then this situation could change. In this sense, the states of the economic conjunctures can be considered as non-crisis and financial crisis, and their probabilities of occurrence are determined as follows: if the probability of a crisis is known, the probability of non-crisis is given by the difference between 1: the probability of a crisis. The question that arises is how can we, in a financial crisis situation, know the probability of occurrence of the financial crisis, the expected returns, and the risks of investors (returns volatility)?

A complementary direction of the study is the determination of discrete and differential Shannon entropy, to measure market uncertainty. We consider this approach necessary because, based on the results obtained, we can observe whether there are differences regarding the degree of uncertainty between the analysis periods considered in the paper, the financial crisis period (2008), and the non-financial crisis period (2019). We consider this complementary approach useful, as it is known that there is a link between the efficiency of markets and their entropy [4] and this may provide additional arguments regarding the use of GBM to make forecasts if in both periods the degree of uncertainty is approximately the same level (a premise of the efficiency of financial markets is that the price of securities has a random evolution—random walk).

Therefore, our paper supports the idea of using GBM for forecasting, and, according to Wilmott in his work “Paul Wilmott introduces quantitative finance” [5], “The widely accepted model for equities, currencies, commodities, and indexes is dS = µS dt + σS dB. It is a continuous-time model of an asset price […] and the foundation of so much finance theory”.

In GBM, constant drift and diffusion coefficients are used, but GBM models can also be used in the cases in which the volatility (necessary in the measurement of the coefficient of diffusion) is stochastic. Numerical solutions can be used through a Monte Carlo simulation in the absence of an analytical solution. In addition, Monte Carlo simulation can be used when there are stochastic diffusion processes with jumps, in which the price of financial security does not fluctuate continuously and regularly (it varies by jumping in a discontinuous way).

The GBM, which we can also call the classic GBM, has proven to be a very useful forecasting tool in finance. However, this tool is less useful in case of a future financial crisis in the financial markets. One solution in this regard would be the following: if we know the probability of a crisis and the expected return, respectively, the risks of investors (return volatility) in a crisis and the coefficients of drift and diffusion can be rewritten to capture it in the differential equation.

Regarding expected returns and volatility in the financial crisis situation, we can consider that their values may be those recorded in 2008, a period that characterizes such a situation well (2008 is our benchmark in the article regarding what we can empirically understand by a financial crisis). Summarizing, we can say that the periods of analysis considered for determining the coefficients of drift and diffusion that characterize the two states of the economic situation in the form of a mix are 2019 (for the non-financial crisis period) and 2008 (for financial crisis period), to make forecasts for 2020. We emphasize that, in our analysis, for the two periods mentioned above, we work with sizes such as the average log-return and the standard deviation of the log-returns, and these can be largely considered representative to characterize the expected returns by the investors and return volatilities in non-crisis and financial crisis situations.

Regarding the likelihood of a financial crisis or economic recession, it is worth noting that these probabilities can be known because of current research increasingly active in this field of study. Thus, in 2019 many researchers, including Nobel laureates (e.g., Robert Engle [6,7]), were concerned about measuring the likelihood of a financial crisis in the US market or in other mature markets. In addition, on 14 October 2019, Bloomberg published a model used to detect the US recession whose result is given by the probability of the US recession calculated for the next 12 months in the future.

Therefore, knowing the appearance probabilities of the two states of the economic conjuncture and knowing the numerical characteristics (average log-return and the standard deviation of the log-returns) corresponding to these states, a rewriting of the GBM model can be performed, referred to as the mGBM model, in which drift and diffusion are calculated considering these states in the form of a mix. The result is a GBM that can better capture the evolution of stock indexes, given the fact that in the construction of drift and diffusion, a possible future financial crisis can also be considered.

That being said, for the present research, we will work with two scenarios regarding the evolution of DAX, S&P 500, and SHANGHAI Composite stock indexes: Scenario A, in which the probability of the financial crisis appearance is zero (in which case the GBM is, in fact, the classical one—GBM), and Scenario B, in which there is a probability of appearance of the financial crisis (in which case the GBM is a modified one—mGBM), as in Figure 1.

We also highlight that the solutions generated by the equation of GBM can be determined both analytically and numerically by GBM using Monte Carlo simulation. We opt for the second option because, on the one hand, we consider it more useful because of the possibility of a graphical representation of possible paths. On the other hand, alternative values for the stock market index (10,000 values) can be obtained by simulation at different times (3, 6, 9, and 12 months). Based on these values, the number higher than the value from the date of analysis can be later determined (30 or 31 of December, the closing date of the stock market). This last fact makes possible the determination of the likelihood that the stock market index will be higher in future than its value at the date of analysis, and so we can capture some nuanced aspects of the analysis of simulated data regarding the forecasts.

That being said, the article is further structured as follows: the literature review, Section 2, presents the most important conceptual approaches; research methodology is described in the third part; the empiric findings and discussions are described in the fourth section of the paper; the conclusions of the study are outlined in the final part of the article.

2. Literature Review

2.1. Financial Crisis Forecasting Models

Determining the probability of the financial crisis has been a topic of interest for economists of all time [8,9]. It is still a topic of interest nowadays; the aspects regarding the determination of the crisis occurrence probability in a specific time horizon and defining optimal early warning systems (EWS) have been researched through various scientific methodologies. Predicting the exact timing of the crisis is a difficult task, but common patterns can be identified before the global economic crisis.

A financial crisis is defined as a rare event that meets the following four characteristics [10]: (a) the economic and social costs generated by the crisis are overwhelming; (b) they appear very quickly and do not give time for reaction and adoption of preventive measures, but their anticipation is essential; (c) the implementation of prevention measures is severe as the citizens consider the crisis unlikely to appear and show reluctance towards such measures; (d) the crisis prevention measures themselves are costly.

Among the first and most widely used financial crisis prediction models are probabilistic models [11], regression-based models (STV model), Developing Country Studies Division (DCSD) model and Kaminsky, Lizondo, Reinhart (KLR) signal model. Of the models mentioned above, studies have shown that the KLR signal model has the best predictive ability [12]. However, these EWS have evolved over the years and have become increasingly sophisticated in capturing economic cyclicality. The probability of a crisis occurrence was also determined by estimating vulnerability levels through crisis probability curves using pooled and panel regression [13].

Sarlin [14] tested the efficiency of parametric models compared to nonparametric models (neural networks) in predicting the financial crisis by applying and testing them on the economic situation during the 2007 crisis. The result of the study promotes the use of nonparametric methods in monitoring financial stability. The International Monetary Fund (IMF), starting from the KLR model, recently adopted nonparametric models to estimate the probability of a crisis, calibrated on different types of crises: growth crisis, fiscal crisis, and financial crisis. The models are based on the choice of variables specific to the type of crises analyzed and on the determination of the threshold of each variable, on groups of countries: emerging markets and advanced economies [15]. Nevertheless, none of the parametric models have been abandoned, being used even in the current period to estimate the probability of a crisis. SRISK is a recent regression-based and well-known econometric model that measures systemic risk for 23 countries [6,7,16]. Another recent parametric model is the one developed for the Bloomberg platform by Pickert, Qiu, and McIntyre [17], and is applied for the United States economy, being updated monthly.

2.2. Rare Events and Uncertainty on Stock Markets

Many economists have studied probability theory, with Zappia [18] conducting a valuable bibliographic study on the theory of probability, uncertainty, and decision-making in the vision of Keynes, Bayes, to the animal spirits of Akerlof and Shiller. Financial crisis forecasting models have evolved with the evolution of mathematical methods, from “the Marginal revolution and the Keynesian revolution” to the Memory Revolution, which includes fractional calculus and “fractional dynamic models of economic processes” [19,20].

The impact of the financial crisis on the price of options was analyzed by El-Khatib, Ali Hajji, and Al-Refai [21], considering the jump-diffusion model and the increase in volatility during a financial crisis.

To estimate the moment when a potential crisis can occur, the persistence and long memory of the stock market was also studied through two theories: “Efficient Market Hypothesis” (EMH) and “Fractal Market Hypothesis” (FMH) [22,23,24,25,26,27].

Studies show that investors ignore rare events, they think of optimal strategies for typical situations, and they have a limited ability to act optimally in rare situations. The expected loss due to suboptimal action in a contingency is inversely proportional to the probability of contingency [28]. From this point of view, the prevention of the effects of rare events began to be studied through entropy and probability theory, in anticipation of crisis, extended to the development of stochastic processes, including Brownian motion [29,30].

Based on the information theory, entropy measures the uncertainty and unpredictability of a discrete or continuous random variable. Although entropy is a concept initially used in thermodynamics, it has also been introduced in the field of finance. Entropy is used in finance and applied mainly in issues related to portfolio selection, asset (options, other derivatives) pricing, and capital increase, being perceived as a form of risk measurement [31,32].

Studies related to entropy reveal that entropy is a measure of uncertainty [33,34] in stochastic processes with random variables and probability of distribution. However, it remains an open topic for research on whether Shannon entropy “is the unique, useful measure of statistical uncertainty” [35,36,37,38,39].

Several types of entropies can be calculated and used in finance, namely, Shannon, Tsallis and Tsallis relative entropy, Kullback Cross, Rényi, Havrda—Charvát, Fermi–Dirac information entropy [40,41]. At the same time, entropy can also be used to measure statistical dispersion for discrete and continuous distributions, but with different properties for the latter ones [42]. Shannon entropy “quantifies the expected value of the information generated from a random variable” [43]; Shannon entropy is a “quantitative measure of the uncertainty associated with a probability distribution” [44]. Entropy density functions were used to analyze financial crisis from the perspective of the yield generated by financial markets; the analysis of the value of entropy allows a thorough and consistent assessment of the risk on the financial market, which could propose an EWS of a financial crisis [45].

2.3. GBM Models for Stock Market Predictions

Monte Carlo simulation and GBM models are used in economic processes to make forecasts, especially for stock prices or stock indexes, and to capture their value fluctuations [46], with increased accuracy, according to studies performed [47,48,49,50,51,52]. Krishna Reddy and Vaughan Clinton have used GBM model for simulating stock process evolution and have demonstrated the validity of the model through three test methods [53]. Brownian motion is the primary tool of modern quantitative finance with which random behaviors can be modeled [54]. The behavior of financial securities and stock indexes can be predicted using a random walk model [55], Monte Carlo simulation, geometric Brownian motion, fractal Brownian motion, and irrational fractional Brownian motion [56,57]. GBM and entropy calculus were used to model the evolution of stock prices and stock options, contributing to a new portfolio optimization theory [58]. GBM can model the price behavior of securities in the Black and Scholes Model [59]. GBM is a useful tool in building a portfolio that optimizes the risk–return relationship, depending on the interest pursued by the investor [60]. The equation motion for the underlying asset from the Black and Scholes model is also a GBM [61,62].

In the present paper, we use the Monte Carlo simulation applied on GBM to generate 10,000 possible paths for the evolution of the three stock indexes at different times (3, 6, 9, 12 months) and in different scenarios. Nonetheless, there are other contributions in this field of research that provide alternative methods to Monte Carlo simulation [63].

3. Research Methodology

3.1. GBM in Non-Crisis and Crisis Conjunctures

Definition 1.

Let $I$ be the value of the stock market index, $t\in \left(0,T\right)$ the time moment, $T$ the total time, and $\Delta t=\frac{1}{T}$ the time lag. The logarithmic return $R\left(t\right)$ of $I$ in the time interval $\left(t, t+\Delta t\right)$ is defined as

$$R\left(t\right)=ln\frac{I\left(t+\Delta t\right)}{I\left(t\right)}=\Delta ln\mathrm{I}.$$

Definition 2.

Let $\left\{B\left(t\right),t\ge 0\right\}$ be a stochastic process; $\left\{B\left(t\right),t\ge 0\right\}$ is a Brownian motion if it verifies:

1. 

The increments $\left\{B\left(t_{i+1}\right)–B\left(t_i\right),i=1,\dots ,n-1\right\}$ are independent, where $0\le t_i\le t_{i+1}, i=1,\dots ,n-1$.

2. 

$B\left(x\right)-B\left(y\right)~N\left(0,x-y\right),\forall x<y$.

3. 

$B\left(0\right)=0$.

Definition 3.

A stochastic process $\left\{I\left(t\right), t\ge 0\right\}$ is a geometric Brownian motion (GBM) if it verifies

$$dI\left(t\right)=\mu I\left(t\right)dt+\sigma I\left(t\right)dB\left(t\right),$$

(1)

where $\mu$ is drift coefficient and $\sigma$ is diffusion coefficient.

Applying Itô Lemma in Equation (1), we obtain

$$d\ln I=\left(\mu -\frac{1}{2}{\sigma }^2\right)dt+\sigma dB\left(t\right),$$

namely,

$$I\left(t\right)=I\left(0\right)exp\left(\mu t-\frac{1}{2}{\sigma }^{2}t+\sigma B\left(t\right)\right),$$

where $B\left(t\right)=\varnothing \sqrt{t},\varnothing ~N\left(0,1\right)$. Therefore,

$$ln\frac{I\left(t\right)}{I\left(0\right)}=\left(\mu -\frac{1}{2}{\sigma }^2\right)t+\sigma \varnothing \sqrt{t}.$$

Over a time lag it follows

$$I\left(t+\Delta t\right)=I\left(t\right)exp\left(\left(\mu -\frac{1}{2}{\sigma }^2\right)\Delta t+\sigma \varnothing \sqrt{\Delta }t\right)$$

(2)

The logarithmic distribution of the stock index return modeled by a GBM is given by

$$R\left(t\right)~N\left[\left(\mu -\frac{1}{2}{\sigma }^2\right)\Delta t,\sigma \sqrt{\Delta }t\right].$$

As mentioned in the introduction, we propose the modeling of the evolution of the stock index value in the form of a stochastic process that evolves as a GBM, but in which drift and diffusion are determined by considering the two economic conjunctures, financial crisis and non-financial crisis. In this sense, the average log-return and the standard deviation of log-returns can be deduced from each state of the economic conjuncture (state of the economy). Given these values and the covariance between logarithmic returns, expected returns and volatility of the two regimes can be determined as a mix that considers the two economic conjunctures to which the weights are assigned in the form of probabilities of the appearance of those conjunctures.

Let $\left(\Omega ,K,P\right)$ be a probability space, where $\Omega =\{s^{\prime },s^{″}\}$ is the space of economic conjunctures with $s^{\prime }\cap s^{″}=\varnothing$ and $\Omega =s^{\prime }\cup s^{″}$. Denote $p^{\prime }=P\left(s^{\prime }\right)$ the probability of non-crisis and $p^{″}=P\left(s^{″}\right)$ the probability of crisis $\left(p^{\prime }=1-p^{″}\right)$.

Define $R^{\prime }=\Delta ln{I}^{\prime }$ and $R^{″}=\Delta ln{I}^{″}$ the return logarithm of the stock market index in the non-crisis period and crisis period, respectively. Consider $R^{\prime }~N\left({\mu }^{\prime },{\sigma }^{\prime }\right)$ and $R^{″}~N\left({\mu }^{″},{\sigma }^{″}\right)$. Let $R~N\left(\mu ,\sigma \right)$ the return logarithm of the stock market index for both periods, where we consider

$$\mu =\left(p^{\prime }{p}^{″}\right)\left(\begin{array}{c}{\mu }^{\prime }\\ {\mu }^{″}\end{array}\right)=p^{\prime }{\mu }^{\prime }+p^{″}{\mu }^{″}$$

(3)

and

$$\begin{gathered} {\sigma }^2=\left(p^{\prime }{p}^{″}\right)\left(\begin{array}{cc}{\sigma }_{R^{\prime }{R}^{\prime }}& {\sigma }_{R^{\prime }{R}^{″}}\\ {\sigma }_{R^{″}{R}^{\prime }}& {\sigma }_{R^{″}{R}^{″}}\end{array}\right)\left(\begin{array}{c}{p}^{\prime }\\ p^{″}\end{array}\right) \\ ={p^{\prime }}^2{{\sigma }^{\prime }}^2+{p^{″}}^2{{\sigma }^{″}}^2+2p^{\prime }{p}^{″}{\sigma }_{R^{″}{R}^{\prime }}. \end{gathered}$$

(4)

If $R^{\prime }$ and $R^{″}$ are independent (${\sigma }_{R^{\prime }{R}^{″}}$ is insignificantly different by zero), then

$${\sigma }^2\approx {p^{\prime }}^2{{\sigma }^{\prime }}^2+{p^{″}}^2{{\sigma }^{″}}^2,$$

(5)

namely,

$$\sigma \approx \sqrt{{p^{\prime }}^2{{\sigma }^{\prime }}^2+{p^{″}}^2{{\sigma }^{″}}^2}.$$

(6)

The time step measures the average profitability. As a result, the larger the unit of time, the greater the average increase in the value of the stock market index over this period. Furthermore, for the standard deviation to remain finite while the time step tends to be zero, the individual terms in the standard deviation expression must be a function of the time step. The standard deviation of profitability after a time step must therefore be a function of the square root of the time step [5]. In Equations (3), (5), and (6), the time factor is added and the values of these numerical characteristics for the total time (T) are defined as follows:

$$\tilde{\mu }=\frac{p^{\prime }{\mu }^{\prime }+p^{″}{\mu }^{″}}{\Delta t},$$

(7)

$$\tilde{\sigma }=\sqrt{\frac{{p^{\prime }}^2{{\sigma }^{\prime }}^2+{p^{″}}^2{{\sigma }^{″}}^2}{\Delta t}}.$$

(8)

In the following, we will call a modified geometric Brownian motion (mGBM) a stochastic process $\left\{\tilde{I}\left(t\right),t\ge 0\right\}$ defined by

$$d\tilde{I}\left(t\right)=\tilde{\mu }\tilde{I}\left(t\right)dt+\tilde{\sigma }\tilde{I}\left(t\right)dB\left(t\right),$$

(9)

where $\tilde{\mu }$ and $\tilde{\sigma }$ are defined in (7) and (8). Then, we obtain

$$\tilde{I}\left(t\right)=\tilde{I}\left(0\right)exp\left(\left(\tilde{\mu }-\frac{1}{2}{\tilde{\sigma }}^2\right)t+\tilde{\sigma }\varnothing \sqrt{t}\right),$$

Over a time lag, it follows

$$\tilde{I}\left(t+\Delta t\right)=\tilde{I}\left(t\right)exp\left(\left(\tilde{\mu }-\frac{1}{2}{\tilde{\sigma }}^2\right)\Delta t+\tilde{\sigma }\varnothing \sqrt{\Delta }t\right).$$

(10)

The variable $ln\tilde{I}\left(t\right)$ has normal distribution see also [64]

$$ln\tilde{I}\left(t\right)~N\left[ln\tilde{I}\left(0\right)+\left(\tilde{\mu }-\frac{1}{2}{\tilde{\sigma }}^2\right)t,\tilde{\sigma }\sqrt{t}\right],$$

with

$$E\left[ln\tilde{I}\left(t\right)|ln\tilde{I}\left(0\right)\right]=ln\tilde{I}\left(0\right)+\left(\tilde{\mu }-\frac{1}{2}{\tilde{\sigma }}^2\right)t$$

and

$$Var\left[ln\tilde{I}\left(t\right)|ln\tilde{I}\left(0\right)\right]={\tilde{\sigma }}^{2}t.$$

From the above relation we obtain

$$E\left[\tilde{I}\left(t\right)|\tilde{I}\left(0\right)\right]=\tilde{I}\left(t\right)e^{\tilde{\mu }t}$$

(11)

and

$$Var\left[\tilde{I}\left(t\right)|\tilde{I}\left(0\right)\right]={\tilde{I}}^2\left(0\right)e^{2\tilde{\mu }t}\left(e^{{\tilde{\sigma }}^{2}t}-1\right).$$

(12)

This being said, due to the structural elements described above, it is now possible to create potential paths for the stock index for the next year, by using the Monte Carlo simulation, and value ranges can be determined at different times, t, in the future. The ranges of values measured on the stock market simulation are roughly equal to the ranges of values used in Equations (13) and (14), thereby

$$\left[E\left(I_{si{m}_{\left(t\right)}}\right)-\varnothing \sqrt{VAR\left(I_{si{m}_{\left(t\right)}}\right)},E\left(I_{si{m}_{\left(t\right)}}\right)+\varnothing \sqrt{VAR\left(I_{si{m}_{\left(t\right)}}\right)}\right]\approx$$

(13)

$$\left[E\left(I\left(t\right)|I\left(0\right)\right)-\varnothing \sqrt{VAR\left(I\left(t\right)|I\left(0\right)\right)},E\left(I\left(t\right)|I\left(0\right)\right)+\varnothing \sqrt{VAR\left(I\left(t\right)|I\left(0\right)\right)}\right],$$

(14)

where $I_{si{m}_{\left(t\right)}}$ is the value of the index simulated at time t by Monte Carlo method.

3.2. Capital Market Entropy

To measure the capital market entropy, we consider the Shannon entropy, as a measure of uncertainty in a stochastic process. A stochastic process can be described by a pattern, a probability distribution of a random variable, and the random variable may be discrete or continuous. If the probability distribution function assigns a small probability to its values, the information entropy is high (high uncertainty), and vice versa, if the probability distribution assigns a high probability to its values, the information entropy is small (the uncertainty is low).

Formally:

We consider the stock index to be a random variable defined as

$$\mathrm{I}\text{:}\left(\begin{array}{ccc}{\mathrm{i}}_1& {\mathrm{i}}_2& \begin{array}{cc}\text{…}& {\mathrm{i}}_{\mathrm{n}}\end{array}\\ {\mathrm{p}}_1& {\mathrm{p}}_2& \begin{array}{cc}\text{…}& {\mathrm{p}}_{\mathrm{n}}\end{array}\end{array}\right)$$

(15)

where ${\mathrm{p}}_{\mathrm{i}}=\mathrm{P}\left({\mathrm{I}=\mathrm{i}}_{\mathrm{i}}\right){;\mathrm{p}}_{\mathrm{i}}\in \left[0,1\right];{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}}=1$. Then, the discrete Shannon entropy is

$$\mathrm{H}\left(\mathrm{I}\right)=-{\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}}{\log }_2{\mathrm{p}}_{\mathrm{i}}$$

(16)

If I is a continuous random variable with normal distribution density f(x), then the differential entropy can be determined as

$$\mathrm{I}\text{~}\mathrm{N}\left({0,\mathsf{\sigma }}^2\right),\mathrm{f}\left(\mathrm{i}\right)=\frac{1}{\mathsf{\sigma }\sqrt{2\mathsf{\pi }}}\exp \left(-\frac{{\mathrm{i}}^2}{{2\mathsf{\sigma }}^2}\right)$$

(17)

Then, the differential Shannon entropy is

$$\mathrm{h}\left(\mathrm{I}\right)=-{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right){\log }_2\mathrm{f}\left(\mathrm{i}\right)\mathrm{di}$$

(18)

but

$${\log }_2\mathrm{f}\left(\mathrm{i}\right)=\mathrm{lnf}\left(\mathrm{i}\right)·{\log }_2\mathrm{e}$$

(19)

From (18) and (19), by way of substitution, the following can be written successively:

$$\mathrm{h}\left(\mathrm{I}\right)=-{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\ln \mathrm{f}\left(\mathrm{i}\right)·{\log }_2 \mathrm{e}\mathrm{di}$$

(20)

$$\mathrm{h}\left(\mathrm{I}\right)=-{\log }_2\mathrm{e}{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\ln \mathrm{f}\left(\mathrm{i}\right)\mathrm{di}$$

(21)

$$\mathrm{h}\left(\mathrm{I}\right)=-{\log }_2\mathrm{e}{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\left[-\frac{{\mathrm{i}}^2}{2{\mathsf{\sigma }}^2}+\ln \frac{1}{\mathsf{\sigma }\sqrt{2\mathsf{\pi }}}\right]\mathrm{di}$$

(22)

$$\mathrm{h}\left(\mathrm{I}\right)=-{\log }_2\mathrm{e}{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\left[-\frac{{\mathrm{i}}^2}{{2\mathsf{\sigma }}^2}-\ln \left(\mathsf{\sigma }\sqrt{2\mathsf{\pi }}\right)\right]\mathrm{di}$$

(23)

$$\mathrm{h}\left(\mathrm{I}\right)=\frac{{\log }_2\mathrm{e}}{{2\mathsf{\sigma }}^2}{{\displaystyle \int }}_{-\infty }^{+\infty }{\mathrm{i}}^2\mathrm{f}\left(\mathrm{i}\right){\mathrm{di}+\log }_2\left(\mathsf{\sigma }\sqrt{2\mathsf{\pi }}\right){{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\mathrm{di}$$

(24)

but:

$$\mathrm{E}\left[{\mathrm{I}}^2\right]{=\mathsf{\sigma }}^2={{\displaystyle \int }}_{-\infty }^{+\infty }{\mathrm{i}}^2\mathrm{f}\left(\mathrm{i}\right)\mathrm{di}\mathrm{and}{{\displaystyle \int }}_{-\infty }^{+\infty }\mathrm{f}\left(\mathrm{i}\right)\mathrm{di}=1$$

(25)

From (24) and (25), by way of substitution, the following can be written:

$$\mathrm{h}\left(\mathrm{I}\right)=\frac{1}{2}{\log }_2\left({2\mathsf{\pi }\mathrm{e}\mathsf{\sigma }}^2\right)$$

(26)

4. Empirical Results and Discussions

In the following, considering the elements described in the methodology, we forecast the values of the major stock indexes of the three capital markets: DAX—German Stock Exchange (U.E.), S&P 500—New York Stock Exchange (U.S.), and SHANGHAI Composite—SHANGHAI Stock Exchange (Asia). We will also measure the degree of uncertainty of the analyzed markets through Shannon entropy, using discrete and continuous distribution.

Based on the methodology, in our empirical approaches we consider the following:

• Log-returns are intraday.
• The analysis period and the forecast period are considered at the level of a stock exchange year (252 days).
• The period through which we characterize the conjuncture of a financial crisis is 2008, and the period through which we characterize the conjuncture of non-financial crisis is 2019.
• The forecasts are made for 2020, at 3, 6, 9, and 12 months.
• The data is taken from Thomson’s Reuters’ Eikon Refinitiv platform [65].

4.1. Probability of the Financial Crisis

In our study, we consider the probability of the financial crisis to be at least equal to the probability of the economic recession (given by Bloomberg in early January 2020 for the next 12 months, see Figure 2) for the following reasons: financial crises do not necessarily determine an installation of an economic recession, their causes being both of a financial nature and a psychological, behavioral nature. Thus, during periods of economic recession, consumption is affected, companies’ earnings are uncertain, inflation can rise, and erode the value of earnings, a state of panic and caution sets in, and investors usually seek to invest in “refuge” assets, and for these mentioned reasons, the period of economic recession also overlaps with a period of a market collapse, financial crisis.

What we cannot know exactly is whether the above recession probability is the measure of a recession comparable to the 2008 recession (the period that characterizes the financial crisis in our analyses). However, as recessionary probability models evolve, we will have a better measure of them. Thus, if we knew the probabilities of the occurrence of different types of recessions, then we would also know the probabilities corresponding to the different types of financial crises. It would be better to know the probabilities of financial crisis corresponding to different types of financial crises, but there may be such scientific concerns in the future given the importance of their knowledge in economic processes. In this context, the methodology proposed by us may better capture the future evolution of stock market indexes.

That being said, we consider that the probability of occurrence of the financial crisis on the US market (considered the mature market) is similar to the probability of occurrence on the other analyzed markets (German and Asian markets), because they are also considered mature markets. In addition, another way in which we can technically capture this aspect of similarity is by calculating the Granger causality through which we can highlight the existence of such a link. In this sense, we analyzed the time series during the financial crisis (2008) of these stock market indexes on account of the Granger causality presented in Appendix A,

Table A1. Granger causality tests, DAX, S&P 500, and SHANGHAI Composite.

Pairwise Granger Causality Tests
Date: 19 December 2020 Time: 12:00
Sample: 3 January 2008–30 December 2008
Lags: 1
Null Hypothesis:	Obs	F-Statistic	Prob.
lnReturnDAX does not Granger Cause lnReturnS_P500	218	0.35254	0.5533
lnReturnS_P500 does not Granger Cause lnReturnDAX		50.6279	2.E-11
lnReturnSHANGHAI_COMPOSITE does not Granger Cause lnReturnS_P500	218	1.38660	0.2403
lnReturnS_P500 does not Granger Cause lnREturnSHANGHAI_COMPOSITE		6.67552	0.0104
lnReturnSHANGHAI_COMPOSITE does not Granger Cause lnReturnDAX	218	1.42410	0.2340
lnReturnDAX does not Granger Cause lnReturnSHANGHAI_COMPOSITE		6.02846	0.0149
Pairwise Granger Causality Tests
Date: 12/19/20 Time: 12:03
Sample: 1/03/2008 12/30/2008
Lags: 2
Null Hypothesis:	Obs	F-Statistic	Prob.
lnReturnDAX does not Granger Cause lnReturnS_P500	203	0.24626	0.7820
lnReturnS_P500 does not Granger Cause lnReturnDAX		26.2816	8.E-11
lnReturnSHANGHAI_COMPOSITE does not Granger Cause lnReturnS_P500	203	2.06087	0.1301
lnReturnS_P500 does not Granger Cause lnReturnSHANGHAI_COMPOSITE		3.14937	0.0450
lnReturnSHANGHAI_COMPOSITE does not Granger Cause lnReturnDAX	203	1.73381	0.1793
lnReturnDAX does not Granger Cause lnReturnSHANGHAI_COMPOSITE		3.42624	0.0344

Source: Authors’ computation in EViews.

. If the obtained results confirm that a US financial crisis Granger-causes the other markets (German and Asian markets) to change, we can conclude that the appearance on the US market of a probability of financial crisis is found to affect the probability of crisis on other markets.

To not distort the analysis, only common daily trading prices in 2008 were used for the three indexes analyzed.

For the F-test result of the Granger causality not to be distorted, we must make sure that the analyzed series are stationary. In this sense, we applied the ADF test; the results obtained are presented in Appendix A,

Table A2. ADF tests, DAX, S&P 500, and SHANGHAI Composite.

Null Hypothesis: lnReturnDAX has a unit root
Exogenous: Constant
Lag Length: 0 (Automatic—based on SIC, maxlag = 14)
		t-Statistic	Prob. *
Augmented Dickey–Fuller test statistic		−15.91247	0.0000
Test critical values:	1% level	−3.460313
	5% level	−2.874617
	10% level	−2.573817
* MacKinnon (1996) one-sided p-values.
Null Hypothesis: lnReturnS_P500 has a unit root
Exogenous: Constant
Lag Length: 0 (Automatic—based on SIC, maxlag = 14)
		t-Statistic	Prob. *
Augmented Dickey–Fuller test statistic		−16.93707	0.0000
Test critical values:	1% level	−3.460313
	5% level	−2.874617
	10% level	−2.573817
* MacKinnon (1996) one-sided p-values.
Null Hypothesis: lnReturnSHANGHAI_COMPOSITE has a unit root
Exogenous: Constant
Lag Length: 0 (Automatic—based on SIC, maxlag = 14)
		t-Statistic	Prob. *
Augmented Dickey–Fuller test statistic		−16.50747	0.0000
Test critical values:	1% level	−3.460313
	5% level	−2.874617
	10% level	−2.573817

* MacKinnon (1996) one-sided p-values. Source: Authors’ computation in EViews.

.

The results of the ADF test confirm that the series are stationary, and the results obtained on Granger causality are not distorted.

According to Granger causality test, we obtained the following for lag 1:

• S&P 500 Granger-cause DAX (p-value = 0.00000000002; p-value < 0.05).
• S&P 500 Granger-cause SHANGHAI Composite (p-value = 0.0104; p-value < 0.05).
• The Granger causality test proves that the reciprocal is not valid, S&P 500 is not Granger caused either by DAX (p-value = 0.5533) or SHANGHAI Composite (p-value = 0.2403).
• According to Granger causality test, we obtained the following for lag 2:
• S&P 500 Granger-cause DAX (p-value = 0.00000000008; p-value < 0.05).
• S&P 500 Granger-cause SHANGHAI Composite (p-value = 0.0450; p-value < 0.05).
• The Granger causality test proves that the reciprocal is not valid, S&P 500 is not Granger-caused either by DAX (p-value = 0.7820) or SHANGHAI Composite (p-value = 0.1301).

As a result, the S&P 500 Granger-caused DAX and SHANGHAI Composite on both lag 1 and lag 2, but the reciprocal is not valid, which means that the probability of the financial crisis on the US market is transmitted to other mature markets (DAX and SHANGHAI Composite).

4.2. Forecasts on Scenarios (A and B) and Graphical Representation

Based on the GBM with Monte Carlo simulation, we estimated the tolerance intervals in which the values of the stock market indexes will be over 3 months, 6 months, 9 months, and 1 year, with tolerance levels of 95% and 75% from the date of analysis (30 or 31 of December 2019, depending on each index) on two Scenarios (A and B), see Appendix A

Table A3. Forecasted values for the index DAX, 2020.

Price on 30 December: 13,249.01
Index	DAX		Crisis	Non-Crisis
Stock exchange	German Stock Exchange	Drift coefficient	−0.4864	0.2278	covariance	−0.000006582
Country	Germany	Diffusion coefficient	0.3796	0.1400	correlation	−0.031204783
The range of values in which we find the price
Probability a	Scenario A b			Scenario B b		Time
95%	12,021.68	21,222.70		9.704.27	17,601.26	12 months
	11,978.67	19,418.23		10,144.20	16,952.26	9 months
	11,950.71	17,695.32		10,677.63	16,216.48	6 months
	12,113.21	15,933.58		11,416.86	15,305.12	3 months
75%	13,956.05	19,342.85		11,331.39	15,952.53	12 months
	13,537.88	17,933.13		11,566.25	15,532.33	9 months
	13,170.76	16,550.29		11,846.40	15,067.76	6 months
	12,911.39	15,159.02		12,219.03	14,478.48	3 months
Scenario	How many of the 10,000 Monte Carlo simulations will be below 13,249.01	The probability that the price will be above 13,249.01		Expected index value	Volatility index value	Time
A	621	93.8%		16,649.45	2342.08	12 months
	859	91.4%		15,735.50	1910.97	9 months
	1300	87%		14,860.52	1469.36	6 months
	2105	79%		14,035.21	977.22	3 months
B	4532	54.7%		13,641.96	2009.18	12 months
	4526	54.7%		13,549.29	1724.38	9 months
	4570	54.3%		13,457.08	1400.58	6 months
	4717	52.8%		13,348.75	2009.18	3 months

Source: Authors’ computation; ^a Tolerance levels; ^b Tolerance intervals.

,

Table A4. Forecasted values for the index S&P 500, 2020.

Price on 31 December: 3230.78
Index	S&P 500		Crisis	Non-Crisis
Stock exchange	New York Stock Exchange	Drift coefficient	−0.4732	0.2534	covariance	0.000013887
Country	United States	Diffusion coefficient	0.4115	0.1250	correlation	0.067985261
The range of values in which we find the price
Probability a	Scenario A b			Scenario B b		Time
95%	3145.29	5177.62		2417.58	4361.33	12 months
	3075.40	4729.59		2513.73	4185.36	9 months
	3030.33	4299.67		2637.96	3978.01	6 months
	3023.5	3859.89		2800.65	3734.98	3 months
75%	3564.06	4772.64		2833.38	3977.93	12 months
	3416.46	4403.81		2871.25	3854.75	9 months
	3291.04	4049.40		2920.64	3714.74	6 months
	3193.31	3694.34		2995.53	3547.84	3 months
Scenario	How many of the 10,000 Monte Carlo simulations will be below 3230.78	The probability that the price will be above 3230.78		Expected index value	Volatility index value	Time
A	255	97.5%		4168.35	525.46	12 months
	448	95.5%		3910.14	429.28	9 months
	846	91.5%		3670.22	329.72	6 months
	1632	83.7%		3443.83	217.73	3 months
B	3866	61.3%		3405.66	497.63	12 months
	4007	59.9%		3363.00	427.61	9 months
	4151	58.5%		3317.69	345.26	6 months
	4444	55.6%		3271.69	240.13	3 months

Source: Authors’ computation; ^a Tolerance levels; ^b Tolerance intervals.

and

Table A5. Forecasted values for the index SHANGHAI Composite, 2020.

Price on 31 December: 3050.124
Index	SHANGHAI Composite		Crisis	Non-crisis
Stock exchange	Shanghai Stock Exchange	Drift coefficient	−1.0344	0.1799	covariance	−0.000000426
Country	China	Diffusion coefficient	0.4500	0.1791	correlation	−0.001331561
The range of values in which we find the price
Probability a	Scenario A b			Scenario B b		Time
95%	2355.08	4976.39		1686.77	3529.50	12 months
	2415.69	4582.90		1877.33	3549.90	9 months
	2516.07	4166.91		2115.50	3524.89	6 months
	2636.12	3747.29		2415.56	3453.72	3 months
75%	2889.35	4398.88		2044.60	3141.72	12 months
	2853.48	4107.65		2208.28	3193.79	9 months
	2846.72	3824.79		2399.05	3225.73	6 months
	2859.72	3521.34		2626.71	3234.44	3 months
Scenario	How many of the 10,000 Monte Carlo simulations will be below 3050.124	The probability that the price will be above 3050.124		Expected index value	Volatility index value	Time
A	1821	81.8%		3649.39	664.26	12 months
	2133	78.7%		3493.29	549.64	9 months
	2573	74.3%		3344.09	429.81	6 months
	3188	68.1%		3194.21	290.08	3 months
B	8367	16.3%		2596.64	466.04	12 months
	7984	20.2%		2702.55	419.26	9 months
	7563	24.4%		2813.09	353.71	6 months
	6861	31.4%		2929.84	263.84	3 months

Source: Authors’ computation; ^a Tolerance levels; ^b Tolerance intervals.

.

Possible paths have been taken in two scenarios:

• Scenario A, in which the probability of a financial crisis is 0 per cent (GBM).
• Scenario B, in which the probability of a financial crisis is: 28 per cent (mGBM).

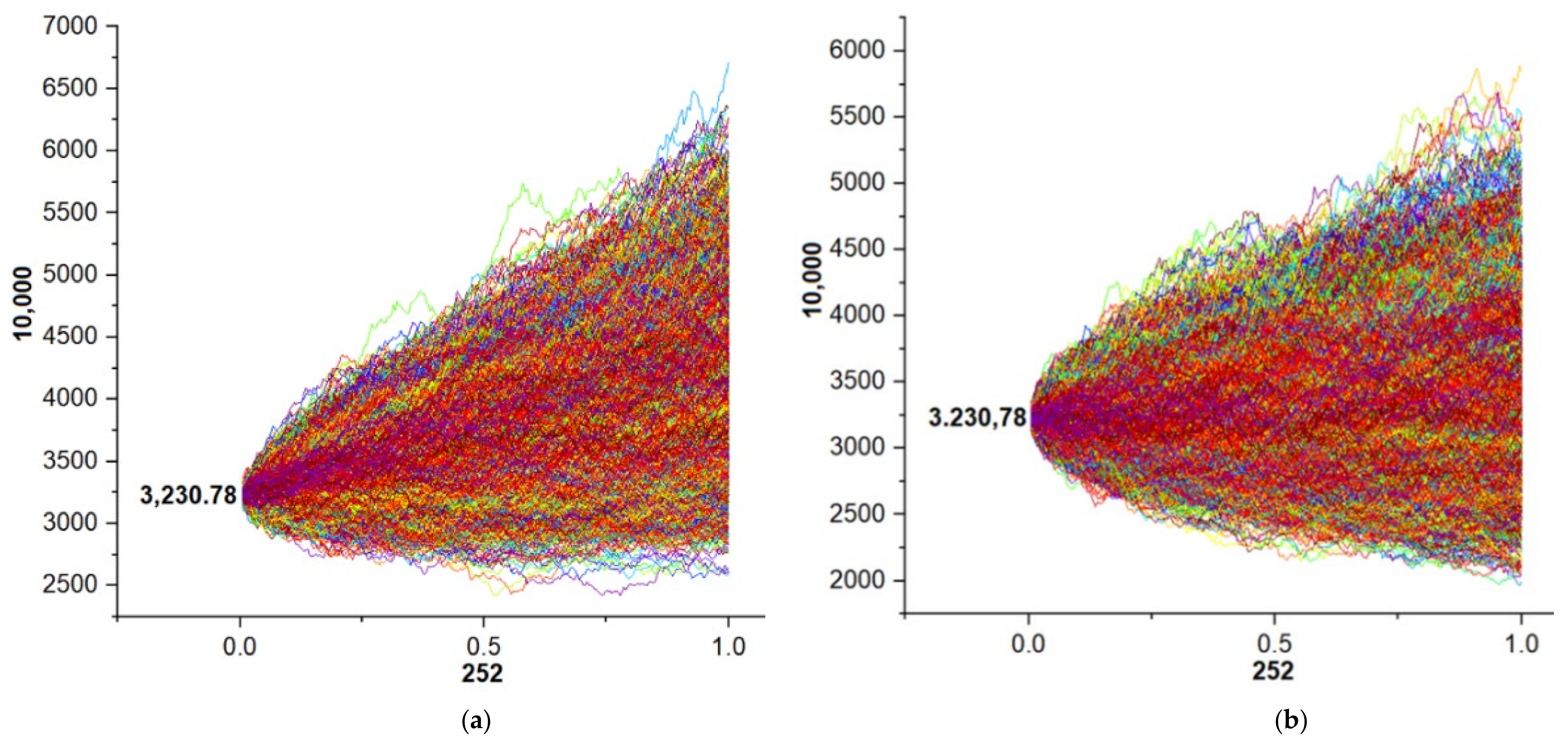
For each stock market index examined, 10,000 potential paths were taken for the next year. In other words, for each stock market index using GBM models with Monte Carlo simulation, 10,000 alternative simulations (see Brătian [66] for dataset) of the index were computed for each stock market day from the next year 2020 (see Appendix A, Figure A1, Figure A2 and Figure A3). In these figures there is a graphic representation of GBM models of 10,000 possible paths: (a) Scenario A; (b) Scenario B.

For simulations obtained by applying GBM and mGBM models at 3 months, 6 months, 9 months, and 12 months, we determined the probability that the values of the indexes will be higher than their corresponding values at the date of analysis (30 or 31 of December 2019, depending on each index) on the two scenarios mentioned above (see Appendix A, Table A3, Table A4 and Table A5).

4.3. Testing the GBM vs. mGBM Models

In the following we will proceed to test the results obtained from the application of GBM and mGBM models by the following methods presented below.

4.3.1. Using Tolerance Intervals with Different Tolerance Levels

The table below shows the situation with the real values of the three indexes analyzed (DAX, S&P 500, and SHANGHAI Composite) observed on these markets at 3, 6, 9, and 12 months, see

Table 1. Indexes values—3, 6, 9, and 12 months.

Index	Closing Date	3 Months a	6 Months b	9 Months c	12 Months d
DAX	30 December 2019	9815.97	12,260.57	12,870.87	13,790.29
S&P 500	31 December 2019	2470.50	3115.86	3363.00	3732.04
SHANGHAI Composite	31 December 2019	2815.37	3443.29	3336.36	3565.90

Source: Refinitiv Eikon, Thomson Reuters’ platform. ^a 63 days since the closing date. ^b 126 days since the closing date. ^c 189 days since the closing date. ^d 252 days since the closing date.

.

Analyzing the forecasted values in Table A3, Table A4 and Table A5 from Appendix A with the real ones observed in Table 1 for the DAX and S&P 500 stock indexes in 2020, we find the following:

• At 3 months, for tolerance level 95% and 75%, tolerance intervals on Scenarios A and B do not contain the real value, which means that the probability of the financial crisis is higher than 28%, but the tolerance interval values in Scenario B generated by mGBM are closer to the actual value compared to the tolerance interval values in Scenario A generated by GBM.
• At 6 months, for tolerance level 95%, the real values are contained in tolerance intervals for both Scenario A and Scenario B, but for tolerance level 75%, the real value is contained only by tolerance intervals from Scenario B generated by mGBM.
• At 9 and 12 months, for tolerance level 95%, the real values are contained in tolerance intervals for both Scenario A and Scenario B, but for tolerance level 75%, the real value is contained only by tolerance intervals from Scenario B generated by mGBM for DAX, and for S&P 500, the real values are contained in both Scenarios A and B for a tolerance level of 75%.
• At 3, 6, 9, and 12 months, the expected index values in Scenario B generated by mGBM are closer to the real values (the expected index value for S&P 500 at 9 months is identical to the real value at 9 months) than expected index values in Scenario A generated by GBM.

Analyzing the forecasted values in Table A3, Table A4 and Table A5 from Appendix A with the real ones observed in Table 1 for SHANGHAI Composite stock index in 2020, we find the following:

• At 3 months, for tolerance level 95%, the real values are contained in tolerance intervals for both Scenario A and Scenario B, but for tolerance level 75%, the real value is contained only by tolerance intervals from Scenario B generated by mGBM. At 3 months, the expected index value in Scenario B generated by mGBM is closer to the real value than the expected index value in Scenario A generated by GBM.
• At 6 months, for tolerance level 95%, the real values are contained in tolerance intervals for both Scenario A and Scenario B, but for tolerance level 75%, the real value is contained only by tolerance intervals from Scenario A generated by GBM.
• At 9 months, for tolerance level 95%, the real values are contained in tolerance intervals for both Scenario A and Scenario B,, but for tolerance level 75%, the real value is contained only by tolerance intervals from Scenario A generated by GBM.
• At 12 months, for both tolerance levels of 95% and 75%, the real values are contained only in Scenario A generated by GBM.
• At 6, 9, and 12 months, the expected index value in Scenario A generated by GBM is closer to real values than the expected index value in Scenario B generated by mGBM; at 3 months, the real value is closed to the expected index value which can be found in Scenario B generated by mGBM.

In conclusion, the real values of the DAX and S&P 500 stock indexes are confirmed at 3, 6, 9, and 12 months on Scenario B generated by mGBM, and for SHANGHAI Composite, the real values are confirmed at 3 months on Scenario B generated by mGBM, and at 6, 9, and 12 months the real values are confirmed on Scenario A generated by GBM.

4.3.2. Probability That the Forecasted Value of the Stock Market Indexes Will Be Higher Than the Value from the Analysis Date (30 or 31 of December 2019)

In

Table 2. Indexes closing dates and prices.

Index	Closing Date	Closing Price
DAX	30 December 2019	13,249.01
S&P 500	31 December 2019	3230.78
SHANGHAI Composite	31 December 2019	3050.124

Source: Refinitiv Eikon, Thomson Reuters’ platform.

below, we present the closing prices at the date of the analysis. From the forecasted results in Table A3, Table A4 and Table A5 from Appendix A, it can be seen the probability that these prices will be higher at 3, 6, 9, and 12 months, based on the simulations performed on the two Scenarios A and B.

What we can observe is that for Scenario A generated by GBM, the probability that the index values will be higher than the closing price is much higher compared to Scenario B generated by mGBM. As a result, the mGBM model better captures the real situation (see Table 1) recorded for DAX and S&P 500 given the real results of these indexes at 3, 6, 9, and 12 months, but it is not capturing the real situation for SHANGHAI Composite for which the real situation is better captured by the GBM model, except for the values at 3 months.

4.3.3. Robustness Testing

To test the robustness of the GBM model compared to the robustness of the mGBM model we used mean average percentage error (MAPE).

MAPE is calculated according to Equation (27), and its values can be interpreted according to

Table 3. MAPE values and interpretation.

MAPE Value	Interpretation
<0.1	Highly accurate forecasting
0.1–0.2	Good forecasting
0.2–0.5	Reasonable forecasting
>0.5	Inaccurate forecasting

Source: [67].

.

$$\mathrm{MAPE}=\frac{1}{\mathrm{n}}{\displaystyle \sum }_{\mathrm{t}=1}^{\mathrm{n}}\left|\frac{\mathrm{At}-\mathrm{St}}{\mathrm{At}}\right|$$

(27)

MAPE was used in the following two forms:

• The smallest MAPE for Scenario A, respectively, the smallest MAPE for Scenario B [67]. In this sense, from the 10,000 simulations, the simulation with the smallest MAPE on each scenario, at 12 months, is chosen (see

  Table 4. MAPE values for DAX, S&P 500, and SHANGHAI Composite.

  Index	Time	Smallest MAPE		Average of MAPE
  		Scenario A	Scenario B	Scenario A	Scenario B
  DAX	12 months	0.05699	0.04537	0.22664	0.14429
  S&P 500	12 months	0.03542	0.03801	0.16336	0.11639
  SHANGHAI Composite	12 months	0.02680	0.02599	0.12036	0.14260

  Source: Authors’ computation.

  ).
• The average of MAPE for scenario A, respectively the average of MAPE for Scenario B. In this sense, the average of MAPE is calculated for the 10,000 simulations, on each scenario, at 12 months (see Table 4).

At = actual value; St = simulated value.

Based on the results obtained after testing, we can conclude the following:

• For the smallest MAPE it is observed that the forecasts are highly accurate for both GBM and mGBM model, but better values are found for mGBM. This fact can also be noticed from the graphic representation (see Figure 3, Figure 4 and Figure 5).
• The average of MAPE shows a good forecast for both the GBM and mGBM models, but better values for mGBM, except for the DAX index for which only mGBM is a good forecast.

4.3.4. Measuring the Degree of Market Uncertainty through Shannon Entropy

Regarding the uncertainty of the markets, calculated using the discrete Shannon entropy and the Shannon differential entropy and whose results are found in

Table 5. Shannon entropy on analyzed indexes.

Index	Discreet Entropy		Differential Entropy
	Crisis Period (2008)	Non-Crisis Period (2019)	Crisis Period (2008)	Non-Crisis Period (2019)
DAX	7.977279923	7.977279923	11.860790049	11.457051386
S&P 500	7.961406908	7.969343416	9.626546525	9.282319764
SHANGHAI Composite	7.977279923	7.977279923	12.099958213	9.460556827

Source: Authors’ computation.

, we can make the following remarks:

• Using a discrete distribution for the periods considered during the financial crisis and the non-financial crisis, the degree of uncertainty of the markets examined is the same with minor variations. This means that, regardless of the economic situation (crisis or non-crisis), the uncertainty in the markets is roughly the same.
• Using continuous distribution for periods considered to be a financial crisis and a non-financial crisis, it is found that the degree of uncertainty in the markets examined varies significantly from the situation discussed above. We note that, in the situation of the financial crisis, the degree of uncertainty in the markets examined is significantly higher than in the situation of the non-financial crisis.

We find a high level of entropy in the analyzed markets both in the crisis period and in the period of non-financial crisis, and, given the fact that there is a direct link between market efficiency and their entropy (high entropy—high efficiency; low entropy—low efficiency), it can be deduced that the analyzed markets are information-efficient, and in this case, the use of GBM for forecasting is justified, as the prices have a random evolution (random walk). In the case of the DAX—German Stock Exchange (U.E.) and S&P 500—New York Stock Exchange (U.S.) stock indices, discreet and differential entropy do not differ in the crisis and non-crisis scenarios; there are insignificant differences in the case of SHANGHAI Composite—Shanghai Stock Exchange (Asia).

5. Conclusions

The GBM proved to be a suitable model for making forecasts of stock market index values, as it describes their future evolution quite well. However, the model proposed by us (mGBM), in which drift and diffusion are determined by considering two states of the economic situation weighted with their probabilities of occurrence, brings some contributions through which some subtle nuances that better describe the future evolution of stock indexes (confirms for two indexes out of three analyzed—DAX, S&P 500, and for SHANGHAI Composite partially confirms at 3 months) are captured. Thus, in general, on account of the analyzed stock market indexes, the model proposed by us better describes the future trajectories of these indexes. We consider these aspects important, because, based on such a model, investors have the possibility of a better understanding of the forecasting process when the probability of a financial crisis appears on the markets.

However, what cannot be very well captured are the temporary shocks on the capital markets, as shown in this case by the shock generated by the COVID-19 pandemic in March, as seen in Figure 3, Figure 4 and Figure 5.

The forecasts for 2020 are supported by the fact that the actual data for this year are compared with the forecast data, and, consequently, the results can be considered verisimilar.

The limitations of this study come from the fact that, in this paper, we model the behavior of random variables, but the factors that generate their effects are unknown. Through quantitative finance, we do not research the structural reasons for the price evolution of a financial security, but instead we use the stochastic calculation to obtain its corresponding value. The analysis of the causes that can justify these results is the topic of behavioral finance, which can analyze the behavior of investors and describe the state of the economy at various times. Another limitation comes from the fact that the results of the analysis are presented on only three stock indices (DAX, S&P 500, and SHANGHAI Composite) associated with large economies, and the results could be different in emerging markets. This aspect will be the subject of future research that will contain analysis of several stock indices from different markets, both mature and emerging.