Prospective Primary Teachers’ Didactic-Mathematical Knowledge in a Service-Learning Project for Inclusion

Abstract

An analysis of the didactic-mathematical knowledge put into play by a sample of 30 prospective primary teachers during their participation in a Service-Learning program focused on mathematical stimulation as a measure of attention to adolescents at risk of social exclusion is presented. The program aimed to respond to current training demands by promoting the development of mathematics-specific professional competencies, as well as social skills to interact with students, and to positively influence the prospective teachers’ affection towards mathematics and its teaching. It was developed during three academic years in two phases: the learning module was oriented to the presentation of the mathematical stimulus program and the didactical analysis of the STEAM activities knocking it into shape; in the service module, the participants implemented the activities in an educational center with students at risk of social exclusion. The analysis was carried out from the video recordings of the sessions, the future teachers’ written reports with the analysis of the activities, questionnaires on the didactic-mathematical knowledge and a satisfaction test. The results show difficulties on the part of the future teachers to analyze some of the activities of the program, which seems to have its origin in their poor command of the common knowledge of the mathematical content, which also limits them when it comes to managing the activities in the way expected for the stimulus program. All in all, participation in the program was positively assessed by them in relation to its usefulness for their training. The potential benefit of Service-Learning programs such as the one addressed here in the face of a positive impact on the affections towards mathematics is concluded, as a necessary step for a more effective acquisition of didactic-mathematical knowledge and skills in the initial training.

1. Introduction

In recent years, universities have internalized that they must face the commitment to project greater social enrichment; they have become aware that the training they offer must be more linked to their community, favoring the transformation and improvement of reality [1]. In promoting what is supposed to be a comprehensive teacher, emphasis is placed on all aspects of teacher development, including attitudes, knowledge, and practice [2], in search of professional skills development that favor educational work conditioned to personal responsibility and the development of awareness and respect for differences and different educational needs [3,4]. Faced with this commitment, the Service Learning (SL) training option, which combines learning processes and community service in a single project where all participants learn and work on real needs [5], has been gaining prominence. The transformative cycles that are assumed for the SL focused on processes at university involve the review of already given knowledge and call on students to create critical knowledge and make decisions about their own practice, promoting both theoretical learning and professional skills, and their agency in the processes of social transformation [6].

The service processes of the SL project to which we will direct attention in this work are part of a research aimed at caring for adolescents at risk of social exclusion [7], a group whose school failure can be manifested or accentuated as a consequence of their personal conditions of a lack of protection and vulnerability. These risk situations have a contextual component (family and environment) and another personal component (demotivation, low self-confidence) that must be considered in any professional intervention. Normally, the support that this type of student receives, whether in the reference classroom or outside of it, focuses on reinforcing content through curricular adaptations supervised by specialist support teachers in therapeutic pedagogy. This task therefore falls most of the time to teachers who are not specialized in mathematics [8], and in many cases, it does not produce the desired result. This suggests the need to test new formulas such as that of [7], which aims to encourage stimulation through motivating activities to approach a more positive attitude towards the subject, and this leads to an improvement in academic performance [9]. The question is not so much that all students can be successful (or not) in mathematics but that the adults responsible for organizing learning opportunities are capable of redirecting attitudes and practices to promote success regardless of gender, social class, ethnic group, or any other predictor of low performance [10].

On the other hand, although there have not been many contrasted experiences until now, the application of SL projects has revealed positive results in the development of mathematical affects. In [11], it was observed that, after participating in a SL project, high school students saw mathematics as more useful, as a worthwhile science. This is a key aspect to consider in order to improve initial teacher training, if we take into account that maths anxiety is one of the phenomena that affects teachers in training [12,13,14,15,16]. It has also been shown that teachers in training not only show anxiety towards mathematics but also anxiety towards teaching mathematics [17,18,19], and that the evolution of affects towards mathematics –attitudes, beliefs, and emotions according to the classification of [20,21]—during initial training in undergraduate studies can even be negative [15].

It seems necessary, therefore, to introduce actions in training programs aimed at strengthening affects towards mathematics, with an emphasis on the gender perspective [22], given most female students in teaching degrees and their apparent greater permeability to prejudices and beliefs [23]. This is not an easy task, given the strength of attitudes towards mathematics to remain stable in the face of change [15,24], but some research has been able to establish a positive correlation between the improvement of beliefs about the nature of mathematics and changes towards more positive attitudes after completing training courses in which creative and diverse learning strategies have been used [15]. These types of actions are presented as useful in improving the affects of girls towards mathematics, particularly if the tasks to be carried out are collaborative, applied to real problems, with the presence of metacognitive elements and in which positive female referents are shown [25]. In a reciprocal sense, the results of [26] suggest the potential role of pedagogical content knowledge in improving teachers’ mathematical beliefs and attitudes.

Taking into account the previous paragraphs, the objectives are described as mobilizing the prospective teachers in order to:

(i)

Develop mathematics-specific professional competencies through the design, analysis, and implementation of inclusive mathematical practices in real contexts;

(ii)

Promote ethical commitment to the teaching profession and develop social skills to interact with students at risk of social exclusion;

(iii)

Positively influence affection towards mathematics and its teaching.

The first two objectives claim the action of the prospective teachers. The third one is different, so the prospective teachers are not influencing themselves.

2. Teacher’s Didactic-Mathematical Knowledge

For the development of this work, we have considered the Didactic-Mathematical Knowledge Model (DMK) of Godino and collaborators [27,28,29,30,31,32,33,34]. The mentioned model, since the Didactics of Mathematics is considered the discipline that systematically articulates the different aspects involved in the teaching and learning processes of mathematics, provides a set of categories and subcategories of knowledge that the teacher must know how to apply and value [29]. In [29,31] three global categories of DMK are proposed: common content knowledge, extended content knowledge, and specialized knowledge.

Common knowledge refers to the knowledge that the teacher must put into practice to solve problematic situations in relation to a specific mathematical topic, not necessarily linked to teaching. Extended knowledge is the knowledge that the teacher needs to identify possible generalizations of the task and connections with other more advanced topics when posing a certain problem situation to their students. Specialized knowledge is the knowledge that a teacher must handle, and it is directly linked to their profession, differentiating them from another person who is not a teacher, even if they have knowledge of mathematics. At the same time, this specialized knowledge is subdivided into four categories [28]: specialized content knowledge, content knowledge in relation to students, content knowledge in relation to teaching, and content knowledge in relation to the curriculum.

Specialized content knowledge involves the identification, by the teacher, of the content involved in a given problem situation. Content knowledge in relation to students refers to the teacher’s ability to develop strategies that help students solve problems, describe, and resolve students learning conflicts, and generally, be able to describe the types of cognitive configurations that students present when solving a problem situation. Content knowledge in relation to teaching implies reflection by teachers on the teaching and learning processes, considering, for example, how the teacher interacts with students, or students with each other, to what extent cognitive progress is produced by students, how the different materials are used. Finally, content knowledge in relation to the curriculum requires that the teacher contemplates the adequacy of the content implemented with the curriculum, the timing, and everything that has to do with the context in which the teaching-learning process occurs. Figure 1 schematically shows the facets considered by the DMK from which these types of knowledge are addressed.

This way, the DMK model interprets the teacher’s knowledge from three dimensions: mathematical, didactical, and meta didactic-mathematical. We will focus here on the first two. The mathematical dimension of knowledge includes two subcategories of knowledge: common content knowledge and extended content knowledge. It refers to the knowledge allowing the teacher to solve a problem or mathematical activity and link it with mathematical objects that can later be found in the school mathematics curriculum. As all models of teacher knowledge point out [29], more than mathematical knowledge is needed, for instance, the knowledge of some features that affects the class planning and management of a specific subject. The didactical dimension so includes the specialized knowledge that requires the teacher to control those factors intervening in the planning and implementation of the teaching of mathematical content, which the DMK model analyzes by the six subcategories or facets showed in Figure 1. As [29] emphasizes, this didactical dimension, associated to specialized knowledge, needs the mathematical knowledge; without it, the teacher would not be able to recognize the knowledge involved in a task and establish different procedures to carry it out (specialized content knowledge), or detect and anticipate possible misconceptions, conflicts, or errors, as well as manage students’ emotions when solving a problem (content knowledge about students). Moreover, the mathematical dimension is essential to plan, evaluate, and reflect on the didactical sequences in the teaching and learning process, including the relevance and potential of different materials and technological resources (content knowledge in relation to teaching) or adapt the contents to a certain educational level or establish intra or interdisciplinary connections (content knowledge in relation to the curriculum).

Based on the above, [28,29] present a series of guidelines and criteria for the creation of items that allow each of the DMK categories to be evaluated and analyzed.

Table 1. Indicators of the DMK categories.

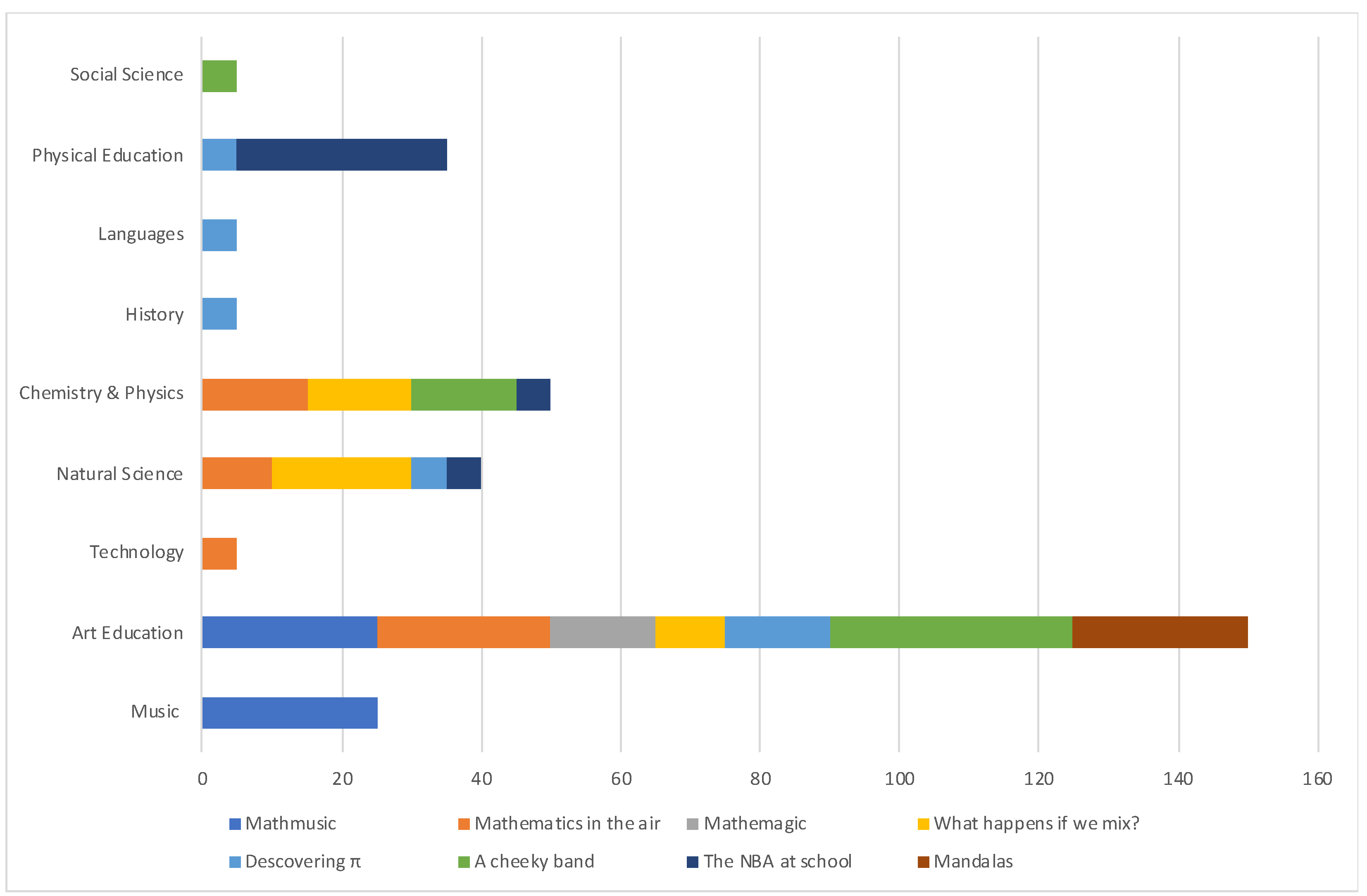
DM Knowledge		Indicators
Common (CK)		CKI1. Carrying out the activity.
Extended (EK)		EKI1. Making connections with other blocks.
		EKI2. Making connections with other subjects.
		EKI3. Considering generalization of the activity.
		EKI4. Making connections with other more advanced topics.
Specialized (SK)	Content (SKCn)	SKI1. Setting the mathematical concepts that can be worked on.
		SKI2. Adapting to the educational level.
	Students (SKSt)	SKI3. Being able to set the types of cognitive configurations that students have developed when solving the task.
		SKI4. Describing difficulties, errors, conflicts that the students could have.
		SKI5. Formulating questions that allow to explain the personal meanings of the students when solving this type of tasks.
		SKI6. Evaluating the learning.
		SKI7. (Attitudes, emotions, beliefs, values) Describing strategies that can be implemented to encourage students to get involved in solving the tasks (or studying the topic). Considering the emotional state of your students at the time of solving the task. Promoting self-concept, self-esteem.
	Teaching (SKTc)	SKI8. Describing, applying, and reflecting on the didactical configuration that is has been implemented using the given mathematical task.
		SKI9. Describing other tasks related to the given one and how to manage the didactical trajectory.
	Curriculum (SKCr)	SKI10. Reflecting/justifying/adapting the activity to different educational levels.

summarizes this analytical tool globally.

In [35], a model to consider the affective domain from the onto-semiotic approach (OSA) to research in mathematics education is advanced. The components of the affective domain (emotions, attitudes, beliefs, and values) and their relations with the DMK facets and components are discussed, and the criteria for assessing the affective suitability in a process of teaching and learning of mathematics are updated. Among others, the notion of affective situation is addressed. When a student faces a problem situation, an affective situation is juxtaposed to the cognitive one, including the purely personal meanings, in the form of emotions, attitudes, beliefs, or values. An emotion of mental blockage towards a type of problem situation, a persevering attitude that facilitates the implementation of problem-solving heuristics, or a specific belief about the nature of the mathematical objects involved would be examples of how the affective components are manifested. Moreover, teaching and learning ecosystems provide constant reference points, such as situations of production, communication or, simply, of individual mathematical study, for the affective domain. Thus, to analyze the affective domain, specific situations in which the students’ affects are brought into play may be posed, and collecting data instruments, as observation record or classroom diary, can help to reflect later [35].

3. Materials and Methods

The project to be analyzed was developed over three academic years, between 2017 and 2021 (with the interruption in the 2019–2020 academic year due to COVID-19) with a sample of 30 pre-service primary teachers at the University of Santiago de Compostela (USC). As it has been said, it is framed within SL methodology [5,6], combining in this case learning processes of didactic-mathematical knowledge with service to a certain sector of the community (students at risk of social exclusion) through the implementation of a socio-educational program. It was intended to contribute to the development of degree-specific professional skills through the analysis, implementation, and reflection of educational practices focused on mathematics and oriented towards students with special educational needs from a multidisciplinary perspective consistent with their training as a generalist teacher [2,3,4]. This can be considered as an affective situation according to [35].

Next, the corresponding Service and Learning modules will be described. In each one, the indicators considered will be related to the categories of the teacher’s DMK [28] that will guide the data analysis, introduced in Section 2 (see Table 1).

3.1. Service Module: Mathematical Stimulus Program for Students at Risk of Social Exclusion

The service module was integrated into the Mathematical Bits (translation of Anaquiños Matemáticos, its original name in Galician language) socio-educational program [7]. This is a mathematical stimulus program implemented in three public secondary schools in the autonomous community of Galicia, outside of school hours. The program is specified in a set of inclusive practices to promote mathematical stimulation with students in the first year of Spanish compulsory secondary education (CSE) who are at risk of social exclusion. It tries to complement, on an emotional level, the support that this type of student receives, usually based on the reinforcement of curricular content. It aims, by way of encouragement, to respond to the demotivation and lack of interest in mathematics that, in general, is shown by students who have some type of educational need due to adverse personal circumstances.

A total of 68 high school adolescents aged between 12 and 15 years participated in Mathematical Bits during three editions. The program was developed in fortnightly sessions after school hours between the months of November and May. In the design of the activities, the recommendations of [36,37,38] have been followed, presenting experiments that provide students with the opportunity to question, investigate, and discover in the context of a globalized approach and collaborative work. In each activity, mathematical content has been worked on in an interdisciplinary way following the STEAM methodology [39]. Most of this mathematical content comes from the school curriculum but presented in real and innovative contexts that seek the active participation of students. The indications of the guidance staff and the characteristics of these students (lack of attention, disruptive behavior) lead to one hour as the recommended duration for each activity.

With the idea of reinforcing this motivating and integrating character, the activities combined manipulative resources (drawing instruments; odometers, meters, scales; geoboards, bascules; laboratory material) and technological resources (robots, tablet apps, dynamic geometry software, 3D printers) and the workspaces were varied (chemistry laboratory, music room, sports pavilion, classroom, corridor, outdoor patio). The intervention process, based on promoting interaction through verbal communication with students [40], was carried out by two researchers, a pre-service primary teacher, and with the participation of a teacher of the orientation staff and a mathematics department teacher of each center. These last two act as external evaluators.

Table 2. Sessions of the Mathematical Bits program and disciplines that are worked on in each of the sessions.

Name of Activity	STEAM Subjects	Mathematical Content
Mathemagic (A1)	Maths and Art	Elementary operations, numbering systems, and mental calculus.
A cheeky band (A2)	Maths and Physics	Cylinder, torus, sphere, face, edge, single-sided surfaces, inner face, outer face, and surfaces with holes.
Mathmusic (A3)	Maths and Art	Bayes’ theorem, probability, random, fractions, equivalences, and units of time measurement.
The combinatorics of Carnaval (A4)	Maths and Social Sciences	Problem solving and combinatorics.
What happens if we mix? (A5)	Maths and Chemistry	Estimation of quantities, control of variables, bar and sector graphs, percentages, and handling of measuring instruments.
Mathematics in the air (A6)	Maths and Physics	Units of the International System of Measurement, graphs, and measures of central tendency.
Discovering π (A7)	Maths and Natural Sciences	Units of the International System of Measurement, arithmetic mean, length and diameter of the circle and the number π.
A world of quadrilaterals (A8)	Maths, Art, and Technology	Recognition, classification and construction of quadrilaterals, concave, convex and convex conjecture, non-conventional units of measurement and handling of the physical and virtual geoboard.
Polyhedrons (A9)	Maths and Technology	Three-dimensional figures, classification of polyhedron, regular polyhedron, concavity, and convexity.
Mandalas (A10)	Maths and Art	Perpendicular line, perpendicular bisector, polygonal and non-polygonal figures, inscribed and circumscribed figures, symmetry, rotation, and translation.
The NBA at school (A11)	Maths and Physical education	Percentages, mean, mode and median.
Reading paintings (A12)	Maths and Art	Cartesian coordinates, estimation, and geometric figures.
Dynamic geometry (A13)	Maths and Technology	Euler’s line. Construction of figures of equal area and different perimeter.
Mental agility with Kahoot (A14)	Maths and Technology	Arithmetic operations.

shows the activities with the STEAM subjects and the mathematical content involved in each of them.

The description of each activity is collected, along with a short illustrative video, at http://gidem-tesela.es/anaquinos/ (accessed on 26 January 2022). Some of them are presented in greater detail in [41,42,43,44].

The proposed interdisciplinary activities try to relate mathematics with at least one of the other curricular areas that make up STEAM. In activity A5, the concept of chemical reaction, dissolution, as well as the use of laboratory material and its terminology, are worked on. The relationship between mathematics and music becomes visible in the A3 activity, with the introduction of musical notes, the construction of a melody and rhythm, involving the measurement of time to build a musical piece. Mathematics and art connect the A12 activity through the creation of color compositions, aesthetics, and the game with different geometric figures to give an artistic sense to the construction of a mandala. Technology is present in activities such as A13, where the dynamic geometry software Geogebra is used to study the relationship between perimeter and area of plane figures. This discipline is also included in practice A14 since it consists of the use of electronic devices (mobile phones, tablets, or computers) to be able to solve arithmetic operations with the Kahoot application. The interdisciplinarity with other disciplines such as Physical Education is manifested in practice A11, in which sport is treated as the content, simulating a basketball game in which data are extracted to carry out a statistical analysis.

On the other hand, we must note that, although the service was not aimed at primary education, the proximity of the first level to the last years of primary school, the academic profile of the students to whom it was addressed, the mathematical contents that it included (which could be covered in primary) and, above all, the inclusive and interdisciplinary approach of the program suggested its potential interest for the participation of prospective teachers.

3.2. Learning Module

The learning part is linked to the subjects of the didactic-disciplinary mathematics module that are taught in the Degree in Primary Education Teacher at USC. Through a volunteer program organized in collaboration with the USC integration service (https://www.usc.gal/en/servizos/sepiu/index.html, accessed on 26 January 2022), a course on inclusive mathematics was organized from which the participants, 30 pre-service primary teachers, were offered the possibility of collaborating as teachers in the Mathematical Bits social integration program.

The Learning module was structured in three phases. In Phase I, implemented during the course, the Mathematical Bits program and the characteristics of STEAM activities were presented to the participants. The future teachers experienced in a group the activities A1, A2, A3, A5, A6, A7, A10, and A11 (Table 2) of the program, which corresponds to the common knowledge of the content (CK). Afterwards, they independently completed, for each activity, a didactical-mathematical analysis questionnaire. In addition to this questionnaire, the future teachers completed a satisfaction questionnaire for each activity.

Phase II of the Learning module connects directly with the Service module, in which 10 of the 30 prospective teachers who had taken the course participated. It corresponds to the moment of intervention of the future teachers in the Mathematical Bits program that takes place in the educational centers, with the supervision of the teachers and researchers involved in the project.

Phase III of the Learning module integrated the reflection part of the intervention carried out by the future teachers (those who had participated in the service module) with the design of a STEAM activity adapted to the students of the socio-educational program. After implementing each activity of the Mathematical Bits program, the future teachers had to record their development in order to carry out a retrospective analysis (SKTc) and contrast the difficulties perceived in the session with what the literature collects and those they had intuited in the pre-analysis (SKSt). To facilitate the realization of this critical reflection, they had the video-recordings of the sessions and the satisfaction questionnaires that the Mathematical Bits students completed at the end of each one of them. This phase was completed with the design by the teachers of a STEAM activity aimed at students at risk of exclusion that involved at least two other disciplines, in addition to mathematics. They were asked to collect: a suggestive title, subjects involved, the age of the students, objective, contents involved, materials, duration, and a description of the methodological sequence (SKTc).

3.3. Data Collection and Analysis Instruments

The data-collection instruments used were didactic-mathematical questionnaires and the satisfaction questionnaires that the future teachers had to fill out for each of the activities experienced, in Phase I of the Learning module, and a critical record of each Mathematical Bits session, along with their STEAM activity proposal, in Phase III. This information was supplemented with the researchers’ field notebook with the notes of the future teachers’ interventions and the video-recordings of the sessions, both analysis during the Service module and intervention in the Learning module. In addition, at the end of the SL project, the future teachers completed a questionnaire of global satisfaction of their participation in the program.

As for the data-collection instruments employed in Phase I of the Learning module, the didactic-mathematical analysis questionnaires consist of the following six questions that explicitly include some of the indicators of specialized knowledge (SK) and extended knowledge (EK) of the content [28]: (1) identification and description of the mathematical concepts that allow the activity to be addressed (SKI1), (2) objective(s) of the activity (SKCn), (3) relationship with other subjects (EKI2), (4) level of adaptation of the activity to primary education (SKI9) and secondary education, (5) possible generalizations (EKI3); and (6) difficulties that the students could find (SKI4).

At the end of each Phase I task, the future teachers completed a satisfaction questionnaire in which they assessed questions related to the organization of the activities presented to them and the level of difficulty of the activity that the students participating in the Mathematical Bits program may encounter. Moreover, the opinion of prospective teachers was collected on the way in which the contents of the different curricular areas were presented, so that they could assess whether it was carried out in a novel way. Finally, a question was introduced regarding the usefulness of the activity within their training as future teachers.

The analytical tools used were the indicators for each of the three categories of the teacher’s didactical knowledge from [28] that were already introduced in Section 2 and that are collected in Table 1.

4. Results and Discussion

To answer to our objective of evaluating the didactic-mathematical knowledge that future teachers put into practice in the two modules of the SL project, this section presents the results based on the three categories of Didactic-Mathematical knowledge of [29]: common, specialized, and extended.

4.1. Common Knowledge

Common knowledge is put into play in Phase I of the Learning module, when future teachers experience STEAM activities. The methodology that was applied to formulate the activities for future teachers was the same that would be followed in the socio-educational program of the Service module: guided teaching by the introduction of activities by probing questions or by the proposal of games, the work group, and sharing of results. For example, in activity A5 (What happens if we mix?), they are asked if they know how to inflate a balloon without air or a magic trick is performed, and they are invited to discover the trick as in activity A1 (Mathemagic). Thus, to be successful in the activities, it is essential to promote a relaxed environment that favors dialogue between equals, respectful of all responses and generating emotions.

In general, all the groups solved the proposed activities (CKI1). However, they found it difficult to remember some mathematical concepts and procedures that would lead them to the solution. For example, in terms of concepts, in activity A10, they only interpreted a regular polygon as the one with equal sides and did not establish what rigid movements lead them to the final composition. In activity A7 (Discovering π), although they come to recognize a constant as the number π, a poor understanding of this number as a constant of proportionality between the length and the diameter (radius) of any circumference is evident. In activities A6 (Mathematics in the air) and A11 (the NBA at school), only three of the 30 future teachers explored the mode and median, concepts that were required to interpret the results obtained by each group (measures of the distances obtained when throwing the paper airplanes and shots made, respectively). Regarding procedures, in activity A10 (Mandalas), they showed difficulties in constructing both the perpendicular bisector of a segment, as well as the bisector of an angle; in activity A6 and A7, they chose the appropriate measuring instrument and perform the measurement with a minimum of precision (place the measuring tape properly between the ends that delimit the distance to be measured, for example, which shows little familiarity with this type of activity). Difficulties were also observed in collecting and representing the data obtained in activities A5, A6, and A11. In activities A1 and A5, they also needed help to find a resolution strategy.

The results obtained show important deficiencies in the common content knowledge, in accordance with what was pointed out in [45]. This is in contrast to the results of [46], where future teachers state that they have sufficient knowledge to carry out their work as mathematics teachers. In fact, in [46], it is already pointed out that future teachers show low self-confidence as mathematics teachers. This could be explained by the doubts they show in relation to their mastery of didactic-mathematical knowledge. In addition, it was observed in carrying out the first activities that future teachers are not used to following this type of methodology, responding in some cases with great insecurity and with awkward silences when probing questions are asked. This supports the results of the study by [46] in that more than half of future teachers do not feel comfortable teaching mathematical topics.

4.2. Extended Knowledge

The extended knowledge appears in Phase I of the Learning module, specifically in the third question (relationship that the activity can have with other subjects) and the fifth (adequacy of the activity to secondary education and possible generalizations) of the analysis questionnaire. Figure 2 illustrates the responses to the first. They were not explicitly asked to justify the connections considered, which would have helped to understand some that are not a priori obvious. For example, in A2 (A cheeky band), 100% of the future teachers marked Plastic and Visual Education, 43% Physical, and 14% Social Sciences.

In the design and choice of most of the activities of the program, mathematical contents from different areas were considered, for example, in activity A7 (Discovering π) statistics and geometry were worked on; in activity A8 (A world of quadrilaterals) geometry, measurement and algebra- future teachers were not asked about intradisciplinary connections. This new issue will have to be considered in future studies since it would have contributed more information to the analysis of specialized content knowledge by revealing all the content involved in each activity and not just the most explicit.

Regarding the fifth question, where future teachers were required to adapt the activity if they did not consider it appropriate for an educational level, the results show that all of them consider that they are appropriate for primary education, although none of them detail the course and they do not propose any adaptation for upper education levels (secondary). This silence can be justified through the study carried out by [16] which concluded that 84.51% of future teachers feel uncomfortable when interacting with the subject and in general are not in favor of expanding their mathematical knowledge, which leaves us with a shadow towards negative attitudes.

4.3. Specialized Knowledge

Specialized knowledge is involved in all phases of the Learning module and in the Service module. Questions one, two, four, and six of the analysis questionnaire connect with a type of specialized content knowledge, as indicated in Section 3. It will be detailed with respect to its four subcategories: content, students, teaching, and curriculum.

4.3.1. Specialized Content Knowledge

The first question on the analysis questionnaire (mathematical concepts involved in the activity) refers to the specialized knowledge of the content. Regarding its mathematical aspect, in the activities of the Mathematical Bits program, elementary contents of the different blocks of the mathematical curriculum are mobilized (see Table 2): calculation (counting, basic operations, estimation, mental calculation, use of the calculator), geometry (plane figures, angles, polygons, perimeter and area, symmetries, circumference, phenomenology of the pi number, coordinates, spatial representation), measurement (SI units, use of measurement instruments and techniques), and statistics and probability (collecting and data representation, statistical graphs, centralization and dispersion parameters, percentages, combinatorics). Some of them also address issues that are not usually dealt with in the official curriculum, such as the intuitive initiation to topology through recurrent examples such as the Möbius band.

In most of the activities, a high percentage of future teachers were able to correctly identify one or more of the intended contents. However, in a few cases, a considerable part of them did so in a very vague way, referring only to the content block (‘measure’ or ‘geometry’), or including implicit content in the development of the activity, but which was not explicitly addressed, or others whose presence is not even clear. For example, in activity A6 (Mathematics in the air), which is analyzed in [42], practically all future teachers indicated measurement as content, but only 16.7% referred to statistical concepts such as the mean, median, and mode, while, to our surprise, a half indicated that geometry was worked on, especially spatial vision, and a third the concept of speed. Although it is the case that caused the greatest difficulty, we believe that the example illustrates that a part of the prospective teachers has had certain difficulties in unraveling the contents of the activities in depth. It stands out that some people included ‘patterns and relationships’ as a content in activity A1 (Mathemagic), positively, and that in general they did not identify the use of the calculator as a content, although the latter is probably explained because they implicitly handled a restricted interpretation of the term content.

In the second question of the analysis questionnaire, the objective of the activity was requested. Most of the groups picked up the mathematical objective, although they could not formulate it in a precise way. In those activities in which this objective is multiple, they clearly focused on the content they were identifying. For example, in activity A6 (Mathematics in the air), they focused on measurement and only a few alluded to the statistical purpose of the activity, referring to ‘interpreting data’. The attitudinal type objectives appear only in the responses to two activities, in A1 (Mathemagic), where a future teacher explicitly writes ‘realize that mathematics never fails’, and in A5 (What happens if we mix?), ‘perceive the importance of the measure’. Probably, the fact that they focused only on objectives related to mathematical knowledge has to do with a restrictive interpretation of the question.

4.3.2. Content Knowledge in Relation to Students

This knowledge is collected through various indicators (Table 1). We will focus on SKI4, SKI5, and SKI6. The SKI4 indicator corresponds to the fifth question of the analysis questionnaire, in which they were asked about the difficulties they had when carrying out each activity and the possible difficulties that the students could encounter. These difficulties should be understood in a broad sense, from difficulties in understanding the content dealt with to obstacles in the possible resolution procedures of the activity. Among the difficulties related to understanding the concepts, some of them are generally argued based on a possible lack of knowledge of the content to be worked on by students at risk of social exclusion (musical concepts, diameter and radius, binary code). For example, in relation to activity A3 (Mathmusic), a group of future teachers reflects that ‘children may find it difficult to understand that there must be four beats in each measure’. In activity A2 (A cheeky band), an intuitive initiation to topology, the difficulties encountered are related to the involved concepts of face and order and the meaning or role they play. In another class, there are procedural difficulties that may appear when performing arithmetic calculations (A1) or geometric constructions, handling measuring or drawing instruments (A7), and making measurements with a certain precision (A5), making estimates (A5, A7, and A11), or interpreting data, graphs, or results. Difficulties associated with the novelty of the procedures also appear, such as ‘calculating times, not knowing how to follow the rhythm, not knowing how to represent symbols...’ (A3). In general, it is observed that, in three of the eight proposed activities, about 30% of the future teachers did not foresee any difficulty, and it is appreciated that many are limited to transferring the difficulties that they may have experienced in the first person when carrying out the activity.

The SKI5 indicator, which refers to whether the future teachers formulate questions that make it possible to explain the personal meanings of the students when solving this type of task, is collected in the Service module when putting into practice the activities addressed in the experimentation part and the other ones designed by them. The future teachers help the students to carry out the procedures that the task requires and even formulate questions to assess to what extent they manage the knowledge they already have, and they need other complementary ones. For example, in activity A11 (Reading paintings), questions are asked about characteristics of flat figures, helping students determine which ones to reproduce on the page or grid. However, it is difficult for them to launch questions that stimulate students to explain their doubts or difficulties. This situation can be illustrated by the following conversation:

• Future teacher [T]. What figure are you trying to make?
• Student [S]. I am trying to build a triangle.
• T. But if you continue like this it will come out very crooked.
• S. Well, I don’t know how to do it better.
• T. If you want, I can help you so that it works out better for you. What kind of triangle is it, do you know?
• S. I have doubts, I don’t remember what it is.
• T. Look, you are trying to make one that has all the sides equal, which is the easiest.

Although future teachers were not explicitly required to assess student learning (SKI6), it was observed that, when managing activities, future teachers focus more on the result than on the process that students must follow to solve the activity in a meaningful way, whether it is the most successful or not.

The SKI7 indicator shows us the knowledge and competence of the teacher in relation to the attitudes, emotions, beliefs, and values of the students. It is evaluated if the teacher encourages students to get involved in solving the tasks (or the study of the topic) and considers the emotional state of their students at the time of solving the task, promoting self-concept and self-esteem. In other words, it considers specialized knowledge from the affective side. In the case of Mathematical Bits, given its nature as a mathematical stimulus program, this facet is highly regarded in the design of the activities and in the methodology followed, which try to promote the involvement of students with a positive attitude. During the participation of future teachers in the Service module, it was evident that they consider it very important that all students develop positive emotional behavior for a significant learning situation to occur, as well as promote changes in their attitudes that help them to show a greater interest in the curricular contents. However, they showed serious difficulties in managing the activities in the manner intended in the program. A directive teaching style was observed, more focused on presenting the activity, giving instructions to the students to solve specific questions (especially calculation operations), than in motivating the meaning of the task and guiding the students towards a solution based on feedbacks. Although they tried to encourage the students to solve the tasks, they focused more on detecting execution errors than on guiding and assessing the entire process, a fundamental aspect given the objective of the program and the nature of the students. We could interpret this anchoring in traditional methodology even as a negative attitude of future teachers towards mathematics, since this is not only characterized by a negative emotional disposition (“I don’t like mathematics”) but also by an incorrect epistemology of mathematics discipline, that is, a vision of the discipline that is not shared by the experts [47]. It also supposes a serious obstruction for the purpose of the SL program, since among the practices that can have potential effects on the anxiety to teach mathematics, the traditional methods do not seem to be effective [19,48].

4.3.3. Content Knowledge in Relation to Teaching

The SKI8 indicator is considered here, which collects if the future teachers describe, apply, and reflect on the didactic configuration that they implement using the given mathematical task. In the activities that they had previously experienced, they tried to reproduce the methodology implemented by the researchers with them in Phase I of the Learning module, starting the activities through a stimulating or probing question and trying to conduct the intervention in a similar way. Despite this, as we have just pointed out in 4.2.2., it was difficult for them to break with the role of transmitting teacher focused on the result. This type of interaction with students by future teachers is closely linked to the basic educational model they have internalized. This teacher–student interaction is very clear in those practices in which the product belongs to the whole group. For example, in activity A3, where the goal is to create a melody composed and performed by all, the degree of success in interpreting the melody clearly depends on the level of trust between teachers and students. The future teachers, in general, did not show the initiative to promote student–student interaction, by means of, for example, the exchange of information between students from different groups or mediation to try to reach a consensus. An example of this can be seen in this transcript:

• Future teacher [T]. Now we have the beats built and the rhythm, so we have to put a letter to it.
• Student1 [S1]. Can we put the letter that we want?
• T. Yes, of course. We are going to start in the first measure putting a short phrase because after that there is a silence.
• Student2 [S2]. That’s it, the best start is like this: “Oh, destruction!”
• T. But it will be better to put another one, type “there is a heart”.
• S1. I like the A2 one better.
• S2. I think mine is much better.
• T. Well we are going to put the other one because the truth sounds better.

This interaction was specifically required in activities in which it was necessary to compare results between different groups, such as activities A5, A6, and A11, where they competed to inflate a balloon, throw a paper plane as far as possible or be the best scoring team, respectively.

At a global level, they value the activities well, but they have difficulties when implementing them fundamentally because they are not capable of detaching themselves from the transmission model, which causes them anxiety. This classic approach to activities does not help to create the climate of trust and interaction that is intended to be achieved. In this sense, as pointed out by [45], the modes of teacher–student and student–student interaction that occur must be effective to create a connecting link that allows the development of a meaningful learning. This poor management of interactions in the classroom was accentuated when they put into practice the activities that they had not previously experienced (A4, A8, A9, A12, A13, and A14). In these cases, it became more evident that they put into practice the pedagogical model that they have naturally internalized, showing a more distant and authoritative attitude in the management of the activities, reducing the management of the activity to an initial explanation about the content involved and the steps and premises necessary to perform the task at hand.

With regard to material resources, the Mathematical Bits program uses a wide variety of resources that includes expendable material such as paper, EVA foam, felt (A2, A6, A4, A10, A12); drawing instruments, odometers, meters, bascules, (A6, A7, A10); specific didactic material such as geoboard or sets to build 3D figures (A8, A9); Erlenmeyer pipettes and laboratory material (A5); technological resources (A11, A13, A14); and musical instruments (A3). Pre-service primary teachers value the variety of material positively, although they often find it difficult to recognize the didactic value of the material itself. For example, in practice A14 (Mental agility with Kahoot), gamification is used as a motivating element and not as a mental calculation tool as many of the future teachers considered.

As for whether the future teachers describe other tasks related to the given one and the way of managing the didactical trajectory (SKI9), in Phase III of the Learning module, they are asked to create an activity according to the following indications: Suggestive title, subjects involved, age of the students, objective, contents involved, materials, duration, and a description of the methodological sequence. All future teachers designed activities for students between 10 and 14 years old, incorporating recycled material such as plastic [41], flowers and leaves, and technological resources such as robots, mathematical apps [49], design and printing 3D [50], cameras [41] and virtual escape-rooms [51], which makes clear their interest in incorporating technology into education and their commitment to environment. The description of these activities can be seen in more detail at http://gidem-tesela.es/anaquinos/ (accessed on 26 January 2022).

Another element that is considered when developing these didactical situations is the duration. As stated above, the duration of the sessions was always 1 h, with the idea of maintaining the degree of attention of students at risk of social exclusion. With the future teachers, in Phase I, the same duration was used, with the idea that this would allow them to control the session based on the content that required more or less time. The activities designed by them were adjusted to that time, except for the escape-room and land-art activities, which required half an hour more to carry them out.

4.3.4. Content knowledge in Relation to the Curriculum

Knowledge of the content in relation to the curriculum (SKI10) is collected in the fourth question of the analysis questionnaire (level of adaptation of the activity to primary education). The future teachers were asked to rate, using a four-level Likert scale, the difficulty that the Mathematical Bits activities, originally designed for students of the first and second year of secondary education (12–14 years). In general, future teachers consider that most of the activities presented are suitable for primary education, giving an average of 2.30 points in terms of difficulty. The 62% of pre-service primary teachers highlighted activity A3 (Mathmusic) as quite difficult for primary school students. However, in the intervention phase they were able to verify, supported by the satisfaction questionnaire of the students of the Mathematical Bits program, that 67% consider it easy or very easy. Note that the future teachers made their assessment of the difficulty in Phase I, before the implementation in the classroom during the Mathematical Bits program. This deviation is explained because they did not consider the activity with the inductive-type methodology inherent in its design, with which they deduce that the probable lack of knowledge of the musical concepts involved by adolescents will be an obstacle to their development. As for the activities designed by the future teachers, they were all adjusted to curricular content and the level at which they put them into practice (10–14 years).

From the results of the satisfaction questionnaire, it is highlighted that the activities that they consider most useful are those that explicitly relate to known content and subjects that they are going to teach in their working lives, as shown by the results obtained for activity A7 (Discovering π) and activity A5 (What happens if we mix?), respectively. The novelty and difficulty of the contents is considered low, which was the objective of the program in trying to show curricular contents already known in other contexts, giving an average of 2.30 for difficulty and an average of 2.13 for novelty of the contents.

5. Conclusions

In this work, a service-learning project has been presented for pre-service primary teachers to serve students at risk of social exclusion through mathematical stimulation. This type of methodology has made it possible to observe the different categories of didactic-mathematical knowledge that future teachers put into operation in a real situation of inclusion.

In relation to common knowledge, although the future teachers ended up solving the activities of the Mathematical Bits program, their superficial understanding of basic mathematical contents was observed, which assumed that they had already partially reviewed in the subjects of the didactic-mathematical module of the degree. In addition, an important part has had difficulty unraveling the contents and objectives of the activities, limiting their responses to those that are most obvious. For the analysis of extended knowledge, little information has been available because of the design of the didactic-mathematical analysis questionnaire that did not consider intradisciplinary connections. It will be necessary to reformulate this point for future research.

The analysis of specialized knowledge shows a mastery of the curriculum on the part of future teachers, but reveals important gaps in terms of content, students, and teaching. Among the difficulties related to the understanding of the concepts, some of them are generally argued based on the lack of knowledge of the content to be worked on by students at risk of social exclusion. Many of them limit themselves to transferring the difficulties that they may have experienced in the first person when carrying out the activity. The future teachers formulate the tasks and accompany the students in carrying them out. However, they do not show the ability to manage the processes involved in the resolution, emphasizing the objective of the activity, promoting student–student interaction, providing questions as feedback or mediating debates so that the group-class can reach significant conclusions. The traditional teaching model that they have internalized was observed in the intervention of the Mathematical Bits program with the activities that they designed and had not experienced. Their reference teaching model was also appreciated when they were questioned about the difficulty of the activities, with respect to the knowledge of the content in relation to the curriculum. We believe that the differences that arose between the difficulty anticipated by the future teachers and the perception of the students of the Mathematical Bits program after carrying out the activities is largely due to the fact that the future teachers at the time of the assessment did not consider some activities with the inductive-type methodology inherent in their design, so the difficulty is deduced in this case from the probable ignorance by adolescents of the concepts involved. Nevertheless, the activities designed by the future teachers did have great potential, partly thanks to a good selection of the resources involved. Difficulties generally appear when visualizing how mathematical knowledge is generated, either when analyzing an activity, its design, or its management in the classroom.

Although a very small sample was analyzed, the results showed greater-than-expected limitations, both in the Learning module analysis and design of activities and in the Service module implementation within the stimulus program. The professional skills that future teachers acquire in their undergraduate studies seem to be far from allowing them to develop inclusive mathematical teaching that goes beyond traditional transmission schemes. It is perceived that their important deficiencies at the level of didactic-mathematical knowledge cause in many cases a state of insecurity that considerably limits them when approaching the teaching of mathematics. This only confirms in our case the importance of a positive impact on the affections towards mathematics and its teaching as a necessary way to promote a more effective acquisition of professional specific mathematical skills.

Despite this, we think the learning and service project offered specific possibilities for the acquisition of mathematical skills future teachers that help them control educational interventions in contexts with a high emotional load, promoting a social and civic awareness that is essential in the development of their teaching work. The future teachers highlight the STEAM activities carried out as key elements to work on motivation and attitudes towards the subject, both for themselves and for the students at risk of social exclusion, recipients of the service. They considered, of great importance, the fact that other subjects teachers carried out activities making explicit reference to the use of mathematics as a determining factor for their vision on this subject. The latter requires a deeper investigation on the affective suitability of the program [35] that allows conclusive results to be drawn on the effect of the SL program on the affections of future teachers towards mathematics and its teaching.

The interest of future teachers shown in the activities could be related to the weight given to the program in the evaluation of the subject. We agree with [35] on the need to rethink evaluation in teacher training, considering varied evaluation instruments and with enough weight to not depend on the written test and to avoid the disaffection that is produced by class tasks.

Considering the above, future action proposals in initial teacher training should be aimed at experiencing teaching situations that place mathematics in context and that relate it to other subjects, not only from the area itself but from other areas of knowledge, as a key point to promote affection towards mathematics. The faculties of education have the necessary infrastructure to carry out a STEAM training/methodology, with professionals from different areas, with a diversity of materials and spaces to achieve it, promoting a broader and richer vision of each one of them and breaking with the idea of compartmentalized and transmitting knowledge that future teachers continue to have and focusing on the evaluation of learning from errors, which fuels a negative attitude and anxiety towards the subject.