Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector
Abstract
:1. Introduction
2. Mathematical Model
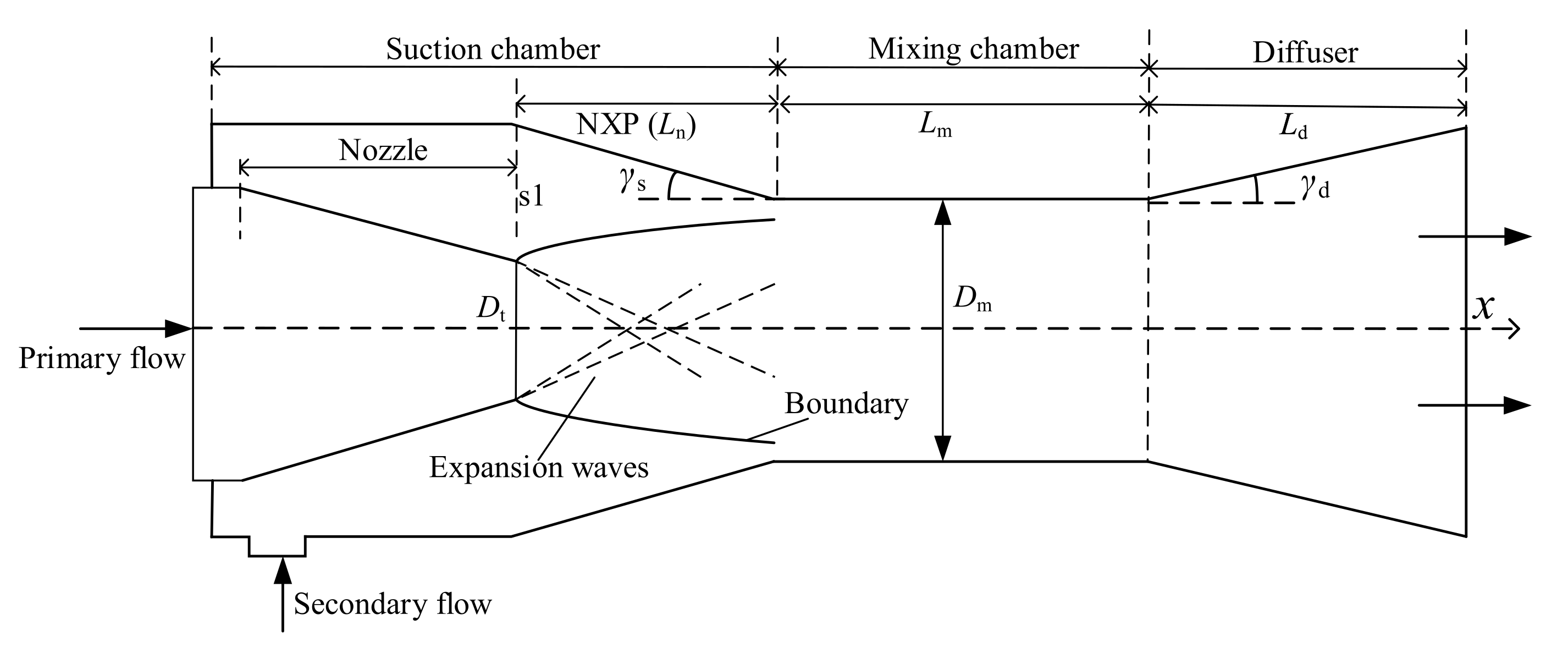
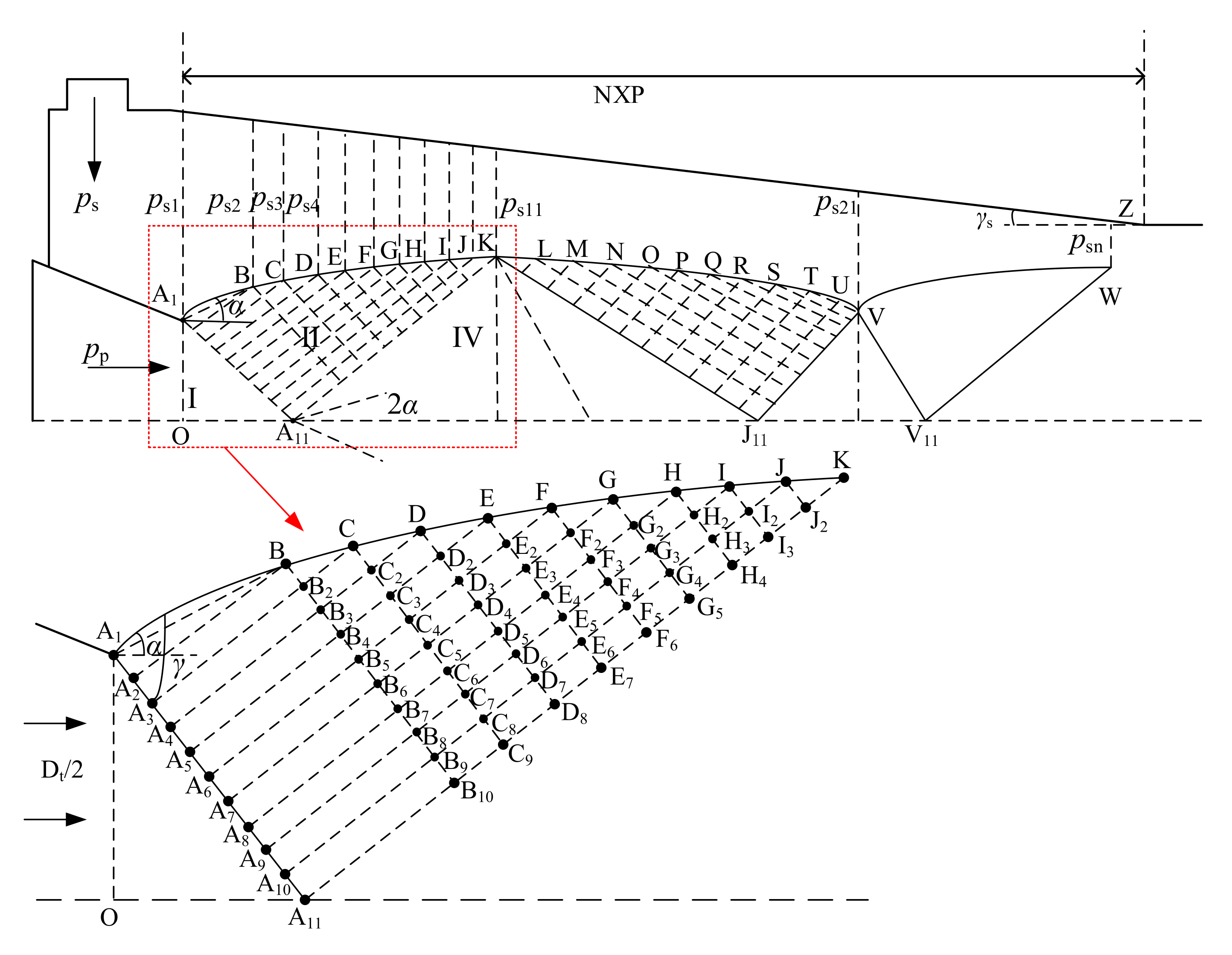
2.1. Motive Nozzle and Suction Chamber
2.2. Mixing Chamber and Diffuser Model
- The fluid in the mixing chamber and diffuser is the steady flow state.
- The external forces are ignored.
- The mass transfer between the two streams is calculated by the condensation and entrainment.
- The momentum transfer is determined by the drag forces of interface between the two streams and the mass transfer resulted in the momentum gain or loss.
- The friction pressure drop is accounted for by the wall boundary layer and the imaginary mixing layer between the two streams.
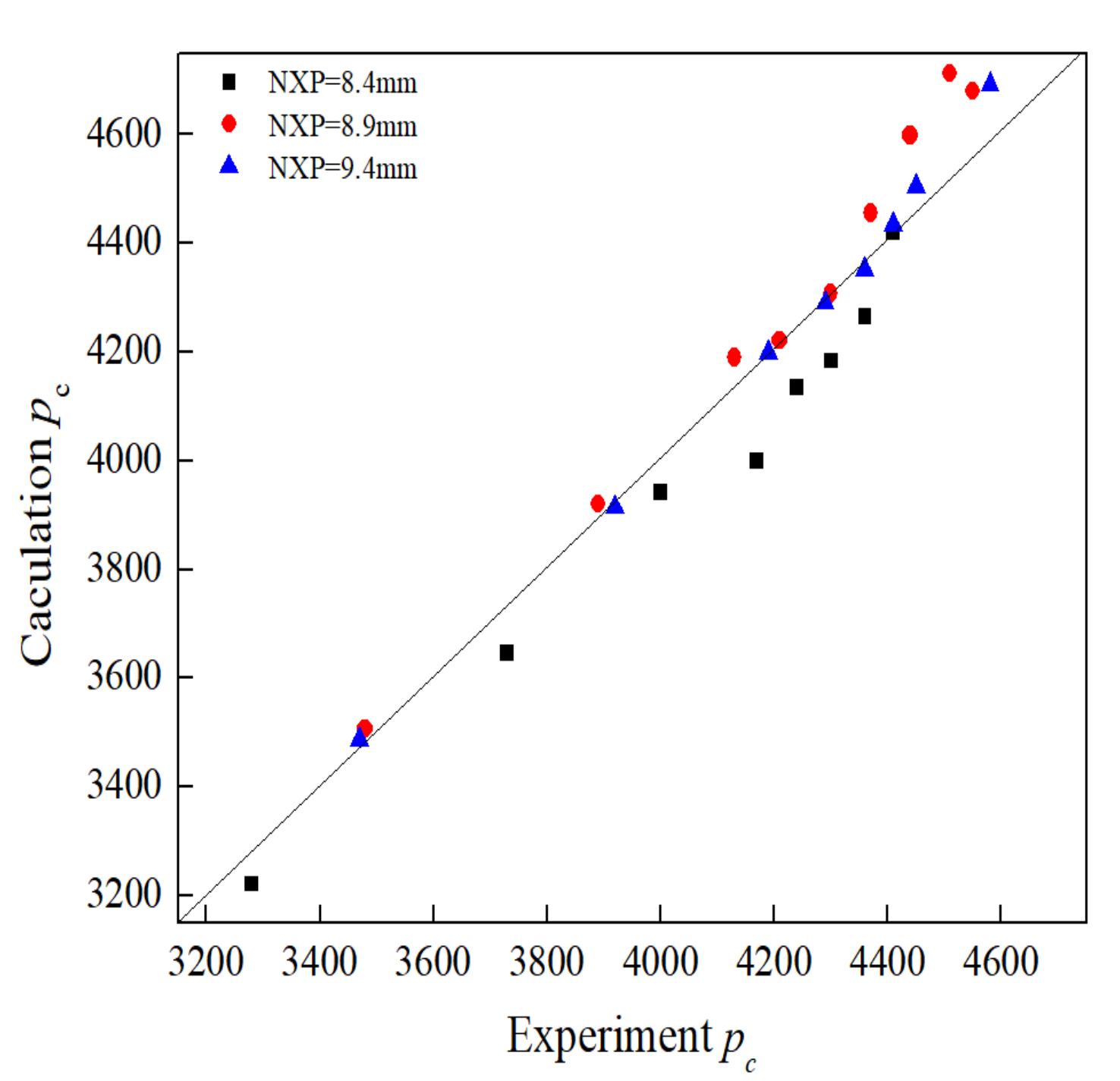
3. Model Validation
4. Result and Discussion
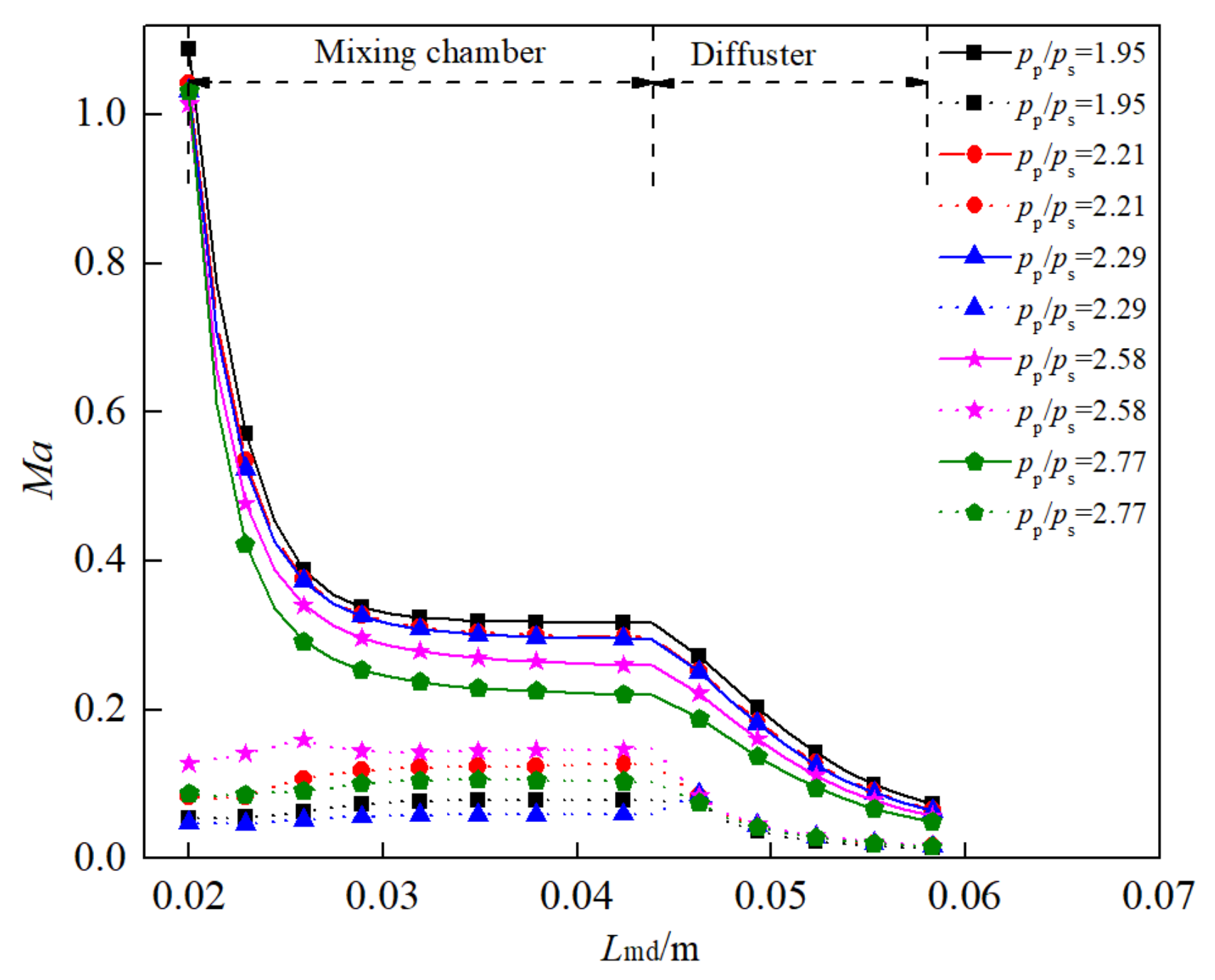
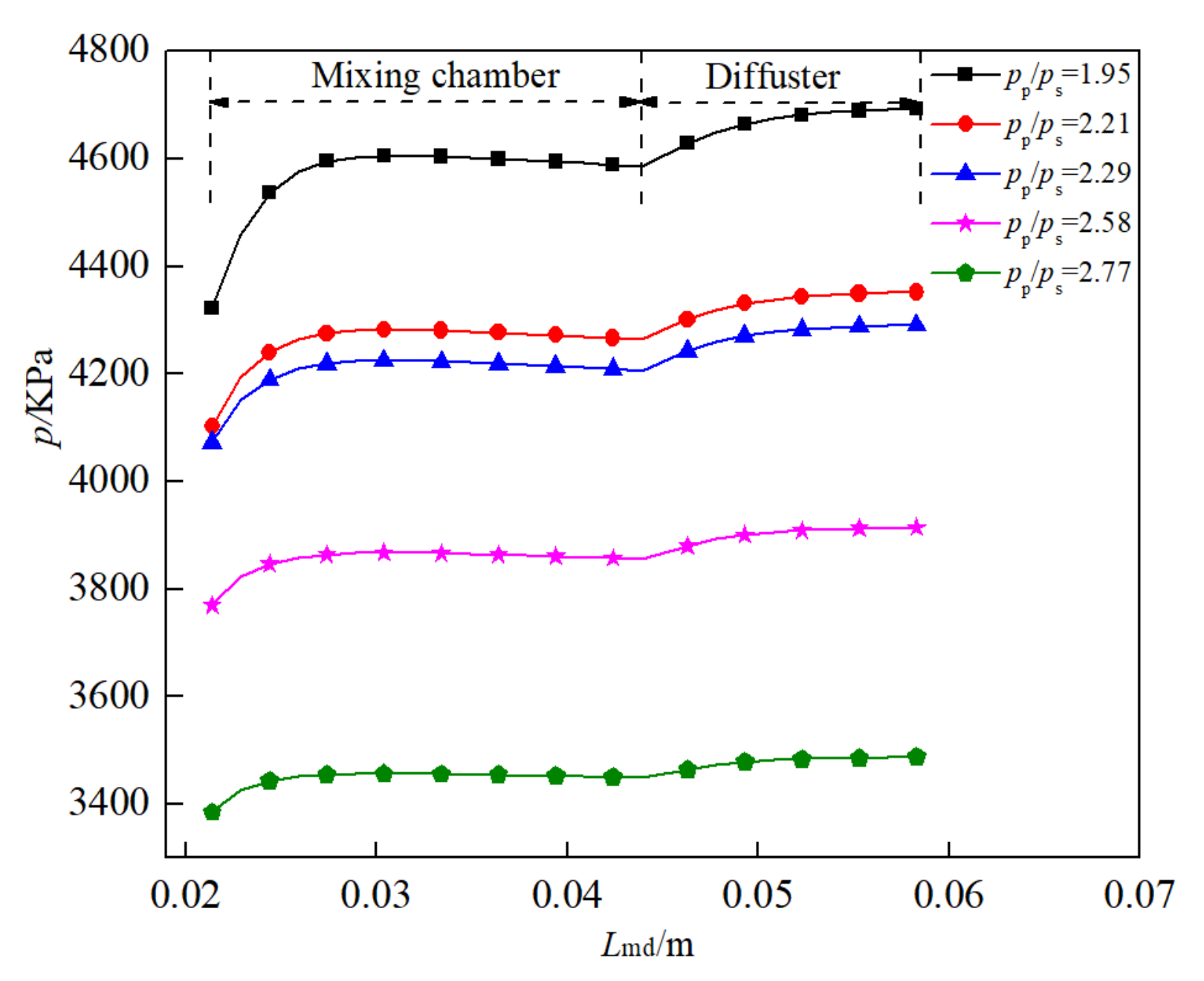
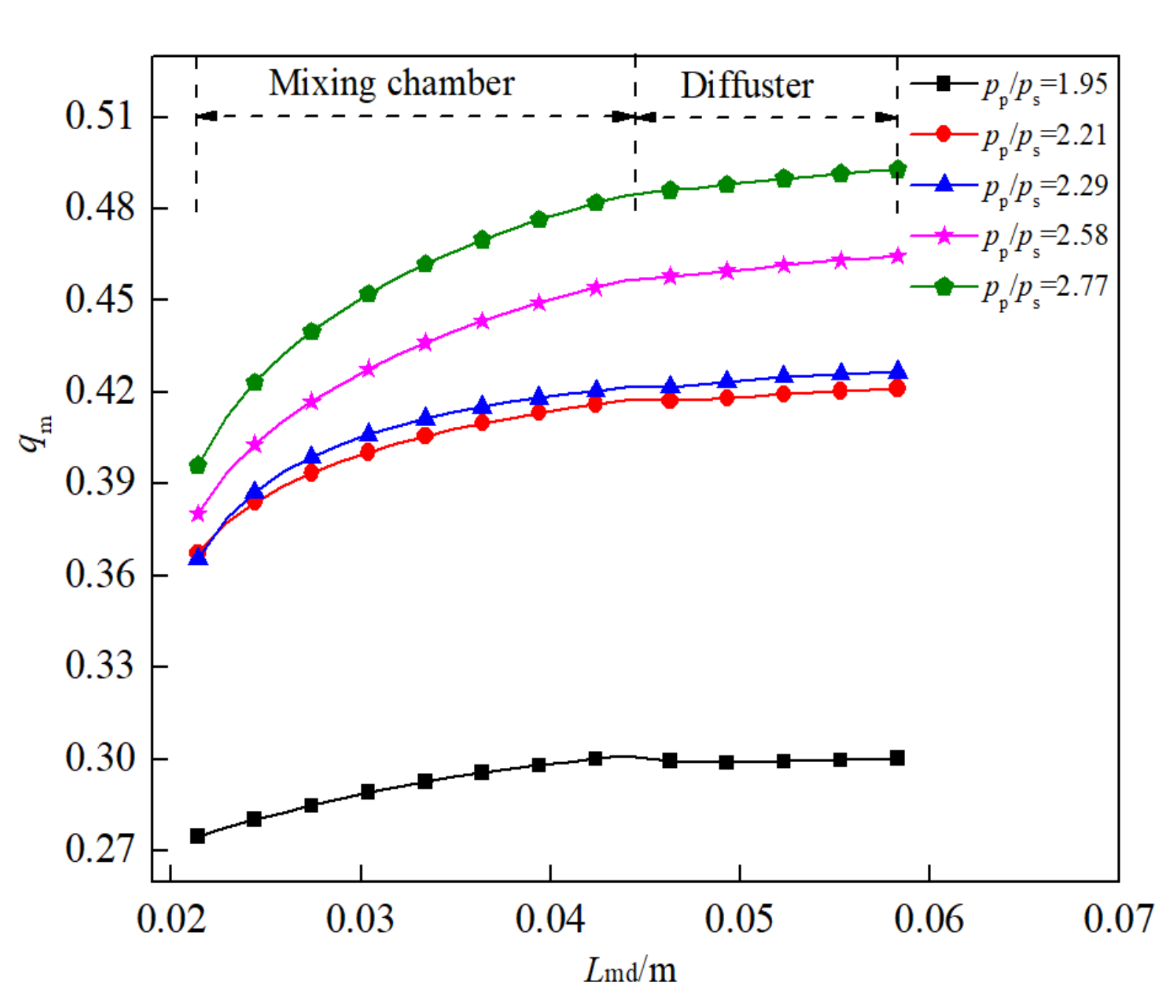
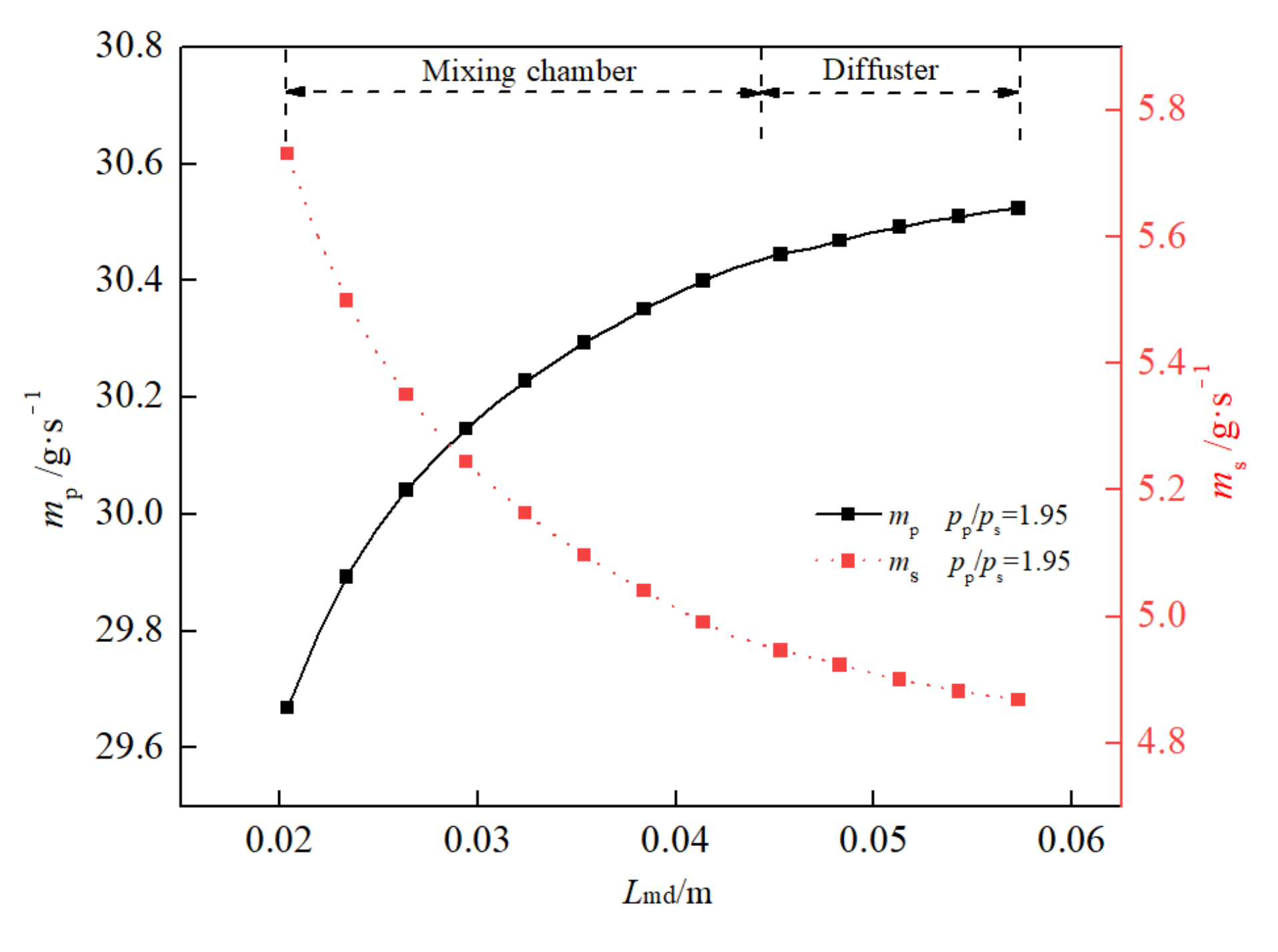
4.1. Flow Distribution
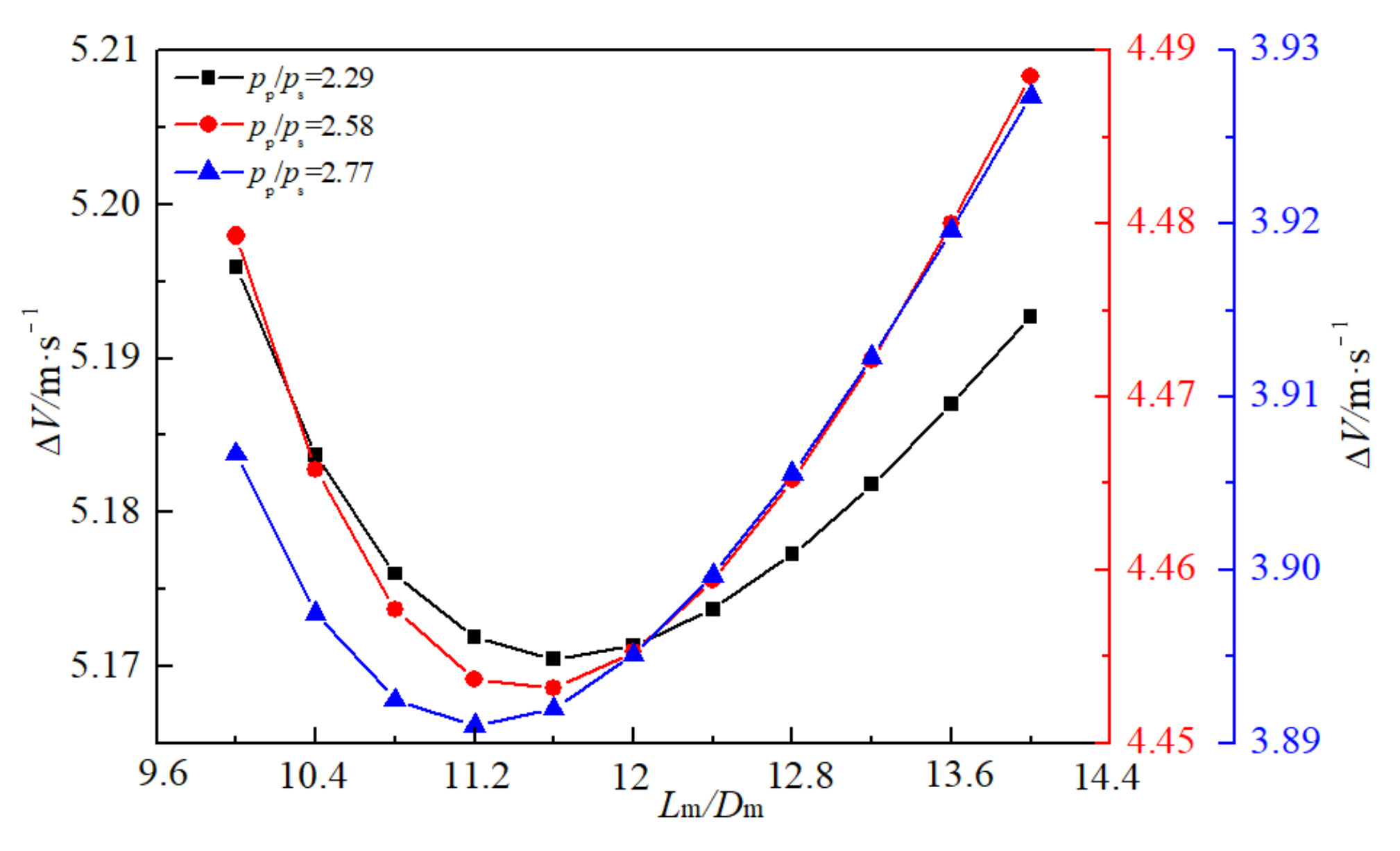
4.2. Optimization of Mixing Chamber Length
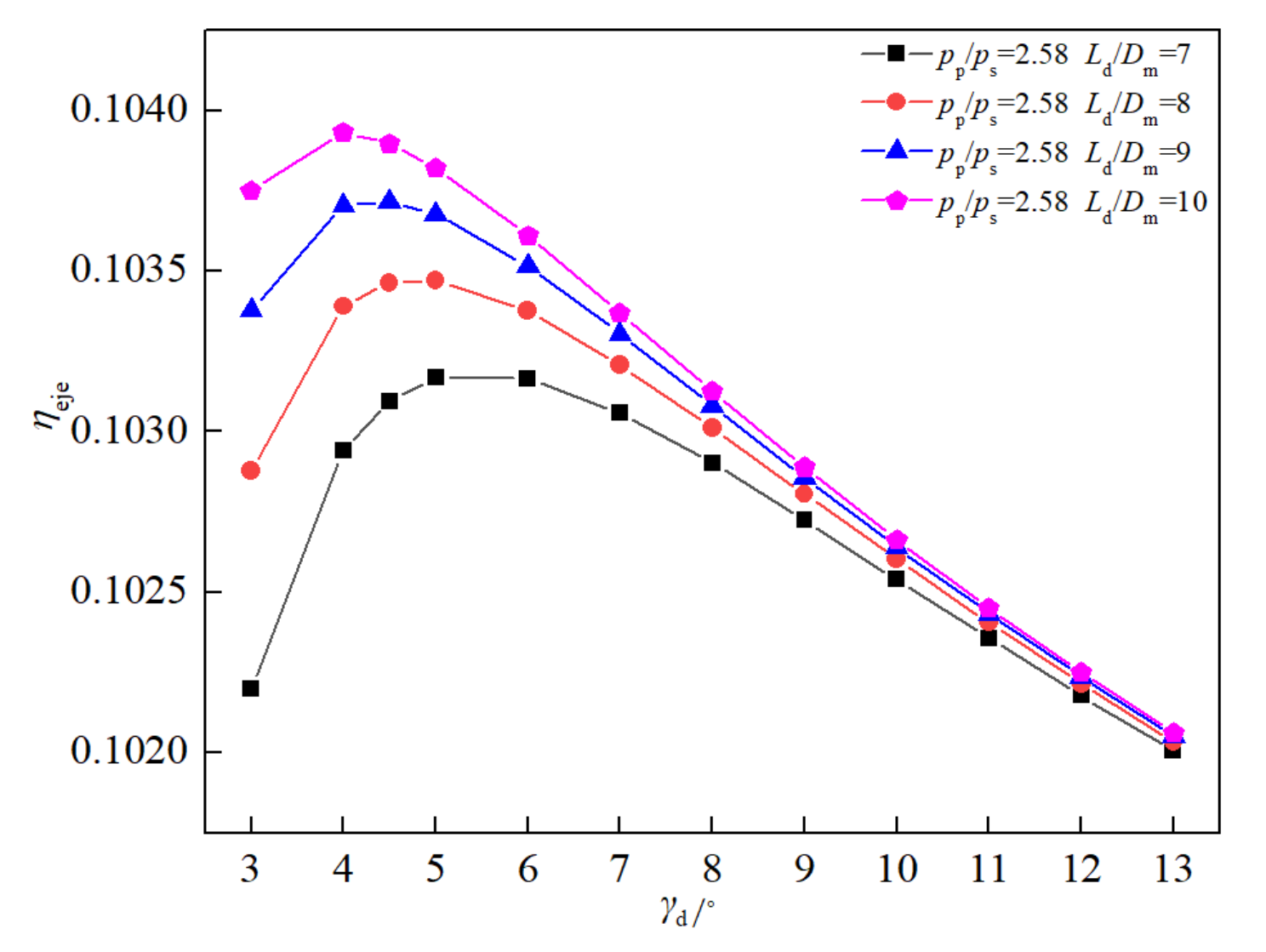
4.3. Optimization of Diffuser Angle
5. Conclusions
- (1)
- The suction chamber model established by the characteristic line method is embedded into the global mathematical model of the CO2 ejector. The expansion wave development in the suction chamber is considered, and its influence on the subsequent mixing process can be obtained. Compared with the experimental values presented in the literature [30], the average deviation of the entrainment ratio µ and the ejector outlet pressure pc calculated by the present model are 4.93% and 1.55%, respectively.
- (2)
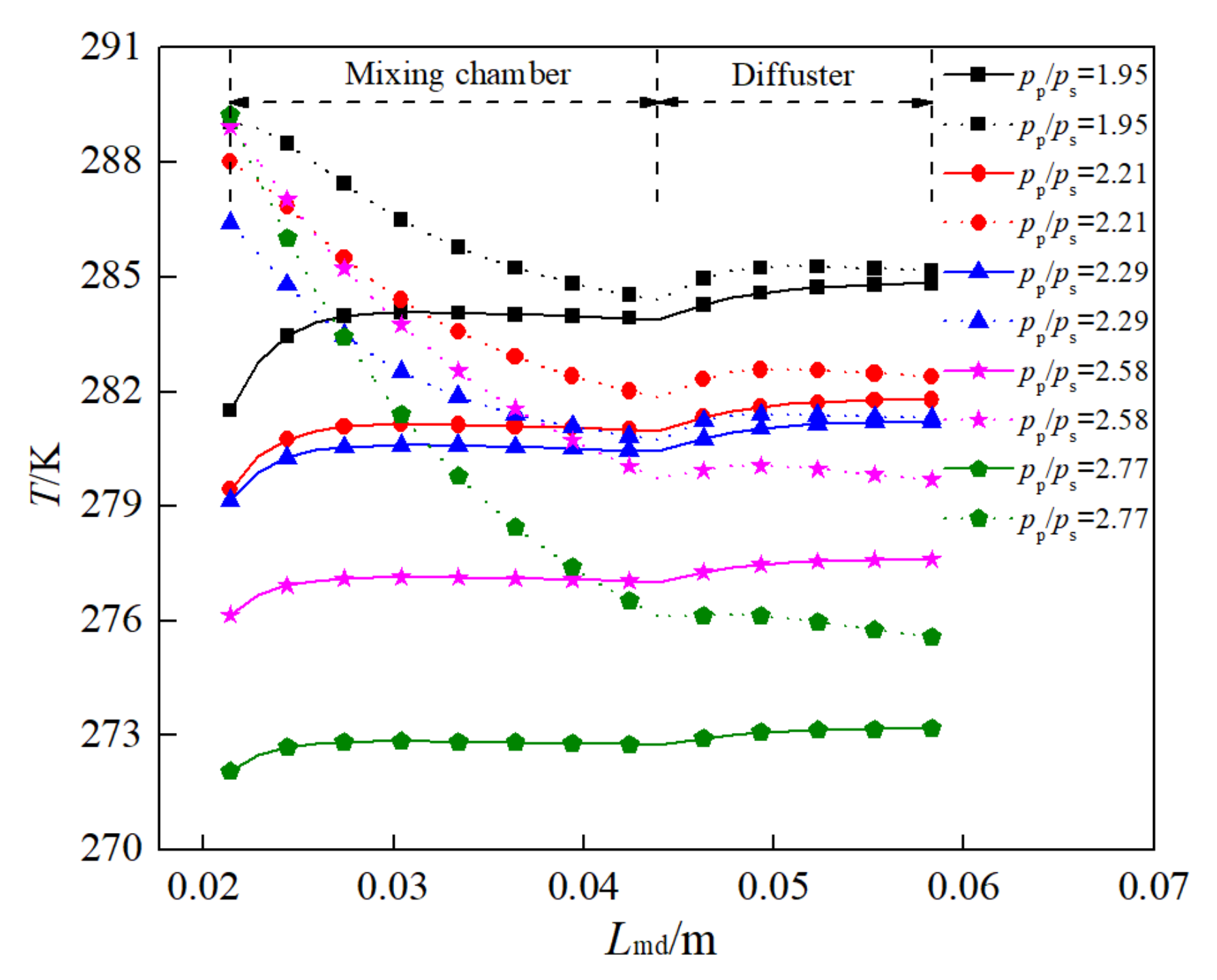
- In the mix chamber and diffuser, the temperature of the primary flow increases gradually along the path, while the Mach number and velocity decrease gradually, while the secondary flow shows an opposite trend. For the small expansion ratios, the temperature of the primary flow rises rapidly with the initial stage of mixing, while the large expansion ratio makes the secondary flow temperature decrease significantly in the mixing process. In the diffuser, the Mach number of the primary flow decreases more obviously than that of the secondary flow. The mass of the secondary flow is continuously transferred to the primary flow, and the gas-phase mass fraction of the primary flow increases gradually due to the transfer of energy and the rise of temperature.
- (3)
- The velocity difference between the two streams in the mixing chamber is proposed as the optimized parameter. It is found that the mixing uniformity is better when the length–diameter ratio of the mixing chamber is 10.8–12, and the ejector has a better ejector efficiency when the semi-cone angle of the diffuser is 4–6°.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramesh, A.S.; Sekhar, S.J. Experimental and numerical investigations on the effect of suction chamber angle and nozzle exit position of a steam-jet ejector. Energy 2018, 164, 1097–1113. [Google Scholar] [CrossRef]
- Bodys, J.; Smolka, J.; Palacz, M. Experimental and numerical study on the R744 ejector with a suction nozzle bypass. Appl. Therm. Eng. 2021, 194, 117015. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef] [Green Version]
- Ker, A.; Ya, A.; Pg, B. A detailed review on CO2 two-phase ejector flow modeling. Therm. Sci. Eng. Prog. 2020, 20, 100647. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Fic, A.; Bulinski, Z.; Nowak, A.J.; Banasiak, K.; Hafner, A. Application range of the HEM approach for CO2 expansion inside two-phase ejectors for supermarket refrigeration systems. Int. J. Refrig. 2015, 59, 251–258. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Ostrowski, Z.; Palacz, M.; Madsen, K.B.; Försterling, S.; Nowak, A.J.; Banasiak, K. Performance mapping of the R744 ejectors for refrigeration and air conditioning supermarket application: A hybrid reduced-order model. Energy 2018, 153, 933–948. [Google Scholar] [CrossRef]
- Haida, M.; Smolka, J.; Hafner, A.; Palacz, M.; Banasiak, K.; Nowak, A.J. Modified homogeneous relaxation model for the R744 trans-critical flow in a two-phase ejector. Int. J. Refrig. 2018, 85, 314–333. [Google Scholar] [CrossRef]
- Nakagawa, M.; Berana, M.S.; Harada, A. Shock waves in supersonic two-phase flow of CO2 in converging-diverging nozzles. HVACR Res. 2009, 15, 1081–1098. [Google Scholar] [CrossRef] [Green Version]
- Fardi, M.; Pishkar, I.; Alidousti, J.; Khan, Y. Numerical investigation of the MHD suction–injection model of viscous fluid using a kernel-based method. Arch. Appl. Mech. 2021, 91, 4205–4221. [Google Scholar] [CrossRef]
- Li, Y.F.; Deng, J.Q.; Ma, L. Experimental study on the primary flow expansion characteristics in transcritical CO2 two-phase ejectors with different primary nozzle diverging angles. Energy 2019, 186, 115839. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A. 1D Computational model of a two-phase R744 ejector for expansion work recovery. Int. J. Therm. Sci. 2011, 50, 2235–2247. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Dang, C.; Hihara, E. Investigations on driving flow expansion characteristics inside ejectors. Int. J. Heat Mass Transf. 2017, 108, 490–500. [Google Scholar] [CrossRef]
- Yan, J.; Li, S.; Liu, Z. Numerical investigation on optimization of ejector primary nozzle geometries with fixed/varied NXP. Appl. Therm. Eng. 2020, 175, 115426. [Google Scholar] [CrossRef]
- Barta, R.B.; Dhillon, P.; Braun, J.E. Design and optimization strategy for ejectors applied in refrigeration cycles. Appl. Therm. Eng. 2021, 189, 116682. [Google Scholar] [CrossRef]
- Elbel, S.; Hrnjak, P. Experimental validation of a prototype ejector designed to reduce throttling losses encountered in transcritical R744 system operation. Int. J. Refrig. 2008, 31, 411–422. [Google Scholar] [CrossRef]
- Chong, D.T.; Yan, J.J.; Wu, G.S. Structural optimization and experimental investigation of supersonic ejectors for boosting low pressure natural gas. Appl. Therm. Eng. 2009, 29, 2799–2807. [Google Scholar] [CrossRef]
- Wen, H.; Yan, J. Effect of mixing chamber length on ejector performance with fixed/varied area ratio under three operating conditions in refrigerated trucks. Appl. Therm. Eng. 2021, 197, 117379. [Google Scholar] [CrossRef]
- Yan, J.; Cai, W.; Li, Y. Geometry parameters effect for air-cooled ejector cooling systems with R134a refrigerant. Renew. Energy 2012, 46, 155–163. [Google Scholar] [CrossRef]
- Wu, H.Q.; Liu, Z.L.; Han, B. Numerical investigation of the influences of mixing chamber geometries on steam ejector performance. Desalination 2014, 353, 15–20. [Google Scholar] [CrossRef]
- Yan, J.; Wen, N.; Wang, L.; Li, X.; Liu, Z.; Li, S. Optimization on ejector key geometries of a two-stage ejector-based multi-evaporator refrigeration system. Energy Convers. Manag. 2018, 175, 142–150. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Lei, W. Configuration dependence and optimization of the entrainment performance for gas–gas and gas–liquid ejectors. Appl. Therm. Eng. 2012, 48, 237–248. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.Z. Investigation of entrainment behavior and characteristics of gas–liquid ejectors based on CFD simulation. Chem. Eng. Sci. 2011, 66, 405–416. [Google Scholar] [CrossRef]
- Kandakure, M.T.; Gaikar, V.G.; Patwardhan, A.W. Hydrodynamic aspects of ejectors. Chem. Eng. Sci. 2005, 60, 6391–6402. [Google Scholar] [CrossRef]
- Balamurugan, S.; Gaikar, V.G.; Patwardhan, A.W. Effect of ejector configuration on hydrodynamic characteristics of gasliquid ejectors. Chem. Eng. Sci. 2008, 63, 721–731. [Google Scholar] [CrossRef]
- Metin, C.; Gök, O.; Atmaca, A.U.; Erek, A. Numerical investigation of the flow structures inside mixing section of the ejector. Energy 2019, 166, 1216–1228. [Google Scholar] [CrossRef]
- Zheng, L.X. Simulation and Experimental Study on Dynamic Characteristics of Transcritical CO2 Ejector Refrigeration System. Ph.D. Thesis, Xi’an Jiaotong University, Xi’an, China, 2018. [Google Scholar]
- NIST. Reference Fluid Thermodynamic and Transport Properties Database (REFPROP); Version 9.0; U.S. Department of Commerce: Gaithersburg, MD, USA, 2002. [Google Scholar]
- Liu, F.; Groll, E.A. Study of ejector efficiencies in refrigeration cycles. Appl. Therm. Eng. 2013, 52, 360–370. [Google Scholar] [CrossRef]
- Liepmann, H.W.; Roshko, A. Elements of Gasdynamics, 1st ed.; John Wiley & Sons: New York, NY, USA, 1957; pp. 98–100. [Google Scholar]
- Zheng, L.X.; Deng, J.Q. Research on CO2 ejector component efficiencies by experiment measurement and distributed-parameter modeling. Energy Convers. Manag. 2017, 142, 244–256. [Google Scholar] [CrossRef]
- Churchill, S.W. Friction factor equation spans all fluid flow regimes. Chem. Eng. 1977, 84, 91–92. [Google Scholar]
- Hwang, Y. Comprehensive Investigation of a Carbon Dioxide Refrigeration Cycle. Ph.D. Thesis, University of Maryland, College Park, MA, USA, 1997. [Google Scholar]
- Faraz, N.; Khan, Y.; Anjum, A.; Kahshan, M. Three-Dimensional Hydro-Magnetic Flow Arising in a Long Porous Slider and a Circular Porous Slider with Velocity Slip. Mathematics 2019, 7, 748. [Google Scholar] [CrossRef] [Green Version]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Li, Y.; Deng, J. Numerical investigation on the performance of transcritical CO2 two-phase ejector with a novel non-equilibrium CFD model. Energy 2022, 238, 121995. [Google Scholar] [CrossRef]
- Elbel, S. Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications. Int. J. Refrig. 2011, 34, 1545–1561. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Hu, H.; Wang, W.; Zhang, Y.; Wang, L. Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector. Mathematics 2022, 10, 693. https://doi.org/10.3390/math10050693
Zheng L, Hu H, Wang W, Zhang Y, Wang L. Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector. Mathematics. 2022; 10(5):693. https://doi.org/10.3390/math10050693
Chicago/Turabian StyleZheng, Lixing, Hongwei Hu, Weibo Wang, Yiyan Zhang, and Lingmei Wang. 2022. "Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector" Mathematics 10, no. 5: 693. https://doi.org/10.3390/math10050693
APA StyleZheng, L., Hu, H., Wang, W., Zhang, Y., & Wang, L. (2022). Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector. Mathematics, 10(5), 693. https://doi.org/10.3390/math10050693




