Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials
Abstract
:1. Introduction
- IGA-FEM is employed for the coupled eigenvalue problems of piezoelectric materials.
- We investigate the influence of different factors on coupled eigenvalue problems.
2. Uncertainty Quantification Based on Monte Carlo Simulation
3. Linear Piezoelectricity Vibration Analysis Theory with IGA-FEM
3.1. Linear Piezoelectricity Formulation
3.2. IGA-FEM Theory for Linear Piezoelectricity Vibration Analysis
3.2.1. Variational Setting
3.2.2. IGA-FEM Discretization
4. Numerical Examples
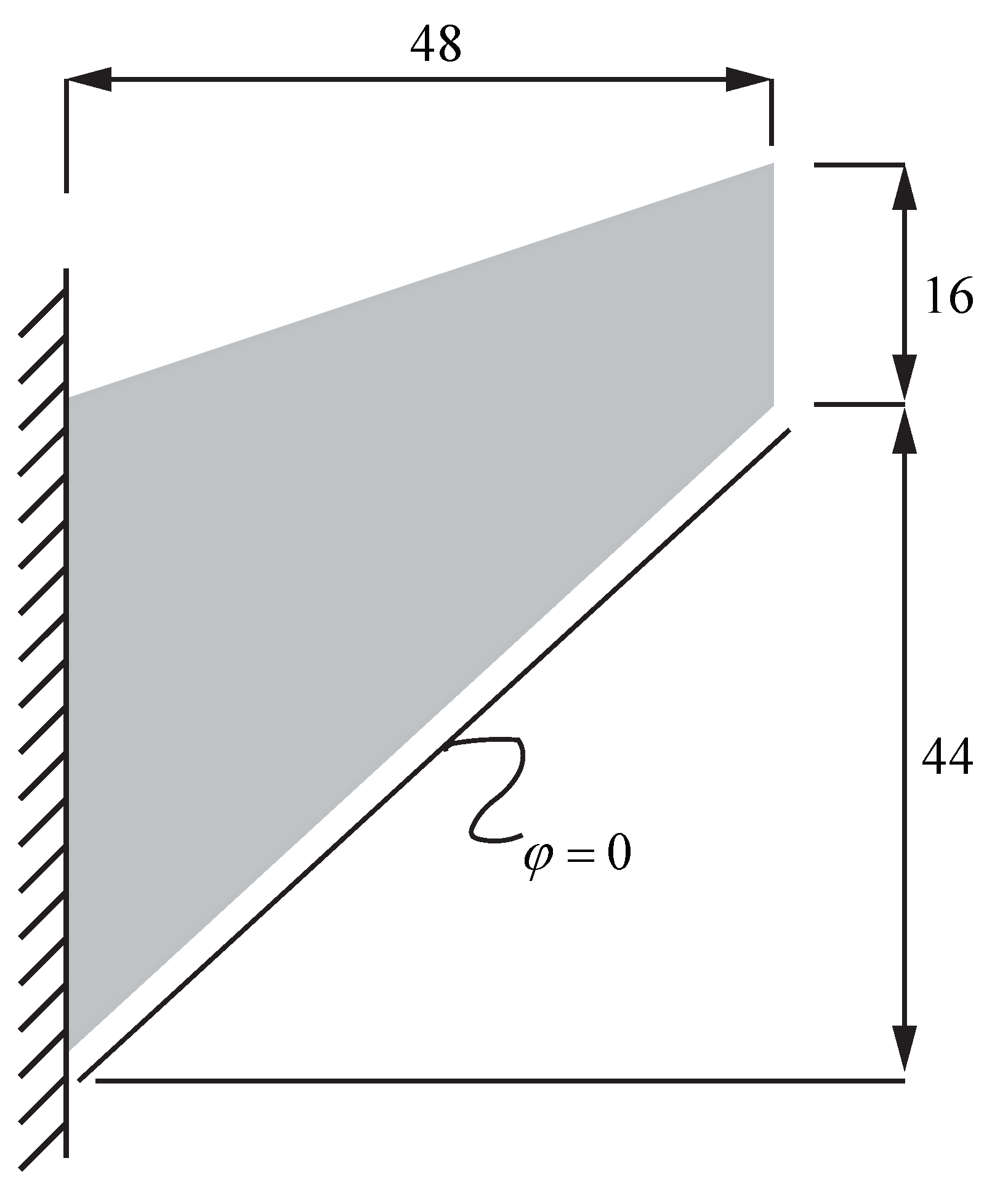
4.1. Piezoelectric Tapered Panel
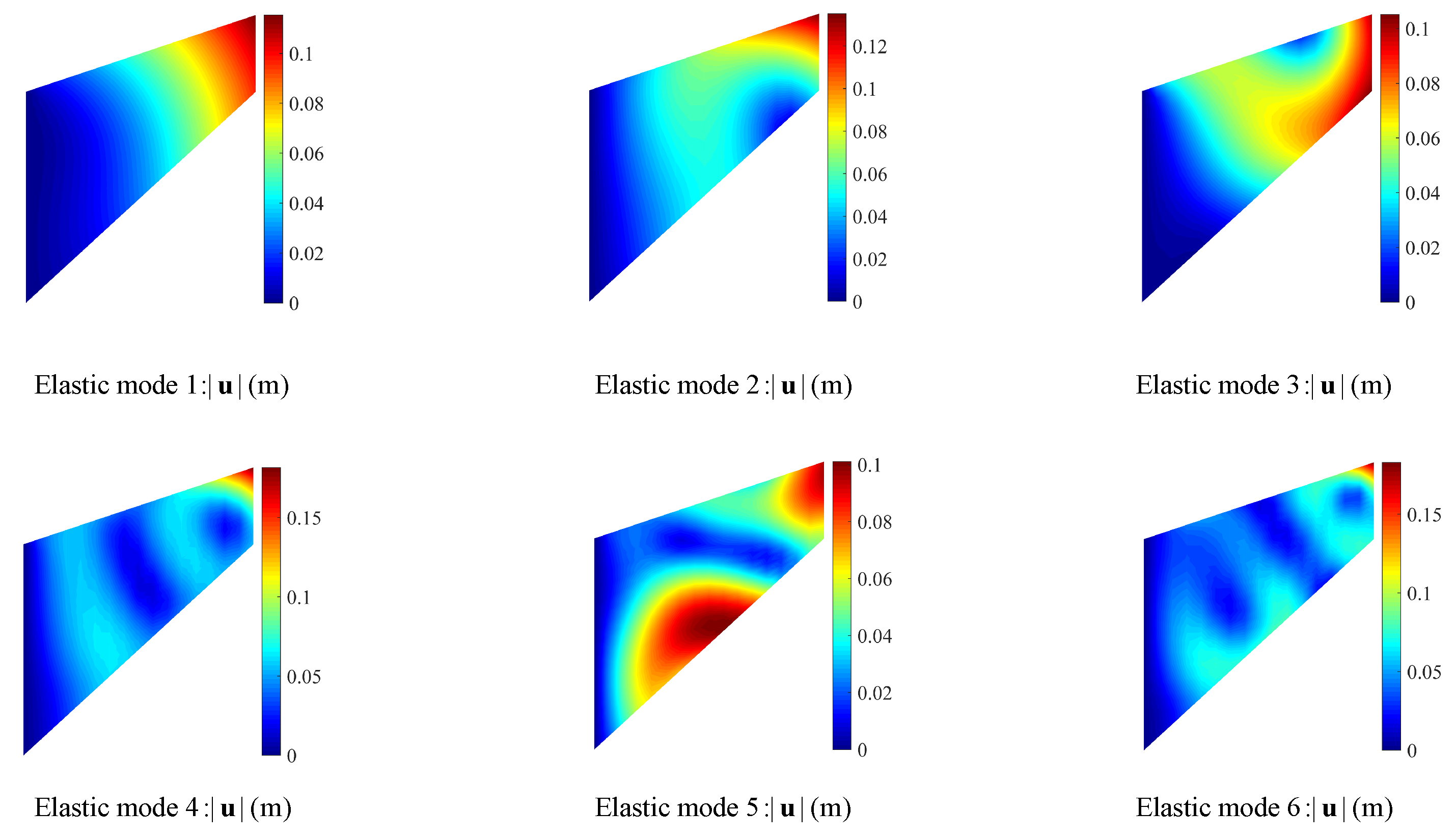
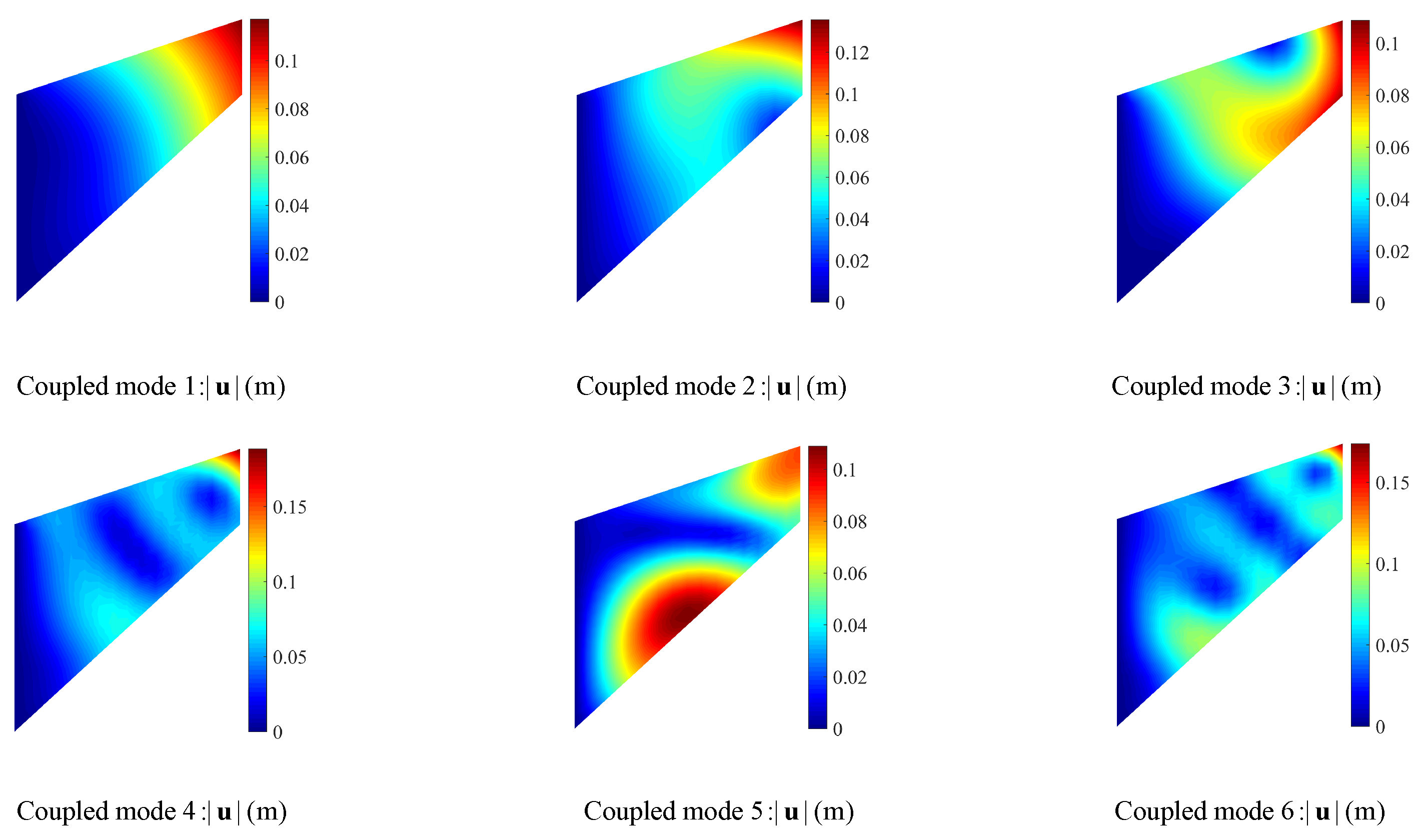
4.1.1. Piezoelectric Tapered Panel Free Vibration Analysis
4.1.2. Uncertainty Quantification for Piezoelectric Tapered Panel Model with MCs
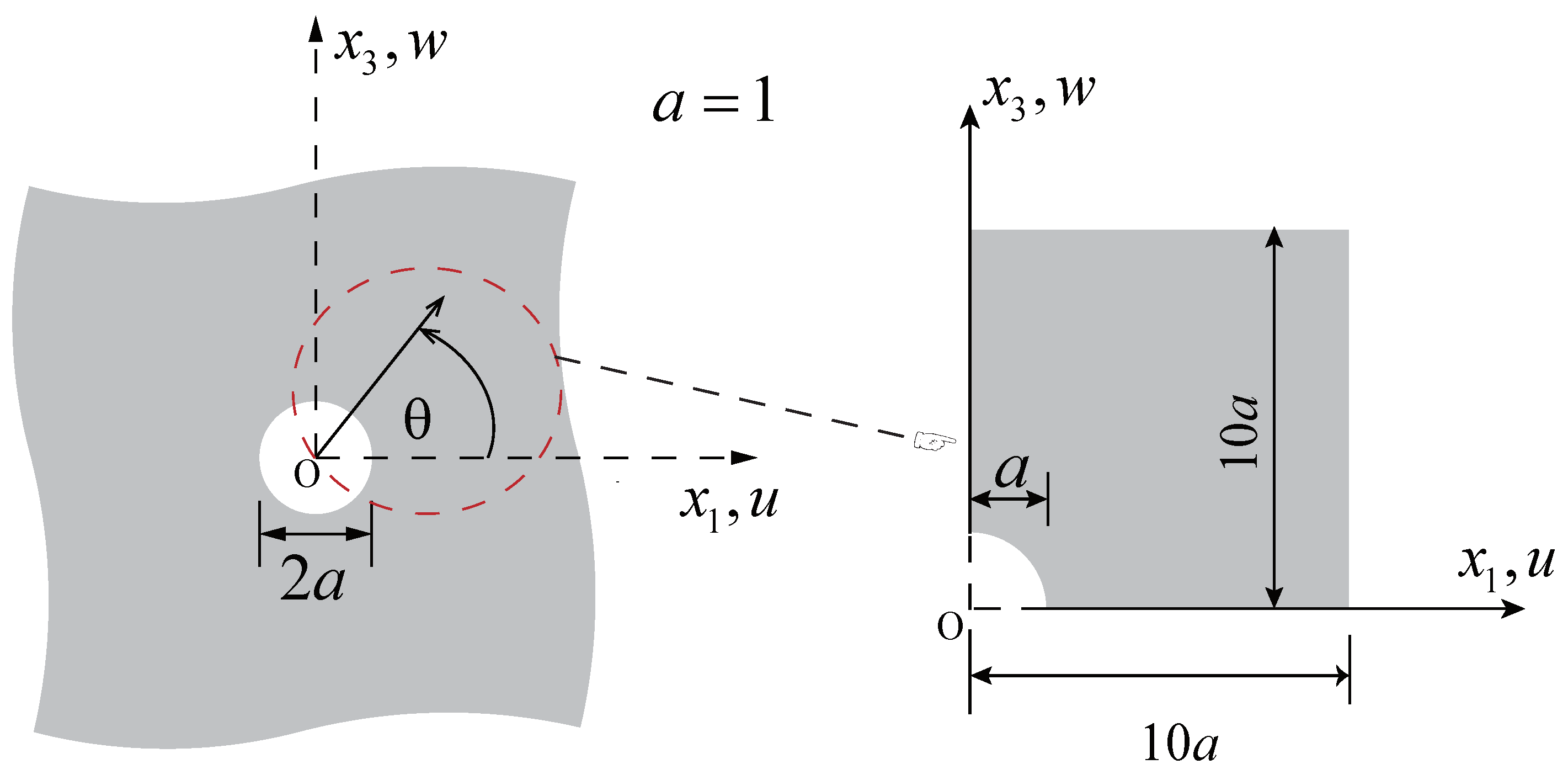
4.2. Infinite Plate with Circular Hole
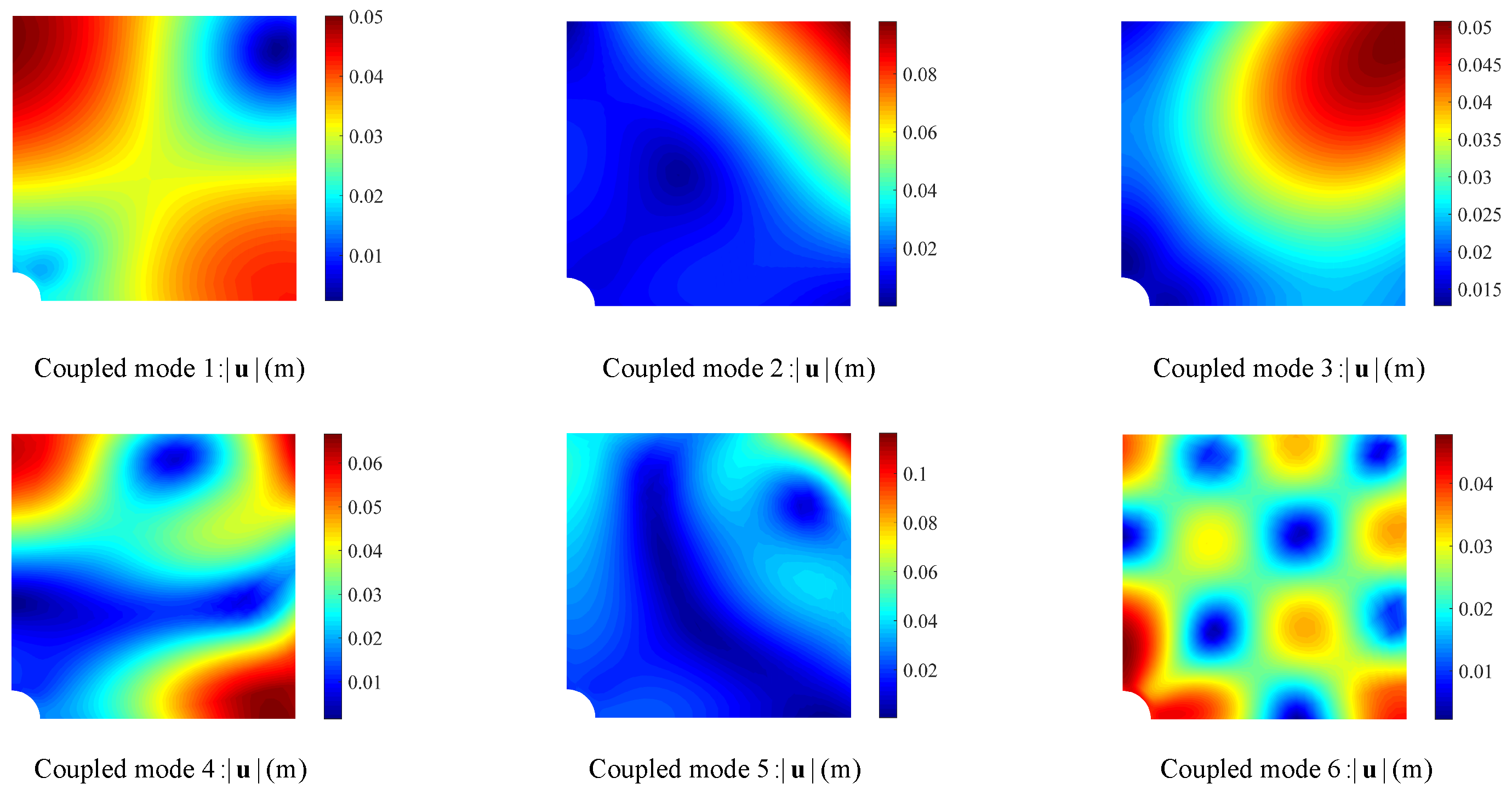
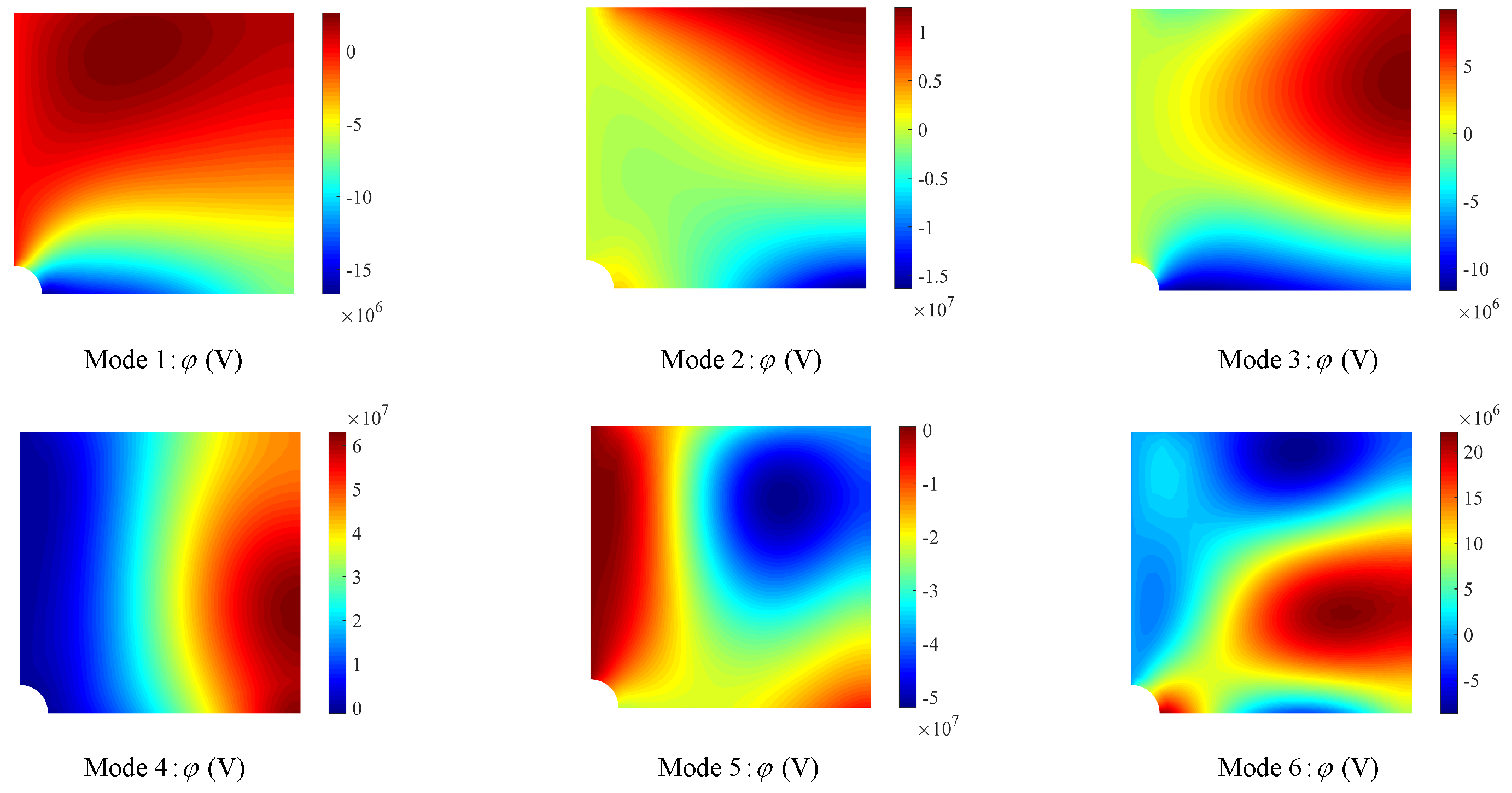
4.2.1. Infinite Plate with Circular Hole Free Vibration Analysis
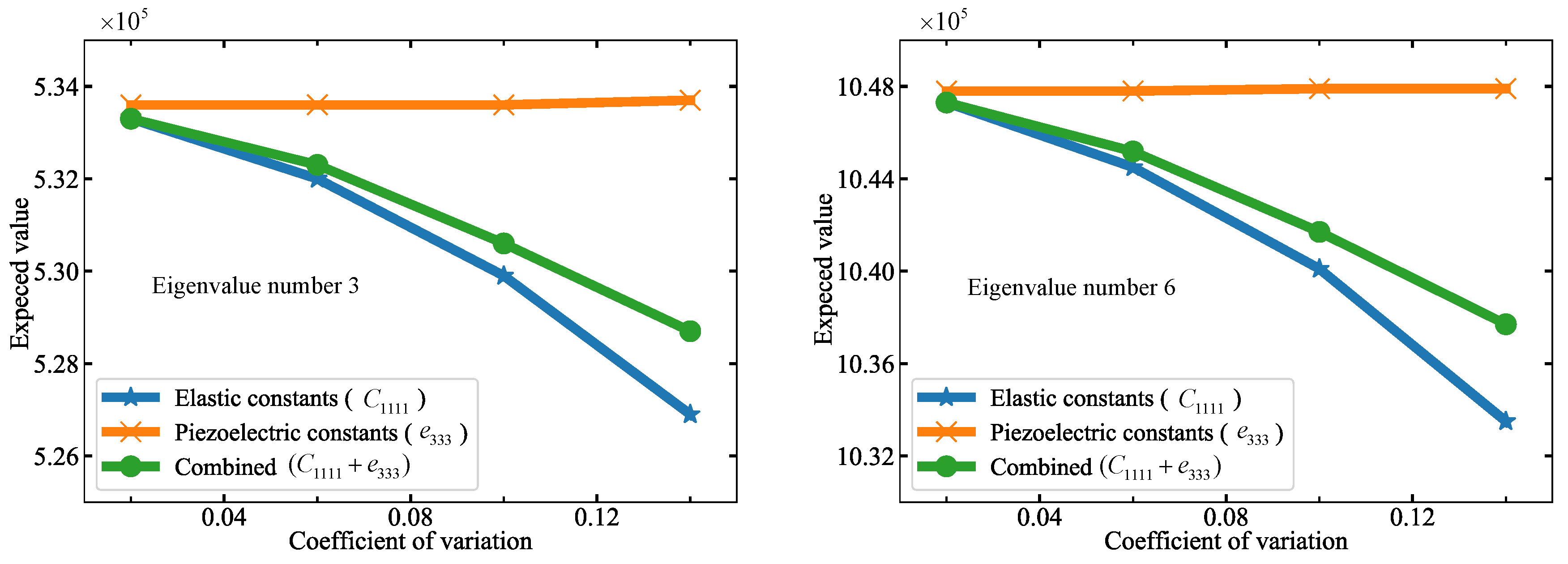
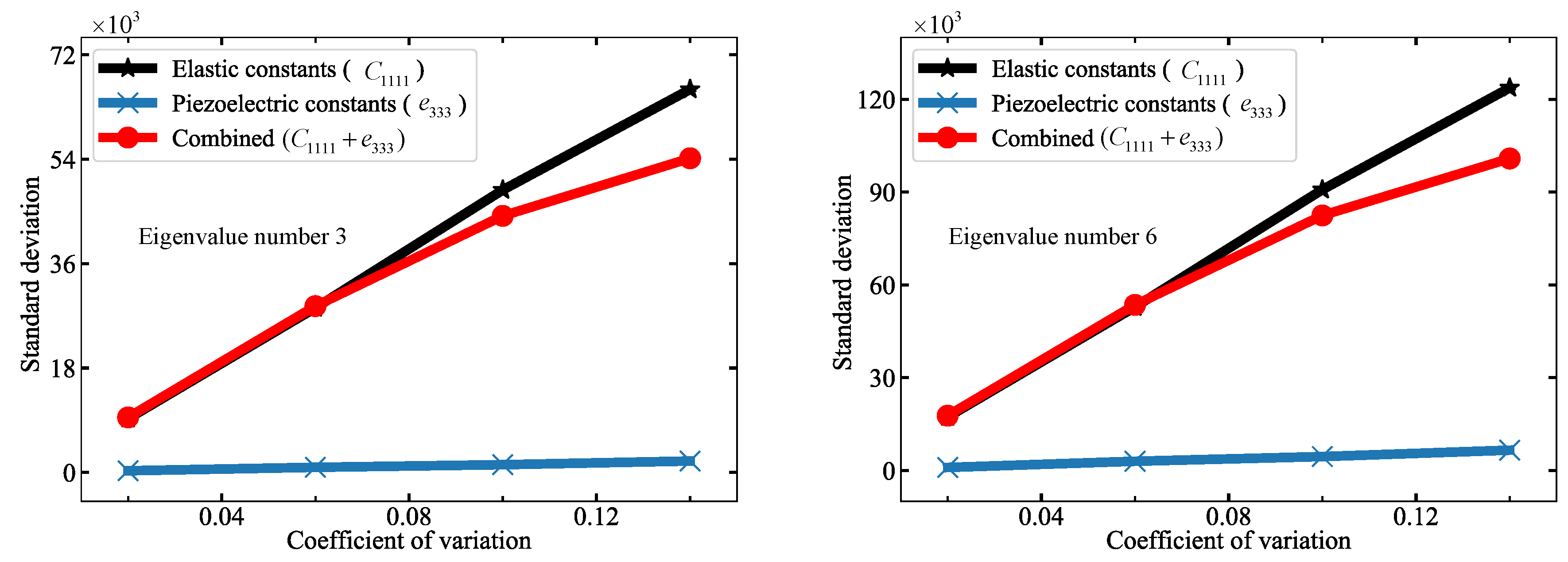
4.2.2. Uncertainty Quantification for Infinite Plate with Circular Hole Model with MCs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Stress Relaxation
References
- Redwood, M. Transient performance of a piezoelectric transducer. J. Acoust. Soc. Am. 1961, 33, 527–536. [Google Scholar] [CrossRef]
- Jaffe, H.; Berlincourt, D. Piezoelectric transducer materials. Proc. IEEE 1965, 53, 1372–1386. [Google Scholar] [CrossRef]
- Abboud, T.; Nédélec, J.; Zhou, B. Improvement of the integral equation method for high frequency problems. In Proceedings of the Third International Conference on Mathematical Aspects of Wave Propagation Phenomena, SIAM, Mandelieu-La Napoule, France, 24–28 April 1995; pp. 178–187. [Google Scholar]
- Tzou, H.; Tseng, C. Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems: A piezoelectric finite element approach. J. Sound Vib. 1990, 138, 17–34. [Google Scholar] [CrossRef]
- Ng, T.; Liao, W. Sensitivity analysis and energy harvesting for a self-powered piezoelectric sensor. J. Intell. Mater. Syst. Struct. 2005, 16, 785–797. [Google Scholar] [CrossRef]
- Safari, A.; Akdogan, E.K. Piezoelectric and Acoustic Materials for Transducer Applications; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NY, USA, 2011. [Google Scholar]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Hurtado, A.C.; Peralta, P.; Ruiz, R.; Alamdari, M.M.; Atroshchenko, E. Shape optimization of piezoelectric energy harvesters of variable thickness. J. Sound Vib. 2022, 517, 116503. [Google Scholar] [CrossRef]
- Benes, E.; Hammer, D. Piezoelectric resonator with acoustic reflectors. J. Acoust. Soc. Am. 1980, 67, 750. [Google Scholar] [CrossRef]
- Nowotny, H.; Benes, E. General one-dimensional treatment of the layered piezoelectric resonator with two electrodes. J. Acoust. Soc. Am. 1987, 82, 513–521. [Google Scholar] [CrossRef]
- Hollkamp, J.J. Multimodal passive vibration suppression with piezoelectric materials and resonant shunts. J. Intell. Mater. Syst. Struct. 1994, 5, 49–57. [Google Scholar] [CrossRef]
- Johannsmann, D. Piezoelectric stiffening. In The Quartz Crystal Microbalance in Soft Matter Research; Springer: New York, NY, USA, 2015; pp. 125–142. [Google Scholar]
- Rahaman, M.N.; De Jonghe, L.C.; Chu, M.Y. Effect of green density on densification and creep during sintering. J. Am. Ceram. Soc. 1991, 74, 514–519. [Google Scholar] [CrossRef]
- Chen, P.; Yi, K.; Liu, J.; Hou, Y.; Chu, B. Effects of density inhomogeneity in green body on the structure and properties of ferroelectric ceramics. J. Mater. Sci. Mater. Electron. 2021, 32, 16554–16564. [Google Scholar] [CrossRef]
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Methods Appl. Mech. Eng. 2009, 198, 1031–1051. [Google Scholar] [CrossRef] [Green Version]
- Kamiński, M. Generalized perturbation-based stochastic finite element method in elastostatics. Comput. Struct. 2007, 85, 586–594. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Courier Corporation: Chelmsford, MA, USA, 2003. [Google Scholar]
- Chen, N.Z.; Soares, C.G. Spectral stochastic finite element analysis for laminated composite plates. Comput. Methods Appl. Mech. Eng. 2008, 197, 4830–4839. [Google Scholar] [CrossRef]
- Hurtado, J.; Barbat, A. Monte Carlo techniques in computational stochastic mechanics. Arch. Comput. Methods Eng. 1998, 5, 3–29. [Google Scholar] [CrossRef]
- Spanos, P.D.; Zeldin, B.A. Monte Carlo Treatment of Random Fields: A Broad Perspective. Appl. Mech. Rev. 1998, 51, 219–237. [Google Scholar] [CrossRef]
- Feng, Y.; Li, C.; Owen, D. A directed Monte Carlo solution of linear stochastic algebraic system of equations. Finite Elem. Anal. Des. 2010, 46, 462–473. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, R.; Li, S.; Lian, H.; Zheng, C.; Bordas, S.P. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic–vibration interaction problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114784. [Google Scholar] [CrossRef]
- Hughes, T.; Cottrell, J.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Lian, H.; Liu, Z.; Chen, H.; Atroshchenko, E.; Bordas, S. Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Comput. Methods Appl. Mech. Eng. 2019, 355, 926–951. [Google Scholar] [CrossRef]
- Yu, B.; Cao, G.; Meng, Z.; Gong, Y.; Dong, C. Three-dimensional transient heat conduction problems in FGMs via IG-DRBEM. Comput. Methods Appl. Mech. Eng. 2021, 384, 113958. [Google Scholar] [CrossRef]
- González-Rodelas, P.; Pasadas, M.; Kouibia, A.; Mustafa, B. Numerical Solution of Linear Volterra Integral Equation Systems of Second Kind by Radial Basis Functions. Mathematics 2022, 10, 223. [Google Scholar] [CrossRef]
- Chen, L.; Marburg, S.; Zhao, W.; Liu, C.; Chen, H. Implementation of Isogeometric Fast Multipole Boundary Element Methods for 2D Half-Space Acoustic Scattering Problems with Absorbing Boundary Condition. J. Theor. Comput. Acoust. 2019, 27, 1850024. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Lu, C.; Zhao, W.; Chen, H.; Zheng, C. Subdivision Surfaces - Boundary Element Accelerated by Fast Multipole for the Structural Acoustic Problem. J. Theor. Comput. Acoust. 2020, 28, 2050011. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Lian, H.; Atroshchenko, E.; Ding, C.; Bordas, S.P. Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on Catmull-Clark subdivision surfaces. Adv. Eng. Softw. 2020, 149, 102879. [Google Scholar] [CrossRef]
- Ibáñez, M.J.; Barrera, D.; Maldonado, D.; Yáñez, R.; Roldán, J.B. Non-Uniform Spline Quasi-Interpolation to Extract the Series Resistance in Resistive Switching Memristors for Compact Modeling Purposes. Mathematics 2021, 9, 2159. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Natarajan, S.; Zhao, W.; Chen, X.; Bordas, S. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput. Methods Appl. Mech. Eng. 2022, 395, 114997. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Yuan, X.; Wu, H. Discontinuous Galerkin Isogeometric Analysis of Convection Problem on Surface. Mathematics 2021, 9, 497. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Zhao, W.; Liu, L. An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Comput. Methods Appl. Mech. Eng. 2018, 336, 507–532. [Google Scholar] [CrossRef]
- Yu, B.; Cao, G.; Huo, W.; Zhou, H.; Atroshchenko, E. Isogeometric dual reciprocity boundary element method for solving transient heat conduction problems with heat sources. J. Comput. Appl. Math. 2021, 385, 113197. [Google Scholar] [CrossRef]
- Peng, X.; Atroshchenko, E.; Kerfriden, P.; Bordas, S.P.A. Linear elastic fracture simulation directly from CAD: 2D NURBS-based implementation and role of tip enrichment. Int. J. Fract. 2017, 204, 55–78. [Google Scholar] [CrossRef]
- Yu, P.; Bordas, S.P.A.; Kerfriden, P. Adaptive Isogeometric analysis for transient dynamics: Space–time refinement based on hierarchical a-posteriori error estimations. Comput. Methods Appl. Mech. Eng. 2022, 394, 114774. [Google Scholar] [CrossRef]
- Peng, X.; Atroshchenko, E.; Kerfriden, P.; Bordas, S.P.A. Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Comput. Methods Appl. Mech. Eng. 2017, 316, 151–185. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Li, K.; Peng, X.; Lian, H.; Lin, X.; Fu, Z. Isogeometric Boundary Element Analysis for 2D Transient Heat Conduction Problem with Radial Integration Method. Comput. Model. Eng. Sci. 2021, 126, 125–146. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Peng, X.; Yang, J.; Wu, P.; Lian, H. Modeling pressurized fracture propagation with the isogeometric BEM. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Liu, Z.; Gong, Y.; Zheng, C.; Bordas, S. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM–BEM. Eng. Anal. Bound. Elem. 2022, 135, 182–195. [Google Scholar] [CrossRef]
- Ghasemi, H.; Park, H.S.; Rabczuk, T. A level-set based IGA formulation for topology optimization of flexoelectric materials. Comput. Methods Appl. Mech. Eng. 2017, 313, 239–258. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Anitescu, C.; Bordas, S.P.; Rabczuk, T. Isogeometric analysis: An overview and computer implementation aspects. Math. Comput. Simul. 2015, 117, 89–116. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.T.; Kumar, P.; Leong, J.Y.C. Finite Element Modelling and Simulations of Piezoelectric Actuators Responses with Uncertainty Quantification. Computation 2018, 6, 60. [Google Scholar] [CrossRef] [Green Version]





| Name | PZT-4 |
|---|---|
| Mass density | 7500 kg/m |
| Elastic constants | |
| 139 GPa | |
| 77.8 GPa | |
| 74 GPa | |
| 115 GPa | |
| 25.6 GPa | |
| Piezoelectric constants | |
| 12.7 C/m | |
| −5.2 C/m | |
| 15.7 C/m | |
| Permittivity | |
| 6.46 × 10 C/(Vm) | |
| 5.62 × 10 C/(Vm) |
| i | (mm, mm) | (mm, mm) | (mm, mm) | |||
|---|---|---|---|---|---|---|
| 1 | (0, 0) | (24, 22) | (48, 44) | 1 | 1 | 1 |
| 2 | (0, 22) | (24, 37) | (48, 52) | 1 | 1 | 1 |
| 3 | (0, 44) | (24, 52) | (48, 60) | 1 | 1 | 1 |
| Eigenvalue Number | Elastic (Hz) | Piezoelectric Coupled (Hz) |
|---|---|---|
| 1 | 3.90 × 10 | 4.23 × 10 |
| 2 | 1.00 × 10 | 1.19 × 10 |
| 3 | 1.21 × 10 | 1.28 × 10 |
| 4 | 2.00 × 10 | 2.29 × 10 |
| 5 | 2.55 × 10 | 2.73 × 10 |
| 6 | 2.83 × 10 | 3.09 × 10 |
| Random Input Variables | The Limits of Input Variables: [Lower, Upper] | ||
|---|---|---|---|
| = 0.02 | = 0.06 | ||
| 1.39 × 10 | [1.31 × 10, 1.46 × 10] | [1.14 × 10, 1.66 × 10] | |
| 15.1 | [14.3, 16.2] | [12.2, 17.7] | |
| Random Input Variables | The Limits of Input Variables: [Lower, Upper] | |||
|---|---|---|---|---|
| = 0.1 | = 0.14 | = 0.18 | ||
| 1.39 × 10 | [8.96 × 10, 1.85 × 10] | [8.59 × 10, 2.08 × 10] | [7.81 × 10, 2.17 × 10] | |
| 15.1 | [10.5, 19.5] | [9.1, 20.8] | [7.5, 22.0] | |
| Dimension of Input | Variable | Samples |
|---|---|---|
| Variables | (,) | |
| 1-D | (500, 500) | |
| (500, 500) | ||
| 2-D | + | (, 625) |
| Name | PZT-5H |
|---|---|
| Mass density | 7500 kg/m |
| Elastic constants | |
| 126 GPa | |
| 79.1 GPa | |
| 83.9 GPa | |
| 117 GPa | |
| 23 GPa | |
| Piezoelectric constants | |
| 17.0 C/m | |
| −6.5 C/m | |
| 23.3 C/m | |
| Permittivity | |
| 1.505 × 10 C/(Vm) | |
| 1.302 × 10 C/(Vm) |
| i | (mm, mm) | (mm, mm) | (mm, mm) | (mm, mm) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | (0, 1) | (0, 3.4278) | (0, 7.75) | (0, 10) | 1 | 1 | 1 | 1 |
| 2 | (0.4142, 1) | (0.5954, 3.4278) | (5.375, 7.75) | (10, 10) | 0.8536 | 1 | 1 | 1 |
| 3 | (1, 0.4142) | (3.4278, 0.5954) | (7.75, 5.375) | (10, 10) | 0.8536 | 1 | 1 | 1 |
| 4 | (1, 0) | (3.4278, 0) | (7.75, 0) | (10, 0) | 1 | 1 | 1 | 1 |
| Eigenvalue Number | Elastic (Hz) | Piezoelectric Coupled (Hz) |
|---|---|---|
| 1 | 3.33 × 10 | 3.46 × 10 |
| 2 | 4.13 × 10 | 4.28 × 10 |
| 3 | 5.23 × 10 | 5.34 × 10 |
| 4 | 7.26 × 10 | 8.10 × 10 |
| 5 | 8.49 × 10 | 9.26 × 10 |
| 6 | 1.01 × 10 | 1.05 × 10 |
| Random Input Variables | Symbol | The Limits of Input Variables: [Lower, Upper] | ||
|---|---|---|---|---|
| = 0.02 | = 0.06 | |||
| Elastic constants | 1.26 × 10 | [1.18 × 10, 1.33 × 10] | [1.04 × 10, 1.53 × 10] | |
| piezoelectric constants | 23.3 | [22.0, 24.8] | [19.1, 29.0] | |
| Random Input Variables | Symbol | The Limits of Input Variables: [Lower, Upper] | ||
|---|---|---|---|---|
| = 0.1 | = 0.14 | |||
| Elastic constants | 1.26 × 10 | [8.86 × 10, 1.61 × 10] | [8.06 × 10, 1.72 × 10] | |
| piezoelectric constants | 23.3 | [17.3, 31.0] | [12.9, 34.1] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Li, H.; Chen, L.; Zhao, J.; Zhang, X. Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials. Mathematics 2022, 10, 1840. https://doi.org/10.3390/math10111840
Xu Y, Li H, Chen L, Zhao J, Zhang X. Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials. Mathematics. 2022; 10(11):1840. https://doi.org/10.3390/math10111840
Chicago/Turabian StyleXu, Yanming, Haozhi Li, Leilei Chen, Juan Zhao, and Xin Zhang. 2022. "Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials" Mathematics 10, no. 11: 1840. https://doi.org/10.3390/math10111840
APA StyleXu, Y., Li, H., Chen, L., Zhao, J., & Zhang, X. (2022). Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials. Mathematics, 10(11), 1840. https://doi.org/10.3390/math10111840







