Rigid-Flexible Coupling Dynamics Modeling of Spatial Crank-Slider Mechanism Based on Absolute Node Coordinate Formulation
Abstract
:1. Introduction
2. Cable Model Based on ANCF Method
2.1. ANCF Cable Element Model
2.2. Element Mass Matrix
2.3. Generalized Elastic Force of Element
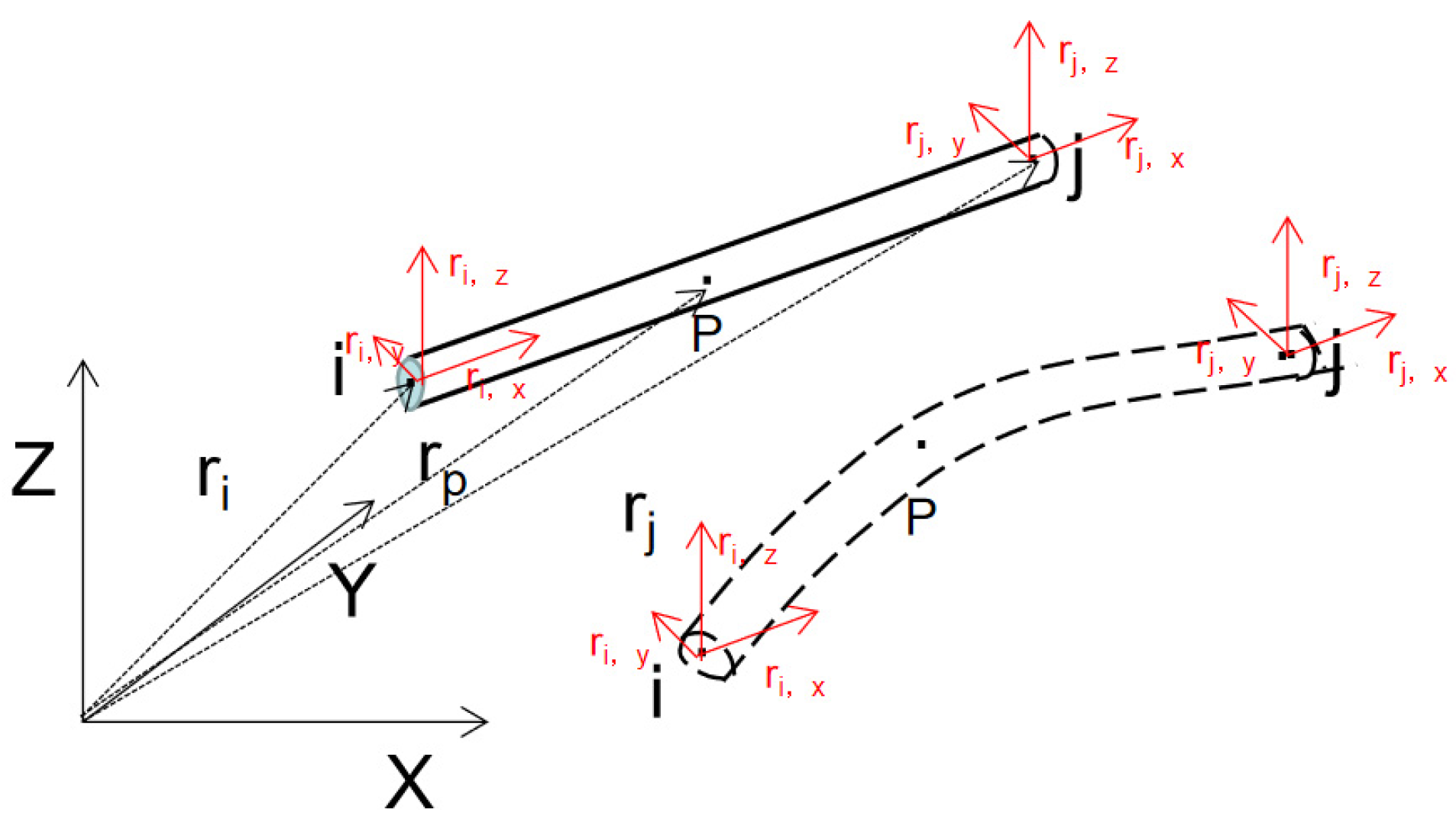
2.4. Generalized External Force of Element
3. Rigid-Flexible Coupling Dynamic Model
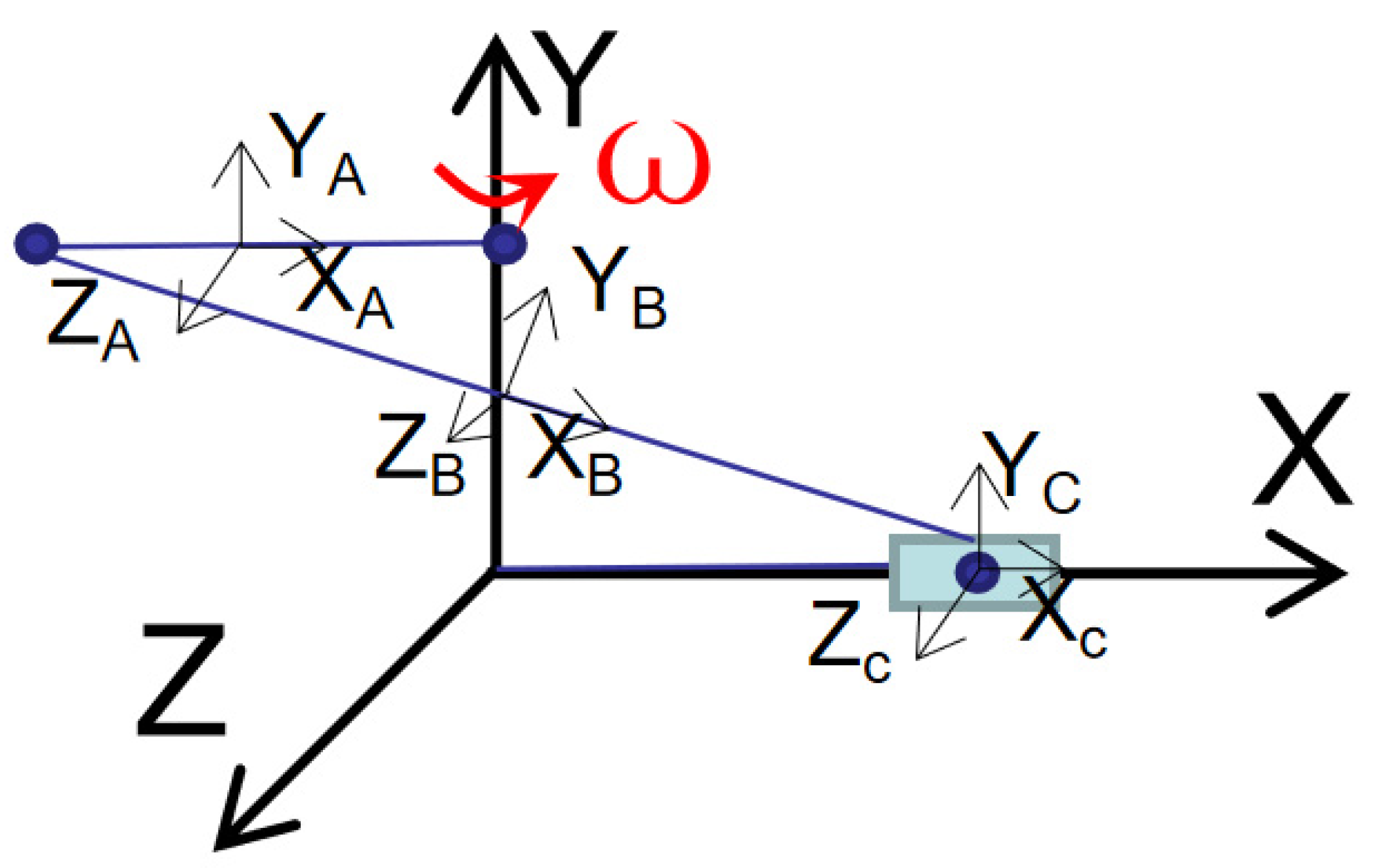
3.1. Mechanism Analysis
3.2. Rigid-Flexible Coupling Dynamic Equation
4. Numerical Simulation and Analysis
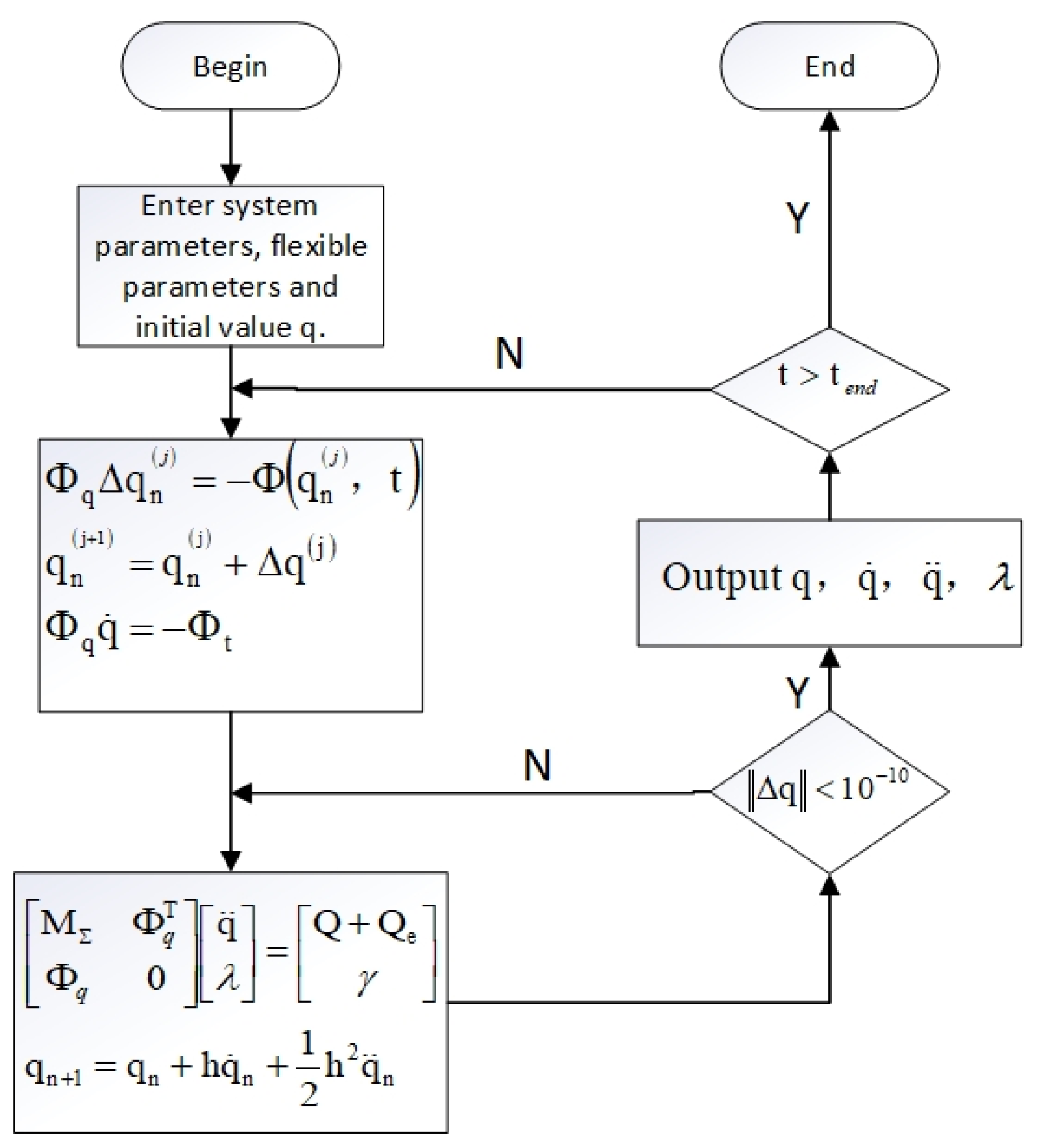
4.1. Simulation Process and Parameters
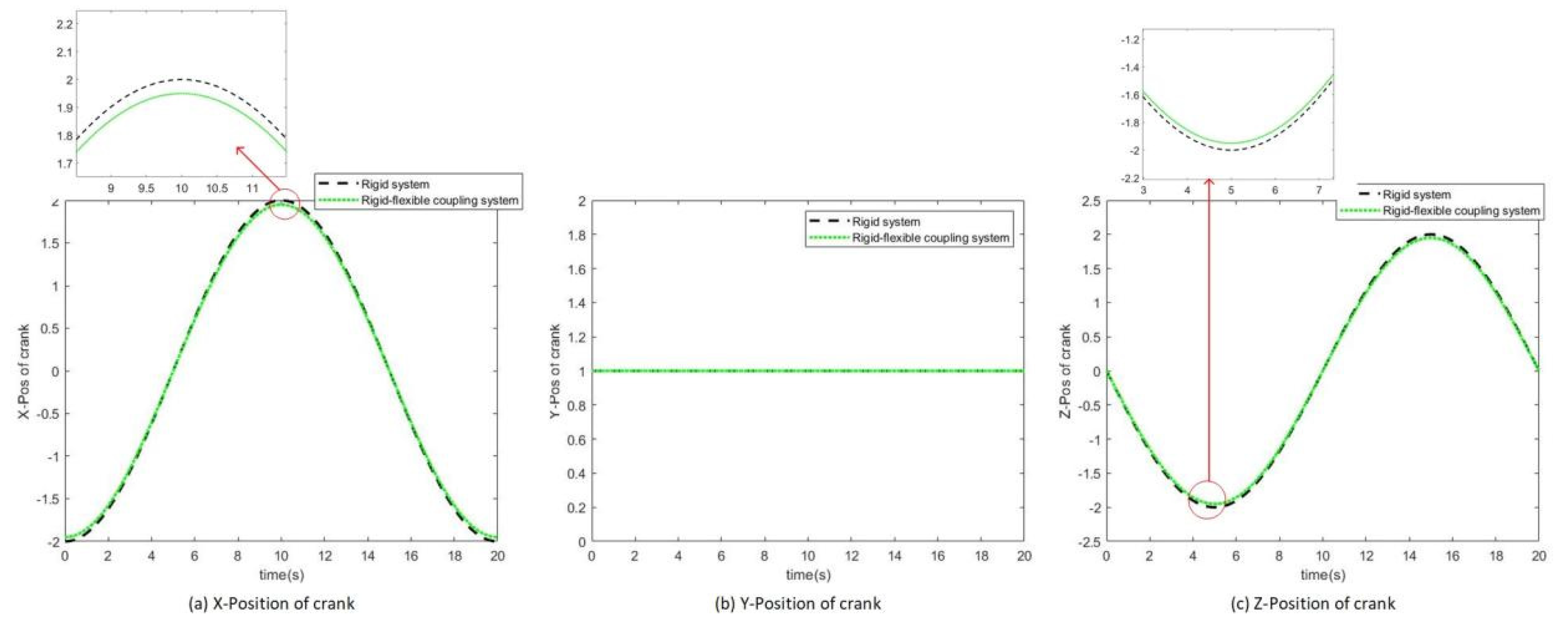
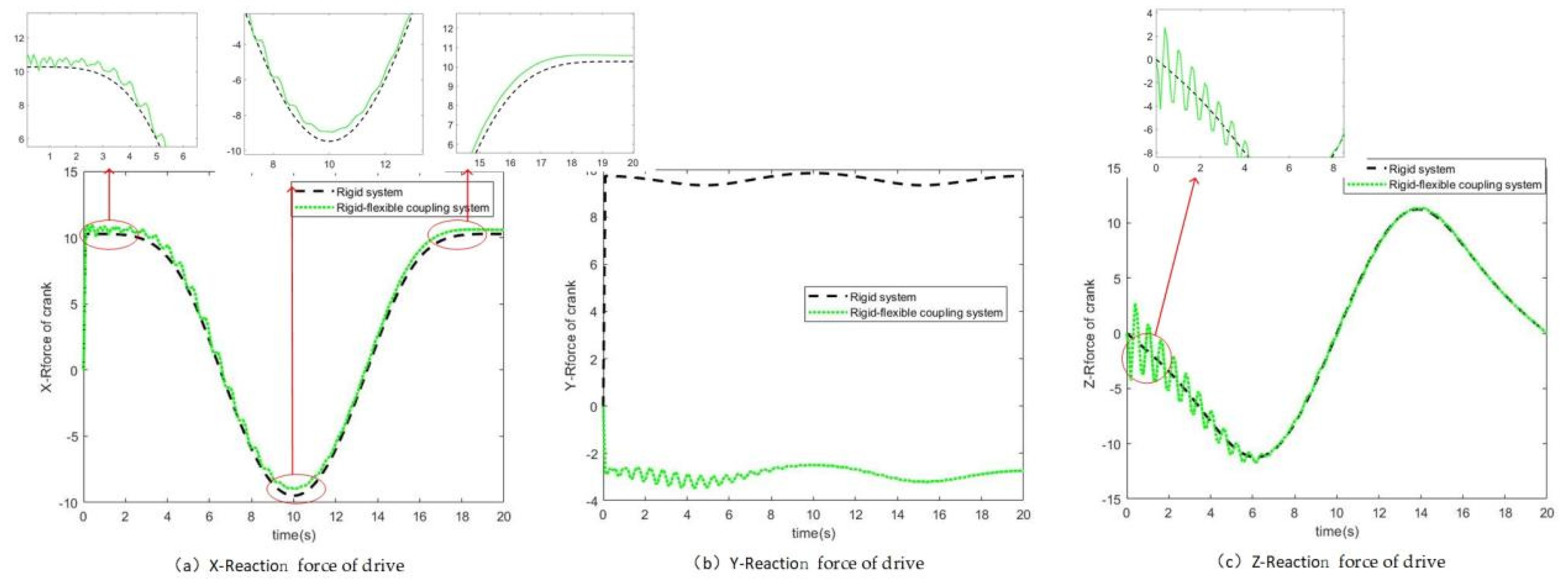
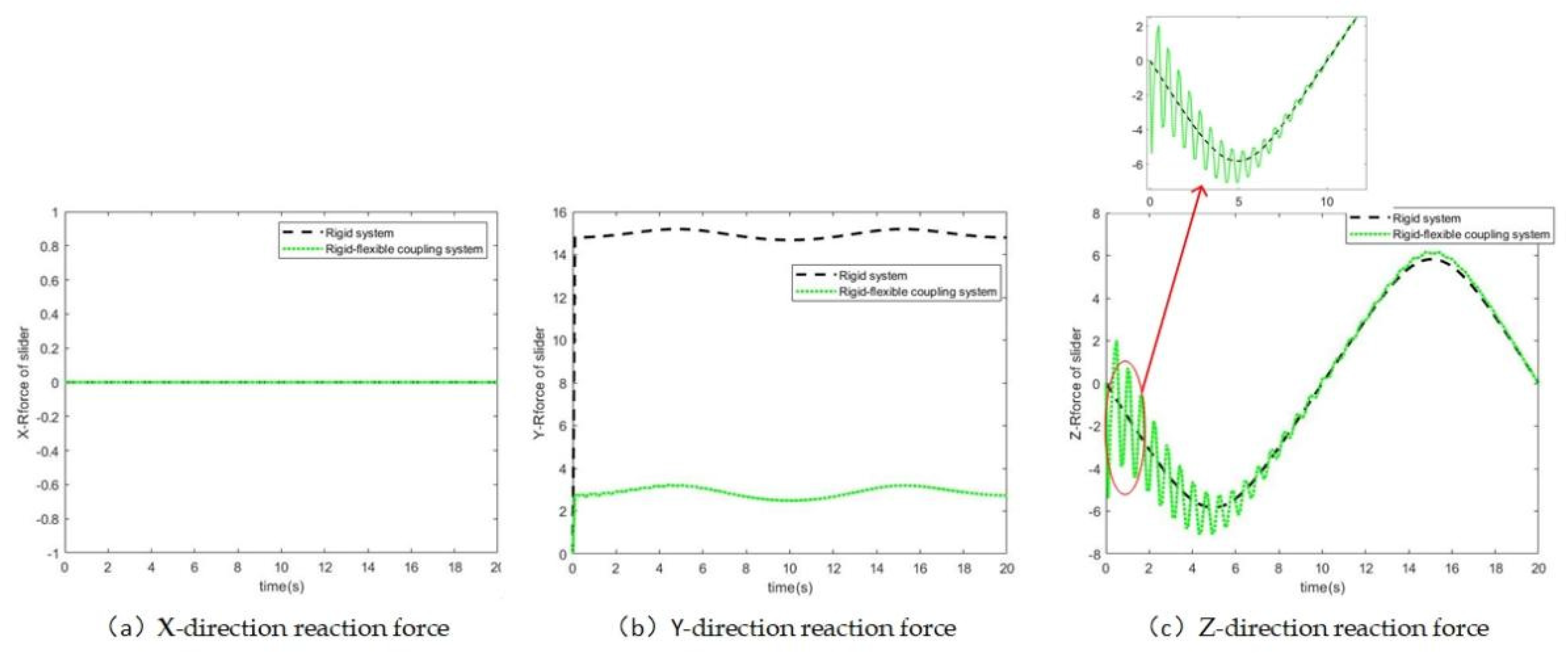
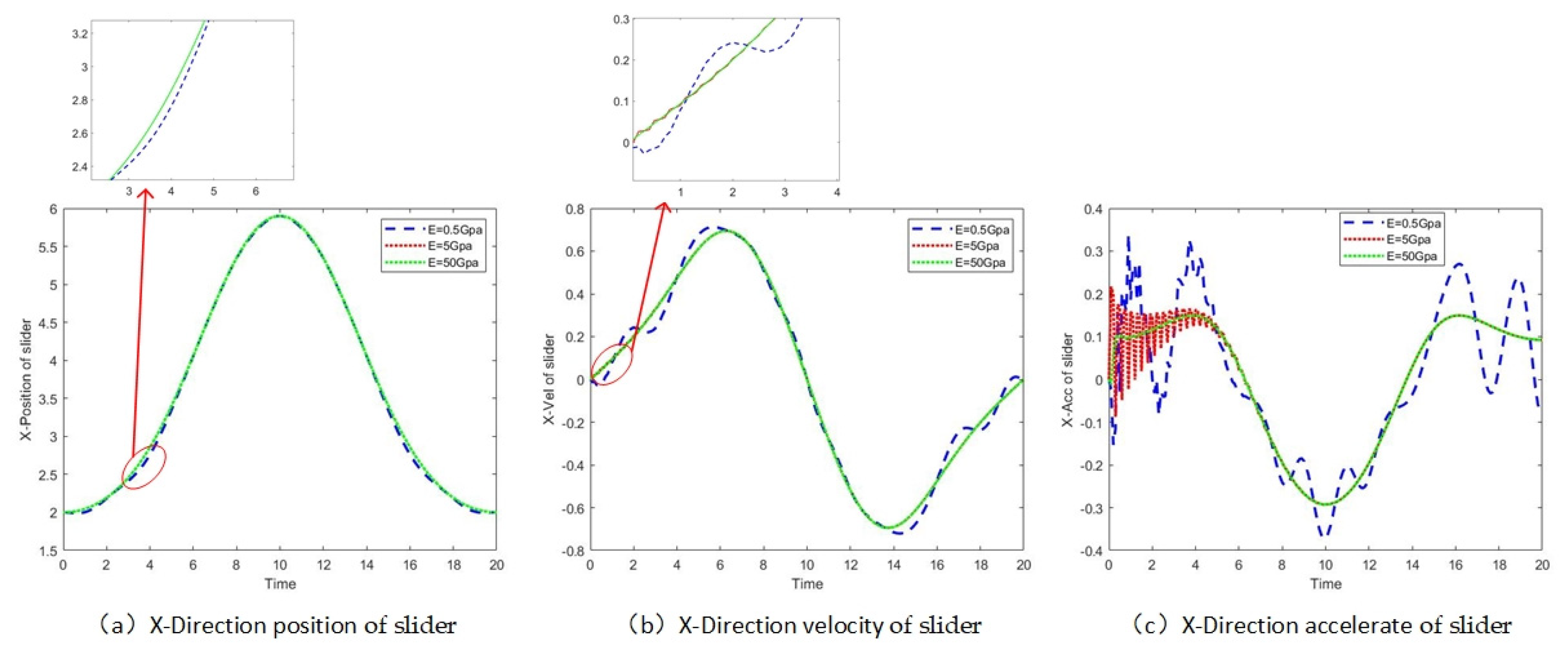
4.2. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dias, J.; Pereira, M.S. Sensitivity Analysis of Rigid-Flexible Multibody Systems. Multibody Syst. Dyn. 1997, 1, 303–322. [Google Scholar] [CrossRef]
- Youwu, L. Application of multi-body dynamics in mechanical engineering. China Mech. Eng. 2000, 11, 6. [Google Scholar]
- Wittenburg, J.; Likins, P. Dynamics of Systems of Rigid Bodies. J. Appl. Mech. 1977, 45, 458. [Google Scholar] [CrossRef]
- Nikravesh, P.E.; Chung, I.S. Application of Euler Parameters to the Dynamic Analysis of Three-Dimensional Constrained Mechanical Systems. J. Mech. Des. 1982, 104, 785–791. [Google Scholar] [CrossRef]
- Haug, E.J.; Wu, S.C.; Yang, S.M. Dynamics of mechanical systems with Coulomb friction, stiction, impact and constraint addition-deletion—III Spatial systems. Mech. Mach. Theory 1986, 21, 401–406. [Google Scholar] [CrossRef]
- Shabana, A.A. Definition of the Slopes and the Finite Element Absolute Nodal Coordinate Formulation. Multi-Body Syst. Dyn. 1997, 1, 339–348. [Google Scholar] [CrossRef]
- Garcia-Vallejo, D.; Mayo, J.; Escalona, J.L.; Domínguez, J. Three-dimensional formulation of rigid-flexible multibody systems with flexible beam elements. Multibody Syst. Dyn. 2008, 20, 1–28. [Google Scholar] [CrossRef]
- Zhang, C. Mechanical Dynamics, 2nd ed.; Higher Education Press: Beijing, China, 2008. [Google Scholar]
- Jiazhen, H.; Chaolan, Y. Research progress of rigid-flexible coupling system dynamics. J. Dyn. Control. 2004, 2, 6. [Google Scholar]
- Jiazhen, H.; Zhuyong, L. Modeling method of rigid-flexible coupling dynamics. J. Shanghai Jiaotong Univ. 2008, 42, 5. [Google Scholar]
- Jiazhen, H.; Lizhong, J. Rigid-flexible coupling dynamics of flexible multi-body system. Mech. Prog. 2000, 30, 6. [Google Scholar]
- Likins, P.W. Finite element appendage equations for hybrid coordinate dynamic analysis. Int. J. Solids Struct. 1972, 8, 709–731. [Google Scholar] [CrossRef]
- Bakr, E.M.; Shabana, A.A. Geometrically nonlinear analysis of multi-body systems. Comput. Struct. 1986, 23, 739–751. [Google Scholar] [CrossRef]
- Lin, B.; Xie, C. Dynamics of Flexible multi-body Systems. Acta Mech. Sin. 1989, 4, 469–478. [Google Scholar]
- Yigi, S.A. The Effect of Flexibility on the Impact Response of a Two-Link Rigid-Flexible Manipulator. J. Sound Vib. 1994, 177, 349–361. [Google Scholar] [CrossRef]
- Choura, S.; Yigit, A.S. Control of a Two-Link Rigid–Flexible Manipulator with a Moving Payload Mass. J. Sound Vib. 2001, 243, 883–897. [Google Scholar] [CrossRef]
- Williams, D.; Fredrickson, G.H. Cylindrical Micelles in Rigid-Flexible Diblock Copolymers. MRS Online Proc. Libr. 1991, 248, 3561–3568. [Google Scholar] [CrossRef]
- Duan, Y.C.; Zhang, D.G. Rigid-Flexible Coupling Dynamics of a Flexible Robot with Impact. Adv. Mater. Res. 2011, 199, 243–250. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, J.; Hong, J. Nonlinear dynamic analysis on rigid-flexible coupling system of an elastic beam. Theor. Appl. Mech. Lett. 2012, 2, 023001. [Google Scholar] [CrossRef] [Green Version]
- Bai, Z.F.; Zhao, Y.; Tian, H. Study on collision dynamics of flexible multibody system. J. Vib. Shock. 2009, 28, 75–78+195–196. [Google Scholar]
- Wang, J.M.; Hong, J.Z. Experimental Study on Flexible Multibody Dynamics. J. Astronaut. 1999, 2, 108–112. [Google Scholar]
- Mo, L. Kinematics and dynamics analysis of crank-slider mechanism based on MATLAB. Automot. Pract. Technol. 2019, 23, 135–137. [Google Scholar] [CrossRef]
- Li, T.T.; Zhang, Z.S.; Cui, G.H.; Guan, L.Z. Dynamic analysis of crank-connecting rod mechanism with coupling hinge clearance and flexibility. Mech. Transm. 2021, 45, 116–122. [Google Scholar] [CrossRef]
- Qian, Y.; Cao, Y.; Liu, Y.W.; Zhou, H. Forward Kinematics Simulation Analysis of Slider-Crank Mechanism. Adv. Mater. Res. 2011, 308–310, 1855–1859. [Google Scholar] [CrossRef]
- Ma, X.G.; Lu, Y.; You, X.M. Multi-body dynamics simulation analysis of planetary gear train based on multi-body dynamics technology. China Mech. Eng. 2009, 20, 1956–1959+1964. [Google Scholar]
- Liu, Y.H.; Miu, B.Q. Theoretical basis and functional analysis of multi-body dynamics simulation software ADAMS. Electron. Packag. 2005, 5, 5. [Google Scholar]
- Shi, Z.X.; Fung, E.; Lie, Y.C. Dynamic modelling of a rigid-flexible manipulator for constrained motion task control. Appl. Math. Model. 1999, 23, 509–525. [Google Scholar] [CrossRef]
- Wu, M.Q.; Mei, H.F.; Zhang, Z.Q. Multi-body dynamics simulation of linkage mechanism based on ADAMS. J. Eng. Des. 2005, 12, 4. [Google Scholar]
- Fan, B.L.; Yang, G.H.; Zhu, X.Y. Research and practice teaching of crank-connecting rod mechanism based on multi-body dynamics simulation. Met. World 2021, 1, 71–75. [Google Scholar]
- Sugiyama, H.; Escalona, J.L.; Shabana, A.A. Formulation of Three-Dimensional Joint Constraints Using the Absolute Nodal Coordinates. Nonlinear Dyn. 2003, 31, 167–195. [Google Scholar] [CrossRef]
- Shabana, A.A. Computational Continuum Mechanics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]





| Component | Crank A | Connecting Rod B | Slider C |
|---|---|---|---|
| / | 0.005 | 0.005 | 0.05 |
| / | 0.1 | 0.1 | 0.05 |
| / | 0.1 | 0.1 | 0.05 |
| Mass/kg | 1 | 0.5 | 1 |
| Length/m | 2 | 0.4 | |
| Section Diameter/m | / | 0.03 | / |
| Young’s Modulus/Pa | / | 5 × 109 | / |
| Number of Elements | / | 9 | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, H.; Zhao, J.; Xu, C.; Luo, Z.; Han, Q. Rigid-Flexible Coupling Dynamics Modeling of Spatial Crank-Slider Mechanism Based on Absolute Node Coordinate Formulation. Mathematics 2022, 10, 881. https://doi.org/10.3390/math10060881
Wang X, Wang H, Zhao J, Xu C, Luo Z, Han Q. Rigid-Flexible Coupling Dynamics Modeling of Spatial Crank-Slider Mechanism Based on Absolute Node Coordinate Formulation. Mathematics. 2022; 10(6):881. https://doi.org/10.3390/math10060881
Chicago/Turabian StyleWang, Xiaoyu, Haofeng Wang, Jingchao Zhao, Chunyang Xu, Zhong Luo, and Qingkai Han. 2022. "Rigid-Flexible Coupling Dynamics Modeling of Spatial Crank-Slider Mechanism Based on Absolute Node Coordinate Formulation" Mathematics 10, no. 6: 881. https://doi.org/10.3390/math10060881
APA StyleWang, X., Wang, H., Zhao, J., Xu, C., Luo, Z., & Han, Q. (2022). Rigid-Flexible Coupling Dynamics Modeling of Spatial Crank-Slider Mechanism Based on Absolute Node Coordinate Formulation. Mathematics, 10(6), 881. https://doi.org/10.3390/math10060881






