Adsorption of Cisplatin Molecules in Nanoporous Inorganic Materials as Drug Delivery Vehicles
Abstract
:1. Introduction
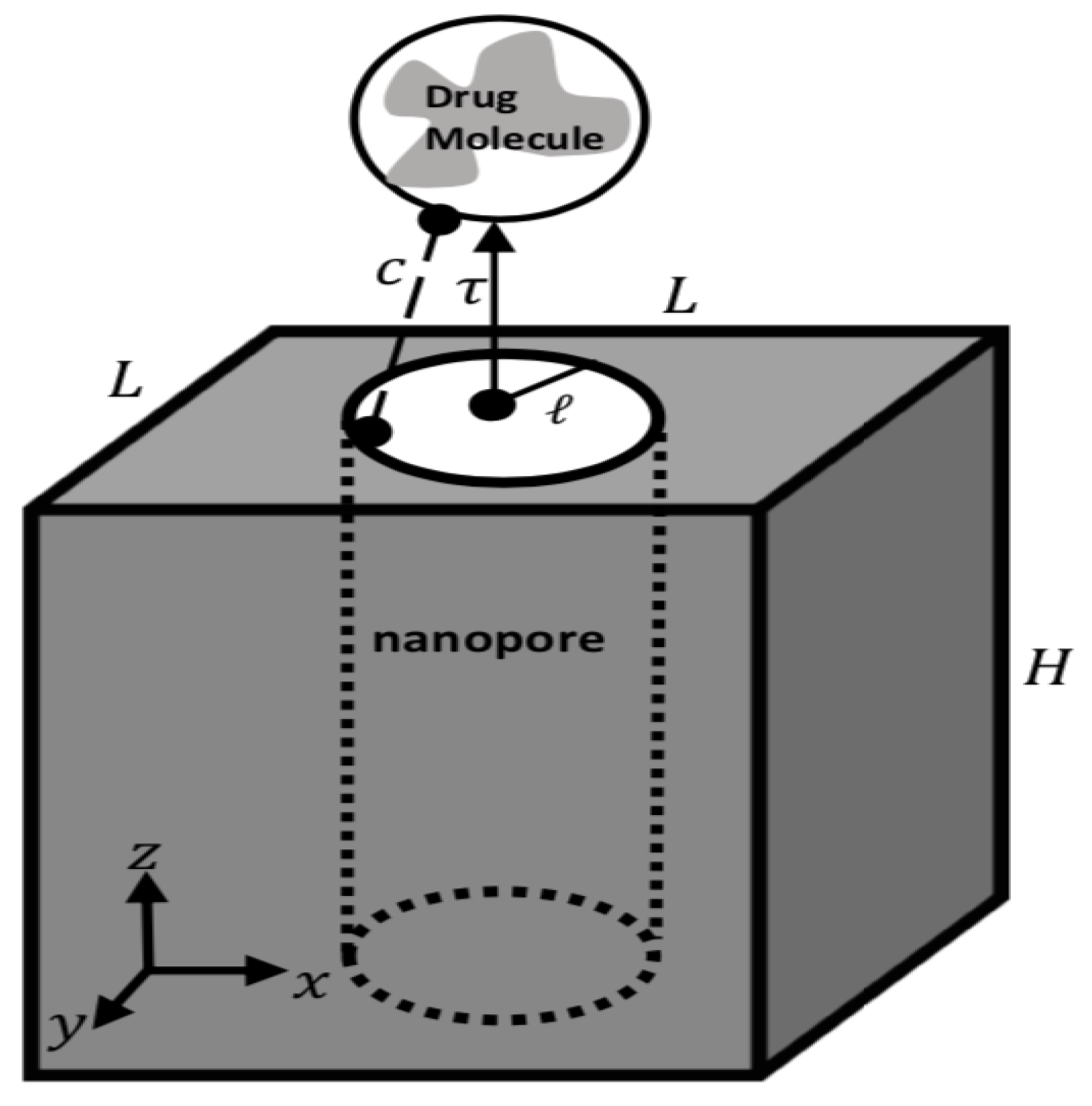
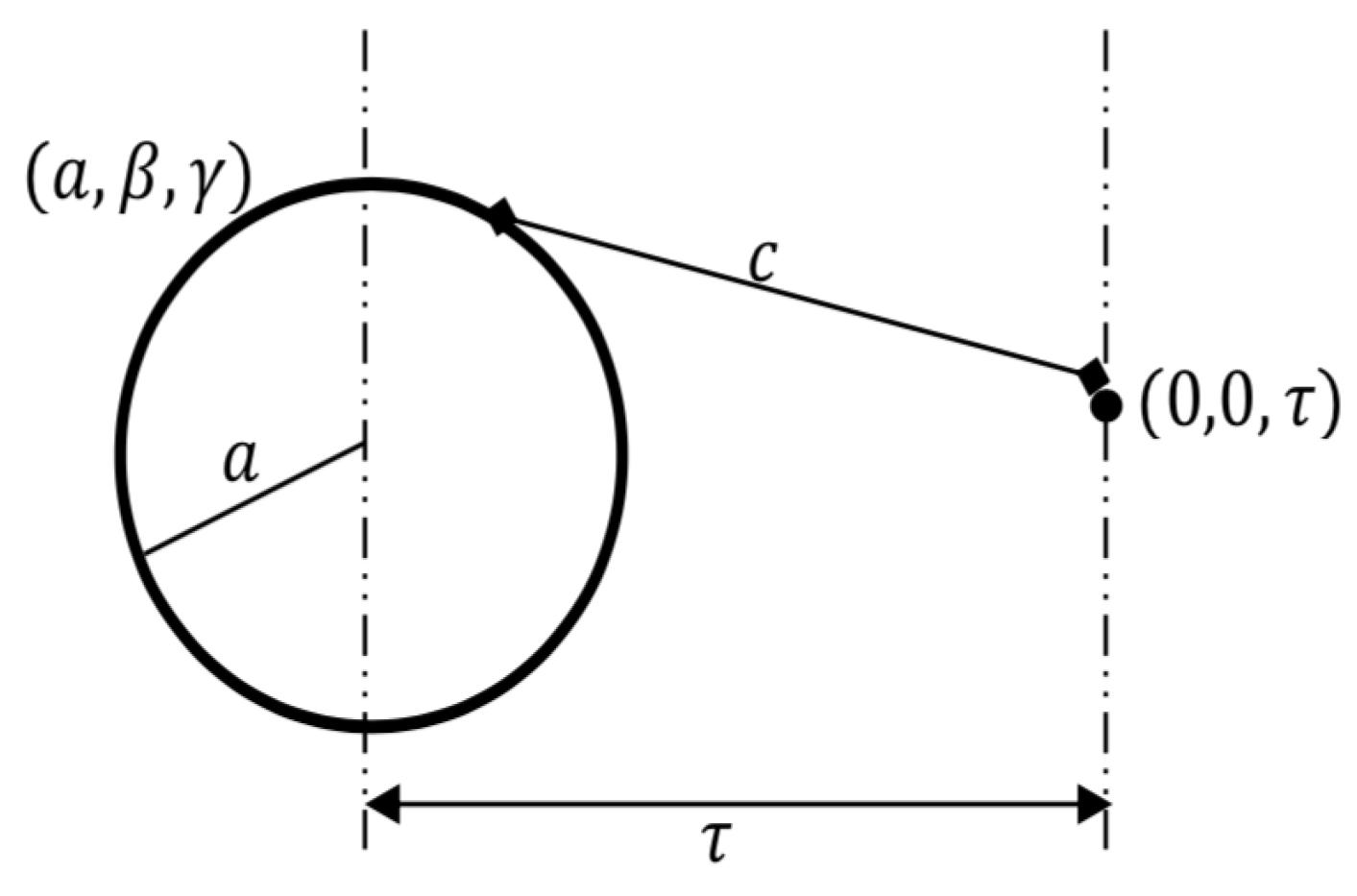
2. Modeling Approach
3. Results and Discussion
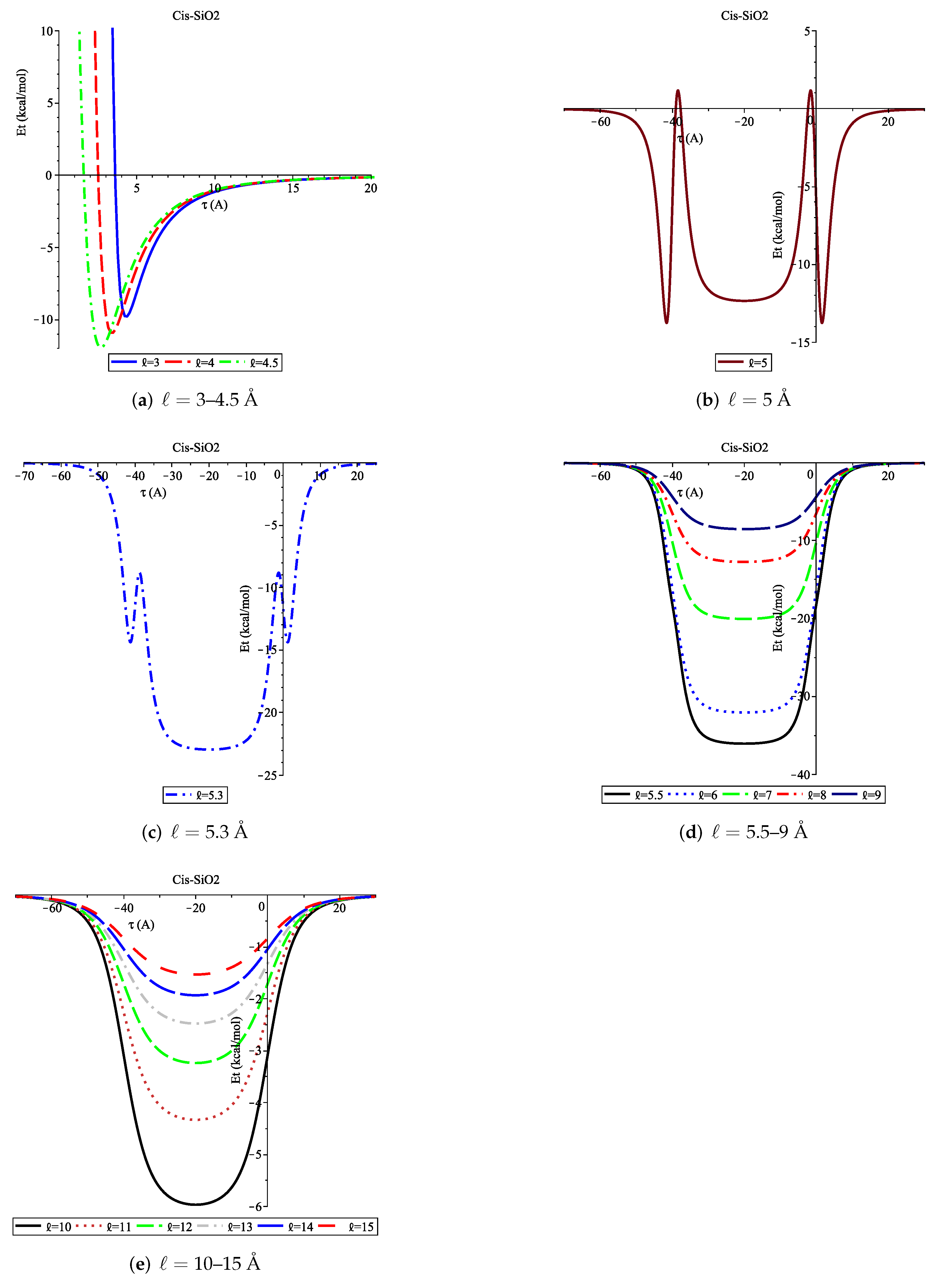
3.1. Adsorption of Cis onto SiO2 Nanopore
3.2. Adsorption of Cis onto Au Nanopore
4. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dasari, S.; Tchounwou, P.B. Cisplatin in cancer therapy: Molecular mechanisms of action. Eur. J. Pharmacol. 2014, 740, 364–378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patra, J.K.; Das, G.; Fraceto, L.F.; Campos, E.V.R.; Rodriguez-Torres, M.d.P.; Acosta-Torres, L.S.; Diaz-Torres, L.A.; Grillo, R.; Swamy, M.K.; Sharma, S.; et al. Nano based drug delivery systems: Recent developments and future prospects. J. Nanobiotechnol. 2018, 16, 71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krishnamachari, Y.; Geary, S.M.; Lemke, C.D.; Salem, A.K. Nanoparticle delivery systems in cancer vaccines. Pharm. Res. 2011, 28, 215–236. [Google Scholar] [CrossRef]
- Sahdev, P.; Ochyl, L.J.; Moon, J.J. Biomaterials for nanoparticle vaccine delivery systems. Pharm. Res. 2014, 31, 2563–2582. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.K.; Lee, D.I.; Park, J.M. Biopolymer-based microgels/nanogels for drug delivery applications. Prog. Polym. Sci. 2009, 34, 1261–1282. [Google Scholar] [CrossRef]
- Zhou, Y.; Quan, G.; Wu, Q.; Zhang, X.; Niu, B.; Wu, B.; Huang, Y.; Pan, X.; Wu, C. Mesoporous silica nanoparticles for drug and gene delivery. Acta Pharm. Sin. B 2018, 8, 165–177. [Google Scholar] [CrossRef]
- Mamaeva, V.; Sahlgren, C.; Linden, M. Mesoporous silica nano- particles in medicine e recent advances. Adv. Drug Deliv. Rev. 2013, 65, 689–702. [Google Scholar] [CrossRef]
- Tabish, T.A.; Dey, P.; Mosca, S.; Salimi, M.; Palombo, F.; Matousek, P.; Stone, N. Smart gold nanostructures for light mediated cancer theranostics: Combining optical diagnostics with photothermal therapy. Adv. Sci. 2020, 7, 1903441. [Google Scholar] [CrossRef]
- Austin, L.A.; Mackey, M.A.; Dreaden, E.C.; El-Sayed, M.A. The optical, photothermal, and facile surface chemical properties of gold and silver nanoparticles in biodiagnostics, therapy, and drug delivery. Arch. Toxicol. 2014, 88, 1391–1417. [Google Scholar] [CrossRef] [Green Version]
- Jazayeri, M.H.; Amani, H.; Pourfatollah, A.A.; Pazoki-Toroudi, H.; Sedighimoghaddam, B. Various methods of gold nanoparticles (GNPs) conjugation to antibodies. Sens. Bio-Sens. Res. 2016, 9, 17–22. [Google Scholar] [CrossRef] [Green Version]
- Sadhu, P.K.; Rajput, A.; Seth, A.K.; Kumar, D.; Dash, N.V.; Kumari, M.; Patel, S. A combined approach of gold nanoparticles with cannabinoids for the treatment of cancer: A Review. Int. J. Pharm. Res. 2020, 12, 393–405. [Google Scholar]
- Nejad, M.A.; Urbassek, H.M. Diffusion of cisplatin molecules in silica nanopores: Molecular dynamics study of a targeted drug delivery system. J. Mol. Graph. Model. 2019, 86, 228–234. [Google Scholar] [CrossRef] [PubMed]
- Nejad, M.A.; Urbassek, H.M. Adsorption and Diffusion of Cisplatin Molecules in Nanoporous Materials: A Molecular Dynamics Study. Biomolecules 2019, 9, 204. [Google Scholar] [CrossRef] [Green Version]
- Rejeeth, C.; Nag, T.C.; Kannan, S. Cisplatin-functionalized silica nanoparticles for cancer chemotherapy. Cancer Nanotechnol. 2013, 4, 127–136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watermann, A.; Juergen, B. Mesoporous silica nanoparticles as drug delivery vehicles in cancer. Nanomaterials 2017, 7, 189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, J.; Liong, M.; Zink, J.I.; Tamanoi, F. Mesoporous silica nanoparticles as a delivery system for hydrophobic anticancer drugs. Small 2007, 3, 1341–1346. [Google Scholar] [CrossRef]
- Ferrari, M. Cancer nanotechnology: Opportunities and challenges. Nat. Rev. Cancer 2005, 5, 161–171. [Google Scholar] [CrossRef]
- Rappi, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skid, W.M. UFF, a full periodic table force field formolecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Alshehri, M.H. Continuum Modelling for Encapsulation of Anticancer Drugs inside Nanotubes. Mathematics 2021, 9, 2469. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Baowan, D.; Thamwattana, N. Modelling selective separation of trypsin and lysozyme using mesoporous silica. Microporous Mesoporous Mater. 2013, 176, 209–214. [Google Scholar] [CrossRef]
- Baowan, D.; Chayantrakom, K.; Satiracoo, P.; Cox, B.J. Mathematical modelling for equilibrium configurations of concentric gold nanoparticles. J. Math. Chem. 2011, 49, 1042–1053. [Google Scholar] [CrossRef]
- Rastegari, E.; Hsiao, Y.-J.; Lai, W.-Y.; Lai, Y.-H.; Yang, T.-C.; Chen, S.-J.; Huang, P.-I.; Chiou, S.-H.; Mou, C.-Y.; Chien, Y. An Update on Mesoporous Silica Nanoparticle Applications in Nanomedicine. Pharmaceutics 2021, 13, 1067. [Google Scholar] [CrossRef] [PubMed]
- German, S.R.; Hurd, T.S.; White, H.S.; Mega, T.L. Sizing Individual Au Nanoparticles in Solution with Sub-Nanometer Resolution. ACS Nano 2015, 9, 7186–7194. [Google Scholar] [CrossRef] [PubMed]
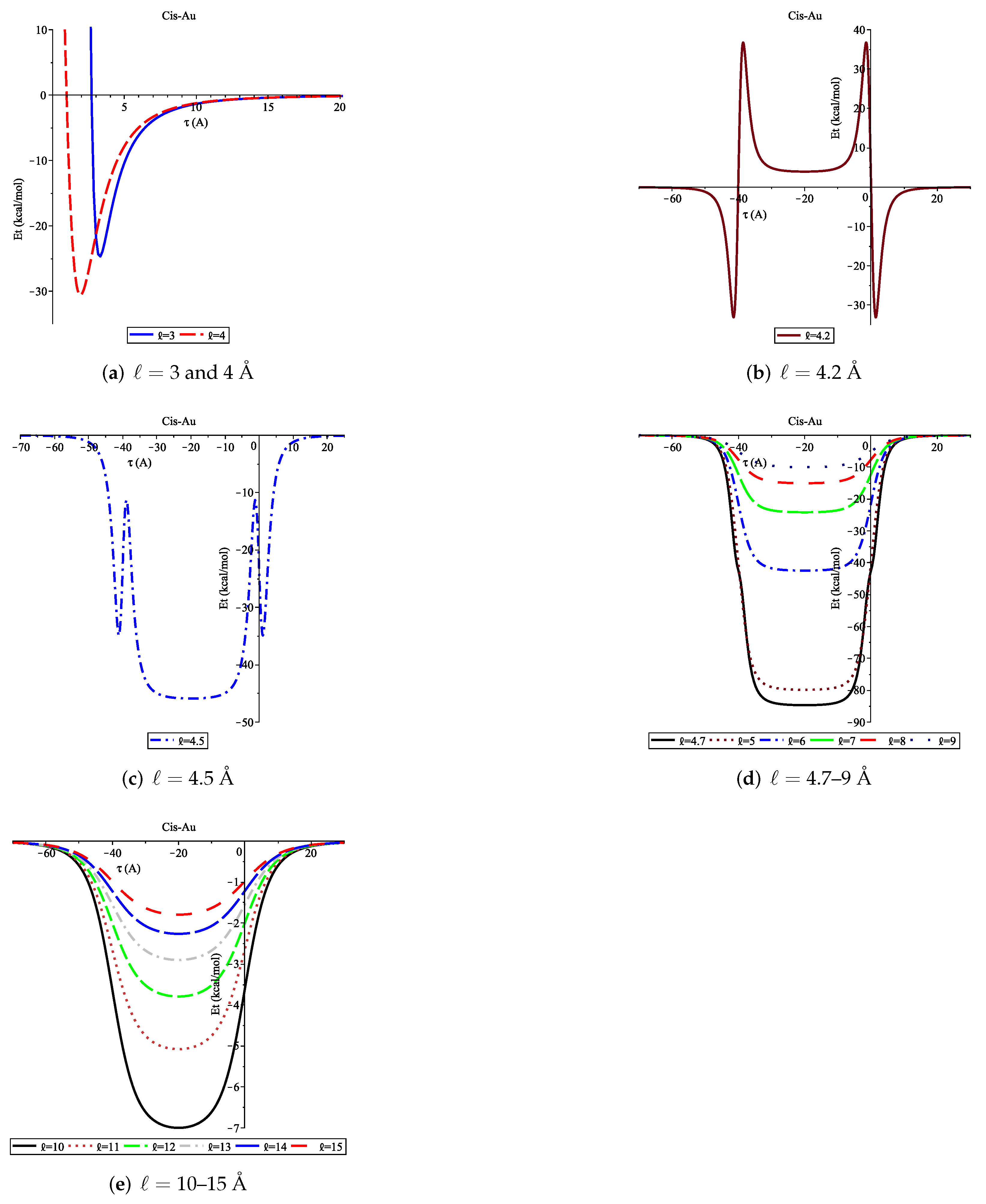
| Atom Type | Si | O | Au | H | N | Pt | Cl |
|---|---|---|---|---|---|---|---|
| D (kcal/mol) | 0.402 | 0.060 | 0.039 | 0.044 | 0.069 | 0.080 | 0.227 |
| R (Å) | 4.295 | 3.500 | 3.293 | 2.886 | 3.660 | 2.754 | 3.947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.H. Adsorption of Cisplatin Molecules in Nanoporous Inorganic Materials as Drug Delivery Vehicles. Mathematics 2022, 10, 1018. https://doi.org/10.3390/math10071018
Alshehri MH. Adsorption of Cisplatin Molecules in Nanoporous Inorganic Materials as Drug Delivery Vehicles. Mathematics. 2022; 10(7):1018. https://doi.org/10.3390/math10071018
Chicago/Turabian StyleAlshehri, Mansoor H. 2022. "Adsorption of Cisplatin Molecules in Nanoporous Inorganic Materials as Drug Delivery Vehicles" Mathematics 10, no. 7: 1018. https://doi.org/10.3390/math10071018
APA StyleAlshehri, M. H. (2022). Adsorption of Cisplatin Molecules in Nanoporous Inorganic Materials as Drug Delivery Vehicles. Mathematics, 10(7), 1018. https://doi.org/10.3390/math10071018






