CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community
Abstract
:1. Introduction
2. Mathematical Formulation
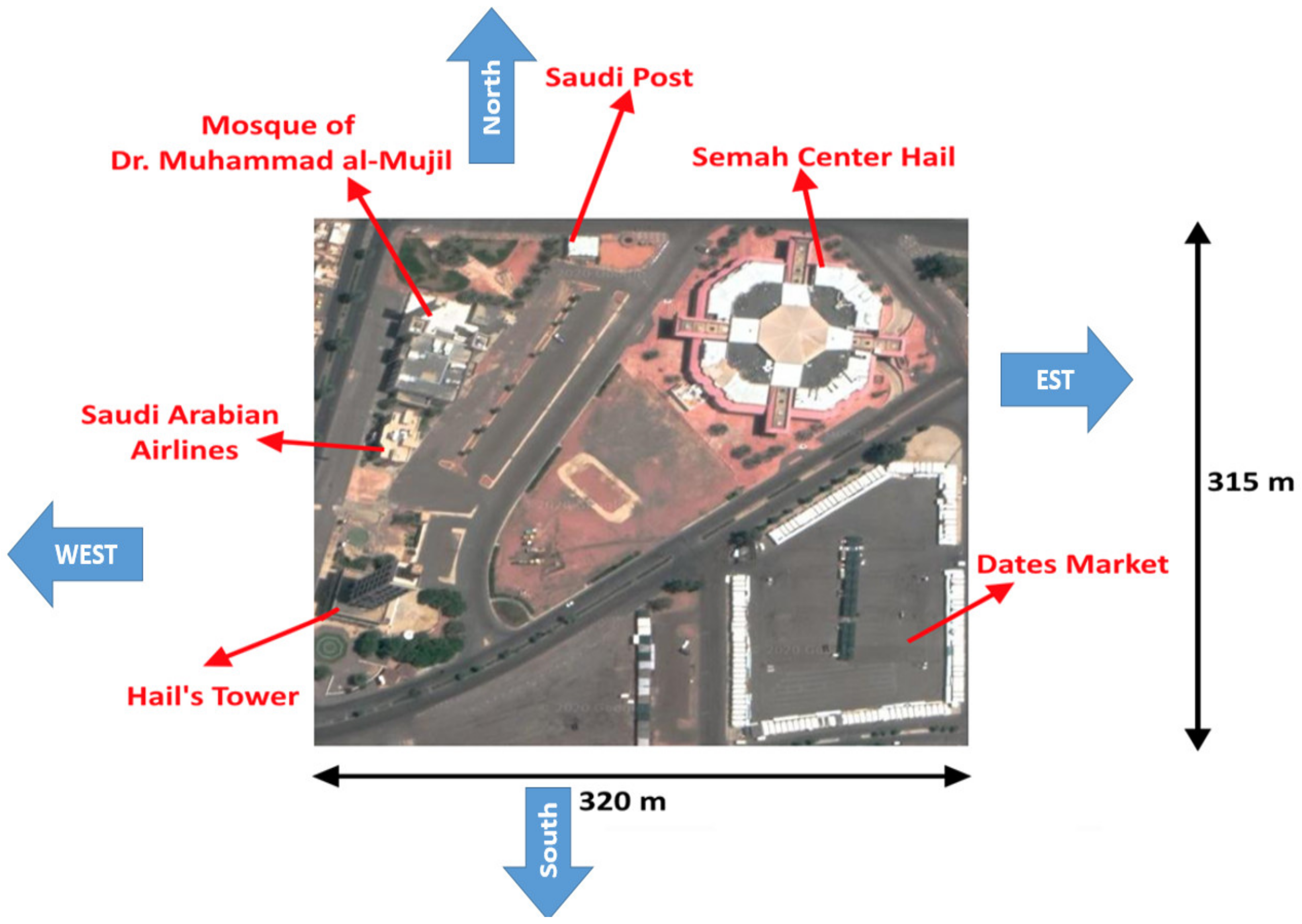
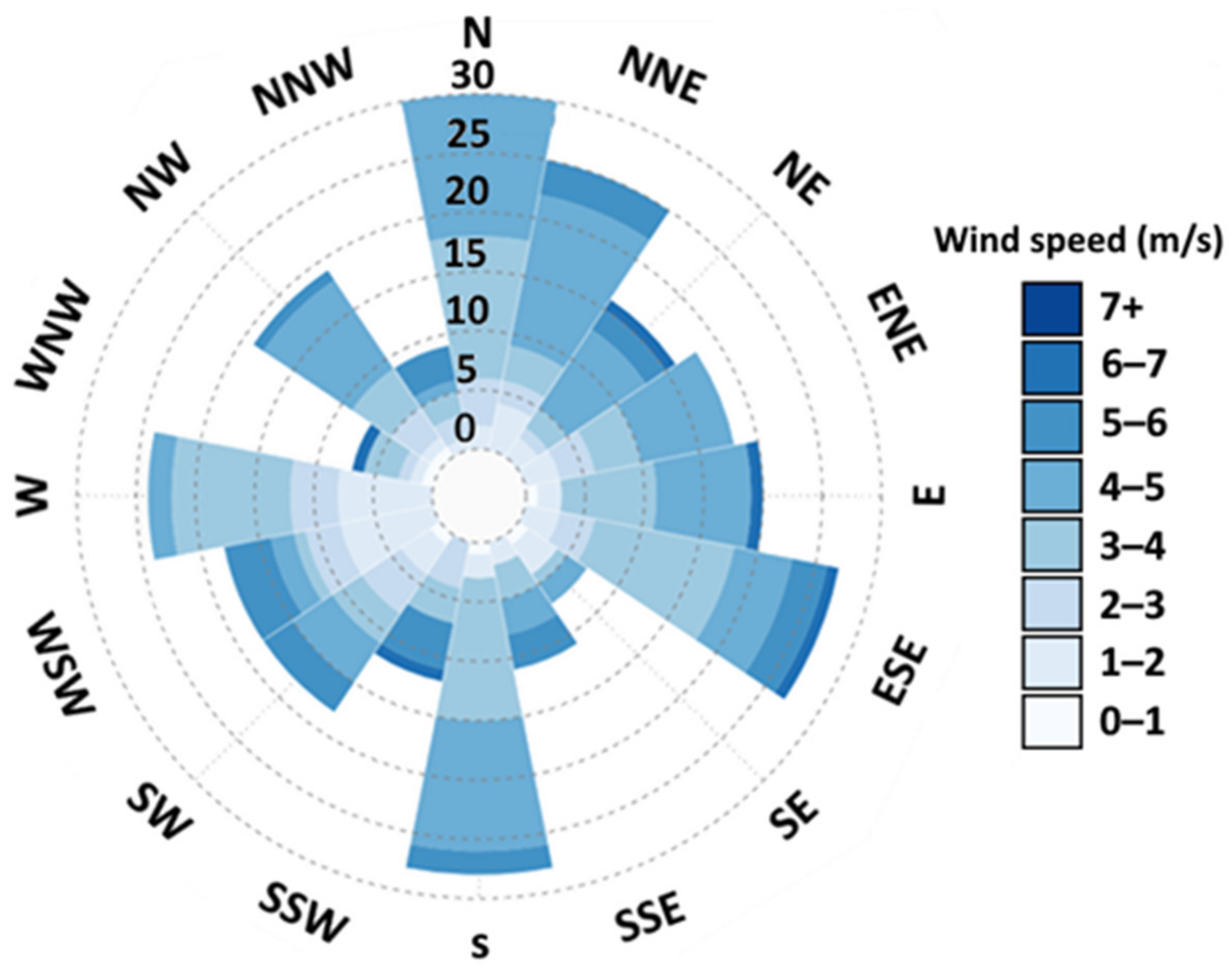
2.1. Real View of the Studied Area
2.2. Hypothesis
- Flow with three-dimensional (3D) aspect in steady state.
- Air is considered as the work fluid with constant physical and thermal properties.
- Flow with turbulent and fully developed aspect.
- Thermal effects due to the thermal gradient between the ground and the ambient air are neglected.
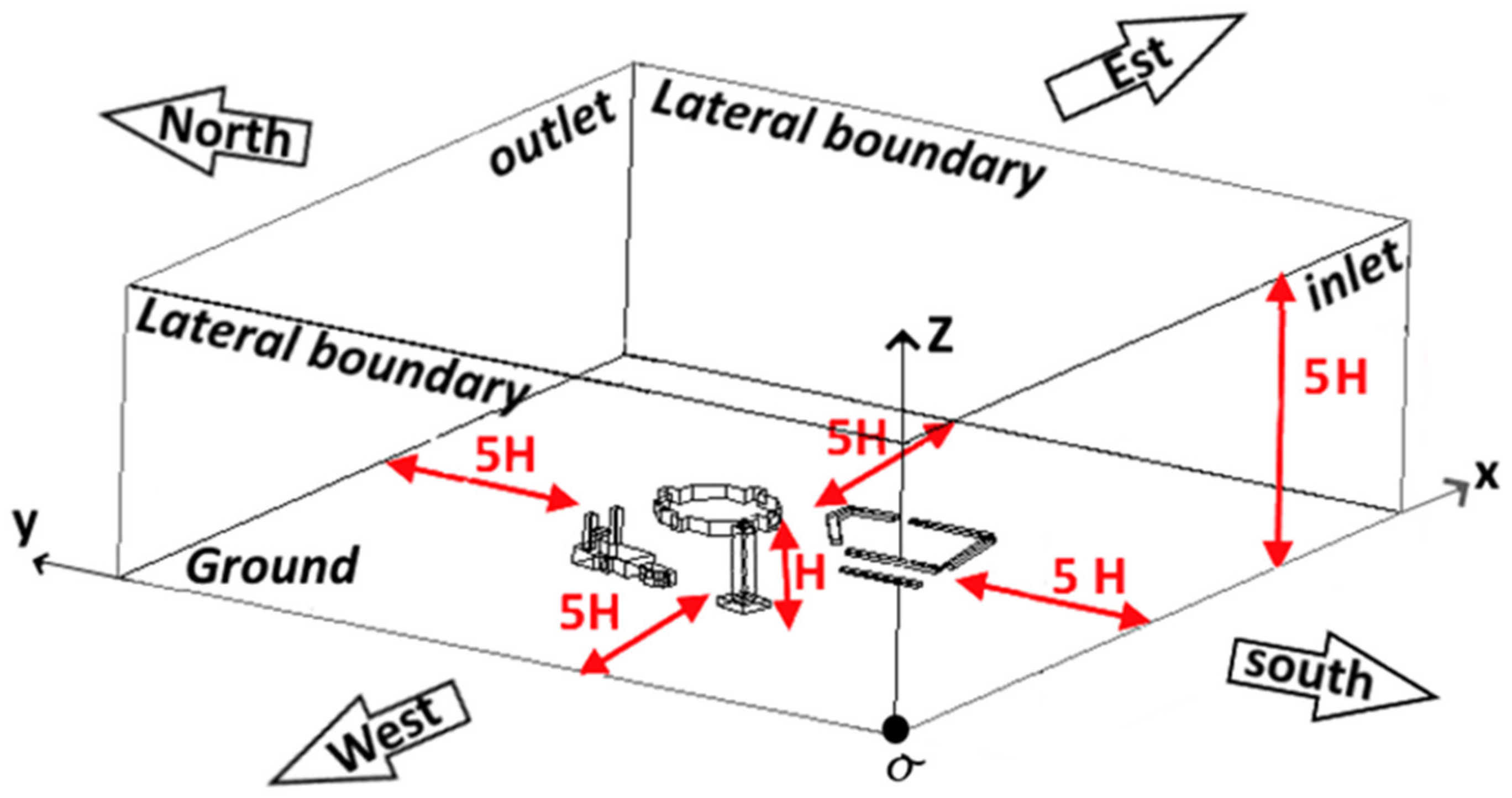
2.3. Geometric Configuration and Numerical Model
2.4. Governing Equations
2.5. Grid Distribution and Boundary Conditions
2.6. Numerical Method
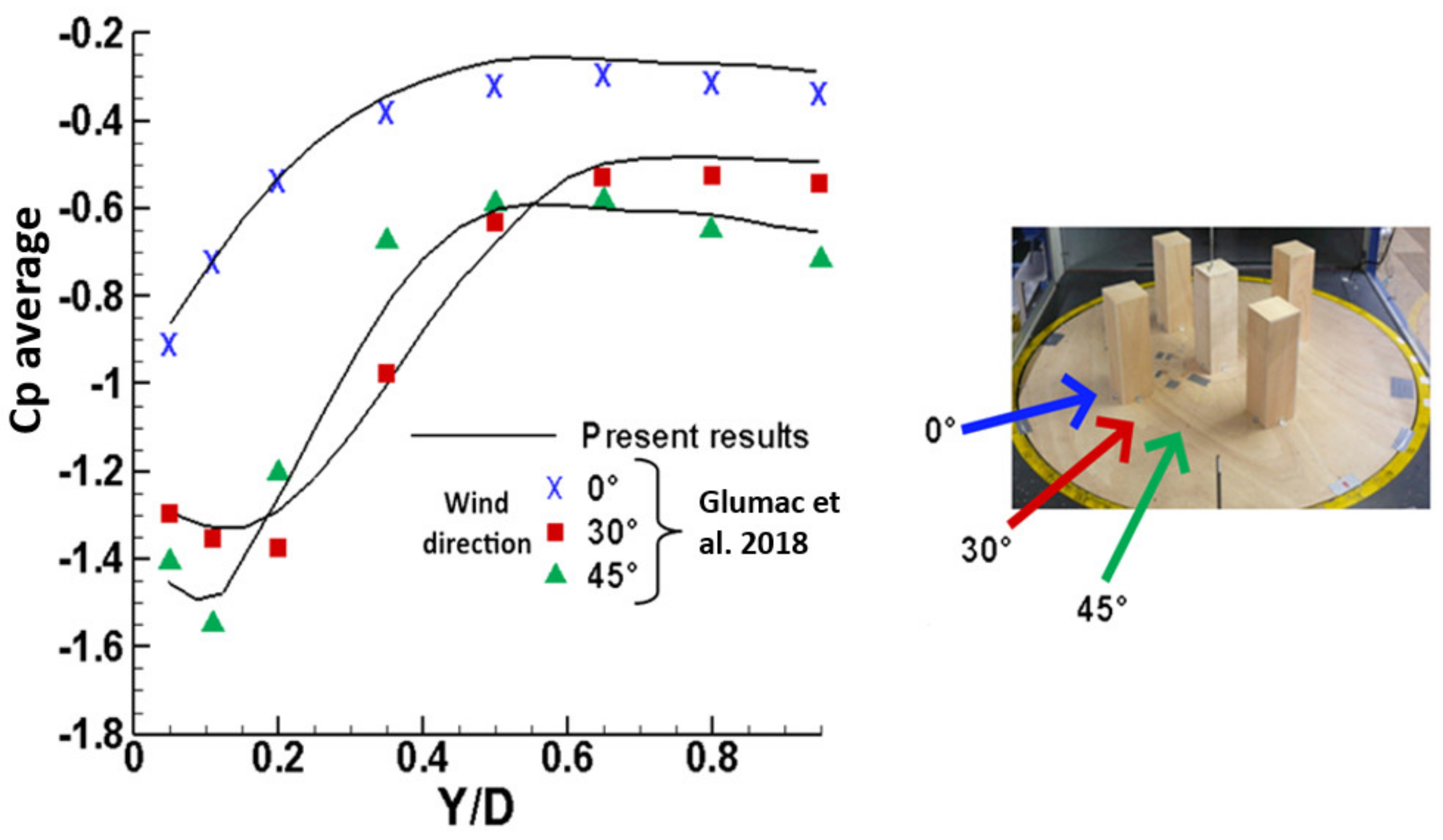
2.7. Validation Test
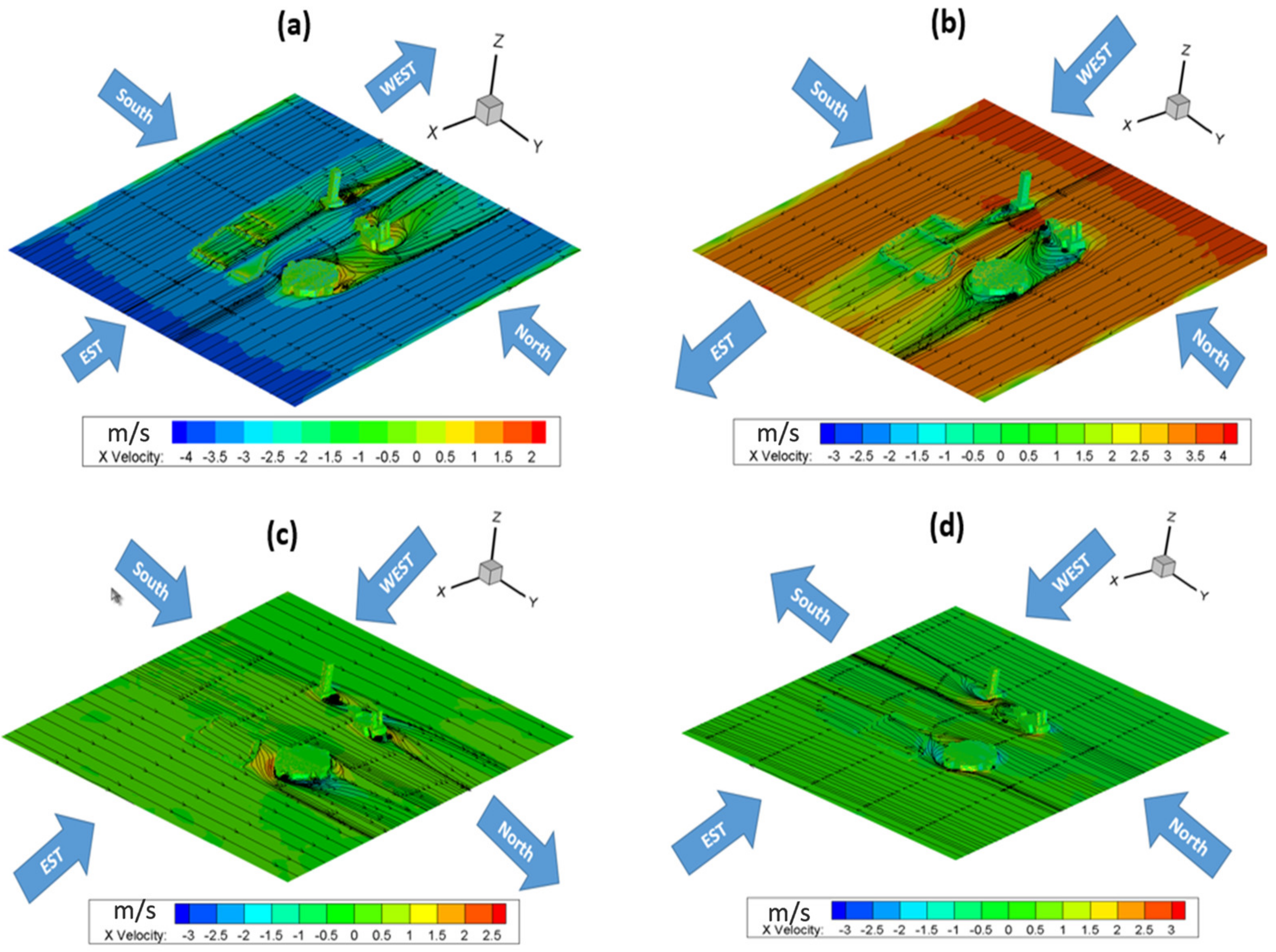
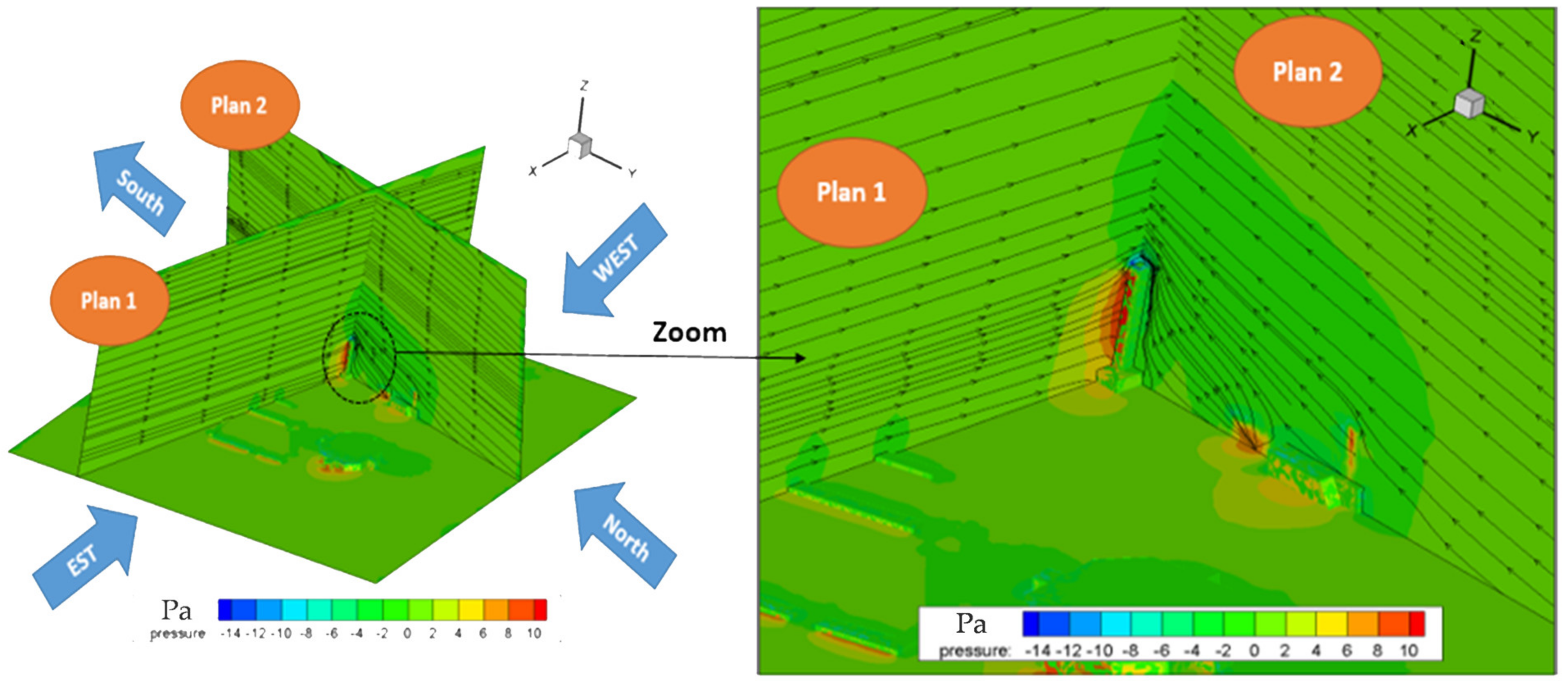
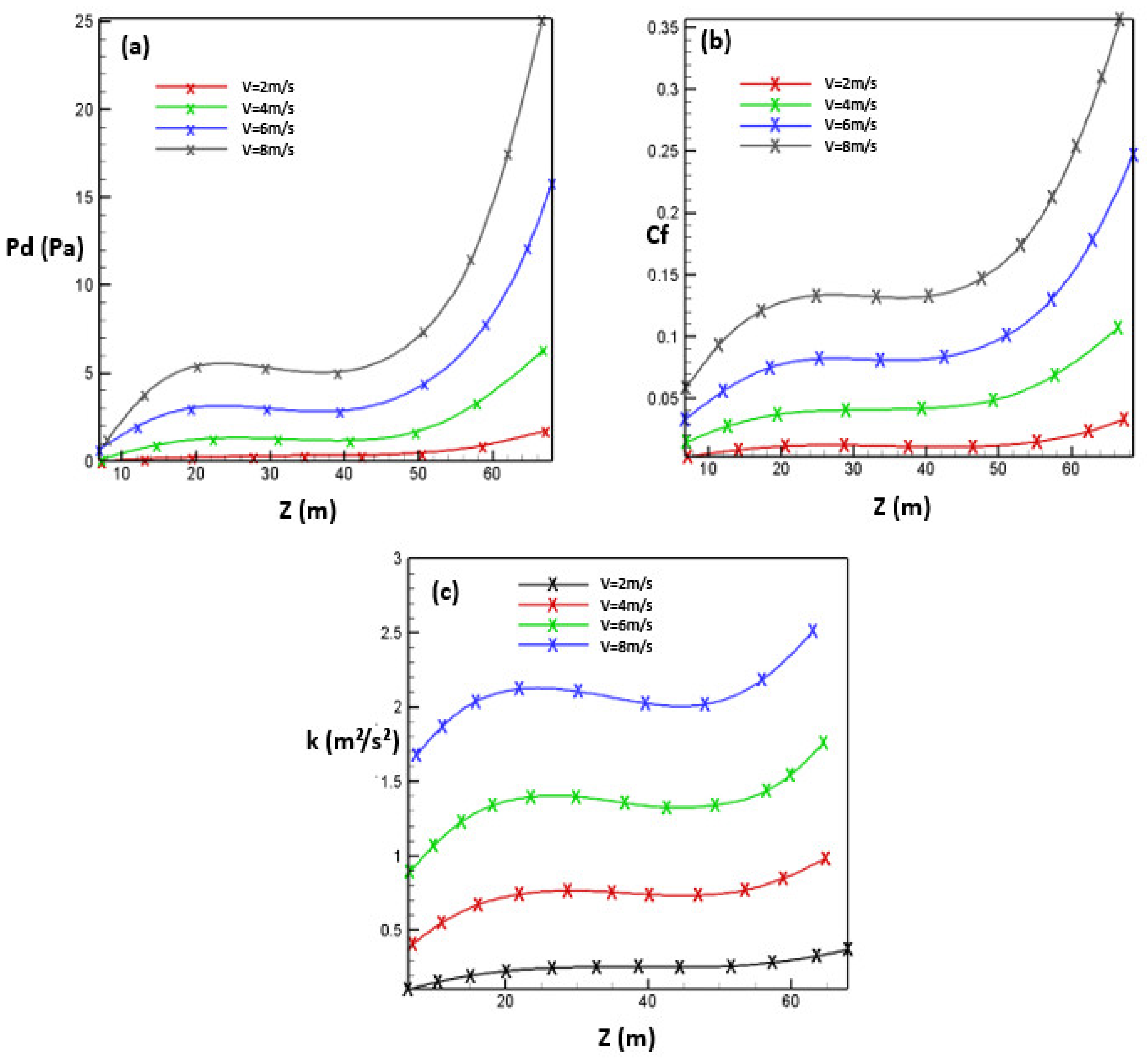
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. A framework for preliminary large-scale urban wind energy potential assessment: Roof-mounted wind turbines. Energy Convers. Manag. 2020, 214, 112770. [Google Scholar] [CrossRef]
- Zinat, T.; Al Noman, A.; Sajal, K. An analytical review on the evaluation of wind resource and wind turbine for urban application: Prospect and challenges. Dev. Built Environ. 2020, 4, 100033. [Google Scholar] [CrossRef]
- Keshavarzian, E.; Jin, R.; Dong, K.; Kwok, K.C.; Zhang, Y.; Zhao, M. Effect of pollutant source location on air pollutant dispersion around a high-rise building. Appl. Math. Model. 2020, 81, 582–602. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.; Prashant, K. Integrated dispersion-deposition modelling for air pollutant reduction via green infrastructure at an urban scale. Sci. Total Environ. 2020, 723, 138078. [Google Scholar] [CrossRef] [PubMed]
- Sarafrazi, V.; Talaee, M.R. Simulation of wall barrier properties along a railway track during a sandstorm. Aeolian Res. 2020, 46, 100626. [Google Scholar] [CrossRef]
- Razak, A.A.; Hagishima, A.; Salim, S.A.Z.S. Progress in wind environment and outdoor air ventilation at pedestrian level in urban area. Appl. Mech. Mater. 2016, 819, 236–240. [Google Scholar] [CrossRef]
- Blocken, B.; Janssen, W.D.; van Hooff, T. CFD simulation for pedestrian wind comfort and wind safety in urban areas: General decision framework and case study for the Eindhoven University campus. Environ. Model. Softw. 2012, 30, 15–34. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Shen, L.; Han, Y.; Zhu, Z.; Hua, X. Numerical study of stable stratification effects on the wind over simplified tall building models using large-eddy simulations. Build. Environ. 2021, 193, 107625. [Google Scholar] [CrossRef]
- Glumac, A.Š.; Hemida, H.; Höffer, R. Wind energy potential above a high-rise building influenced by neighboring buildings: An experimental investigation. J. Wind Eng. Ind. Aerodyn. 2018, 175, 32–42. [Google Scholar] [CrossRef] [Green Version]
- Jin, M.; Zuo, W.; Chen, Q. Simulating natural ventilation in and around buildings by fast fluid dynamics. Numer. Heat Transf. Part A Appl. 2013, 64, 27–289. [Google Scholar] [CrossRef]
- Chen, Q.; Glicksman, L.R.; Lin, J. Chapter 7: Design of natural ventilation with CFD. In Sustainable Urban. Housing in China; Springer: Berlin/Heidelberg, Germany, 2006; pp. 116–123. [Google Scholar] [CrossRef]
- Ramponi, R.; Blocken, B.; De Coo, L.B.; Janssen, W.D. CFD simulation of outdoor ventilation of generic urban configurations with different urban densities and equal and unequal street widths. Build. Environ. 2015, 92, 152–166. [Google Scholar] [CrossRef] [Green Version]
- Sheremet, M.A.; Miroshnichenko, I.V. Numerical study of turbulent natural convection in a cube having finite thickness heat-conducting walls. Heat Mass Transf. 2015, 51, 1559–1569. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A. Turbulent natural convection heat transfer in rectangular enclosures using experimental and numerical approaches: A review. Renew. Sustain. Energy Rev. 2018, 82, 40–59. [Google Scholar] [CrossRef]
- Liu, S.; Pan, W.; Zhang, H.; Cheng, X.; Long, Z.; Chen, Q. CFD simulations of wind distribution in an urban community with a full-scale geometrical model. Build. Environ. 2017, 117, 11–23. [Google Scholar] [CrossRef]
- Ricci, A.; Kalkman, I.; Blocken, B.; Burlando, M.; Repetto, M.P. Impact of turbulence models and roughness height in 3D steady RANS simulations of wind flow in an urban environment. Build. Environ. 2020, 171, 106617. [Google Scholar] [CrossRef]
- Kang, G.; Kim, J.J.; Choi, W. Computational fluid dynamics simulation of tree effects on pedestrian wind comfort in an urban area. Sustain. Cities Soc. 2020, 56, 102086. [Google Scholar] [CrossRef]
- Chu, A.K.M.; Kwok, R.C.W.; Yu, K.N. Study of pollution dispersion in urban areas using Computational Fluid Dynamics (CFD) and Geographic Information System (GIS). Environ. Model. Softw. 2005, 20, 273–277. [Google Scholar] [CrossRef]
- Toja-Silva, F.; Pregel-Hoderlein, C.; Chen, J. On the urban geometry generalization for CFD simulation of gas dispersion from chimneys: Comparison with Gaussian plume model. J. Wind Eng. Ind. Aerodyn. 2018, 177, 1–18. [Google Scholar] [CrossRef]
- Feng, C.; Gu, M. Numerical simulation of wind veering effects on square-section super high-rise buildings under various wind directions. J. Build. Eng. 2021, 44, 102954. [Google Scholar] [CrossRef]
- Fan, M.; Li, W.J. Parameterised drag model for the underlying surface roughness of buildings in urban wind environment simulation. Build. Environ. 2022, 209, 108651. [Google Scholar] [CrossRef]
- Tominaga, Y.; Shirzadi, M. Wind tunnel measurement of three-dimensional turbulent flow structures around a building group: Impact of high-rise buildings on pedestrian wind environment. Build. Environ. 2021, 206, 108389. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, Y.; Zhai, Z.; Xue, Y.; Duanmu, L. Characteristics of wind flow around a target building with different surrounding building layers predicted by CFD simulation. Build. Environ. 2021, 201, 107962. [Google Scholar] [CrossRef]
- Lee, K.Y.; Mak, C.M. Effects of wind direction and building array arrangement on airflow and contaminant distributions in the central space of buildings. Build. Environ. 2021, 205, 108234. [Google Scholar] [CrossRef]
- Kim, B.; Lee, D.E.; Preethaa, K.R.S.; Hu, G.; Natarajan, Y.; Kwok, K.C.S. Predicting wind flow around buildings using deep learning. J. Wind Eng. Ind. Aerodyn. 2021, 219, 104820. [Google Scholar] [CrossRef]
- Sumei, L.; Pana, W.; Zhaoa, X. Influence of surrounding buildings on wind flow around a building predicted by CFD simulations. Build. Environ. 2018, 140, 1–10. [Google Scholar] [CrossRef]
- Tamura, Y.; Xu, X.; Yang, Q. Characteristics of pedestrian-level Mean wind speed around square buildings: Effects of height, width, size and approaching flow profile. J. Wind Eng. Ind. Aerodyn. 2019, 192, 74–87. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, Z.; Zhang, J.; Wu, Y.; Jin, Z.; Chen, Y. Effect of the combined aerodynamic control on the amplitude characteristics of wind loads on a tall building. Eng. Struct. 2021, 245, 112967. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, G.; Tse, K.T.; He, X. Twisted-wind effect on the flow field of tall building. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104778. [Google Scholar] [CrossRef]
- Han, M.; Ooka, R.; Kikumoto, H. Validation of lattice Boltzmann method-based large-eddy simulation applied to wind flow around single 1:1:2 building model. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104277. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar] [CrossRef]
- Liu, W.; Sun, H.; Lai, D.; Xue, Y.; Kabansh, A.; Hu, S. Performance of fast fluid dynamics with a semi-Lagrangian scheme and an implicit upwind scheme in simulating indoor/outdoor airflow. Build. Environ. 2021, 207, 108477. [Google Scholar] [CrossRef]



| 1 | 0.52 | 1/9 | 0.09 | 0.072 | 8 | 6 | 2.95 | 1.5 | 0.25 | 2 | 2 |
| u0 (m/s) | k0 (m²/s) | ω0 (1/s) |
|---|---|---|
| 2 | 0.015 | 0.007 |
| 4 | 0.06 | 0.014 |
| 6 | 0.135 | 0.021 |
| 8 | 0.24 | 0.028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hnaien, N.; Hassen, W.; Kolsi, L.; Mesloub, A.; Alghaseb, M.A.; Elkhayat, K.; Abdelhafez, M.H.H. CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community. Mathematics 2022, 10, 1118. https://doi.org/10.3390/math10071118
Hnaien N, Hassen W, Kolsi L, Mesloub A, Alghaseb MA, Elkhayat K, Abdelhafez MHH. CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community. Mathematics. 2022; 10(7):1118. https://doi.org/10.3390/math10071118
Chicago/Turabian StyleHnaien, Nidhal, Walid Hassen, Lioua Kolsi, Abdelhakim Mesloub, Mohammed A. Alghaseb, Khaled Elkhayat, and Mohamed Hssan Hassan Abdelhafez. 2022. "CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community" Mathematics 10, no. 7: 1118. https://doi.org/10.3390/math10071118
APA StyleHnaien, N., Hassen, W., Kolsi, L., Mesloub, A., Alghaseb, M. A., Elkhayat, K., & Abdelhafez, M. H. H. (2022). CFD Analysis of Wind Distribution around Buildings in Low-Density Urban Community. Mathematics, 10(7), 1118. https://doi.org/10.3390/math10071118










