Measurement and Analysis of High Frequency Assert Volatility Based on Functional Data Analysis
Abstract
:1. Introduction
2. Methods
2.1. Determination of Basis Function
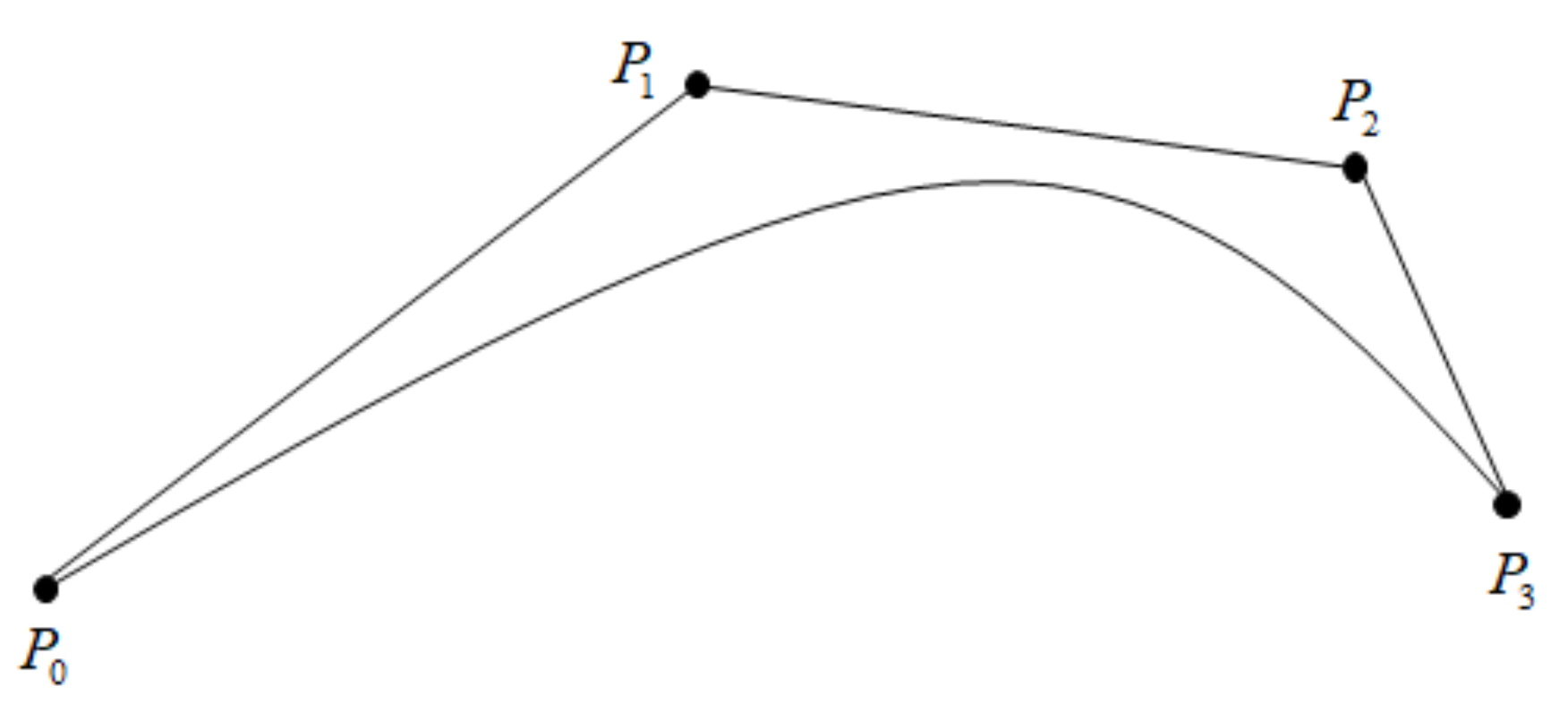
2.2. Bernstein Basis Function Modeling
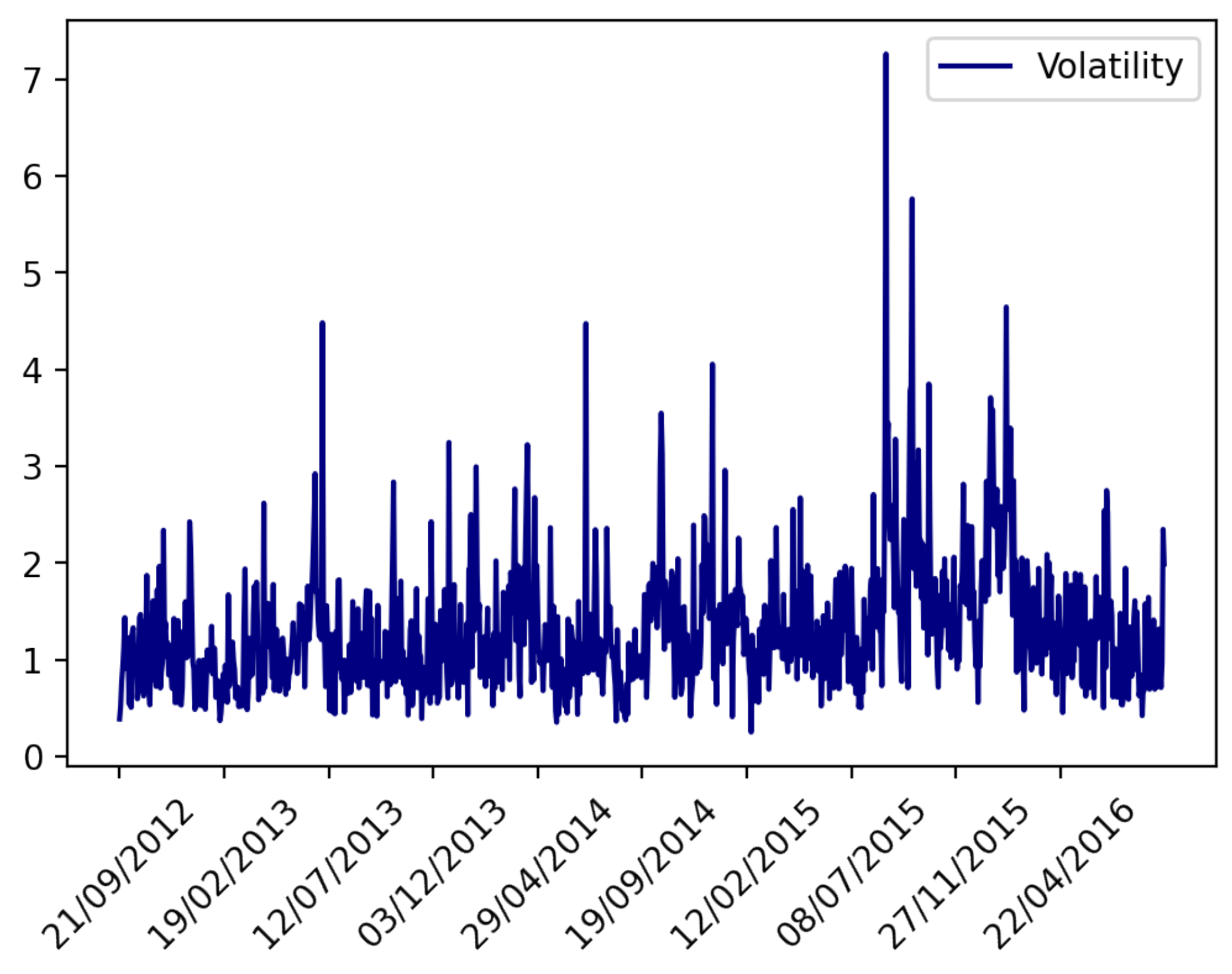
2.3. Volatility Measurement
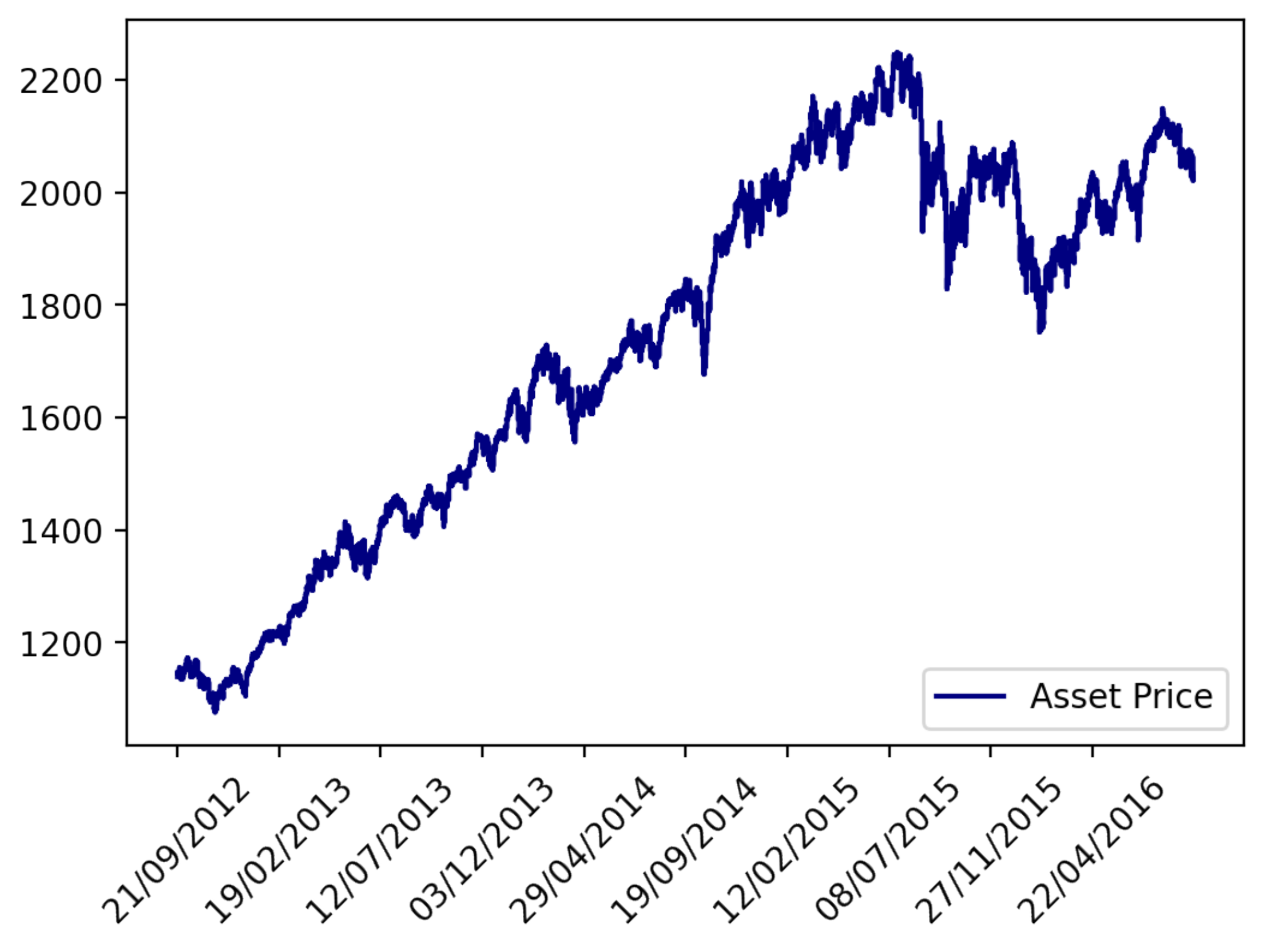
3. Experimental Analysis
- We randomly remove a certain proportion of data from the original daily data, that is, produce non-equidistant high-frequency data. The corresponding proportion is controlled by DropRate.
- We randomly add noise to the original data, where r is randomly chosen from 0 to 1. Parameter determines the degree of the added noise.
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Weng, F.; Zhang, H.; Yang, C. Volatility forecasting of crude oil futures based on a genetic algorithm regularization online extreme learning machine with a forgetting factor: The role of news during the COVID-19 pandemic. Resour. Policy 2021, 73, 102148. [Google Scholar] [CrossRef] [PubMed]
- Duttilo, P.; Gattone, S.; Di Battista, T. Volatility modeling: An overview of equity markets in the euro area during COVID-19 Pandemic. Mathematics 2021, 9, 1212. [Google Scholar] [CrossRef]
- Andersen, T.; Bollerslev, T.; Diebold, F.; Labys, P. The distribution of realized exchange rate volatility. J. Am. Stat. Assoc. 2001, 96, 42–55. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.; Huang, Z.; Shek, H. Realized GARCH: A joint model for returns and realized measures of volatility. J. Appl. Econom. 2012, 27, 877–906. [Google Scholar] [CrossRef]
- Poon, S.; Granger, C. Practical issues in forecasting volatility. Financ. Anal. J. 2005, 61, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Andersen, T.; Bollerslev, T.; Diebold, F. Parametric and nonparametric volatility measurement. In Handbook of Financial Econometrics: Tools and Techniques; North-Holland: Chicago, IL, USA, 2010; pp. 67–137. [Google Scholar]
- Hurvich, C.; Moulines, E.; Soulier, P. Estimating long memory in volatility. Econometrica 2005, 73, 1283–1328. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Maheu, J. Are there structural breaks in realized volatility? J. Financ. Econom. 2008, 6, 326–360. [Google Scholar] [CrossRef]
- Bandi, F.M.; Russell, J.R. Separating microstructure noise from volatility. J. Financ. Econ. 2006, 79, 655–692. [Google Scholar] [CrossRef]
- Hansen, P.; Lunde, A. Realized variance and market microstructure noise. J. Bus. Econ. Stat. 2006, 24, 127–161. [Google Scholar] [CrossRef]
- Zhang, L.; Mykland, P.A.; Aït-Sahalia, Y. A tale of two time scales: Determining integrated volatility with noisy high-frequency data. J. Am. Stat. Assoc. 2005, 100, 1394–1411. [Google Scholar] [CrossRef]
- Duong, D.; Swanson, N. Empirical evidence on the importance of aggregation, asymmetry, and jumps for volatility prediction. J. Econom. 2015, 187, 606–621. [Google Scholar] [CrossRef] [Green Version]
- Breidt, F.; Crato, N.; Delima, P. The detection and estimation of long memory in stochastic volatility. J. Econom. 1998, 83, 325–348. [Google Scholar] [CrossRef] [Green Version]
- Baillie, R.; Cecen, A.; Han, Y. High frequency Deutsche Mark-US Dollar returns: FIGARCH representations and non linearities. Multinatl. Financ. J. 2000, 4, 247–267. [Google Scholar] [CrossRef]
- Granger, C. Long memory relationships and the aggregation of dynamic models. J. Econom. 1980, 14, 227–238. [Google Scholar] [CrossRef]
- Alvarez, A.; Panloup, F.; Pontier, M.; Savy, N. Estimation of the instantaneous volatility. Stat. Inference Stoch. Process. 2012, 15, 27–59. [Google Scholar] [CrossRef] [Green Version]
- Müller, H.; Sen, R.; Stadtmüller, U. Functional data analysis for volatility. J. Econom. 2011, 165, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Shang, H. Forecasting intraday S&P 500 index returns: A functional time series approach. J. Forecast. 2017, 36, 741–755. [Google Scholar]
- Kokoszka, P.; Miao, H.; Zhang, X. Functional dynamic factor model for intraday price curves. J. Financ. Econom. 2015, 13, 456–477. [Google Scholar] [CrossRef] [Green Version]
- Shang, H.; Yang, Y.; Kearney, F. Intraday forecasts of a volatility index: Functional time series methods with dynamic updating. Ann. Oper. Res. 2019, 282, 331–354. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Fang, Y.; Li, Z.; Zhang, B.; Zhao, X. Non-Parametric Estimation of High-Frequency Spot Volatility for Brownian Semimartingale with Jumps. J. Time Ser. Anal. 2014, 35, 572–591. [Google Scholar] [CrossRef]
- Wang, J.; Chiou, J.; Müller, H. Functional data analysis. Annu. Rev. Stat. Its Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef] [Green Version]
- Ramsay, J. When the data are functions. Psychometrika 1982, 47, 379–396. [Google Scholar] [CrossRef]
- Kokoszka, P.; Reimherr, M. Introduction to Functional Data Analysis; Chapman and Hall/CR: London, UK, 2017. [Google Scholar]
- Ler, K. A brief proof of a maximal rank theorem for generic double points in projective space. Trans. Am. Math. Soc. 2001, 353, 1907–1920. [Google Scholar]
- Beaton, A.; Tukey, J. The fitting of power series, meaning polynomials, illustrated on band-spectroscopic data. Technometrics 1974, 16, 147–185. [Google Scholar] [CrossRef]
- Hatefi, E.; Hatefi, A. Nonlinear Statistical Spline Smoothers for Critical Spherical Black Hole Solutions in 4-dimension. arXiv 2022, arXiv:2201.00949. [Google Scholar]
- Dahiya, V. Analysis of Lagrange Interpolation Formula. IJISET-Int. J. Innov. Sci. Eng. Technol. 2014, 1, 619–624. [Google Scholar]
- Wang, X.; Wang, J.; Wang, X.; Yu, C. A Pseudo-Spectral Fourier Collocation Method for Inhomogeneous Elliptical Inclusions with Partial Differential Equations. Mathematics 2022, 10, 296. [Google Scholar] [CrossRef]
- Farouki, R. The Bernstein polynomial basis: A centennial retrospective. Comput. Aided Geom. Des. 2012, 29, 379–419. [Google Scholar] [CrossRef]
- Farouki, R.; Goodman, T. On the optimal stability of the Bernstein basis. Math. Comput. 1996, 65, 1553–1566. [Google Scholar] [CrossRef] [Green Version]
- Kühnel, W. Differential Geometry; American Mathematical Society: Providence, RI, USA, 2015. [Google Scholar]
- Jianping, Z.; Zhiguo, L.; Caiyun, C. A New Predictive Model on Data Mining—Predicting Arithmetic of Bernstein Basic Function Fitting and Its Application for Stock Market. Syst. Eng. Theory Pract. 2003, 9, 35–41. [Google Scholar]
- Shaojun, Z.; Hong, L. An improved model based on fitting predictions to Bernstein Basic Function. Stat. Decis. 2015, 8, 20–23. [Google Scholar]
- Wang, S. A class of distortion operators for pricing financial and insurance risks. J. Risk Insur. 2000, 1, 15–36. [Google Scholar] [CrossRef] [Green Version]
- Levitin, D.; Nuzzo, R.; Vines, B.; Ramsay, J. Introduction to functional data analysis. Can. Psychol. Can. 2007, 48, 135. [Google Scholar] [CrossRef] [Green Version]
- Ferraty, F.; Mas, A.; Vieu, P. Nonparametric regression on functional data: Inference and practical aspects. Aust. N. Z. J. Stat. 2007, 49, 267–286. [Google Scholar] [CrossRef] [Green Version]
- Mas, A.; Pumo, B. Functional linear regression with derivatives. J. Nonparametr. Stat. 2009, 21, 19–40. [Google Scholar] [CrossRef] [Green Version]
- Farin, G. Class a Bézier curves. Comput. Aided Geom. Des. 2006, 7, 573–581. [Google Scholar] [CrossRef]
| DropRate | sub | avg | std |
|---|---|---|---|
| 0.1 | 0.003993 | 0.000017 | 0.000192 |
| 0.2 | 0.035771 | 0.000225 | 0.001836 |
| 0.3 | 0.115362 | 0.000767 | 0.006560 |
| Sigma | sub | avg | std |
|---|---|---|---|
| 0.1 | 0.032560 | 0.016152 | 0.009657 |
| 0.2 | 0.065114 | 0.031076 | 0.019011 |
| 0.3 | 0.097928 | 0.049194 | 0.029173 |
| 0.4 | 0.130392 | 0.064272 | 0.038869 |
| DropRate | sub | avg | std |
|---|---|---|---|
| 0.1 | 0.001301 | 0.000209 | 0.000108 |
| 0.2 | 0.012924 | 0.000368 | 0.000861 |
| 0.3 | 0.239079 | 0.001688 | 0.012562 |
| Sigma | sub | avg | std |
|---|---|---|---|
| 0.1 | 0.000072 | 0.00004 | 0.000571 |
| 0.2 | 0.000145 | 0.000114 | 0.002248 |
| 0.3 | 0.097928 | 0.000116 | 0.001764 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Weng, F.; Ma, Y.; Xu, Y.; Zhu, M.; Yang, C. Measurement and Analysis of High Frequency Assert Volatility Based on Functional Data Analysis. Mathematics 2022, 10, 1140. https://doi.org/10.3390/math10071140
Liang Z, Weng F, Ma Y, Xu Y, Zhu M, Yang C. Measurement and Analysis of High Frequency Assert Volatility Based on Functional Data Analysis. Mathematics. 2022; 10(7):1140. https://doi.org/10.3390/math10071140
Chicago/Turabian StyleLiang, Zhenjie, Futian Weng, Yuanting Ma, Yan Xu, Miao Zhu, and Cai Yang. 2022. "Measurement and Analysis of High Frequency Assert Volatility Based on Functional Data Analysis" Mathematics 10, no. 7: 1140. https://doi.org/10.3390/math10071140
APA StyleLiang, Z., Weng, F., Ma, Y., Xu, Y., Zhu, M., & Yang, C. (2022). Measurement and Analysis of High Frequency Assert Volatility Based on Functional Data Analysis. Mathematics, 10(7), 1140. https://doi.org/10.3390/math10071140






