GR-GNN: Gated Recursion-Based Graph Neural Network Algorithm
Abstract
:1. Introduction
1.1. Research Status of GNN
1.2. Related Work
2. Overview
2.1. Symbols and Definitions
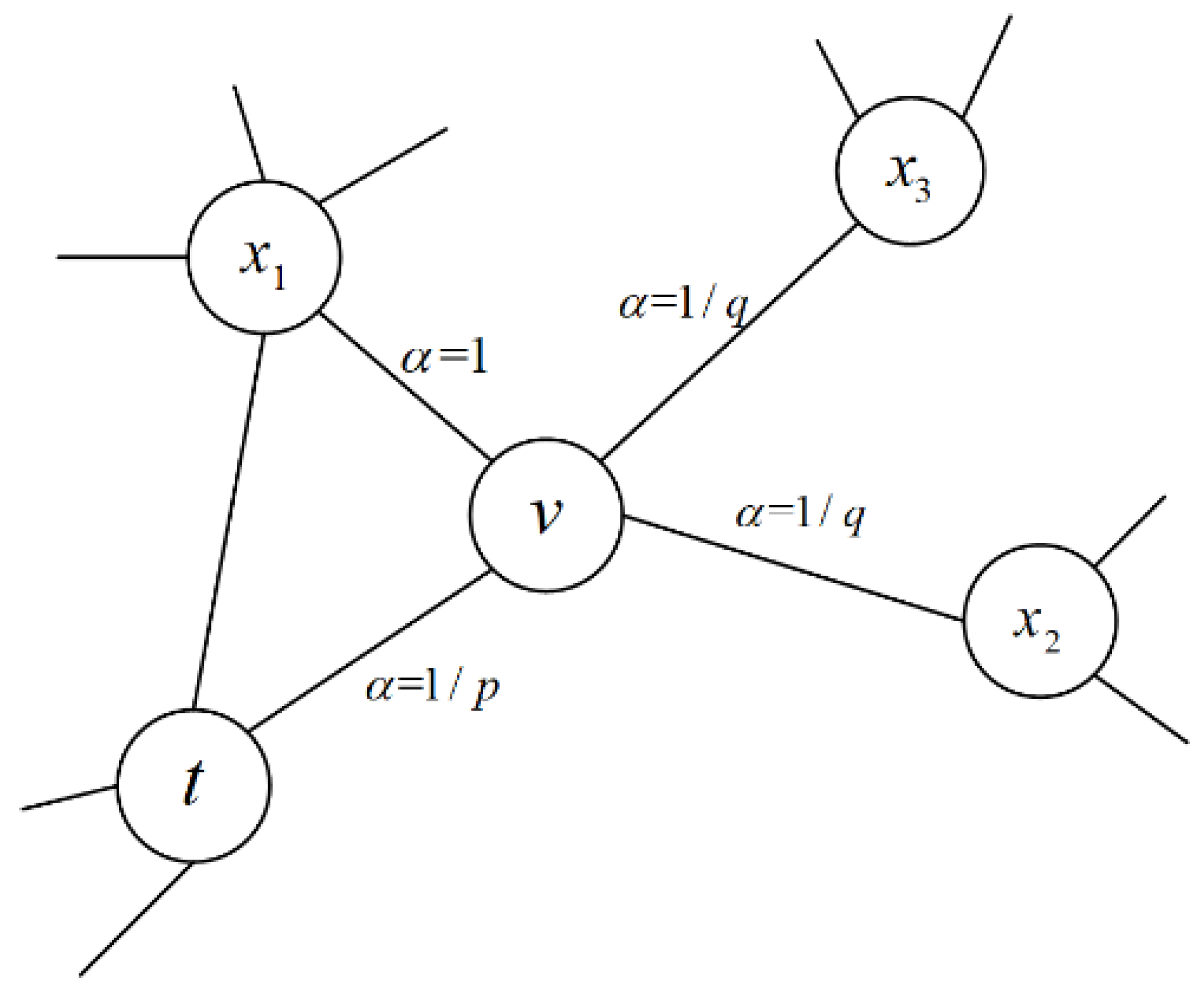
2.2. Node2Vec Algorithm
- Conditional independence assumption: given a node v, any two nodes and in its neighbor node , and v becoming neighbors have nothing to do with and v becoming neighbors; that is:
- Spatial symmetry: given a node v, it shares the same representation vector as a source node and as a neighbor node, so the conditional probability is constructed by the Softmax function:
2.3. GRU Model
3. Gated Recursion-Based Graph Neural Network (GR-GNN) Algorithm
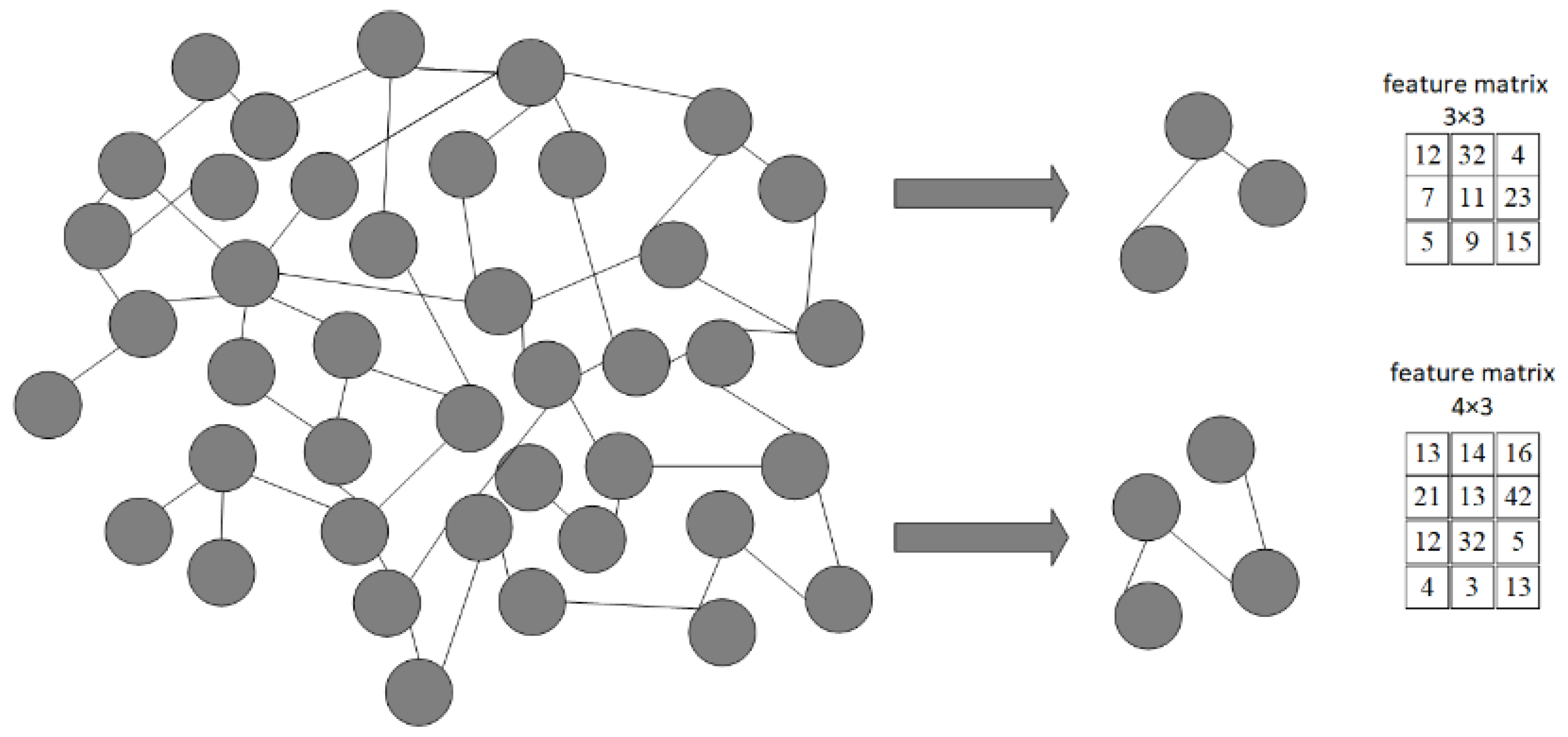
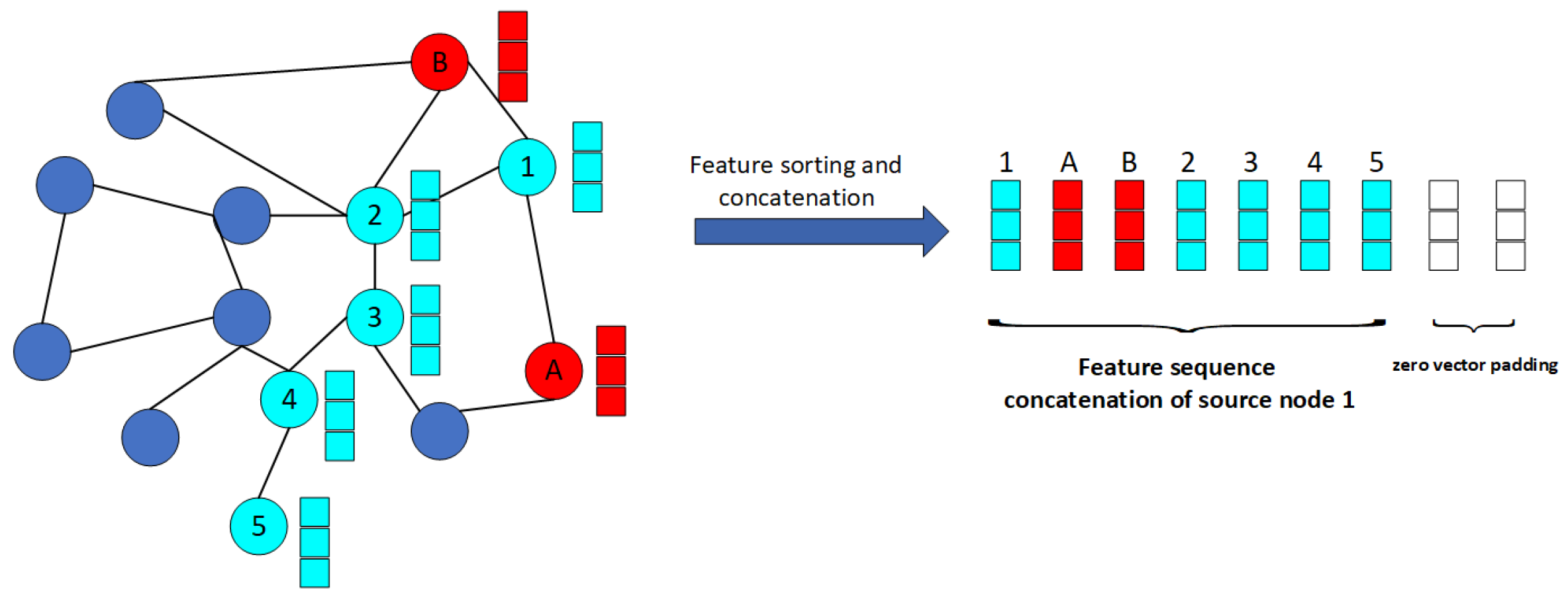
3.1. Feature Pre-Training
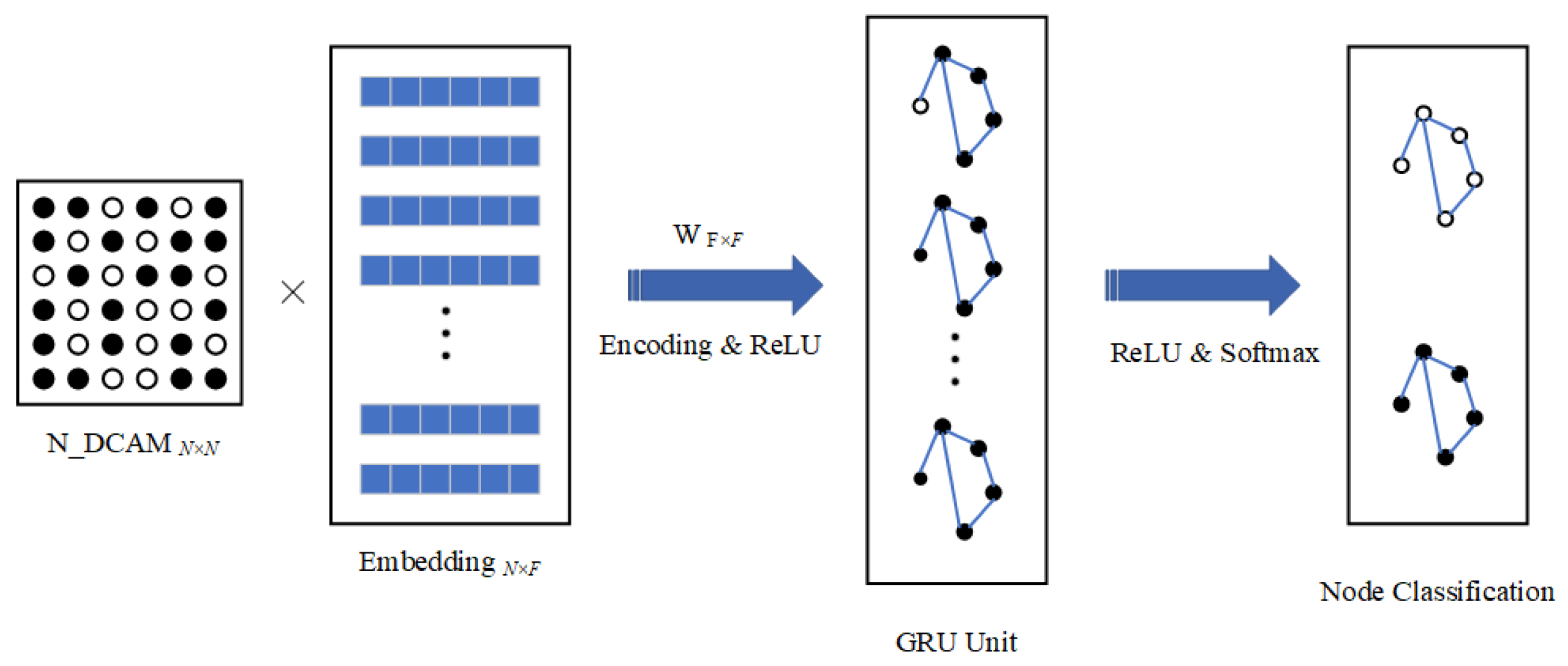
3.2. Model Construction
4. Experimental Evaluation
4.1. Experiment Preparation
4.1.1. Experimental Environment
4.1.2. Evaluation Index
4.1.3. Data Preparation
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, F.; Jin, L.; Dong, J. A Survey of Convolutional Neural Network Research. Chin. J. Comput. 2017, 40, 1229–1251. [Google Scholar]
- Gori, M.; Monfardini, G.; Scarselli, F. A new model for learning in graph domains. In Proceedings of the International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; pp. 729–734. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Qi, J.; Liang, X.; Li, Z. Representation Learning for Large-Scale Complex Information Networks: Concepts, Methods and Challenges. Chin. J. Comput. 2018, 41, 222–248. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Defferrard, M.; Bresson, X.V.; Ergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 258–276. [Google Scholar]
- Levie, R.; Monti, F.; Bresson, X.; Bronstein, M.M. CayleyNets: Graph convolutional neural networks with complex rational spectral filters. IEEE Trans. Signal Process. 2019, 67, 97–109. [Google Scholar] [CrossRef] [Green Version]
- Spinelli, I.; Scardapane, S.; Uncini, A. Adaptive propagation graph convolutional network. IEEE Trans. Neural Networks Learn. Syst. 2020, 32, 4755–4760. [Google Scholar] [CrossRef]
- Duvenaud, D.K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional networks on graphs for learning molecular fingerprints. Adv. Neural Inf. Process. Syst. 2015, 28, 1594–1603. [Google Scholar]
- Zhao, Z.; Zhou, H.; Qi, L.; Chang, L.; Zhou, M. Inductive representation learning via cnn for partially-unseen attributed networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 695–706. [Google Scholar] [CrossRef]
- Liang, M.; Zhang, F.; Jin, G.; Zhu, J. FastGCN: A GPU accelerated tool for fast gene co-expression networks. PLoS ONE 2015, 10, e0116776. [Google Scholar] [CrossRef] [PubMed]
- Kou, S.; Xia, W.; Zhang, X.; Gao, Q.; Gao, X. Self-supervised graph convolutional clustering by preserving latent distribution. Neurocomputing 2021, 437, 218–226. [Google Scholar] [CrossRef]
- Luo, J.X.; Du, Y.J. Detecting community structure and structural hole spanner simultaneously by using graph convolutional network based Auto-Encoder. Neurocomputing 2020, 410, 138–150. [Google Scholar] [CrossRef]
- Li, C.; Welling, M.; Zhu, J.; Zhang, B. Graphical generative adversarial networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 6072–6083. [Google Scholar]
- Gharaee, Z.; Kowshik, S.; Stromann, O.; Felsberg, M. Graph representation learning for road type classification. Pattern Recognit. 2021, 120, 108174. [Google Scholar] [CrossRef]
- Zhang, S.; Ni, W.; Fu, N. Differentially private graph publishing with degree distribution preservation. Comput. Secur. 2021, 106, 102285. [Google Scholar] [CrossRef]
- Ruiz, L.; Gama, F.; Ribeiro, A. Gated graph recurrent neural networks. IEEE Trans. Signal Process. 2020, 68, 6303–6318. [Google Scholar] [CrossRef]
- Bach, F.R.; Jordan, M.I. Learning graphical models for stationary time series. IEEE Trans. Signal Process. 2004, 52, 2189–2199. [Google Scholar] [CrossRef]
- Liu, J.; Kumar, A.; Ba, J.; Kiros, J.; Swersky, K. Graph normalizing flows. Adv. Neural Inf. Process. Syst. 2019, 32, 5876. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 20. [Google Scholar]
- Zhao, Y.; Zhou, H.; Zhang, A.; Xie, R.; Li, Q.; Zhuang, F. Connecting Embeddings Based on Multiplex Relational Graph Attention Networks for Knowledge Graph Entity Typing. IEEE Trans. Knowl. Data Eng. 2022. Early Access. [Google Scholar] [CrossRef]
- Wu, J.; Pan, S.; Zhu, X.; Zhang, C.; Philip, S.Y. Multiple structure-view learning for graph classification. IEEE Trans. Neural Networks Learn. Syst. 2017, 29, 3236–3251. [Google Scholar] [CrossRef] [PubMed]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar]



| Graph Neural Network Classification | Improved Variant Algorithm | Research Content |
|---|---|---|
| Network embedding [4] | DeepWalk [5], LINE [6], Node2Vec [7]. | These algorithms mainly learn fixed-length feature representations for each node by integrating the graph structure information of source nodes and neighbor nodes. |
| Spectral decomposition graph convolution: Chebyshev [8], CayleyNet [9], AGCN [10]. | The algorithm mainly performs feature extraction by convolving the eigenvectors of the Laplacian matrix of the graph. | |
| Graph convolution network | Spatial graph convolution: PATCHY-SAN [11], GraphSAGE [12], FastGCN [13]. | The algorithm mainly performs feature extraction using convolution operations on the structural information of the source node and neighbor nodes. |
| Graph auto-encoder (GAE) | MGAE [14], AutoGCN [15]. | The algorithm mainly designs a stack denoising autoencoder to extract features from the structural information generated by the random walk model. |
| Graph generative network (GGN) [16] | Graph-GAN [17], NetGAN [18]. | The algorithm mainly uses the Bayesian network to learn the dependency structure between random node variables and uses the expectation propagation algorithm to train the generator and discriminator. |
| Graph recurrent network (GRN) [19] | GGT-NN [20], GraphRNN [21]. | The GRN algorithm is one of the earliest GNN models. It generally uses bidirectional RNN (Bi-RNN) and the long short-term memory network (LSTM) as the network structure and feature extraction. |
| Graph attention network (GAT) | GATE [22], RGAT [23], GAM [24]. | The algorithm builds a multi-head attention mechanism on the basis of spatial graph convolution, and uses it to generate a feature aggregation function of a stacked spatial graph convolution for feature extraction. |
| Name | Value |
|---|---|
| Operating system | Ubuntu 18.04 |
| Programming language | Python |
| Development framework | PyTorch |
| CPU | Intel(R) Core(TM) i9-10900K |
| RAM | 64G |
| GPU | RTX 3090 |
| Cora | CiteseerX | PubMed | |
|---|---|---|---|
| Nodes | 2708 | 3327 | 19,717 |
| Edges | 5429 | 4732 | 44,338 |
| Features/node | 1433 | 3703 | 500 |
| Classes | 7 | 6 | 3 |
| Training nodes | 140 | 120 | 60 |
| Validation nodes | 500 | 500 | 500 |
| Test nodes | 1000 | 1000 | 1000 |
| Methods | Cora | CiteseerX | PubMed |
|---|---|---|---|
| GCN | 81.5% | 70.3% | 79.0% |
| GAT | 83.0% | 72.5% | 79.0% |
| GraphSAGE | 82.3% | 71.7% | 78.3% |
| GR-GNN | 83 ± 0.5% | 73 ± 0.7% | 79.3 ± 0.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, K.; Zhao, J.-Q.; Zhao, Y.-Y. GR-GNN: Gated Recursion-Based Graph Neural Network Algorithm. Mathematics 2022, 10, 1171. https://doi.org/10.3390/math10071171
Ge K, Zhao J-Q, Zhao Y-Y. GR-GNN: Gated Recursion-Based Graph Neural Network Algorithm. Mathematics. 2022; 10(7):1171. https://doi.org/10.3390/math10071171
Chicago/Turabian StyleGe, Kao, Jian-Qiang Zhao, and Yan-Yong Zhao. 2022. "GR-GNN: Gated Recursion-Based Graph Neural Network Algorithm" Mathematics 10, no. 7: 1171. https://doi.org/10.3390/math10071171
APA StyleGe, K., Zhao, J.-Q., & Zhao, Y.-Y. (2022). GR-GNN: Gated Recursion-Based Graph Neural Network Algorithm. Mathematics, 10(7), 1171. https://doi.org/10.3390/math10071171






