Impact of Third-Degree Price Discrimination on Welfare under the Asymmetric Price Game
Abstract
:1. Introduction
2. Literature Review
3. The Model
3.1. Basic Model
3.2. Model Solution
- (1)
- Under uniform pricing vs. uniform pricing
- (2)
- Under price discrimination vs. price discrimination
- (3)
- Under price discrimination vs. uniform pricing
4. Model Analysis
4.1. Total Social Welfare Analysis
- (1)
- ;
- (2)
- ;
- (3)
- .
- (1)
- ;
- (2)
- , when,, when.
4.2. Local Social Welfare Analysis
- (1)
- ;
- (2)
- ;
- (3)
- .
- (1)
- (2)
- , when; , when.
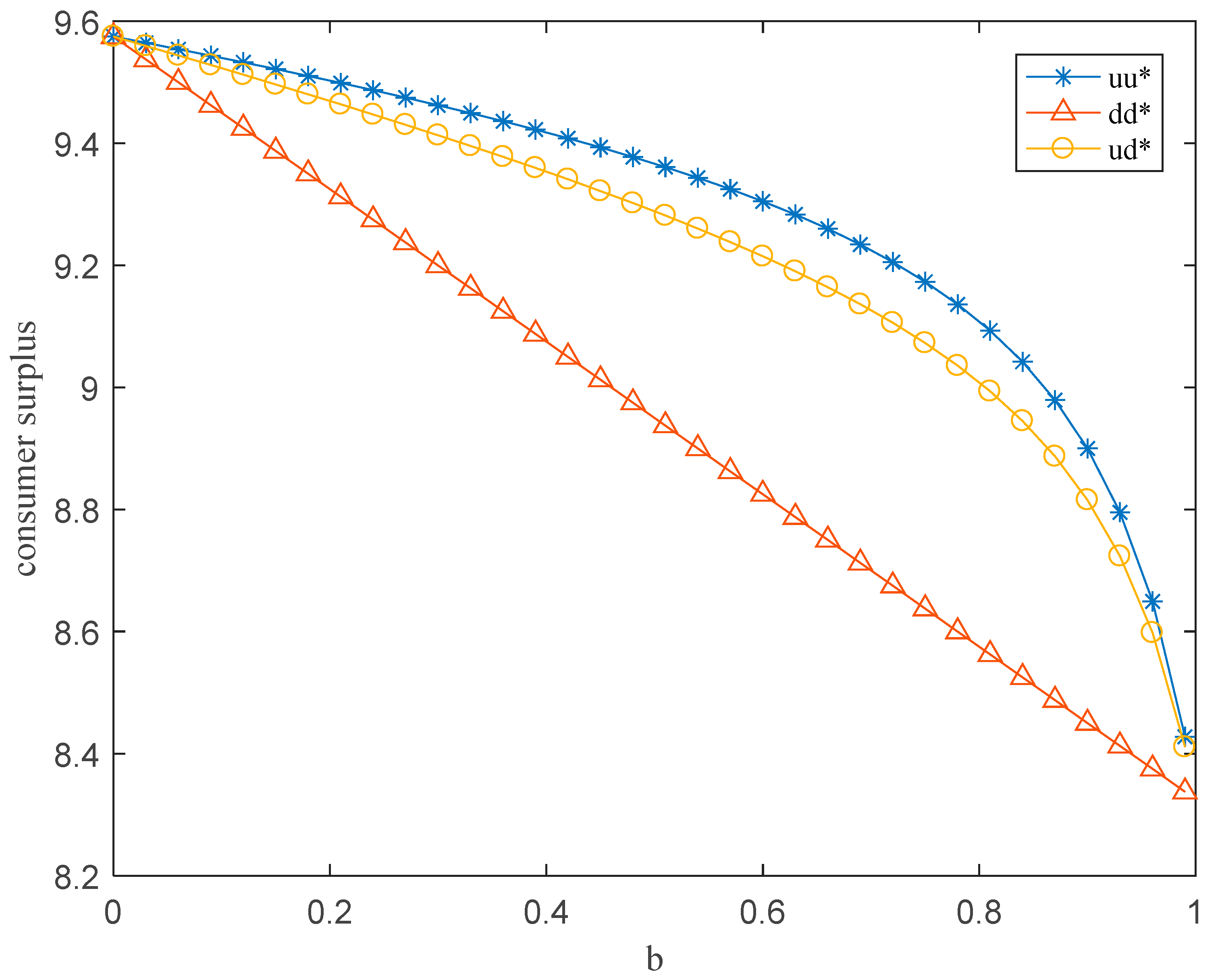
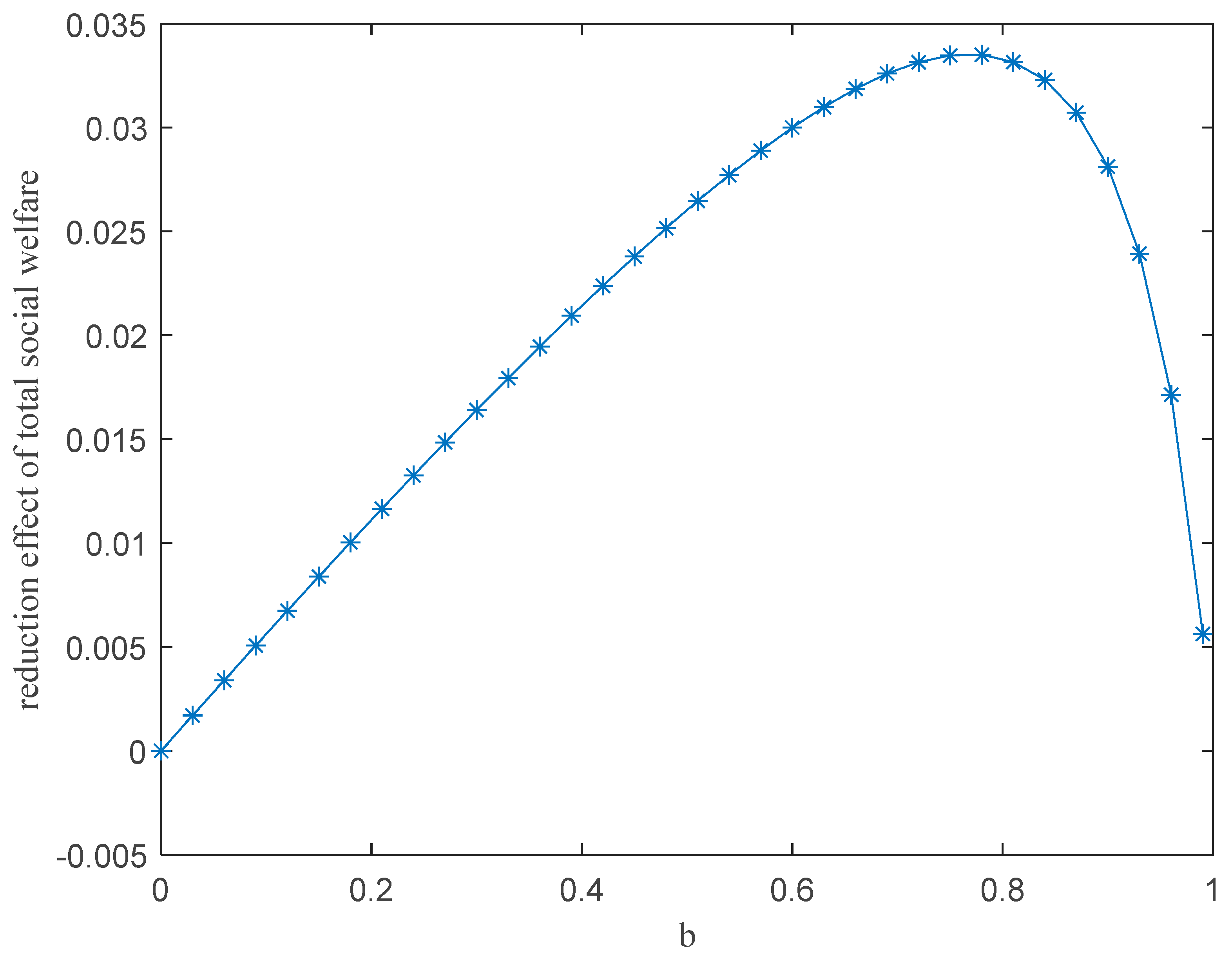
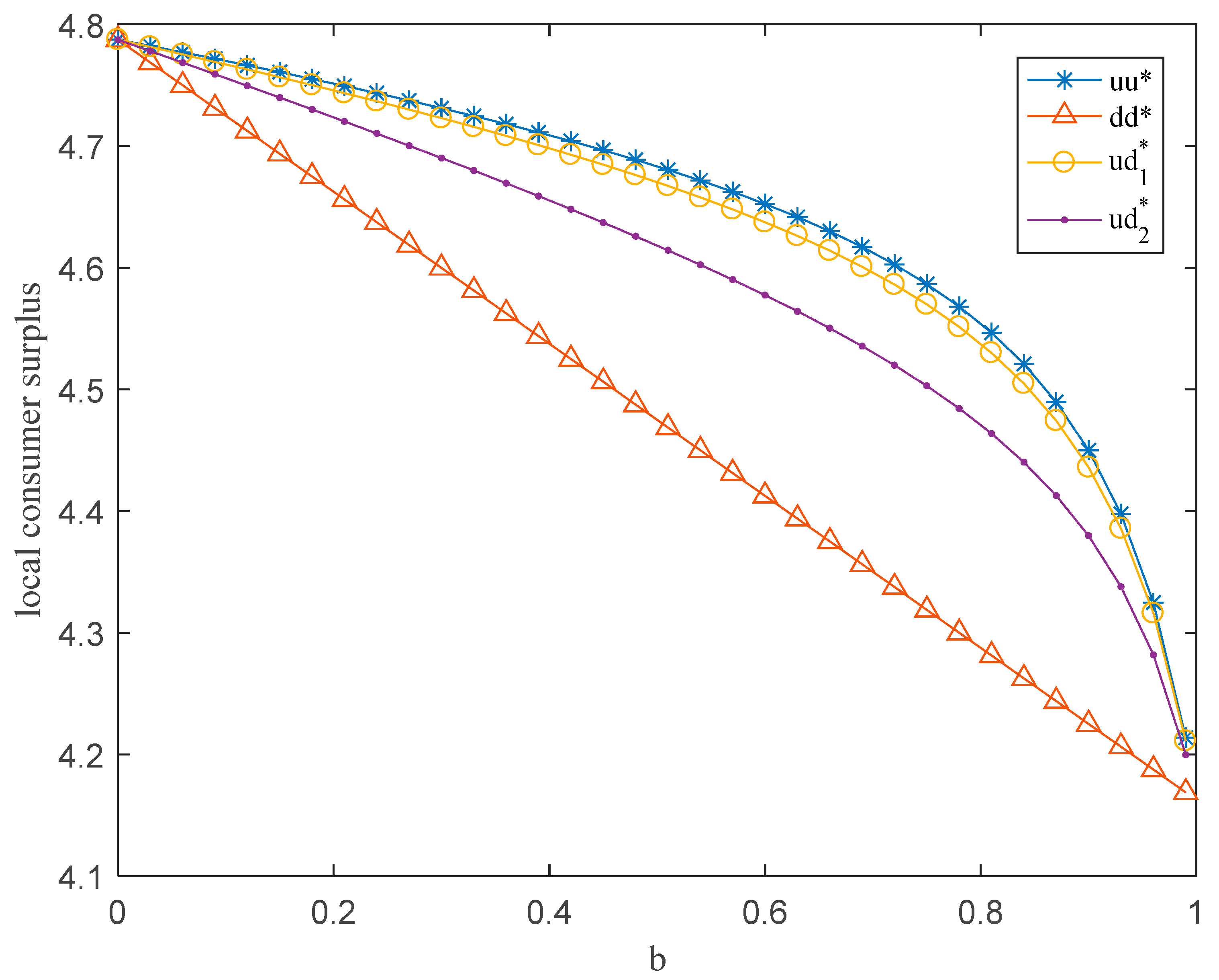
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Varian, H.R. Price Discrimination and Social Welfare. Am. Econ. Rev. 1985, 75, 870–875. [Google Scholar]
- Askar, S.; Foul, A.; Mahrous, T.; Djemele, S.; Ibrahim, E. Global and Local Analysis for a Cournot Duopoly Game with Two Different Objective Functions. Mathematics 2021, 9, 3119. [Google Scholar] [CrossRef]
- Robinson, J. The Economics of Imperfect Competition; Springer Macmillan: London, UK, 1993. [Google Scholar]
- Clempner, J.B.; Poznyak, A.S. Analytical Method for Mechanism Design in Partially Observable Markov Games. Mathematics 2021, 9, 321. [Google Scholar] [CrossRef]
- Schmalensee, R. Output and Welfare Implications of Monopolistic Third-degree Price Discrimination. Am. Econ. Rev. 1981, 71, 242–247. [Google Scholar]
- Namin, A.; Gauri, D.K.; Kwortnik, R.J. Improving Revenue Performance with Third-degree Price Discrimination in the Cruise Industry. Int. J. Hosp. Manag. 2020, 89, 102597. [Google Scholar] [CrossRef]
- Schwartz, M. Third-degree price discrimination and output: Generalizing welfare result. Am. Econ. Rev. 1990, 80, 1259–1262. [Google Scholar]
- Adams, C.F. A Note on Pricing with Market Power: Third-degree Price Discrimination with Quality-differentiated Demand. Am. Econ. 2019, 64, 183–187. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L. Monopolistic third-degree price discrimination, welfare, and vertical market structure. Rev. Econ. Des. 2021, 26, 75–86. [Google Scholar] [CrossRef]
- Holmes, T.J. The effects of third-degree price discrimination in oligopoly. Am. Econ. Rev. 1989, 79, 244–250. [Google Scholar]
- Corts, K.S. Third-degree Price Discrimination in Oligopoly: All-out Competition and Strategic Commitment. RAND J. Econ. 1998, 29, 306–323. [Google Scholar] [CrossRef]
- Miklós-Thal, J.; Shaffer, G. Third-degree price discrimination in oligopoly with endogenous input costs. Int. J. Ind. Organ. 2021, 79, 102713. [Google Scholar] [CrossRef]
- Aguirre, I. Oligopoly Price Discrimination, Competitive Pressure and Total Output. Economics 2019, 13, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, M.; Vickers, J. Competitive price discrimination. RAND J. Econ. 2001, 32, 579–605. [Google Scholar] [CrossRef]
- Chen, Y.; Schwartz, M. Beyond price discrimination: Welfare under differential pricing when costs also differ. MPRA Pap. 2012, 11, 1–29. [Google Scholar]
- Adachi, T.; Matsushima, N. The welfare effects of –third-degree price discrimination in a differentiated oligopoly. Econ. Inq. 2014, 52, 1231–1244. [Google Scholar] [CrossRef] [Green Version]
- Galera, F.; Mendi, P.; Molero, J.C. Quality differences, third-degree price discrimination, and welfare. Econ. Inq. 2017, 55, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Feng, H.; Ma, J. Location choices and third-degree spatial price discrimination. Scot. J. Polit. Econ. 2018, 2, 142–153. [Google Scholar] [CrossRef]
- Zhang, T.; Huo, Y.; Zhang, X.; Shuai, J. Endogenous third-degree price discrimination in Hotelling model with elastic demand. J. Econ. 2019, 127, 125–145. [Google Scholar] [CrossRef]
- Galera, F.; Garcia-del-Barrio, P.; Mendi, P. Consumer surplus bias and the welfare effects of price discrimination. J. Regul. Econ. 2019, 55, 33–45. [Google Scholar] [CrossRef]
- Chung, H.S. Welfare impacts of behavior-based price discrimination with asymmetric firms. Asia-Pac. J. Bus. Adm. 2020, 11, 17–26. [Google Scholar] [CrossRef]
- Yl, A.; Jie, S.B. Monopolistic competition, price discrimination, and welfare. Econ. Lett. 2019, 174, 114–117. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, Y.; Meng, Q.; Han, Q. Impact of Third-Degree Price Discrimination on Welfare under the Asymmetric Price Game. Mathematics 2022, 10, 1215. https://doi.org/10.3390/math10081215
Zhang Z, Wang Y, Meng Q, Han Q. Impact of Third-Degree Price Discrimination on Welfare under the Asymmetric Price Game. Mathematics. 2022; 10(8):1215. https://doi.org/10.3390/math10081215
Chicago/Turabian StyleZhang, Zheng, Yingtong Wang, Qingchun Meng, and Qiang Han. 2022. "Impact of Third-Degree Price Discrimination on Welfare under the Asymmetric Price Game" Mathematics 10, no. 8: 1215. https://doi.org/10.3390/math10081215
APA StyleZhang, Z., Wang, Y., Meng, Q., & Han, Q. (2022). Impact of Third-Degree Price Discrimination on Welfare under the Asymmetric Price Game. Mathematics, 10(8), 1215. https://doi.org/10.3390/math10081215





