Abstract
In a previous work by the same authors, a hollow annular membrane structure loaded transversely and uniformly was proposed, and its closed-form solution was presented; its anticipated use is for designing elastic shells of revolution. Since the height–span ratio of shells of revolution is generally desired to be as large as possible, to meet the need for high interior space, especially for the as-small-as-possible horizontal thrust at the base of shells of revolution, the closed-form solution should be able to cover annular membranes with a large deflection–outer radius ratio. However, the previously presented closed-form solution cannot meet such an ability requirement, because the previous out-of-plane equilibrium equation used the assumption of a small deflection–outer radius ratio. In this study, the out-of-plane equilibrium equation is re-established without the assumption of a small deflection–outer radius ratio, and a new and more refined closed-form solution is presented. The new closed-form solution is numerically discussed regarding its convergence and effectiveness, and compared with the old one. The new and old closed-form solutions agree quite closely for lightly loaded cases but diverge as the load intensifies. Differences in deflections, especially in stresses, are very significant when the deflection–outer radius ratio exceeds 1/4, indicating that, in this case, the new closed-form solution should be adopted in preference to the old one.
Keywords:
annular membrane; uniform transverse loading; axisymmetric deformation; large deflection; power series method; closed-form solution MSC:
74G10; 74K15
1. Introduction
Circular and annular membrane structures are often favored in many technical applications due to their axisymmetric characteristics that are convenient to deal with analytically, such as in non-contact or contact capacitive pressure sensors [1,2,3,4], bulge tests [5,6,7], blister tests [8,9,10] or constrained blister tests [11,12,13,14]. Essential to achieving these technical applications is the ability to deal analytically with the mechanical behaviors of these circular or annular membranes, i.e., the ability to obtain closed-form solutions. In the literature, however, attentions are more often devoted to circular membranes than to annular membranes.
The problem of axisymmetric deformation of a peripherally fixed and uniformly transversely loaded circular membrane was analytically dealt with originally by H. Hencky in 1915 [15], and a closed-form solution of the problem was given in terms of power series. Chien [16] and Alekseev [17] each corrected a computational error in [15] in 1948 and 1953, respectively. This solution is the first solution of circular membrane problems, usually known as Hencky’s solution, and is often cited by related studies [18,19,20,21,22]. However, the well-known Hencky’s solution is unsatisfactory when applied to heavily loaded membranes owing to its limited accuracy in calculation, and it has thus been repeatedly improved [23,24,25]. Another type of circular membrane problem involves the axisymmetric deformation problem of a peripherally fixed and uniformly normally loaded circular membrane [26], where the loading direction of a normal load is always perpendicular to the membrane before and after deformation (while the loading direction of a transverse load is always perpendicular to the membrane before deformation). Gas pressure is typical normal loading, while structural dead weight is typical transverse loading. In addition, circular membrane problems also involve cases where the circular membrane is transversely loaded at its central region [27].
Investigations into annular membrane problems, in the literature, began with S.A. Alekseev [28], who gave a closed-form solution for the axisymmetric deformation problem of a peripherally fixed annular membrane connected centrally with a flat, concentric and circular stiff thin plate that is transversely loaded at its center point. The closed-form solution given by Alekseev [28] is valid only for thin films with Poisson’s ratios less than 1/3. However, many widely used thin films, such as polymers, often have Poisson’s ratios greater than 1/3, sparking the further investigation of Alekseev’s problem by Sun et al. [29]. The closed-form solution presented by Sun et al. [29] can be used for Alekseev’s problem where the Poisson’s ratio of thin films may be less than, or equal to, or greater than 1/3. Incidentally, the solutions presented by Alekseev [28] and Sun et al. [29] are derived by solving nonlinear differential equations algebraically, and they are therefore in the form of algebraic functions, rather than in the form of power series like the solutions of circular membranes. The annular membrane in Alekseev’s problem, as mentioned above, bears the concentrated force that is applied at the center point of the flat, concentric and circular stiff thin plate through its inner edge, without direct contact with an external load. Lian et al. [30] used the Alekseev-type annular membrane structure to directly bear the applied external load—a uniformly distributed transverse load that is applied onto the annular membrane and the centrally connected flat, concentric and circular stiff thin plate—developing a capacitive pressure sensor based on membrane elastic deflection and a parallel plate capacitor. The closed-form solution presented by Lian et al. [30] is in the form of a power series, making it the first power series solution for annular membrane problems. The useful lesson from [30] is that the power series method for differential equations usually converges easily when applied to circular membrane problems, but often does not when applied to annular membrane problems. This limitation means that the power series solution of an annular membrane problem should be verified in terms of its convergence before use.
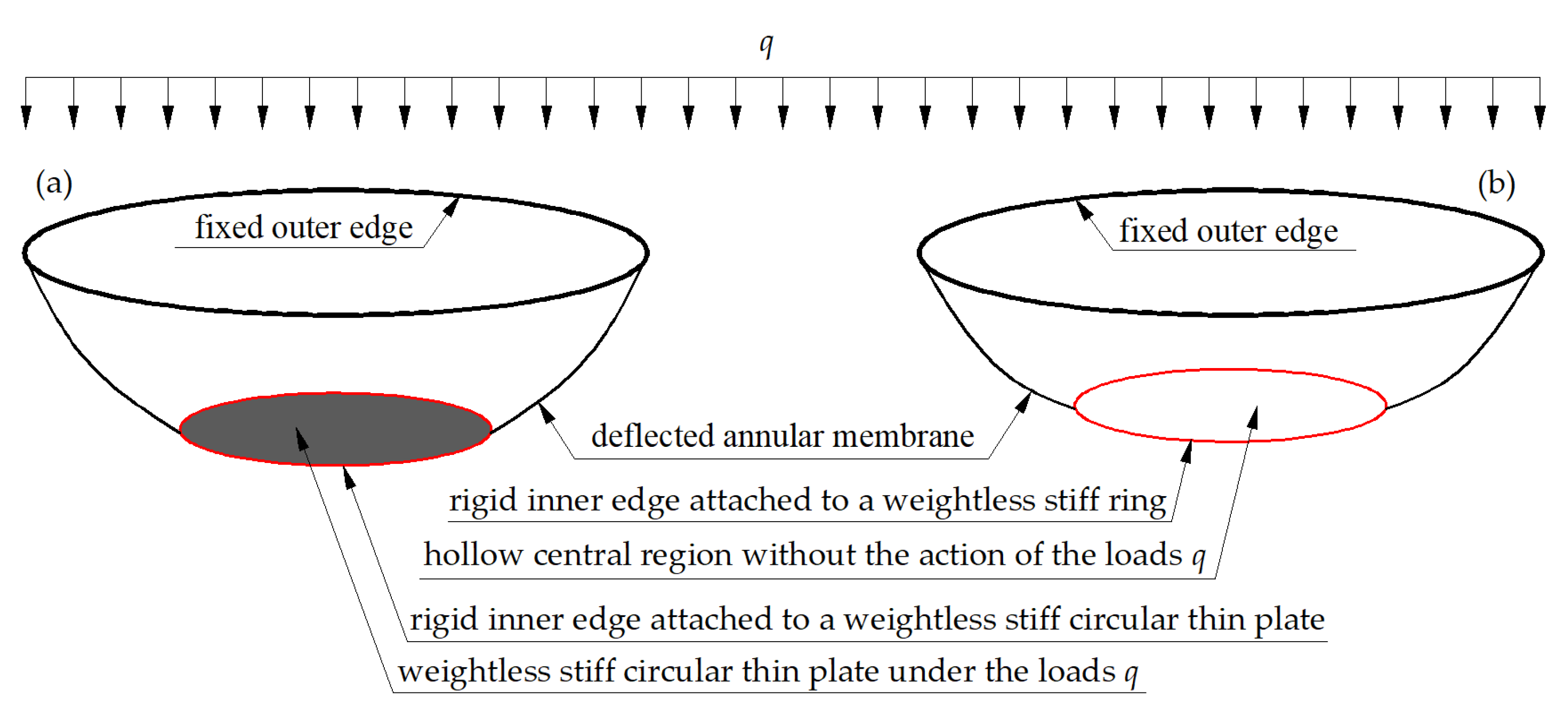
Sun et al. [31], for the first time, proposed a new type of annular membrane structure, a hollow annular membrane structure, different from the Alekseev-type annular membrane structure [28]. The main difference between the Alekseev-type [28] and Sun-type [31] annular membrane structures is that the central region of the annular membranes is filled with a flat, concentric and circular stiff thin plate in the Alekseev-type annular membrane structure, as shown in Figure 1a, and is hollow in the Sun-type annular membrane structure, as shown in Figure 1b. If the Alekseev- and Sun-type annular membrane structures have the same annular membranes and bear the same uniformly distributed transverse load, this difference in central regions may cause the elastic response of the annular membranes to differ greatly, resulting in a large difference in the ratio of the maximum deflection to the outer radius of the annular membranes, especially when the ratio of the inner radius to the outer radius of the annular membranes is relatively large. In the Alekseev-type annular membrane structure, the annular membrane, in addition to being directly subjected to the uniformly distributed transverse load q, is acted on at its rigid inner edge by the flat, concentric and circular stiff thin plate that is also under the action of the uniformly distributed transverse load q, while in the Sun-type annular membrane structure, the annular membrane is only directly subjected to the uniformly distributed transverse load q; see Figure 1. Therefore, under the same uniformly distributed transverse load q, the bigger the inner radius–outer radius ratio is, the bigger the contribution of the central regions to the elastic response is, the bigger the difference in elastic responses is, and the bigger the difference in the ratio of the maximum deflection to the outer radius of the annular membranes is. This is why Lian et al. [30] gave the closed-form solution of the Alekseev-type annular membrane structure under uniformly distributed transverse load, while Sun et al. [31] still need to analytically solve the problem of axisymmetric deformation of the hollow annular membrane structure loaded transversely and uniformly.
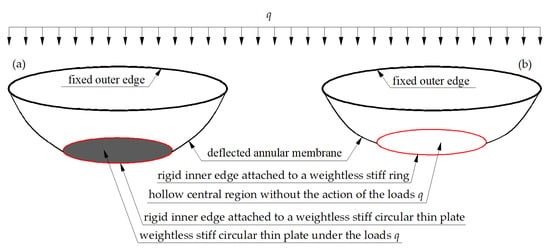
Figure 1.
Two types of transversely and uniformly loaded annular membrane structures. (a) Alekseev-type annular membrane structure, where the inner edge is attached to a weightless stiff circular thin plate; (b) Sun-type annular membrane structure, where the inner edge is attached to a weightless stiff ring, resulting in a hollow central region without the action of the load q.
Sun et al. [31] proposed to generate the initial spatial shape of a shell of revolution with the “conjugate” of the spatial geometry of the transversely and uniformly loaded hollow annular membrane structure; that is, the spatial shape of a shell of revolution that is not vertically loaded is a mirror image of the spatial geometry of the transversely and uniformly loaded hollow annular membrane structure. Essential to the design of such “conjugate shells of revolution” (which are obtained by such doing) is the ability to obtain the closed-form solutions of deflection and stress of the transversely and uniformly loaded hollow annular membrane. Usually, the height–span ratio of a shell of revolution to be designed is often desired to be as large as possible to meet the need for high interior space, especially for the as-small-as-possible horizontal thrust at the base of shells of revolution. This requires a closed-form solution capable of covering annular membranes with a large maximum deflection–outer radius ratio (corresponding to a large rotation angle of the deflected membrane). However, the closed-form solution that was presented by Sun et al. [31] is not competent for such a task, because it was obtained based on the assumption that the maximum deflection—outer radius ratio or rotation angle of the membrane is relatively small, or not too large. However, in the present study, such an assumption is not made during the derivation of the closed-form solution.
The paper is organized as follows. In the following section, the hollow annular membrane problem—the problem of axisymmetric deformation with large deflection of a transversely uniformly loaded hollow annular membrane with a fixed outer edge and a moveable rigid inner edge—is reformulated and solved, where the out-of-plane equilibrium equation is re-established without the assumption of a small maximum deflection–outer radius ratio, and a new and more refined closed-form solution of the problem is given. In Section 3, the convergence and validity of the closed-form solution given in Section 2 are discussed, and a numerical comparison between the new and old closed-form solutions is presented to study the dependence of the ranges of application of the new and old solutions on deflection–outer radius ratio. Concluding remarks are given in Section 4.
2. Membrane Equations and Solution
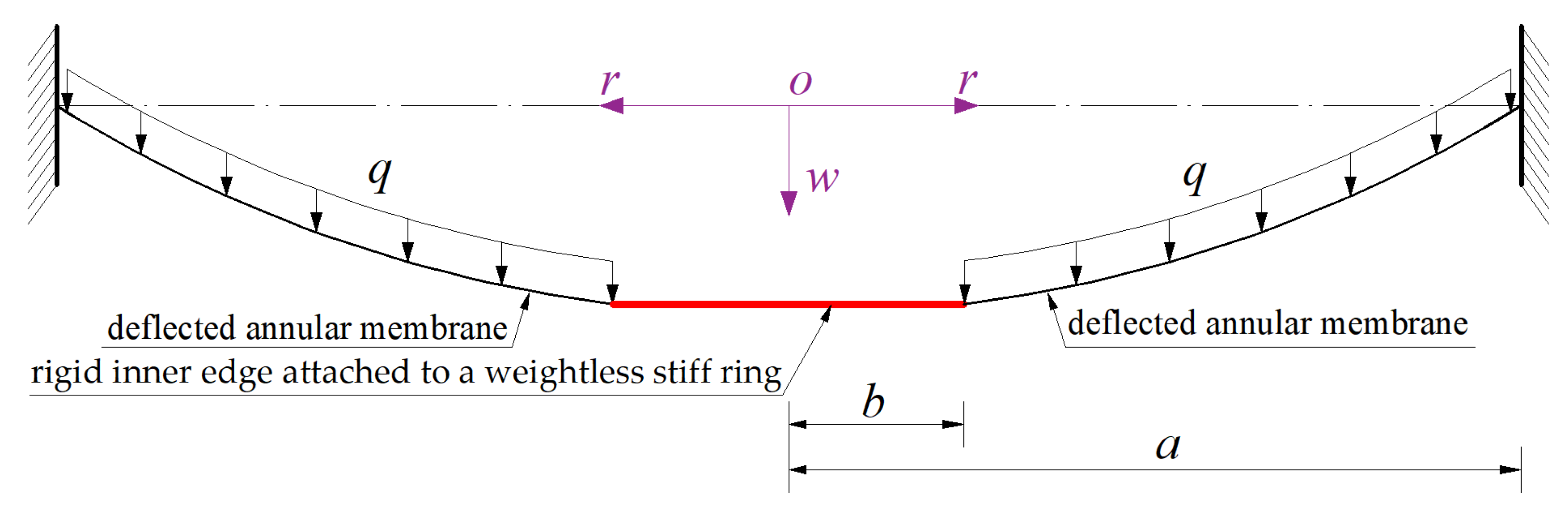
A linearly elastic and initially flat annular membrane with Young’s modulus of elasticity E, Poisson’s ratio v, outer radius a, inner radius b and thickness h is fixed at its outer edge and tightly clamped at its inner edge by a movable but weightless stiff ring, resulting in a hollow annular membrane structure with a movable but indeformable rigid inner edge and an immovable and indeformable fixed outer edge. A uniformly distributed load q is transversely applied to the hollow annular membrane structure, resulting in the load q acting only on the annular membrane due to the hollowness, as shown in Figure 2, where the dash-dotted line represents the geometric intermediate plane of the initially flat annular membrane; the coordinate origin of the introduced cylindrical coordinate system (r, φ, w), o, is placed in the centroid of the geometric intermediate plane; the polar coordinate plane (r, φ) passes through the geometric intermediate plane; r is the radial coordinate; φ is the angle coordinate (not represented in Figure 2); and w is the axial coordinate and is in the same direction as the deflection of the annular membrane.
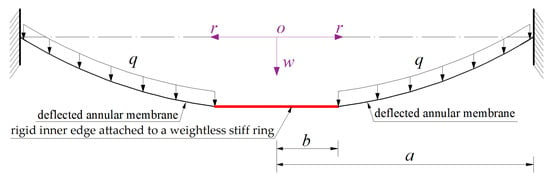
Figure 2.
Sketch of the transversely and uniformly loaded hollow annular membrane.
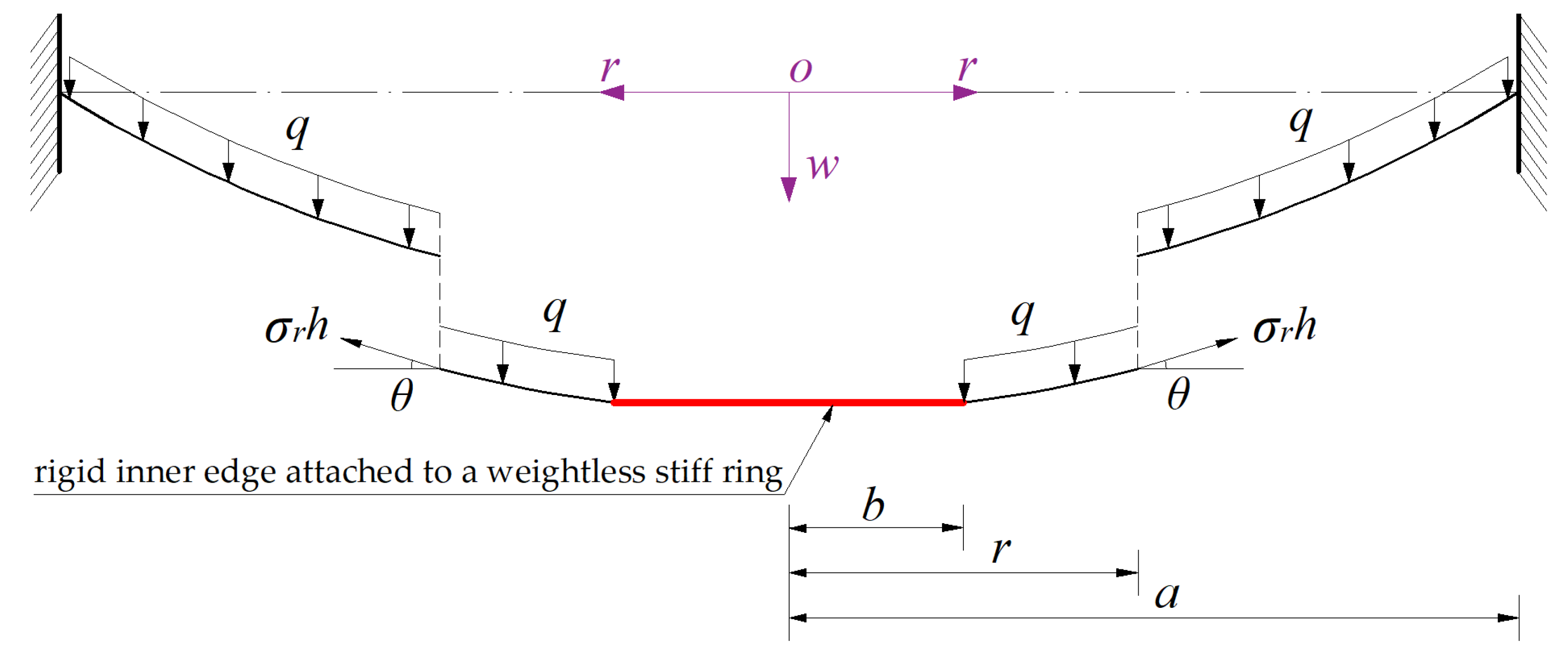
A free body with radius r (b ≤ r ≤ a) is removed from the central portion of the deflected annular membrane to study the static problem of equilibrium of this free body under the joint action of the active force (πr2 − πb2)q produced by the load q and the reactive force 2πrσrh produced by the membrane force σrh acting on the boundary with radius r, as shown in Figure 3, where σr denotes the radial stress and θ denotes the slope angle of the deflected annular membrane.
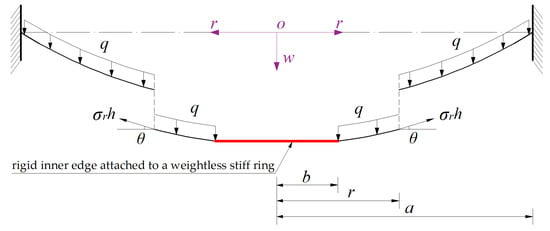
Figure 3.
Sketch of the free body with radius r (b ≤ r ≤ a).
The equilibrium condition in the transverse direction perpendicular to the initially flat annular membrane requires that the resultant force acting on the free body in Figure 3 be equal to zero, i.e.,
If w(r) is the transverse displacement at point r, then
Substitution of Equation (2) into Equation (1) results in a new out-of-plane equilibrium equation different from the one in [31]:
If the circumferential stress is denoted by σt, the so-called in-plane equilibrium equation can be derived by analyzing the radial equilibrium of an infinitesimal element taken away from the deflected membrane and given by
If the radial strain is denoted by er, circumferential strain is denoted by et, and radial displacement is denoted by u(r), then the usually so-called geometric equations (i.e., the relationship between strain and displacement) may be written as
and
The relationship between stress and strain (i.e., the so-called physical equations) is still assumed to satisfy linear elasticity:
and
Eliminating er and et from Equations (5)–(8) yields
and
By means of Equations (9) and (10), σr and σt may be written as
and
After the dw/dr in Equations (11) and (12) is eliminated, Equation (4) can be further used to obtain
Substituting the u in Equation (13) into Equation (11) yields
Therefore, σr, σt and w can be solved by Equations (3), (4) and (14).
The boundary conditions for solving σr, σt and w are
and
After introducing the nondimensionalization
Equations (3), (4), and (13)–(17) can be transformed into
and
Eliminating dW/dx from Equations (19) and (22), an equation containing only Sr can be obtained:
In a real physical phenomenon, the displacement, strain and stress are all finite within α ≤ x ≤ 1. Therefore, Sr and W can be expanded into power series of x − β:
and
where β = (1 + α)/2. After introducing X = x − β, Equations (19) and (26)–(28) can be transformed into
and
The recursive relations for the coefficients ci can be determined as follows. After Equation (31) is substituted into Equation (30), all the coefficients of the same powers of X can be added together to form sums of coefficients. By letting all the sums of coefficients be simultaneously equal to zero, all the coefficients ci (i = 2, 3, 4, …) can be expressed in the polynomials with regard to the first two coefficients c0 and c1; these are listed in Appendix A. Further, after Equations (32) and (31) are substituted into Equation (29), where ci should be first expressed in terms of c0 and c1, all the coefficients di (i = 1, 2, 3, …) can also be expressed in terms of c0 and c1; these are listed in Appendix B.
The remaining coefficients c0, c1 and d0 are three undetermined constants, which can be determined by using the boundary conditions Equations (23)–(25). After expressing each ci in terms of c0 and c1, substituting Equation (27) into Equations (23) and (24) yields two equations containing only c0 and c1:
and
Therefore, c0 and c1 can be determined by simultaneously solving Equations (33) and (34); thus, the expression of Sr can be determined. Further, substituting Equation (28) into the boundary condition Equation (25) yields
Therefore, with the known c0 and c1, the values of di (i = 1, 2, 3, …) can be determined by using the expressions in Appendix B, and with the known di values (i = 1, 2, 3, …), the value of d0 can be determined from Equation (35). Thus, the expression of W can also be determined.
As for the expression of St, it can easily be determined by using Equation (20) based on the known expression of Sr. It is not necessary to address this easy problem here.
3. Results and Discussion
In this section, we first analyze the convergence of the closed-form solution obtained in Section 2, then discuss its validity and, finally, compare it with the closed-form solution presented in [31].
3.1. Convergence Analysis
From the derivation in Section 2, it can be seen that the obtained closed-form solutions of stress Sr and deflection W are given in the form of power series, and all the coefficients di (i = 1, 2, 3, …) and ci (i = 2, 3, 4, …) are expressed in the somewhat complex polynomials with regard to c0 and c1 (see Appendix A and Appendix B). Therefore, due to these complex polynomials, the convergence of the power series solutions of stress and deflection must be discussed by examining the special solutions, rather than general solutions. To this end, let us consider a numerical example, where an annular membrane with Young’s modulus of elasticity E = 7.84 MPa, Poisson’s ratio v = 0.47, outer radius a = 20 mm, inner radius b = 10 mm and thickness h = 0.2 mm is subjected to uniformly distributed transverse load q = 0.0003 MPa. After substituting the values of E, ν, a, b, h and q into Equation (18), it was found that α = 1/2, β = (1 + α)/2 = 3/4 and Q = 0.00382653.
In the actual calculation operation, the infinite power series in Equations (33)–(35) have to be used in truncated form, resulting in
and
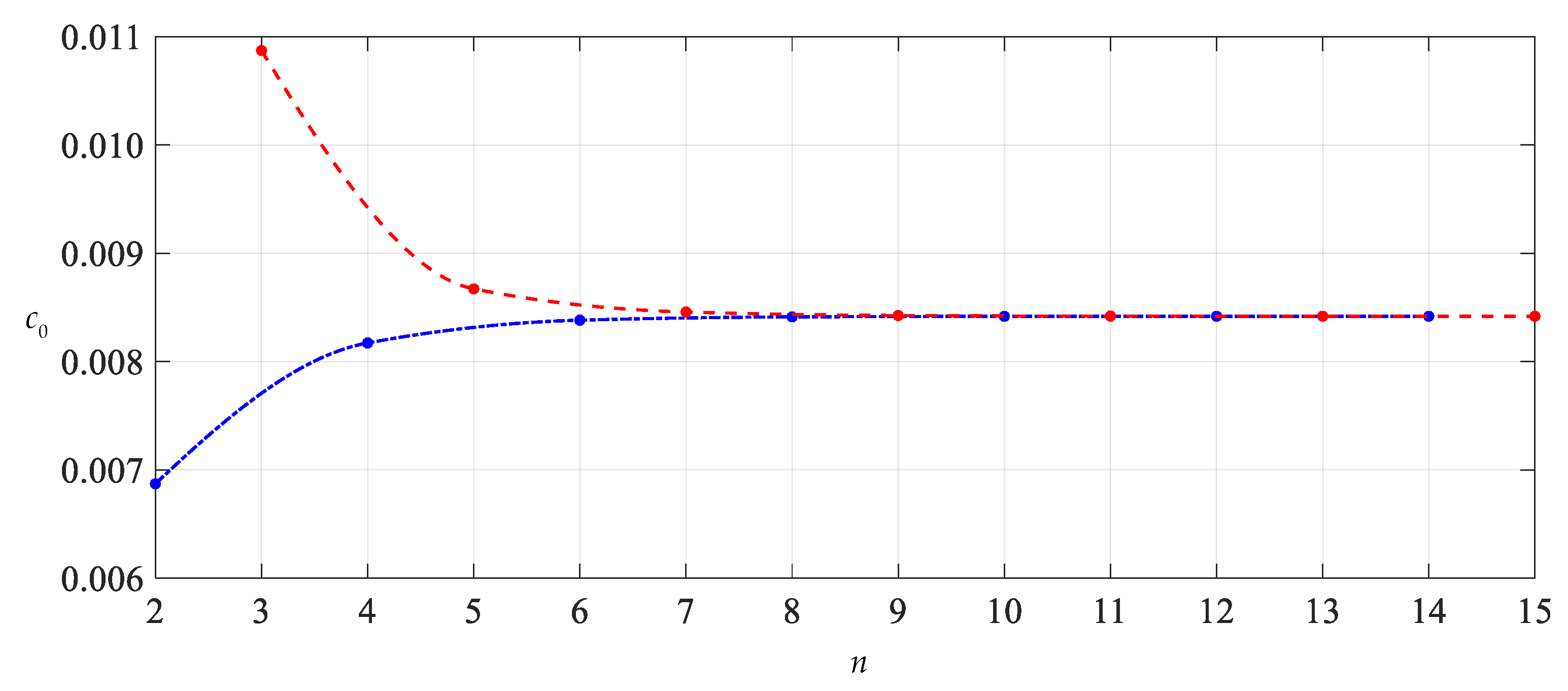
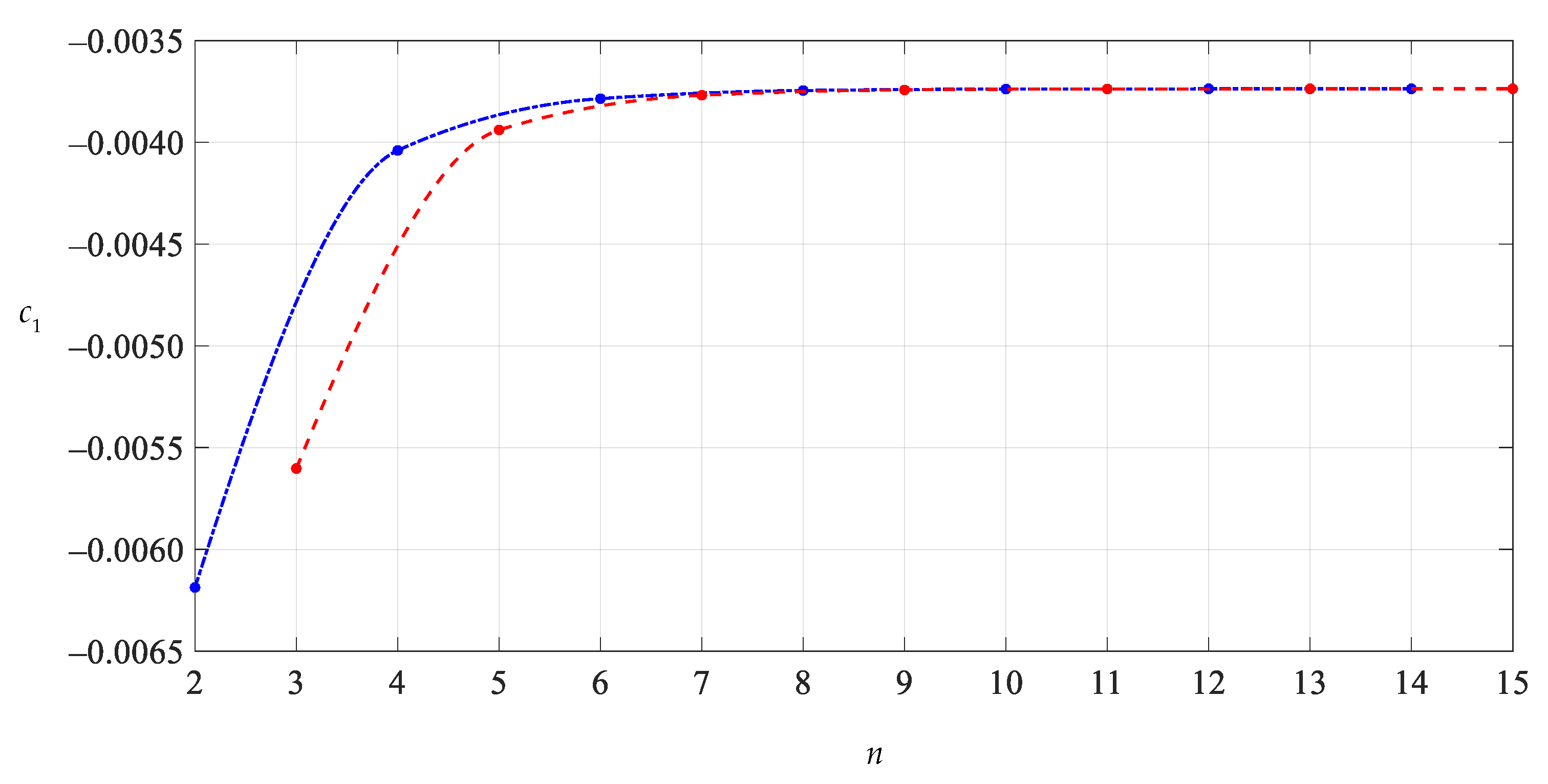
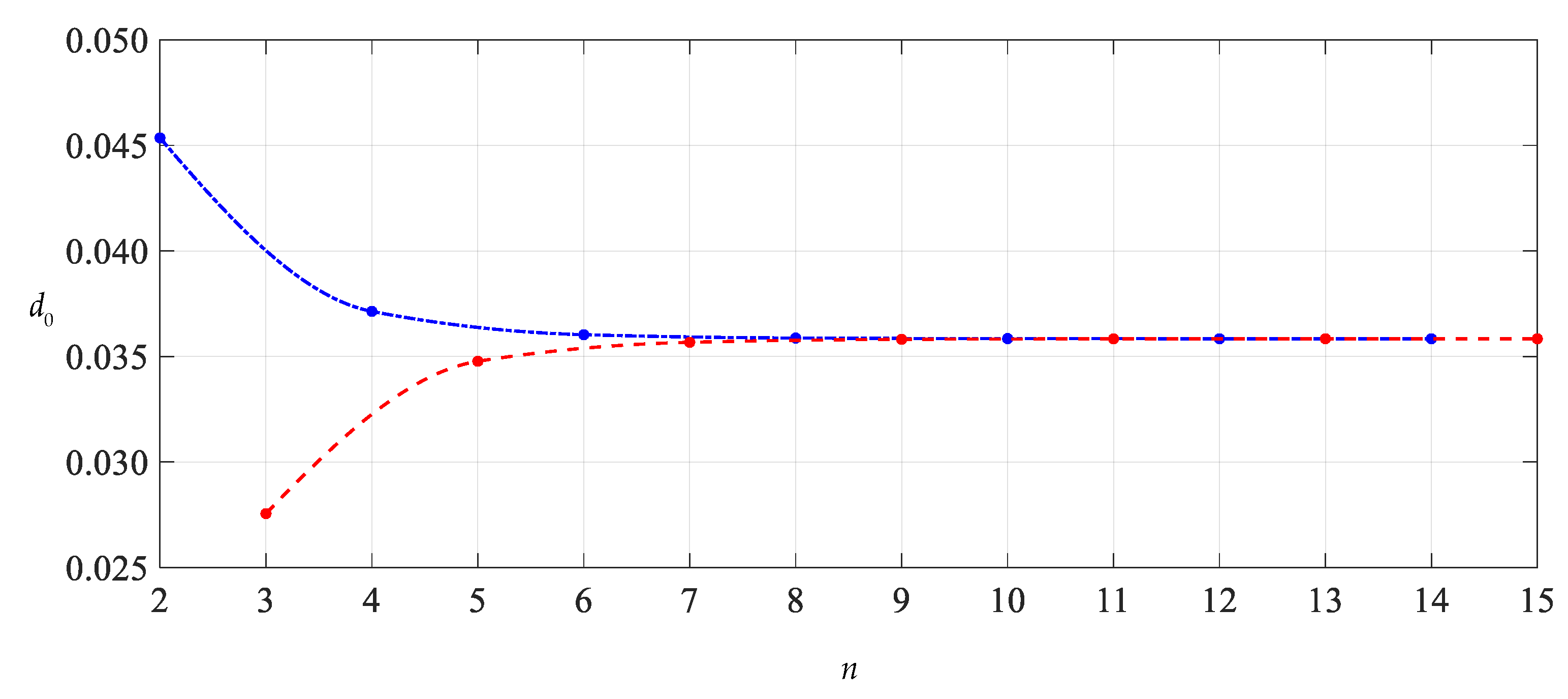
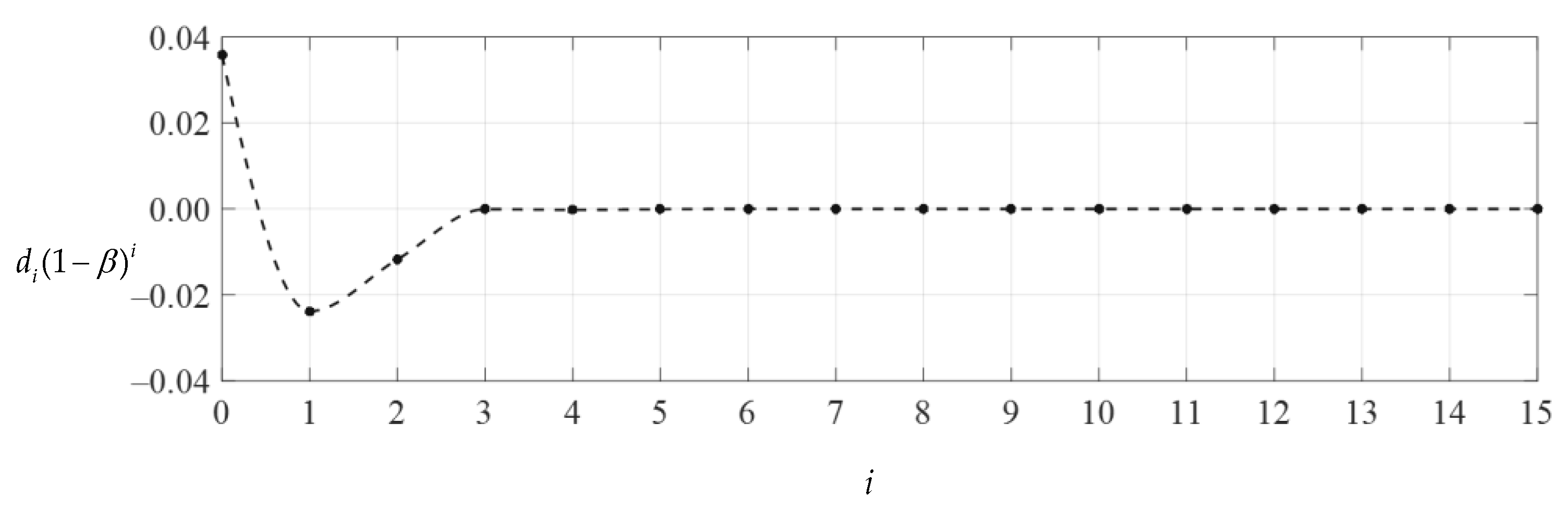
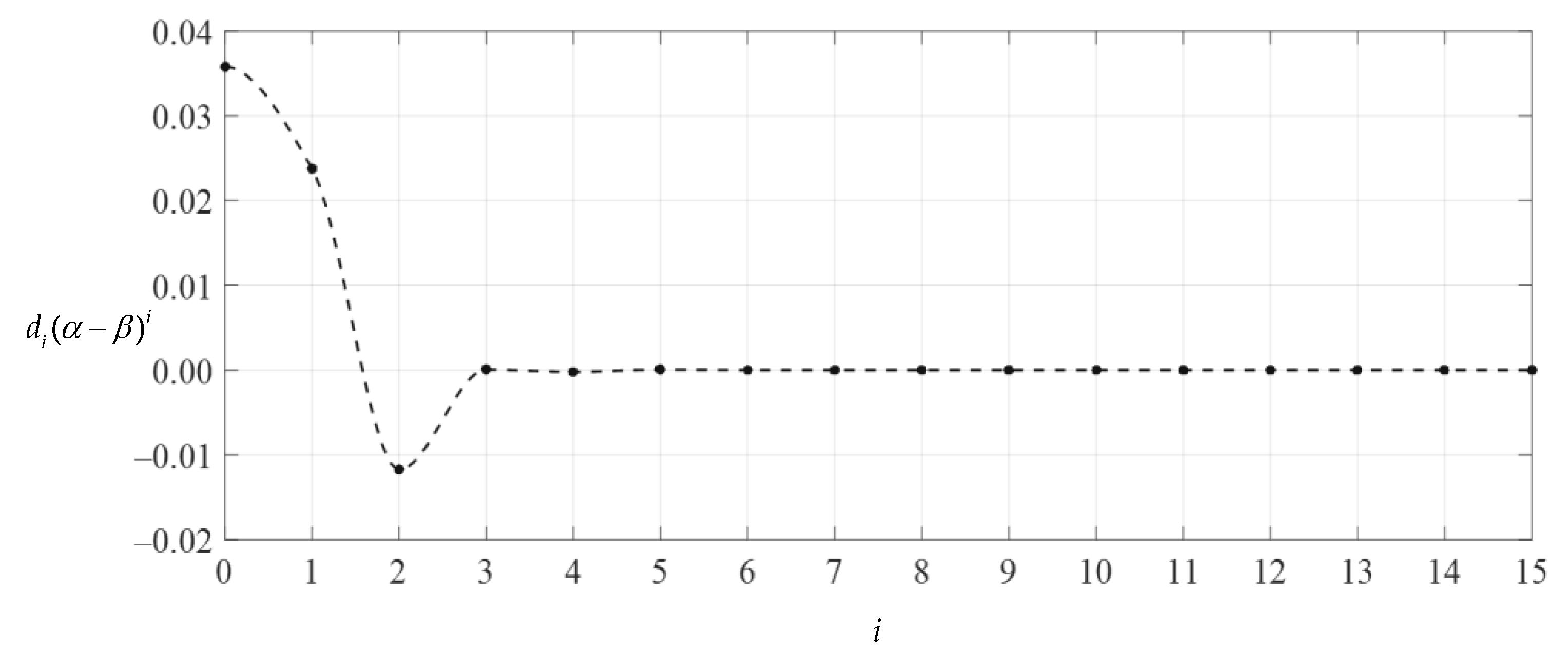
After expressing di (i = 1, 2, 3, …) and ci (i = 2, 3, 4, …) in the polynomials with regard to c0 and c1 (see Appendixe A and Appendixe B), with a given value of the parameter n in Equations (36), (37) and (38), the undetermined constants c0 and c1 can be determined by Equations (36) and (37), and with the known c0 and c1, the value of d0 can be further determined by Equation (38). We numerically calculated the values of the undetermined constants c0, c1 and d0 from n = 2. The results of numerical values of c0, c1 and d0 are listed in Table 1. The convergence trends of c0, c1 and d0 with n are shown in Figure 4, Figure 5 and Figure 6, where the connection lines of data points indicated by a dash-dotted line show the convergence trend of even terms (n = 2, 4, 6…) and those indicated by a dashed line show the convergence trend of odd terms (n = 3, 5, 7…). Of course, we can also make no distinction between odd and even terms to give an oscillation convergence trend, as shown in Figure 7, Figure 8, Figure 9 and Figure 10. However, sometimes it is very useful to distinguish between odd and even terms, as it can help to find the data points (invalid roots) that make connection lines not smooth. The smoothness can be used to judge the effective roots of higher-order equations of c0, c1 and d0, such as Equations (36)–(38).

Table 1.
The results of numerical calculation of c0, c1 and d0.
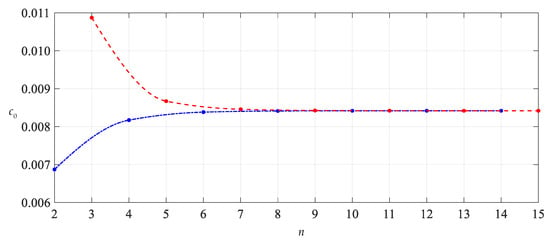
Figure 4.
Variation of c0 with n.
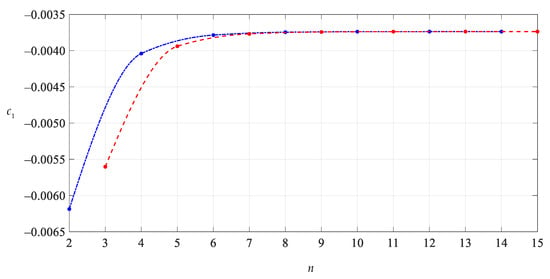
Figure 5.
Variation of c1 with n.
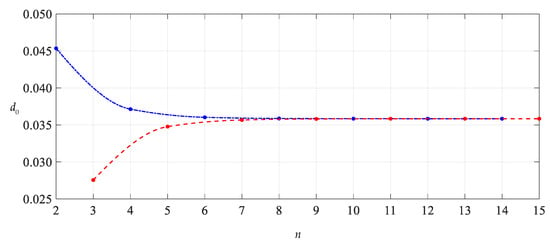
Figure 6.
Variation of d0 with n.
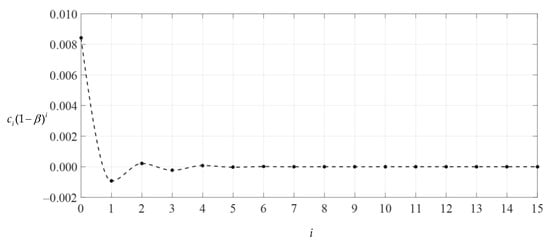
Figure 7.
Variation of ci(1 − β)i with i.
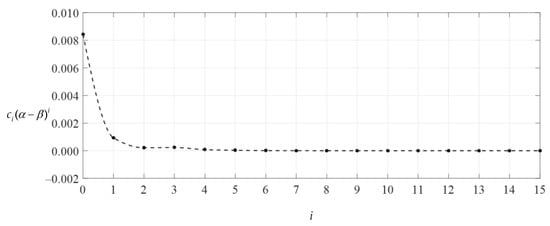
Figure 8.
Variation of ci(α − β)i with i.
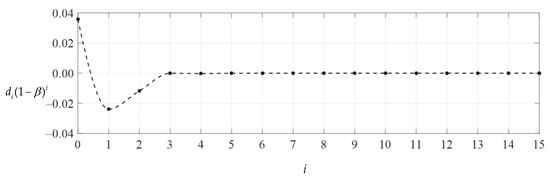
Figure 9.
Variation of di(1 − β)i with i.
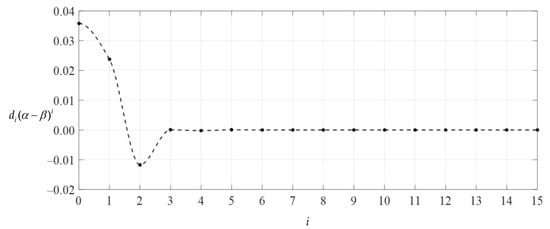
Figure 10.
Variation of di(α − β)i with i.
As can be seen from Figure 4, Figure 5 and Figure 6, when the parameter n is equal to 8 or 9, the data sequences for c0, c1 and d0 show very good convergence, indicating that the infinite power series in Equations (33)–(35) need only be truncated to the ninth terms when used. It should be pointed out that drawing Figure 4, Figure 5 and Figure 6 is very important for the proper use of the power series method for ordinary differential equations. The convergence shown in Figure 4, Figure 5 and Figure 6 is the basis for determining the true value of the undetermined constants c0, c1 and d0. The convergence of the special solutions of stress and deflection can be discussed only after the undetermined constants c0, c1 and d0 are correctly and accurately determined.
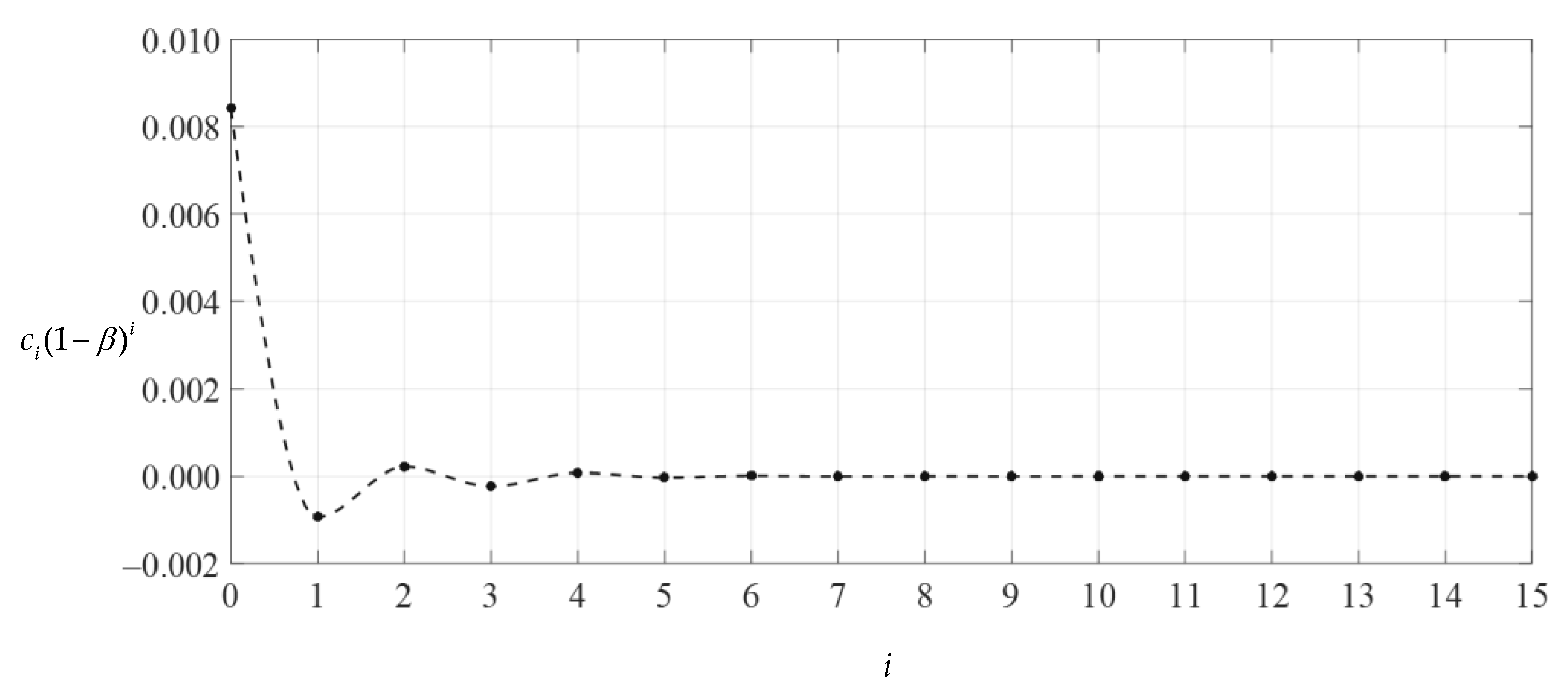
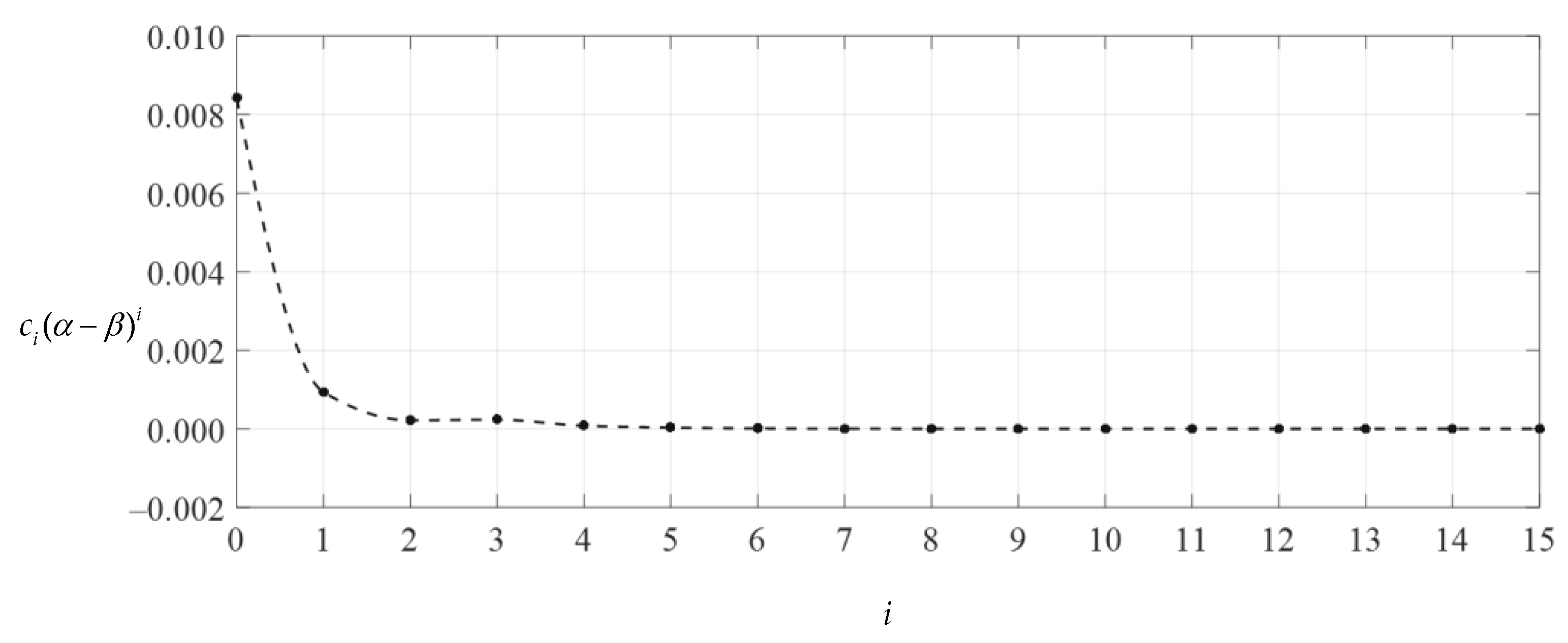
Obviously, if the special solutions of stress and deflection converge at both ends of the closed interval of the independent variable, i.e., at x = 1/2 (r = 10 mm) and at x = 1 (r = 20 mm), then they converge throughout the closed interval [1/2, 1]. Table 2 and Table 3 show the numerical values of stress and deflection of ci(1 − β)i, ci(α − β)i, di(1 − β)i and di(α − β)i, which were calculated by using Equations (31) and (32), where Q = 0.00382653, α = 1/2, β = (1 + α)/2 = 3/4, and the undetermined constants c0, c1 and d0 take the values 0.00841875, −0.00373713 and 0.03584094, respectively (i.e., the values at n = 15 in Table 1). Figure 7, Figure 8, Figure 9 and Figure 10 show the variations in di(α − β)i, di(1 − β)i, ci(α − β)i and ci(1 − β)I with i, indicating that the special solutions of stress and deflection converge very well at x = 1/2 and x = 1 and therefore converge throughout the closed interval [1/2, 1]. Moreover, it can be seen from Figure 7 and Figure 8 that when i is equal to about 5 or 6, the data sequences for ci(1 − β)i and ci(α − β)i show very good convergence, indicating that the infinite power series Equation (31) may be truncated to the sixth terms when used to express the stress special solution of the numerical example considered. However, it can also be seen from Figure 9 and Figure 10 that when i is equal to about 4 or 5, the data sequences for di(1 − β)i and di(α − β)i show very good convergence, indicating that the infinite power series Equation (32) may be truncated to the fifth terms when used to express the deflection special solution of the numerical example considered. Thus, drawing Figure 7, Figure 8, Figure 9 and Figure 10 is very important for the proper use of the power series solutions.

Table 2.
Numerical values of ci(1 − β)i and ci(α − β)i.

Table 3.
Numerical values of di(1 − β)i and di(α − β)i.
3.2. Discussion on Effectiveness
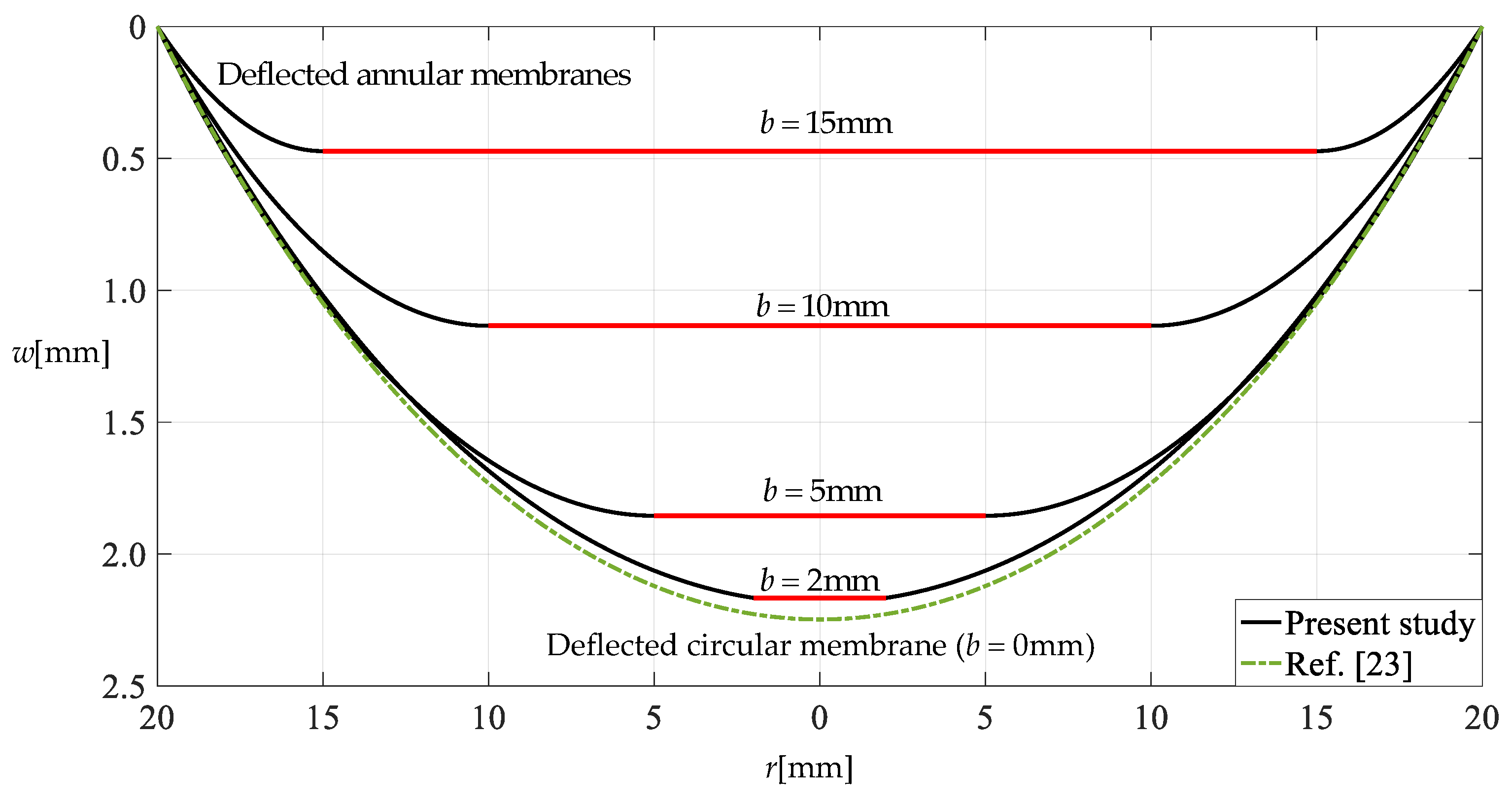
Although the closed-form solution given in Section 2 has been proved to have good convergence, it still needs to be proved whether it can correctly describe the elastic behavior of the hollow annular membrane. Obviously, under the same uniformly distributed transverse load, the hollow annular membrane structure with inner radius b and outer radius a should have the same shape as a circular membrane structure with outer radius a as the inner radius b→0. Therefore, the effectiveness of the closed-form solution given in Section 2 can be proved with the aid of a classical, mature closed-form solution for circular membrane problems. Here we used the closed-form solution that was presented in [23], because this closed-form solution was also obtained without the assumption of a small deflection–outer radius ratio or a small rotation angle of the membrane.
Figure 11 shows that the deflection profiles of the annular membranes gradually approach the deflection profile of the circular membrane as the inner radius b of the annular membranes gradually decreases from 15 mm to 2 mm, where the annular and circular membranes have the same Young’s modulus of elasticity E = 7.84 MPa, Poisson’s ratio v = 0.47, thickness h = 0.2 mm and outer radius a = 20 mm and are subjected to the same load q = 0.0005 MPa. The deflection profiles were calculated for the annular membranes using the closed-form solution given in Section 2 (“Present study” in Figure 11) and for the circular membrane using the closed-form solution presented in [23] (“Ref. [23]” in Figure 11). Therefore, it can be concluded from Figure 11 that the closed-form solution given in Section 2 is reliable to a certain extent.
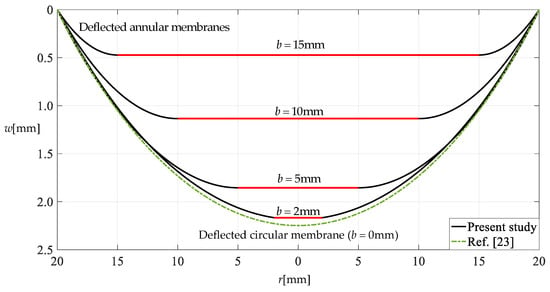
Figure 11.
The deflection profiles of the annular membranes gradually approaching that of the circular membrane as inner radius b decreases from 15 to 2.
3.3. Comparison of the Closed-Form Solutions before and after Improvement
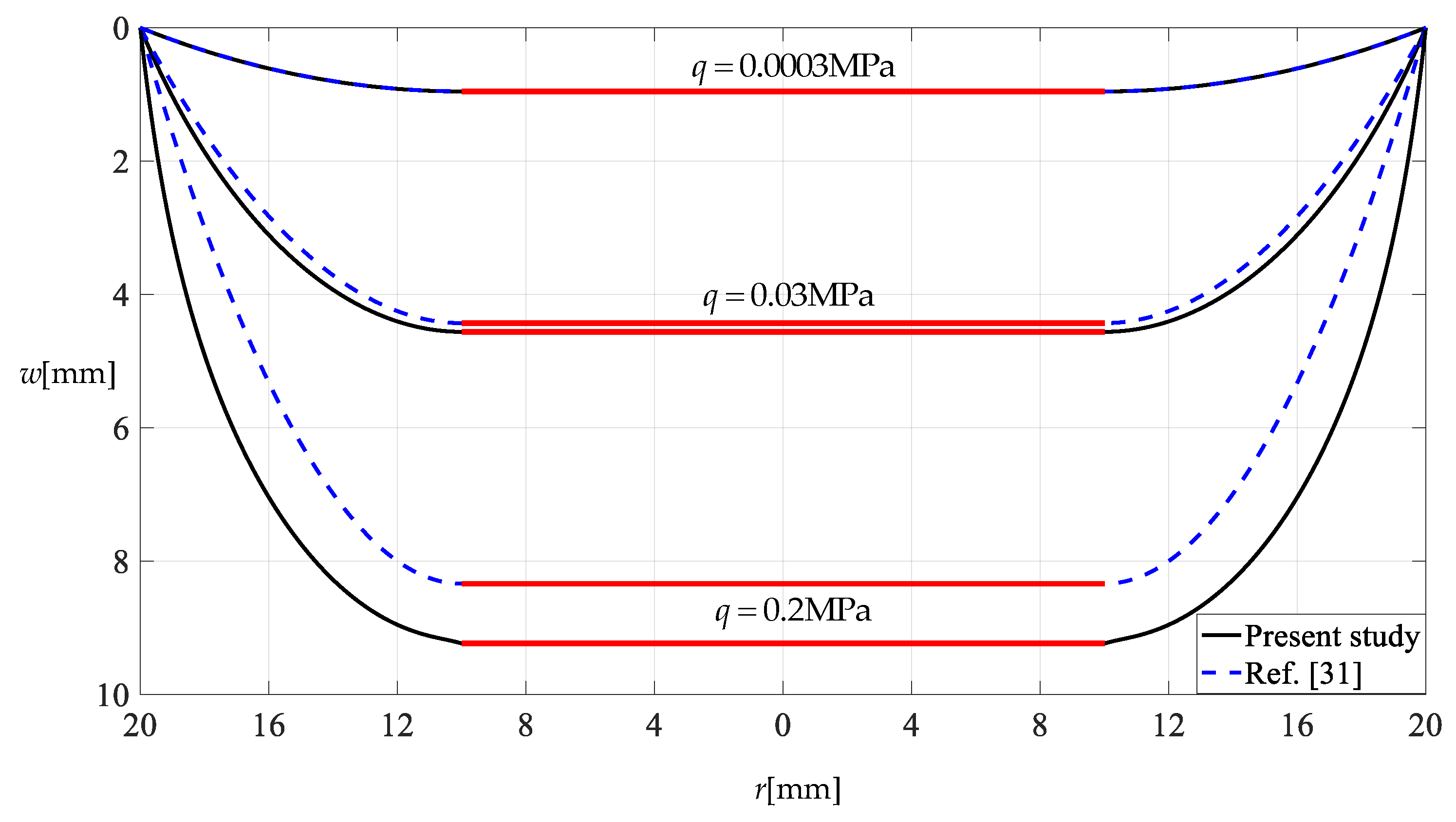
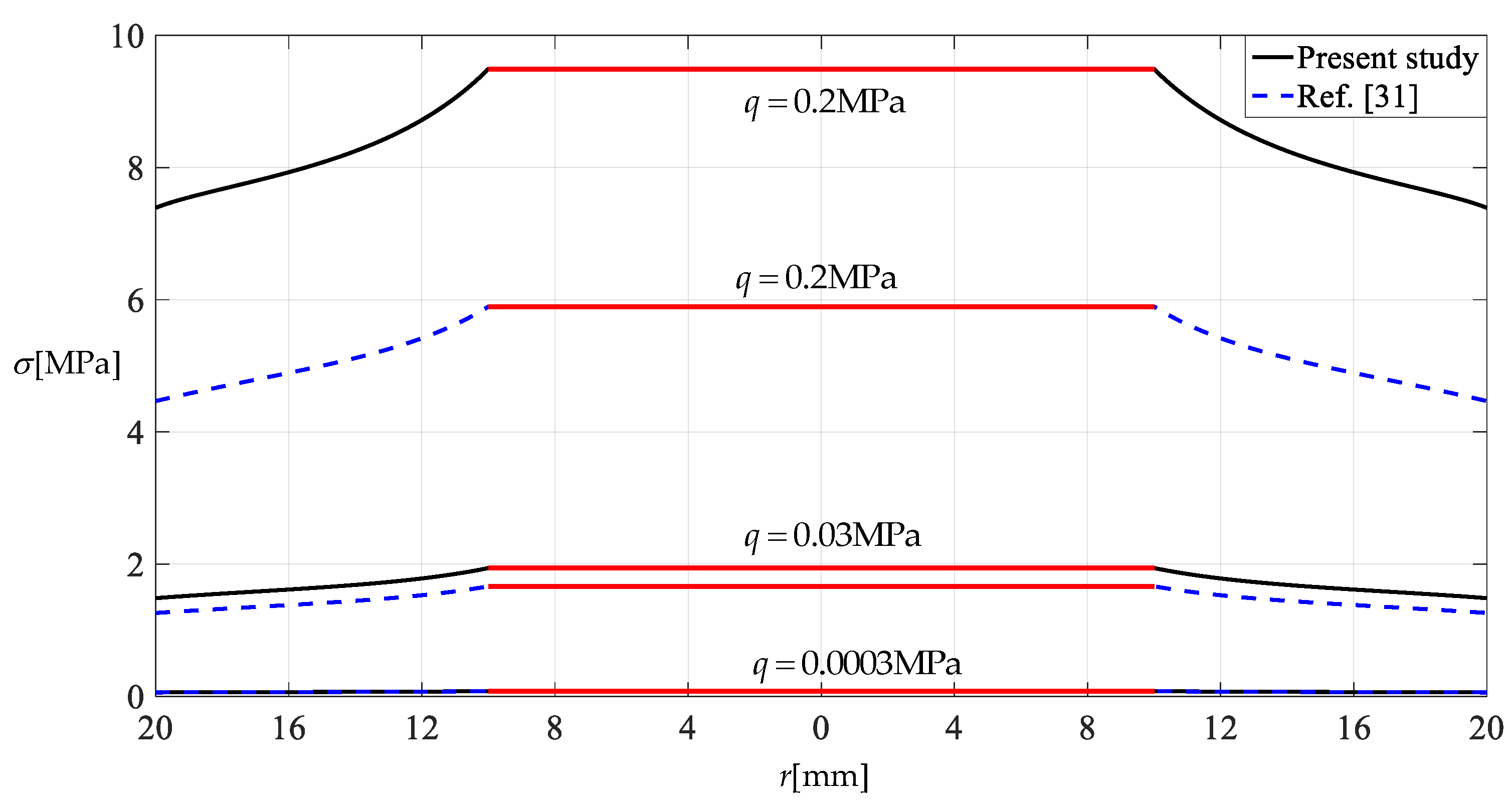
Figure 12 and Figure 13 show the variation in the deflection and stress of an annular membrane with uniformly distributed transverse load q, where the annular membrane has Poisson’s ratio v = 0.47, Young’s modulus of elasticity E = 7.84 MPa, outer radius a = 20 mm, inner radius b = 10 mm and thickness h = 0.2 mm and is subjected to loads q = 0.0003 MPa, 0.03 MPa and 0.02 MPa. “Present study” refers to the closed-form solution given in Section 2, and “Ref. [31]” refers to the closed-form solution given in [31]. The difference between this study and the previous study [31] mainly lies in the out-of-plane equilibrium equations, that is, the difference between Equation (3) in this paper and Equation (3) in [31]. The out-of-plane equilibrium equation in [31] used the assumption of a small deflection–outer radius ratio or small rotation angle of the membrane, while the new out-of-plane equilibrium equation in this study makes no such assumption.
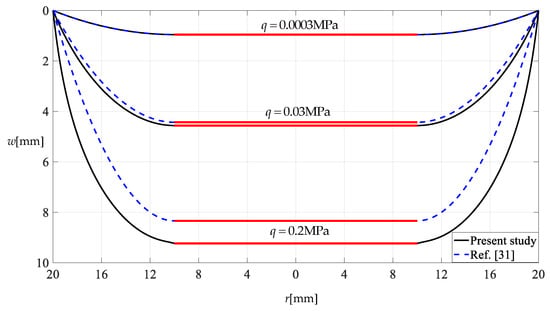
Figure 12.
Variation of deflection difference with load q.
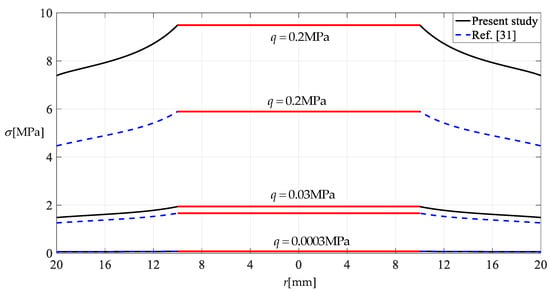
Figure 13.
Variation of stress difference with load q.
It can be seen from Figure 12 and Figure 13 that the differences in both deflection and stress increase with increasing uniformly distributed transverse load q, especially when q = 0.2 MPa, where the difference in deflection is about 0.9 mm while the difference in stress is as high as about 3.6 MPa. As mentioned above, the closed-form solutions in [31] and in this study are primarily for application to the design of “conjugate shells of revolution”. Therefore, Figure 12 and Figure 13 show that for a conjugate shell of revolution with a given large height–span ratio, if it is designed using the closed-form solution presented in [31], then there is a stress design error that increases as the height–span ratio increases, and such an error will affect its safe service. Therefore, for the design of conjugate shells of revolution with large height–span ratios, the new closed-form solution presented in this paper should be adopted in preference to the old one presented in [31].
4. Concluding Remarks
In this study, the problem of axisymmetric deformation of a hollow annular membrane structure under uniformly distributed transverse load, which was, for the first time, proposed and dealt with in a previous work by the same authors [31], was analytically solved again, resulting in a new and more refined closed-form solution suitable for cases where the annular membrane is allowed to exhibit a larger deflection–outer radius ratio or larger rotation angle of the membrane. The resulting new and more refined closed-form solution makes the design of conjugate shells of revolution with large height–span ratios possible. The following main conclusions can be drawn from this study.
The assumption of a small deflection–outer radius ratio or small rotation angle of the membrane can make the closed-form solutions based on this assumption lose too much computational accuracy, especially for heavily loaded membranes.
The closed-form solution presented in [31] agrees quite closely with the closed-form solution presented in this paper for lightly loaded membranes, but as the uniformly distributed transverse load intensifies, it slowly diverges from the closed-form solution presented in this paper, due to the adopted assumption of a small deflection–outer radius ratio or small rotation angle of the membrane.
For the design of conjugate shells of revolution with large height–span ratios, the closed-form solution presented in this paper should be adopted in preference to the closed-form solution presented in [31]; otherwise, a design error that affects the safe service of the designed conjugate shells of revolution may be caused.
In addition, the limitation of this study is that only the out-of-plane equation was improved, while the classical equations were still adopted for the in-plane equations and geometric equations. Therefore, further research is still necessary. The work presented here can be further integrated into the design of conjugate shells of revolution, and it is also of great significance for the structural design of annular thin films or thin plates.
Author Contributions
Conceptualization, J.-Y.S.; methodology, Q.Z., X.L. and J.-Y.S.; validation, X.-T.H.; writing—original draft preparation, Q.Z. and X.L.; writing—review and editing, X.L. and X.-T.H.; visualization, Q.Z. and X.L.; funding acquisition, J.-Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 11772072).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix B
References
- Molla-Alipour, M.; Ganji, B.A. Analytical Analysis of Mems Capacitive Pressure Sensor with Circular Diaphragm under Dynamic Load Using Differential Transformation Method (DTM). Acta Mech. Solida Sin. 2015, 28, 400–408. [Google Scholar] [CrossRef]
- Lee, H.Y.; Choi, B. Theoretical and Experimental Investigation of the Trapped Air Effect on Air-Sealed Capacitive Pressure Sensor. Sens. Actuators A 2015, 221, 104–114. [Google Scholar] [CrossRef]
- Mishra, R.B.; Khan, S.M.; Shaikh, S.F. Low-Cost Foil/Paper Based Touch Mode Pressure Sensing Element as Artificial Skin Module for Prosthetic Hand. In Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 194–200. [Google Scholar]
- Meng, G.Q.; Ko, W.H. Modeling of Circular Diaphragm and Spreadsheet Solution Programming for Touch Mode Capacitive Sensors. Sens. Actuators A 1999, 75, 45–52. [Google Scholar] [CrossRef]
- Delfani, M.R. Nonlinear Elasticity of Monolayer Hexagonal Crystals: Theory and Application to Circular Bulge Test. Eur. J. Mech. A-Solid. 2018, 68, 117–132. [Google Scholar] [CrossRef]
- Dai, Z.; Lu, N. Poking and Bulging of Suspended Thin Sheets: Slippage, Instabilities, and Metrology. J. Mech. Phys. Solids 2021, 149, 104320. [Google Scholar] [CrossRef]
- Gutscher, G.; Wu, H.C.; Ngaile, G.; Altan, T. Determination of Flow Stress for Sheet Metal Forming Using the Viscous Pressure Bulge (VPB) Test. J. Mater. Process. Technol. 2004, 146, 1–7. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.R.; Chen, Y.L.; Long, D.; Guan, Y.C.; Liu, L.Q.; Zhang, Z. Extended Hencky Solution for the Blister Test of Nanomembrane. Extreme Mech. Lett. 2018, 22, 69–78. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; Li, S.Z.; Zheng, Z.L. A Refined Theory for Characterizing Adhesion of Elastic Coatings on Rigid Substrates Based on Pressurized Blister Test Methods: Closed-Form Solution and Energy Release Rate. Polymers 2020, 12, 1788. [Google Scholar] [CrossRef]
- Cao, Z.; Tao, L.; Akinwande, D.; Huang, R.; Liechti, K.M. Mixed-Mode Traction-Separation Relations between Graphene and Copper by Blister Tests. Int. J. Solids Struct. 2016, 84, 147–159. [Google Scholar] [CrossRef]
- Napolitanno, M.J.; Chudnovsky, A.; Moet, A. The Constrained Blister Test for the Energy of Interfacial Adhesion. J. Adhes. Sci. Technol. 1988, 2, 311–323. [Google Scholar] [CrossRef]
- Pervier, M.L.A.; Hammond, D.W. Measurement of the Fracture Energy in Mode I of Atmospheric Ice Accreted on Different Materials Using a Blister Test. Eng. Fract. Mech. 2019, 214, 223–232. [Google Scholar] [CrossRef]
- Zhu, T.T.; Li, G.X.; Müftü, S. Revisiting the Constrained Blister Test to Measure Thin Film Adhesion. J. Appl. Mech.-T ASME 2017, 84, 071005. [Google Scholar] [CrossRef]
- Zhu, T.T.; Müftü, S.; Wan, K.T. One-Dimensional Constrained Blister Test to Measure Thin Film Adhesion. J. Appl. Mech.-Trans. ASME 2018, 85, 054501. [Google Scholar] [CrossRef]
- Hencky, H. On the Stress State in Circular Plates with Vanishing Bending Stiffness. Z. Angew. Math. Phys. 1915, 63, 311–317. [Google Scholar]
- Chien, W.Z. Asymptotic Behavior of a Thin Clamped Circular Plate under Uniform Normal Pressure at Very Large Deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic Circular Membranes under the Uniformly Distributed Loads. Eng. Corpus 1953, 14, 196–198. [Google Scholar]
- Li, X.; Sun, J.Y.; Zhao, Z.H.; He, X.T. Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads. Symmetry 2020, 12, 1343. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-Form Solution of Axisymmetric Deformation of Prestressed Föppl-Hencky Membrane under Constrained Deflecting. Stuct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
- Huang, P.F.; Song, Y.P.; Li, Q.; Liu, X.Q.; Feng, Y.Q. A Theoretical Study of Circular Orthotropic Membrane under Concentrated Load: The Relation of Load and Deflection. IEEE Access 2020, 8, 126127–126137. [Google Scholar] [CrossRef]
- Sun, J.Y.; Qian, S.H.; Li, Y.M.; He, X.T.; Zheng, Z.L. Theoretical Study of Adhesion Energy Measurement for Film/Substrate Interface Using Pressurized Blister Test: Energy Release Rate. Measurement 2013, 46, 2278–2287. [Google Scholar] [CrossRef]
- Rao, Y.; Qiao, S.; Dai, Z.; Lu, N. Elastic Wetting: Substrate-Supported Droplets Confined by Soft Elastic Membranes. J. Mech. Phys. Solids 2021, 151, 104399. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Yang, Z.X. Closed-Form Solution of Well-Known Hencky Problem without Small-Rotation-Angle Assumption. Z. Angew. Math. Me. 2016, 96, 1434–1441. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; He, X.T. A Revisit of the Boundary Value Problem for Föppl–Hencky Membranes: Improvement of Geometric Equations. Mathematics 2020, 8, 631. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Sun, J.Y.; Zhao, Z.H.; Li, S.Z.; He, X.T. A New Solution to Well-Known Hencky Problem: Improvement of In-Plane Equilibrium Equation. Mathematics 2020, 8, 653. [Google Scholar] [CrossRef]
- Shi, B.B.; Sun, J.Y.; Huang, T.K.; He, X.T. Closed-Form Solution for Circular Membranes under In-Plane Radial Stretching or Compressing and Out-Of-Plane Gas Pressure Loading. Mathematics 2021, 9, 1238. [Google Scholar] [CrossRef]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The Symmetrical Deformation of Circular Membrane under the Action of Uniformly Distributed Loads in Its Central Portion. Appl. Math. Mech. 1981, 2, 599–612. [Google Scholar]
- Alekseev, S.A. Elastic Annular Membranes with a Stiff Centre under the Concentrated Force. Eng. Cor. 1951, 10, 71–80. [Google Scholar]
- Sun, J.Y.; Hu, J.L.; He, X.T.; Zheng, Z.L. A Theoretical Study of a Clamped Punch-Loaded Blister Configuration: The Quantitative Relation of Load and Deflection. Int. J. Mech. Sci. 2010, 52, 928–936. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Ge, X.M.; Yang, Z.X.; He, X.T.; Zheng, Z.L. A Theoretical Study of an Improved Capacitive Pressure Sensor: Closed-Form Solution of Uniformly Loaded Annular Membranes. Measurement 2017, 111, 84–92. [Google Scholar] [CrossRef]
- Sun, J.Y.; Zhang, Q.; Li, X.; He, X.T. Axisymmetric Large Deflection Elastic Analysis of Hollow Annular Membranes under Transverse Uniform Loading. Symmetry 2021, 13, 1770. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).