Influences of Boundary Temperature and Angular Velocity on Thermo-Elastic Characteristics of a Functionally Graded Circular Disk Subjected to Contact Forces
Abstract
:1. Introduction
2. Materials and Methods
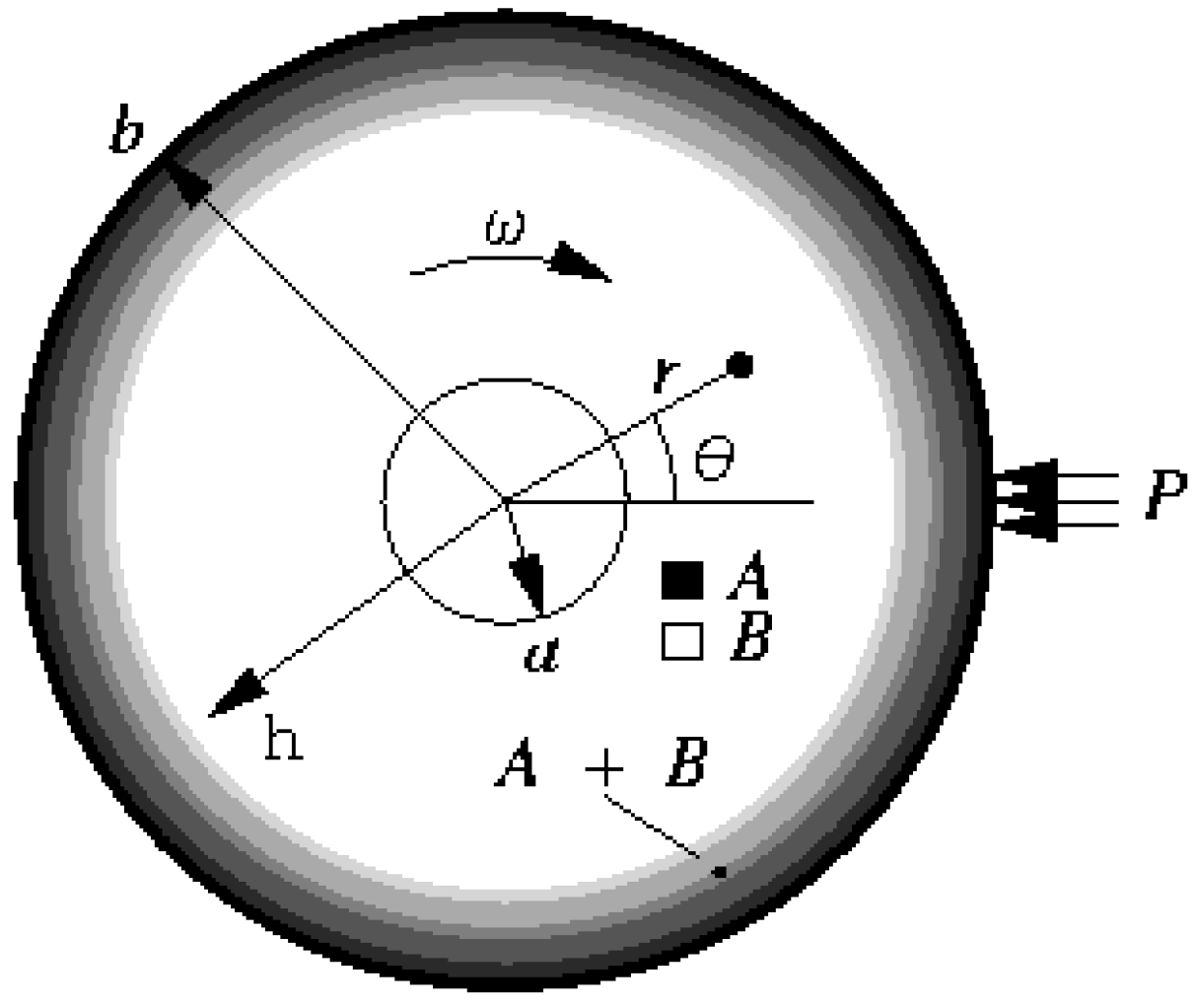
2.1. Mathematical Formulation
2.2. Temperature Distribution Profiles
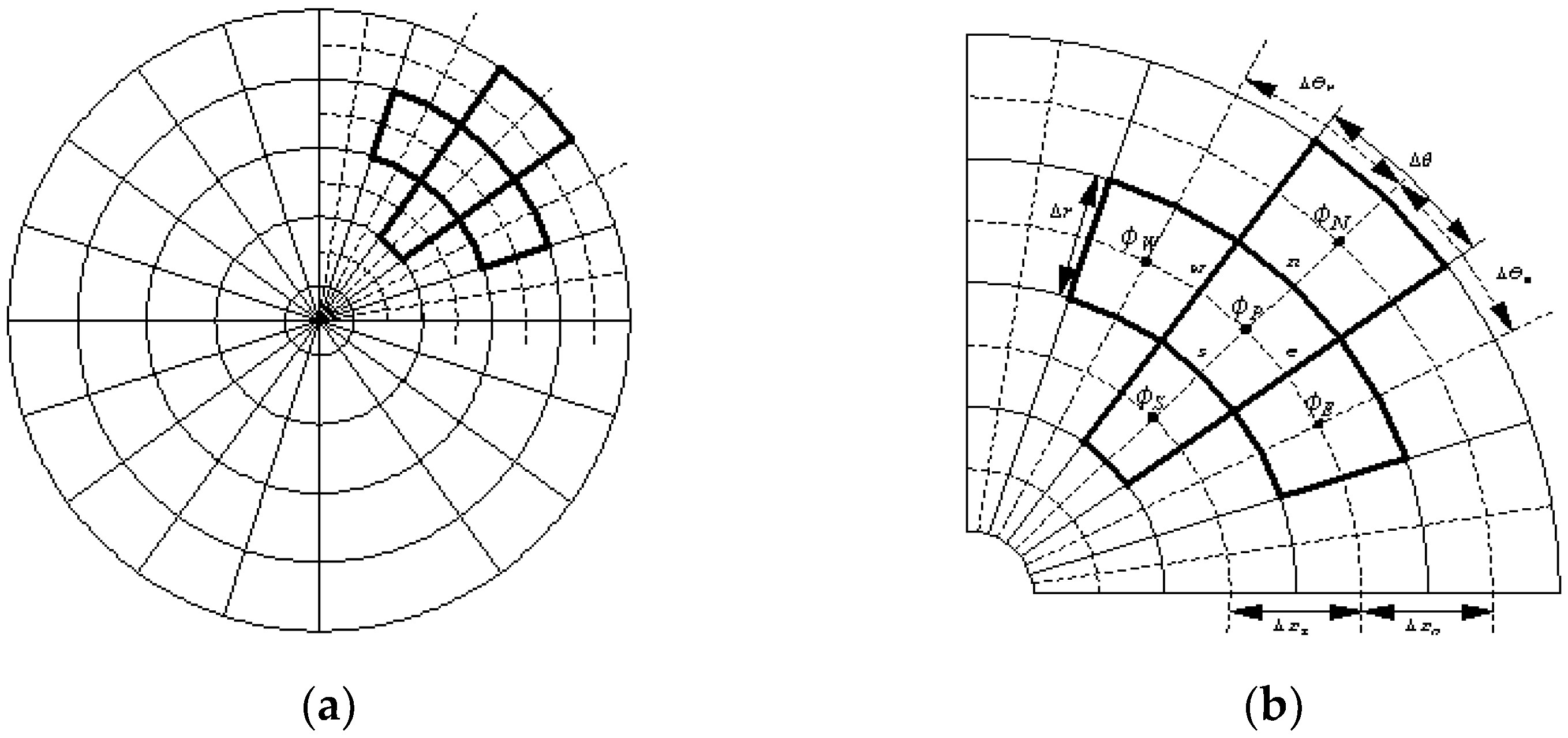
2.3. Finite Volume Formulation
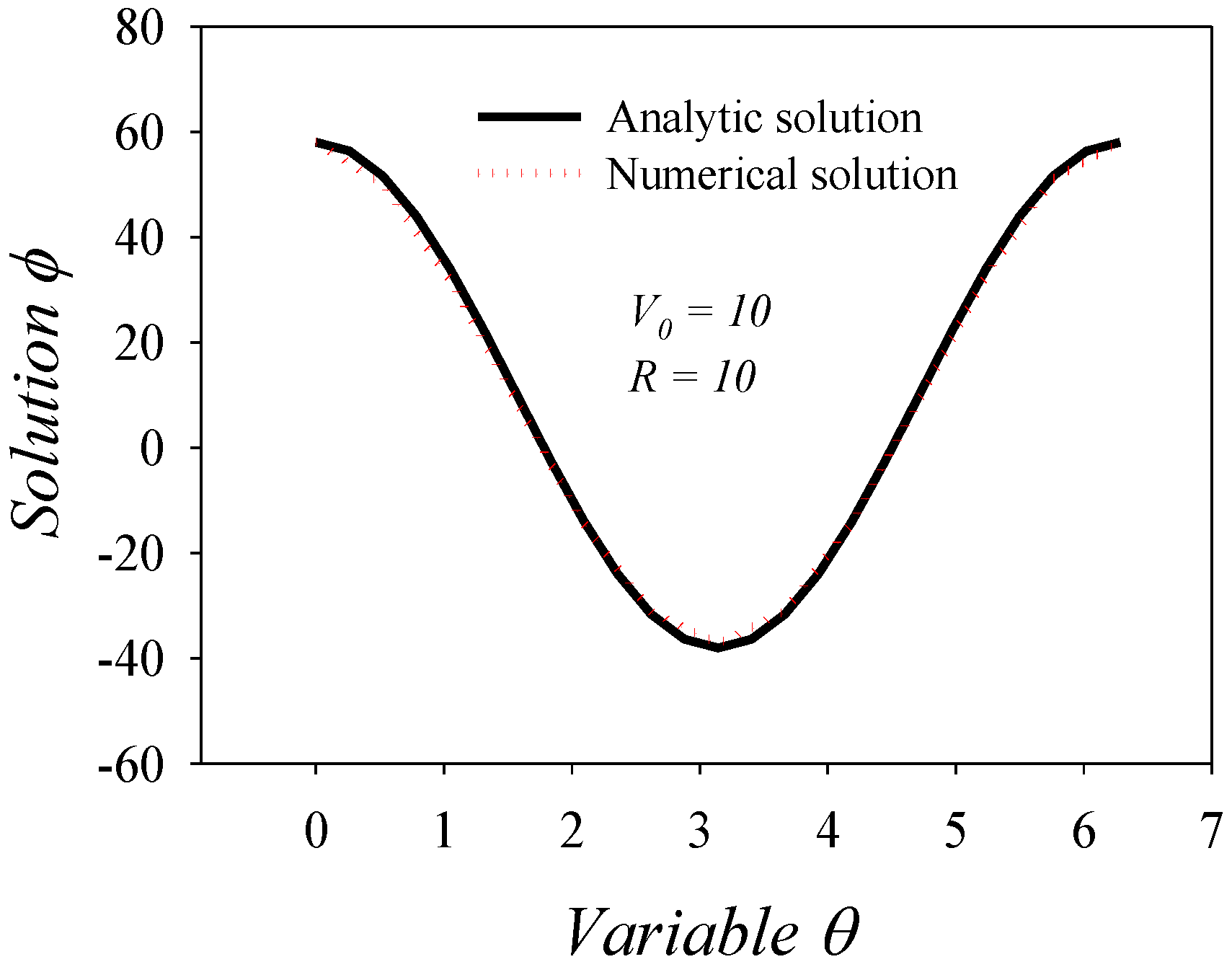
2.4. Validation of Numerical Approach
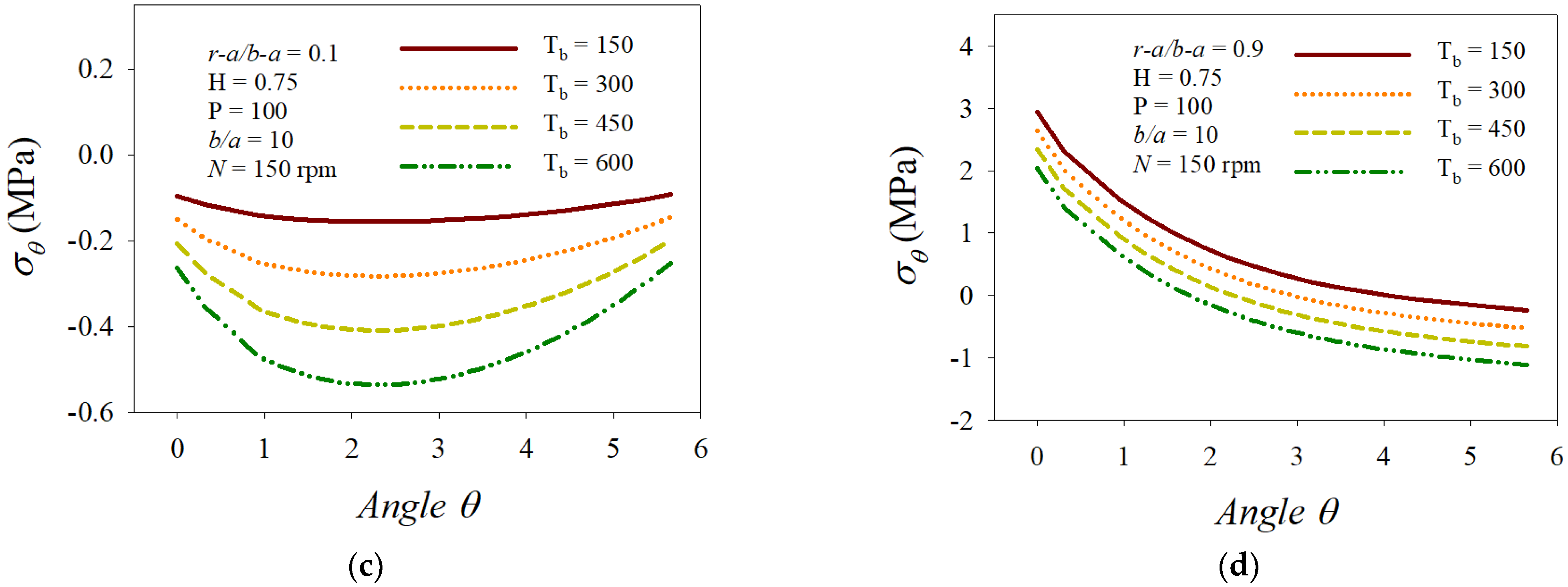
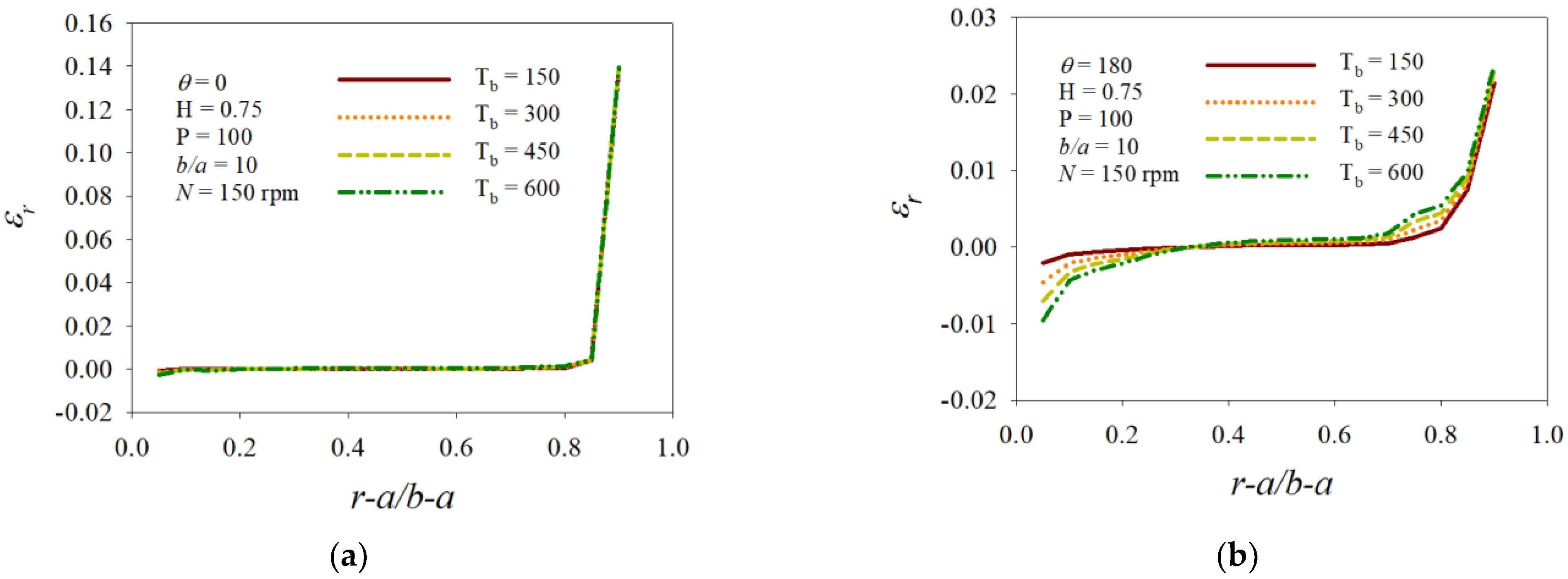
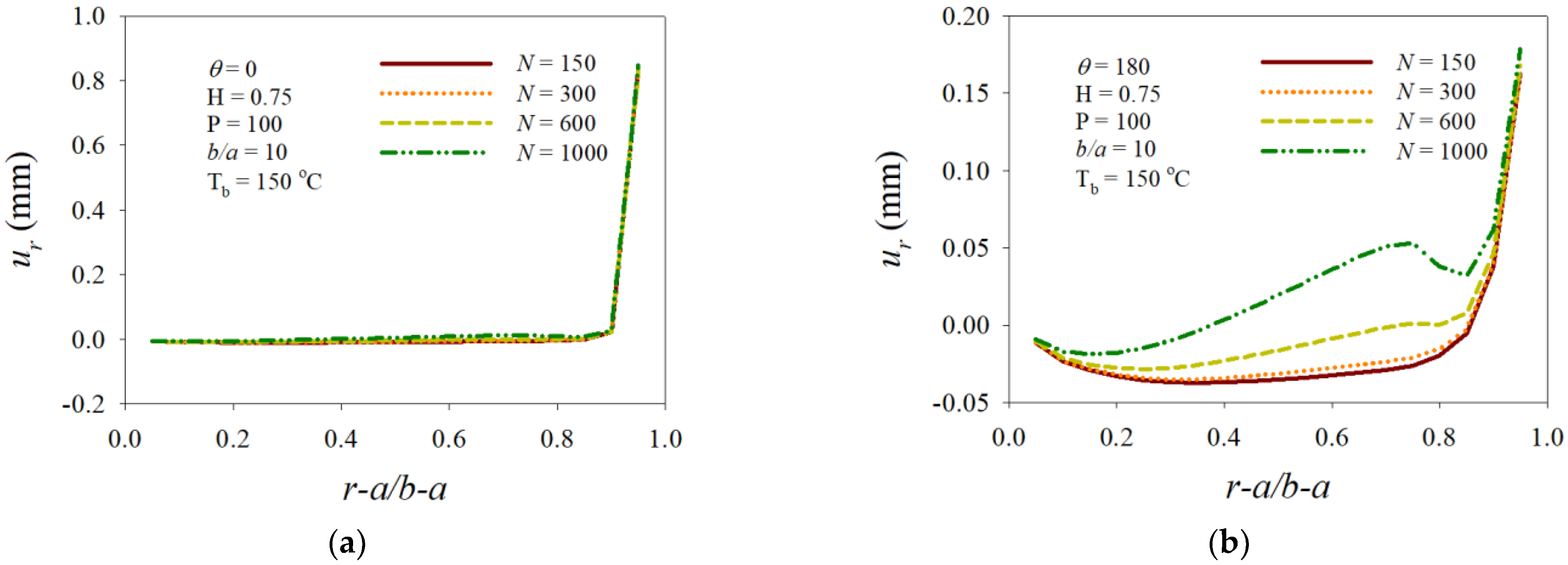
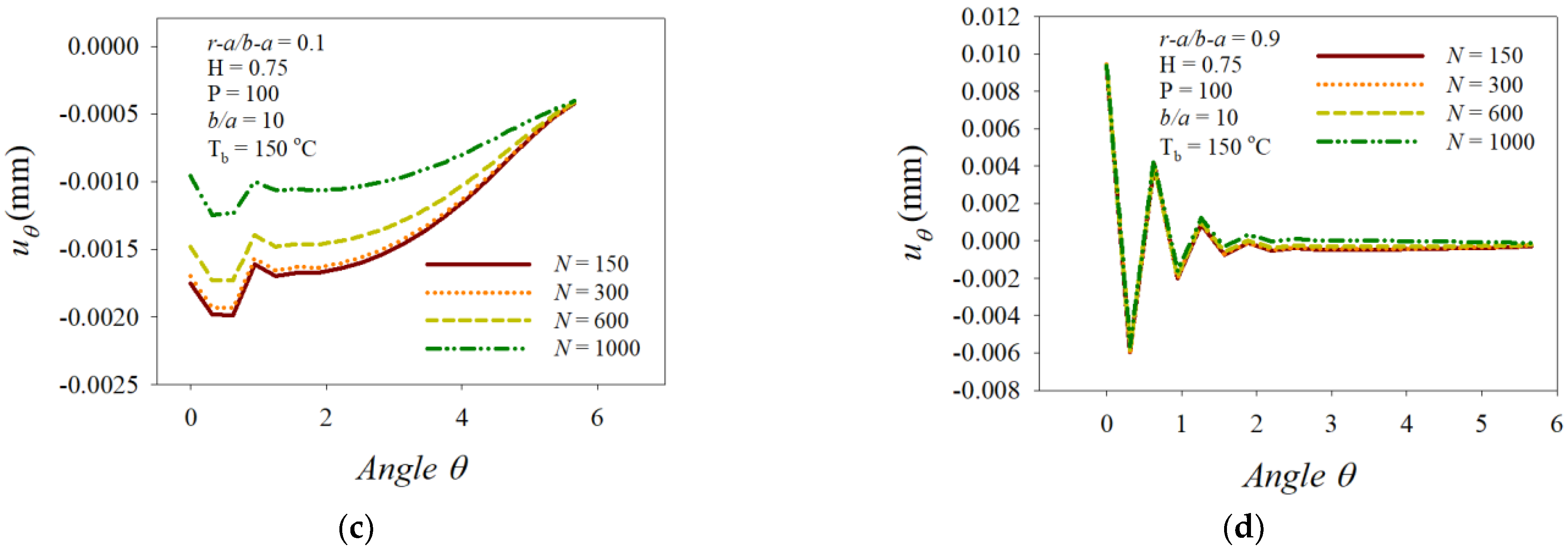
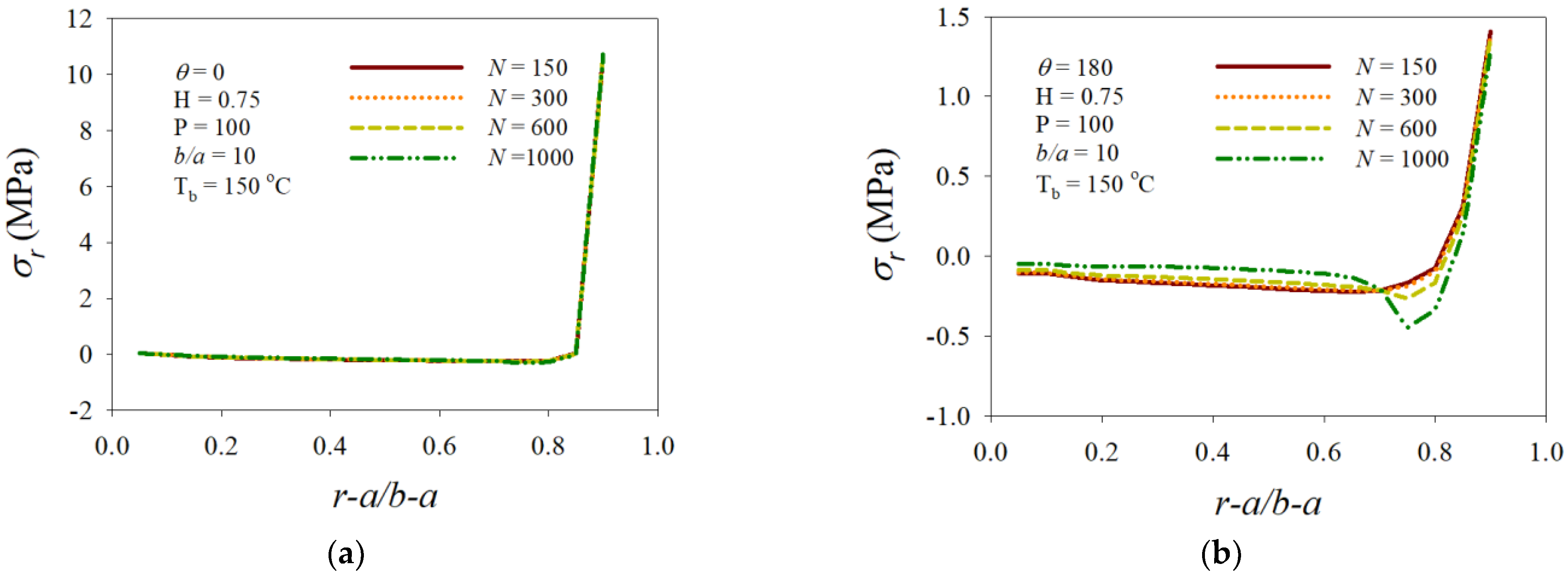
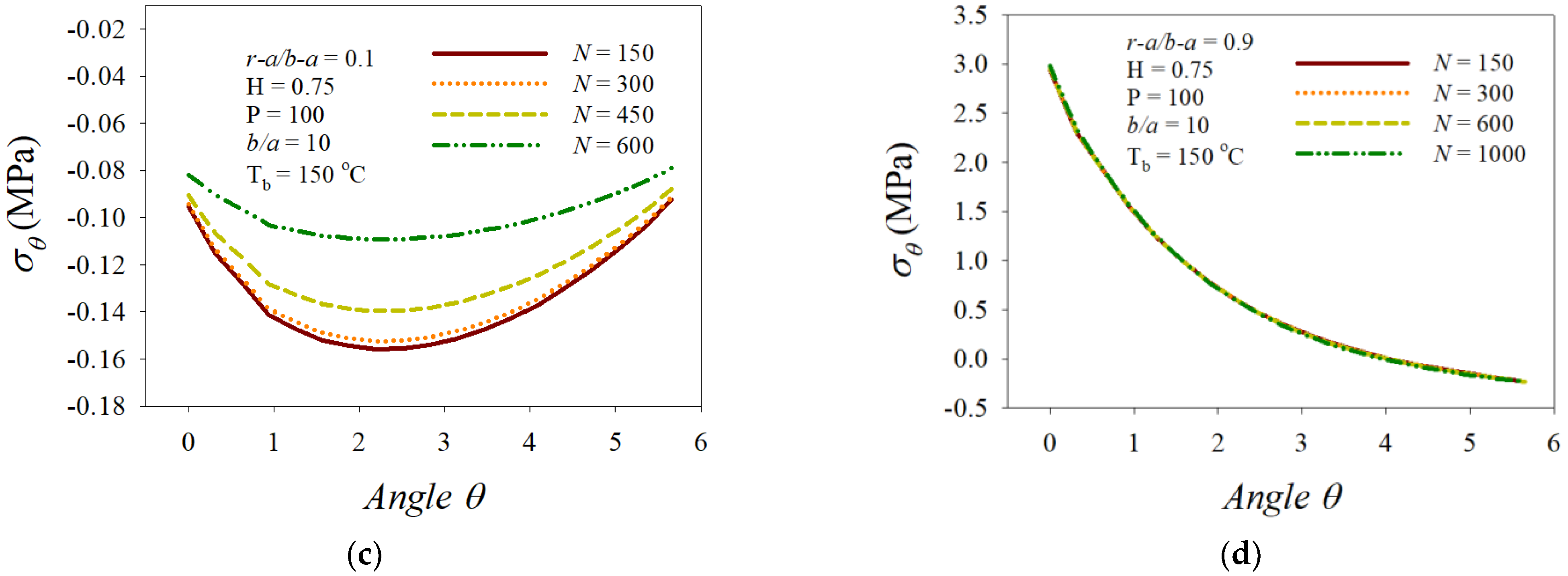
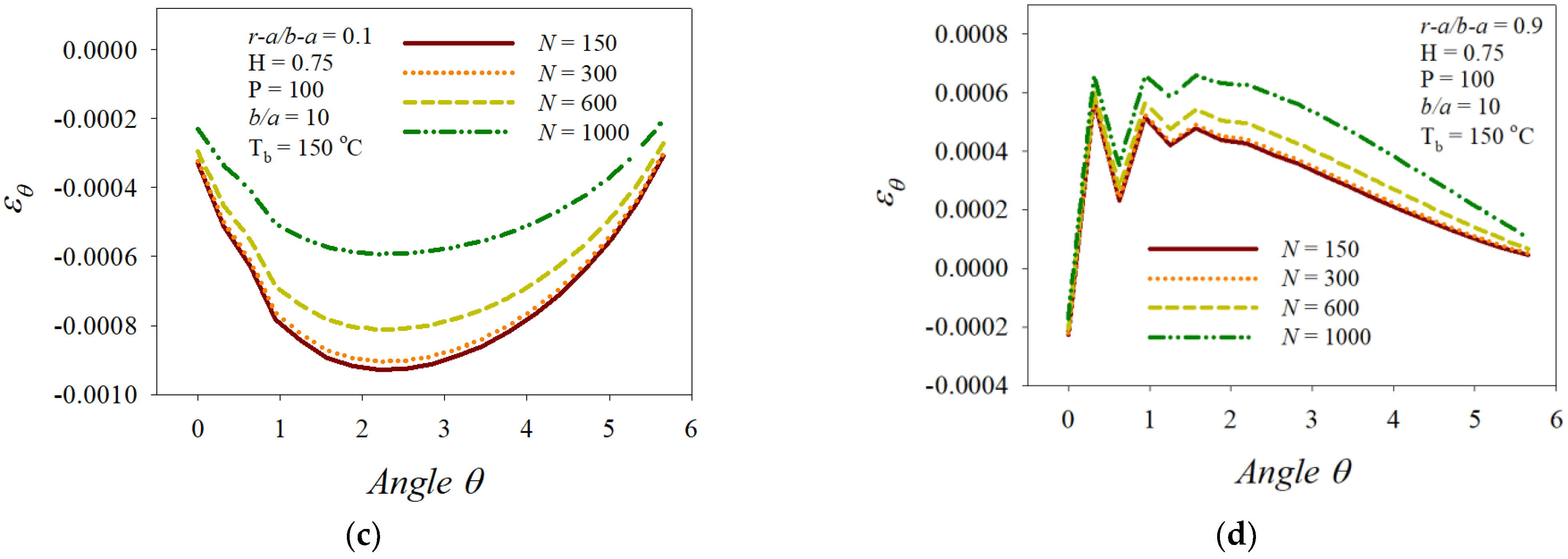
3. Numerical Results and Discussion
4. Conclusions
- (i)
- A larger displacement distribution developed in the concentric direction.
- (ii)
- The magnitudes of the displacement, stress, and strain distribution profiles increased over the area of the inner surface.
- (iii)
- The opposite side to the loading point reacted sensitively and the magnitudes of the displacement, stress, and strain distribution profiles increased over the opposite area.
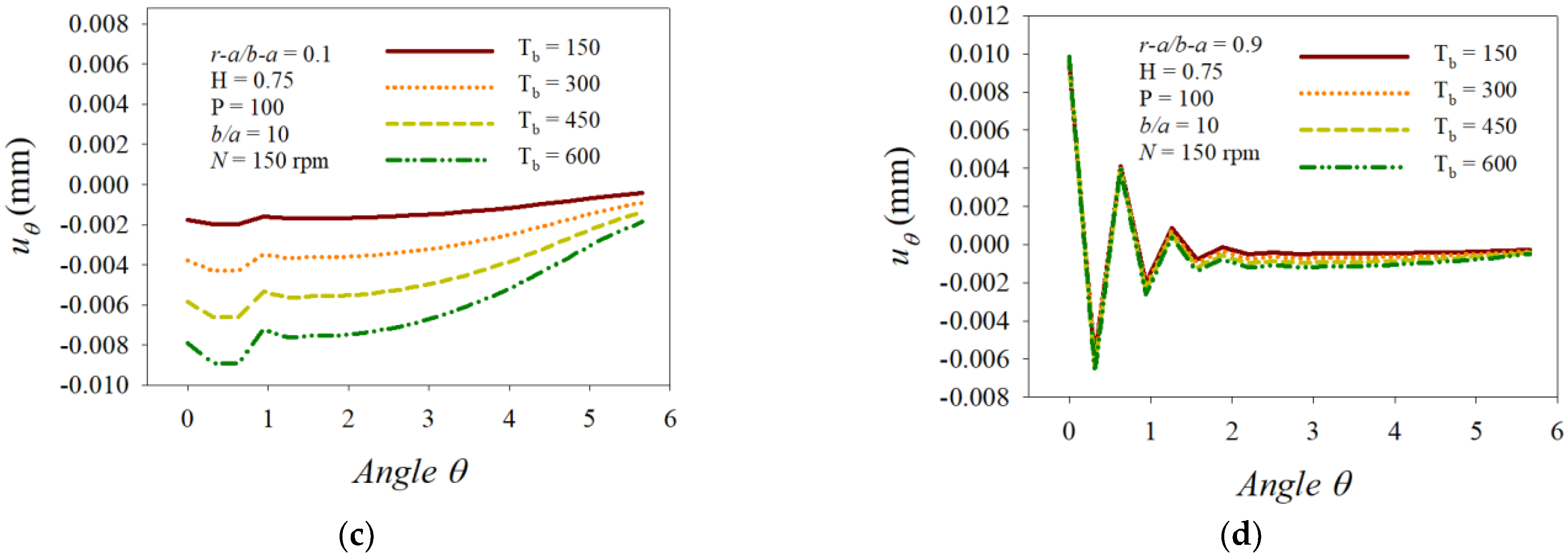
- (i)
- The radial displacement distributions displayed complex change patterns over the opposite side to the loading point.
- (ii)
- The distribution profiles of the displacement, stress, and strain over the near area of the inner surface moved in the outer-surface direction and the magnitudes decreased.
- (iii)
- The interval < 0.9 was the most susceptible area to the variation in the angular velocity, and a dramatic drop appeared at around = 0.73 of N = 1000.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| u | radial displacement component |
| circumferential displacement component | |
| radial strain | |
| circumferential strain | |
| shearing strain | |
| radial stress | |
| circumferential stress | |
| shearing stress | |
| Poisson’s ratio | |
| angular velocity | |
| N | revolutions per minute (rpm) |
| r | radius of circular disk |
| E | Young’s modulus |
| initial amount of Young’s modulus | |
| thermal expansion coefficient | |
| initial amount of thermal expansion coefficient | |
| density of disk | |
| initial amount of density | |
| growth rate of | |
| growth rate of | |
| growth rate of | |
| temperature on circular domain | |
| thickness of homogeneous part | |
| contact force | |
| hole radius of circular disk | |
| b | outer-surface radius of circular disk |
References
- Dai, T.; Dai, H.-L. Thermo-elastic analysis of a functionally graded rotating hollow circular disk with variable thickness and angular speed. Appl. Math. Model. 2016, 40, 7689–7707. [Google Scholar] [CrossRef]
- Yildirim, S. Hydrogen elasticity solution of functionally-graded spheres, cylinders and Disks. Int. J. Hydrogen Energy 2020, 45, 22094–22101. [Google Scholar] [CrossRef]
- Entezari, A.; Filippi, M.; Carrera, E.; Kouchakzadeh, M.A. 3D-wave propagation in generalized thermoelastic functionally graded disks. Compos. Struct. 2018, 206, 941–951. [Google Scholar] [CrossRef]
- Pal, S.; Das, D. Free vibration behavior of rotating bidirectional functionally-graded micro-disk for flexural and torsional modes in thermal environment. Int. J. Mech. Sci. 2020, 179, 105635. [Google Scholar] [CrossRef]
- Madan, R.; Bhowmick, S.; Saha, K. Limit angular speed of L-FGM rotating disk for both temperature dependent and temperature independent mechanical properties. Mater. Today Proc. 2019, 18, 2366–2373. [Google Scholar] [CrossRef]
- Arani, A.G.; Maraghi, Z.K.; Mozdianfard, M.R.; Shajari, A.R. Thermo-piezo-magneto-mechanical stresses analysis of FGPM hollow rotating thin disk. Int. J. Mech. Mater. Des. 2010, 6, 341–349. [Google Scholar] [CrossRef]
- Eraslan, A.N. Elastic-plastic deformations of rotating variable thickness annular disks with free, pressurized and radially constrained boundary conditions. Int. J. Mech. Sci. 2000, 45, 643–667. [Google Scholar] [CrossRef]
- Sondhi, L.; Thawait, A.M.; Sanyal, S.; Bhowmick, S. Stress and deformation analysis of functionally graded varying thickness profile orthotropic rotating disk. Mater. Today Proc. 2020, 33, 5455–5460. [Google Scholar] [CrossRef]
- Bayat, M.; Saleem, M.; Sahari, B.B.; Hamouda, A.M.S.; Mahdi, E. Analysis of functionally graded rotating disks with variable thickness. Mech. Res. Commun. 2008, 86, 283–309. [Google Scholar] [CrossRef]
- Yildirim, S.; Tutuncu, N. On the inertio-elastic instability of variable-thickness functionally-graded disks. Mech. Res. Commun. 2018, 91, 1–6. [Google Scholar] [CrossRef]
- Mahdavi, E.; Ghaseme, A.; Alashti, R.A. Elastic-plastic analysis of functionally graded rotating disk with variable thickness and temperature-dependent material properties under mechanical loading and unloading. Aetospace Sci. Technol. 2016, 59, 57–68. [Google Scholar] [CrossRef]
- Kadkhodayan, M.; Golmakani, M.E. Non-linear bending analysis of shear deformable functionally graded rotating disk. Int. J. Non-Linear Mech. 2014, 58, 41–56. [Google Scholar] [CrossRef]
- Khorsand, M.; Tang, Y. Design functionally graded rotating disks under thermoelastic loads: Weight optimization. Int. J. Press. Vessel. Pip. 2018, 161, 33–40. [Google Scholar] [CrossRef]
- Zeinkiewics, O.C.; Campbell, J.S. Shape Optimization and Sequential Linear Programming in Optimum Structural Design; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Jafari, S.; Hojjati, M.H.; Fathi, A. Classical and modern optimization methods in minimum weight design of elastic rotating disk with variable thickness and density. Int. J. Pres. Ves. Pip. 2012, 92, 41–47. [Google Scholar] [CrossRef]
- Saini, R.; Ahlawat, N.; Rai, P.; Khadimallah, M.A. Thermal stability analysis of functionally graded non-uniform asymmetric circular and annular nano discs: Size-dependent regularity and boundary conditions. Eur. J. Mech. 2022, 94, 104607. [Google Scholar] [CrossRef]
- Gayen, D.; Chakraborty, D.; Tiwari, R. Stability behavior of two-crack functionally graded shaft in a rotor-disk system: Finite element approach. Mater. Today Proc. 2020, 24, 432–441. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Habibi, M.; Ghabussi, A.; Safarpour, H.; Safarpour, M.; Tounsi, A. Non-polynomial framework for stress and strain response of the FG-GPLRC disk using three-dimensional refined higher-order theory. Eng. Struct. 2021, 228, 111496. [Google Scholar] [CrossRef]
- Sathujoda, P. A novel corrosion detection method using wavelet transformed mode shapes of a functionally graded rotor-bearing system. Compos. Part C Open Access 2021, 5, 100134. [Google Scholar] [CrossRef]
- Saeedi, S.; Kholdi, M.; Loghman, A.; Ashrafi, H.; Arefi, M. Thermo-elasto-plastic analysis of thick-walled cylinder made of functionally graded materials using successive approximation method. Int. J. Press. Vessel. Pip. 2021, 194, 104481. [Google Scholar] [CrossRef]
- Liu, J.; Migórski, S.; Yang, X.; Zeng, S. Existence and convergence results for a nonlinear thermoelastic contact problem. J. Nonlinear Var. Anal. 2021, 5, 647–664. [Google Scholar]
- Chawde, D.P.; Bhandakkar, T.K. Mixed boundary value problems in power-law functionally graded circular annulus. Int. J. Press. Vessel. Pip. 2021, 192, 10442. [Google Scholar] [CrossRef]
- Howell, P.; Ockendon, J.; Shillor, M. Mathematical theories for two classes of thermoelastic contact problems. Int. J. Solid Struct. 2022; in press. [Google Scholar]
- Paoli, L.; Shillor, M. A dynamic thermo-mechanical actuator system with contact and Barber’s heat exchange boundary conditions. Proc. Roy. Soc. Edinb. Sect. A 2021, 151, 734–760. [Google Scholar] [CrossRef]
- Cao-Rial, M.T.; Castiñeira, G.; Rodriguez-Aros, A.; Roscani, S. Mathematical and asymptotic analysis of thermoelastic shells in normal damped response contact. Commun. Nonlinear Sci. Numer. Similation 2021, 103, 105995. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]




| Material/Property | Elastic Module (MPa) | Thermal Coefficient | Thermal Conductivity | Density |
|---|---|---|---|---|
| Substrate (Al) | 71 | 23.1 | 237 | 2.70 |
| Top | 380 | 8.0 | 30 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Go, J. Influences of Boundary Temperature and Angular Velocity on Thermo-Elastic Characteristics of a Functionally Graded Circular Disk Subjected to Contact Forces. Mathematics 2022, 10, 1518. https://doi.org/10.3390/math10091518
Go J. Influences of Boundary Temperature and Angular Velocity on Thermo-Elastic Characteristics of a Functionally Graded Circular Disk Subjected to Contact Forces. Mathematics. 2022; 10(9):1518. https://doi.org/10.3390/math10091518
Chicago/Turabian StyleGo, Jaegwi. 2022. "Influences of Boundary Temperature and Angular Velocity on Thermo-Elastic Characteristics of a Functionally Graded Circular Disk Subjected to Contact Forces" Mathematics 10, no. 9: 1518. https://doi.org/10.3390/math10091518
APA StyleGo, J. (2022). Influences of Boundary Temperature and Angular Velocity on Thermo-Elastic Characteristics of a Functionally Graded Circular Disk Subjected to Contact Forces. Mathematics, 10(9), 1518. https://doi.org/10.3390/math10091518






