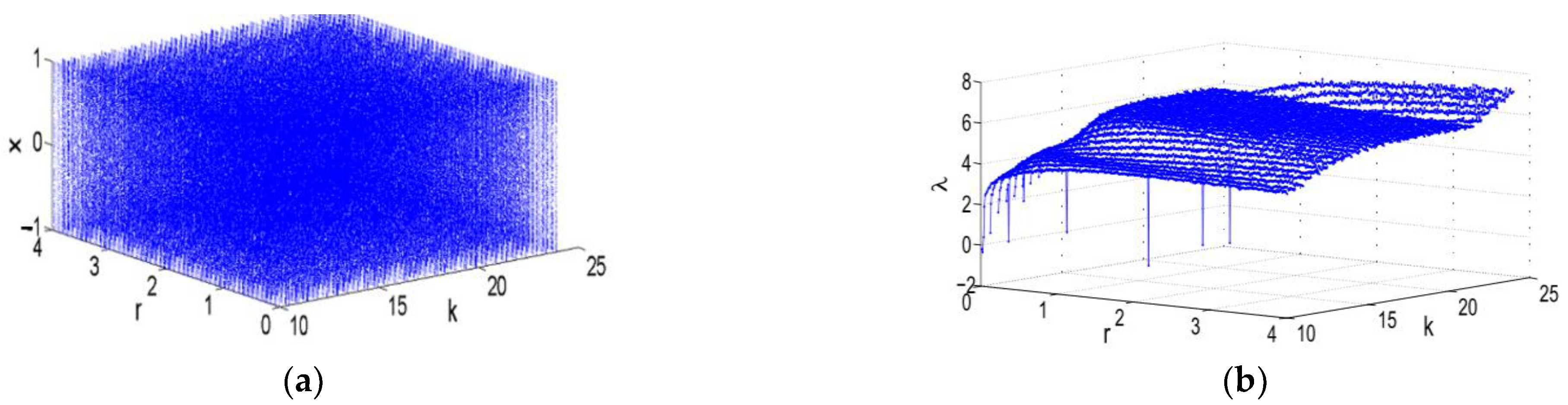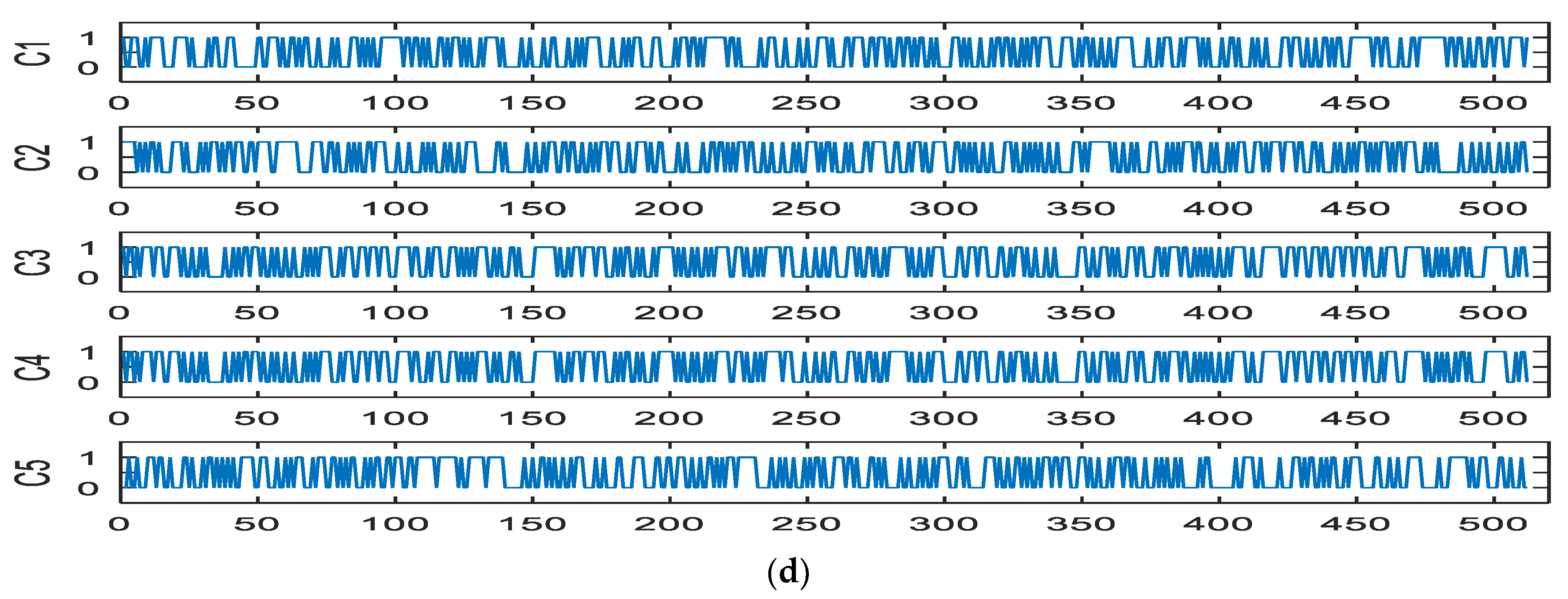A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps

Abstract

This paper aims to improve SHA-512 security without increasing complexity; therefore, we focused on hash functions depending on DNA sequences and chaotic maps. After analysis of 45 various chaotic map types, only 5 types are selected in this proposal—namely, improved logistic, cosine logistic map, logistic sine system, tent sine system, and hybrid. Using DNA features and binary coding technology with complementary rules to hide information is a key challenge. This article proposes improving SHA-512 in two aspects: the modification of original hash buffer values, and the modification of additive constants K_t. This proposal is to make hash buffer values (a, b, c, d, e, f, g, and h) and K_t dependent on one-dimensional discrete chaotic maps and DNA sequences instead of constant. This modification complicates the relationship between the original message and hash value, making it unexpected. The performance of the proposed hash function is tested and analyzed the confusion, diffusion, and distributive and compared with the original SHA-512. The performance of security is analyzed by collision analysis, for which the maximum number of hits is only three, showing that the proposed hash function enhances the security and robustness of SHA-512. The statistical data and experimental analysis indicate that the proposed scheme has good properties and satisfies high-performance requirements for secure hash functions.

1. Introduction

Cryptographic algorithms can be categorized into three classes: symmetric cryptography, or single-key cryptography, which uses a single key to encrypt data [1,2,3,4]; asymmetric cryptography, or public-key cryptography, which uses two keys (one to encrypt the message and the other to decrypt the ciphertext); hashing functions, which do not need any key and protect the data using a one-way function [5].

In recent years, hash functions have played important roles in message authentication [6], integrity protection, digital signatures [1,7,8,9], and even blockchain [10,11,12,13,14,15]. Hash functions map an arbitrary size input into an output of fixed length hash values or message digest h = H(M). The most used algorithm in hash function has been the Secure Hash Algorithm (SHA) [16]. SHA was published by the National Institute of Standards and Technology (NIST) as a FIPS in 1993. Hash values produced by SHA-0 are 160 bits long but, after publication, SHA-0 was rejected for use due to the presence of a “significant flaw”. In 1995, SHA-1 was published to resolve SHA-0′s security problem. Its design is close to that of the MD5 hash function. In 2005, SHA-1 fell from use due to the discovery of security vulnerabilities that prompted a transition to SHA-2 [17].

SHA-2 consists of hash functions with different lengths: SHA-256 is a 256-bit model, SHA-384 is a 384-bit model, and SHA-512 is a 512-bit model [18]. All SHA-2 variants use the same types of logical binary operation and modular arithmetic. SHA-512 is used in applications due to three factors: computational efficiency, security, and compatibility. This algorithm is widely used for password hashing, digital record verification, and blockchain technology [19,20].

Chaotic systems have come to be used in many applications of engineering, mathematics, physics, biology, chemistry, and cryptography over the past few years because of properties such as their sensitivity to small changes in initial conditions and control parameters [21]. A small change in the initial states will lead to completely different results, whether a completely different path or a transition to a continuous state. This property is referred to as the butterfly effect [22]. Chaotic systems can be continuous or discrete. Continuous chaotic systems are based on differential equations, while discrete systems are based on difference equations. Numerically solving differences rather than using differential equations can significantly increase the encryption speed, and there are no merits in using continuous over simple discrete chaotic systems; therefore, any continuous chaotic system can be replaced by a discrete one without loss of security [23]. Discrete chaotic systems can be represented as digital chaos due to being expressible by iteration and difference equations. Many researchers choose the logistic map, Baker map, and tent maps, which are discrete-time maps due to their easy implementation [22]. Digital chaotic systems can be classified into two types: one dimensional (1D) and multidimensional (MD). MD chaos maps are increasingly used in image security due to their complex structure and multiple parameters. However, their complexity increases the difficulty of both hardware and software implementation and the associated computational complexity, but 1D chaos systems have the advantages of simple structure, low computation, and easy-to-implement process.

DNA computing is a new technique for securing data from unauthorized access using the biological structure of DNA. It was invented by Adleman in 1994. DNA stands for deoxyribose nucleic acid. Each cell in living organisms has a unique, complete set of DNA, which is responsible for bearing the genetic characteristic from parents to offspring. The DNA strands are polymers of millions of linked nucleotides. These nucleotides consist of adenine, guanine, cytosine, and thymine [24].

Currently, these simple hash buffers values and additive constants in SHA-512 will carry considerable security threats; therefore, we used chaotic maps with DNA in making additive constants and hash buffers, thus increasing unpredictability and uncertainty.

2. Materials and Methods

2.1. SHA-512 Hash Algorithm

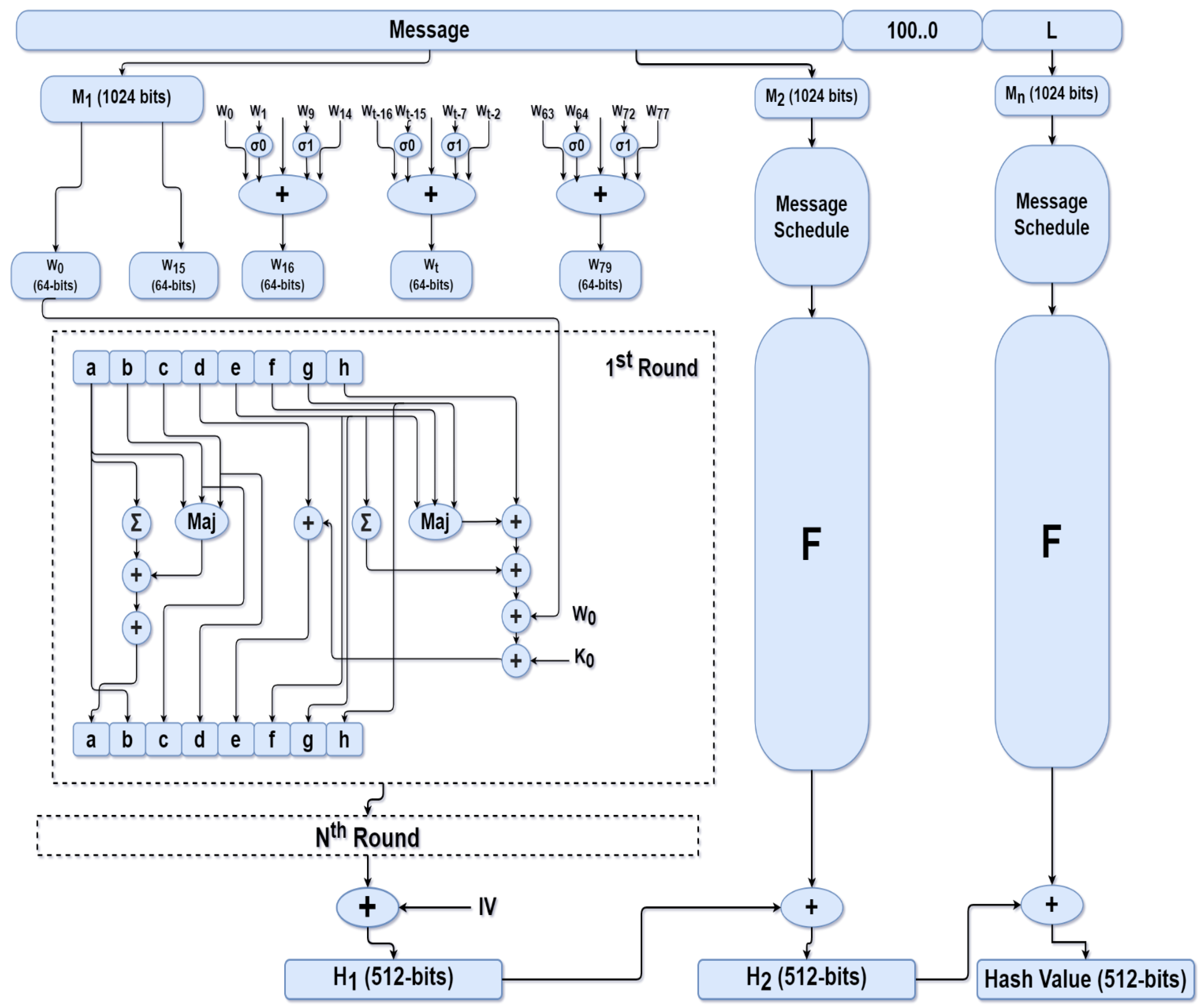
In this algorithm, the maximum length of the input message is 2¹²⁸ bits, and a message digest with a fixed size of 512 bits is created. The block size of SHA-512 is 1024 bits, and the number of iterations—known as rounds—is 80. Figure 1 shows the complete processing of a message to its resultant message digest [25,26].

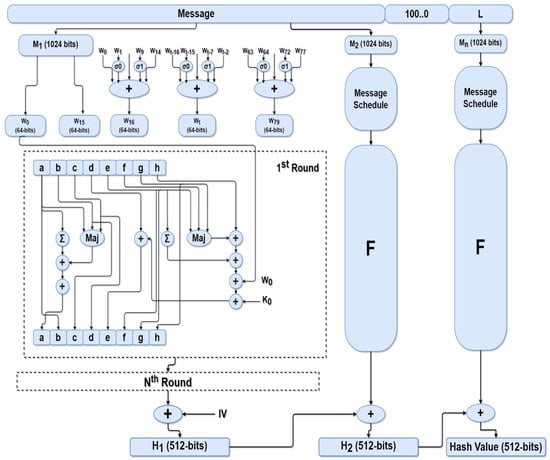
Figure 1. SHA-512 algorithm.

SHA-512 proceeds as follows:

• Step 1: Message preprocessing by padding and appending its length

Padding is added to the original message to match its length with 896 modulo 1024. Padding consists of a single 1, followed by as many 0 s as needed. Space is left after padding to append the length of the original message, achieving the target length.

• Step 2: Initializing hash buffer

SHA-512 uses 8 buffers of 64 bits each, denoted a, b, c, d, e, f, g and h, to hold temporary and final results of the compression function. These eight buffers are initialized to the following 64-bit (hexadecimal) values:

• a = 6A09E667F3BCC908 b = BB67AE8584CAA73B
• c = 3C6EF372FE94F82B d = A54FF53A5F1D36F1
• e = 510E527FADE682D1 f = 9B05688C2B3E6C1F
• g = 1F83D9ABFB41BD6B h = 5BE0CDI9137E2179

• Step 3: Compression function

The compression function in SHA-512 consists of 80 rounds. The input of each round is the hash buffer (a, b, c, d, e, f, g, and h). Calculations are made on these buffers to create hash buffers with new values to input in the next round. Each round takes, as input, the 64-bit value W_t, which is derived from a 1024-bit block using a message schedule, as shown in Figure 1. Each round also takes an additive constant K_t, progressing from 1 to 80, which has a constant value based on the number of the round. The output of the last round is added to the input hash of the first round to produce H_i.

• Step 4: Output

The output of the last 1024-bit block is the 512-bit message digest.

2.2. Chaotic Maps

One-dimensional chaos systems have the advantages of simple structure, low computation, and easy-to-implement process [27,28,29,30]. However, they also face the three following issues:

• A limited range of chaotic behavior;
• Less possibility of computational analysis using iteration and correlation functions;
• Uneven distribution of chaotic output sequences.

Therefore, new chaotic systems need to be developed with better chaotic performance. For this purpose, two existing 1D chaotic maps can be integrated to generate a new chaotic map with superior properties such as time evolution, bifurcation diagram, and Lyapunov exponent.

2.2.1. Improved Logistic Map

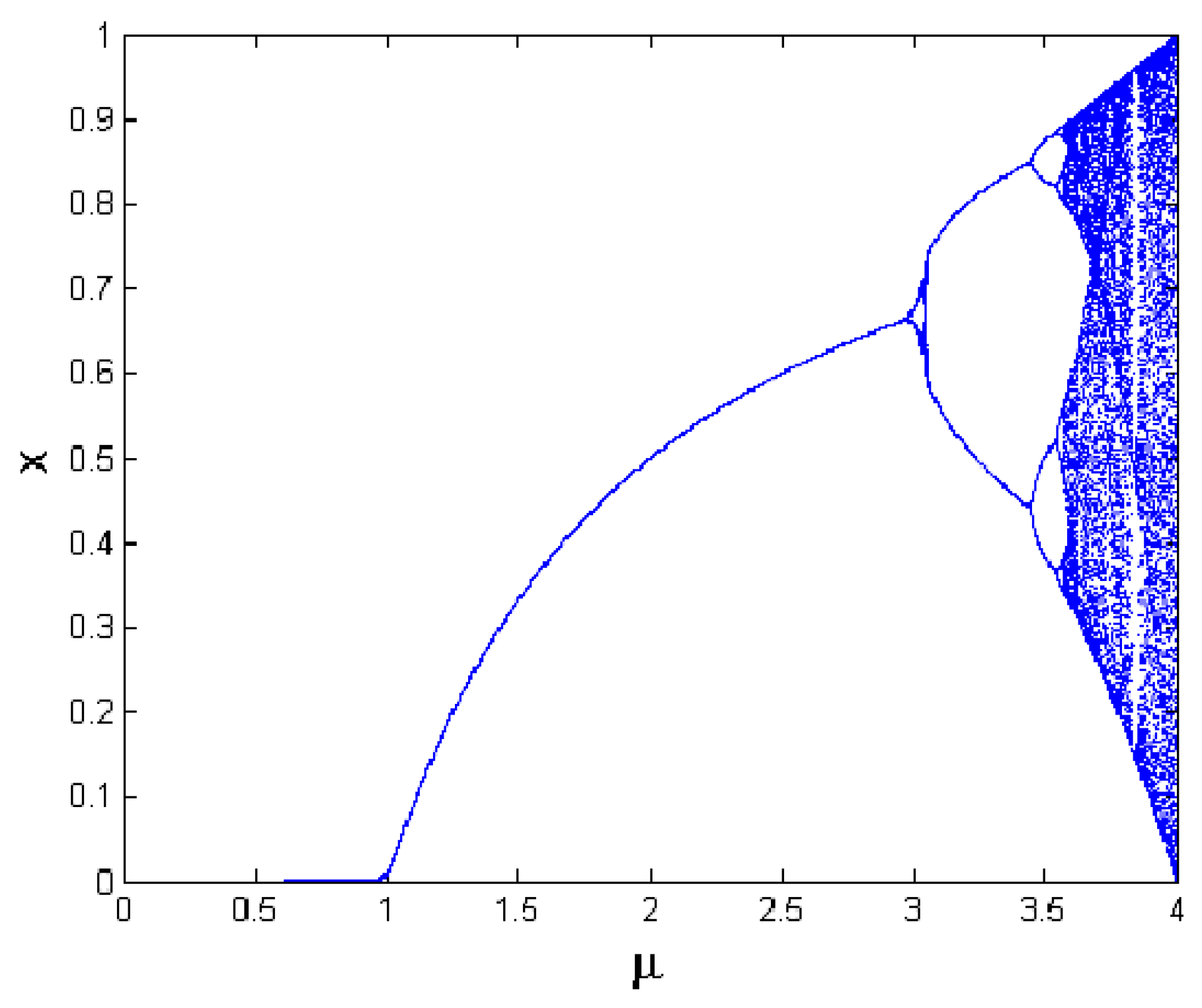
The logistic map is widely used for its simplicity, having fast and low computational overhead, and its sensitivity to initial conditions. The output sequences differ depending on the initial value of X₀ (0 ≤ X₀ ≤ 1) and μ as input [31,32,33,34]. Figure 2 shows a logistic pap plotted from Formula (1).

X_n+1 = μ X_n (1 − X_n)

(1)

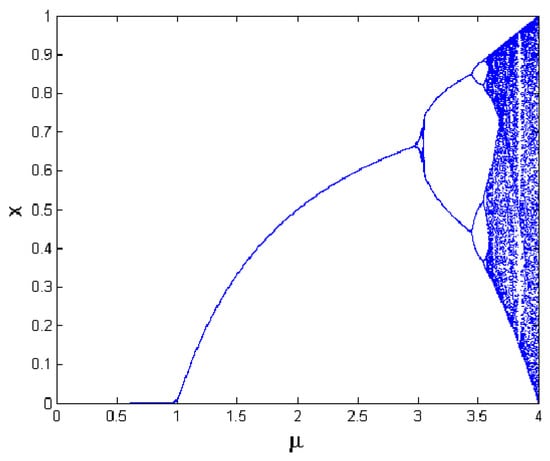
Figure 2. Bifurcation diagram of logistic map.

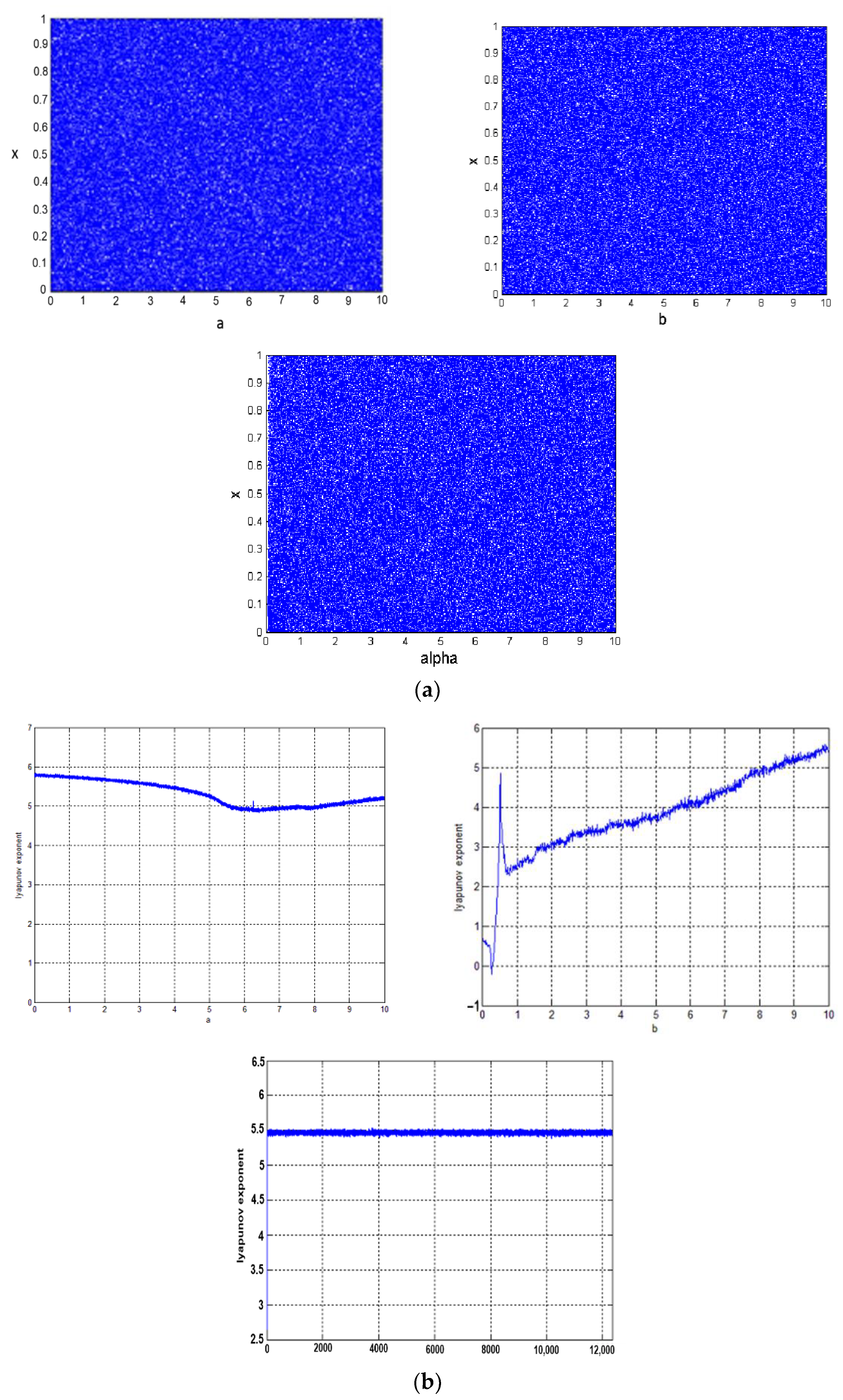
Although it offers benefits, logistic maps face some obstacles such as their limited chaotic range and non-uniform distribution of the variant density function. Thus, there is also an improved logistic map, as defined in Formula (2) [35]. X_n is a state variable that is bounded in [0, 1], and the control parameters (a, b, and alpha) do not have any limited range. However, for simulation analysis of dynamical behavior of the chaotic map, the values are initialed as X₀ = 0.123456789, a ∈ (0, 10], b ∈ (0, 10], alpha = 12,345. The values of the improved logistic map are distributed regularly over [0, 1] intervals for values of all three control parameters, as shown in Figure 3a.

f (X_n, a, b) = a X_n(1 − X_n) + b (1 + X_n) tan(X_n)
X_n+1 = f (X_n, a, b) × alpha − floor (f (X_n, a, b) × alpha)

(2)

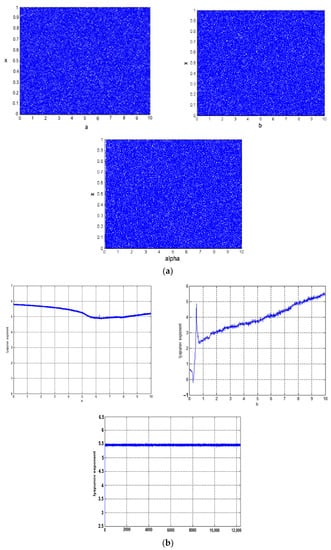
Figure 3. (a) Bifurcation plot versus parameter of improved logistic map; (b) Lyapunov exponent versus parameter of improved logistic map.

A chaotic map with a positive Lyapunov exponent (LE) will have completely diverged paths after a number of iterations, while a larger LE value is an indicator of higher sensitivity and unpredictability, as shown in Figure 3b.

The Lyapunov exponent refers to the separation pace of infinitesimally close trajectories [36]. Mathematically, it is defined as

$${\mathrm{LE}}_{\mathrm{i}}=\underset{\mathrm{n}\to \infty }{ \lim }\left(\frac{1}{\mathrm{t}} {\log }_2\frac{\mathrm{pi}\left(\mathrm{t}\right)}{\mathrm{pi}\left(0\right)}\right)$$

(3)

where p_i(t) denotes the respective ellipsoidal length principal axis. An n-D system has n number of LE. The existence of a positive exponent shows the presence of chaotic behavior on the map. It has been shown that, for alpha ∈ [0, 12,345], and a, b ∈ [1, 10], the chaotic map shows positive exponents for a wider range of all three parameters. LE becomes larger with an increase in parameter b. When a = 4, alpha = 12,345 and b = 10⁸, the largest LE obtained is 42.0616.

2.2.2. Cosine Logistic System

Any chaotic map can be used as the seed map in the cosine chaotic map (CCM) to improve the range and complexity of its chaotic parameter. The CCM model is bounded in the range of [−1, 1]. Merging the cosine and logistic maps produces the cosine logistic map (CLM) described as Formula (4) [37].

X_n+1 = cos (2^k+(r×X_n^×(1−X_n⁾⁾)

(4)

where X_n is the state variable, which is bounded in [0, 1]; k ∈ [10, 24] and r ∈ [0, 4] are the control parameters, as shown in Figure 4a. The CLM models have larger positive values of LE, as shown in Figure 4b.

Figure 4. Dynamical behavior of CLM: (a) bifurcation plot; (b) Lyapunov exponent.

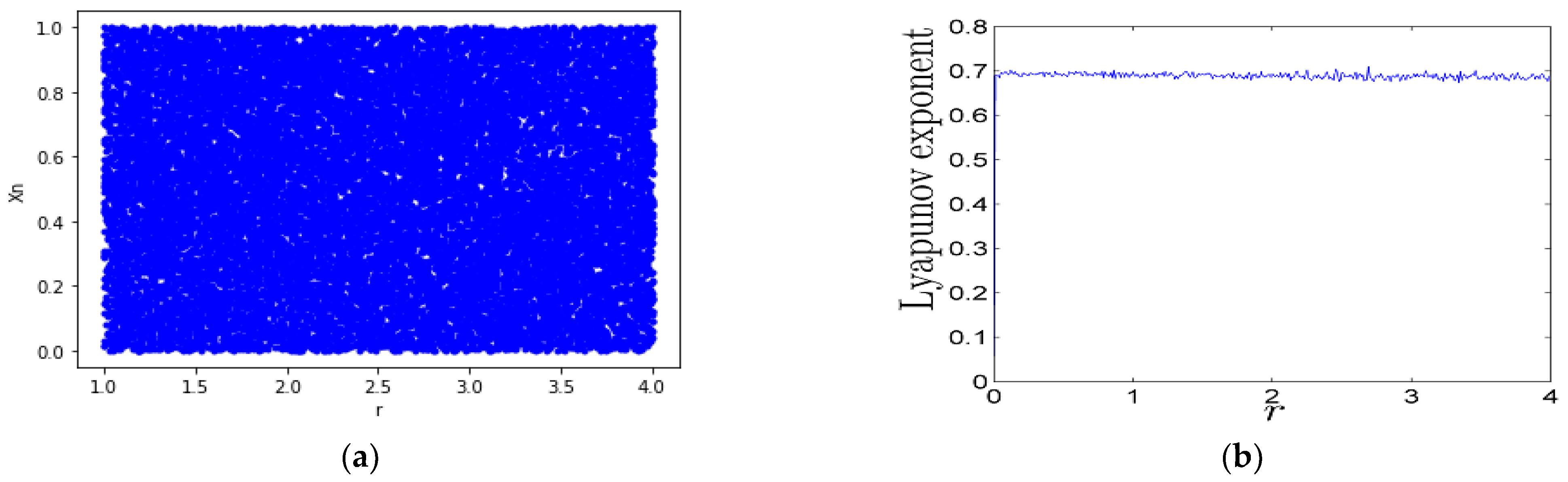
2.2.3. Logistic Sine System

The logistic and sine maps can be used as seed maps to construct a new chaotic system called the logistic sine system (LSS), defined in Formula (5) [38]. Figure 5b shows its lyapunov exponent. The LSS behaves chaotically when parameter r ∈ [0, 4], and its chaotic sequences are distributed uniformly within a range of [0, 1] as shown in Figure 5a.

X_n+1 = (r·X_n(1 − X_n) + (4 − r) sin(π·X_n)/4)·mod·1

(5)

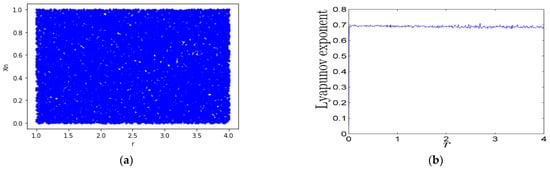
Figure 5. Dynamical behavior of LLS: (a) bifurcation plot; (b) Lyapunov exponent.

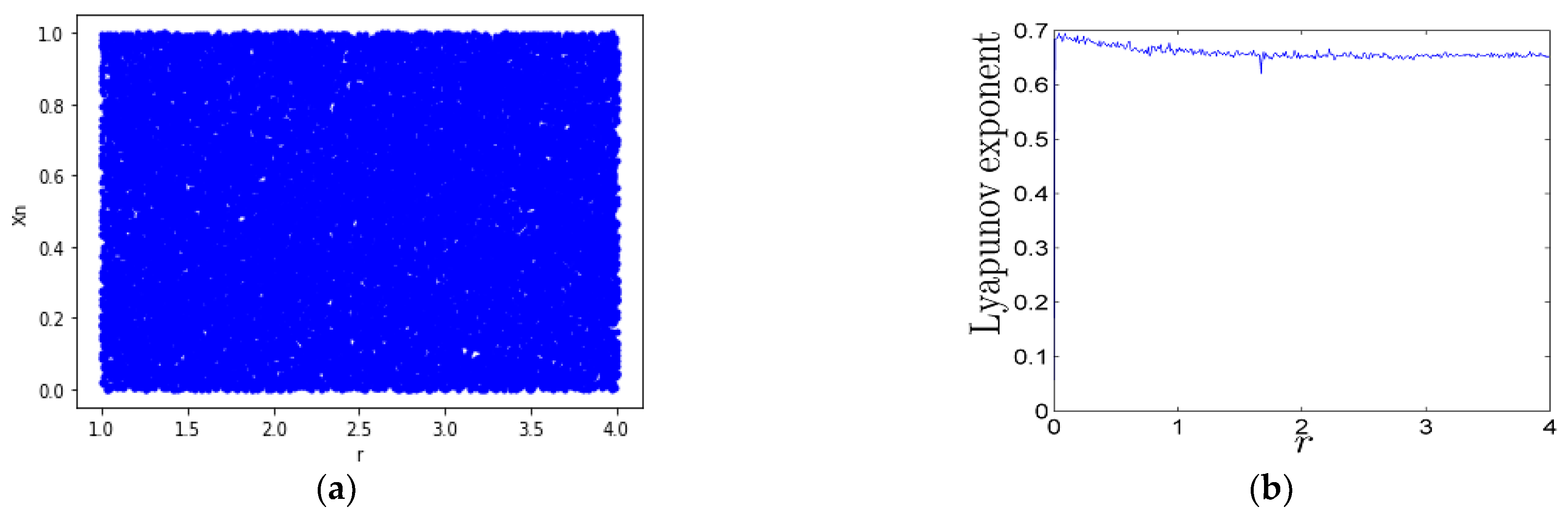
2.2.4. Tent Sine System

The tent map shares the problems associated with logistic maps—namely, limited chaotic range and non-uniform distribution in the range of [0, 1]. Combining the tent and sine maps as seed maps generates a new chaotic system called the tent sine system (TSS) [38]. Its definition is described in Formula (6), after unifying its parameters X_n ∈ [0, 1] and r ∈ [0, 4]. As shown in Figure 6a, the TSS has perfect chaotic properties. The LSS and TSS Lyapunov exponents have values greater than zero in the range of r ∈ [0, 4], as shown in Figure 6b, but their seed maps have positive values of LE within a limited range.

$${\mathrm{x}}_{\mathrm{n}+1}=\{\begin{array}{c}\left(\frac{{\mathrm{rx}}_{\mathrm{n}}}{2}+\frac{\left(4-\mathrm{r}\right)\sin \left({\mathsf{\pi }\mathrm{x}}_{\mathrm{n}}\right)}{4}\right)\mathrm{mod}·1 {\mathrm{x}}_{\mathrm{n}}<0.5\\ \left(\frac{\mathrm{r}(1-{\mathrm{x}}_{\mathrm{n}})}{2}+\frac{\left(4-\mathrm{r}\right)\sin \left({\mathsf{\pi }\mathrm{x}}_{\mathrm{n}}\right)}{4}\right)\mathrm{mod}·1 {\mathrm{x}}_{\mathrm{n}}\ge 0.5\end{array}$$

(6)

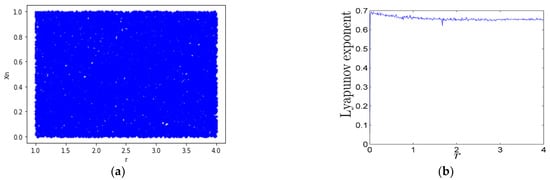
Figure 6. Dynamical behavior of TSS: (a) bifurcation plot; (b) Lyapunov exponent.

2.2.5. Hybrid Chaotic Map

This type of chaotic map uses a hybrid combination of three different 1D chaotic maps—tent, logistic, and sine—as its seed maps [39,40]. Figure 7B shows the LE values versus parameters. The LE values in the three subplots are all positive, indicating the chaotic behavior of the proposed map with γ ∈ [1, 1.9], a ∈ [0.975, 0.995], and μ ∈ [0.5, 0.9]. Figure 7A shows the bifurcation plot of the Hybrid Chaotic map.

$${\mathrm{x}}_{\mathrm{n}+1}=\{\begin{array}{c}\left(\mathrm{a}\sin \left({\mathsf{\mu }\mathsf{\pi }\mathrm{x}}_{\mathrm{n}}\right)+{\mathsf{\gamma }\mathsf{\mu }\mathrm{x}}_{\mathrm{n}}\left(1-{\mathsf{\mu }\mathrm{x}}_{\mathrm{n}}\right)\right)\mathrm{mod}·1 0\le {\mathrm{x}}_{\mathrm{n}}\le 0.5\\ \left(\mathrm{a}\sin \left(\mathsf{\mu }\mathsf{\pi }(1-{\mathrm{x}}_{\mathrm{n}}\right))+\mathsf{\gamma }\mathsf{\mu }\left(1-{\mathrm{x}}_{\mathrm{n}}\right)\left(1-\mathsf{\mu }(1-{\mathrm{x}}_{\mathrm{n}})\right)\right)\mathrm{mod}·1 0.5<{\mathrm{x}}_{\mathrm{n}}\le 1\end{array}$$

(7)

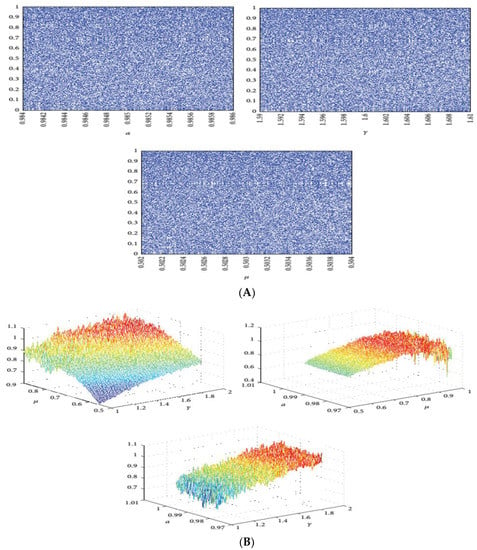
Figure 7. (A) Bifurcation plot versus parameter of hybrid chaotic map: (B) Lyapunov exponent versus parameter of hybrid chaotic map.

2.3. DNA Sequence and Complementary Rules

There are four types of DNA nitrogen bases: adenine (A), guanine (G), cytosine (C), and thymine (T); in addition, (A, T) and (C, G) are complementary pairs. DNA sequence (C, G, A, T) can be represented in binary code, in which each nucleotide has two bits. By using the Watson–Crick rule, nucleotides were represented by eight encoding rules, as shown in Table 1 [41].

Table 1. DNA encoding rule.

Binary\Rule	1	2	3	4	5	6	7	8
00	C	C	G	G	T	T	A	A
01	T	A	T	A	C	G	C	G
10	A	T	A	T	G	C	G	C
11	G	G	C	C	A	A	T	T

There are six legal group complementary rules that each nucleotide (n_i) must satisfy, which are

n_i ≠ C(n_i) ≠ C(C(n_i)) ≠ C(C(C(n_i)))
n_i = C(C(C(C(n_i))))

where C(n_i) is a DNA complementary rule; group 1 is (A → T) (T → C) (C → G) (G → A), etc. up to group 6, as shown in Table 2 [41].

Table 2. DNA complementary rules.

ni\Group	G1	G2	G3	G4	G5	G6
A	T	T	C	C	G	G
T	C	G	G	A	C	A
C	G	A	T	G	A	T
G	A	C	A	T	T	C

2.4. Method

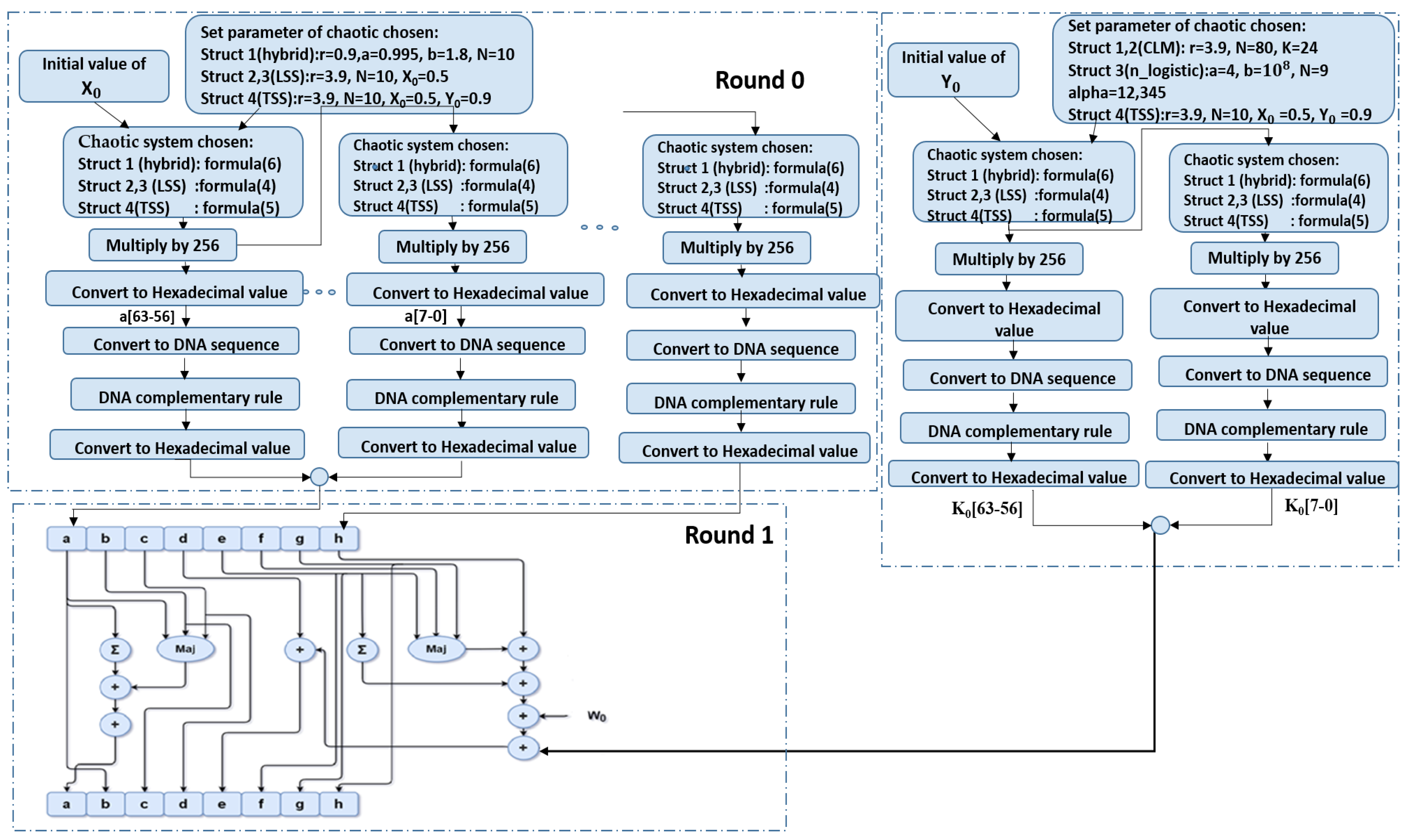
The main objective of a proposed hash is to generate a hash based on a 1D chaotic map and DNA sequences and compare that with the original SHA-512. The hash value is produced as follows, also shown in Figure 8:

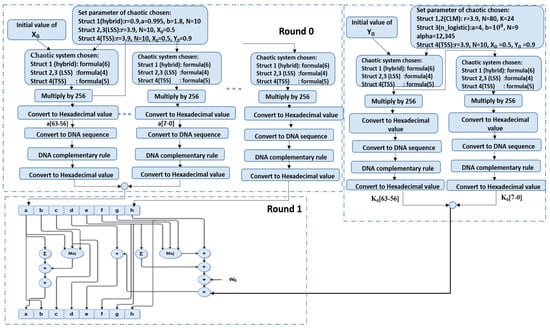
Figure 8. Proposed Hash-512.

• Step 1: The original message is encoded into an ASCII binary stream. The message is padded with a 1, followed by 0 values, and the length of the original message is appended at the final 128 bits. The number of zeroes is chosen so that the message length, after padding and appending the message length, is a multiple of 1024.
• Step 2: Chaotic maps are chosen for the hash buffers—either hybrid, LSS, or TSS—and for the additive constant—either CLM, improved logistic, or TSS.
• Step 3: The secret values for X₀ ∈ [0, 1] are selected as initial values to obtain X_n+1 of the hash buffer (a, b, c, d, e, f, g, h) and Y₀ ∈ [0, 1] to obtain Y_n+1 additive constant K_t.
• Step 4: X_n+1 is multiplied by 256 and the output value, expressed in hexadecimal, is converted to a DNA sequence.
• Step 5: Complementary rule is applied to the output of the DNA sequence, and then it is turned back to hexadecimal value, which is written to the last eight bits in the hash buffer a.
• Step 6: X_n+1 from step 3 is used again to obtain the second 8 bits of hash buffer a, and the same process continues until 64 bits of buffer a are obtained; steps 4 and 5 are repeated for each eight-bit set.
• Step 7: The last X_n+1 obtained from buffer a is considered X₀ for buffer b, and steps 4 and 5 are repeated until all remaining hash buffers (c, d, e, f, g, and h) are obtained.
• Step 8: Each round takes, as input, the 512-bit buffer value, and updates the buffer values using the 64-bit value derived from the current 1024-bit message schedule. Each round also makes use of an additive constant indicating which of the 80 rounds is currently in progress.
• Step 9: To obtain the first additive constant, steps 3 to 7 are repeated.

When we applied 45 various chaotic map types to the hash buffer and additive constants of SHA-512 and conducted all simulation experiments, it was found that using these chaotic maps (improved logistic, CLM, TSS, LSS, and Hybrid) on SHA-512 with specific types of DNA encoding rules and complementary rules, explained in structure 1, 2, 3, and 4, provide strong confusion and diffusion, as well as excellent distribution, sensitivity, and robustness against collisions and meet-in-the-middle attacks.

• Structure 1: a hybrid chaotic map is used by initializing buffer hash and CLM in adaptive constant k_t and using DNA encoding rule 0 and G6 complementary rule;
• Structure 2: the buffer hash is initialized with LSS, CLM is applied to adaptive constant k_t, and DNA encoding rule 5 and G1 complementary rule are used;
• Structure 3: the buffer hash is initialized with LSS, the improved logistic chaotic map is applied to adaptive constant k_t, and DNA encoding rule 5 and G3 complementary rule are used;
• Structure 4: the buffer hash is initialized with TSS, which is then applied to adaptive constant k_t, and DNA encoding rule 2 and G5 complementary rule are used.

Table 3 shows that each structure has initial hash buffer values and additive constant corresponding to the type of chaotic map and certain parameters.

Table 3. Lookup table for initializing hash buffer and additive constant.

	Parameter	Initial Hash Buffer	Additive Constant
Structure 1	Hybrid: r = 0.9, a = 0.995, b = 1.8, N = 10, X0 = 0.5 CLM: r = 3.9, N = 80, K = 24, Y0 = 0.5	a = 6d5b3ce95e42fd09 b = ac2bb11e816c5938 c = 8e6045061c786753 d = aa2fc0f52ebcfe05 e = 675227a241f91e7e f = 5a39e27c6b5835d3 g = 165f440108249951 h = 9c4c17654e1f836a	k1 = a99c8684073fdcf6 k2 = d708ff9ebf9cf7f4 k3 = 4ed248e568f52a86 k4 = 8be68516d917dbef k77 = fbb5fe2f58e7ef1b k78 = 830eeab0eff1aeae k79 = e8f8dfac50b5fe4d k80 = f88bfb8d813e7aed
Structure 2	LSS: r = 3.9, N = 10, X0 = 0.5 CLM: r = 3.9, N = 80, K = 24, Y0 = 0.5	a = fffffb1550d687fe b = 113bace070f3349d c = 52e070f33399f527 d = f4319af52883f336 e = db76fe081a5ceb4b f = 9bf335a4e753e070 g = 3299f42e9bf136aa h = 70f3349de854de6e	k1 = a99c8684073fdcf6 k2 = d708ff9ebf9cf7f4 k3 = 4ed248e568f52a86 k4 = 8be68516d917dbef k77 = fbb5fe2f58e7ef1b k78 = 830eeab0eff1aeae k79 = e8f8dfac50b5fe4d k80 = f88bfb8d813e7aed
Structure 3	LSS: r = 3.9, N = 10, X0 = 0.5 Improved logistic: a = 4, b = 108, alpha = 12,345, N = 9, Y0 = 0.5	a = fffffb1550d687fe b = 113bace070f3349d c = 52e070f33399f527 d = f4319af52883f336 e = db76fe081a5ceb4b f = 9bf335a4e753e070 g = 3299f42e9bf136aa h = 70f3349de854de6e	k1 = 64ca97e7026df731 k2 = f47e896ca60190e k3 = 5ea7206d450fa092 k4 = 4a6eca97e7026df7 k77 = fa092fc8ae5ac98 k78 = e5e5d4116787cf4c k79 = 3b131174ea4a6eca k80 = 8330a1437ff2982c
Structure 4	TSS: r = 3.9 N = 10, X0 = 0.5, Y0 = 0.9	a = 6b43d9f2a25da192 b = 30e087e0f925d9e c = caf3af5094d9c598 d = 9688d7e837d134cc e = 60ba87b1989540bf f = fe3e91c22e5f044c g = 6dad2a49859f1e18 h = f979897995e4d17	k1 = 3139d540b95ff723 k2 = 90e8e811355ffc4b k3 = 6b173f9a382490e5 k4 = 6cf4fe2c859e63b0 k77 = 9dc80f916a938ed1 k78 = b21cc378aa9d2900 k79 = d6c101d634aff73a k80 = 9b087c315739b7c2

3. Results

To show the advantage of the proposed hash function, we present a performance analysis that considers the distribution of hash value, diffusion and confusion, sensitivity to the message, and the collision resistance. The proposed hash function can work on a message up to 2¹²⁸.

3.1. Hash Value Distribution

One of the most important characteristics of hash functions is to produce uniformly distributed output. Simulation experiments were performed on the following sentence as a simple example: “The people of Egypt are intelligent people with glorious history who left their mark on civilization”.

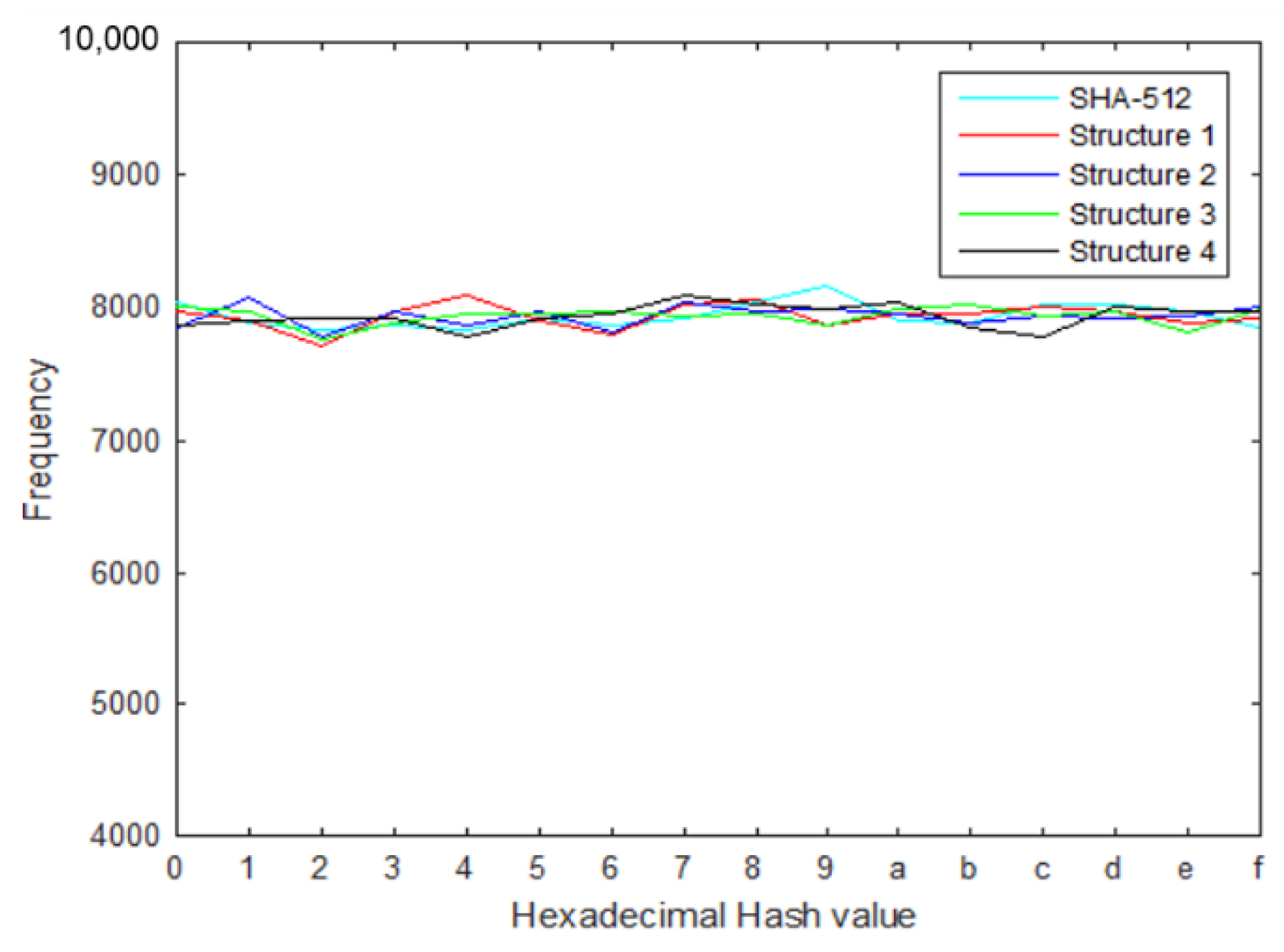
In this paper, the distribution of the hash value was evaluated by hashing 1000 different messages and representing the hash values in hexadecimal for distributional analysis. Figure 9 shows the distributions for all test structures (noted in Section 2.4) by counting the occurrence of all hexadecimal digits (0-F).

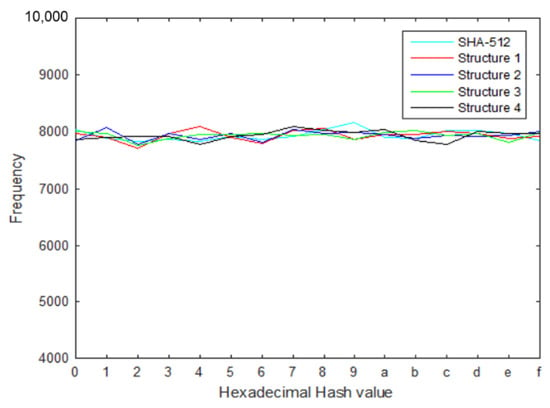
Figure 9. Hash value distribution for 1000 messages.

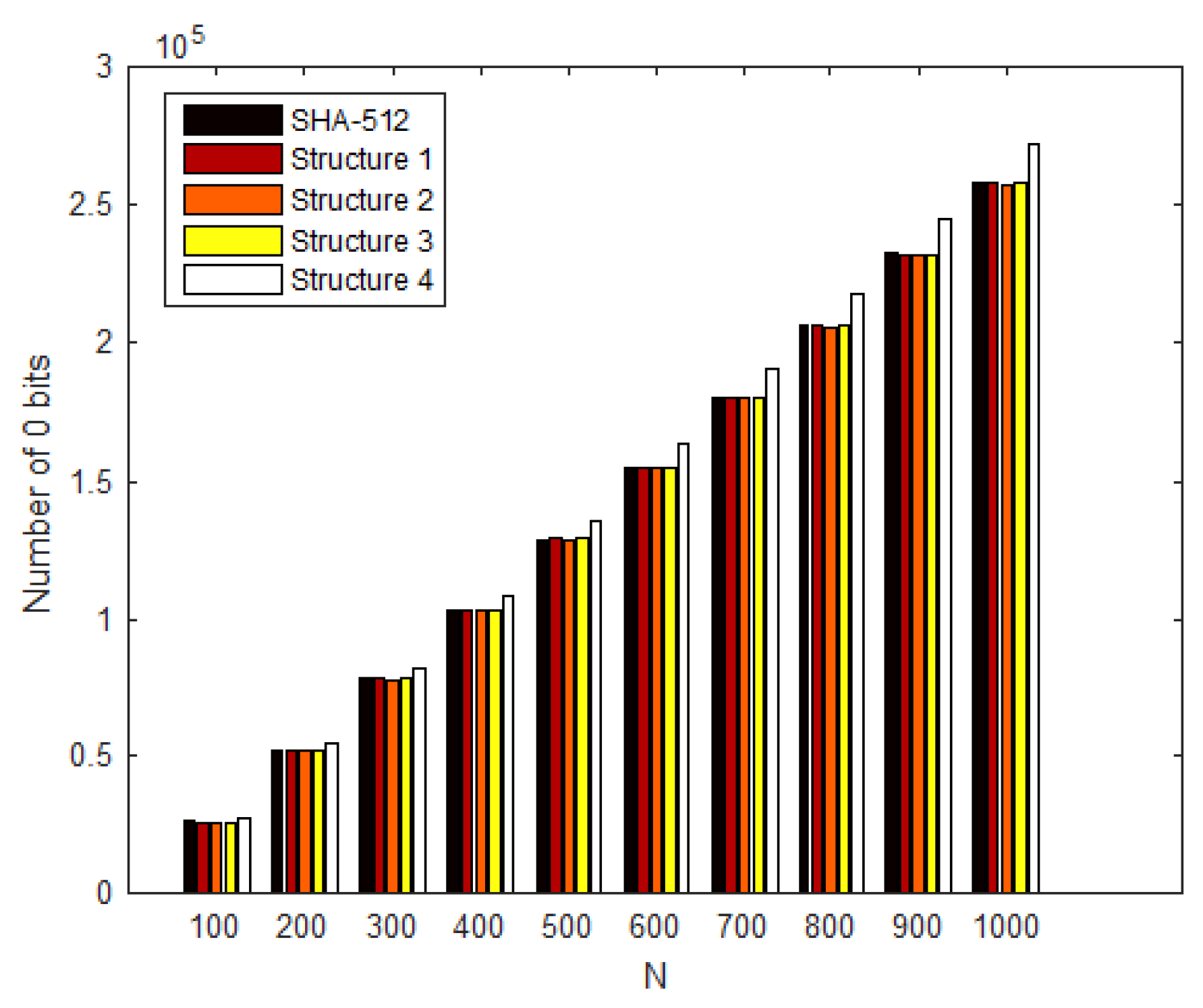
3.2. Linear Complexity

To determine this property [42], the 0 s and 1 values were counted in the binary-encoded hash output. For an ideal hash function, the two counts should be equal. Figure 10 shows the linear complexity of hash values for 1000 input different messages.

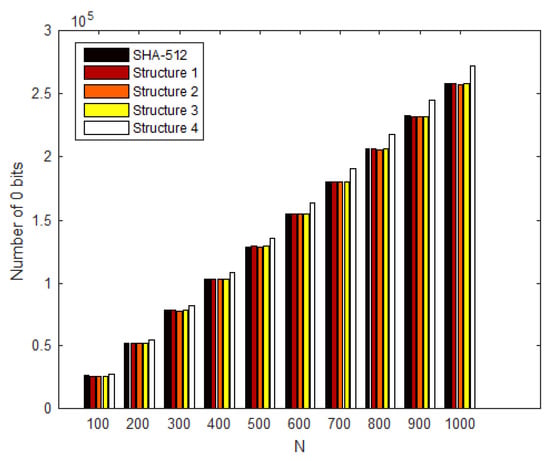
Figure 10. Linear complexity of hash for 1000 different messages.

3.3. Sensitivity Analysis

We investigated the sensitivity of the proposed hash function by comparing the effects of five variants to the input message, which means that a small change in its input message will generate a considerable change in the hash value.

• C1: The original plaintext message;
• C2: Alter ‘.’ At the end of a sentence to ‘/’;
• C3: Flip all letters (a) in a sentence to (o);
• C4: Change E in Egypt word to e;
• C5: Add 5 before history.

Table 4, Table 5, Table 6 and Table 7 show the resulting hash values listed in hexadecimal format for all cases, followed by the number of changed bits compared with the hash value for C1.

Table 4. Hash values of first structure.

	Hash Value of 1st Case (Hash_Hybrid_CLM)	Changed Bits
C1	76ec2e55956e3d03d56391b1db4ddadb7beb8b003 afcb8ad6fef744314f1ef55418a84c62c3a00ca6306 4686befa06aeca58cfaa0289a1dc0e915da54e42f333	___
C2	54947ac5855264797ee1f4eee2b619a359548fd78c 8b640c5276793dff60e90b69e3d0a06fab29b2fc8f3 30cc6fc2530c6862e92ce331922c3482fa5cffa7151	257
C3	39f72e29f55a7daa1b1fa0abbb595fba0f3f06f2e160 dd219022def05641ff0849689b9986a5e064e18a49 70ee8da76c47c3ff37fe8f4c7965f19f6e7d1f3b6f	270
C4	9bb66539582bf4d443e158aa565c111a924c113d07 16e5e42193ce3d9fdd31b183d09ed06f40e1f4d60ce 4d7b9117737dc74acbcae7f3817cce119adbb2994c8	259
C5	54c94f2c6dc95bf68982a8519433161c48134ad6d8 d928c5173713f5e0d6915344f5b28c4e8e29c10404 0554faa512d8d8fae363d73e7c5b628603ddf2b9d0ae	238

Table 5. Hash values of second structure.

	Hash Value of 2nd Case (Hash_LSS_CLM)	Changed Bits
C1	5cde39d1a7e0ce19e1550c37e8befc57551c4d2949b 864e2da0f714edd2941cd952dde5e7c780dfec773f4 4487d768929bf34cd731e2106a743312f475846bc5	___
C2	a954350f1ac222201c41176199ac7e6297075848b4 02e8a61048b6c76af076b3fb2f73c7af8ab69e14d2f 6049995654179cc2cd6e45af6049f0de757a5655168	257
C3	7b923f81f921fa6d1ccef45d4f3d672c99d2a5775d6 5ef635c65fc24c4f4b483838417335603e72b31578 1d2fd4ee01a2ec297508c0e2f20447f15bb0feecfae	265
C4	797584a71b64c1a882d1d0d438ca9d9dc367ff5899a 48ade6ec2d3eae25cae60d594f04477a807c588b490 8deb9ca40e81022600328e767dbad5be0854daed21	261
C5	7d64060613bb02ed718cbdbb901b6d2e61c898d0ed 3a549876047c8a94012900995d0abb5d826419f84e 0a6477d6be5d3f06cf07b813585f8e931d5e198a586	251

Table 6. Hash values of third structure.

	Hash Value of the 3rd Structure (Hash_LSS_ Nlogistic)	Changed Bits
C1	a74901fcb8376c137a81a0c84deba7c4dc8781a5dd5 256736e755fdf33bf0873b9f7bdf62a9600051b1a68 7c3551d21890fcc7d87305a22557b6821f47608972	___
C2	81c74c921f7f8e53dafb76c02c5e3e1a15537fefc791 4aab1f5886452a258ae6b972d24311c65c183a4ec0 997d46614baab20b6b59aef712e5e674553b13b011	245
C3	c0431d33acf8e118a0e8a2be0d1d7c67f43458f5f26 f92c70c028c970a4cf8b4f9b974cf8c2cae52aa393d 8a2cf221713061af521ae20b2718cac6225b3a6a5a	254
C4	512f1247e20d1b18d208300842071dfa72fa926c5c 1ac13d89f2c530e067e7c383067d5431d68395e661 a9e5e50a582b16c6238341d4b1c19cc3676752392768	259
C5	26f05090636b04f1c123060f3655591fa315801c2d f47c6eea2330bf62041ae5f6d73d784b887ed9d2e35 310e097d1adce93db522785cee9eafa7dd206a59010	261

Table 7. Hash values of fourth structure.

	Hash Value of the 4th Structure (Hash_TSS_TSS)	Changed Bits
C1	9cbe1f41638067a6b10a1d53fdb51aea2fa0484c257 c22b8705daff6809c4247a1bcdd36b283a88b695bc 3cb493f045c5f509a1483b926b1fed846ffdb266e7d	___
C2	fab43d0aeb737cff079a2a6f0885452780d0125cd92 bb89e9824136aec488a7ad1437c62e9f1aa4874aa4 83aff49438abd8a2b8ebdec6852babade2a01124496	262
C3	b5ee7a4a04add2922af173bb8fb171d5794683fd2e f715945fa94af9d2bf708930e9a5fd25e0cee19748 900e4ea3b0d7b2a92f91fcee7677762f1fd2a5a0ff16	270
C4	66380959269b1de562517ea65a3ed64c4c042b5e2e6 050a73d16a07ae72a69c1e676180c321c56c1fb0b8b 0d3f14e415ce8320c61849b59b64a7d6e66336c6f5	244
C5	24764345aa9f3895c5cd58acdcdfdfd3f7e024d4970 90c3c333926aefe0948ad1ed0d4122978d03d26a5d b8e917688a940b004f2043acac5e0c48f811fd38644	258

The simulation results in Figure 11 show that the proposed hash function has a high sensitivity to the least-different bits in the message.

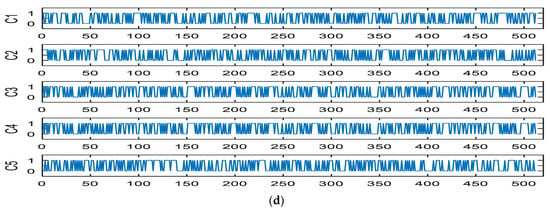
Figure 11. Hash values under different conditions: (a) first structure; (b) second structure; (c) third structure; (d) fourth structure.

3.4. Confusion and Diffusion Analyses

The confusion and diffusion of the hashing procedures were evaluated as follows:

• The hash value for an input message was calculated;
• Single bits in the message, and the hash value was calculated again;
• The two hashes were compared to identify the difference between them;
• Steps (1–3) were repeated for N times.

Table 8 shows the six statistics used in the analysis defined above and compared with previous studies [41,42,43,44]. Ref. [41] used chaotic sponge construction and DNA sequence on a hash function; specifically, DNA sequence was used to design state transition rules of (DCFSA). Ref. [42] used a hyperchaotic Lorenz system in the hash algorithm to absorb input messages via multiple parameters time-varying perturbation. Ref. [43] analyzed two-keyed hash function structures by proposing the use of a chaotic neural network Sponge construction was applied in these structures, resulting in two variants of hash value lengths, i.e., 256 and 512 bits. Ref. [44] used a hash function based on two Tinkerbell maps filtered with an irregular decimation rule.

Table 8. Confusion and diffusion test results for 1000-message tests.

	Bmin	Bmax	Mean	P%	ΔB	ΔP
SHA-512	212	297	256.09	50.018	11.13	2.174
Structure1	219	291	256.0586	50.011	11.67	2.279
Structure 2	219	293	256.032	50.006	10.92	2.133
Structure 3	222	291	255.9648	49.993	11.34	2.214
Structure 4	226	292	256.0244	50.0068	11.46	2.24
Ref. [42]–Structure 1	223	291	256.496	50.05	11.41	2.229
Ref. [42]–Structure 2	215	293	254.862	49.778	10.95	2.138
Ref. [43]	222	287	256.39	50.08	11.39	2.22
Ref. [44]–Structure 1	217	293	256.2	50.04	11.20	2.18
Ref. [44]–Structure 2	214	291	255.90	49.98	11.37	2.22
Ref. [44]–Structure 3	215	296	255.53	49.90	11.41	2.23
Ref. [45]–Structure 1	214	287	256.03	50.01	11.48	2.24
Ref. [45]–Structure 2	229	292	256.45	50.08	11.32	2.21

• Minimum number of changed bit: B_min =min ${\left({\mathrm{B}}_{\mathrm{i}}\right)}_1^{\mathrm{N}}$;
• Maximum changed bit number: B_max = max ${\left({\mathrm{B}}_{\mathrm{i}}\right)}_1^{\mathrm{N}}$;
• Mean number of changed bits: $\overline{\mathrm{B}}={{\displaystyle \sum }}_1^{\mathrm{N}}\frac{{\mathrm{B}}_{\mathrm{i}}}{\mathrm{N}}$;
• Mean changed probability: $\mathrm{P}=\frac{\overline{\mathrm{B}}}{512}\times 100\%$;
• Standard variance of the changed bit number ΔB = $\sqrt{\frac{1}{\mathrm{N}-1}{{\displaystyle \sum }}_1^{\mathrm{N}}{\left(\mathrm{Bi}-\overline{\mathrm{B}}\right)}^2}$;
• Standard variance of probability ΔP= $\sqrt{\frac{1}{\mathrm{N}-1}{{\displaystyle \sum }}_1^{\mathrm{N}}{\left(\frac{{\mathrm{B}}_{\mathrm{i}}}{\mathrm{N}}-\mathrm{P}\right)}^2}$.

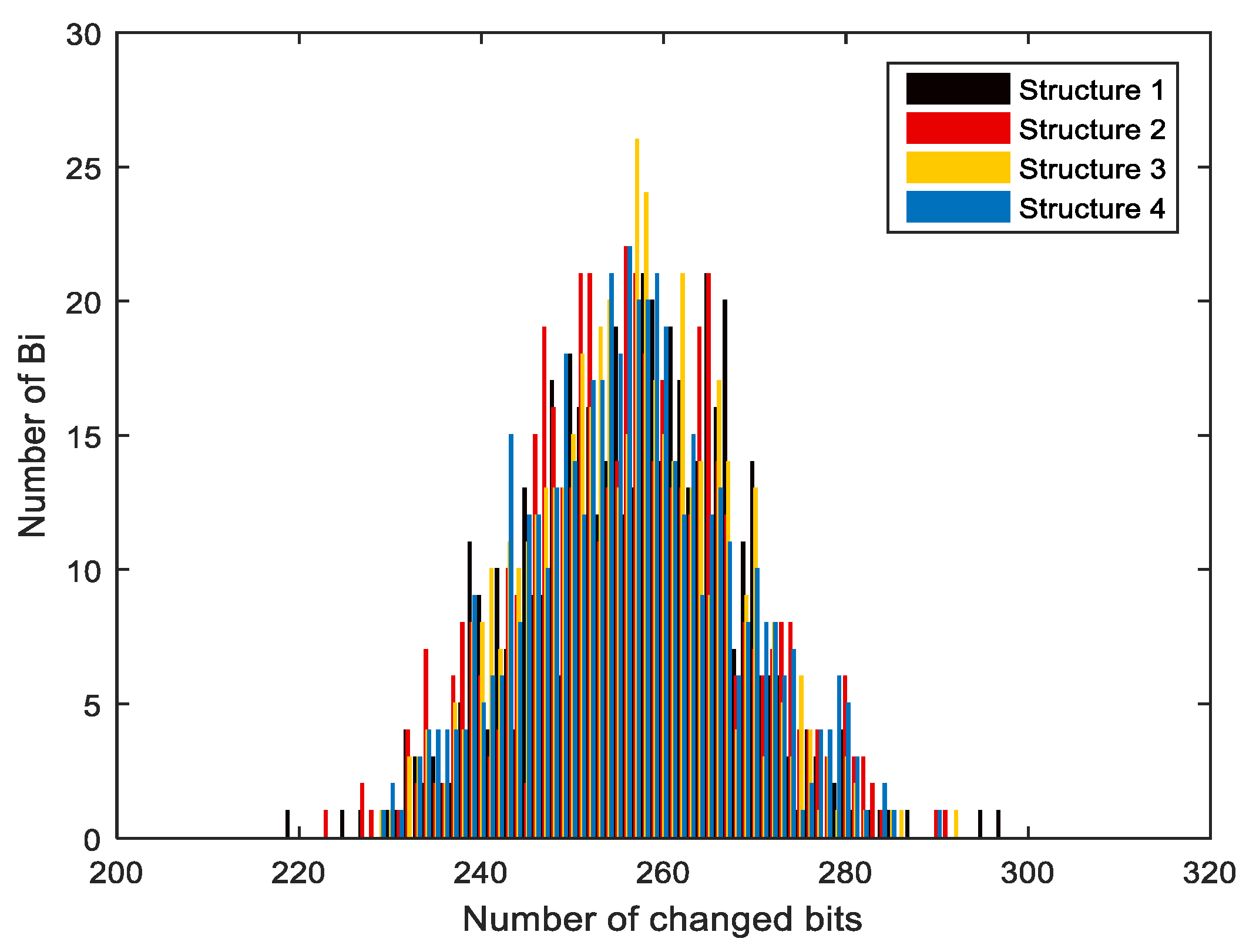
The same analysis was undertaken with N = 256, 512, 1024, 2048, and 10,000, as shown in Table 9, Table 10, Table 11 and Table 12, where N is the number of the different messages. According to the data evaluation in Table 8, the mean number of changed bits $\overline{\mathrm{B}}$ and the mean changed probability P% are both very close to the ideal value of 256 bits and 50, respectively. In addition, ΔB and ΔP indicate the degree of stability; the closer to zero, the more stable. Figure 12 shows that the mean number of changed bits $\overline{\mathrm{B}}$ is close to value of 256, and this is the perfect value of $\overline{\mathrm{B}}$that can be reached. The standard variances are low, indicating that the confusion and diffusion of the proposed hash function are ideal.

Table 9. Statically results for structure 1 for a number of different tests.

	N = 256	512	1024	2048	10,000
Bmin	228	224	219	214	210
Bmax	287	287	291	297	303
Mean	256.336	256.5	256.059	256.106	256.178
P%	50.066	50.098	50.011	50.021	50.034
ΔB	11.401	11.164	11.144	11.364	11.202
ΔP	2.227	2.180	2.176	2.220	2.20

Table 10. Statically results for structure 2 for a number of different tests.

	N = 256	512	1024	2048	10,000
Bmin	227	219	219	219	217
Bmax	293	293	293	298	303
Mean	255.648	255.628	256.189	256.320	255.911
P%	49.931	49.928	50.037	50.062	49.983
ΔB	11.1031	10.791	10.907	11.073	10.80
ΔP	2.169	2.107	2.130	2.162	2.05

Table 11. Statically results for structure 3 for a number of different tests.

	N = 256	512	1024	2048	10,000
Bmin	228	226	222	212	213
Bmax	290	290	291	294	300
Mean	256.402	255.978	255.965	255.668	256.024
P%	50.079	49.995	49.9931	49.935	50.005
ΔB	11.265	11.412	11.336	11.394	11.20
ΔP	2.200	2.229	2.214	2.225	2.110

Table 12. Statically results for structure 4 for a number of different tests.

	N = 256	512	1024	2048	10,000
Bmin	226	226	226	225	207
Bmax	283	292	292	292	300
Mean	256.063	256.433	256.024	256.388	255.963
P%	50.012	50.085	50.005	50.076	49.993
ΔB	11.127	11.641	11.505	11.404	10.95
ΔP	2.173	2.274	2.247	2.227	2.175

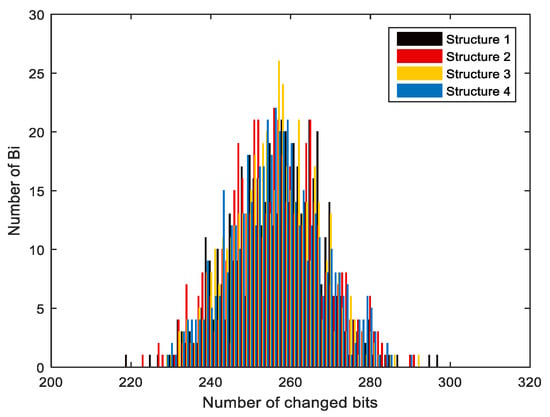
Figure 12. Results and histograms of the average number of changed bits.

3.5. Hash Attacks

Attacking in a hash means breaking a security property of hash functions. Attacks may focus on the algorithm of compression functions or the structure of hash functions [46]. There are two types of attacks on hash functions: brute force and cryptanalysis.

3.5.1. Brute Force Attack

Brute force attacks depend not on the algorithm but on the bit length of the hash algorithm. For a hash code of length n, the effort level required to resist different brute force classical attacks on hash functions is as follows:

Preimage and Second Preimage Attacks

In a preimage attack, the attacker has the hash of a particular message and tries to determine what this message is, such that H(M) = h. In the second preimage attack, the attacker has the message M₁ and hash value of H₁, and it tries to find another message M₂ that maps to the same hash value H₁.

Collision Resist Attack

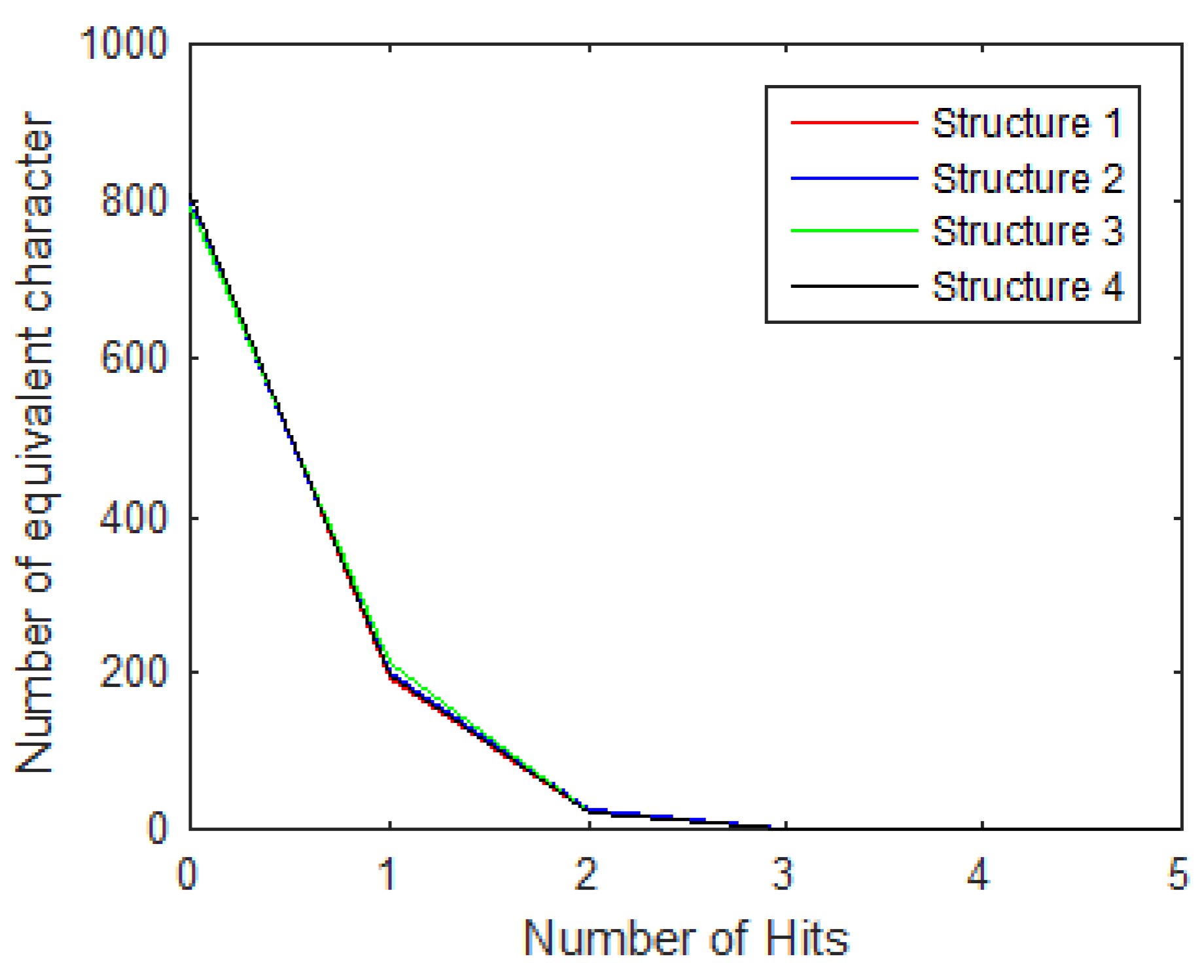
Collision resistance is also used to measure the security of the hash algorithm. Hash collision attacks attempt to find two string messages that hash to the same value. The collision can be analyzed by calculating the hash value of the chosen message and extracting a thousand different messages from the original by toggling one bit at a time with “0” and “1”, and then comparing the resulting hash values. This is conveniently performed via ASCII encoding, comparing characters at matching locations to count the number of hits ω. Figure 13 shows the distribution of the number of hits. The relation between a number of different tests and the number of hits is explained in [47].

$$\mathrm{WN}(\mathsf{\omega })=\mathrm{N}\times \mathrm{prob}(\mathsf{\omega })=\mathrm{N}\frac{\mathrm{s}!}{\mathsf{\omega }!(\mathrm{s}-\mathsf{\omega })!}{(\frac{1}{2^8})}^{\mathsf{\omega }}{(1-\frac{1}{2^8})}^{\mathrm{s}-\mathsf{\omega }}$$

(8)

where N is the number of tests, and s = L/8 where L is the length of the hash function. WN(ω) in Formula (8) is the theoretical value given in Table 13, which also shows how the outputs differ between hashing under test structures 1, 2, 3, and 4. Therefore, an absolute difference can be proved as shown in Formula (9).

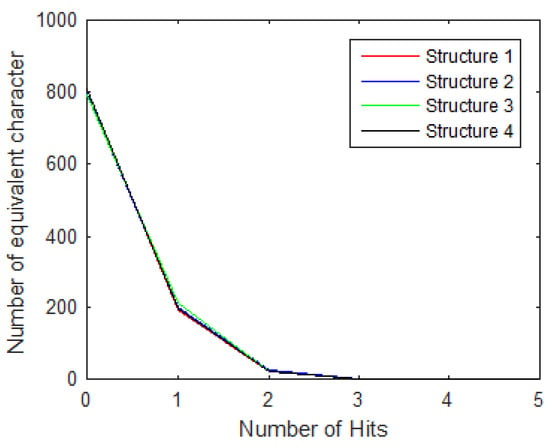
Figure 13. Distribution of the number of hits.

Table 13. Number of hits for all structures of the proposed hash function for N = 1000.

	Number of Hits (ω)
	0	1	2	3	4	64
Theoretical value	797.10	200.05	24.71	2.00	0.11	1.42 × 10−56
Structure 1	820	176	27	1	0	0
Structure 2	812	187	23	2	0	0
Structure 3	802	198	22	2	0	0
Structure 4	809	194	0	0	0	0

$$\mathrm{D}\_\mathrm{hash}= {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{N}}\left(\left|\mathrm{t}\left({\mathrm{m}}_{\mathrm{i}}\right)-\mathrm{t}\left({{\mathrm{m}}^{\prime }}_{\mathrm{i}}\right)\right|\right)$$

(9)

Converting the hash value from ASCII format to decimal and calculating the differences between them is repeated 1000 times. Absolute differences are compared in Table 14. The theoretical value of mean/character is close to 177.66, as explained in Formula (10) for 512-bit hash value length (L = 512). Basing a cryptographic hash algorithm on chaotic maps provides increased security against brute force attacks.

$$\overline{\mathrm{X}}(\mathrm{mean}/\mathrm{character})=\mathrm{L}/3$$

(10)

Table 14. Absolute differences between two hash values for 1000 different messages.

	Absolute Difference
	Max.	Min.	Mean	Mean/Character
SHA-512	-	-	5461.33	170.67
Structure 1	6785	3863	5447.148	170.22
Structure 2	7008	3946	5295.425	165.48
Structure 3	6926	4143	5462.526	170.70
Structure 4	6908	3801	5451.65	170.36

3.5.2. Cryptanalytic Attacks

In this type of attack, some attacks are performed to find specific weaknesses in the structure of a hash algorithm, and the amount of effort is expected to be less than the effort in the brute force attack. The meet-in-the-middle attack is considered a generic cryptographic approach that is applied to cryptographic systems based on block ciphers.

Meet-in-the-Middle Attack

This attack seeks collisions on intermediate hash values instead of the final hash value [48]. Meet-in-the-middle (MITM) attacks can be analyzed by substitution of the last block in the original message to find conflicts. In this attack process, we kept the final hash unchanged but replaced Msg1 with Msg2. The following steps were performed:

• Msg1 = (M₁, M₂, M₃, …, M_n) can be replaced by Msg2 = (M₁, M₂, M₃, …, M_n″). The second time, “advanced culture” was replaced with “civilization”;
• The hash value was calculated for both the original message and the replaced message;
• The number of bits different between the original and replaced message was counted.

For an ideal hash function, the number of differing bits should be close to 256 bits, as shown in Table 15.

Table 15. Different bits in meet-in-the-middle attack.

	Different Bits in Meet in the Middle Attack
Structure 1	254
Structure 2	259
Structure 3	260
Structure 4	245

4. Conclusions

This proposal described improvements to SHA-512 by using the different types of 1D chaotic maps (improved logistic, CLM, TSS, LSS, and hybrid) and DNA sequences. The main improvements focused on changing the fixed role of the hash buffer and additive constant to one that depends on the sensitivity of changes in initial condition and control parameters and uses DNA features and binary coding technology with complementary rules instead of constant values. This paper proposed four different structures to maximize improvements in the performance and security of SHA-512. Several analyses were conducted on the four structures, with simulation experiments results showing that the proposed design had superior distribution and sensitivity, as well as strong confusion and diffusion and robustness against collisions and meet-in-the-middle attacks.