A Two-Stage DEA Approach to Measure Operational Efficiency in Vietnam’s Port Industry
Abstract
1. Introduction
- (1)
- An effective two-stage DEA approach integrating resampling technique and Malmquist is first proposed to assess performance efficiency in the context of the Vietnamese port industry.
- (2)
- The DEA resampling is applied to forecast the next 3 years of seaport performance based on the efficiency score to confirm the suitable data in this case study.
- (3)
- The DEA Malmquist model estimates total productivity change through technical and technological changes based on selected inputs (terminal length, equipment, ship calls) and outputs (cargo throughput, TEUs).
2. Literature Review
3. Methodology
3.1. Validation of Data
3.2. DEA Resampling Model
3.2.1. Past-Present Model
3.2.2. Past–Present–Future Model
3.3. DEA Malmquist Model
- MPI values > 1: Increasing productivity
- MPI values = 1: Constant productivity
- MPI values < 1: Decreasing productivity.
4. Empirical Analysis
4.1. Case Study
4.2. Results of DEA Resampling Model
4.2.1. Results of DEA Resampling Model for Historical Data
4.2.2. Results of DEA Resampling Model for Future Data
4.3. Results of DEA Malmquist Model
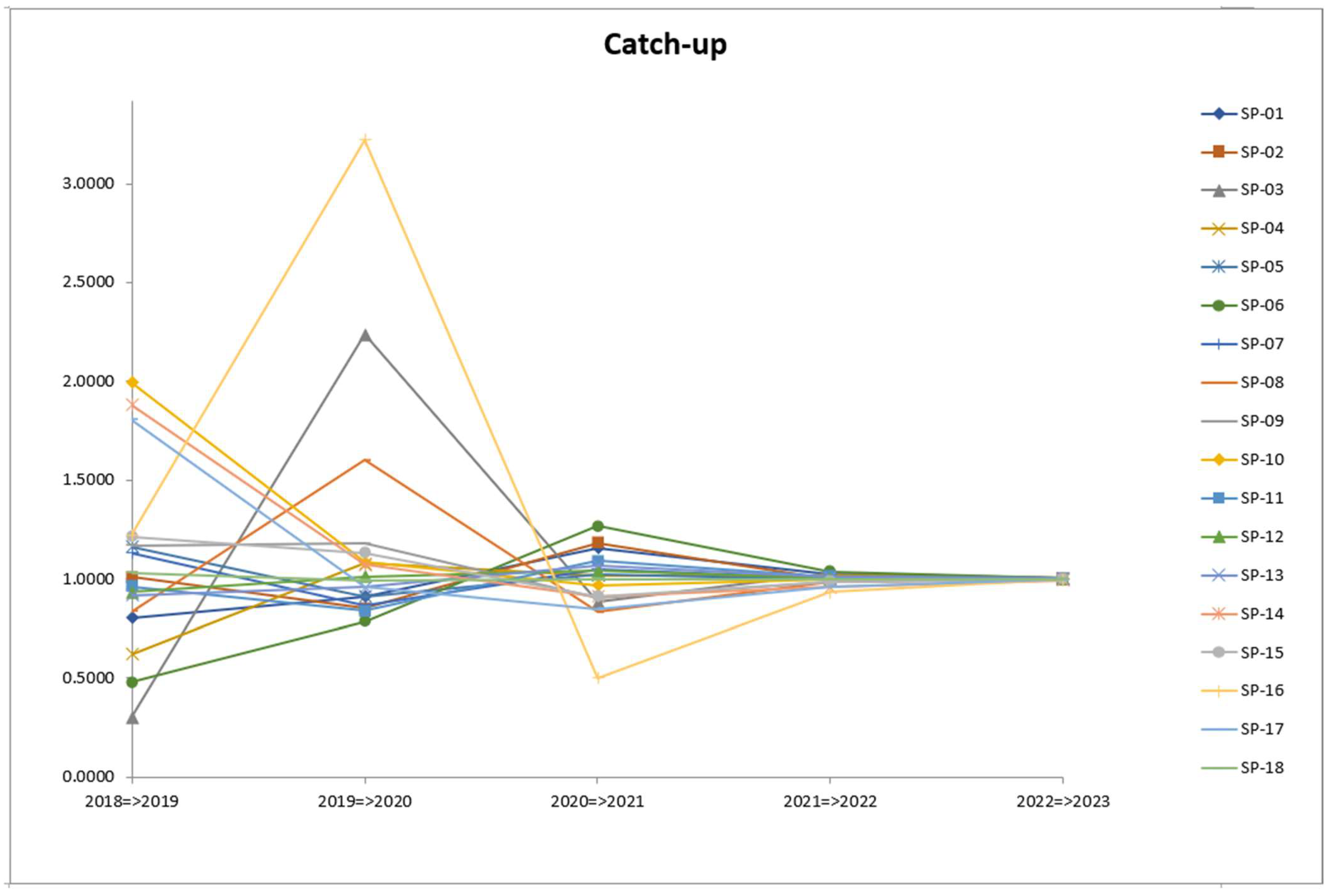
4.3.1. Technical Efficiency Change
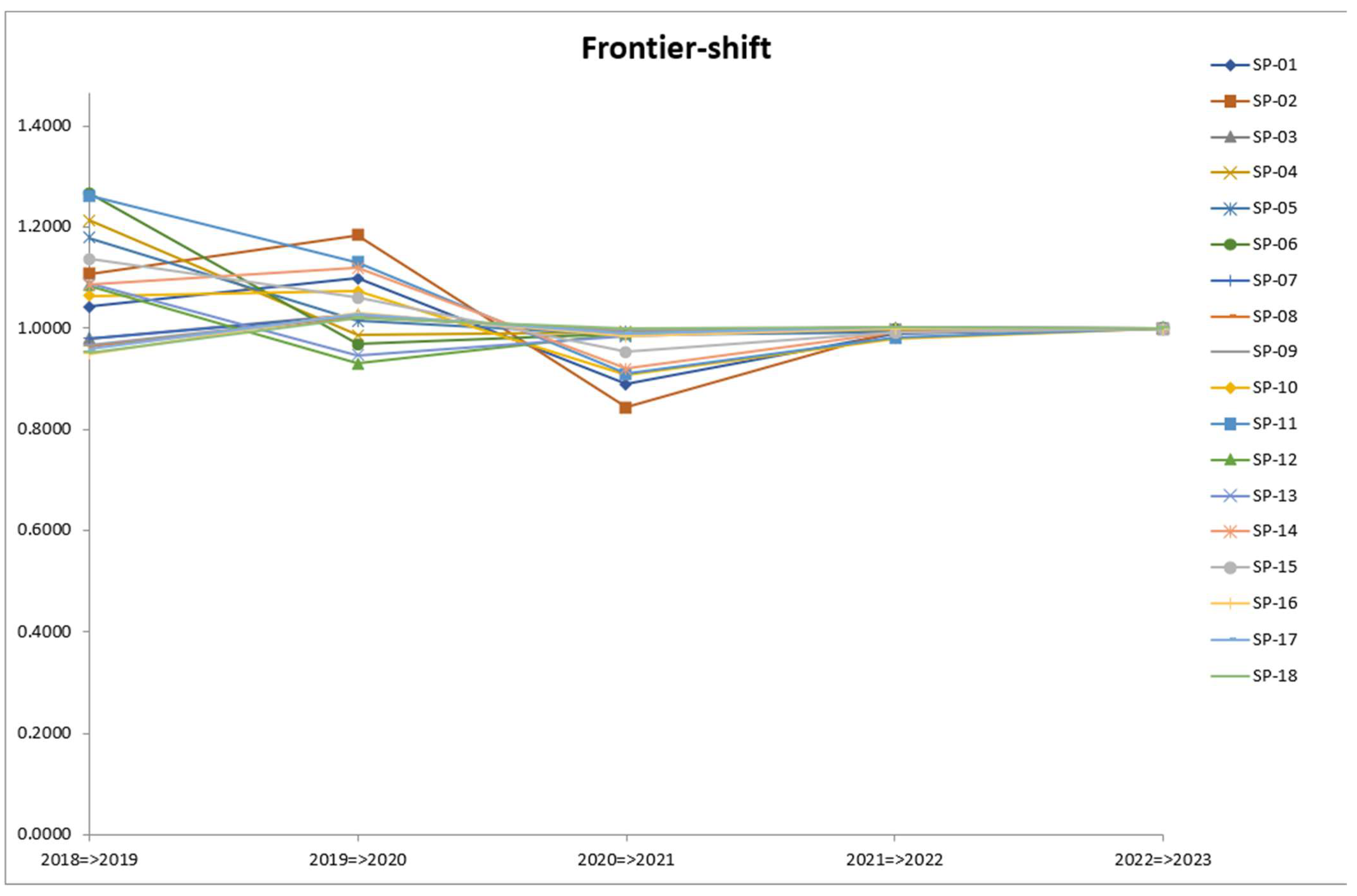
4.3.2. Technological Efficiency Change
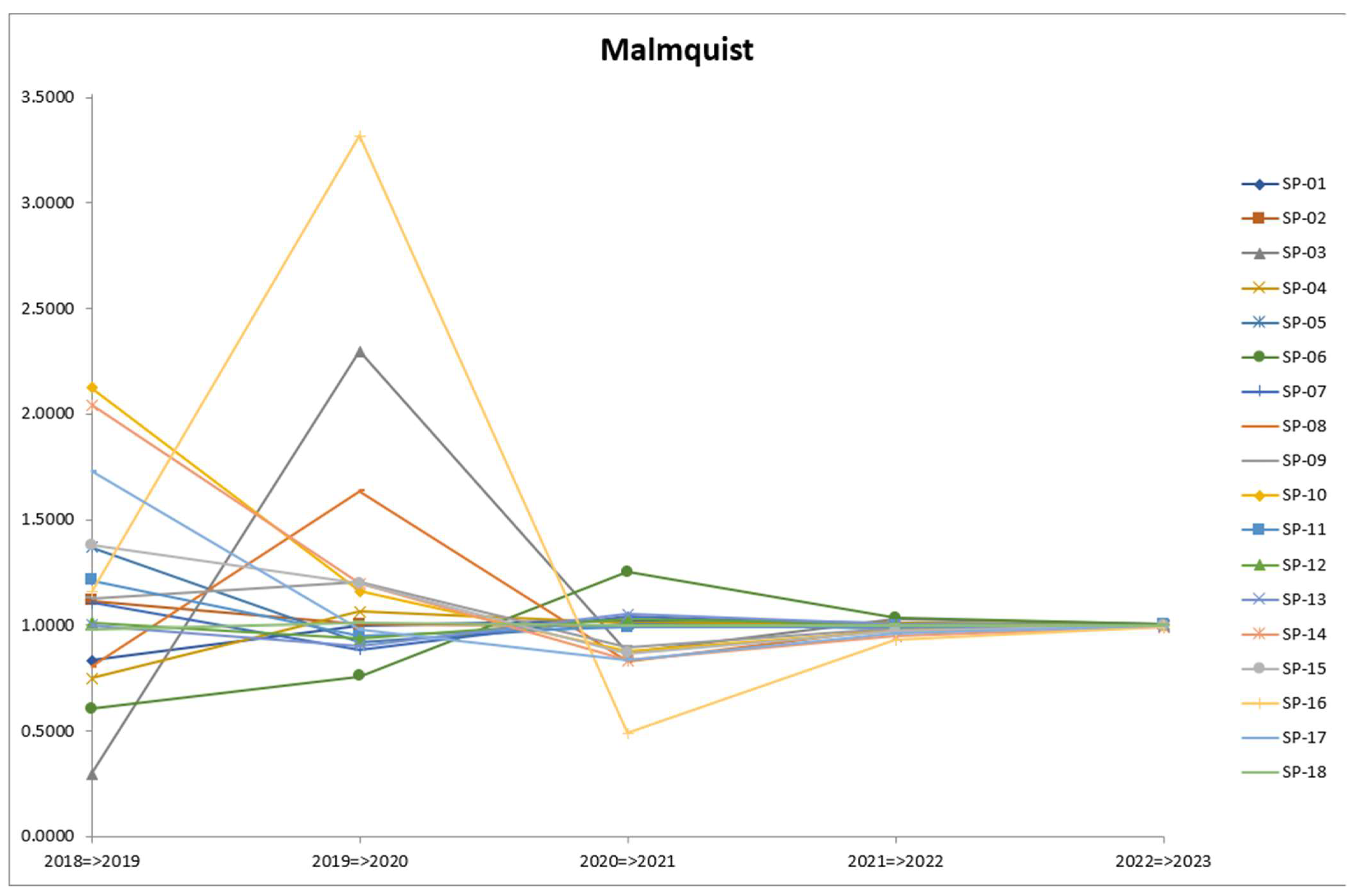
4.3.3. Total Productivity Change
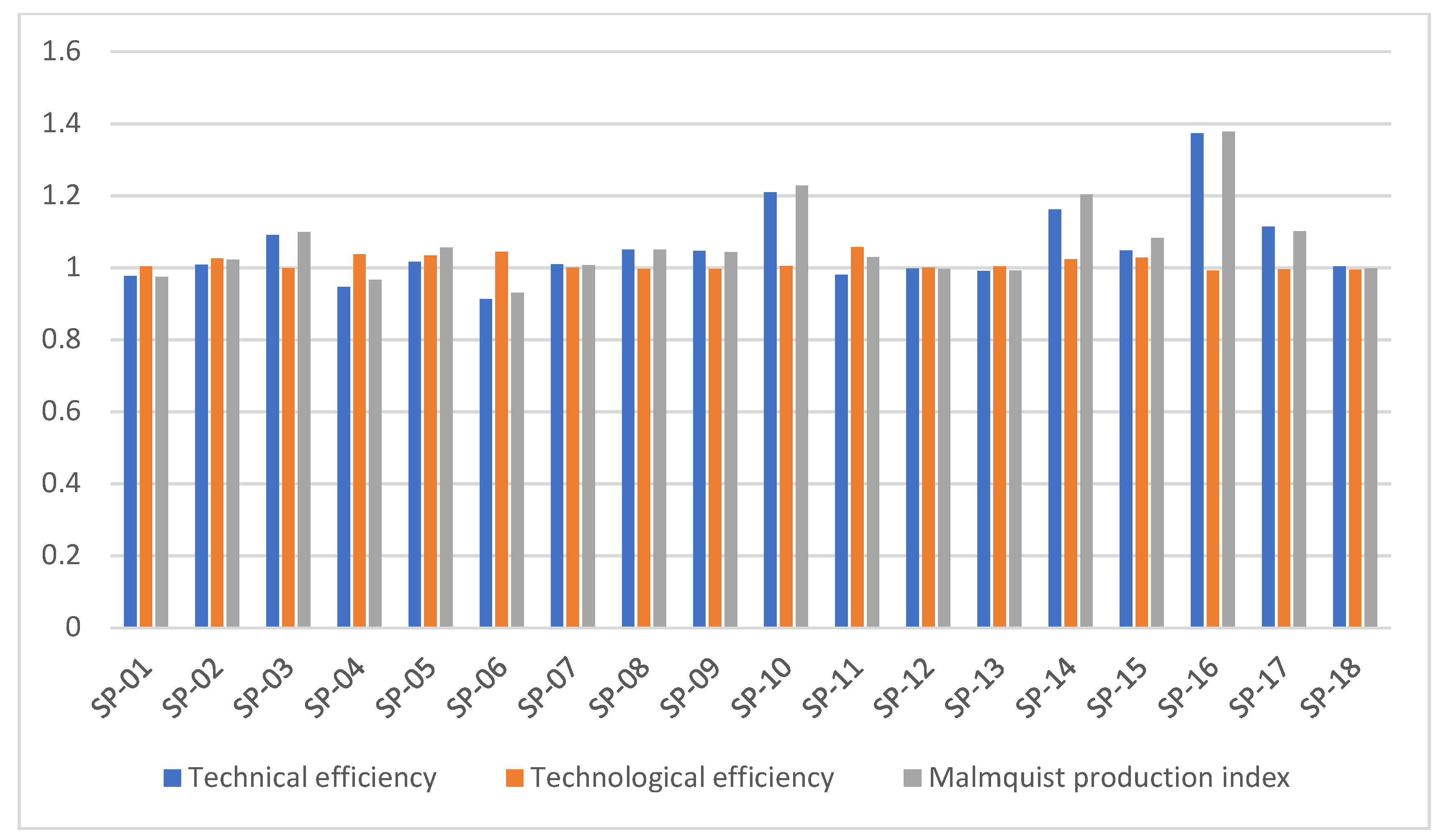
4.3.4. Comparative Analysis
4.4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thai, V.V.; Yeo, G.-T.; Pak, J.-Y. Comparative analysis of port competency requirements in Vietnam and Korea. Marit. Policy Manag. 2016, 43, 614–629. [Google Scholar] [CrossRef]
- Nguyen, T.L.H.; Park, S.H.; Kim, Y.; Yeo, G.T. An efficiency analysis of container terminals in Southern Vietnam using DEA dynamic efficiency evaluation. Asian J. Shipp. Logist. 2021, 37, 329–336. [Google Scholar] [CrossRef]
- Nguyen, P.N.; Woo, S.H.; Beresford, A.; Pettit, S. Competition, market concentration, and relative efficiency of major container ports in Southeast Asia. J. Transp. Geogr. 2020, 83, 102653. [Google Scholar] [CrossRef]
- Castellano, R.; Ferretti, M.; Musella, G.; Risitano, M. Evaluating the economic and environmental efficiency of ports: Evidence from Italy. J. Clean. Prod. 2020, 271, 122560. [Google Scholar] [CrossRef]
- Pham, H.T.; Lee, H. Developing a Green Route Model for Dry Port Selection in Vietnam. Asian J. Shipp. Logist. 2019, 35, 96–107. [Google Scholar] [CrossRef]
- Tran, T.-T.; Ngo, T.Q.-A.; Cung, T.N.-A.; Nguyen, T.-G.; Vu, D.-D.; Nguyen, P.-H.; Tsai, J.-F. Influencing Factors of the International Payment Service Quality at Joint Stock Commercial Bank for Investment and Development of Vietnam. J. Asian Financ. Econ. Bus. 2020, 7, 241–254. [Google Scholar] [CrossRef]
- Vietnam Investment Review. Container Throughput via Vietnamese Seaports Grows in Double-Digit up to August. Available online: https://vir.com.vn/container-throughput-via-vietnamese-seaports-grows-in-double-digit-up-to-august-86797.html#:~:text=ContainerthroughputviaVietnameseseaportsgrowsindouble-digituptoAugust,-August18%2C2021&text=ContainerthroughputviaVietname (accessed on 3 August 2021).
- Nam Dinh Vu News. The Developing Situation of Vietnam Seaports System—2022 Updated. Available online: https://namdinhvu.com/en/the-developing-situation-of-vietnam-seaports-system-2022-updated/ (accessed on 8 March 2022).
- Hanoi Times Vietnam to Pour $13.8-Billion into Seaport System. Available online: https://hanoitimes.vn/vietnam-to-pour-138-billion-into-seaport-system-318812.html (accessed on 8 March 2022).
- Vietnam Plus News. Vietnam’s Seaports Set to Handle 1.14–1.42 Billion Tonnes of Cargo by 2030. Available online: https://en.vietnamplus.vn/vietnams-seaports-set-to-handle-114142-billion-tonnes-of-cargo-by-2030/208564.vnp#:~:text=%7CVietnam%2B(VietnamPlus)-,Vietnamsseaportssettohandle1.14-1.42billiontonnesof,afreshlyapprovedmasterplan (accessed on 8 March 2022).
- Wilmsmeier, G.; Monios, J.; Pérez-Salas, G. Port system evolution—The case of Latin America and the Caribbean. J. Transp. Geogr. 2014, 39, 208–221. [Google Scholar] [CrossRef]
- Suárez-Alemán, A.; Morales Sarriera, J.; Serebrisky, T.; Trujillo, L. When it comes to container port efficiency, are all developing regions equal? Transp. Res. Part A Policy Pract. 2016, 86, 56–77. [Google Scholar] [CrossRef]
- Kuo, K.C.; Lu, W.M.; Le, M.H. Exploring the performance and competitiveness of Vietnam port industry using DEA. Asian J. Shipp. Logist. 2020, 36, 136–144. [Google Scholar] [CrossRef]
- Chang, Y.T.; Jo, A.; Choi, K.S.; Lee, S. Port efficiency and international trade in China. Transp. A Transp. Sci. 2021, 17, 801–823. [Google Scholar] [CrossRef]
- Nguyen, H.O.; Nguyen, H.V.; Chang, Y.T.; Chin, A.T.H.; Tongzon, J. Measuring port efficiency using bootstrapped DEA: The case of Vietnamese ports. Marit. Policy Manag. 2016, 43, 644–659. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Odeck, J.; Bråthen, S. A meta-analysis of DEA and SFA studies of the technical efficiency of seaports: A comparison of fixed and random-effects regression models. Transp. Res. Part A Policy Pract. 2012, 46, 1574–1585. [Google Scholar] [CrossRef]
- Tovar, B.; Wall, A. Environmental efficiency for a cross-section of Spanish port authorities. Transp. Res. Part D Transp. Environ. 2019, 75, 170–178. [Google Scholar] [CrossRef]
- Wu, D.; Lu, C.C.; Tang, P.Y.; Wang, M.L.; Yang, A.C. A resampling slack-based energy efficiency analysis: Application in the G20 economies. Energies 2022, 15, 67. [Google Scholar] [CrossRef]
- Statistics. VPA—Summary of Throughput. Available online: http://www.vpa.org.vn/statistics-2020/ (accessed on 8 March 2022).
- General Statistics Office (GSO). Developing Vietnam’s Seaport System to Meet International Integration. Available online: https://www.gso.gov.vn/en/data-and-statistics/2021/06/developing-vietnams-seaport-system-to-meet-international-integration/ (accessed on 8 March 2022).
- Debreu, G. The coefficient of resource utilization. Econ. J. Econ. Soc. 1951, 19, 273–292. [Google Scholar] [CrossRef]
- Farrell, M.J. The measurement of productive efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253–281. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Wang, G.; Li, K.X.; Xiao, Y. Measuring marine environmental efficiency of a cruise shipping company considering corporate social responsibility. Mar. Policy 2019, 99, 140–147. [Google Scholar] [CrossRef]
- Bjurek, H. The Malmquist total factor productivity index. Scand. J. Econ. 1996, 98, 303–313. [Google Scholar] [CrossRef]
- Bichou, K. An empirical study of the impacts of operating and market conditions on container-port efficiency and benchmarking. Res. Transp. Econ. 2013, 42, 28–37. [Google Scholar] [CrossRef]
- Tongzon, J. Efficiency measurement of selected Australian and other international ports using data envelopment analysis. Transp. Res. Part A Policy Pract. 2001, 35, 107–122. [Google Scholar] [CrossRef]
- Cullinane, K.; Wang, T.-F. Data envelopment analysis (DEA) and improving container port efficiency. Res. Transp. Econ. 2006, 17, 517–566. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J. DEA-based performance measurement of seaports in NorthEast Asia: Radial and non-radial approach. Asian J. Shipp. Logist. 2009, 25, 219–236. [Google Scholar] [CrossRef]
- Sharma, M.J.; Yu, S.J. Benchmark optimization and attribute identification for improvement of container terminals. Eur. J. Oper. Res. 2010, 201, 568–580. [Google Scholar] [CrossRef]
- Lim, S.; Bae, H.; Lee, L.H. A study on the selection of benchmarking paths in DEA. Expert Syst. Appl. 2011, 38, 7665–7673. [Google Scholar] [CrossRef]
- Núñez-Sánchez, R.; Coto-Millán, P. The impact of public reforms on the productivity of Spanish ports: A parametric distance function approach. Transp. Policy 2012, 24, 99–108. [Google Scholar] [CrossRef]
- Wanke, P.F. Physical infrastructure and shipment consolidation efficiency drivers in Brazilian ports: A two-stage network-DEA approach. Transp. Policy 2013, 29, 145–153. [Google Scholar] [CrossRef]
- Bray, S.; Caggiani, L.; Dell′Orco, M.; Ottomanelli, M. Measuring transport systems efficiency under uncertainty by fuzzy sets theory based data envelopment analysis. Procedia Social Behav. Sci. 2014, 111, 770–779. [Google Scholar] [CrossRef][Green Version]
- Almawsheki, E.S.; Shah, M.Z. Technical efficiency analysis of container terminals in the middle eastern region. Asian J. Shipp. Logist. 2015, 31, 477–486. [Google Scholar] [CrossRef]
- Sun, J.; Yuan, Y.; Yang, R.; Ji, X.; Wu, J. Performance evaluation of Chinese port enterprises under significant environmental concerns: An extended DEA-based analysis. Transp. Policy 2017, 60, 75–86. [Google Scholar] [CrossRef]
- Huang, T.; Chen, Z.; Wang, S.; Jiang, D. Efficiency evaluation of key ports along the 21st-Century Maritime Silk Road based on the DEA–SCOR model. Marit. Policy Manag. 2021, 48, 378–390. [Google Scholar] [CrossRef]
- Mustafa, F.S.; Khan, R.U.; Mustafa, T. Technical efficiency comparison of container ports in Asian and Middle East region using DEA. Asian J. Shipp. Logist. 2021, 37, 12–19. [Google Scholar] [CrossRef]
- Kim, S.; Kim, C.; Kim, S.; Choi, S. Rationalization in Korea container terminal using DEA cross-efficiency and cluster analysis. Asian J. Shipp. Logist. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Xu, L.; Xu, S. Evaluation and Forecast of Port Enterprise Innovation Efficiency Based on ES-DEA. In Proceedings of the 2021 5th Annual International Conference on Data Science and Business Analytics (ICDSBA), Changsha, China, 24–26 September 2021; IEEE: New York, NY, USA, 2021; pp. 362–365. [Google Scholar]
- Liu, S.; Park, S.-H.; Choi, Y.-S.; Yeo, G.-T. Efficiency evaluation of major container terminals in the top three cities of the Pearl River Delta using SBM-DEA and undesirable DEA. Asian J. Shipp. Logist. 2022, 3, 1–8. [Google Scholar] [CrossRef]
- Chang, T.-S.; Tone, K.; Wu, C.-H. Past-present-future Intertemporal DEA models. J. Oper. Res. Soc. 2015, 66, 16–32. [Google Scholar] [CrossRef]
- Tone, K.; Ouenniche, J. Dea Score Confidence Intervals with Past–Present and Past–Present–Future-Based Resampling. In Advances in DEA Theory and Applications: With Extensions to Forecasting Models; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 459–479. [Google Scholar]
- Wang, C.-N.; Le, A.L. Measuring the macroeconomic performance among developed countries and Asian developing countries: Past, present, and future. Sustainability 2018, 10, 3664. [Google Scholar] [CrossRef]
- Chiu, Y.; Lin, T.; Chang, T.; Lin, Y.; Chiu, S. Prevaluating efficiency gains from potential mergers and acquisitions in the financial industry with the Resample Past–Present–Future data envelopment analysis approach. Manag. Decis. Econ. 2021, 42, 369–384. [Google Scholar] [CrossRef]
- Bai, X.J.; Zeng, J.; Chiu, Y.H. Pre-evaluating efficiency gains from potential mergers and acquisitions based on the resampling DEA approach: Evidence from China′s railway sector. Transp. Policy 2019, 76, 46–56. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The economic theory of index numbers and the measurement of input, output, and productivity. Econ. J. Econ. Soc. 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lindgren, B.; Roos, P. Productivity changes in Swedish pharamacies 1980–1989: A non-parametric Malmquist approach. J. Product. Anal. 1992, 3, 85–101. [Google Scholar] [CrossRef]
- Li, Z.; Crook, J.; Andreeva, G. Dynamic prediction of financial distress using Malmquist DEA. Expert Syst. Appl. 2017, 80, 94–106. [Google Scholar] [CrossRef]
- Pan, W.-T.; Zhuang, M.-E.; Zhou, Y.-Y.; Yang, J.-J. Research on sustainable development and efficiency of China′s E-Agriculture based on a data envelopment analysis-Malmquist model. Technol. Forecast. Soc. Change 2021, 162, 120298. [Google Scholar] [CrossRef]
- Wan, B.; Zhou, E. Research of Total Factor Productivity and Agricultural Management Based on Malmquist-DEA Modeling. Math. Probl. Eng. 2021, 2021, 2828061. [Google Scholar] [CrossRef]
- Kong, M.; Wang, X.; Wu, Q. The development efficiency of China′s innovative industrial clusters-based on the DEA-Malmquist model. Arab. J. Geosci. 2021, 14, 638. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2000; ISBN 0130661899. [Google Scholar]
- Nguyen, H.K. Combining DEA and ARIMA models for partner selection in the supply chain of Vietnam’s construction industry. Mathematics 2020, 8, 866. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, T.L.; Dang, T.T. Analyzing operational efficiency in real estate companies: An application of GM (1,1) and dea malmquist model. Mathematics 2021, 9, 202. [Google Scholar] [CrossRef]
- Zhu, N.; Zhu, C.; Emrouznejad, A. A combined machine learning algorithms and DEA method for measuring and predicting the efficiency of Chinese manufacturing listed companies. J. Manag. Sci. Eng. 2021, 6, 435–448. [Google Scholar] [CrossRef]
- Tone, K. Resampling in DEA; GRIPS Discussion Papers 13–23; National Graduate Institute for Policy Studies: Tokyo, Japan, 2013. [Google Scholar]
- Färe, R.; Grosskopf, S.; Primont, D. Aggregation, Efficiency, and Measurement; Springer Science & Business Media: Cham, Switzerland, 2010. [Google Scholar]
- Cho, H.; Lee, J. Does transportation size matter for competitiveness in the logistics industry? The cases of maritime and air transportation. Asian J. Shipp. Logist. 2020, 36, 214–223. [Google Scholar] [CrossRef]
- Pham, T.Y.; Jeon, J.W.; Dang, V.L.; Cha, Y.D.; Yeo, G.T. A Longitudinal Analysis of Concentration Developments for Container Terminals in Northern Vietnam. Asian J. Shipp. Logist. 2016, 32, 157–164. [Google Scholar] [CrossRef]
- Vietcombank. Báo Cáo Triển VỌNG ngành Cảng Biển—Logistics 2022. Available online: http://vcbs.com.vn/vn/Communication/GetReport?reportId=9257 (accessed on 8 March 2022).
- Ministry of Transportation. 647 Triệu Tấn Hàng HOÁ Thông Qua Cảng Biển Việt Nam Trong 11 Tháng. Available online: https://mt.gov.vn/vn/tin-tuc/77309/647-trieu-tan-hang-hoa-thong-qua-cang-bien-viet-nam-trong-11-thang.aspx (accessed on 8 March 2022).
- SSIT News. SSIT Lập Kỷ Lục 500.000 TEU Sản Lượng Tàu Mẹ Cập Cảng. Available online: https://www.ssit.com.vn/tin-tuc/ssit-lap-ky-luc-500-000-teu-san-luong-tau-me-cap-cang.html#:~:text=Ngày11tháng12năm,củahãngtàuCMA-CGM (accessed on 8 March 2022).
- Raconteur Media. How Technology Is Creating the Digital Ports of the Future. Available online: https://www.raconteur.net/technology/technology-digital-port/ (accessed on 8 March 2022).
- Polat, I.; Erdoğan, D.; Sesliokuyucu, O.S. The Impact of Attitude and Subjective Norm on Airline Passengers′ Travel Intention in the COVID-19 Era: Mediating Role of Perceived Risk. An. Bras. Estud. Tur. 2021, 11, 1–15. [Google Scholar]
- Tsao, Y.C.; Thanh, V. Van A multi-objective mixed robust possibilistic flexible programming approach for sustainable seaport-dry port network design under an uncertain environment. Transp. Res. Part E Logist. Transp. Rev. 2019, 124, 13–39. [Google Scholar] [CrossRef]
- Ashaari, M.A.; Singh, K.S.D.; Abbasi, G.A.; Amran, A.; Liebana-Cabanillas, F.J. Big data analytics capability for improved performance of higher education institutions in the Era of IR 4.0: A multi-analytical SEM & ANN perspective. Technol. Forecast. Soc. Change 2021, 173, 121119. [Google Scholar] [CrossRef]

| Authors/Year | Inputs/Criteria | Outputs/Responses | Method | Sample and Region |
|---|---|---|---|---|
| Tongzon (2001) [28] | Number of cranes Number of container berths Number of tugs Terminal area Delay time labor | Throughput Number of ship calls | CCR Additive DEA. | Brazilian ports |
| Cullinane and Wang (2006) [29] | Terminal area Quay cranes Yard cranes straddle carriers | Container throughput | CCR BCC | container ports |
| Jiang and Li (2009) [30] | Import/Export by customs GDP by regions Berth length Crane number | Container throughput | Radial Non-radial | Northeast Asian container ports |
| Sharma and Yu (2010) [31] | Quay cranes Transfer cranes Straddle carriers Reach stackers Quay length terminal area | Container throughput | Context-DEA | Container terminals |
| Lim et al. (2011) [32] | Quay length Total area Gantry cranes | Container throughput | Additive non-oriented DEA RAM | Asian container terminals |
| Sánchez and Millán (2012) [33] | Number of employees Intermediate consumption Capital | Liquid bulk solid bulk Containerized general cargo Non-containerized general cargo | MPI | Ports in Spain |
| Wanke (2013) [34] | Number of berths Warehousing area yard area Shipments frequency | Container throughput | Network-DEA | Brazilian ports |
| Bray et al. (2014) [35] | Number of cranes Container berths Number of tugs Terminal area Delay time Number of port authority employees | Container throughput Shiprate Ship calls Crane Productivity | Fuzzy DEA | Container ports |
| Almawsheki and Shah (2015) [36] | Terminal Area Quay length Quay cranes Yard equipment Maximum Draft | Container throughput | CCR | Middle East container terminals |
| Sun et al. (2017) [37] | Staff number Fixed assets | Operating cost Net profit Cargo throughput NOx | Non-radial DEA | Chinese port enterprises |
| Huang et al. (2021) [38] | Quay length Number of container berths Gantry cranes | Container throughput | CCR BCC SCOR | Ports along the twenty-first-century Maritime Silk Road |
| Mustafa et al. (2021) [39] | Number of berths Number of cranes Berth length Berth depth | TEUs | CCR BCC | Ports in South & Middle Eastern and East Asian region |
| Kim et al. (2021) [40] | Quay length Depth of water Crane | Cargo volume Loading capacity per hour | DEA cross-efficiency Cluster analysis | Korean Container Terminals |
| Xu and Xu (2021) [41] | R&D Proportion of technical personnel | Business income Container throughput | Exponential smoothing CCR | Ports in China |
| Liu et al. (2022) [42] | Gross Crane Productivity Crane Intensity Berth Length Berth Depth | Calls Moves Finish | SBM Undesirable | Ports in China |
| DMUs | Seaport | Area |
|---|---|---|
| SP-01 | Quang Ninh | Northern |
| SP-02 | Hai Phong | Northern |
| SP-03 | Doan Xa | Northern |
| SP-04 | Dinh Vu | Northern |
| SP-05 | Nam Dinh Vu | Northern |
| SP-06 | Tan Cang 128 | Northern |
| SP-07 | Nghe Tinh | Central |
| SP-08 | Da Nang | Central |
| SP-09 | Quy Nhon | Central |
| SP-10 | Dong Nai | Southern |
| SP-11 | Cat Lai | Southern |
| SP-12 | Sai Gon | Southern |
| SP-13 | Ben Nghe | Southern |
| SP-14 | Lotus | Southern |
| SP-15 | TCIT+TCCT | Southern |
| SP-16 | SSIT | Southern |
| SP-17 | Can tho | Southern |
| SP-18 | An Giang | Southern |
| Variables | Definitions | Units | References |
|---|---|---|---|
| Terminal Length (I1) | The length of berths at which container ship anchor | m2 | [2,13] |
| Equipment (I2) | The major number of equipment cargo-handling in port | Items | [13,60] |
| Ship calls (I3) | The number of vessels which call or arrive at a particular port at any given time | Call | [11,12] |
| Cargo throughput (O1) | The weighted quantity of cargo handled annually | MT | [15,61] |
| TEUs (O2) | The terminal’s annual container | TEU | [13,15] |
| DMUs | 5000 Replicas | 500 Replicas | Difference | |||||
|---|---|---|---|---|---|---|---|---|
| 97.50% | DEA | 2.50% | 97.50% | DEA | 2.50% | 97.50% | 2.50% | |
| SP-01 | 1.0107 | 0.7801 | 0.6251 | 1.0082 | 0.7801 | 0.6251 | 0.0025 | 0 |
| SP-02 | 1.1436 | 0.8952 | 0.6545 | 1.1449 | 0.8952 | 0.6623 | −0.0013 | −0.0078 |
| SP-03 | 0.3698 | 0.2484 | 0.1077 | 0.3698 | 0.2484 | 0.1083 | 0 | −0.0006 |
| SP-04 | 2.0137 | 1.3668 | 1.3012 | 2.006 | 1.3668 | 1.2965 | 0.0077 | 0.0047 |
| SP-05 | 1.4568 | 1.0705 | 0.6937 | 1.4653 | 1.0705 | 0.6834 | −0.0085 | 0.0103 |
| SP-06 | 1.3138 | 0.376 | 0.3236 | 1.3079 | 0.376 | 0.3236 | 0.0059 | 0 |
| SP-07 | 0.2325 | 0.1966 | 0.1805 | 0.2385 | 0.1966 | 0.1791 | −0.006 | 0.0014 |
| SP-08 | 0.4094 | 0.3855 | 0.2377 | 0.4174 | 0.3855 | 0.2373 | −0.008 | 0.0004 |
| SP-09 | 0.5723 | 0.5266 | 0.3683 | 0.5763 | 0.5266 | 0.3872 | −0.004 | −0.0189 |
| SP-10 | 2.909 | 1.1525 | 0.5062 | 2.9088 | 1.1525 | 0.5007 | 0.0002 | 0.0055 |
| SP-11 | 0.4002 | 0.2801 | 0.263 | 0.4229 | 0.2801 | 0.263 | −0.0227 | 0 |
| SP-12 | 0.3883 | 0.3367 | 0.2613 | 0.3918 | 0.3367 | 0.2613 | −0.0035 | 0 |
| SP-13 | 0.5701 | 0.4683 | 0.3766 | 0.5735 | 0.4683 | 0.3766 | −0.0034 | 0 |
| SP-14 | 0.1772 | 0.1279 | 0.0519 | 0.1787 | 0.1279 | 0.0536 | −0.0015 | −0.0017 |
| SP-15 | 5.9669 | 2.3891 | 3.9871 | 6.0392 | 2.3891 | 3.9797 | −0.0723 | 0.0074 |
| SP-16 | 1.2658 | 1.1213 | 0.2484 | 1.2665 | 1.1213 | 0.2585 | −0.0007 | −0.0101 |
| SP-17 | 0.2038 | 0.1771 | 0.1088 | 0.2054 | 0.1771 | 0.1088 | −0.0016 | 0 |
| SP-18 | 0.4413 | 0.4098 | 0.3703 | 0.4441 | 0.4098 | 0.3689 | −0.0028 | 0.0014 |
| Terminal Length | Equipment | Ship Calls | Cargo Throughput | TEUs | |
|---|---|---|---|---|---|
| Terminal Length | 1.000 | 0.981 | 0.852 | 0.912 | 0.922 |
| Equipment | 0.981 | 1.000 | 0.829 | 0.953 | 0.968 |
| Ship calls | 0.852 | 0.829 | 1.000 | 0.834 | 0.795 |
| Cargo throughput | 0.912 | 0.953 | 0.834 | 1.000 | 0.988 |
| TEUs | 0.922 | 0.968 | 0.795 | 0.988 | 1.000 |
| DMUs | 97.50% | Forecasted Score | Actual Score | 2.50% |
|---|---|---|---|---|
| SP-01 | 1.0346 | 0.9746 | 0.7801 | 0.6427 |
| SP-02 | 1.1402 | 1.0625 | 0.8952 | 0.6322 |
| SP-03 | 0.3687 | 0.1907 | 0.2484 | 0.1100 |
| SP-04 | 2.1020 | 1.4263 | 1.3794 | 1.3219 |
| SP-05 | 1.4928 | 1.1642 | 1.1065 | 0.7053 |
| SP-06 | 1.2317 | 0.5695 | 0.3760 | 0.4479 |
| SP-07 | 0.2386 | 0.2187 | 0.1966 | 0.1978 |
| SP-08 | 0.3011 | 0.2566 | 0.3855 | 0.2242 |
| SP-09 | 0.4601 | 0.4251 | 0.5266 | 0.3718 |
| SP-10 | 2.7488 | 1.9320 | 1.7165 | 0.4815 |
| SP-11 | 0.4002 | 0.3369 | 0.2801 | 0.3074 |
| SP-12 | 0.3879 | 0.3639 | 0.3367 | 0.2799 |
| SP-13 | 0.5719 | 0.5321 | 0.4683 | 0.4064 |
| SP-14 | 0.1702 | 0.0912 | 0.1279 | 0.0521 |
| SP-15 | 5.6958 | 4.9512 | 4.5446 | 3.9764 |
| SP-16 | 0.3943 | 0.2900 | 1.1352 | 0.2198 |
| SP-17 | 0.1859 | 0.1395 | 0.1771 | 0.1116 |
| SP-18 | 0.4373 | 0.4086 | 0.4098 | 0.3759 |
| Frontier | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 | Average |
|---|---|---|---|---|---|---|
| SP-01 | 0.8013 | 0.9098 | 1.1547 | 1.0192 | 1.0017 | 0.9773 |
| SP-02 | 1.0079 | 0.8499 | 1.1825 | 0.9985 | 0.9999 | 1.0077 |
| SP-03 | 0.3028 | 2.2371 | 0.8811 | 1.0271 | 1.0024 | 1.0901 |
| SP-04 | 0.6178 | 1.0791 | 1.0180 | 1.0153 | 1.0014 | 0.9463 |
| SP-05 | 1.1625 | 0.9076 | 1.0195 | 0.9939 | 0.9995 | 1.0166 |
| SP-06 | 0.4777 | 0.7826 | 1.2653 | 1.0354 | 1.0030 | 0.9128 |
| SP-07 | 1.1312 | 0.8632 | 1.0488 | 1.0013 | 1.0001 | 1.0089 |
| SP-08 | 0.8359 | 1.5990 | 0.8326 | 0.9838 | 0.9985 | 1.0500 |
| SP-09 | 1.1683 | 1.1768 | 0.9042 | 0.9836 | 0.9985 | 1.0463 |
| SP-10 | 1.9953 | 1.0825 | 0.9671 | 0.9985 | 0.9999 | 1.2087 |
| SP-11 | 0.9610 | 0.8390 | 1.0888 | 1.0115 | 1.0010 | 0.9803 |
| SP-12 | 0.9343 | 1.0099 | 1.0408 | 1.0029 | 1.0003 | 0.9976 |
| SP-13 | 0.9181 | 0.9566 | 1.0690 | 1.0067 | 1.0006 | 0.9902 |
| SP-14 | 1.8819 | 1.0703 | 0.9076 | 0.9574 | 0.9924 | 1.1619 |
| SP-15 | 1.2128 | 1.1298 | 0.9104 | 0.9839 | 0.9986 | 1.0471 |
| SP-16 | 1.2213 | 3.2211 | 0.4971 | 0.9320 | 0.9938 | 1.3731 |
| SP-17 | 1.8041 | 0.9582 | 0.8462 | 0.9617 | 0.9968 | 1.1134 |
| SP-18 | 1.0297 | 0.9915 | 0.9986 | 0.9988 | 0.9999 | 1.0037 |
| Average | 1.0813 | 1.2036 | 0.9796 | 0.9951 | 0.9993 | 1.0127 |
| Max | 1.9953 | 3.2211 | 1.2653 | 1.0354 | 1.003 | 1.0839 |
| Min | 0.3028 | 0.7826 | 0.4971 | 0.932 | 0.9924 | 0.951 |
| SD | 0.4503 | 0.6077 | 0.1686 | 0.0255 | 0.0027 | 0.0372 |
| Frontier | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 | Average |
|---|---|---|---|---|---|---|
| SP-01 | 1.0424 | 1.0992 | 0.8886 | 0.9899 | 0.9991 | 1.0038 |
| SP-02 | 1.1074 | 1.1827 | 0.8435 | 0.9938 | 0.9994 | 1.0254 |
| SP-03 | 0.9787 | 1.0265 | 0.9895 | 0.9997 | 1.0000 | 0.9989 |
| SP-04 | 1.2125 | 0.9858 | 0.9929 | 0.9943 | 0.9995 | 1.0370 |
| SP-05 | 1.1789 | 1.0136 | 0.9862 | 0.9907 | 0.9992 | 1.0337 |
| SP-06 | 1.2662 | 0.9684 | 0.9887 | 0.9996 | 1.0000 | 1.0446 |
| SP-07 | 0.9788 | 1.0259 | 0.9927 | 1.0001 | 1.0000 | 0.9995 |
| SP-08 | 0.9629 | 1.0226 | 0.9950 | 1.0009 | 1.0001 | 0.9963 |
| SP-09 | 0.9660 | 1.0241 | 0.9940 | 1.0006 | 1.0001 | 0.9970 |
| SP-10 | 1.0644 | 1.0732 | 0.9074 | 0.9792 | 0.9981 | 1.0044 |
| SP-11 | 1.2625 | 1.1304 | 0.9099 | 0.9822 | 0.9984 | 1.0567 |
| SP-12 | 1.0848 | 0.9291 | 0.9889 | 0.9995 | 1.0000 | 1.0005 |
| SP-13 | 1.0884 | 0.9459 | 0.9838 | 0.9983 | 0.9999 | 1.0033 |
| SP-14 | 1.0859 | 1.1192 | 0.9190 | 0.9918 | 0.9999 | 1.0232 |
| SP-15 | 1.1362 | 1.0593 | 0.9531 | 0.9905 | 0.9992 | 1.0276 |
| SP-16 | 0.9484 | 1.0299 | 0.9832 | 0.9987 | 0.9999 | 0.9920 |
| SP-17 | 0.9577 | 1.0267 | 0.9897 | 1.0006 | 1.0001 | 0.9949 |
| SP-18 | 0.9514 | 1.0201 | 0.9983 | 1.0016 | 1.0001 | 0.9943 |
| Average | 1.0707 | 1.0379 | 0.9614 | 0.9951 | 0.9996 | 1.0129 |
| Max | 1.2662 | 1.1827 | 0.9983 | 1.0016 | 1.0001 | 1.0567 |
| Min | 0.9484 | 0.9291 | 0.8435 | 0.9792 | 0.9981 | 0.9920 |
| SD | 0.1072 | 0.0647 | 0.0466 | 0.0066 | 0.0006 | 0.0200 |
| Frontier | 2018–2019 | 2019–2020 | 2020–2021 | 2021–2022 | 2022–2023 | Average |
|---|---|---|---|---|---|---|
| SP-01 | 0.8353 | 1.0000 | 1.0261 | 1.0089 | 1.0008 | 0.9742 |
| SP-02 | 1.1161 | 1.0051 | 0.9974 | 0.9922 | 0.9993 | 1.0220 |
| SP-03 | 0.2964 | 2.2964 | 0.8718 | 1.0268 | 1.0023 | 1.0987 |
| SP-04 | 0.7491 | 1.0638 | 1.0107 | 1.0095 | 1.0008 | 0.9668 |
| SP-05 | 1.3704 | 0.9200 | 1.0055 | 0.9847 | 0.9986 | 1.0558 |
| SP-06 | 0.6049 | 0.7579 | 1.2510 | 1.0349 | 1.0030 | 0.9304 |
| SP-07 | 1.1071 | 0.8855 | 1.0412 | 1.0014 | 1.0001 | 1.0071 |
| SP-08 | 0.8048 | 1.6351 | 0.8285 | 0.9846 | 0.9986 | 1.0503 |
| SP-09 | 1.1287 | 1.2051 | 0.8988 | 0.9842 | 0.9986 | 1.0431 |
| SP-10 | 2.1237 | 1.1617 | 0.8775 | 0.9778 | 0.9980 | 1.2277 |
| SP-11 | 1.2133 | 0.9484 | 0.9907 | 0.9935 | 0.9994 | 1.0291 |
| SP-12 | 1.0135 | 0.9383 | 1.0293 | 1.0024 | 1.0002 | 0.9968 |
| SP-13 | 0.9993 | 0.9048 | 1.0516 | 1.0050 | 1.0004 | 0.9922 |
| SP-14 | 2.0435 | 1.1979 | 0.8341 | 0.9496 | 0.9923 | 1.2035 |
| SP-15 | 1.3779 | 1.1968 | 0.8677 | 0.9746 | 0.9977 | 1.0829 |
| SP-16 | 1.1583 | 3.3176 | 0.4888 | 0.9307 | 0.9937 | 1.3778 |
| SP-17 | 1.7278 | 0.9838 | 0.8374 | 0.9623 | 0.9969 | 1.1016 |
| SP-18 | 0.9796 | 1.0114 | 0.9969 | 1.0004 | 1.0000 | 0.9977 |
| Average | 1.1472 | 1.2461 | 0.9392 | 0.9902 | 0.9989 | 1.0643 |
| Max | 2.1237 | 3.3176 | 1.251 | 1.0349 | 1.003 | 1.3778 |
| Min | 0.2964 | 0.7579 | 0.4888 | 0.9307 | 0.9923 | 0.9304 |
| SD | 0.4642 | 0.6235 | 0.1546 | 0.0256 | 0.0027 | 0.1096 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-N.; Nguyen, P.-H.; Nguyen, T.-L.; Nguyen, T.-G.; Nguyen, D.-T.; Tran, T.-H.; Le, H.-C.; Phung, H.-T. A Two-Stage DEA Approach to Measure Operational Efficiency in Vietnam’s Port Industry. Mathematics 2022, 10, 1385. https://doi.org/10.3390/math10091385
Wang C-N, Nguyen P-H, Nguyen T-L, Nguyen T-G, Nguyen D-T, Tran T-H, Le H-C, Phung H-T. A Two-Stage DEA Approach to Measure Operational Efficiency in Vietnam’s Port Industry. Mathematics. 2022; 10(9):1385. https://doi.org/10.3390/math10091385
Chicago/Turabian StyleWang, Chia-Nan, Phi-Hung Nguyen, Thi-Ly Nguyen, Thi-Giang Nguyen, Duc-Thinh Nguyen, Thi-Hoai Tran, Hong-Cham Le, and Huong-Thuy Phung. 2022. "A Two-Stage DEA Approach to Measure Operational Efficiency in Vietnam’s Port Industry" Mathematics 10, no. 9: 1385. https://doi.org/10.3390/math10091385
APA StyleWang, C.-N., Nguyen, P.-H., Nguyen, T.-L., Nguyen, T.-G., Nguyen, D.-T., Tran, T.-H., Le, H.-C., & Phung, H.-T. (2022). A Two-Stage DEA Approach to Measure Operational Efficiency in Vietnam’s Port Industry. Mathematics, 10(9), 1385. https://doi.org/10.3390/math10091385









