Knacks of Fractional Order Swarming Intelligence for Parameter Estimation of Harmonics in Electrical Systems

Abstract

The efficient parameter estimation of harmonics is required to effectively design filters to mitigate their adverse effects on the power quality of electrical systems. In this study, a fractional order swarming optimization technique is proposed for the parameter estimation of harmonics normally present in industrial loads. The proposed fractional order particle swarm optimization (FOPSO) effectively estimates the amplitude and phase parameters corresponding to the first, third, fifth, seventh and eleventh harmonics. The performance of the FOPSO was evaluated for ten fractional orders with noiseless and noisy scenarios. The robustness efficiency of the proposed FOPSO was analyzed by considering different levels of additive white Gaussian noise in the harmonic signal. Monte Carlo simulations confirmed the reliability of the FOPSO for a lower fractional order ($\lambda$ = 0.1) with a faster convergence rate and no divergent run compared to other fractional orders as well as to standard PSO ($\lambda$ = 1).

1. Introduction

Parameter estimation is an essential or fundamental step in solving various engineering and applied sciences problems [1,2,3,4] including monitoring power quality and assessing reliability in electrical systems [5]. Parameter estimation of electrical harmonics is required to compensate or mitigate their adverse effects in electrical systems that may lead to reduced lifetime of complex/sensitive equipment due to circuit breaker failure, enhanced core losses in electrical devices/components, instrumentation malfunctioning and excessive heat generation [6,7,8]. Researchers have proposed various local/global search parameter estimation methods to address the power systems harmonics issue. For instance, Singh et al. presented a Kalman filtering approach [9], Joorabian et al. proposed a novel method by hybridizing least squares with Adaline [10], Enayati et al. designed a hybrid algorithm integrating recursive least squares with an iterated Kalman filter [11], Sarkar et al. introduced a self-organized ADALINE mechanism [12], Liu et al. presented a hierarchical iterative estimation approach [13], and Xu et al. proposed various modifications in least squares and gradient descent algorithms in [14,15], and references cited therein, for the parameter estimation of power signals.

The efficacy of evolutionary and swarm optimization techniques is well-established in the literature for solving different optimization and estimation problems [16,17,18]. The researchers exploited their renowned strength to estimate the parameters of harmonics in electrical systems. Some of the relevant examples are as follows: Ray et al. proposed a bacterial foraging optimization technique [19], Mehmood et al. exploited differential evolution and backtracking search algorithms [20,21], Elvira-Ortiz et al. presented a genetic algorithm approach [22], Nascimento Sepulchro et al. introduced an evolutionary strategy [23], Subramaniyan et al. developed an improved football game optimization approach [24], Singh at al. designed a hybrid firefly algorithm [25], and Kabalci et al. introduced an artificial bee colony mechanism [26].

In the last decade, a new concept of designing fractional order algorithms has emerged [27,28]. Fractional order algorithms have been developed by exploiting the theories and concepts of fractional calculus in conventional algorithms. Fractional calculus generalizes the standard integer calculus to real values and provides better modeling and insight to the system under study due to promising features that include history information or the long memory principle [29,30,31]. Fractional order approaches are exploited to effectively solve different problems. Examples include the following: Khan et al. developed fractional order gradient algorithms for recommender systems [32,33], Yousri et al. designed fractional cuckoo search, fractional flower pollination and fractional modified Harris Hawks optimization algorithms for different applications [34,35,36], Chaudhary and Zubair et al. proposed fractional least-mean-squares-based methods for the parameter estimation of power signals [37,38,39], Machado et al. introduced the concept of particle swarm optimization (PSO) with fractional velocity [40]. and Couceiro et al. introduced the concept of a fractional order Darwinian PSO [41,42]. Later, different fractional order variants of PSO were introduced for diverse applications [43,44,45] including power and electrical engineering [46,47]. These successful applications of the fractional order PSO techniques motivated the authors to investigate exploiting the fractional order swarming optimization paradigm for efficient parameter estimation of harmonics in electrical systems.

The contributions of the current study are summarized as:

• A fractional order swarming optimization approach exploiting the inherited legacy of the fractional calculus is presented for the nonlinear parameter estimation problem of electrical harmonics.
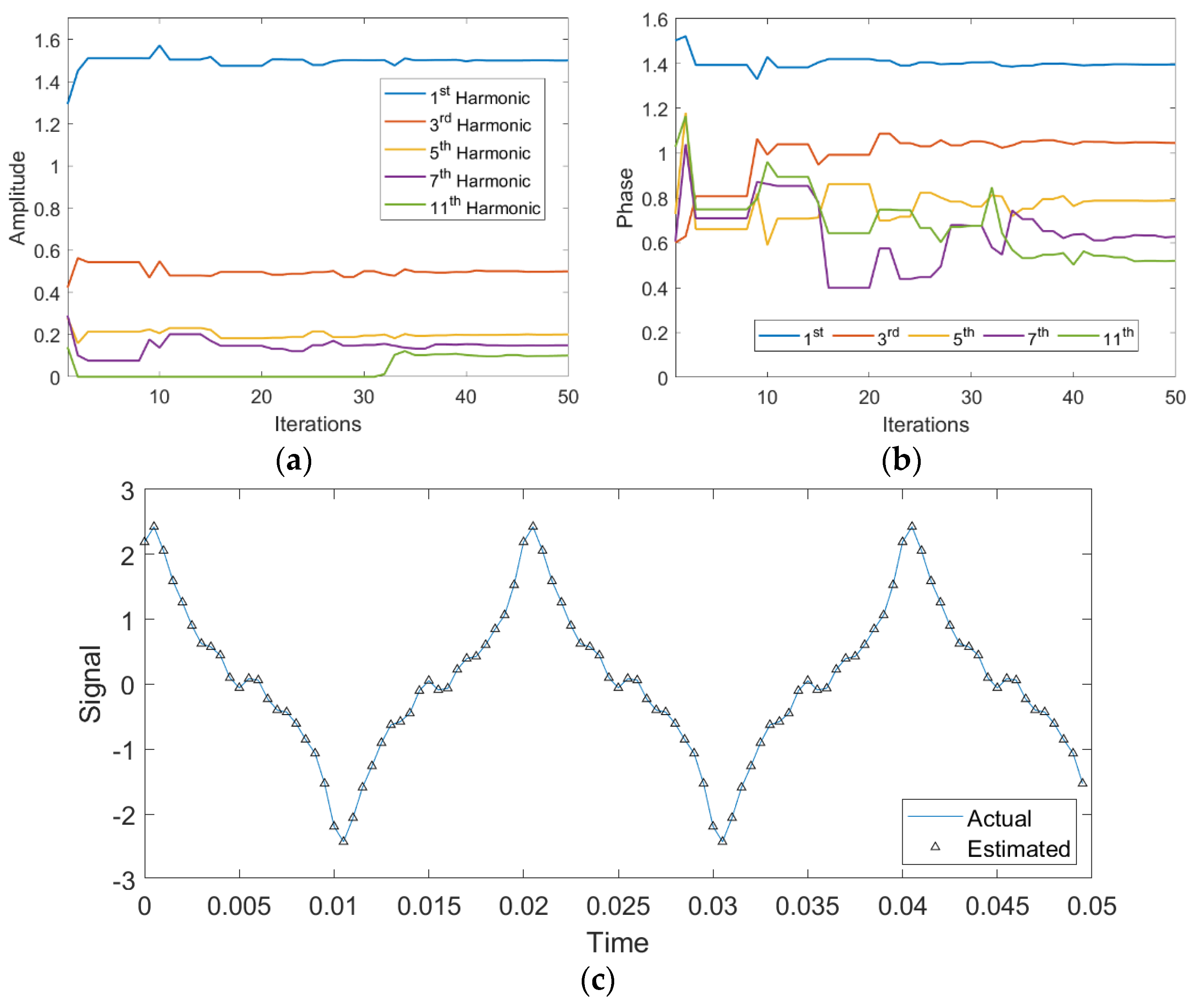
• The proposed fractional order particle swarm optimization (FOPSO) effectively estimates the amplitude and phase parameters of the harmonic signal compared with the standard counterpart for different scenarios of additive white Gaussian noise.
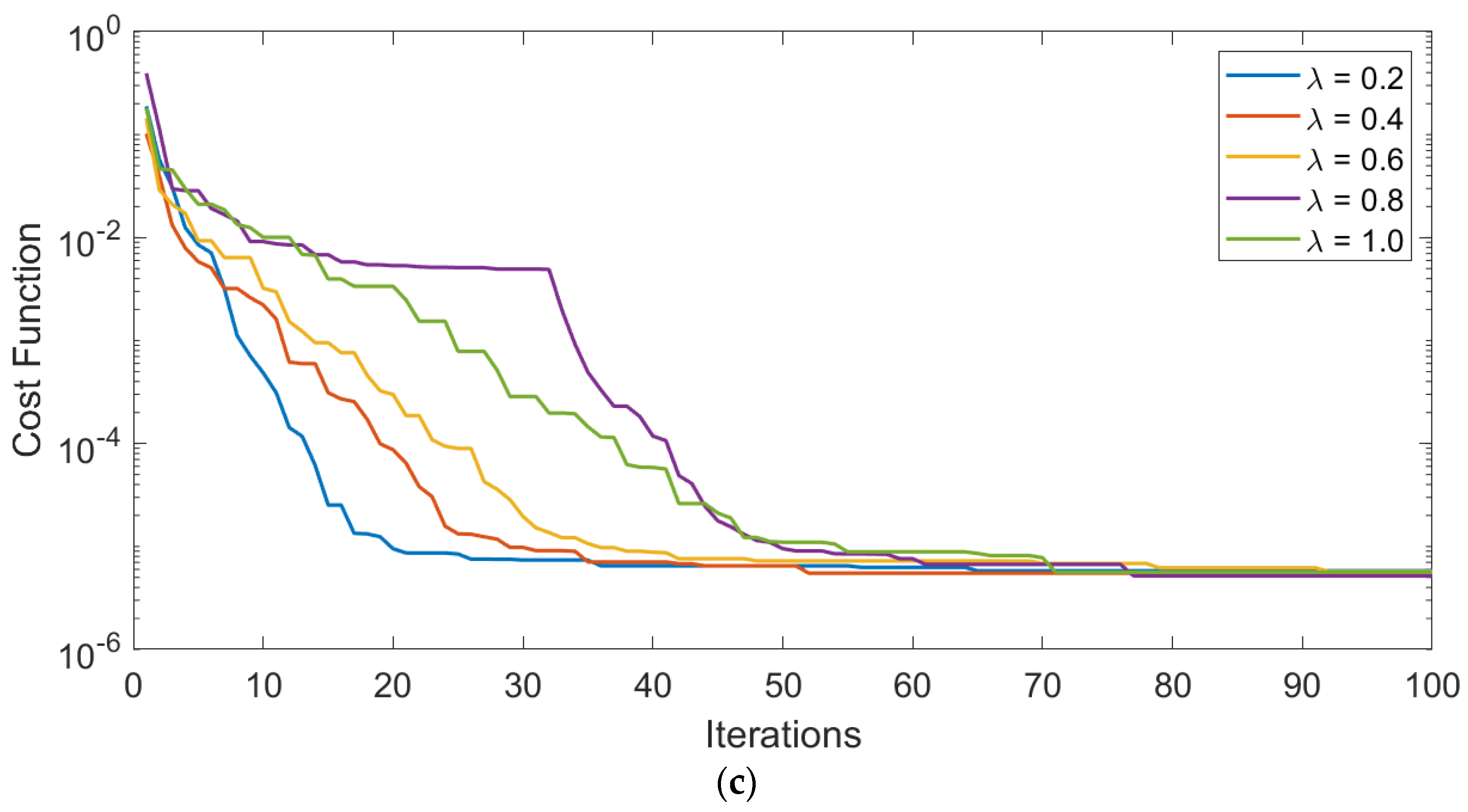
• The best convergence performance of the FOPSO is obtained for a fractional order of 0.1 that reduces gradually with increase in the fractional order until unity (standard PSO).
• The reliability analyses, through autonomous executions of the FOPSO for harmonics parameter identification, confirm superior performance in the case of a fractional order of 0.1 for all noise variations.

The remaining article is structured as follows: A mathematical model for harmonics estimation is provided in Section 2. The proposed methodology for the problem is presented in Section 3. Simulation results, in terms of different tabular and graphical illustrations, are provided in Section 4. The conclusions of the study are provided in Section 5.

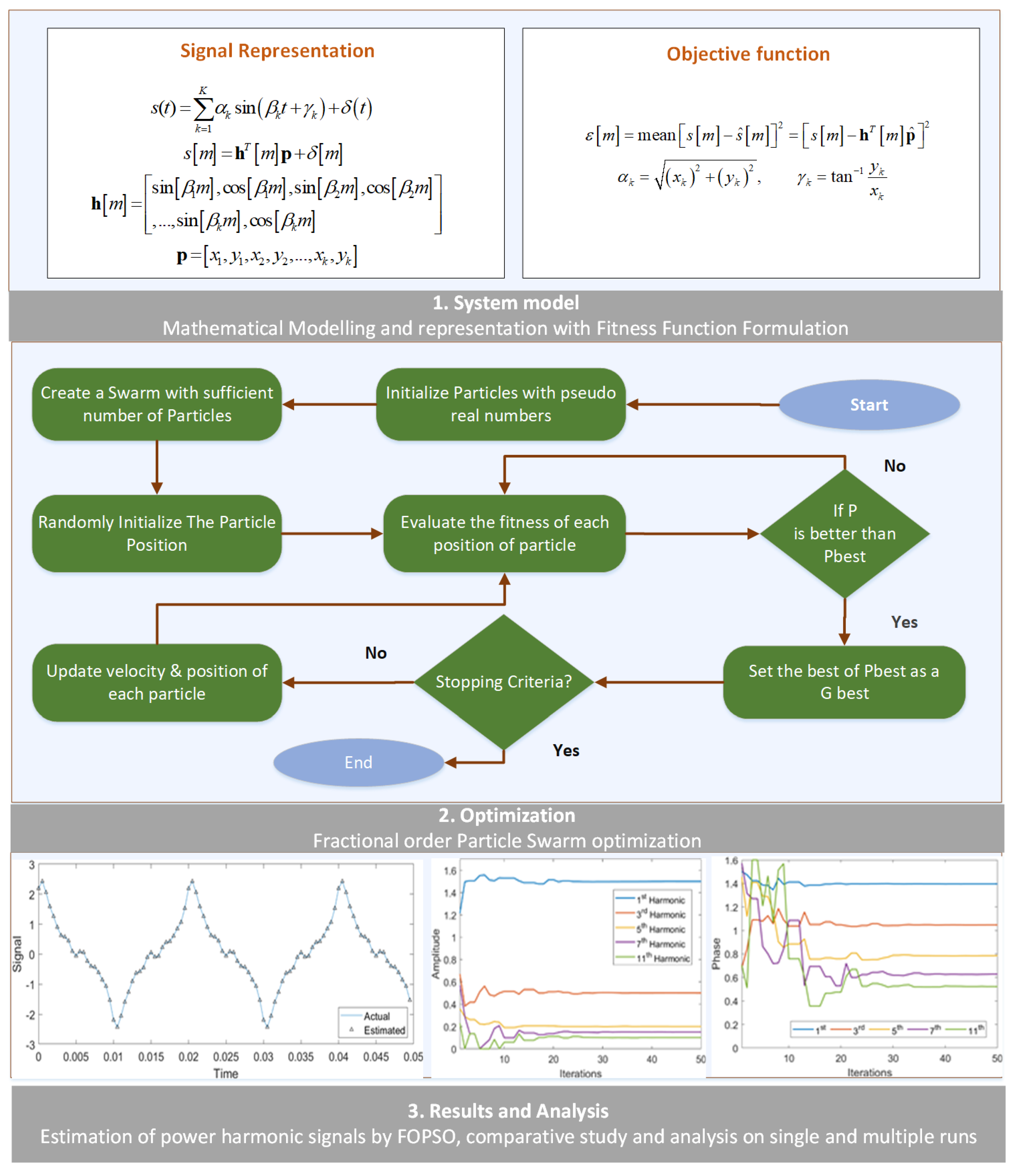
2. Harmonics Identification Model

Mathematically, the electrical harmonic signal, in terms of the amplitude, frequency and phase parameters signal, can be written as [13,14]:

$$s(t)={\displaystyle \sum _{k=1}^K{\alpha }_k\sin \left({\beta }_{k}t+{\gamma }_k\right)}+\delta \left(t\right),$$

(1)

where K is order of the harmonic, ${\beta }_k$ denotes the angular frequency of the kth harmonic, defined as ${\beta }_k=k2\pi f_0$ with $f_0$ as fundamental frequency, ${\alpha }_k$ and ${\gamma }_k$ are the amplitude and phase corresponding to the kth harmonic, while $\delta$ is used to represent additive white Gaussian noise. Writing Equation (1) in discrete form by sampling the signal s(t) with period l, then $t_m=ml$

$$s\left[t_m\right]={\displaystyle \sum _{k=1}^K{\alpha }_k\sin \left[{\beta }_k{t}_m+{\gamma }_k\right]}+\delta \left[t_m\right].$$

(2)

For simplicity, assume $s\left(t_m\right)=s\left(m\right)$ and rewriting (2) as

$$s\left[m\right]={\displaystyle \sum _{k=1}^K{\alpha }_k\sin \left[{\beta }_{k}m+{\gamma }_k\right]}+\delta \left[t_m\right].$$

(3)

Applying the trigonometric identity to (2) and expressing this in terms of the combination of cosine and sine forms

$$s\left[m\right]={\displaystyle \sum _{k=1}^K\left[{\alpha }_k\sin \left[{\beta }_{k}m\right]\cos {\gamma }_k+{\alpha }_k\cos \left[{\beta }_{k}m\right]\sin {\gamma }_k\right]}+\delta \left[m\right],$$

(4)

assuming $x_k={\alpha }_k\cos {\gamma }_k$ and $y_k={\alpha }_k\sin {\gamma }_k$. Then, rewriting (4) in simplified form as

$$s\left[m\right]={\displaystyle \sum _{k=1}^K\left[x_k\sin \left[{\beta }_{k}m\right]+y_k\cos \left[{\beta }_{k}m\right]\right]}+\delta \left[m\right].$$

(5)

Equation (5) in terms of the identification model is expressed as

$$s\left[m\right]=h^T\left[m\right]p+\delta \left[m\right].$$

(6)

where

$$h\left[m\right]=\left[\sin \left[{\beta }_{1}m\right],\cos \left[{\beta }_{1}m\right],\sin \left[{\beta }_{2}m\right],\cos \left[{\beta }_{2}m\right],\dots ,\sin \left[{\beta }_{k}m\right],\cos \left[{\beta }_{k}m\right]\right].$$

(7)

and

$$p=\left[x_1,y_1,x_2,y_2,\dots ,x_k,y_k\right].$$

(8)

The objective is to estimate the parameters of the harmonics by minimizing the difference between the actual harmonic signal $s\left[m\right]$ and the estimated harmonic signal $\widehat{s}\left[m\right]$ through the proposed fractional order swarming optimization approach. Thus, defining the cost/objective function as

$$\epsilon \left[m\right]=\mathrm{mean}{\left[s\left[m\right]-\widehat{s}\left[m\right]\right]}^2={\left[s\left[m\right]-h^T\left[m\right]\widehat{p}\right]}^2,$$

(9)

since the identification model presented in Equation (6) and the cost function given in Equation (9) considers the intermediate variable as parameters to be identified, it is necessary to use the expressions relating the intermediate variables of (8) with the actual parameters of the harmonics signal (3). The required relations are given as

$${\alpha }_k=\sqrt{{\left(x_k\right)}^2+{\left(y_k\right)}^2},{\gamma }_k={\tan }^{-1}\frac{y_k}{x_k},$$

(10)

3. Methodology

The methodology for the fractional swarming optimization approach for the harmonic identification model is described concisely in terms of mathematical development, process flow illustrations and pseudocodes. An overview of the methodology in terms of fundamental block structures is presented in Figure 1.

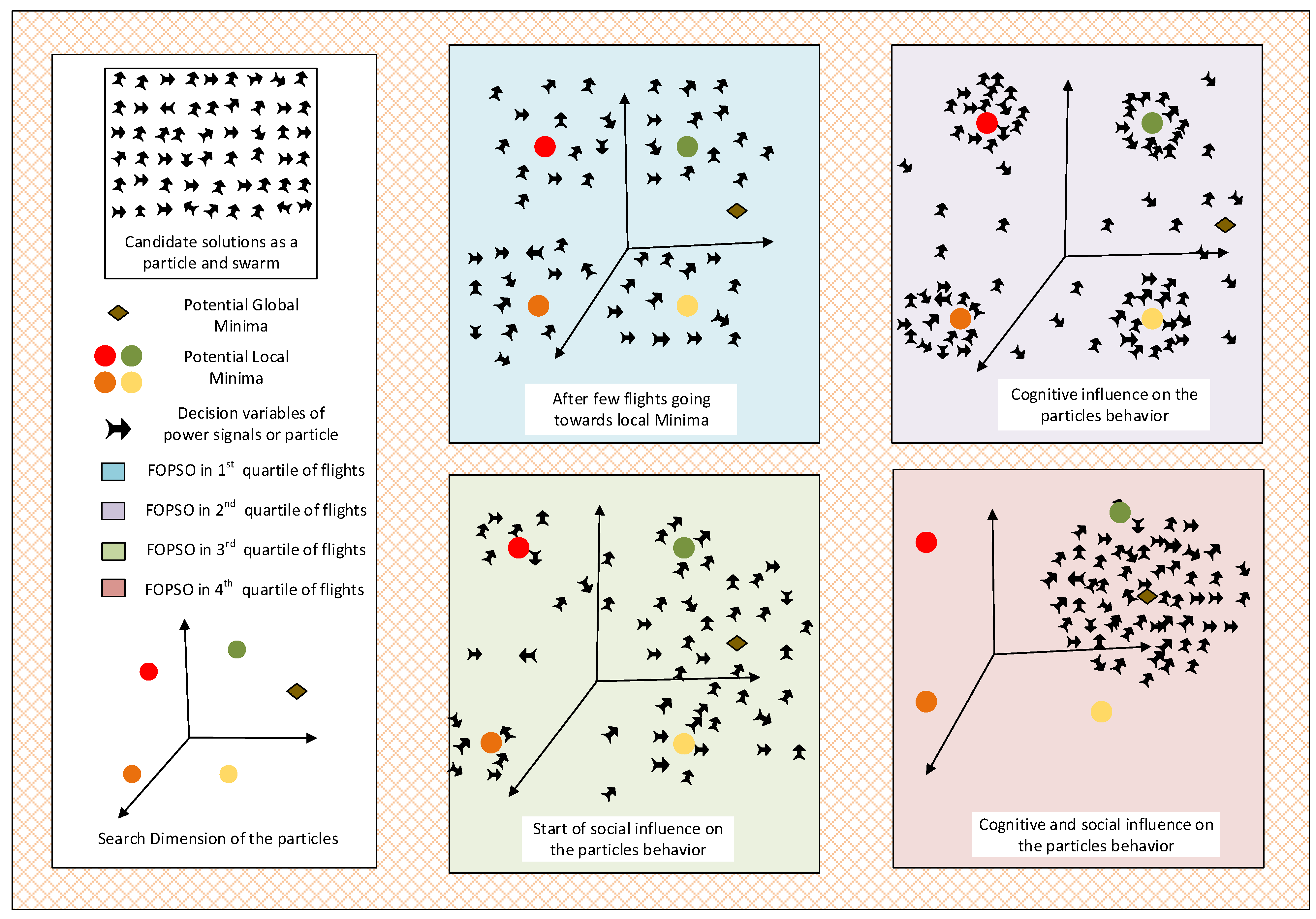
Optimization Procedure: Fractional Swarming Computing Paradigm

A heuristic computing strategy represented with fractional order particle swarm optimization (FOPSO) was first presented by Machado with a team of researchers by introducing the fractional order velocity in the standard PSO [40]. Since its introduction, the FOPSO has been extensively used by the research community for various optimization tasks with performance better than that in integer counterparts [41,42,43,44]

The FOPSO is designed by introducing the definition of the fractional order velocity in standard PSO and the definition of the fractional derivative is given in a variety of ways, such as Grünwald–Letnikov (GL), Riemann–Liouville, Weyl, Marchaud, Caputo, Hadamard, Davidson–Essex and many others [48,49]. The similarity of all these definitions is well-established for some of their own functions and they have their own significance for different applications; however, the mathematical expressions for FOPSO with a fractional velocity are derived by implementing the GL definition for the fractional order $\lambda$, i.e., $D^{\lambda }$ of signal s(t) using the concept of a Euler gamma function Γ, as [50]:

$$D^{\lambda }[s(t)]=\underset{h\to 0}{\lim }\left[\frac{1}{h^{\lambda }}{\displaystyle \sum _{k=0}^{\infty }\frac{{\left(-1\right)}^k\Gamma \left(\lambda +1\right)s\left(t-kh\right)}{\Gamma \left(k+1\right)\Gamma \left(\lambda -k+1\right)}}\right],$$

(11)

where h is the incremental step size and the Euler gamma function is defined as, $\Gamma \left(z\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{z-1}}$.

The finite time representation of Equation (11) can be given as follows:

$$D^{\lambda }[s(t)]=\frac{1}{T^{\lambda }}{\displaystyle \sum _{k=0}^{kr}\frac{{\left(-1\right)}^k\Gamma \left(\lambda +1\right)s\left(t-kT\right)}{\Gamma \left(k+1\right)\Gamma \left(\lambda -k+1\right)}},$$

(12)

where Kr represents the order of truncation and T denotes the sampling period. Before proceeding regarding how Equations (11) and (12) are used to derive FOPSO, first, we introduce the mathematical expressions for the velocity v and position x of traditional PSO in the case of the nth particle as follows:

$$v^n(j+1)=\omega v^n(j)+{\rho }_1{r}_1\left(L{b}^n(j)-x^n(j)\right)+{\rho }_2{r}_2\left(G{b}^n(j)-x^n(j)\right),$$

(13)

$$x^n(j+1)=x^n(j)+v^n(j+1),$$

(14)

where j is used to represent the flight index, ω stands for the inertia weight, Lb is a local best particle, Gb is the representation for the global best particle, ρ₁ and ρ₂ are cognitive and social acceleration parameters, respectively, while r₁ and r₂ are the pseudo-random values taken between 0 and 1.

By assuming ω = 1 in (13), while T = 1, $s(t)=v^n(t)$ and replacing j by j + 1 in (12), one may obtain the mathematical relation of the fractional velocity in FOPSO as follows [50]:

$$\begin{array}{l}{v}^n(j+1)=-{\displaystyle \sum _{k=1}^{kr}\frac{{\left(-1\right)}^k\Gamma \left(\lambda +1\right)v^n(j+1-k)}{\Gamma \left(k+1\right)\Gamma \left(\lambda -k+1\right)}}+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\rho }_1{r}_1\left(L{b}^n(j)-x^n(j)\right)+{\rho }_2{r}_2\left(G{b}^n(j)-x^n(j)\right)\end{array}$$

(15)

The fractional velocity representation of FOPSO for n^th particle with k^th term, i.e., kr = 1, 2, …, k, as:

$$\begin{array}{ll}{v}^n(j+1)=& \lambda v^n(j)+\frac{1}{2}\lambda (1-\lambda )v^n(j-1)+\cdots \\ & +\frac{1}{\Gamma (k+1)}\left(\lambda (1-\lambda )(2-\lambda )\cdots (k-1-\lambda )\right)v^n(j-k+1)\\ & +{\rho }_1{r}_1\left(L{b}^n(j)-x^n(j)\right)+{\rho }_2{r}_2\left(G{b}^n(j)-x^n(j)\right)\end{array}$$

(16)

The velocity update Equation (16) and position update Equation (14) formulate the FOPSO. Further details regarding the FOPSO can be found in [50].

For implementation of the FOPSO for the harmonic identification model, the workflow procedure of methodology is shown in Figure 1, the genetic flow diagram of the FOPSO in the form of procedural steps is given in Figure 2, while the performance of cognitive and social learning behavior of FOPSO is illustrated in Figure 3. The pseudocode of the FOPSO for the harmonic identification model is provided in Algorithm 1. The velocity update equation of FOPSO for Kr = 4 is used as given below:

$$\begin{array}{ll}{v}^n(j+1)=& \lambda v^n(j)+\frac{1}{2}\lambda (1-\lambda )v^n(j-1)+\cdots \\ & +\frac{1}{24}\left(\lambda (1-\lambda )(2-\lambda )\cdots (3-\lambda )\right)v^n(j-3)\\ & +{\rho }_1{r}_1\left(L{b}^n(j)-x^n(j)\right)+{\rho }_2{r}_2\left(G{b}^n(j)-x^n(j)\right),\end{array}$$

(17)

and the position update is given as

$$x^n(j+1)=x^n(j)+v^n(j+1)$$

(18)

The parameter settings for implementation of the FOPSO were adopted through experience and much experimentation. All the parameters were set after conducting exhaustive experiments since small variations in these settings can result in premature convergence and/or some time divergence. The parameter settings are given as follows: eight decision variables for the optimization problem were set, i.e., particle size = 8, swarm size = 250 particles, flights or iterations = 100, cognitive and global acceleration factors = 2, inertia weight = 0.97, $\lambda$, maximum/minimum velocities = [0.4, −0.4], and fractional order $\lambda$ = [0.1, 0.2, …, 1]. The computer simulations for FOPSO were performed in the MATLAB software package in a Windows 10 environment.

Algorithm 1. Pseudocode for FOPSO to solve the harmonics identification model

Inputs:  Create particle p with elements equivalent to number of unknown parameters in the signal s(t) as $$\mathit{p}=\left[\begin{array}{cc}\mathit{\alpha }& \mathit{\gamma }\end{array}\right]=\left[\begin{array}{cc}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{n_a}\right)& \left({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_{n_{\gamma }}\right)\end{array}\right],$$ and set of P formulate a swarm. Inputs:  Swarm position $\mathit{X}=\left[\begin{array}{c}{\mathit{x}}_1\\ {\mathit{x}}_2\\ ⋮\\ {\mathit{x}}_m\end{array}\right]=\left[\begin{array}{cc}\left({\alpha }_{1,1},{\alpha }_{2,1},\dots ,{\alpha }_{n_a,1}\right)& \left({\gamma }_{1,1},{\gamma }_{2,1},\dots ,{\gamma }_{n,1}\right)\\ \left({\alpha }_{1,1},{\alpha }_{2,1},\dots ,{\alpha }_{n_a,1}\right)& \left({\gamma }_{1,1},{\gamma }_{2,1},\dots ,{\gamma }_{n,1}\right)\\ ⋮& ⋮\\ \left({\alpha }_{1,1},{\alpha }_{2,1},\dots ,{\alpha }_{n_a,1}\right)& \left({\gamma }_{1,1},{\gamma }_{2,1},\dots ,{\gamma }_{n,1}\right)\end{array}\right]$, Inputs:  for m number of p = x in X. The associated velocity V with position is created similarly. Output:  The particle x of FOPSO with best fitness as defined in (9) Start FOPSO   Step 1:  Initialization: Bound pseudo-real numbers are randomly generated to form an initial swarm X with m number of particles x. Accordingly, associate the initialize velocities v to each particle. Set the values of decision variables, i.e., particle size, swarm size, flights or iterations, cognitive and global acceleration factors, inertia weight, maximum and minimum velocities, and fractional order Step 2:  Fitness evaluation: Determine the fitness of each particle x of X using Equation (9). Step 3:  Termination: Stop the execution of FOPSO for fulfilment of any of the following: (a) Total number of flights/iterations are executed (b) Tolerance limits are attained, i.e., via calculation of the difference between present and previous local/global best particles If termination conditions are fulfilled then proceed from step 5, otherwise continue Step 4:  Updating mechanism: The velocity and position of FOPSO algorithms, as defined in Equaitons (14) and (16), respectively, are updated on each flight taking into consideration the local/global best particle x of the swarm X. Go to Step 2 with updated swarm X. Step 5:  Analysis of fractional order: Repeat steps 1 to 4 by varying the fractional order α of the velocity in the FOPSO algorithms. Step 6:  Storage: Store the values of the parameter for global best particle x, align the fitness, execution time for the current run of FOPSO with different fractional orders. Step 7:  Replication: Conduct repetition of steps 1 to 6 for the harmonic identification model with small as well as large signal-to-noise ratios. Step 8:  Statistics: Create a resaonable dataset by repetition of the FOPSO algorithm from step 1 to 7 for multiple trials to perform a reliable and exhaustive statistical analysis. End FOPSO

4. Results and Discussion

In this section, numerical experimentation for power systems harmonics estimation was conducted through FOPSO and the results are presented in tabular/graphical illustrations, along with necessary discussion. The estimation was not real-time and the measurement data needed to be provided before the estimation. The following example representing the harmonics signal normally present in industrial loads was considered [25,26].

$$s(t)=\left[\begin{array}{l}1.5\sin \left(2\pi f_{1}t+1.396\right)+0.5\sin \left(2\pi f_{3}t+1.047\right)+\\ 0.2\sin \left(2\pi f_{5}t+0.785\right)+0.15\sin \left(2\pi f_{7}t+0.628\right)+\\ 0.1\sin \left(2\pi f_{11}t+0.523\right)\end{array}\right].$$

(19)

The parameters of the harmonics signal to be estimated were

$$\left[\begin{array}{c}\left({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5\right)\\ \left({\gamma }_1,{\gamma }_2,{\gamma }_3,{\gamma }_4,{\gamma }_5\right)\end{array}\right]=\left[\begin{array}{c}1.50,0.50,0.20,0.15,0.10\\ 1.396,1.047,0.785,0.628,0.523\end{array}\right].$$

(20)

The actual harmonic signal s(t) in (19) was generated in Matlab, and was sampled at a 2 kHz sampling frequency. In (19), $f_1$ = 50, $f_3$ = 150, $f_5$ = 250, $f_7$ = 350, $f_{11}$ = 550 and additive white Gaussian noise $\delta$ with 200 dB, 70 dB and 50 dB levels were added to assess the robustness of the proposed FOPSO scheme. The FOPSO was deeply analyzed for the harmonics estimation problem by considering ten fractional orders $\lambda$, ranging from 0.1 to 1, i.e., $\lambda =\left[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0\right]$.

The graphs of iterative learning of the FOPSO for harmonics estimation are presented in Figure 4 for $\lambda =\left[0.2,0.4,0.6,0.8,1.0\right]$. Figure 4a provides the plots for $\delta =200\mathrm{dB}$, while Figure 4b,c gives the graphs for $\delta =70 \mathrm{dB}$ and, $\delta =50 \mathrm{dB}$ respectively. The convergence speed was faster for lower $\lambda$ and decreased gradually with increasing $\lambda$, as seen in Figure 4. In order to assess the accuracy of the parameter estimates, the results of the obtained parameters through FOPSO at different iterations are presented in

Table 1. Fitness results along with the estimated values for $\lambda$ = 0.1.

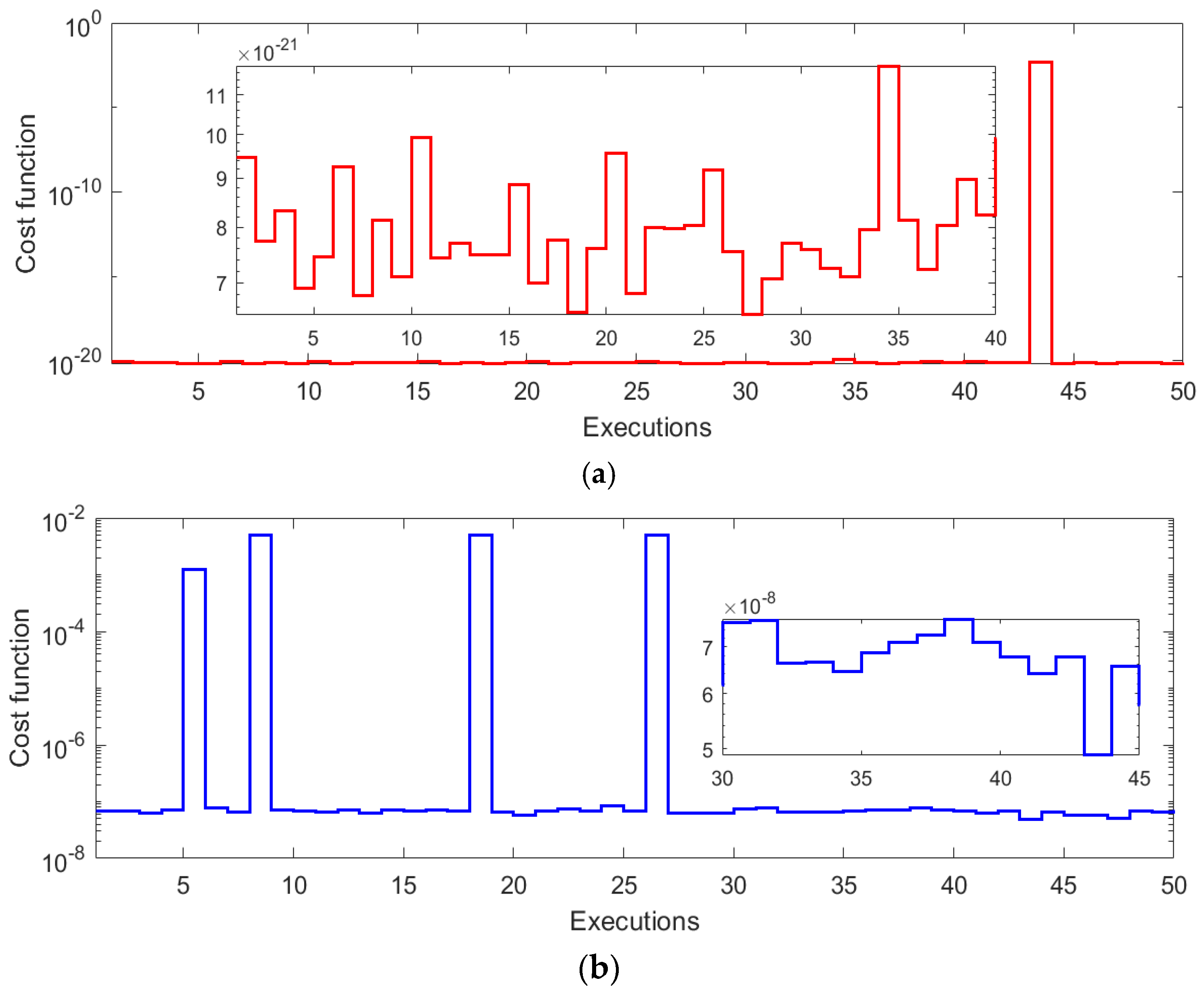
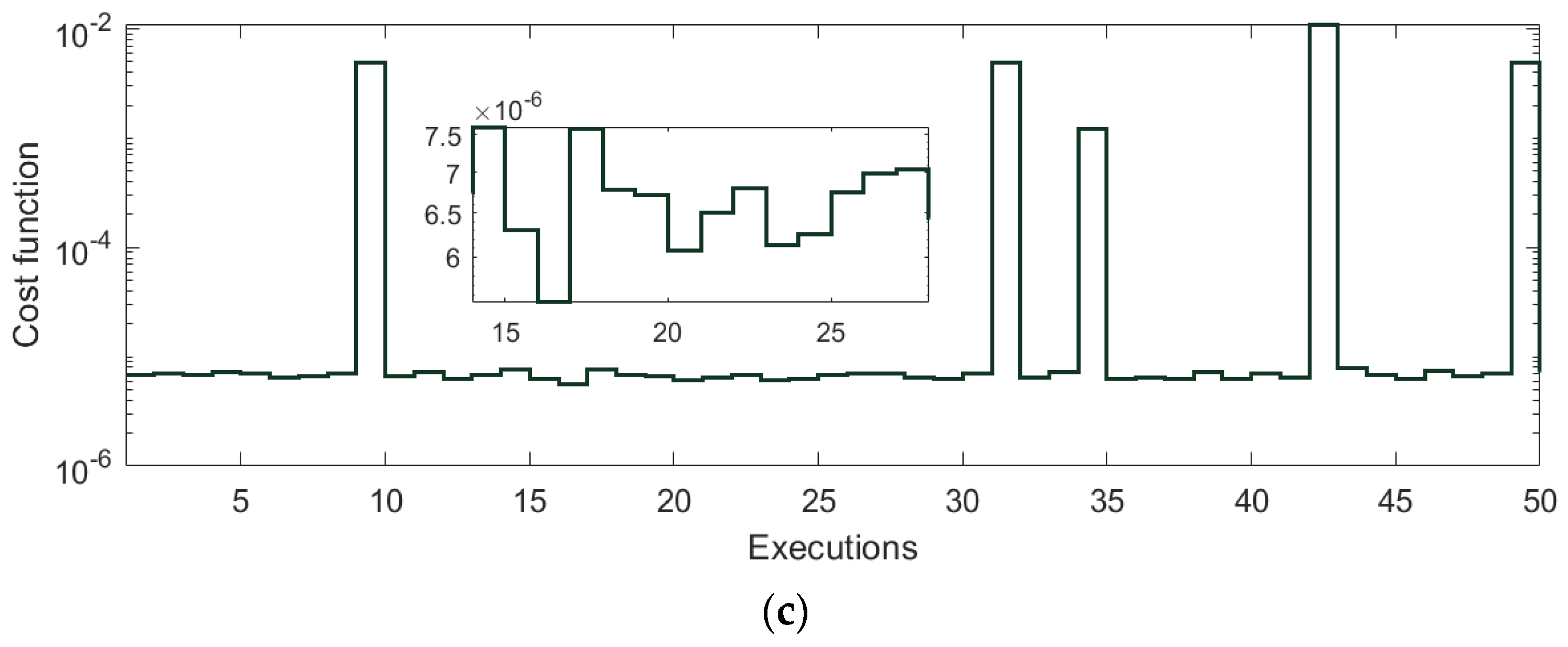
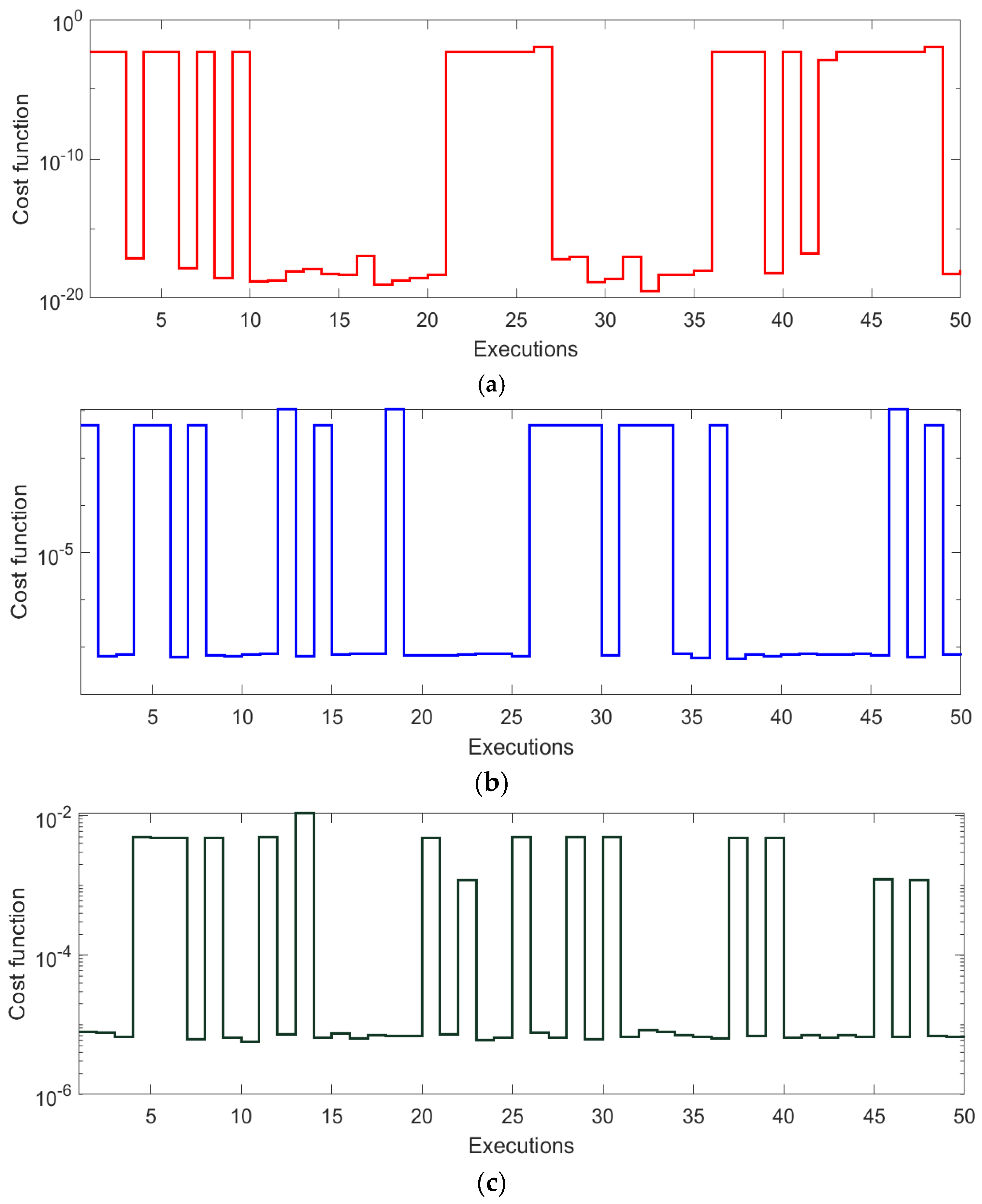
δ	t	α1	α2	α3	α4	α5	γ1	γ2	γ3	γ4	γ5	ε
200	10	1.3877	0.4372	0.3642	0.3479	0.3401	1.5774	1.2000	1.4482	1.2608	0.4896	1.32 × 10−1
	20	1.4907	0.4986	0.2045	0.1439	0.1062	1.3967	1.0491	0.7894	0.6153	0.5417	9.76 × 10−5
	30	1.5000	0.5001	0.1998	0.1499	0.0998	1.3962	1.0466	0.7853	0.6287	0.5228	1.24 × 10−7
	40	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5229	1.12 × 10−10
	50	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	2.51 × 10−13
	60	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	7.46 × 10−17
	70	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	8.40 × 10−20
	80	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	8.05 × 10−21
	90	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	7.90 × 10−21
	100	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	6.43 × 10−21
70	10	1.2489	0.7684	0.1411	0.1246	0.3677	0.9979	0.6191	1.3253	1.2996	1.1829	3.02 × 10−1
	20	1.4961	0.5006	0.1952	0.1432	0.1041	1.3980	1.0495	0.8365	0.6433	0.5207	1.11 × 10−4
	30	1.5000	0.5001	0.1997	0.1500	0.1000	1.3960	1.0470	0.7860	0.6279	0.5258	1.75 × 10−7
	40	1.4999	0.5001	0.1998	0.1501	0.1001	1.3960	1.0471	0.7849	0.6278	0.5238	9.86 × 10−8
	50	1.4999	0.5000	0.1999	0.1500	0.1000	1.3960	1.0470	0.7850	0.6277	0.5236	7.05 × 10−8
	60	1.4999	0.5000	0.1999	0.1500	0.1000	1.3960	1.0470	0.7850	0.6277	0.5236	7.05 × 10−8
	70	1.4999	0.5000	0.1999	0.1500	0.1000	1.3960	1.0471	0.7850	0.6277	0.5236	6.76 × 10−8
	80	1.4999	0.5000	0.1999	0.1500	0.1000	1.3960	1.0471	0.7850	0.6277	0.5236	6.76 × 10−8
	90	1.5000	0.5000	0.1999	0.1500	0.1000	1.3960	1.0470	0.7850	0.6277	0.5235	5.45 × 10−8
	100	1.5000	0.5000	0.1999	0.1500	0.1000	1.3960	1.0470	0.7850	0.6277	0.5235	5.45 × 10−8
50	10	1.4930	0.8742	0.1745	0.2108	0.3877	1.2681	0.9908	1.1505	1.4367	0.9066	1.47 × 10−1
	20	1.4996	0.5051	0.2012	0.1467	0.1043	1.3972	1.0443	0.7541	0.6253	0.5286	5.76 × 10−5
	30	1.5002	0.5000	0.1993	0.1505	0.0999	1.3958	1.0477	0.7860	0.6285	0.5187	6.83 × 10−6
	40	1.5003	0.5000	0.1992	0.1505	0.0999	1.3963	1.0477	0.7860	0.6282	0.5187	6.33 × 10−6
	50	1.5003	0.5000	0.1992	0.1505	0.0999	1.3963	1.0477	0.7860	0.6282	0.5187	6.33 × 10−6
	60	1.5003	0.5000	0.1992	0.1505	0.0999	1.3963	1.0477	0.7860	0.6282	0.5187	6.33 × 10−6
	70	1.5003	0.5000	0.1992	0.1505	0.0999	1.3963	1.0477	0.7860	0.6282	0.5187	6.33 × 10−6
	80	1.5003	0.5000	0.1992	0.1501	0.0999	1.3963	1.0480	0.7859	0.6275	0.5168	4.64 × 10−6
	90	1.5003	0.5000	0.1992	0.1501	0.0999	1.3963	1.0480	0.7859	0.6275	0.5168	4.64 × 10−6
	100	1.5003	0.5000	0.1992	0.1501	0.0999	1.3963	1.0480	0.7859	0.6275	0.5168	4.64 × 10−6
		1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	0

,

Table 2. Fitness results along with the estimated values for $\lambda$ = 0.5.

δ	t	α1	α2	α3	α4	α5	γ1	γ2	γ3	γ4	γ5	ε
200	10	1.7149	0.8193	0.2604	0.3166	0.0804	1.1801	0.9806	0.9897	1.1337	0.7780	1.58 × 10−1
	20	1.4966	0.4795	0.1939	0.1439	0.0000	1.3913	0.9986	0.7302	0.6952	0.5229	5.67 × 10−3
	30	1.5018	0.4988	0.2040	0.1509	0.1030	1.3982	1.0404	0.7921	0.6052	0.5065	3.39 × 10−5
	40	1.5001	0.5003	0.2004	0.1502	0.1003	1.3961	1.0477	0.7860	0.6303	0.5165	5.68 × 10−7
	50	1.5000	0.4999	0.2000	0.1500	0.0999	1.3960	1.0471	0.7845	0.6277	0.5226	1.43 × 10−8
	60	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	1.16 × 10−11
	70	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	2.84 × 10−14
	80	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	1.28 × 10−17
	90	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	2.32 × 10−20
	100	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	8.05 × 10−21
70	10	1.4459	0.5354	0.2790	0.5387	0.2333	1.0436	1.2585	0.7510	1.3152	1.1649	2.52 × 10−1
	20	1.4894	0.5209	0.2076	0.1430	0.0312	1.4307	1.0613	0.6887	0.7014	1.3438	5.31 × 10−3
	30	1.4894	0.5037	0.1941	0.1530	0.1050	1.3910	1.0508	0.8394	0.6228	0.5125	1.84 × 10−4
	40	1.4997	0.5004	0.1998	0.1508	0.1009	1.3955	1.0476	0.7831	0.6226	0.5192	1.69 × 10−6
	50	1.4999	0.5001	0.2000	0.1500	0.1000	1.3961	1.0472	0.7847	0.6286	0.5233	9.23 × 10−8
	60	1.4999	0.5000	0.2000	0.1500	0.1000	1.3960	1.0469	0.7848	0.6277	0.5231	6.43 × 10−8
	70	1.4999	0.5000	0.2000	0.1500	0.1000	1.3960	1.0469	0.7848	0.6277	0.5231	6.18 × 10−8
	80	1.4999	0.5000	0.2000	0.1500	0.1000	1.3960	1.0469	0.7848	0.6277	0.5231	4.89 × 10−8
	90	1.4999	0.5000	0.2000	0.1500	0.1000	1.3960	1.0469	0.7848	0.6277	0.5231	4.89 × 10−8
	100	1.4999	0.5000	0.2000	0.1500	0.1000	1.3960	1.0469	0.7848	0.6277	0.5231	4.89 × 10−8
50	10	1.3047	0.6259	0.3958	0.3571	0.2654	1.4606	0.7557	1.1532	0.8701	1.2466	1.12 × 10−1
	20	1.5127	0.4693	0.2060	0.1364	0.0201	1.3911	1.0300	0.8900	0.6272	1.8194	5.59 × 10−3
	30	1.5050	0.5031	0.2086	0.1531	0.1055	1.4021	1.0264	0.7782	0.6881	0.4985	2.15 × 10−4
	40	1.4993	0.5008	0.1981	0.1501	0.1000	1.3964	1.0508	0.7831	0.6198	0.5258	1.48 × 10−5
	50	1.5006	0.4999	0.2015	0.1499	0.0996	1.3958	1.0480	0.7879	0.6253	0.5195	8.72 × 10−6
	60	1.4996	0.5002	0.2001	0.1501	0.0996	1.3965	1.0473	0.7839	0.6175	0.5195	7.21 × 10−6
	70	1.4996	0.5002	0.2001	0.1501	0.0996	1.3965	1.0473	0.7839	0.6175	0.5195	7.21 × 10−6
	80	1.4996	0.5005	0.1997	0.1501	0.0998	1.3964	1.0470	0.7839	0.6302	0.5203	6.65 × 10−6
	90	1.4996	0.5004	0.2001	0.1501	0.0998	1.3964	1.0471	0.7839	0.6302	0.5213	6.01 × 10−6
	100	1.4996	0.5004	0.2001	0.1501	0.0998	1.3964	1.0471	0.7839	0.6302	0.5213	6.01 × 10−6
		1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	0

and

Table 3. Fitness results along with the estimated values for $\lambda$ = 1.

δ	t	α1	α2	α3	α4	α5	γ1	γ2	γ3	γ4	γ5	ε
200	10	1.4720	0.3721	0.1285	0.4860	0.3704	1.6671	0.3728	0.6035	0.5516	0.1737	2.28 × 10−1
	20	1.5674	0.4953	0.1743	0.1362	0.0507	1.4016	0.9911	0.6795	0.8966	0.9360	5.70 × 10−3
	30	1.4885	0.5049	0.2047	0.1766	0.0768	1.4086	1.0527	0.6944	0.7198	0.7086	1.30 × 10−3
	40	1.4919	0.5047	0.2056	0.1569	0.0956	1.3961	1.0382	0.7966	0.6743	0.6329	1.89 × 10−4
	50	1.4993	0.5008	0.1996	0.1498	0.1008	1.3967	1.0397	0.7948	0.6177	0.5172	1.15 × 10−5
	60	1.5001	0.5000	0.2002	0.1498	0.0996	1.3956	1.0473	0.7842	0.6292	0.5216	3.39 × 10−7
	70	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0471	0.7850	0.6279	0.5225	3.06 × 10−9
	80	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	1.17 × 10−11
	90	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	1.14 × 10−14
	100	1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	2.99 × 10−17
70	10	1.2932	0.4226	0.2798	0.2903	0.1402	1.5028	0.6010	0.7288	0.6064	1.0279	7.18 × 10−2
	20	1.5047	0.4803	0.2312	0.2018	0.0000	1.3832	1.0399	0.7084	0.8538	0.8948	8.14 × 10−3
	30	1.5053	0.4840	0.1851	0.1331	0.0000	1.4128	1.0874	0.7003	0.5753	0.7488	6.08 × 10−3
	40	1.5007	0.5009	0.1953	0.1508	0.0000	1.4056	1.0537	0.7632	0.6765	0.6764	5.16 × 10−3
	50	1.5017	0.5035	0.1986	0.1537	0.1001	1.3918	1.0516	0.7845	0.6395	0.5623	4.66 × 10−5
	60	1.5000	0.5006	0.2005	0.1505	0.1003	1.3960	1.0454	0.7843	0.6269	0.5236	9.40 × 10−7
	70	1.5001	0.4999	0.1999	0.1501	0.0999	1.3961	1.0471	0.7846	0.6281	0.5215	1.25 × 10−7
	80	1.5000	0.5000	0.1999	0.1501	0.0999	1.3960	1.0470	0.7847	0.6277	0.5235	5.63 × 10−8
	90	1.5000	0.5000	0.1999	0.1501	0.0999	1.3960	1.0470	0.7847	0.6277	0.5235	5.63 × 10−8
	100	1.5000	0.5000	0.1999	0.1501	0.0999	1.3960	1.0470	0.7847	0.6277	0.5235	5.63 × 10−8
50	10	1.3944	0.6793	0.3021	0.2184	0.4664	1.4693	0.4017	0.3648	0.8624	0.9475	1.81 × 10−1
	20	1.5278	0.3971	0.2207	0.1943	0.0615	1.3839	0.9626	0.8229	0.6980	1.1946	1.01 × 10−2
	30	1.5164	0.4768	0.1746	0.1624	0.0547	1.3931	1.0690	0.9385	0.5258	0.5986	2.48 × 10−3
	40	1.5042	0.4994	0.1987	0.1366	0.0978	1.3983	1.0246	0.8289	0.6534	0.6263	2.86 × 10−4
	50	1.5027	0.4948	0.1966	0.1521	0.0993	1.3954	1.0362	0.7925	0.6314	0.5302	5.65 × 10−5
	60	1.5008	0.5022	0.1980	0.1493	0.0991	1.3962	1.0479	0.7838	0.6311	0.5326	1.10 × 10−5
	70	1.5004	0.4992	0.1989	0.1482	0.0991	1.3963	1.0478	0.7831	0.6265	0.5328	8.87 × 10−6
	80	1.4997	0.4998	0.2001	0.1501	0.0993	1.3965	1.0480	0.7838	0.6325	0.5262	5.62 × 10−6
	90	1.4997	0.4998	0.2001	0.1501	0.0993	1.3965	1.0480	0.7838	0.6325	0.5262	5.62 × 10−6
	100	1.4997	0.4998	0.2001	0.1501	0.0993	1.3965	1.0480	0.7838	0.6325	0.5262	5.62 × 10−6
		1.5000	0.5000	0.2000	0.1500	0.1000	1.3960	1.0470	0.7850	0.6280	0.5230	0

for $\lambda$ = 0.1, 0.5 and 1.0, respectively. The final fitness values for the case of $\lambda$ = 0.1 were 8.99 × 10⁻²¹, 5.46 × 10⁻⁸ and 5.80 × 10⁻⁶ for $\delta$ = 200 dB, 70 dB and 50 dB, respectively. While the respective values for the case of $\lambda$ = 0.5 and $\lambda$ = 1.0 were 8.05 × 10⁻²¹, 4.89 × 10⁻⁸ and 6.01 × 10⁻⁶, and 2.99 × 10⁻¹⁷, 5.63 × 10⁻⁸ and 5.62 × 10⁻⁶, respectively. The parameter estimates results for the remaining fractional orders, $\lambda$ = 0.2, 0.3, 0.4, 0.6, 0.7, 0.8 and 0.9 are provided in Supplementary Tables S1–S7 in the Supplementary Material. The results indicated that the FOPSO was accurate and convergent in estimating the parameters of the power system harmonics for all $\lambda$ and $\delta$, with decrease in the precision of the estimates as the noise $\delta$ increased.

The learning plots of the amplitude and phase parameters estimates, along with the constructed harmonic signal from the estimated parameters, are presented in Figure 5, Figure 6, Figure 7 and Figure 8 for $\lambda$ = 0.1, 0.4, 0.7 and 1.0, respectively, for the case of $\delta$ = 70 dB, while the respective plots for $\delta$ = 200 dB and 50 dB are provided in Supplementary Figures S1–S8, respectively, in the Supplementary Material. The results indicated that the FOPSO correctly estimated the amplitude and phase parameters of the harmonic signal and hence accurately reconstructed the actual signal through the estimated parameters.

Furthermore, the reliability of the FOPSO was investigated through 50 autonomous executions; the results are presented in Figure 9, Figure 10 and Figure 11 for $\lambda$ = 0.1, 0.5 and 1.0, respectively. Figure 9a, Figure 10a and Figure 11a present the plots for $\delta$ = 200 dB, while Figure 9b, Figure 10b and Figure 11b present the plots for $\delta$ = 70 dB. Figure 9c, Figure 10c and Figure 11c present the plots for $\delta$ = 50 dB. The results indicated that the proposed FOPSO was more reliable for $\lambda$ = 0.1, with almost the same trend in independent trials of the scheme, while for the case of standard PSO (FOPSO for $\lambda$ = 1.0), variation in the results was observed, i.e., sometimes giving good results and sometimes not, as shown in Figure 11.

Analyses in terms of statistical indices of the minimum (Mini) value of cost function, the mean and standard deviation (STDD) were conducted and the results are reported in

Table 4. Values of statistical indices through Monte Carlo simulations.

	δ= 200 dB			δ= 70 dB			δ= 50 dB
$\mathsf{\lambda }$	Mini	Mean	STDD	Mini	Mean	STDD	Mini	Mean	STDD
0.1	6.03 × 10−21	7.24 × 10−21	6.23 × 10−22	5.45 × 10−8	6.75 × 10−8	5.79 × 10−9	4.64 × 10−6	6.69 × 10−6	6.36 × 10−7
0.2	5.39 × 10−21	1.00 × 10−4	7.07 × 10−4	5.46 × 10−8	4.24 × 10−4	1.85 × 10−3	5.80 × 10−6	1.04 × 10−4	6.86 × 10−4
0.3	6.23 × 10−21	3.00 × 10−4	1.20 × 10−3	5.38 × 10−8	2.99 × 10−4	1.20 × 10−3	5.31 × 10−6	6.62 × 10−6	5.76 × 10−7
0.4	5.66 × 10−21	6.00 × 10−4	1.64 × 10−3	5.17 × 10−8	5.98 × 10−4	1.64 × 10−3	5.51 × 10−6	8.11 × 10−4	2.17 × 10−3
0.5	6.48 × 10−21	1.00 × 10−4	7.07 × 10−4	4.89 × 10−8	3.24 × 10−4	1.20 × 10−3	5.52 × 10−6	5.43 × 10−4	1.92 × 10−3
0.6	6.47 × 10−21	9.00 × 10−4	1.94 × 10−3	5.96 × 10−8	1.12 × 10−3	2.42 × 10−3	5.71 × 10−6	1.23 × 10−3	2.71 × 10−3
0.7	7.08 × 10−21	1.02 × 10−3	2.36 × 10−3	5.84 × 10−8	7.23 × 10−4	1.75 × 10−3	5.82 × 10−6	1.05 × 10−3	2.30 × 10−3
0.8	8.51 × 10−21	1.42 × 10−3	2.58 × 10−3	5.89 × 10−8	1.72 × 10−3	3.14 × 10−3	5.18 × 10−6	1.52 × 10−3	2.55 × 10−3
0.9	1.52 × 10−20	2.13 × 10−3	3.19 × 10−3	5.69 × 10−8	2.37 × 10−3	3.65 × 10−3	5.45 × 10−6	1.93 × 10−3	2.91 × 10−3
1.0	9.89 × 10−20	2.47 × 10−3	3.03 × 10−3	5.63 × 10−8	2.07 × 10−3	3.23 × 10−3	5.62 × 10−6	1.37 × 10−3	2.45 × 10−3

. The Mini values indicated that the FOPSO was accurate and convergent for all $\lambda$ and $\delta$ with decrease in the precision of the estimates as the noise $\delta$ increased. The small STDD values in the case of $\lambda$ = 0.1 were 6.23 × 10⁻²², 5.79 × 10⁻⁹ and 6.36 × 10⁻⁷ for $\delta$ = 200 dB, 70 dB and 50 dB, respectively, confirming the more reliable and consistently accurate behavior of the FOPSO for $\lambda$ = 0.1. While the respective STDD values in the case of $\lambda$ = 0.5 and $\lambda$ = 1.0 were 7.07 × 10⁻⁴, 1.20 × 10⁻³ and 1.92 × 10⁻³, and 3.03 × 10⁻³, 3.23 × 10⁻³ and 2.45 × 10⁻³, respectively.

5. Conclusions

The findings/conclusions of the study are presented below.

A fractional order particle swarm optimization, FOPSO, was presented for solving nonlinear problems of harmonics estimation required for monitoring power quality in electrical systems to avoid any adverse effect of harmonic pollution. The FOPSO integrates the inherited legacy of fractional calculus with standard PSO to enhance its optimization capabilities with more controlling parameters. The FOPSO effectively estimated the amplitude and phase parameters of the harmonic signal compared with the standard counterpart for different scenarios of additive white Gaussian noise.

The FOPSO provided faster convergence speeds for a lower value of fractional order, i.e., 0.1 $\lambda$; and the convergence speed decreased gradually with increase in the fractional order, i.e., 0.1 $\lambda$ to 1.0 $\lambda$. The FOPSO was robust against different levels of additive white Gaussian noise with relatively low estimation accuracy for high noise levels. The estimation errors for 200 db, 70 db and 50 db were approximately 10⁻²¹, 10⁻⁸ and 10⁻⁶, respectively. The statistical indices obtained through Monte Carlo simulations confirmed that the FOPSO was accurate and robust for all $\lambda$ values in terms of best fitness, while, in terms of mean fitness values, the FOPSO with 0.1 $\lambda$ was the best among all other fractional order variations.

In future, the proposed scheme can be exploited to solve different control and estimation problems [51,52,53,54]. Moreover, investigations can be carried out in implementing proposed schemes to solve the challenges involved in current power systems, such as, estimating the components that are not integer multiples of the fundamental harmonic, fault detection in power systems and machines, and estimating the exact frequency of the fundamental in real time.