Mathematical Modeling: Cisplatin Binding to Deoxyribonucleic Acid
Abstract
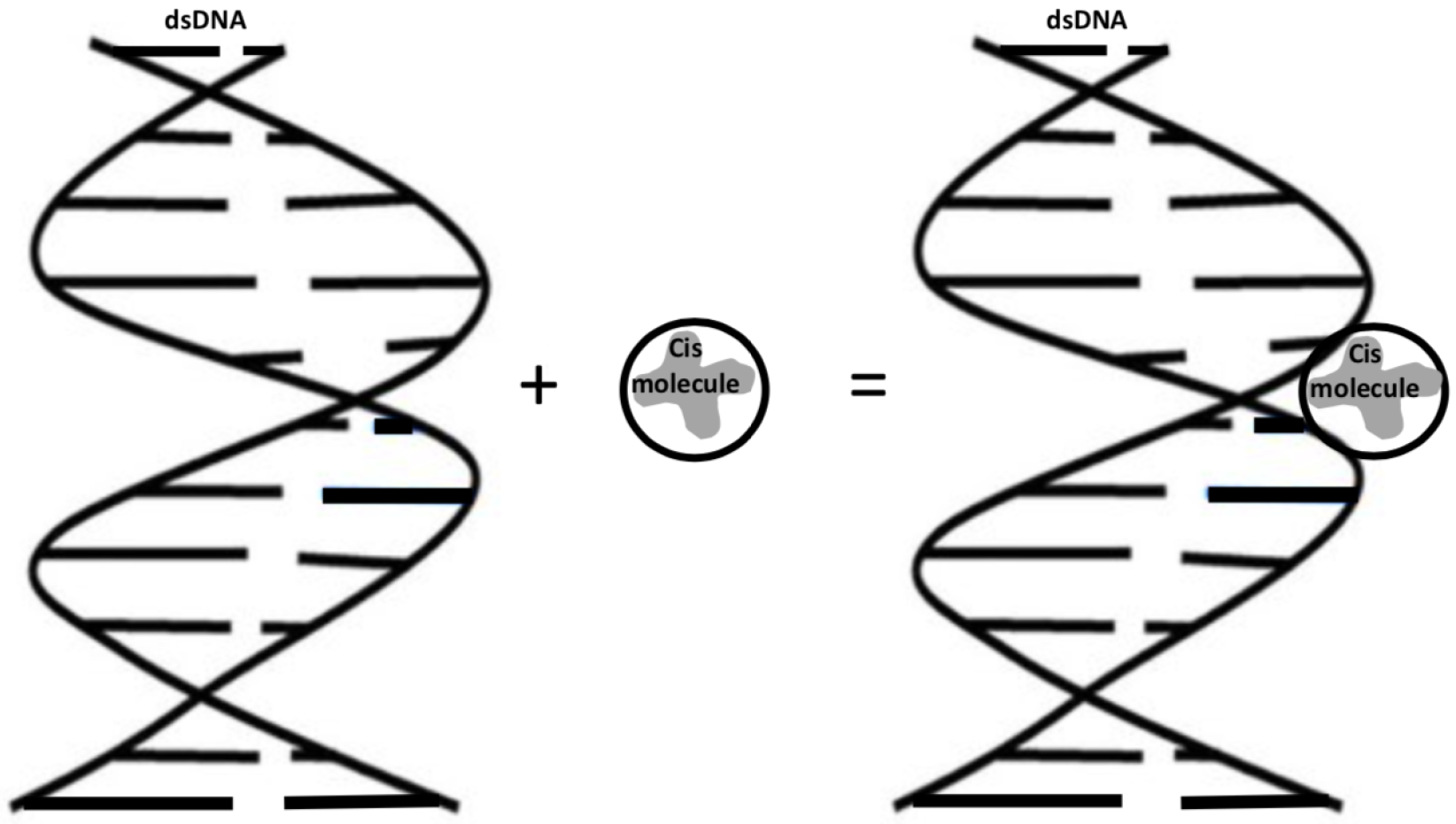
:1. Introduction
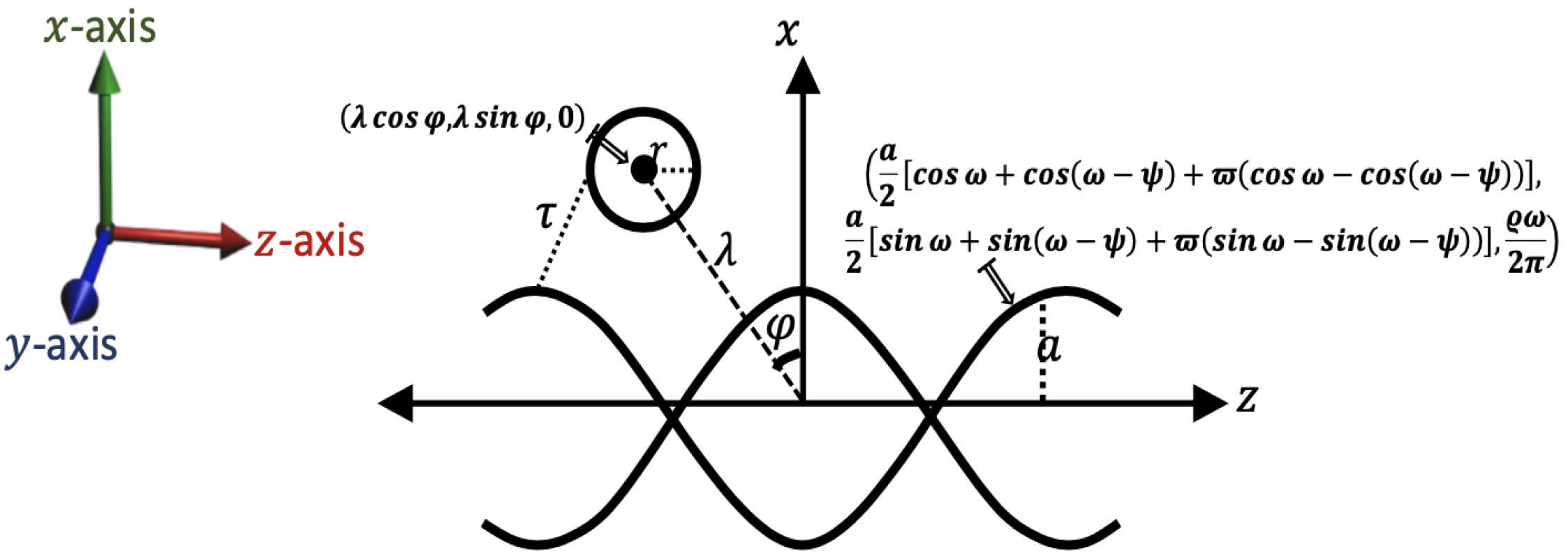
2. Mathematical Modeling
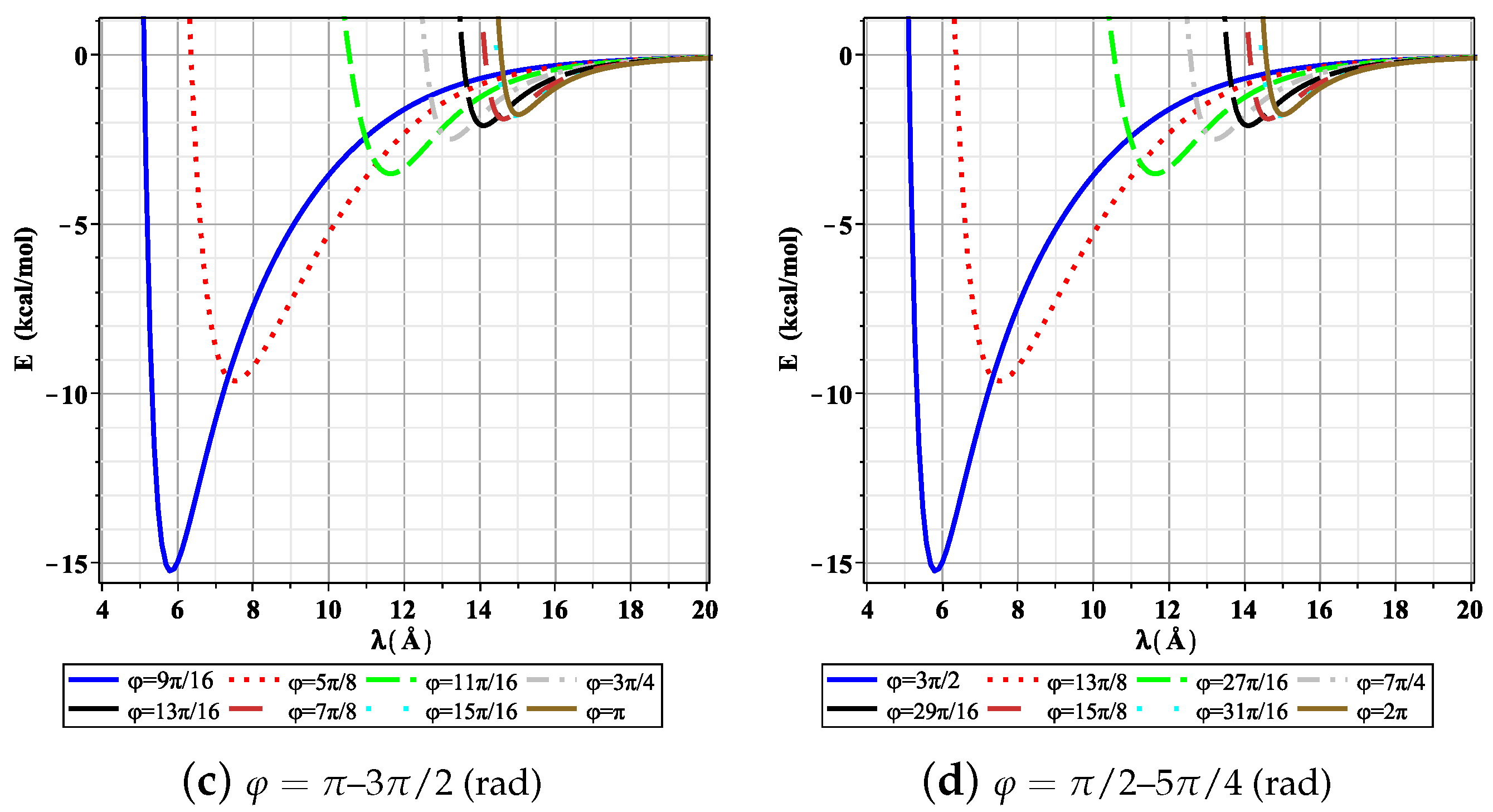
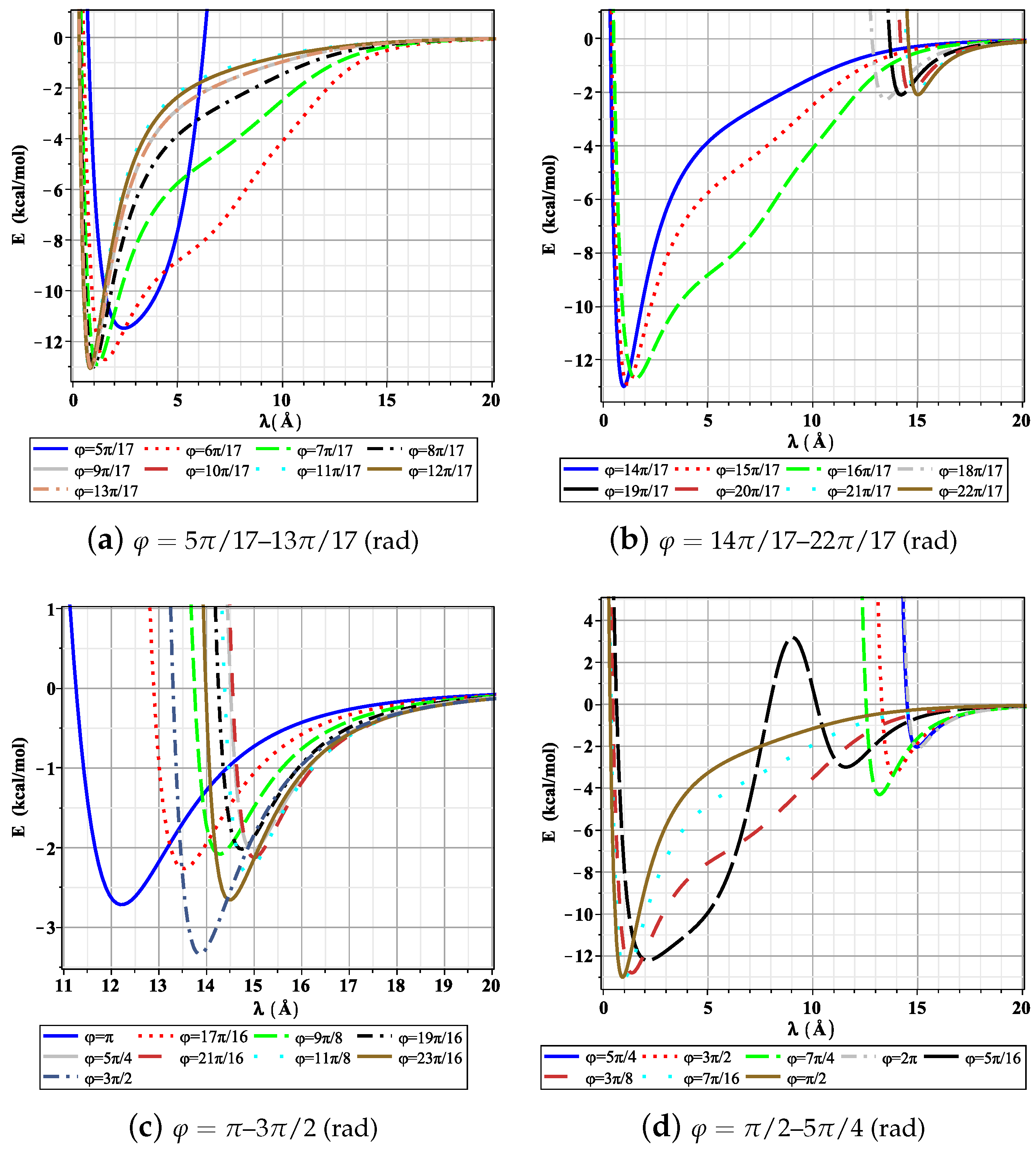
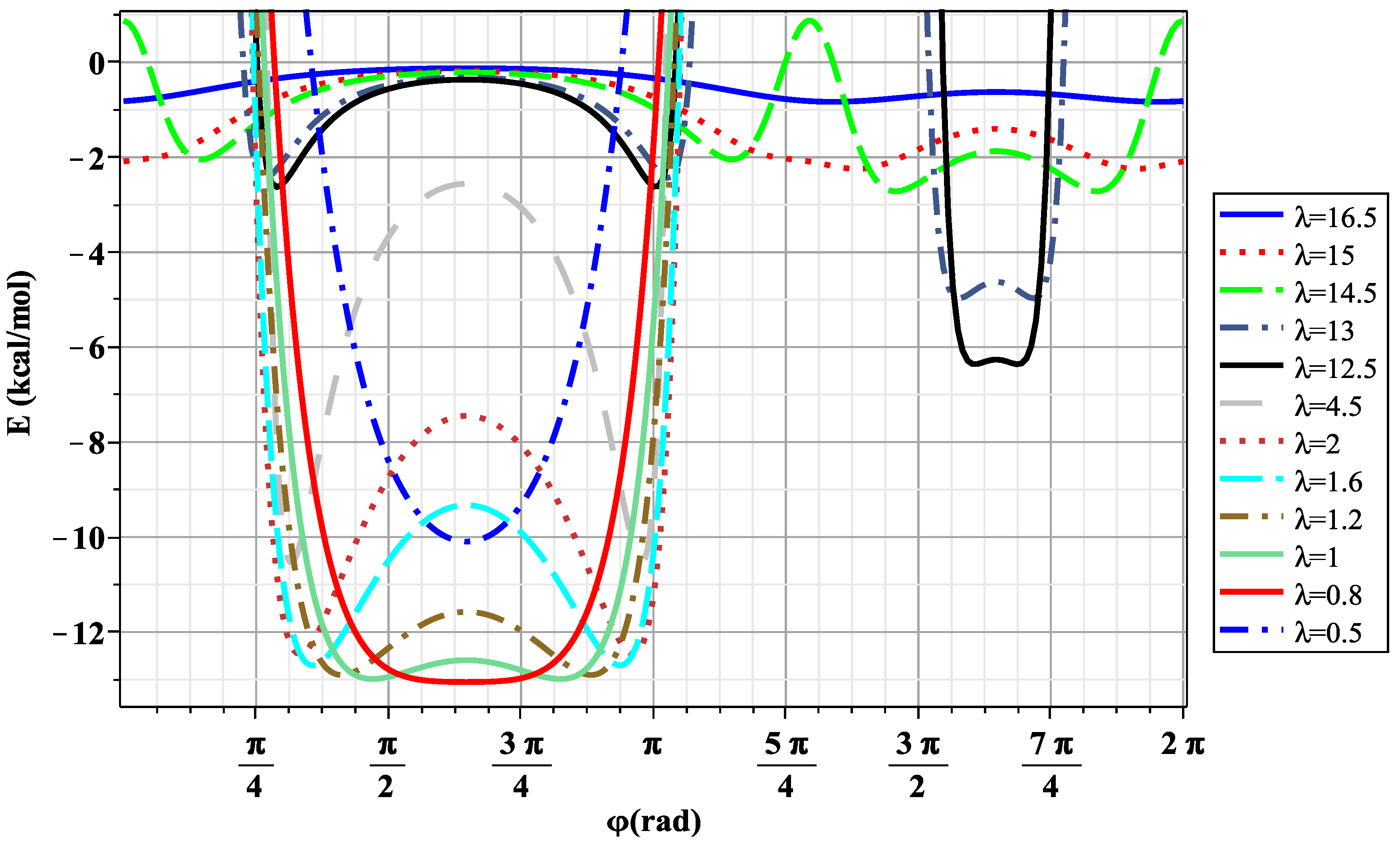
3. Results and Discussion
4. Summary
Funding
Data Availability Statement
Conflicts of Interest
References
- Drexler, K.E. Nanosystems: Molecular Machinery, Manufacturing, and Computation; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1992. [Google Scholar]
- Cui, D. Biomolecules functionalized carbon nanotubes and their applications. In Medicinal Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotubes; Carbon Materials: Chemistry and Physics; Springer: Dordrecht, The Netherlands, 2008; Volume 1, pp. 181–221. [Google Scholar]
- Xu, X.; Li, R.; Ma, M.; Wang, X.; Wang, Y.; Zou, H. Multidrug Resistance Protein P-Glycoprotein Does Not Recognize Nanoparticle C60: Experiment and Modeling. Soft Matt. 2012, 8, 2915–2923. [Google Scholar] [CrossRef]
- Kamiya, K.; Okada, S. Energetics and Electronic Structure of Encapsulated Single-Stranded DNA in Carbon Nanotubes. Phys. Rev. B 2011, 83, 155444. [Google Scholar] [CrossRef] [Green Version]
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science: New York, NY, USA, 2008. [Google Scholar]
- Duderstadt, K.E.; Chuang, K.; Berger, J.M. DNA stretching by bacterial initiators promotes replication origin melting. Nature 2011, 478, 209–213. [Google Scholar] [CrossRef] [PubMed]
- Dasari, S.; Tchounwou, P.B. Cisplatin in cancer therapy: Molecular mechanisms of action. Eur. J. Pharmacol. 2014, 5, 364–378. [Google Scholar] [CrossRef] [Green Version]
- Jamieson, E.R.; Lippard, S.J. Structure, recognition, and processing of cisplatin-DNA adducts. Chem. Rev. 1999, 99, 2467–2498. [Google Scholar] [CrossRef]
- Dutta, S.; Rivetti, C.; Gassman, N.R.; Young, C.G.; Jones, B.T.; Scarpinato, K.; Guthold, M. Analysis of single, cisplatin-induced DNA bends by atomic force microscopy and simulations. J. Mol. Recognit. 2018, 31, e2731. [Google Scholar] [CrossRef]
- Wing, R.M.; Pjura, P.; Drew, H.R.; Dickerson, R.E. The primary mode of binding of cisplatin to a B-DNA dodecamer: C-G-C-G-A-A-T-T-C-G-C-G. EMBO J. 1984, 3, 1201–1206. [Google Scholar] [CrossRef]
- Takahara, P.; Rosenzweig, A.; Frederick, C.; Lippard, S.J. Crystal structure of double-stranded DNA containing the major adduct of the anticancer drug cisplatin. Nature 1995, 377, 649–652. [Google Scholar] [CrossRef]
- Takahara, P.M.; Frederick, C.A.; Lippard, S.J. Crystal Structure of the Anticancer Drug Cisplatin Bound to Duplex DNA. J. Am. Chem. Soc. 1996, 118, 12309–12321. [Google Scholar] [CrossRef]
- van Boom, S.S.G.E.; Yang, D.; Reedijk, J.; van der Marel, G.A.; Wang, A.H.-J. Structural Effect of Intra-strand Cisplatin-crosslink on Palindromic DNA Sequences. J. Biomol. Struct. Dyn. 1996, 13, 989–998. [Google Scholar] [CrossRef] [PubMed]
- Gasior-Glogowska, M.; Malek, K.; Zajac, G.; Baranska, M. A new insight into the interaction of cisplatin with DNA: ROA spectroscopic studies on the therapeutic effect of the drug. Analyst 2016, 141, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Sip, M.; Schwartz, A.; Vovelle, F.; Ptak, M.; Leng, M. Distortions Induced in DNA by cis-Platinum Interstrand Adducts. Biochemistry 1992, 31, 2508–2513. [Google Scholar] [CrossRef] [PubMed]
- Gelasco, A.; Lippard, S.J. NMR Solution Structure of a DNA Dodecamer Duplex Containing a cis-Diammineplatinum(II) d(GpG) Intrastrand Cross-Link, the Major Adduct of the Anticancer Drug Cisplatin. Biochemistry 1998, 37, 9230. [Google Scholar] [CrossRef]
- Bellon, S.F.; Lippard, S.J. Bending studies of DNA site-specifically modified by cisplatin, trans-diamminedichloroplatinum(II) and cis-[Pt(NH3)2(N3-cytosine)Cl]+. Biophys. Chem. 1990, 35, 179–188. [Google Scholar] [CrossRef]
- Bellon, S.F.; Coleman, J.H.; Lippard, S.J. DNA Unwinding Produced by Site-Specific Intrastrand Cross-Links of the Antitumor Drug cis-Diamminedichloroplatinum(II). Biochemistry 1991, 30, 8026–8035. [Google Scholar] [CrossRef]
- Crisafuli, F.A.P.; Cesconetto, E.C.; Ramos, E.B.; Rocha, M.S. DNA—Cisplatin interaction studied with single molecule stretching experiments. Integr. Biol. 2012, 4, 568–574. [Google Scholar] [CrossRef]
- Huang, H.; Zhu, L.M.; Reid, B.R.; Drobny, G.P.; Hopkins, P.B. Solution structure of a cisplatin-induced DNA interstrand cross-link. Science 1995, 270, 1842–1845. [Google Scholar] [CrossRef]
- Baowan, D.; Cox, B.J.; Hilder, T.A.; Hill, J.M.; Thamwattana, N. Modelling and Mechanics of Carbon-Based Nanostructured Materials, 1st ed.; William Andrew: Norwich, NY, USA, 2017. [Google Scholar]
- Jan, R.; Shah, Z.; Deebani, W.; Alzahrani, E. Analysis and dynamical behavior of a novel dengue model via fractional calculus. Int. J. Biomath. 2022, 15, 2250036. [Google Scholar] [CrossRef]
- Alshehri, M.H. Continuum Modelling for Encapsulation of Anticancer Drugs inside Nanotubes. Mathematics 2021, 9, 2469. [Google Scholar] [CrossRef]
- Pico, J.; Tang, T.-Q.; Shah, Z.; Bonyah, E.; Jan, R.; Shutaywi, M. Alreshidi, N. Modeling and Analysis of Breast Cancer with Adverse Reactions of Chemotherapy Treatment through Fractional Derivative. Comput. Math. Methods Med. 2022, 2022, 5636844. [Google Scholar]
- Shah, Z.; Jan, R.; Kumam, P.; Deebani, W.; Shutaywi, M. Fractional Dynamics of HIV with Source Term for the Supply of New CD4+ T-Cells Depending on the Viral Load via Caputo-Fabrizio Derivative. Molecules 2021, 26, 1806. [Google Scholar] [CrossRef]
- Ferrari, M. Cancer nanotechnology: Opportunities and challenges. Nat. Rev. Cancer 2005, 5, 161–171. [Google Scholar] [CrossRef]
- Maitland, G.C.; Rigby, M.; Smith, E.B.; Wakeham, W.A. Intermolecular Forces–Their Origin and Determination; Clarendon Press: Oxford, UK, 1981. [Google Scholar]
- Rappi, A.K.; Casewit, C.J.; Colwell, K.S.; I, W.A.G.I.I.; Skid, W.M. UFF, a full periodic table force field formolecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Cox, B.J.; Thamwattana, N.; Hill, J.M. Mechanics of atoms and fullerenes in single-walled carbon nanotubes. I. Acceptance and suction energies. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 461–477. [Google Scholar] [CrossRef]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions Vol I; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.H. Mathematical Modeling: Cisplatin Binding to Deoxyribonucleic Acid. Mathematics 2023, 11, 235. https://doi.org/10.3390/math11010235
Alshehri MH. Mathematical Modeling: Cisplatin Binding to Deoxyribonucleic Acid. Mathematics. 2023; 11(1):235. https://doi.org/10.3390/math11010235
Chicago/Turabian StyleAlshehri, Mansoor H. 2023. "Mathematical Modeling: Cisplatin Binding to Deoxyribonucleic Acid" Mathematics 11, no. 1: 235. https://doi.org/10.3390/math11010235
APA StyleAlshehri, M. H. (2023). Mathematical Modeling: Cisplatin Binding to Deoxyribonucleic Acid. Mathematics, 11(1), 235. https://doi.org/10.3390/math11010235






