Coverage, Rate, and Last Hop Selection in Multi-Hop Communications in Highway Scenarios
Abstract
:1. Introduction
1.1. Related Studies
1.2. Contributions
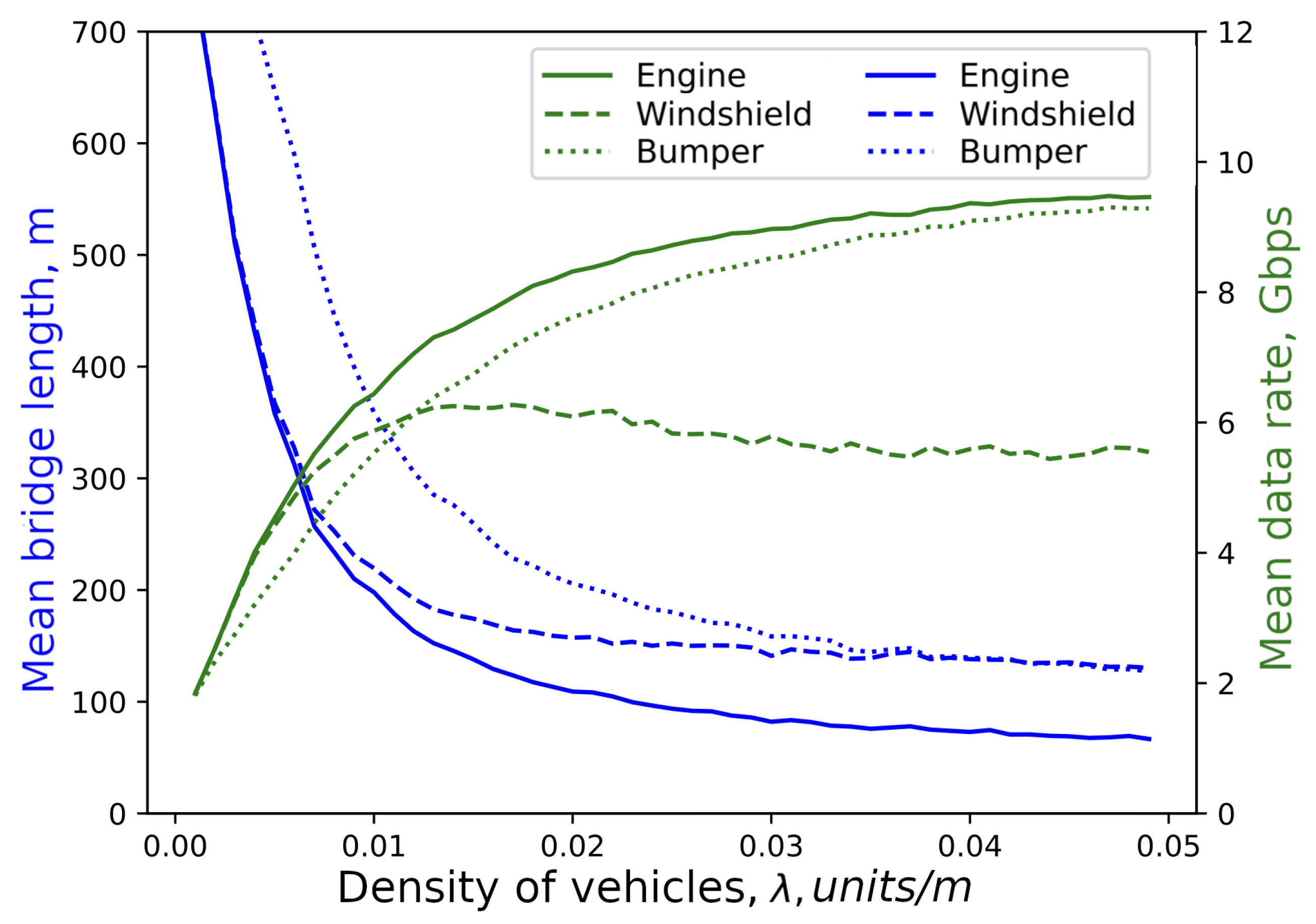
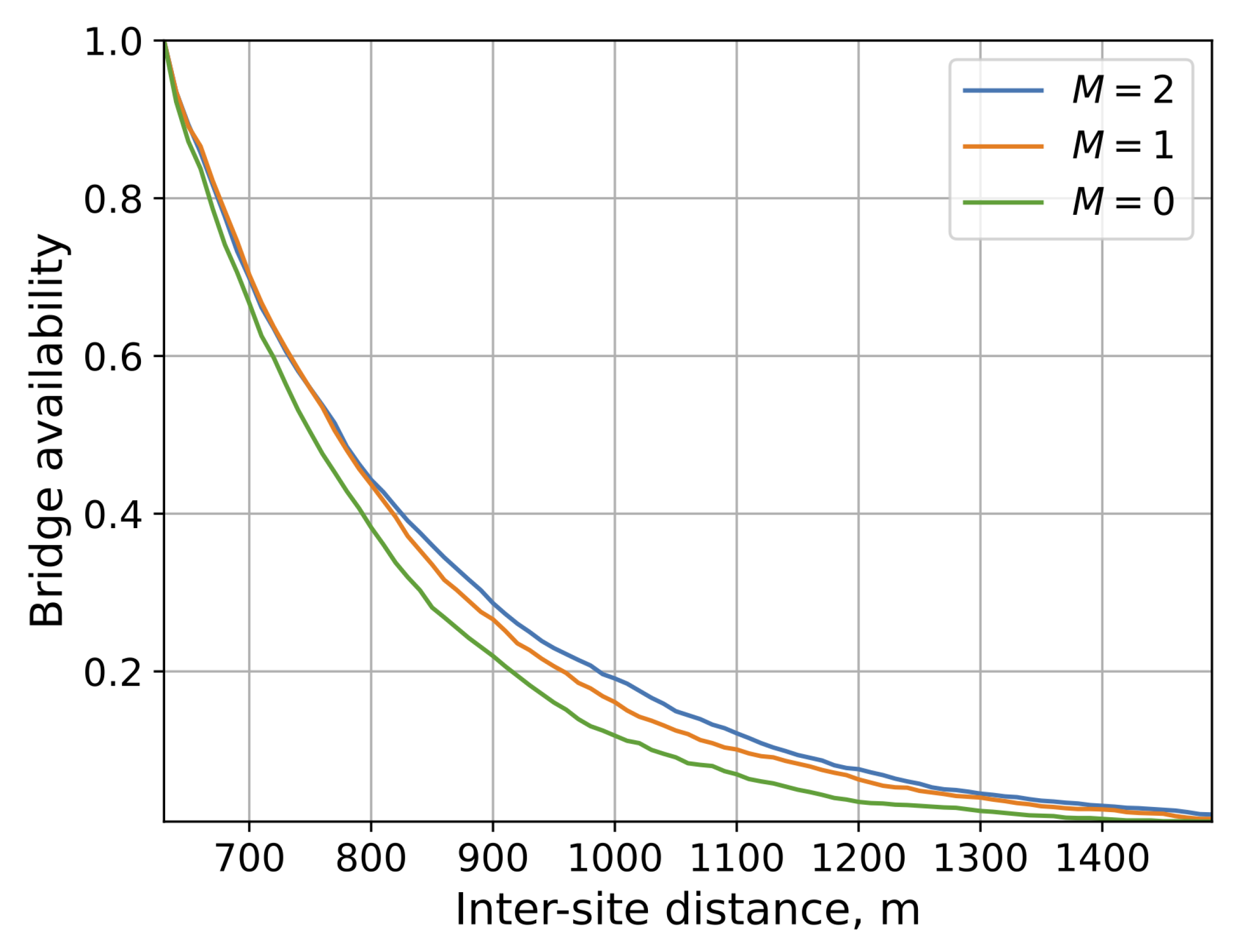
- In terms of optimal antenna locations: (i) bumper location is better in terms of bridge length; (ii) the bumper and engine locations coincide in terms of the data rate, and (iii) engine level location is characterized by the least number of hops thus requiring the least signaling overhead;
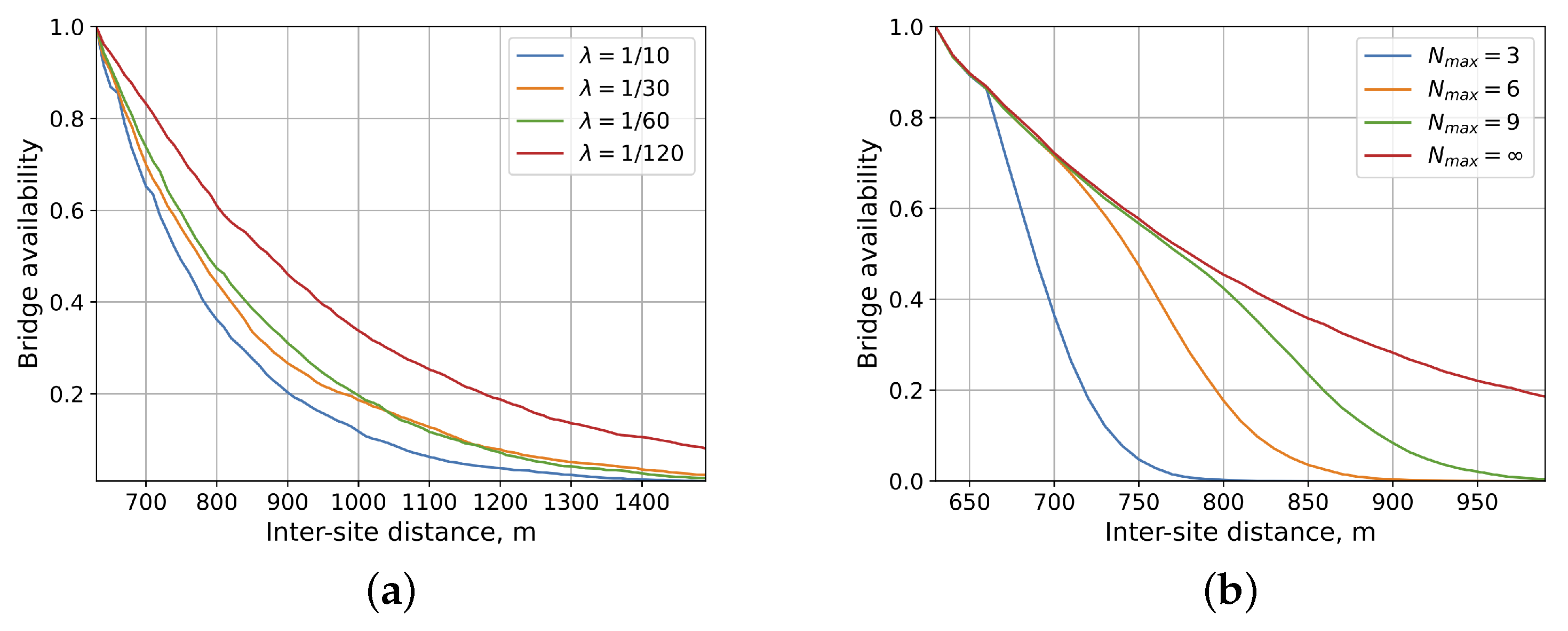
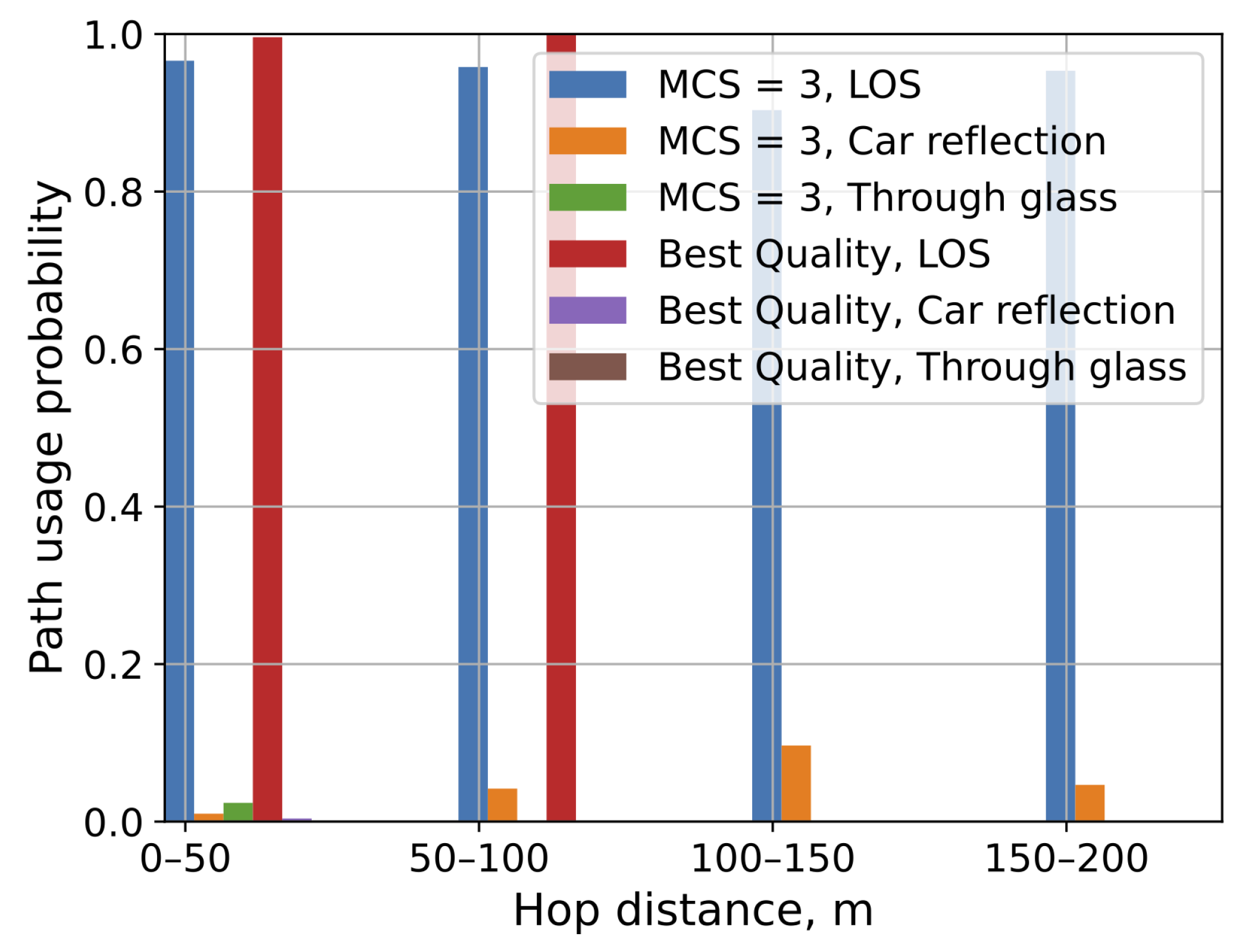
- Since the LoS propagation is dominant for all the considered last hop selection strategies contributing more than 90% of all the paths, for reasonable road traffic conditions, the lower the traffic density, the higher the bridge availability and linear increase in the number of hops leads to a linear increase in the bridge availability;
- The proposed last hop selection strategy leads to extreme performance gains in terms of data rate as compared to the “first opportunity” strategy reaching 100% for large inter-site distance (ISD) and 400–500% for small ISDs.
2. System Model
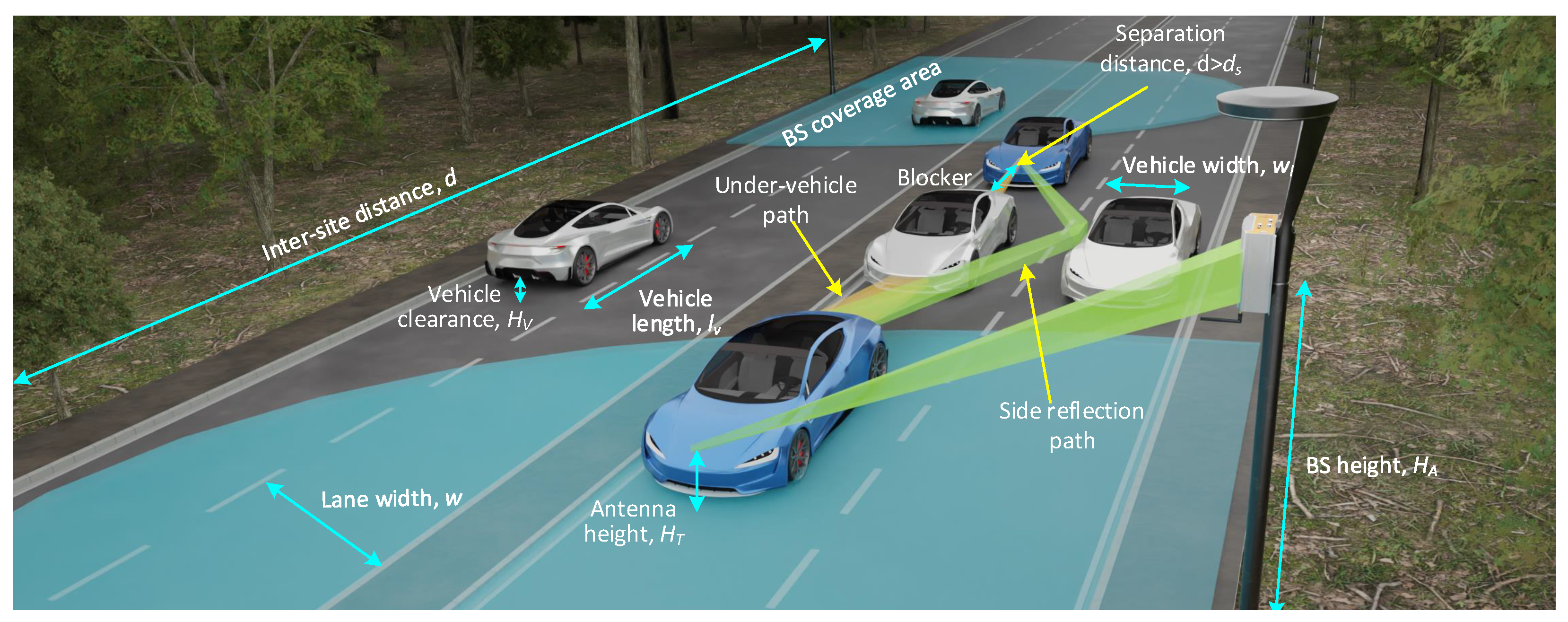
2.1. Deployment Model
2.2. Relaying, Antenna Locations, and Propagation Paths
2.3. Propagation Model
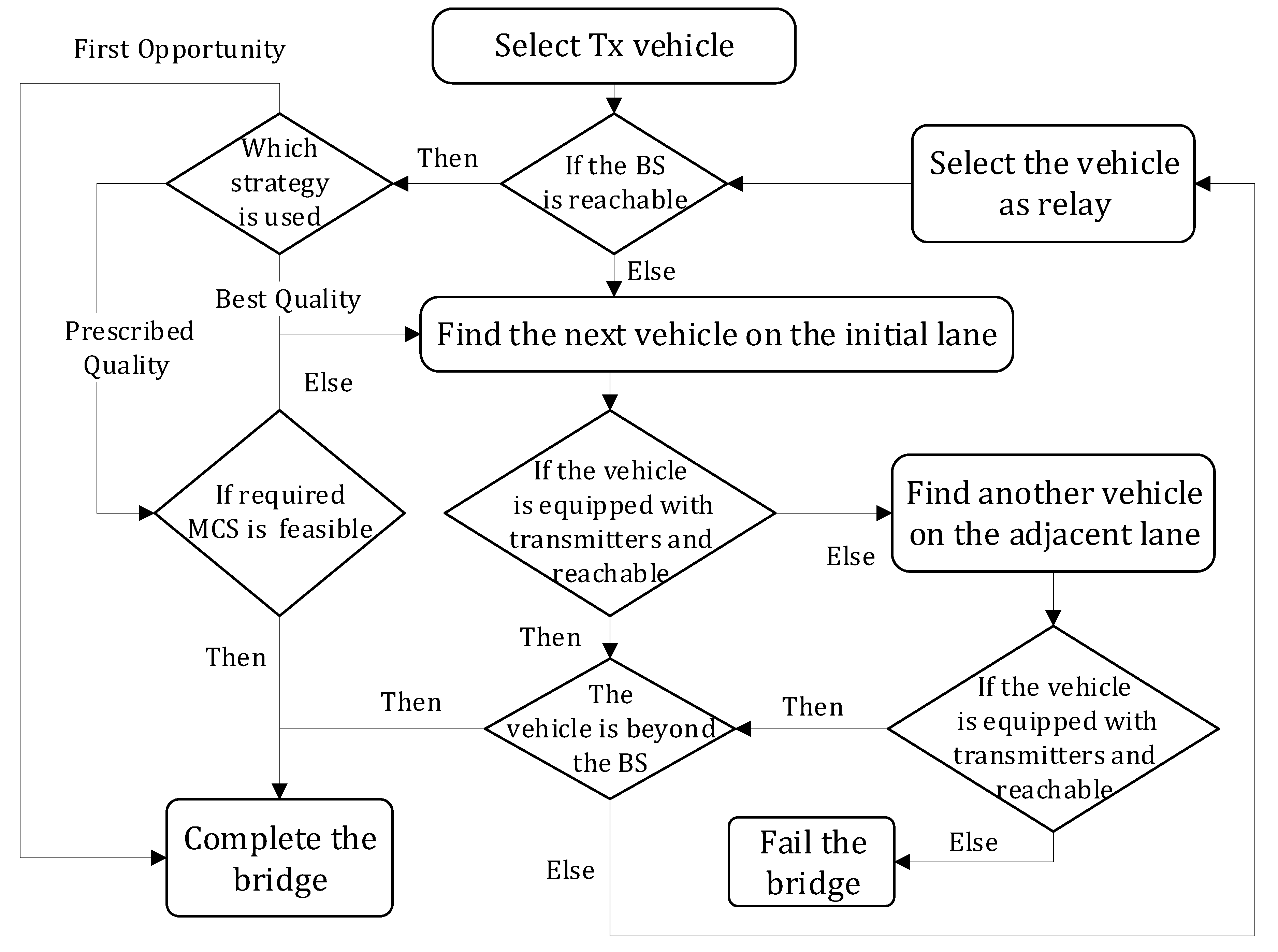
2.4. Last Hop Selection
2.5. Metrics of Interest
3. System Performance Analysis
3.1. Communications Distances and Attained Rates
3.2. Relaying Model Formalization
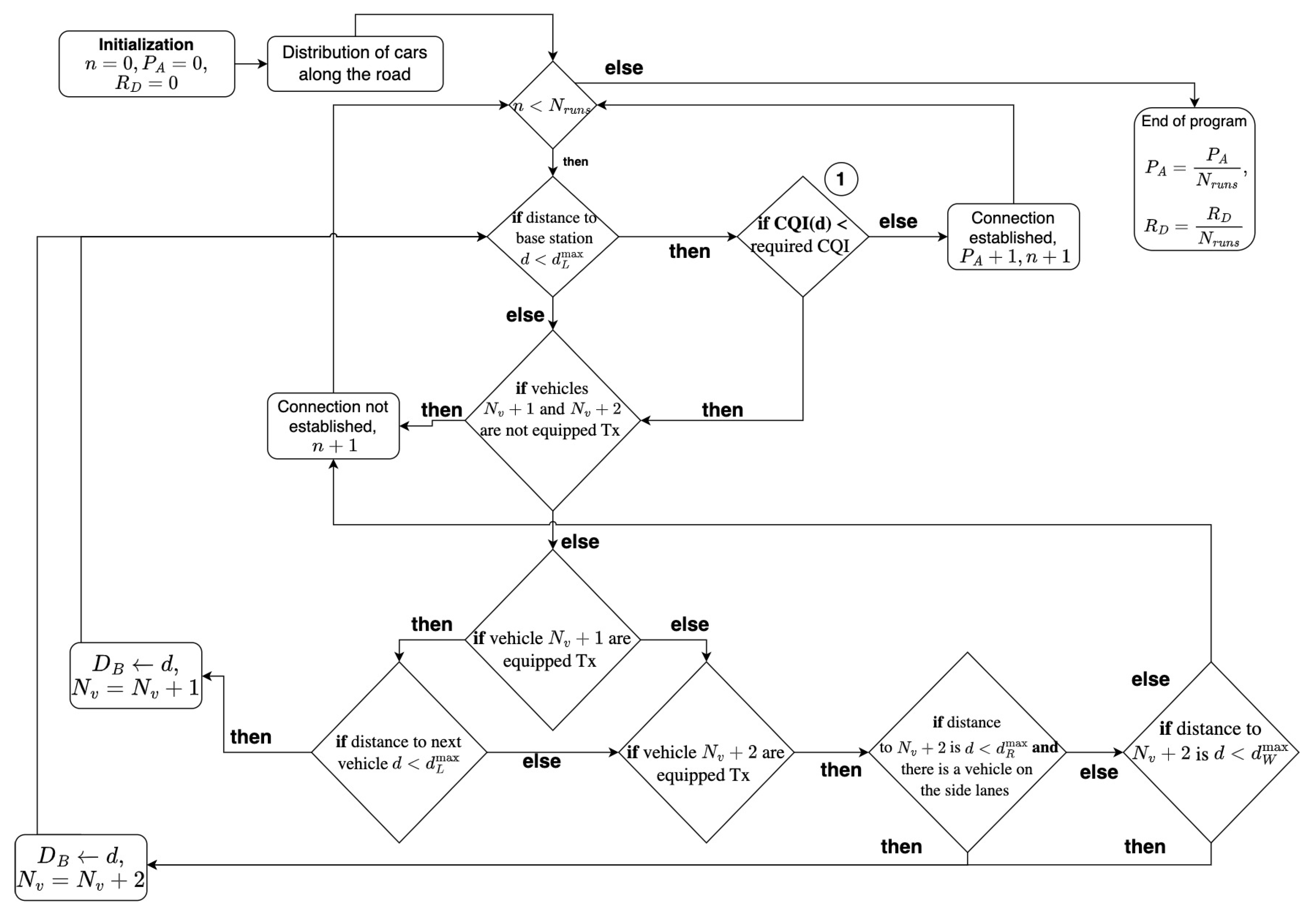
3.3. System-Level Simulation Tool
| Algorithm 1 Simulation algorithm of establishing relaying communications |
|
4. Numerical Results
4.1. Different Antenna Locations
4.2. Impact of System Parameters
4.3. The Impact of Link/Hop Selection Strategies
4.4. Path Usage
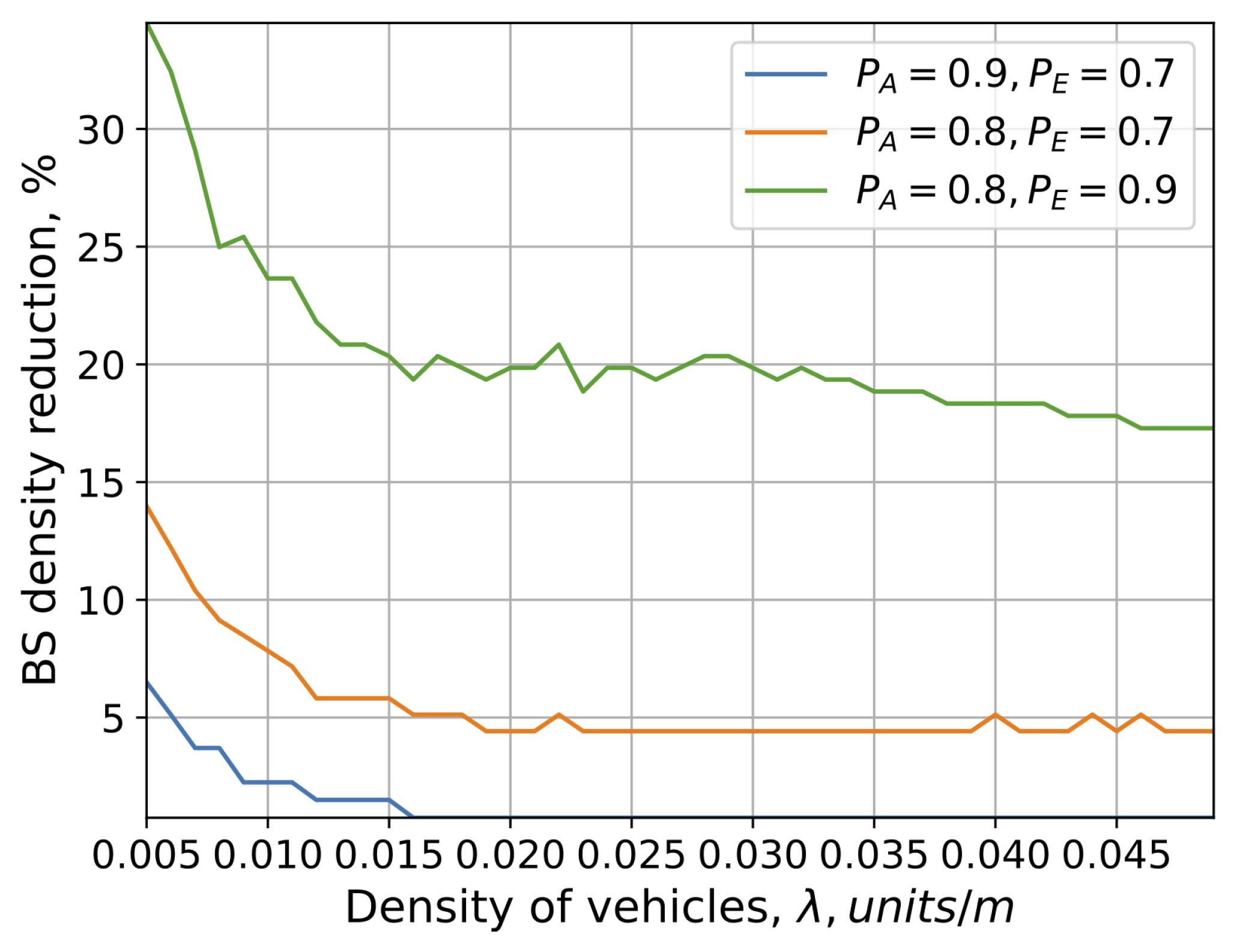
4.5. The Required BS Density
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | 3rd Generation Partnership Project |
| 5G | Fifth-Generation |
| 6G | Sixth-Generation |
| BS | Base Station |
| BQ | Best Quality |
| CQI | Channel Quality Indicator |
| EMBB | Enhanced Mobile Broadband |
| FO | First Opportunity |
| HPBW | Half-Power Bandwidth |
| IAB | Integrated Access and Backhaul |
| IEEE | Institute of Electrical and Electronics Engineers |
| ISD | Inter-Site Distance |
| IMG | Incremental Multicast Grouping |
| LoS | Line-of-Sight |
| MCS | Modulation and Coding Scheme |
| mmWave | Millimeter Wave |
| NLoS | Non Line-of-Sight |
| NOMA | Non-Orthogonal Multiple Access |
| NR | New Radio |
| OMA | Orthogonal Multiple Access |
| PPP | Poisson Point Process |
| PQ | Prescribed Quality |
| SINR | Signal-Interference + Noise Ratio |
| V2X | Vehicle to Everything |
| V2V | Vehicle to Vehicle |
| Vehicle density on a lane, unit/m | |
| Antenna deployment height, m | |
| mmW BS height, m | |
| Road clearance, m | |
| d | Distance between BSs, m |
| Minimum separation distance between vehicles, m | |
| v | Vehicle speed, m/s |
| Length of vehicle, m | |
| Number of lanes | |
| M | Number of lanes of the same direction |
| w | Lane width, m |
| Vehicle width, m | |
| Technology penetration rate | |
| Absorption loss, dB | |
| transmittance of the medium | |
| K | absorption coefficient |
| , | BS emitted power, dB/W |
| , | Antenna array gain, dBi |
| Path loss exponent | |
| Thermal noise, dBi | |
| Array HPBW, | |
| Received signal power, dB | |
| Minimum required Rx sensitivity, dB | |
| Operational frequency, GHz | |
| I | Interference, dB |
| limit of hops within a bridre | |
| Achievable distance for considered path (L, U, R, W), m | |
| Maximum distance for considered path (L, U, R, W), m | |
| Distance to the next vehicle, m | |
| r | Single hop distance, m |
| PDF of distances to the i-th neighbor in PPP | |
| PDF of distances to the i-th neighbor in shifted PPP | |
| Number of hops in a bridge | |
| Probability of non-blocked side reflection | |
| Minimum distance between a blocker and antenna, m | |
| bridge availability | |
| Mean bridge rate, bit/s |
References
- Gapeyenko, M.; Moltchanov, D.; Andreev, S.; Heath, R.W. Line-of-sight probability for mmwave-based UAV communications in 3D urban grid deployments. IEEE Trans. Wirel. Commun. 2021, 20, 6566–6579. [Google Scholar] [CrossRef]
- Gapeyenko, M.; Samuylov, A.; Gerasimenko, M.; Moltchanov, D.; Singh, S.; Aryafar, E.; Yeh, S.p.; Himayat, N.; Andreev, S.; Koucheryavy, Y. Analysis of human-body blockage in urban millimeter-wave cellular communications. In Proceedings of the Communications (ICC), 2016 IEEE International Conference, Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–7. [Google Scholar]
- Moltchanov, D.; Ometov, A.; Andreev, S.; Koucheryavy, Y. Upper bound on capacity of 5G mmWave cellular with multi-connectivity capabilities. Electron. Lett. 2018, 54, 724–726. [Google Scholar] [CrossRef]
- Begishev, V.; Sopin, E.; Moltchanov, D.; Kovalchukov, R.; Samuylov, A.; Andreev, S.; Koucheryavy, Y.; Samouylov, K. Joint use of guard capacity and multiconnectivity for improved session continuity in millimeter-wave 5g nr systems. IEEE Trans. Veh. Technol. 2021, 70, 2657–2672. [Google Scholar] [CrossRef]
- Gapeyenko, M.; Petrov, V.; Moltchanov, D.; Akdeniz, M.R.; Andreev, S.; Himayat, N.; Koucheryavy, Y. On the degree of multi-connectivity in 5G millimeter-wave cellular urban deployments. IEEE Trans. Veh. Technol. 2018, 68, 1973–1978. [Google Scholar] [CrossRef]
- ITU-R. M.2410-0: Minimum Requirements Related to Technical Performance for IMT-2020 Radio Interface(s). Technical Recommendation. ITU-R. 2017. Available online: https://www.itu.int/pub/R-REP-M.2410-2017 (accessed on 15 September 2022).
- Polese, M.; Jornet, J.M.; Melodia, T.; Zorzi, M. Toward end-to-end, full-stack 6G terahertz networks. IEEE Commun. Mag. 2020, 58, 48–54. [Google Scholar] [CrossRef]
- Petrov, V.; Pyattaev, A.; Moltchanov, D.; Koucheryavy, Y. Terahertz band communications: Applications, research challenges, and standardization activities. In Proceedings of the 8th International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Lisbon, Portugal, 18–20 October 2016; pp. 183–190. [Google Scholar]
- 3GPP. Study on Integrated Access and Backhaul (Release 17). TR 38.874 V17.0.0, 3GPP. 2020. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3232 (accessed on 15 September 2022).
- Monteiro, V.F.; Lima, F.; Rafael, M.; Moreira, D.C.; Sousa, D.A.; Maciel, T.F.; Makki, B.; Hannu, H. Paving the Way Towards Mobile IAB: Problems, Solutions and Challenges. arXiv 2022, arXiv:2206.14946. [Google Scholar] [CrossRef]
- Tafintsev, N.; Moltchanov, D.; Gerasimenko, M.; Gapeyenko, M.; Zhu, J.; Yeh, S.p.; Himayat, N.; Andreev, S.; Koucheryavy, Y.; Valkama, M. Aerial access and backhaul in mmWave B5G systems: Performance dynamics and optimization. IEEE Commun. Mag. 2020, 58, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Park, J.J.; Lee, J.; Kim, K.W.; Lee, K.C.; Kim, M.D. Vehicle Antenna Position Dependent Path Loss for Millimeter-Wave V2V Communication. In Proceedings of the 11th Global Symposium on Millimeter Waves (GSMM), Boulder, CO, USA, 22–24 May 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Ozpolat, M.; Bhargava, K.; Kampert, E.; Higgins, M.D. Multi-lane urban mmWave V2V networks: A path loss behaviour dependent coverage analysis. Veh. Commun. 2021, 30, 100348. [Google Scholar] [CrossRef]
- Saraereh, O.A.; Ali, A.; Khan, I.; Rabie, K. Interference Analysis for Vehicle-to-Vehicle Communications at 28 GHz. Electronics 2020, 9, 262. [Google Scholar] [CrossRef]
- Kanhere, O.; Chopra, A.; Thornburg, A.; Rappaport, T.S.; Ghassemzadeh, S.S. Performance Impact Analysis of Beam Switching in Millimeter Wave Vehicular Communications. In Proceedings of the IEEE 93rd Vehicular Technology Conference (VTC-Spring), Bengaluru, India, 4–8 January 2021; pp. 1–7. [Google Scholar]
- Petrov, V.; Kokkoniemi, J.; Moltchanov, D.; Lehtomäki, J.; Juntti, M.; Koucheryavy, Y. The impact of interference from the side lanes on mmWave/THz band V2V communication systems with directional antennas. IEEE Trans. Veh. Technol. 2018, 67, 5028–5041. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; He, D.; Guan, Y.; Huang, Y.; Xu, Y.; Chen, Z. Beamwidth Optimization for Millimeter-Wave V2V Communication Between Neighbor Vehicles in Highway Scenarios. IEEE Access 2021, 9, 4335–4350. [Google Scholar] [CrossRef]
- Belmekki, B.E.Y.; Hamza, A.; Escrig, B. Outage Analysis of Cooperative NOMA for Millimeter Wave Vehicular Networks at Intersections. In Proceedings of the IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ajam, H.; Najafi, M.; Jamali, V.; Schober, R. Ergodic Sum Rate Analysis of UAV-Based Relay Networks With Mixed RF-FSO Channels. IEEE Open J. Commun. Soc. 2020, 1, 164–178. [Google Scholar] [CrossRef] [Green Version]
- Alkama, D.; Ouamri, M.A.; Alzaidi, M.S.; Shaw, R.N.; Azni, M.; Ghoneim, S.S.M. Downlink Performance Analysis in MIMO UAV-Cellular Communication With LOS/NLOS Propagation Under 3D Beamforming. IEEE Access 2022, 10, 6650–6659. [Google Scholar] [CrossRef]
- Tafintsev, N.; Moltchanov, D.; Andreev, S.; Yeh, S.p.; Himayat, N.; Koucheryavy, Y.; Valkama, M. Handling Spontaneous Traffic Variations in 5G+ via Offloading Onto mmWave-Capable UAV “Bridges”. IEEE Trans. Veh. Technol. 2020, 69, 10070–10084. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Kato, N. Networking and communications in autonomous driving: A survey. IEEE Commun. Surv. Tutorials 2018, 21, 1243–1274. [Google Scholar] [CrossRef]
- Eckhardt, J.M.; Petrov, V.; Moltchanov, D.; Koucheryavy, Y.; Kürner, T. Channel Measurements and Modeling for Low-Terahertz Band Vehicular Communications. IEEE J. Sel. Areas Commun. 2021, 39, 1590–1603. [Google Scholar] [CrossRef]
- Petrov, V.; Eckhardt, J.M.; Moltchanov, D.; Koucheryavy, Y.; Kurner, T. Measurements of reflection and penetration losses in low terahertz band vehicular communications. In Proceedings of the 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–5. [Google Scholar]
- Boronin, P.; Petrov, V.; Moltchanov, D.; Koucheryavy, Y.; Jornet, J.M. Capacity and throughput analysis of nanoscale machine communication through transparency windows in the terahertz band. Nano Commun. Netw. 2014, 5, 72–82. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Channel modeling and capacity analysis for electromagnetic wireless nanonetworks in the terahertz band. IEEE Trans. Wirel. Commun. 2011, 10, 3211–3221. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Femtosecond-long pulse-based modulation for terahertz band communication in nanonetworks. IEEE Trans. Commun. 2014, 62, 1742–1754. [Google Scholar] [CrossRef] [Green Version]
- Rothman, L.S. High-Resolution Transmission Molecular Absorption Database. Harvard-Smithson Center for Astrophysics. HITRAN. 2014. Available online: www.cfa.harvard.edu (accessed on 15 September 2022).
- Petrov, V.; Kurner, T.; Hosako, I. IEEE 802.15. 3d: First Standardization Efforts for Sub-Terahertz Band Communications toward 6G. IEEE Commun. Mag. 2020, 58, 28–33. [Google Scholar] [CrossRef]
- Moltchanov, D. Distance distributions in random networks. Elsevier Ad. Hoc. Networks 2012, 10, 1146–1166. [Google Scholar] [CrossRef]
- Basharin, G.; Gaidamaka, Y.V.; Samouylov, K.E. Mathematical theory of teletraffic and its application to the analysis of multiservice communication of next generation networks. Autom. Control. Comput. Sci. 2013, 47, 62–69. [Google Scholar] [CrossRef]
- Fishman, G.S.; Yarberry, L.S. An implementation of the batch means method. INFORMS J. Comput. 1997, 9, 296–310. [Google Scholar] [CrossRef]



| Scenario | Propagation Path | Model | Losses |
|---|---|---|---|
| Single-lane | LoS | FSPL | 0 dB |
| Vehicle–body block. | FSPL + height-dependent | 30–50 dB | |
| Under-vehicle prop. | FSPL + , where and | ||
| are as in Table I in [23] | |||
| Front/rear reflection | FSPL + reflection loss | ∼25 dB | |
| Multi-lane | Sym. side reflection | FSPL + reflection loss | ∼3 dB |
| Assym. side reflection | FSPL + angle-dependent loss | 16–20 dB | |
| Front reflection | FSPL + angle-dependent loss | 24–42 dB | |
| Rear reflection | FSPL + angle-dependent loss | 15–30 dB |
| MCS ID | Modulation | Data Rate | Receiver |
|---|---|---|---|
| (Gb/s) | Sensitivity (dBm) | ||
| 0 | BPSK | 1.29 | −67 |
| 2 | QPSK | 2.58 | −64 |
| 3 | QPSK | 3.29 | −60 |
| 4 | 8-PSK | 3.87 | −59 |
| 8 | 16-QAM | 5.16 | −57 |
| 9 | 16-QAM | 6.57 | −53 |
| 10 | 64-QAM | 7.74 | −52 |
| 11 | 64-QAM | 9.86 | −47 |
| Notation | Value | Description |
|---|---|---|
| m | Vehicle length | |
| s | Minimal inter-vehicle distance | |
| un./m | Mean vehicle density | |
| m | Antenna heights | |
| m | Vehicle clearance | |
| v | 25 m/s | Default vehicle speed |
| GHz | Carrier frequency [23] | |
| W | BS/vehicle antenna emitted power [29] | |
| dBm | Emitted power in dBm [29] | |
| dBm | Noise power [29] | |
| −56 dBm | Minimal SINR [29] | |
| , | 17.58 dBi | Transmit and receive side gains [29] |
| 2.1 | Path loss exponent [23] | |
| 23,000 | Propagation coefficient at 0.4 m [23] | |
| 3.4 | Propagation coefficient at 0.4 m [23] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beschastnyi, V.; Machnev, E.; Ostrikova, D.; Gaidamaka, Y.; Samouylov, K. Coverage, Rate, and Last Hop Selection in Multi-Hop Communications in Highway Scenarios. Mathematics 2023, 11, 26. https://doi.org/10.3390/math11010026
Beschastnyi V, Machnev E, Ostrikova D, Gaidamaka Y, Samouylov K. Coverage, Rate, and Last Hop Selection in Multi-Hop Communications in Highway Scenarios. Mathematics. 2023; 11(1):26. https://doi.org/10.3390/math11010026
Chicago/Turabian StyleBeschastnyi, Vitalii, Egor Machnev, Darya Ostrikova, Yuliya Gaidamaka, and Konstantin Samouylov. 2023. "Coverage, Rate, and Last Hop Selection in Multi-Hop Communications in Highway Scenarios" Mathematics 11, no. 1: 26. https://doi.org/10.3390/math11010026
APA StyleBeschastnyi, V., Machnev, E., Ostrikova, D., Gaidamaka, Y., & Samouylov, K. (2023). Coverage, Rate, and Last Hop Selection in Multi-Hop Communications in Highway Scenarios. Mathematics, 11(1), 26. https://doi.org/10.3390/math11010026







