Free Vibration Characteristics of Bidirectional Graded Porous Plates with Elastic Foundations Using 2D-DQM
Abstract
:1. Introduction
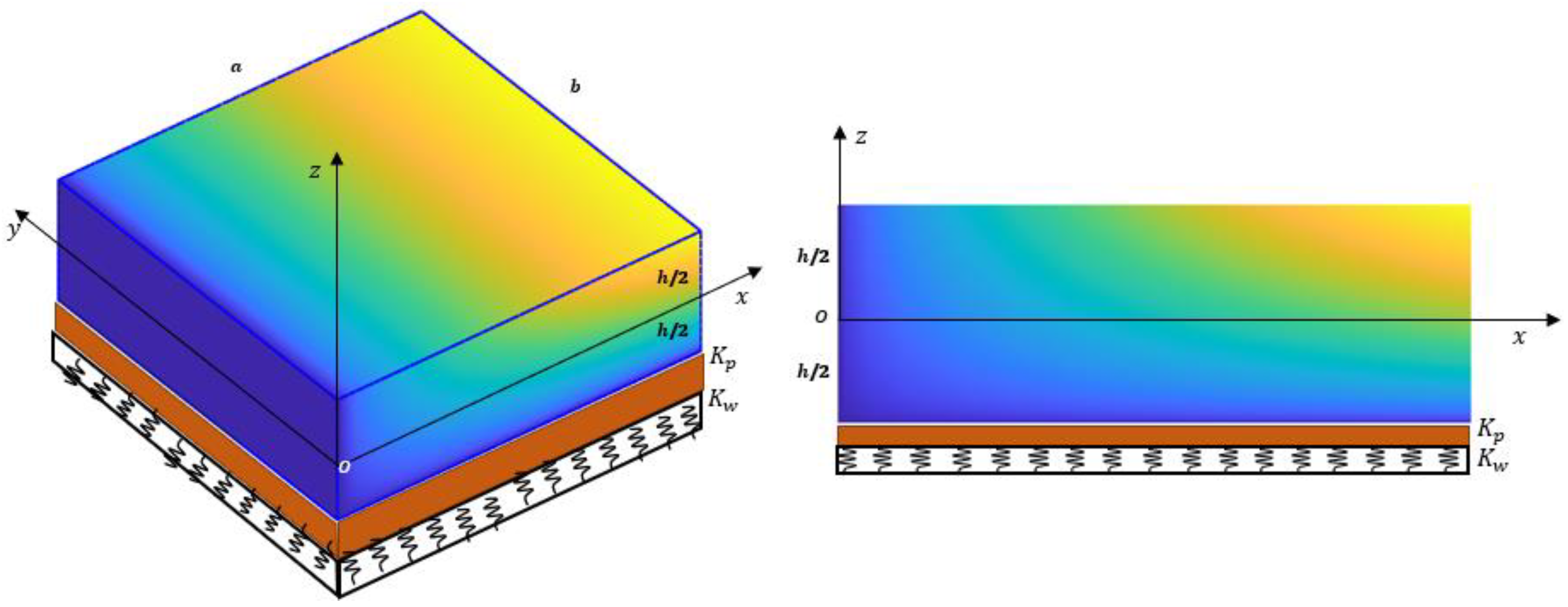
2. Mathematical Formulation
2.1. Displacement Field and Constitutive Relations
2.2. Governing Equations of Motion
3. Solution Methodology
4. Numerical Results
4.1. Model Validations
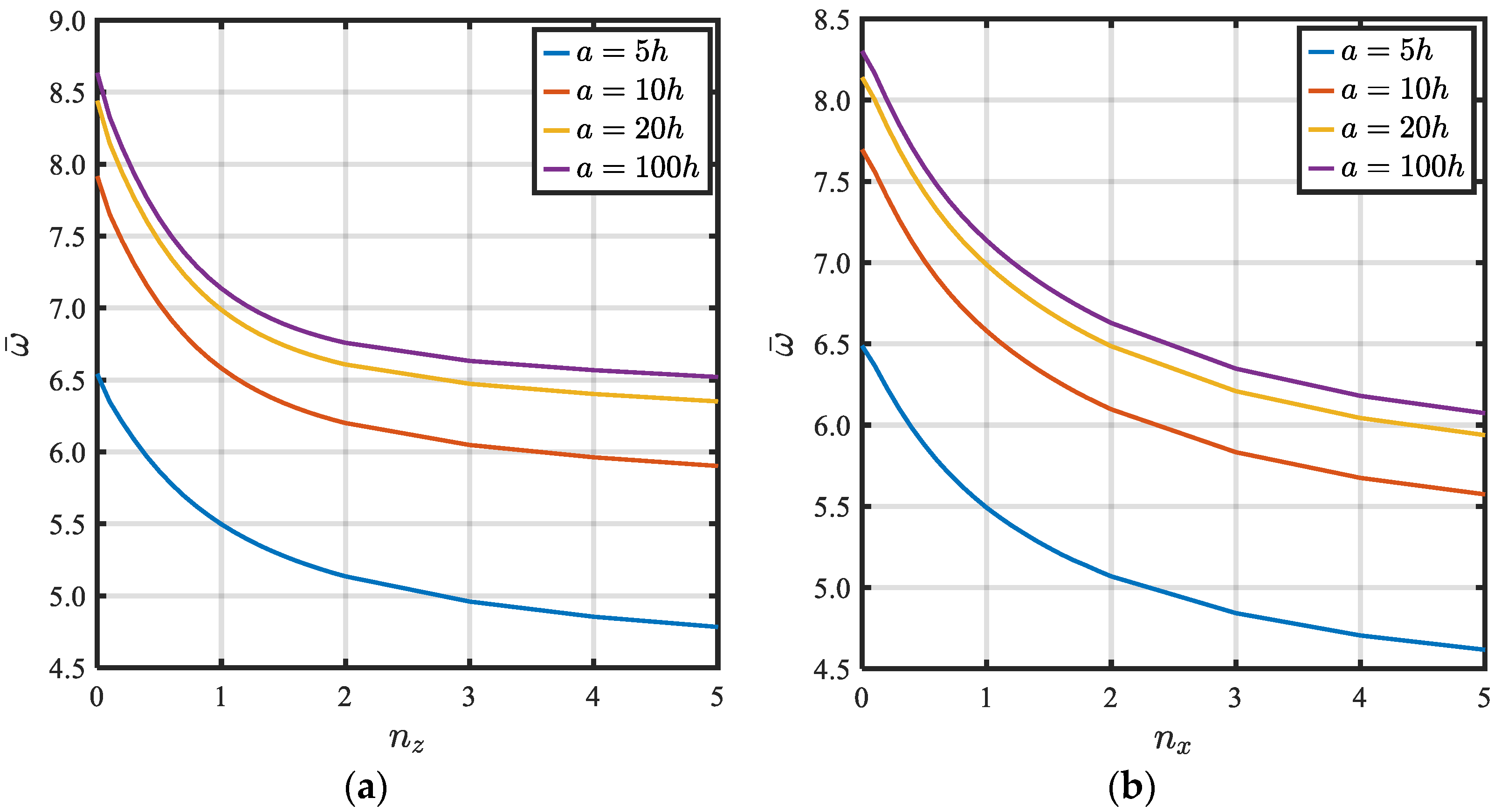
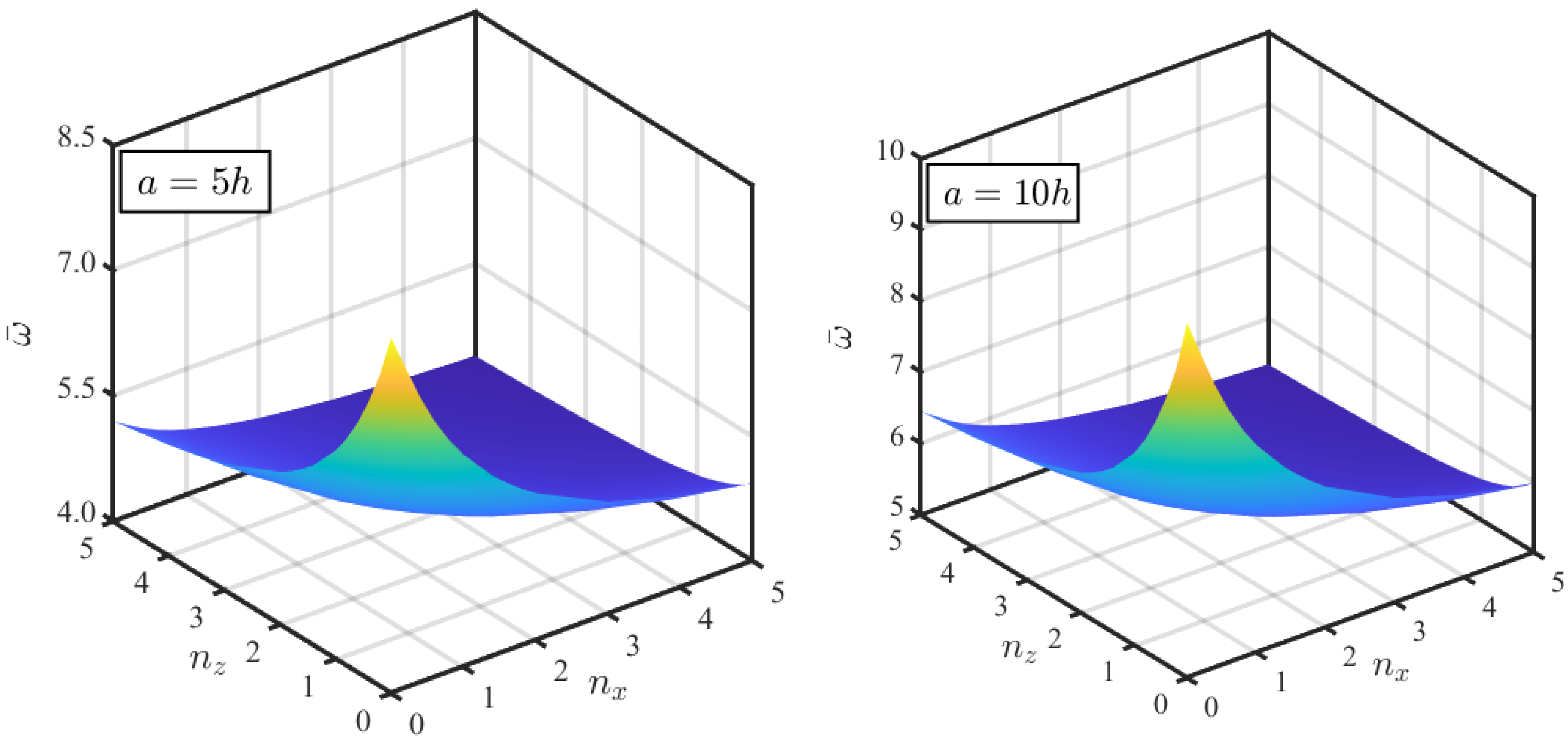
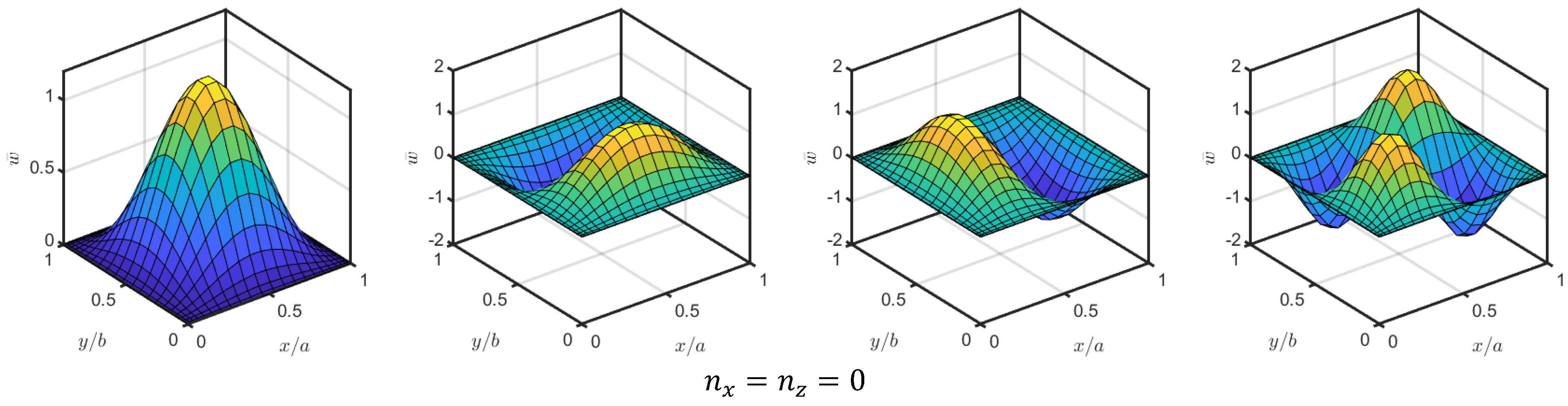
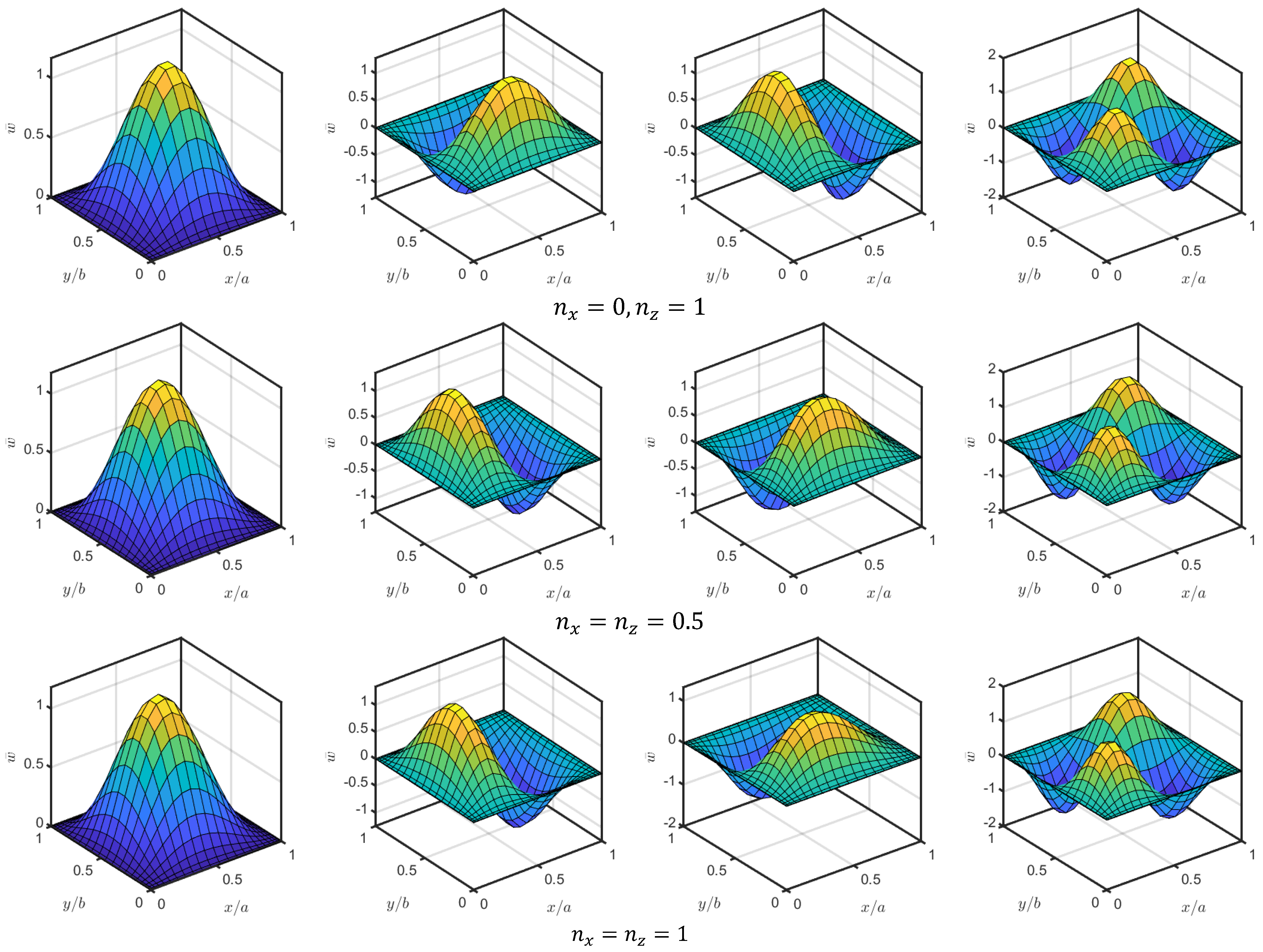
4.2. Parametric Analysis
- a.
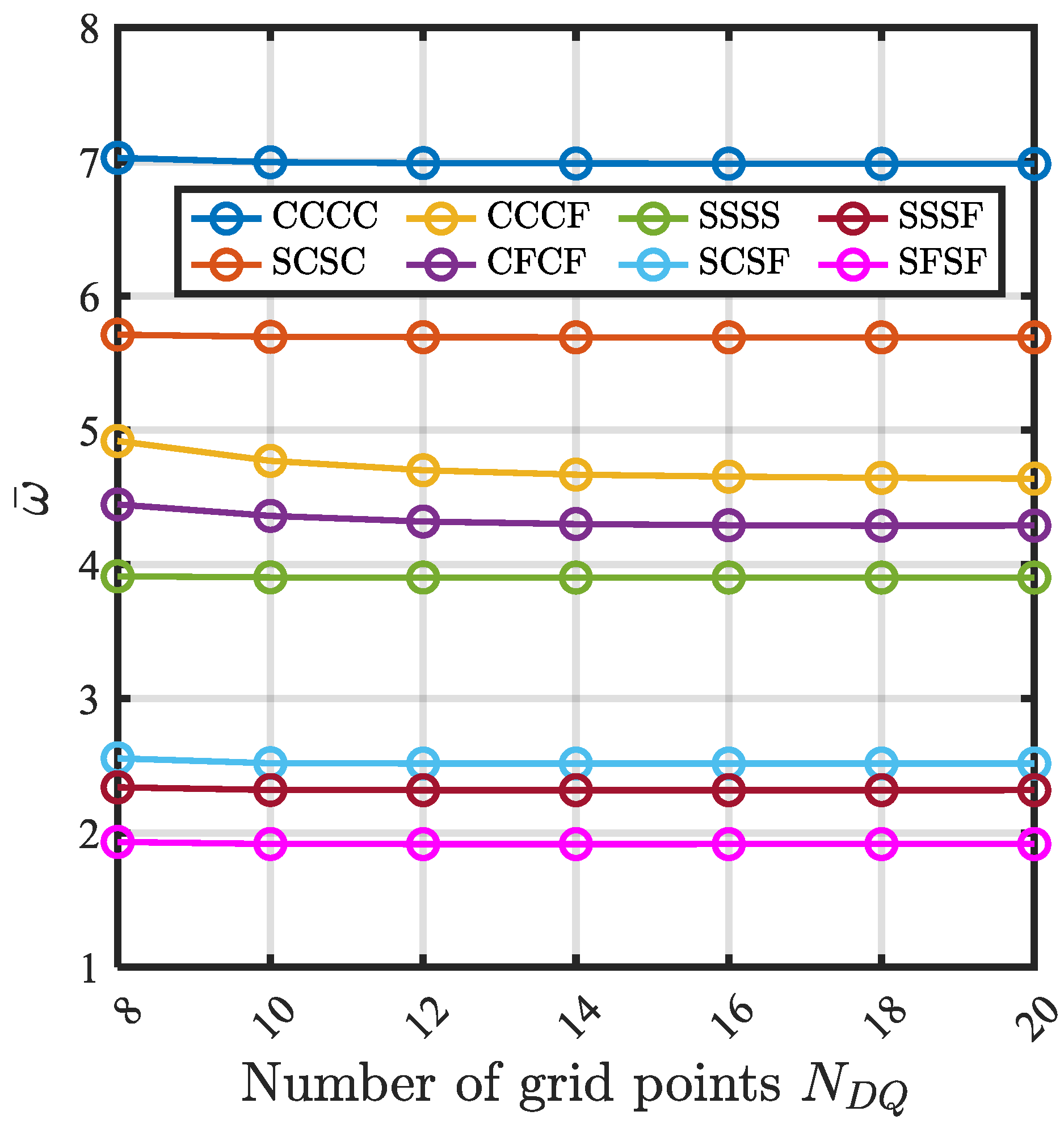
- Convergence Study
- b.
- Effect of Shear shape functions
- c.
- Effect of Slenderness ratio
- d.
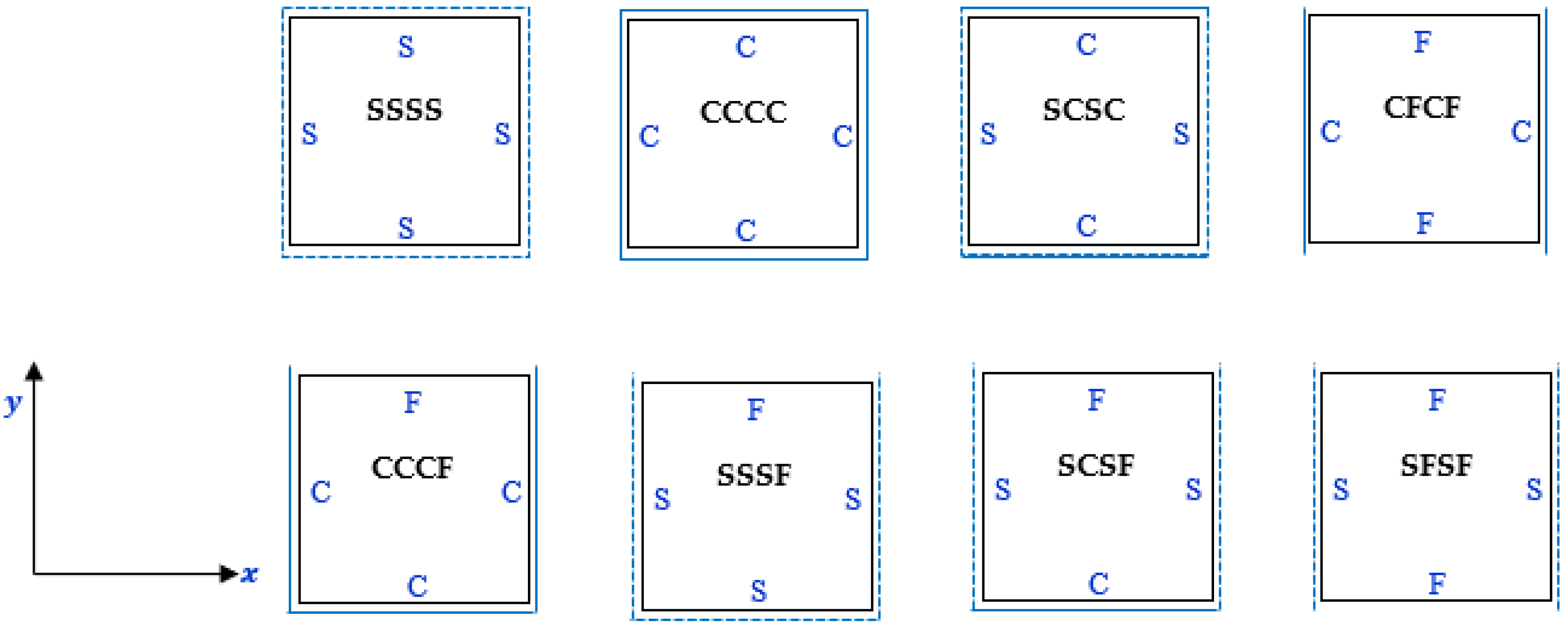
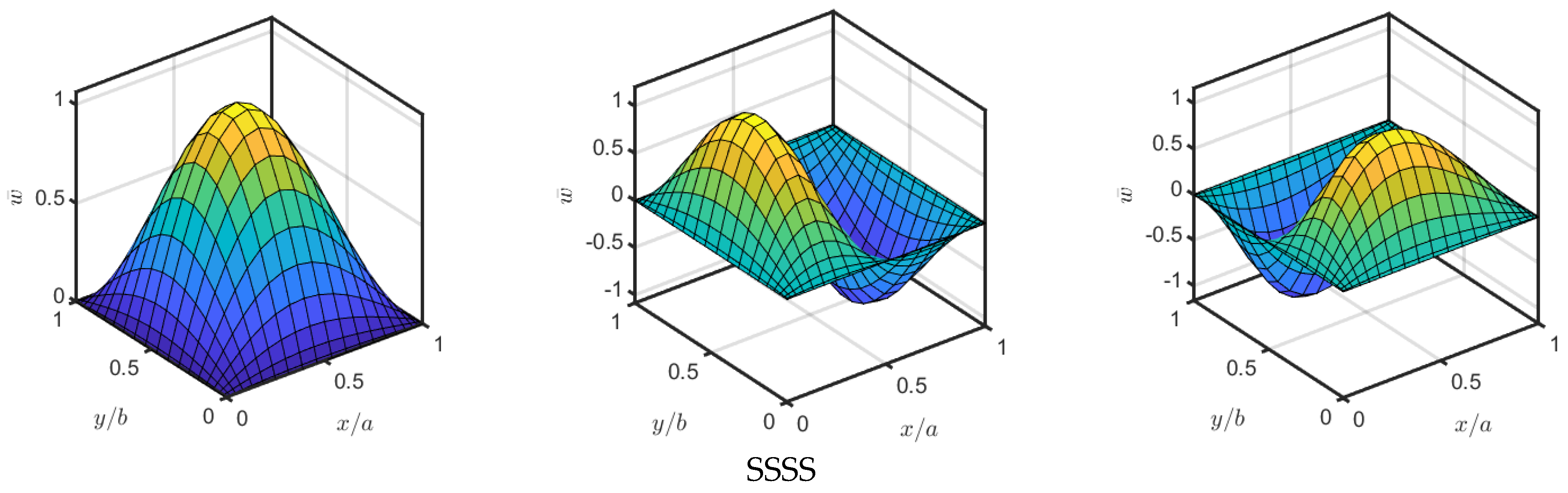
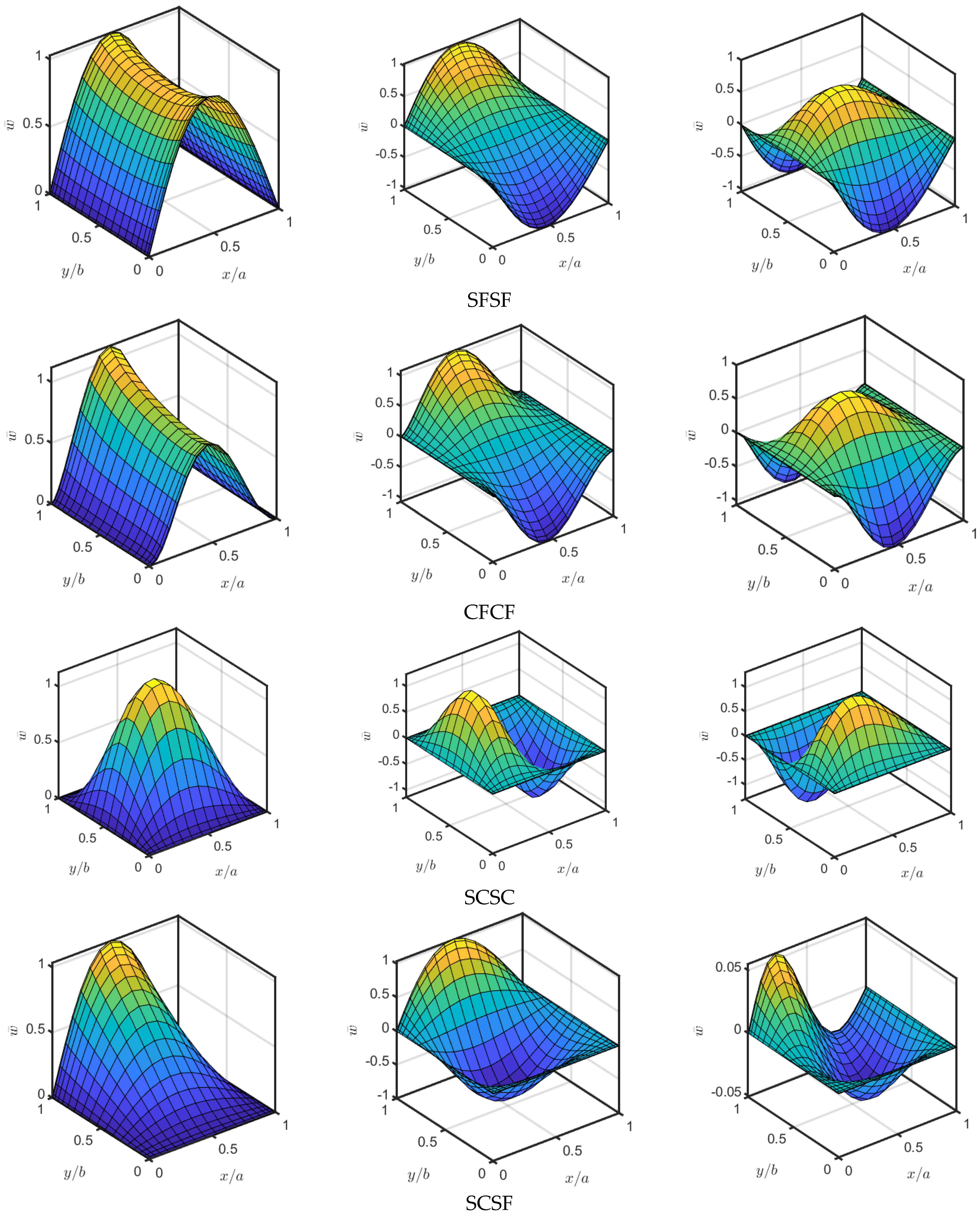
- Effect of Boundary Conditions
- e.
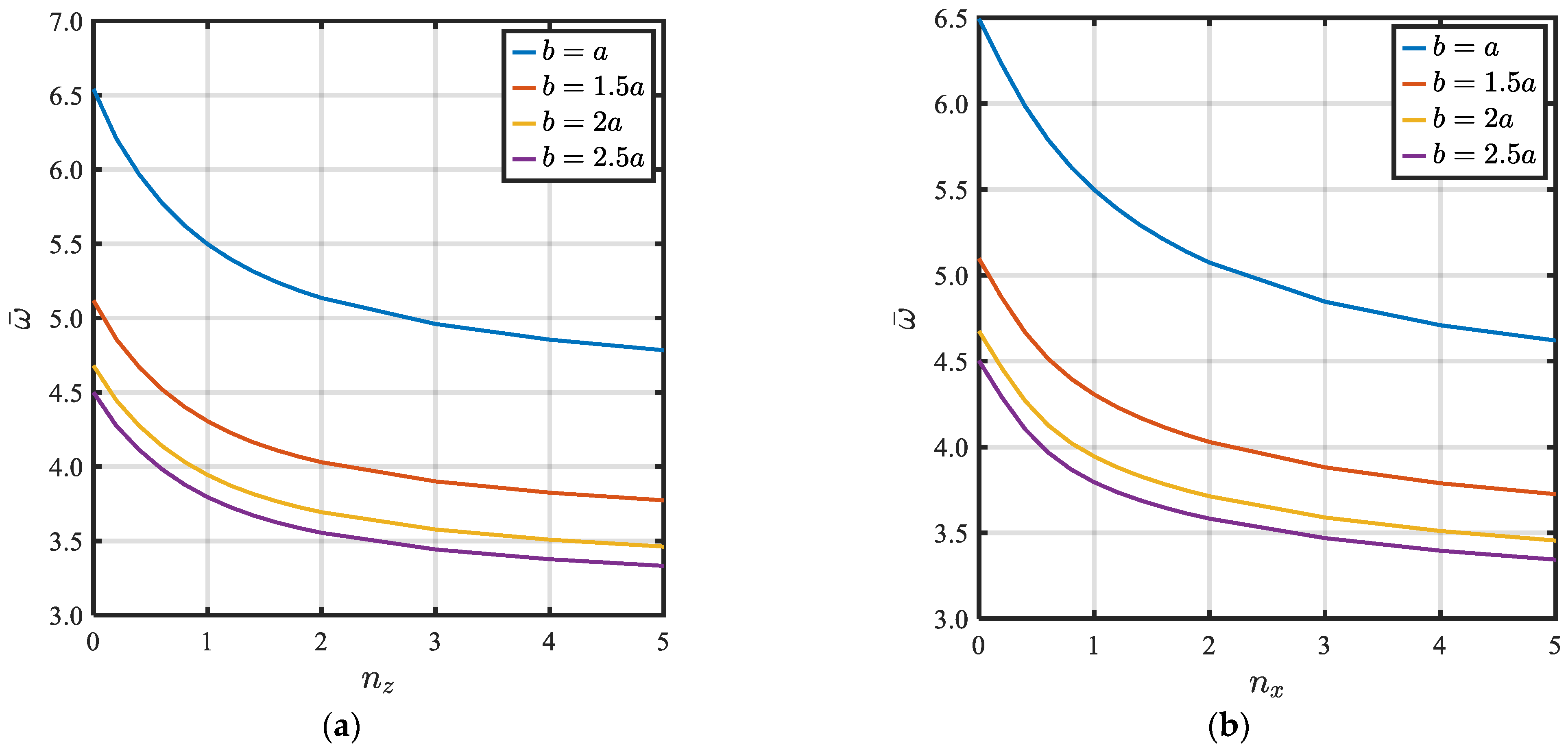
- Effect of Geometrical Dimensions
- f.
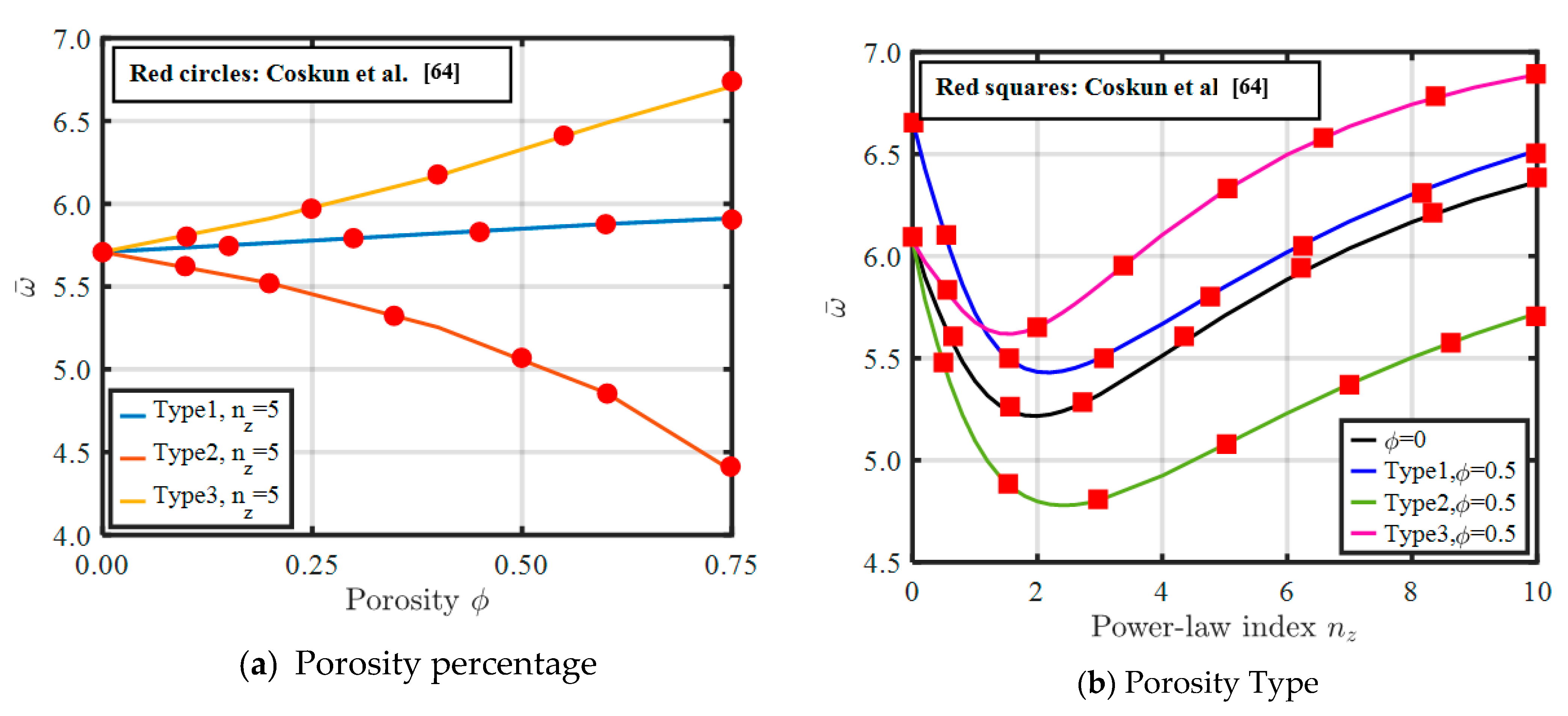
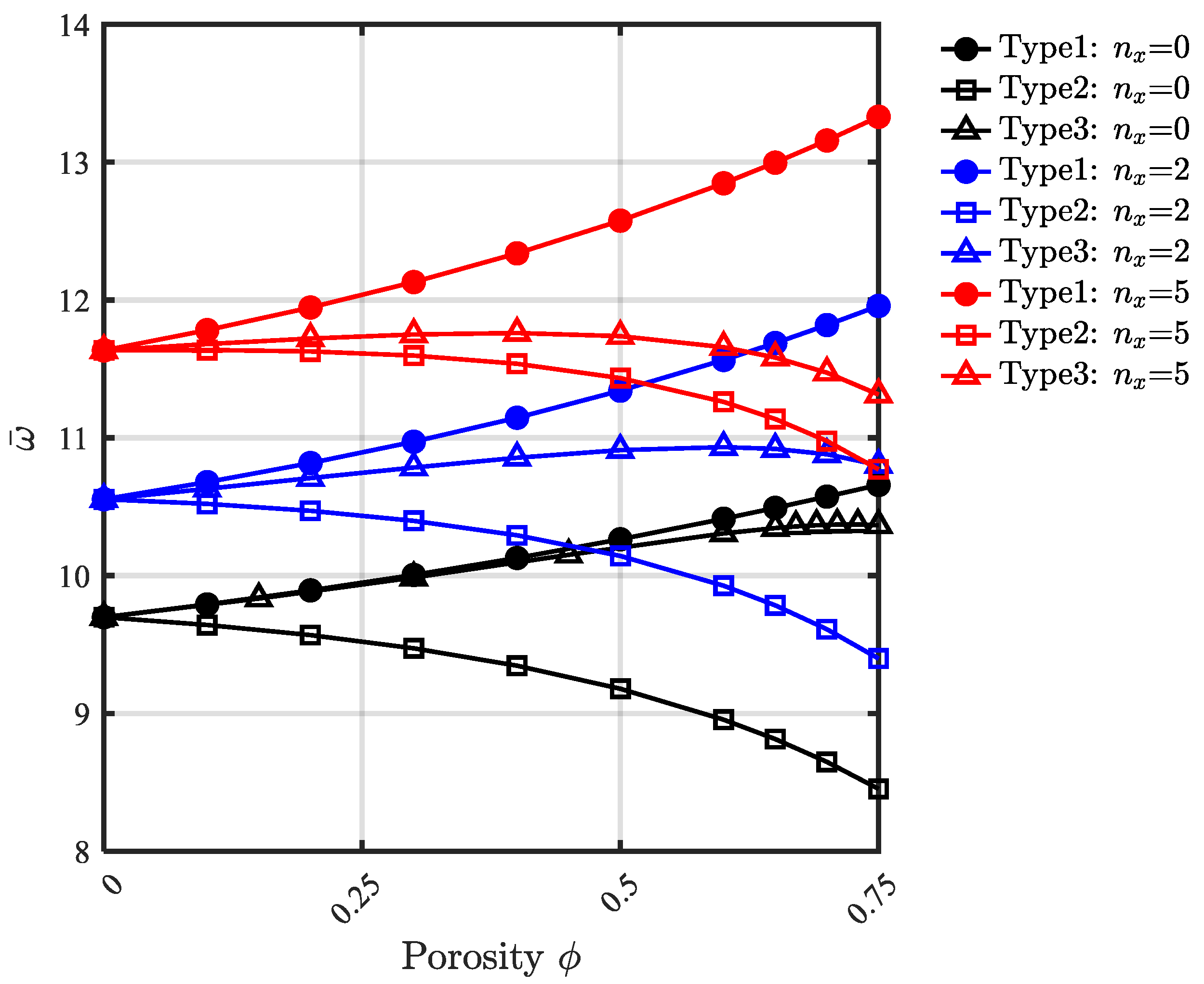
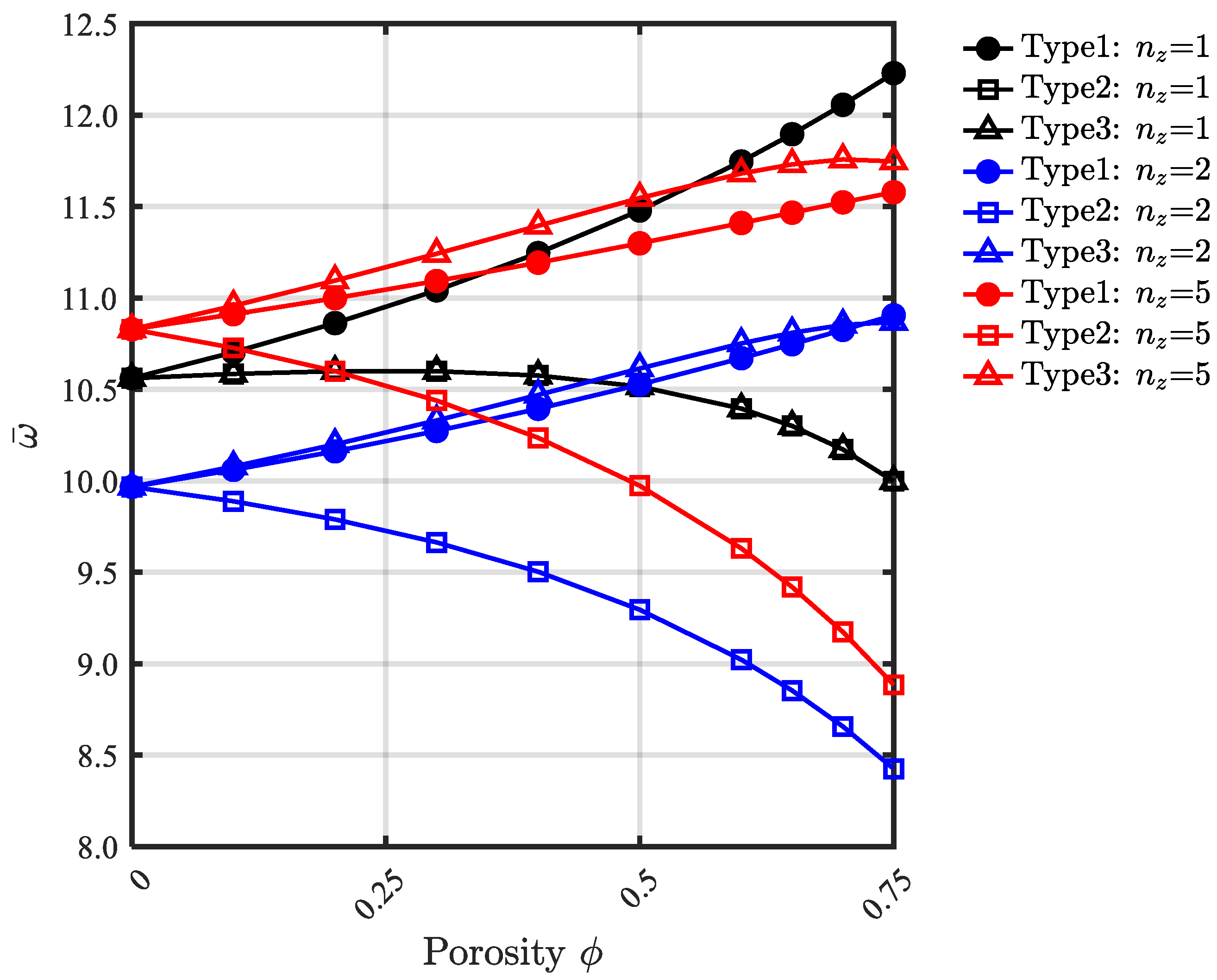
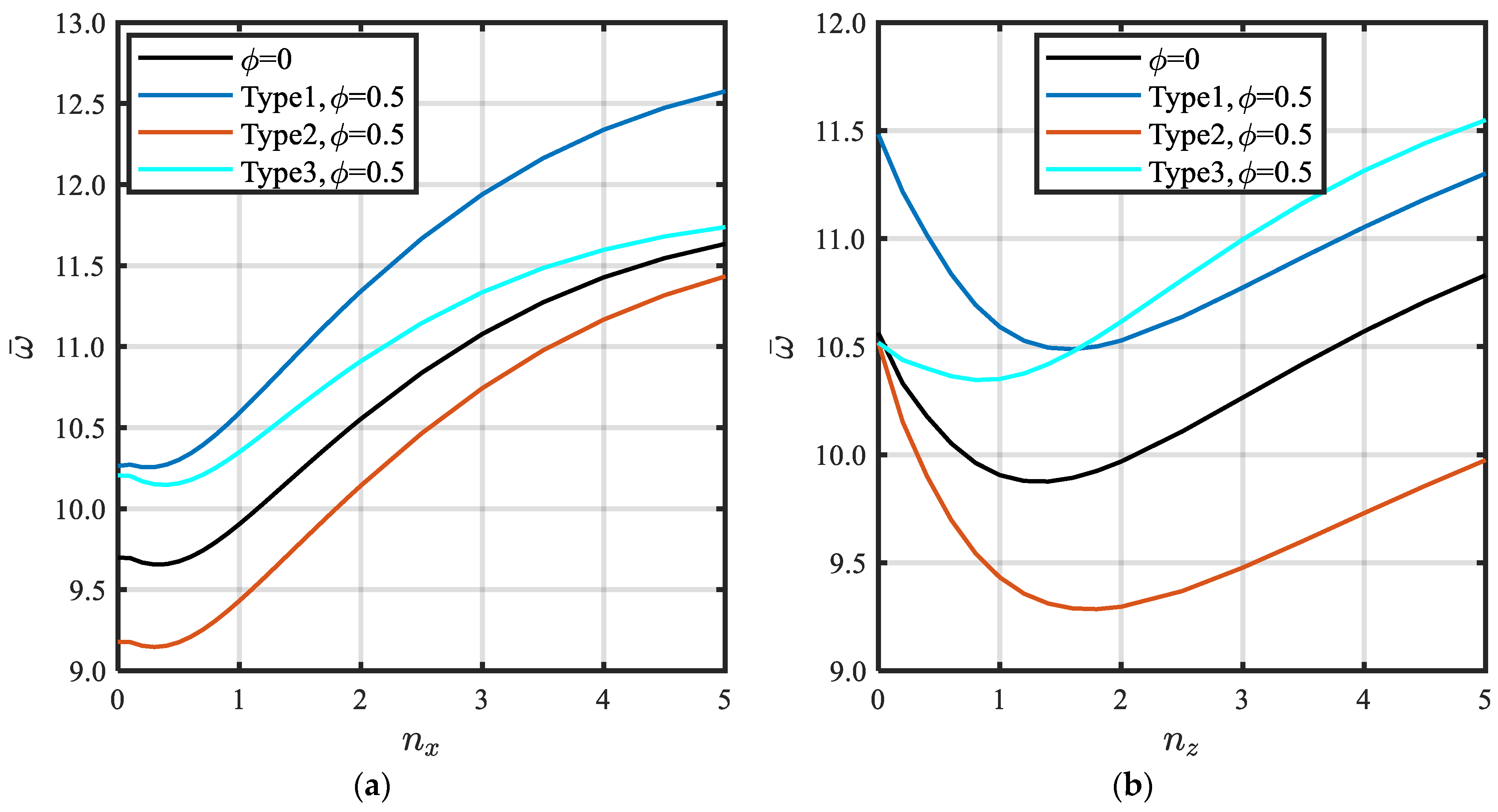
- Effect of porosity type
- g.
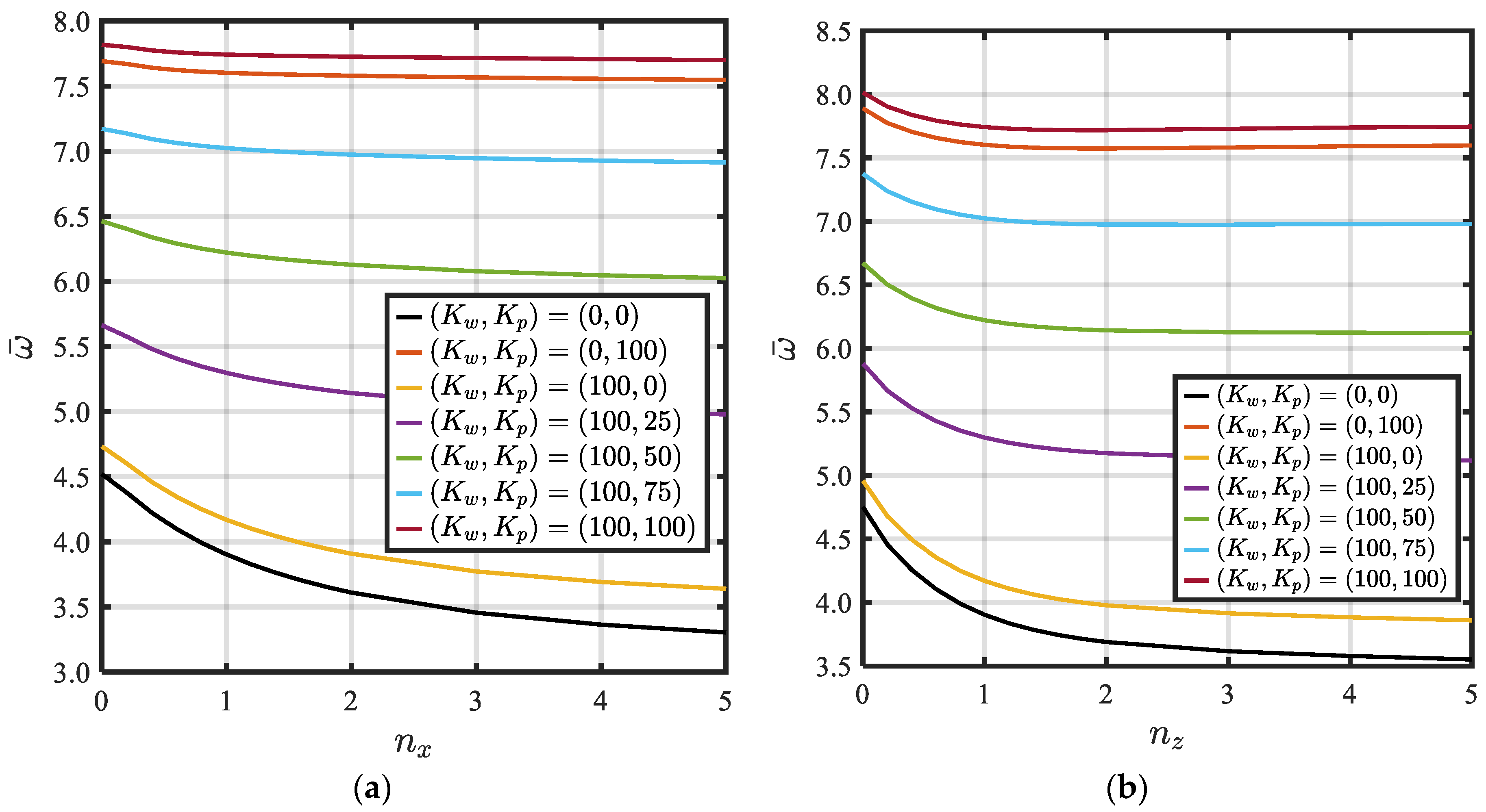
- Effect of Elastic foundation parameters
5. Conclusions
- ➢
- The natural frequencies for all BCs are convergent after .
- ➢
- The Reddy and Thai–Kim shear functions are identical for any modes and slenderness ratios. All shear functions give identical values for the third natural frequency at a/h = 5. The Karama shear function gives overestimated natural frequencies for all modes and all slenderness ratios.
- ➢
- The gradation indices in both thickness and axial directions tend to reduce the natural frequencies, due to the decreasing percentage of ceramic phase in the constituent, which causes a reduction in the stiffness.
- ➢
- The greatest natural frequency is noticed in the CCCC case and the minimum is recorded for SFSF boundary conditions. It was found that the natural frequencies for CCCF, CFCF, and SSSS boundary conditions are very close to each other.
- ➢
- It was found that the influence of the side ratio (b/a) on the natural frequency is decreased for higher side ratios.
- ➢
- The natural frequency is dependent on the coupled effects of porosity type, porosity value, and gradation indices.
- ➢
- The fundamental frequency is raised by raising the elastic foundation parameters . However, it is observed that the impact of is more significant than the impact of on the fundamental frequency.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| The displacement field of unified plate theory | Thickness of the plate | ||
| Thickness coordinate | Metal material property | ||
| Shape shear distribution function | Ceramic material property | ||
| Young modulus | Shear correction factor | ||
| Poisson’s ratio | Winkler modulus parameter | ||
| density | First-order derivative weighting coefficient matrix | ||
| graded indices in the z-direction | Hadamard product operator | ||
| graded indices in the x-direction | Kronecker product | ||
| porosity distribution function | Stiffness and mass matrices, respectively | ||
| porosity coefficient | Fundamental linear frequency |
Appendix A
- Clamped edge:
- Simply supported edge:
- Free edge:
Appendix B
References
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Flexomagneticity in Functionally Graded Nanostructures. In Advanced Materials Modelling for Mechanical, Medical and Biological Applications; Springer: Cham, Germany, 2022; pp. 321–335. [Google Scholar]
- Sasaki, M.; Hirai, T. Thermal fatigue resistance of CVD SiC/C functionally gradient material. J. Eur. Ceram. Soc. 1994, 14, 257–260. [Google Scholar]
- Esmaeilzadeh, M.; Kadkhodayan, M. Dynamic analysis of stiffened bi-directional functionally graded plates with porosities under a moving load by dynamic relaxation method with kinetic damping. Aerosp. Sci. Technol. 2019, 93, 105333. [Google Scholar] [CrossRef]
- Dorduncu, M.; Olmus, I.; Rabczuk, A.T. Peridynamic approach for modeling of two dimensional functionally graded plates. Compos. Struct. 2022, 279, 114743. [Google Scholar] [CrossRef]
- Esen, I.; Özarpa, C.; Eltaher, M.A. Free vibration of a cracked FG microbeam embedded in an elastic matrix and exposed to magnetic field in a thermal environment. Compos. Struct. 2021, 261, 113552. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Nemat-Alla, M. Reduction of thermal stresses by developing two-dimensional functionally graded materials. Int. J. Solids Struct. 2003, 40, 7339–7356. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, S.; Kang, J.; Lee, J. Bending and free vibration analyses of in-plane bi-directional functionally graded plates with variable thickness using isogeometric analysis. Compos. Struct. 2018, 192, 434–451. [Google Scholar] [CrossRef]
- Wu, C.P.; Yu, L.T. Free vibration analysis of bi-directional functionally graded annular plates using finite annular prism methods. J. Mech. Sci. Technol. 2019, 33, 2267–2279. [Google Scholar] [CrossRef]
- Hashemi, S.; Jafari, A.A. Nonlinear Free and Forced Vibrations of In-Plane Bi-Directional Functionally Graded Rectangular Plate with Temperature-Dependent Properties. Int. J. Struct. Stab. Dyn. 2020, 20, 2050097. [Google Scholar] [CrossRef]
- Ghatage, P.S.; Kar, V.R.; Sudhagar, P.E. On the numerical modelling and analysis of multi-directional functionally graded composite structures: A review. Compos. Struct. 2020, 236, 111837. [Google Scholar] [CrossRef]
- Pham, Q.H.; Nguyen, P.C.; Tran, V.K.; Nguyen-Thoi, T. Isogeometric analysis for free vibration of bidirectional functionally graded plates in the fluid medium. Def. Technol. 2022, 18, 1311–1329. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Huang, S.; Li, M.; Li, X. Nonlinear forced vibration of in-plane bi-directional functionally graded materials rectangular plate with global and localized geometrical imperfections. Appl. Math. Model. 2021, 93, 443–466. [Google Scholar] [CrossRef]
- Mohammadian, M. Nonlinear free vibration of damped and undamped bi-directional functionally graded beams using a cubic-quintic nonlinear model. Compos. Struct. 2021, 255, 112866. [Google Scholar] [CrossRef]
- Abo-Bakr, H.M.; Abo-Bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Multi-objective shape optimization for axially functionally graded microbeams. Compos. Struct. 2021, 258, 113370. [Google Scholar] [CrossRef]
- Abo-Bakr, R.M.; Shanab, R.A.; Attia, M.A. Multi-objective optimization for lightweight design of bi-directional functionally graded beams for maximum frequency and buckling load. Compos. Struct. 2021, 278, 114691. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M.; Vo, T.P. A comprehensive study on the size-dependent analysis of strain gradient multi-directional functionally graded microplates via finite element model. Aerosp. Sci. Technol. 2021, 111, 106550. [Google Scholar] [CrossRef]
- Patpatiya, P.; Chaudhary, K.; Shastri, A.; Sharma, S. A review on polyjet 3D printing of polymers and multi-material structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 09544062221079506. [Google Scholar] [CrossRef]
- Attia, M.A.; Shanab, R.A. On the dynamic response of bi-directional functionally graded nanobeams under moving harmonic load accounting for surface effect. Acta Mech. 2022, 233, 3291–3317. [Google Scholar] [CrossRef]
- Attia, M.A.; Shanab, R.A. Vibration characteristics of two-dimensional FGM nanobeams with couple stress and surface energy under general boundary conditions. Aerosp. Sci. Technol. 2021, 111, 106552. [Google Scholar] [CrossRef]
- Whitney, J.M.; Pagano, N.J. Shear deformation in heterogeneous anisotropic plates. J. Appl. Mech. 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Reddy, J.N. Free vibration of antisymmetric, angle-ply laminated plates including transverse shear deformation by the finite element method. J. Sound Vib. 1979, 66, 565–576. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Assie, A.E.; Mohamed, S.M.; Shanab, R.A.; Abo-bakr, R.M.; Eltaher, M.A. Static Buckling of 2D FG Porous Plates Resting on Elastic Foundation based on Unified Shear Theories. J. Appl. Comput. Mech. 2023, 9, 239–258. [Google Scholar] [CrossRef]
- Assie, A.E.; Eltaher, M.A.; Mahmoud, F.F. Behavior of a viscoelastic composite plates under transient load. J. Mech. Sci. Technol. 2011, 25, 1129–1140. [Google Scholar] [CrossRef]
- Assie, A.E.; Kabeel, A.M.; Mahmoud, F.F. Optimum design of laminated composite plates under dynamic excitation. Appl. Math. Model. 2012, 36, 668–682. [Google Scholar] [CrossRef]
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Thermal buckling of functionally graded piezomagnetic micro-and nanobeams presenting the flexomagnetic effect. Contin. Mech. Thermodyn. 2022, 34, 1051–1066. [Google Scholar] [CrossRef]
- Vu, T.V.; Nguyen, H.T.; Nguyen-Van, H.; Nguyen, T.P.; Curiel-Sosa, J.L. A refined quasi-3D logarithmic shear deformation theory-based effective meshfree method for analysis of functionally graded plates resting on the elastic foundation. Eng. Anal. Bound. Elem. 2021, 131, 174–193. [Google Scholar] [CrossRef]
- Raissi, H. Stress analysis in adhesive layers of a five-layer circular sandwich plate subjected to temperature gradient based on layerwise theory. Mech. Based Des. Struct. Mach. 2022, 50, 2274–2300. [Google Scholar] [CrossRef]
- Van Vinh, P. Deflections, stresses and free vibration analysis of bi-functionally graded sandwich plates resting on Pasternak’s elastic foundations via a hybrid quasi-3D theory. Mech. Based Des. Struct. Mach. 2021, 1–32. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Eltaher, M.A. A novel nonlocal strain gradient Quasi-3D bending analysis of sigmoid functionally graded sandwich nanoplates. Compos. Struct. 2021, 262, 113347. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Belarbi, M.O.; Mohamed, S.A.; Eltaher, M.A. Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory. Def. Technol. 2021, 18, 1778–1809. [Google Scholar] [CrossRef]
- Li, M.; Soares, C.G.; Yan, R. Free vibration analysis of FGM plates on Winkler/Pasternak/Kerr foundation by using a simple quasi-3D HSDT. Compos. Struct. 2021, 264, 113643. [Google Scholar] [CrossRef]
- Duc, N.D.; Minh, P.P. Free vibration analysis of cracked FG CNTRC plates using phase field theory. Aerosp. Sci. Technol. 2021, 112, 106654. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, P.C.; Pham, Q.H. Vibration analysis of FGM plates in thermal environment resting on elastic foundation using ES-MITC3 element and prediction of ANN. Case Stud. Therm. Eng. 2021, 24, 100852. [Google Scholar] [CrossRef]
- Sadgui, A.; Tati, A. A novel trigonometric shear deformation theory for the buckling and free vibration analysis of functionally graded plates. Mech. Adv. Mater. Struct. 2021, 1–16. [Google Scholar] [CrossRef]
- Naghsh, M.A.; Sarrami-Foroushani, S.; Azhari, M.; Mohajeri, S. Static and dynamic instability analysis of tapered CNTRC sandwich plates under uniform and non-uniform in-plane loadings using spline finite strip method. Aerosp. Sci. Technol. 2021, 110, 106514. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. 3D Stress Analysis of Multilayered Functionally Graded Plates and Shells under Moisture Conditions. Appl. Sci. 2022, 12, 512. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Abdalla, A.W.; Othman, R.; Almitani, K.H.; Eltaher, M.A. Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Wagih, A.; Othman, R.; Almitani, K.H.; Eltaher, M.A. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics 2022, 10, 408. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Hamed, M.A.; Abo-Bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Influence of axial load function and optimization on static stability of sandwich functionally graded beams with porous core. Eng. Comput. 2020, 36, 1929–1946. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Kiarasi, F. Static response and free-vibration analysis of a functionally graded annular elliptical sector plate made of saturated porous material based on 3D finite element method. Mech. Based Des. Struct. Mach. 2020, 1–25. [Google Scholar] [CrossRef]
- Esmaeilzadeh, M.; Golmakani, M.E.; Sadeghian, M. A nonlocal strain gradient model for nonlinear dynamic behavior of bi-directional functionally graded porous nanoplates on elastic foundations. Mech. Based Des. Struct. Mach. 2020, 1–20. [Google Scholar] [CrossRef]
- Li, S.; Zheng, S.; Chen, D. Porosity-dependent isogeometric analysis of bi-directional functionally graded plates. Thin Walled Struct. 2020, 156, 106999. [Google Scholar] [CrossRef]
- Katiyar, V.; Gupta, A. Vibration response of a geometrically discontinuous bi-directional functionally graded plate resting on elastic foundations in thermal environment with initial imperfections. Mech. Based Des. Struct. Mach. 2021, 1–29. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Gholami, R.; Rouhi, H. Free vibration analysis of postbuckled arbitrary-shaped FG-GPL-reinforced porous nanocomposite plates. Thin Walled Struct. 2021, 163, 107701. [Google Scholar] [CrossRef]
- Abdollahi, M.; Saidi, A.R.; Bahaadini, R. Aeroelastic analysis of symmetric and non-symmetric trapezoidal honeycomb sandwich plates with FG porous face sheets. Aerosp. Sci. Technol. 2021, 119, 107211. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Bashiri, A.H.; Assie, A.E.; Eltaher, M.A. Dynamic analysis of thick beams with functionally graded porous layers and viscoelastic support. J. Vib. Control 2021, 27, 1644–1655. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Fageehi, Y.A.; Assie, A.E.; Eltaher, M.A. Dynamic analysis of viscoelastic functionally graded porous thick beams under pulse load. Eng. Comput. 2022, 38, 365–377. [Google Scholar] [CrossRef]
- Sah, S.K.; Ghosh, A. Influence of porosity distribution on free vibration and buckling analysis of multi-directional functionally graded sandwich plates. Compos. Struct. 2022, 279, 114795. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; CRC Press: Florida, CA, USA, 2006. [Google Scholar]
- Thai, H.T.; Kim, S.E. Closed-form solution for buckling analysis of thick functionally graded plates on elastic foundation. Int. J. Mech. Sci. 2013, 75, 34–44. [Google Scholar] [CrossRef]
- Taibi, F.Z.; Benyoucef, S.; Tounsi, A.; Bachir Bouiadjra, R.; Adda Bedia, E.A.; Mahmoud, S.R. A simple shear deformation theory for thermo-mechanical behaviour of functionally graded sandwich plates on elastic foundations. J. Sandw. Struct. Mater. 2015, 17, 99–129. [Google Scholar] [CrossRef]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science Business Media: Berlin, Germany, 2012. [Google Scholar]
- Zong, Z. Advanced Differential Quadrature Methods; Chapman and Hall/CRC: London, UK, 2009. [Google Scholar]
- Mohamed, S.A.; Mohamed, N.A.; Abo-Hashem, S.I. A novel differential-integral quadrature method for the solution of nonlinear integro-differential equations. Math. Methods Appl. Sci. 2021, 44, 13945–13967. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Application of generalized differential quadrature element method to free vibration of FG-GPLRC T-shaped plates. Eng. Struct. 2021, 242, 112510. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Free vibration analysis of FG-GPLRC L-shaped plates implementing GDQE approach. ThinWalled Struct. 2021, 162, 107600. [Google Scholar] [CrossRef]
- Coskun, S.; Kim, J.; Toutanji, H. Bending, free vibration, and buckling analysis of functionally graded porous micro-plates using a general third-order plate theory. J. Compos. Sci. 2019, 3, 15. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.N.; Hong, T.T.; Vinh, P.V.; Quang, N.D.; Thom, D.V. A refined simple first-order shear deformation theory for static bending and free vibration analysis of advanced composite plates. Materials 2019, 12, 2385. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 101, 332–340. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Fadaee, M.; Atashipour, S.R. A new exact analytical approach for free vibration of Reissner–Mindlin functionally graded rectangular plates. Int. J. Mech. Sci. 2011, 53, 11–22. [Google Scholar] [CrossRef]
- Reddy, J. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates. Appl. Math. Model. 2013, 37, 3269–3281. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Ehteshami, H. Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]

| Property/ Material | Metal | Ceramic | |||||
|---|---|---|---|---|---|---|---|
| Aluminum | Stainless Steel | Coskun et al. [64] | Alumina | Silicon Nitride | Silicon Carbide (SiC) | Coskun et al. [64] | |
| E(GPa) | 70 | 201.04 | 1.44 | 380 | 348.43 | 420 | 14.4 |
| 0.3 | 0.24 | 0.38 | 0.3 | 0.3 | 0.3 | 0.3 | |
| 2707 | 2370 | 1220 | 3800 | 8166 | 3800 | 12,200 | |
| 0 | 0.5 | 1 | 4 | 10 | ||
|---|---|---|---|---|---|---|
| Touratier | 2 | 0.9308 | 0.8113 | 0.7364 | 0.5921 | 0.5417 |
| Karama | 0.9327 | 0.8127 | 0.7377 | 0.5924 | 0.5428 | |
| Reddy | 0.9297 | 0.8105 | 0.7356 | 0.5924 | 0.5414 | |
| Thai & Kim | 0.9297 | 0.8105 | 0.7356 | 0.5924 | 0.5414 | |
| Taibi | 0.9294 | 0.8103 | 0.7354 | 0.5931 | 0.5417 | |
| Nguyen et al. [65] | 0.9114 | 0.8099 | 0.7445 | 0.6165 | 0.5417 | |
| Matsunaga [66] | 0.9400 | 0.8233 | 0.7477 | 0.5997 | 0.5460 | |
| Thai and Choi [67] | 0.9265 | 0.8062 | 0.7333 | 0.6116 | 0.5644 | |
| Touratier | 5 | 0.2113 | 0.1806 | 0.1631 | 0.1377 | 0.1301 |
| Karama | 0.2114 | 0.1807 | 0.1632 | 0.1377 | 0.1301 | |
| Reddy | 0.2113 | 0.1806 | 0.1631 | 0.1378 | 0.1301 | |
| Thai&Kim | 0.2113 | 0.1806 | 0.1631 | 0.1378 | 0.1301 | |
| Taibi | 0.2113 | 0.1806 | 0.1631 | 0.1379 | 0.1302 | |
| Nguyen et al. [65] | 0.2100 | 0.1808 | 0.1639 | 0.1401 | 0.1304 | |
| Matsunaga [66] | 0.2121 | 0.1819 | 0.1640 | 0.1383 | 0.1306 | |
| Thai and Choi [67] | 0.2112 | 0.1805 | 0.1631 | 0.1397 | 0.1324 | |
| Touratier | 10 | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 |
| Karama | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 | |
| Reddy | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 | |
| Thai&Kim | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 | |
| Taibi | 0.0577 | 0.0490 | 0.0442 | 0.0381 | 0.0364 | |
| Nguyen et al. [65] | 0.0576 | 0.0490 | 0.0443 | 0.0383 | 0.0364 | |
| Matsunaga [66] | 0.0578 | 0.0492 | 0.0443 | 0.0381 | 0.0364 | |
| Thai and Choi [67] | 0.0577 | 0.0490 | 0.0442 | 0.0382 | 0.0366 | |
| 0.5 | 1 | 2 | 5 | 8 | ||
|---|---|---|---|---|---|---|
| Touratier | 1(1,1) | 3.1430 | 2.8353 | 2.5771 | 2.4402 | 2.3924 |
| Karama | 3.1430 | 2.8353 | 2.5771 | 2.4401 | 2.3924 | |
| Reddy | 3.1429 | 2.8352 | 2.5771 | 2.4403 | 2.3925 | |
| Thai&Kim | 3.1429 | 2.8352 | 2.5771 | 2.4403 | 2.3925 | |
| Taibi | 3.1430 | 2.8353 | 2.5771 | 2.4404 | 2.3926 | |
| Nguyen et al. [65] | 3.1457 | 2.8358 | 2.5785 | 2.4423 | 2.3933 | |
| Hosseini et al. [68] | 3.1456 | 2.8352 | 2.5777 | 2.4425 | 2.3948 | |
| Reddy [69] | 3.1458 | 2.8352 | 2.5771 | 2.4403 | 2.3923 | |
| Thai and Vo [70] | 3.1458 | 2.8353 | 2.5771 | 2.4401 | 2.3922 | |
| Touratier | 2(1,2) | 5.0135 | 4.5228 | 4.1100 | 3.8881 | 3.8108 |
| Karama | 5.0136 | 4.5229 | 4.1101 | 3.8879 | 3.8108 | |
| Reddy | 5.0134 | 4.5228 | 4.1100 | 3.8884 | 3.8110 | |
| Thai&Kim | 5.0134 | 4.5228 | 4.1100 | 3.8884 | 3.8110 | |
| Taibi | 5.0135 | 4.5228 | 4.1101 | 3.8887 | 3.8113 | |
| Nguyen et al. [65] | 5.0179 | 4.5244 | 4.1136 | 3.8936 | 3.8134 | |
| Hosseini et al. [68] | 5.0175 | 4.5228 | 4.1115 | 3.8939 | 3.8170 | |
| Reddy [69] | 5.0180 | 4.5228 | 4.1100 | 3.8884 | 3.8107 | |
| Thai and Vo [70] | 5.0180 | 4.5228 | 4.1100 | 3.8881 | 3.8105 | |
| Touratier | 3(1,3) | 8.1062 | 7.3133 | 6.6432 | 6.2753 | 6.1476 |
| Karama | 8.1066 | 7.3137 | 6.6434 | 6.2749 | 6.1474 | |
| Reddy | 8.1061 | 7.3132 | 6.6433 | 6.2761 | 6.1481 | |
| Thai&Kim | 8.1061 | 7.3132 | 6.6433 | 6.2761 | 6.1481 | |
| Taibi | 8.1061 | 7.3133 | 6.6435 | 6.2769 | 6.1488 | |
| Nguyen et al. [65] | 8.1133 | 7.3176 | 6.6527 | 6.2896 | 6.1547 | |
| Hosseini et al. [68] | 8.1121 | 7.3132 | 6.6471 | 6.2903 | 6.1639 | |
| Reddy [69] | 8.1133 | 7.3132 | 6.6433 | 6.2760 | 6.1476 | |
| Thai and Vo [70] | 8.1135 | 7.3133 | 6.6432 | 6.2753 | 6.1471 | |
| 0 | 0.5 | 1 | 2 | ||
|---|---|---|---|---|---|
| Touratier | 0.4151 | 0.3548 | 0.3205 | 0.2892 | |
| Karama | 0.4153 | 0.3550 | 0.3207 | 0.2893 | |
| Reddy | 0.4150 | 0.3548 | 0.3205 | 0.2892 | |
| Thai&Kim | 0.4150 | 0.3548 | 0.3205 | 0.2892 | |
| Taibi | 0.4151 | 0.3548 | 0.3205 | 0.2893 | |
| Vu et al. [28] | 0.4199 | 0.3603 | 0.3282 | 0.3001 | |
| Baferani et al. [71] | 0.4154 | 0.3606 | 0.3299 | 0.3016 | |
| Touratier | 0.6075 | 0.5856 | 0.5753 | 0.5695 | |
| Karama | 0.6076 | 0.5857 | 0.5753 | 0.5695 | |
| Reddy | 0.6075 | 0.5856 | 0.5753 | 0.5694 | |
| Thai&Kim | 0.6075 | 0.5856 | 0.5753 | 0.5694 | |
| Taibi | 0.6075 | 0.5856 | 0.5753 | 0.5695 | |
| Vu et al. [28] | 0.6134 | 0.5916 | 0.5823 | 0.5776 | |
| Baferani et al. [71] | 0.6080 | 0.5932 | 0.5876 | 0.5861 | |
| Touratier | 0.4270 | 0.3700 | 0.3381 | 0.3096 | |
| Karama | 0.4271 | 0.3701 | 0.3382 | 0.3097 | |
| Reddy | 0.4269 | 0.3700 | 0.3381 | 0.3097 | |
| Thai&Kim | 0.4269 | 0.3700 | 0.3381 | 0.3097 | |
| Taibi | 0.4269 | 0.3700 | 0.3381 | 0.3097 | |
| Vu et al. [28] | 0.4309 | 0.3745 | 0.3445 | 0.3189 | |
| Baferani et al. [71] | 0.4273 | 0.3758 | 0.3476 | 0.3219 | |
| Touratier | 0.6157 | 0.5949 | 0.5852 | 0.5754 | |
| Karama | 0.6158 | 0.5950 | 0.5853 | 0.5754 | |
| Reddy | 0.6156 | 0.5949 | 0.5852 | 0.5754 | |
| Thai&Kim | 0.6156 | 0.5949 | 0.5852 | 0.5754 | |
| Taibi | 0.6156 | 0.5949 | 0.5852 | 0.5754 | |
| Vu et al. [28] | 0.6210 | 0.6004 | 0.5917 | 0.5876 | |
| Baferani et al. [71] | 0.6162 | 0.6026 | 0.5978 | 0.5970 | |
| 0 | 2 | 5 | |
|---|---|---|---|
| Touratier | 1.1355 | 0.8738 | 0.8191 |
| Karama | 1.1357 | 0.8739 | 0.8193 |
| Reddy | 1.1355 | 0.8737 | 0.8191 |
| Thai&Kim | 1.1355 | 0.8737 | 0.8191 |
| Taibi | 1.1355 | 0.8738 | 0.8191 |
| Pham et al. [12] | 1.1371 | 0.8726 | 0.8179 |
| Li et al. [47] | 1.1066 | 0.8604 | 0.8082 |
| BCs | |||||||
|---|---|---|---|---|---|---|---|
| 8 | 10 | 12 | 14 | 16 | 18 | 20 | |
| CCCC | 7.0292 | 6.9962 | 6.9898 | 6.9873 | 6.9859 | 6.9849 | 6.9841 |
| SCSC | 5.7122 | 5.6956 | 5.6933 | 5.6924 | 5.6920 | 5.6918 | 5.6915 |
| CCCF | 4.9200 | 4.7720 | 4.7020 | 4.6694 | 4.6544 | 4.6460 | 4.6392 |
| CFCF | 4.4474 | 4.3620 | 4.3200 | 4.3012 | 4.2927 | 4.2887 | 4.2899 |
| SSSS | 3.9122 | 3.9040 | 3.9027 | 3.9025 | 3.9025 | 3.9025 | 3.9025 |
| SCSF | 2.5560 | 2.5197 | 2.5173 | 2.5173 | 2.5173 | 2.5173 | 2.5173 |
| SSSF | 2.3402 | 2.3203 | 2.3188 | 2.3188 | 2.3189 | 2.3189 | 2.3189 |
| SFSF | 1.9330 | 1.9180 | 1.9171 | 1.9172 | 1.9172 | 1.9173 | 1.9173 |
| Mode | ||||
|---|---|---|---|---|
| 5 | 10 | 20 | ||
| Touratier | 1(1,1) | 3.4964 | 3.8073 | 3.9025 |
| Karama | 3.4979 | 3.8078 | 3.9026 | |
| Reddy | 3.4958 | 3.8072 | 3.9025 | |
| Thai&Kim | 3.4958 | 3.8072 | 3.9025 | |
| Taibi | 3.4960 | 3.8072 | 3.9025 | |
| Touratier | 2(1,2) | 6.6013 | 9.0607 | 9.5980 |
| Karama | 6.6013 | 9.0633 | 9.5987 | |
| Reddy | 6.6013 | 9.0598 | 9.5977 | |
| Thai&Kim | 6.6013 | 9.0598 | 9.5977 | |
| Taibi | 6.6013 | 9.0602 | 9.5979 | |
| Touratier | 3(1,3) | 6.7222 | 9.0717 | 9.6068 |
| Karama | 6.7222 | 9.0742 | 9.6075 | |
| Reddy | 6.7222 | 9.0708 | 9.6065 | |
| Thai&Kim | 6.7222 | 9.0708 | 9.6065 | |
| Taibi | 6.7222 | 9.0711 | 9.6067 | |
| BC | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 2 | 5 | ||
| Touratier | CCCC | 8.7451 | 7.6046 | 7.0130 | 6.5025 | 6.1207 |
| Karama | 8.7490 | 7.6079 | 7.0156 | 6.5042 | 6.1204 | |
| Reddy | 8.7434 | 7.6036 | 7.0121 | 6.5020 | 6.1229 | |
| Thai&Kim | 8.7437 | 7.6037 | 7.0117 | 6.5024 | 6.1229 | |
| Taibi | 8.7445 | 7.6036 | 7.0119 | 6.5033 | 6.1260 | |
| Touratier | SCSC | 7.3299 | 6.3311 | 5.8215 | 5.3949 | 5.0984 |
| Karama | 7.3324 | 6.3330 | 5.8227 | 5.3957 | 5.0983 | |
| Reddy | 7.3291 | 6.3310 | 5.8208 | 5.3945 | 5.0999 | |
| Thai&Kim | 7.3296 | 6.3308 | 5.8209 | 5.3948 | 5.1000 | |
| Taibi | 7.3302 | 6.3307 | 5.8208 | 5.3954 | 5.1017 | |
| Touratier | CCCF | 5.8655 | 5.1114 | 4.7346 | 4.4128 | 4.1799 |
| Karama | 5.8677 | 5.1233 | 4.7478 | 4.4075 | 4.1814 | |
| Reddy | 5.8552 | 5.1197 | 4.7431 | 4.4072 | 4.1877 | |
| Thai&Kim | 5.8662 | 5.1297 | 4.7415 | 4.4160 | 4.1792 | |
| Taibi | 5.8611 | 5.1204 | 4.7434 | 4.4163 | 4.1819 | |
| Touratier | CFCF | 5.3721 | 4.6941 | 4.3482 | 4.0508 | 3.8393 |
| Karama | 5.3668 | 4.6960 | 4.3495 | 4.0529 | 3.8383 | |
| Reddy | 5.3757 | 4.6942 | 4.3482 | 4.0508 | 3.8397 | |
| Thai&Kim | 5.3663 | 4.6948 | 4.3483 | 4.0521 | 3.8397 | |
| Taibi | 5.3738 | 4.6951 | 4.3466 | 4.0530 | 3.8411 | |
| Touratier | SSSS | 5.1177 | 4.4128 | 4.0581 | 3.7699 | 3.5860 |
| Karama | 5.1184 | 4.4133 | 4.0586 | 3.7702 | 3.5859 | |
| Reddy | 5.1175 | 4.4126 | 4.0579 | 3.7700 | 3.5866 | |
| Thai&Kim | 5.1175 | 4.4126 | 4.0579 | 3.7700 | 3.5866 | |
| Taibi | 5.1176 | 4.4126 | 4.0580 | 3.7702 | 3.5873 | |
| Touratier | SCSF | 3.3319 | 2.8695 | 2.6379 | 2.4520 | 2.3386 |
| Karama | 3.3321 | 2.8697 | 2.6378 | 2.4520 | 2.3384 | |
| Reddy | 3.3329 | 2.8695 | 2.6379 | 2.4521 | 2.3389 | |
| Thai&Kim | 3.3323 | 2.8694 | 2.6377 | 2.4519 | 2.3389 | |
| Taibi | 3.3308 | 2.8694 | 2.6380 | 2.4522 | 2.3392 | |
| Touratier | SSSF | 3.0791 | 2.6508 | 2.4365 | 2.2649 | 2.1611 |
| Karama | 3.0793 | 2.6510 | 2.4366 | 2.2650 | 2.1610 | |
| Reddy | 3.0791 | 2.6507 | 2.4364 | 2.2650 | 2.1613 | |
| Thai&Kim | 3.0791 | 2.6507 | 2.4364 | 2.2650 | 2.1613 | |
| Taibi | 3.0791 | 2.6508 | 2.4365 | 2.2651 | 2.1615 | |
| Touratier | SFSF | 2.5710 | 2.2086 | 2.0274 | 1.8832 | 1.7968 |
| Karama | 2.5711 | 2.2087 | 2.0275 | 1.8832 | 1.7967 | |
| Reddy | 2.5709 | 2.2085 | 2.0274 | 1.8832 | 1.7969 | |
| Thai&Kim | 2.5709 | 2.2085 | 2.0274 | 1.8832 | 1.7969 | |
| Taibi | 2.5710 | 2.2086 | 2.0274 | 1.8833 | 1.7971 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melaibari, A.; Mohamed, S.A.; Assie, A.E.; Shanab, R.A.; Eltaher, M.A. Free Vibration Characteristics of Bidirectional Graded Porous Plates with Elastic Foundations Using 2D-DQM. Mathematics 2023, 11, 46. https://doi.org/10.3390/math11010046
Melaibari A, Mohamed SA, Assie AE, Shanab RA, Eltaher MA. Free Vibration Characteristics of Bidirectional Graded Porous Plates with Elastic Foundations Using 2D-DQM. Mathematics. 2023; 11(1):46. https://doi.org/10.3390/math11010046
Chicago/Turabian StyleMelaibari, Ammar, Salwa A. Mohamed, Amr E. Assie, Rabab A. Shanab, and Mohamed A. Eltaher. 2023. "Free Vibration Characteristics of Bidirectional Graded Porous Plates with Elastic Foundations Using 2D-DQM" Mathematics 11, no. 1: 46. https://doi.org/10.3390/math11010046






