The Unfolding: Origins, Techniques, and Applications within Discrete Event Systems
Abstract
:1. Introduction
2. Concurrent Systems
- -
- A representation of the system;
- -
- A representation of the properties to be checked;
- -
- Semantics according to which the representations of the system and of the properties are compared; and
- -
- A method (in most cases automated) for performing this comparison.
3. Prerequisites on Petri Nets
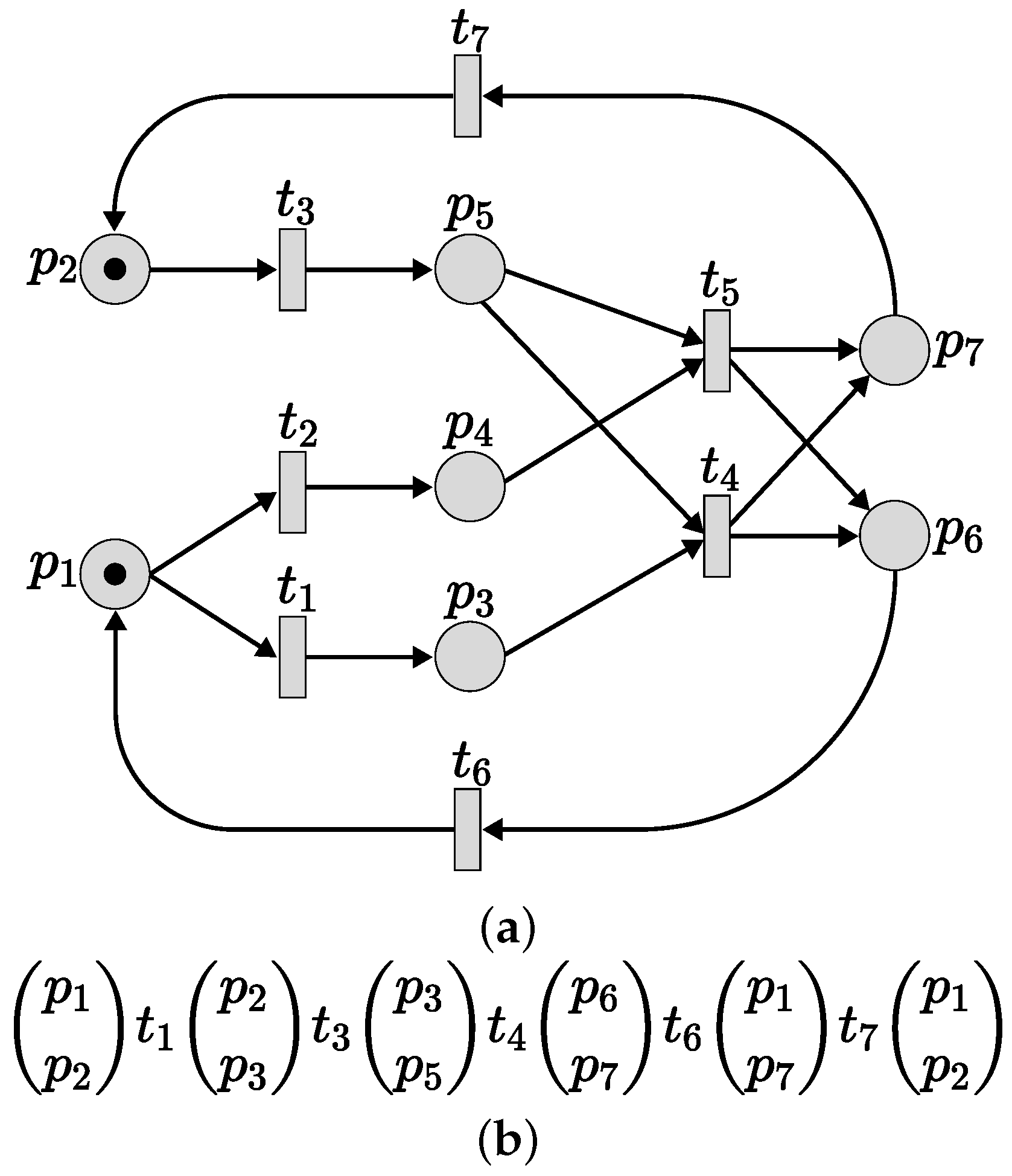
4. Unfolding
4.1. History of Net Unfolding
| Title | Refs. |
|---|---|
| Mathematical theory of computation | [33] |
| Data types as lattices | [34] |
| Net theory | [32] |
| The non-sequential processes | [9] |
| TIme, clocks, and the ordering of events | [23] |
| Denotational semantics and programming language theory | [35] |
| Petri nets, event structures and domains | [15] |
| The non-sequential behavior of Petri nets | [29] |
| Trace theory | [24] |
| Modeling concurrency with partial orders | [25] |
| Event structures | [26] |
| Sequential and concurrent behaviors in net theory | [30] |
| Non-sequential processes | [31] |
| Elementary net systems and behaviours | [36] |
| Pomtrees and behavior machines | [44] |
| The reduced sets “Stubborn sets” | [27] |
| The reduced sets “Persistent sets” | [14] |
| Branching processes of Petri nets | [17] |
| Persistent sets and non-sequential processes | [54] |
| The unfolding technique and deadlock checking (McMillan algorithm) | [16] |
| The reduced sets “Ample sets” | [28] |
| Transition systems, event structures, and unfoldings | [37] |
| Trace verification using unfoldings | [43] |
| Partial-order methods and concurrent systems | [13] |
| The state explosion problem | [55] |
| Foata normal forms (ERV algorithm) | [45,46] |
| Net unfolding and deadlock verification | [49] |
| Products and unfoldings | [47] |
| Stable model semantics for deadlock and reachability problems | [50] |
| Integer Linear Programming with partial-order methods for deadlock verification | [51] |
| Net unfolding as an approach for reachability analysis | [52] |
4.2. Occurrence Nets
- -
- We say that x is a causal predecessor of y, denoted by , if there is a path of arcs from x to y.
- -
- We say that x and y are in conflict, denoted by , if there is a place z, different from x and y, from which one can reach x and y.
- -
- We say that x and y are concurrent, denoted by , if x and y are neither causally related nor in conflict.
- (1)
- For every , ;
- (2)
- is acyclic, or, equivalently, the causal relation is a partial order;
- (3)
- is finitely preceded, i.e., for every , the set of elements such that is finite;
- (4)
- No element is in conflict with itself.
4.3. Branching Processes
- (1)
- and ;
- (2)
- for every , the restriction of to is a bijection between (in ) and (in ). The same goes for postset and . Simply put, preserves the environments of transitions (the preset and postset of transitions);
- (3)
- The restriction of to is a bijection between and . In other words, a net homomorphism also preserves the initial marking.
- (1)
- is an occurrence net;
- (2)
- is a net homomorphism from to N such that for every , if and , then ( does not duplicate the transactions of ).
4.4. Cuts and Configurations
- (1)
- if , then implies ;
- (2)
- contains no mutually conflict events.
4.5. Finite Complete Prefix
- (1)
- , or ;
- (2)
- .
5. Net Unfolding Applications
5.1. Properties & Formal Verification
5.1.1. Fundamental Properties’ Verification
5.1.2. Security
5.1.3. Supervisory Control
5.1.4. Fault Detection and Diagnosis
5.2. Generalizations
| Title | Refs. |
|---|---|
| McMillan’s unfolding technique | [16] |
| ERV unfolding technique | [45,46] |
| ILP-based approaches | [49,51] |
| SAT-based, Symbolic-based approaches | [41,50,60,94,95] |
| Graph-based (CLIQUES) | [52] |
| Goal-driven | [59] |
| Canonical Prefixes | [98] |
| Merged processes | [100] |
| Trellis processes | [91] |
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ho, Y.C. Introduction to special issue on dynamics of discrete event systems. Proc. IEEE 1989, 77, 3–6. [Google Scholar] [CrossRef]
- Silva, M. On the history of discrete event systems. Annu. Rev. Control 2018, 45, 213–222. [Google Scholar] [CrossRef]
- Petri, C.A. Kommunikation Mit Automaten. Ph.D. Thesis, University of Bonn, Bonn, Germany, 1962. [Google Scholar]
- Rozenberg, G. Behaviour of elementary net systems. In Petri Nets: Central Models and Their Properties; Springer: Berlin/Heidelberg, Germany, 1987; pp. 60–94. [Google Scholar]
- Esparza, J.; Heljanko, K. Unfoldings: A Partial-Order Approach to Model Checking; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Godefroid, P.; Wolper, P. Using partial orders for the efficient verification of deadlock freedom and safety properties. In Proceedings of the International Conference on Computer Aided Verification, Aalborg, Denmark, 1–4 July 1991; pp. 332–342. [Google Scholar]
- Cabasino, M.P.; Giua, A.; Seatzu, C. Fault detection for discrete event systems using Petri nets with unobservable transitions. Automatica 2010, 46, 1531–1539. [Google Scholar] [CrossRef] [Green Version]
- Tong, Y.; Li, Z.; Seatzu, C.; Giua, A. Verification of state-based opacity using Petri nets. IEEE Trans. Autom. Control 2016, 62, 2823–2837. [Google Scholar] [CrossRef] [Green Version]
- Petri, C.A. Nichtsequentielle Prozesse Arbeitsberichte des IMMD, Bd. 9, Heft. 8, p.57ff. In Non-Sequential Processes; Krause, P.; Low, J., Translators; Internal Report GMD-ISF-77-05; Universität Erlangen-Nürnberg: Bonn, Germany, 1977. [Google Scholar]
- Mazurkiewicz, A. Concurrent Program Schemes and their Interpretations. DAIMI Rep. Ser. 1977, 6, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Winskel, G. Events in Computation. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 1980. [Google Scholar]
- Valmari, A. Stubborn sets for reduced state space generation. In Proceedings of the Advances in Petri Nets, Bonn, Germany, 13 March 1990; Rozenberg, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 491–515. [Google Scholar]
- Godefroid, P. Partial-Order Methods for the Verification of Concurrent Systems: An Approach to the State-Explosion Problem; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Godefroid, P. Using partial orders to improve automatic verification methods. In Proceedings of the International Conference on Computer Aided Verification, New Brunswick, NJ, USA, 18–21 June 1990; pp. 176–185. [Google Scholar]
- Nielsen, M.; Plotkin, G.; Winskel, G. Petri nets, event structures and domains, part I. Theor. Comput. Sci. 1981, 13, 85–108. [Google Scholar] [CrossRef] [Green Version]
- McMillan, K.L. Using unfoldings to avoid the state explosion problem in the verification of asynchronous circuits. In Proceedings of the International Conference on Computer Aided Verification, Montreal, QC, Canada, 29 June–1 July 1992; pp. 164–177. [Google Scholar]
- Engelfriet, J. Branching processes of Petri nets. Acta Inform. 1991, 28, 575–591. [Google Scholar] [CrossRef]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems; Springer: New York, NY, USA, 2008. [Google Scholar]
- Li, Z.; Zhou, M. Deadlock Resolution in Automated Manufacturing Systems: A Novel Petri Net Approach; Springer Science & Business Media: London, UK, 2009. [Google Scholar]
- Ramadge, P.J.; Wonham, W.M. The control of discrete event systems. Proc. IEEE 1989, 77, 81–98. [Google Scholar] [CrossRef]
- Grumberg, O.; Veith, H. 25 Years of Model Checking: History, Achievements, Perspectives; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5000. [Google Scholar]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Lamport, L. Time, clocks, and the ordering of events in a distributed system. In Concurrency: The Works of Leslie Lamport; Association for Computing Machinery: New York, NY, USA, 2019; pp. 179–196. [Google Scholar]
- Mazurkiewicz, A. Trace theory. In Proceedings of the Advanced Course on Petri Nets, Bad Honnef, Germany, 8–19 September 1986; pp. 278–324. [Google Scholar]
- Pratt, V. Modeling concurrency with partial orders. Int. J. Parallel Program. 1986, 15, 33–71. [Google Scholar] [CrossRef]
- Winskel, G. Event structures. In Proceedings of the Advanced Course on Petri Nets, Bad Honnef, Germany, 8–19 September 1986; pp. 325–392. [Google Scholar]
- Valmari, A. A stubborn attack on state explosion. In Proceedings of the International Conference on Computer Aided Verification, New Brunswick, NJ, USA, 18–21 June 1990; pp. 156–165. [Google Scholar]
- Peled, D. Combining partial order reductions with on-the-fly model-checking. In Proceedings of the International Conference on Computer Aided Verification, Stanford, CA, USA, 21–23 June 1994; pp. 377–390. [Google Scholar]
- Goltz, U.; Reisig, W. The non-sequential behaviour of Petri nets. Inf. Control. 1983, 57, 125–147. [Google Scholar] [CrossRef] [Green Version]
- Best, E.; Devillers, R. Sequential and concurrent behaviour in Petri net theory. Theor. Comput. Sci. 1987, 55, 87–136. [Google Scholar] [CrossRef] [Green Version]
- Best, E.; Fernandez, C.C. Nonsequential Processes: A Petri Net View; EATCS Monographs on Theoretical Computer Science; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Petri, C. General net theory. communication disciplines. In Proceedings of the Joint IBM University of Newcastle upon, Tyne Seminar, Newcastle, GB, USA, 6–9 September 1977. [Google Scholar]
- Scott, D. Outline of a Mathematical Theory of Computation; Oxford University Computing Laboratory, Programming Research Group Oxford: Oxford, UK, 1970. [Google Scholar]
- Scott, D. Data types as lattices. Siam J. Comput. 1976, 5, 522–587. [Google Scholar] [CrossRef] [Green Version]
- Stoy, J.E. Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory; MIT press: Cambridge, MA, USA, 1981. [Google Scholar]
- Nielsen, M.; Rozenberg, G.; Thiagarajan, P.S. Behavioural notions for elementary net systems. Distrib. Comput. 1990, 4, 45–57. [Google Scholar] [CrossRef]
- Nielsen, M.; Rozenberg, G.; Thiagarajan, P. Transition-systems, event structures, and unfoldings. Inf. Comput. 1995, 118, 191–207. [Google Scholar] [CrossRef] [Green Version]
- Winskel, G. An introduction to event structures. In Proceedings of the Workshop/School/Symposium of the REX Project (Research and Education in Concurrent Systems), Noordwijkerhout, The Netherlands, 30 May–3 June 1988; pp. 364–397. [Google Scholar]
- Khomenko, V.; Koutny, M. Branching processes of high-level Petri nets. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Warsaw, Poland, 7–11 April 2003; pp. 458–472. [Google Scholar]
- Liu, F.; Heiner, M.; Yang, M. An efficient method for unfolding colored Petri nets. In Proceedings of the 2012 Winter Simulation Conference (WSC), Berlin, Germany, 9–12 December 2012; pp. 1–12. [Google Scholar]
- Chatain, T.; Jard, C. Symbolic diagnosis of partially observable concurrent systems. In Proceedings of the International Conference on Formal Techniques for Networked and Distributed Systems, Madrid, Spain, 27–30 September 2004; pp. 326–342. [Google Scholar]
- Baldan, P.; Corradini, A.; König, B.; Schwoon, S. McMillan’s complete prefix for contextual nets. In Transactions on Petri Nets and Other Models of Concurrency I; Springer: Berlin/Heidelberg, Germany, 2008; pp. 199–220. [Google Scholar]
- McMillan, K.L. Trace theoretic verification of asynchronous circuits using unfoldings. In Proceedings of the International Conference on Computer Aided Verification, Liege, Belgium, 3–5 July 1995; pp. 180–195. [Google Scholar]
- Probst, D.K.; Li, H.F. Using partial-order semantics to avoid the state explosion problem in asynchronous systems. In Proceedings of the International Conference on Computer Aided Verification, New Brunswick, NJ, USA, 18–21 June 1990; pp. 146–155. [Google Scholar]
- Esparza, J.; Römer, S.; Vogler, W. An improvement of McMillan’s unfolding algorithm. In Proceedings of the International Workshop on Tools and Algorithms for the Construction and Analysis of Systems, Passau, Germany, 27–29 March 1996; pp. 87–106. [Google Scholar]
- Esparza, J.; Römer, S.; Vogler, W. An improvement of McMillan’s unfolding algorithm. Form. Methods Syst. Des. 2002, 20, 285–310. [Google Scholar] [CrossRef]
- Esparza, J.; Römer, S. An unfolding algorithm for synchronous products of transition systems. In Proceedings of the International Conference on Concurrency Theory, Eindhoven, The Netherlands, 24–27 August 1999; pp. 2–20. [Google Scholar]
- McMillan, K.L. Symbolic model checking. In Symbolic Model Checking; Springer: Dordrecht, The Netherlands, 1993; pp. 25–60. [Google Scholar]
- Melzer, S.; Römer, S. Deadlock checking using net unfoldings. In Proceedings of the International Conference on Computer Aided Verification, Haifa, Israel, 22–25 June 1997; pp. 352–363. [Google Scholar]
- Heljanko, K. Using logic programs with stable model semantics to solve deadlock and reachability problems for 1-safe Petri nets. Fundam. Inform. 1999, 37, 247–268. [Google Scholar] [CrossRef]
- Khomenko, V.; Koutny, M. LP deadlock checking using partial order dependencies. In Proceedings of the International Conference on Concurrency Theory, University Park, PA, USA, 22–25 August 2000; pp. 410–425. [Google Scholar]
- Schröter, C.; Esparza, J. Reachability analysis using net unfoldings. In Proceedings of the International Workshop on Concurrency, Specification and Programming (CS&P 2000), University Park, PA, USA, 22–25 August 2000. [Google Scholar]
- Probst, D.K.; Li, H.F. Partial-order model checking: A guide for the perplexed. In Proceedings of the International Conference on Computer Aided Verification, New Brunswick, NJ, USA, 18–21 June 1991; pp. 322–331. [Google Scholar]
- Best, E.; Esparza, J. Model checking of persistent Petri nets. In Proceedings of the International Workshop on Computer Science Logic, Berne, Switzerland, 7–11 October 1991; pp. 35–52. [Google Scholar]
- Valmari, A. The state explosion problem. In Proceedings of the Advanced Course on Petri Nets, Bad Honnef, Germany, 8–19 September 1996; pp. 429–528. [Google Scholar]
- Esparza, J. Model checking using net unfoldings. Sci. Comput. Program. 1994, 23, 151–195. [Google Scholar] [CrossRef] [Green Version]
- Girault, C.; Valk, R. Petri Nets for Systems Engineering: A Guide to Modeling, Verification, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bradfield, J.C. Proving temporal properties of Petri nets. In Proceedings of the International Conference on Application and Theory of Petri Nets, Bonn, Germany, 1 June 1989; pp. 29–47. [Google Scholar]
- Chatain, T.; Paulevé, L. Goal-driven unfolding of Petri nets. arXiv 2016, arXiv:1611.01296. [Google Scholar]
- Abdulla, P.A.; Iyer, S.P.; Nylén, A. Unfoldings of unbounded Petri nets. In Proceedings of the International Conference on Computer Aided Verification, Chicago, IL, USA, 15–19 July 2000; pp. 495–507. [Google Scholar]
- He, K.X.; Lemmon, M.D. Liveness verification of discrete event systems modeled by n-safe ordinary Petri nets. In Proceedings of the International Conference on Application and Theory of Petri Nets, Aarhus, Denmark, 26–30 June 2000; pp. 227–243. [Google Scholar]
- Xie, X.; Giua, A. Counterexamples to “liveness-enforcing supervision of bounded ordinary Petri nets using partial-order methods”. IEEE Trans. Autom. Control 2004, 49, 1217–1219. [Google Scholar] [CrossRef]
- Goguen, J.A.; Meseguer, J. Security policies and security models. In Proceedings of the 1982 IEEE Symposium on Security and Privacy, Oakland, CA, USA, 26–28 April 1982; p. 11. [Google Scholar]
- Bryans, J.W.; Koutny, M.; Ryan, P.Y. Modelling opacity using Petri nets. Electron. Notes Theor. Comput. Sci. 2005, 121, 101–115. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.; Seatzu, C.; Giua, A. Decidability of opacity verification problems in labeled Petri net systems. Automatica 2017, 80, 48–53. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.; Seatzu, C.; Giua, A. Current-state opacity enforcement in discrete event systems under incomparable observations. Discret. Event Dyn. Syst. 2018, 28, 161–182. [Google Scholar] [CrossRef]
- Cong, X.; Fanti, M.P.; Mangini, A.M.; Li, Z. On-line verification of current-state opacity by Petri nets and integer linear programming. Automatica 2018, 94, 205–213. [Google Scholar] [CrossRef]
- Baldan, P.; Carraro, A. Non-interference by unfolding. In Proceedings of the International Conference on Applications and Theory of Petri Nets and Concurrency, Tunis, Tunisia, 23–27 June 2014; pp. 190–209. [Google Scholar]
- Baldan, P.; Burato, F.; Carraro, A. Intransitive non-interference by unfolding. In Proceedings of the International Conference on Formal Aspects of Component Software, Bertinoro, Italy, 10–12 September 2014; pp. 269–287. [Google Scholar]
- Li, Z.; Zhang, J.; Zhao, M. Liveness-enforcing supervisor design for a class of generalised Petri net models of flexible manufacturing systems. IET Control. Theory Appl. 2007, 1, 955–967. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, M. On controllability of dependent siphons for deadlock prevention in generalized Petri nets. IEEE Trans. Syst. Man-Cybern. Part Syst. Hum. 2008, 38, 369–384. [Google Scholar]
- Wang, A.; Li, Z.; Jia, J.; Zhou, M. An effective algorithm to find elementary siphons in a class of Petri nets. IEEE Trans. Syst. Man-Cybern. Part Syst. Hum. 2009, 39, 912–923. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, S.; Zhou, M. A divide-and-conquer strategy to deadlock prevention in flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2009, 39, 156–169. [Google Scholar]
- Chen, Y.; Li, Z. Design of a maximally permissive liveness-enforcing supervisor with a compressed supervisory structure for flexible manufacturing systems. Automatica 2011, 47, 1028–1034. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z. On structural minimality of optimal supervisors for flexible manufacturing systems. Automatica 2012, 48, 2647–2656. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Al-Ahmari, A. Nonpure Petri net supervisors for optimal deadlock control of flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Syst. 2012, 43, 252–265. [Google Scholar] [CrossRef]
- Liu, G.; Li, Z.; Barkaoui, K.; Al-Ahmari, A.M. Robustness of deadlock control for a class of Petri nets with unreliable resources. Inf. Sci. 2013, 235, 259–279. [Google Scholar] [CrossRef]
- Uzam, M.; Li, Z.; Gelen, G.; Zakariyya, R.S. A divide-and-conquer-method for the synthesis of liveness enforcing supervisors for flexible manufacturing systems. J. Intell. Manuf. 2016, 27, 1111–1129. [Google Scholar] [CrossRef]
- He, K.X.; Lemmon, M.D. Liveness-enforcing supervision of bounded ordinary Petri nets using partial order methods. IEEE Trans. Autom. Control. 2002, 47, 1042–1055. [Google Scholar] [CrossRef]
- Giua, A.; Xie, X. Control of safe ordinary Petri nets with marking specifications using unfolding. IFAC Proc. Vol. 2004, 37, 63–68. [Google Scholar] [CrossRef]
- Giua, A.; Xie, X. Control of safe ordinary Petri nets using unfolding. Discret. Event Dyn. Syst. 2005, 15, 349–373. [Google Scholar] [CrossRef] [Green Version]
- Buy, U.; Darabi, H.; Lehene, M.; Venepally, V. Supervisory control of time Petri nets using net unfolding. In Proceedings of the 29th Annual International Computer Software and Applications Conference (COMPSAC’05), Scotland, UK, 25–28 July 2005; Volume 2, pp. 97–100. [Google Scholar]
- Sampath, M.; Sengupta, R.; Lafortune, S.; Sinnamohideen, K.; Teneketzis, D. Diagnosability of discrete-event systems. IEEE Trans. Autom. Control 1995, 40, 1555–1575. [Google Scholar] [CrossRef] [Green Version]
- Cong, X.; Fanti, M.P.; Mangini, A.M.; Li, Z. Decentralized diagnosis by Petri nets and integer linear programming. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1689–1700. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.; Giua, A. On the equivalence of observation structures for Petri net generators. IEEE Trans. Autom. Control 2015, 61, 2448–2462. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Li, Z.; Wu, N. Model-based fault identification of discrete event systems using partially observed Petri nets. Automatica 2018, 96, 201–212. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Z.; Giua, A. Characterization of admissible marking sets in Petri nets with conflicts and synchronizations. IEEE Trans. Autom. Control 2016, 62, 1329–1341. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Li, Z.; Wu, N.; Al-Ahmari, A. Fault identification of discrete event systems modeled by Petri nets with unobservable transitions. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 333–345. [Google Scholar] [CrossRef]
- Benveniste, A.; Fabre, E.; Haar, S.; Jard, C. Diagnosis of asynchronous discrete-event systems: A net unfolding approach. IEEE Trans. Autom. Control 2003, 48, 714–727. [Google Scholar] [CrossRef]
- Fabre, E.; Benveniste, A.; Haar, S.; Jard, C. Distributed monitoring of concurrent and asynchronous systems. Discret. Event Dyn. Syst. 2005, 15, 33–84. [Google Scholar] [CrossRef] [Green Version]
- Fabre, E. Trellis processes: A compact representation for runs of concurrent systems. Discret. Event Dyn. Syst. 2007, 17, 267–306. [Google Scholar] [CrossRef] [Green Version]
- Fabre, E.; Benveniste, A. Partial order techniques for distributed discrete event systems: Why you cannot avoid using them. Discret. Event Dyn. Syst. 2007, 17, 355–403. [Google Scholar] [CrossRef]
- Haar, S. Unfold and cover: Qualitative diagnosability for Petri nets. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 1886–1891. [Google Scholar]
- Haar, S. Types of asynchronous diagnosability and the reveals-relation in occurrence nets. IEEE Trans. Autom. Control 2010, 55, 2310–2320. [Google Scholar] [CrossRef] [Green Version]
- Haar, S.; Rodríguez, C.; Schwoon, S. Reveal your faults: It’s only fair! In Proceedings of the 2013 13th International Conference on Application of Concurrency to System Design, Barcelona, Spain, 8–10 July 2013; pp. 120–129. [Google Scholar]
- Hélouët, L.; Marchand, H. On the cost of diagnosis with disambiguation. In Proceedings of the International Conference on Quantitative Evaluation of Systems, Berlin, Germany, 5–7 September 2017; pp. 140–156. [Google Scholar]
- Khomenko, V.; Koutny, M. Towards an efficient algorithm for unfolding Petri nets. In Proceedings of the International Conference on Concurrency Theory, Aalborg, Denmark, 20–25 August 2001; pp. 366–380. [Google Scholar]
- Khomenko, V.; Koutny, M.; Vogler, W. Canonical prefixes of Petri net unfoldings. Acta Inform. 2003, 40, 95–118. [Google Scholar] [CrossRef]
- Khomenko, V. Model Checking Based on Prefixes of Petri Net Unfoldings. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 2003. [Google Scholar]
- Khomenko, V.; Kondratyev, A.; Koutny, M.; Vogler, W. Merged processes: A new condensed representation of Petri net behaviour. Acta Inform. 2006, 43, 307–330. [Google Scholar] [CrossRef]
- Schwoon, S.; Rodríguez, C. Construction and SAT-based verification of contextual unfoldings. In Proceedings of the International Workshop on Descriptional Complexity of Formal Systems, Giessen/Limburg, Germany, 25–27 July 2011; pp. 34–42. [Google Scholar]
- Hayman, J.; Winskel, G. The unfolding of general Petri nets. In Proceedings of the IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, Bangalore, India, 9–11 December 2008. [Google Scholar]
- Benito, F.C.V.V.; Kunzle, L.A. Relaxed unfolding for time Petri nets. In Proceedings of the 2013 International Conference on Computer Sciences and Applications, Washington, DC, USA, 14–15 December 2013; pp. 833–839. [Google Scholar]
- Frumin, D.; Lomazova, I.A. Branching processes of conservative nested Petri nets. VPT@ CAV 2014, 19, 35. [Google Scholar]
- Jezequel, L.; Chatain, T.; Comlan, M.; Delfieu, D.; Roux, O.H. Pomsets and unfolding of reset Petri nets. In Proceedings of the LATA 2018-12th International Conference on Language and Automata Theory and Applications, Ramat Gan, Israel, 9–11 April 2018. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouabah, Y.; Li, Z. The Unfolding: Origins, Techniques, and Applications within Discrete Event Systems. Mathematics 2023, 11, 47. https://doi.org/10.3390/math11010047
Rouabah Y, Li Z. The Unfolding: Origins, Techniques, and Applications within Discrete Event Systems. Mathematics. 2023; 11(1):47. https://doi.org/10.3390/math11010047
Chicago/Turabian StyleRouabah, Younes, and Zhiwu Li. 2023. "The Unfolding: Origins, Techniques, and Applications within Discrete Event Systems" Mathematics 11, no. 1: 47. https://doi.org/10.3390/math11010047
APA StyleRouabah, Y., & Li, Z. (2023). The Unfolding: Origins, Techniques, and Applications within Discrete Event Systems. Mathematics, 11(1), 47. https://doi.org/10.3390/math11010047






