Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area
Abstract
:1. Introduction
2. Background for Positioning and Dilution of Precision in Ultra-Dense Networks
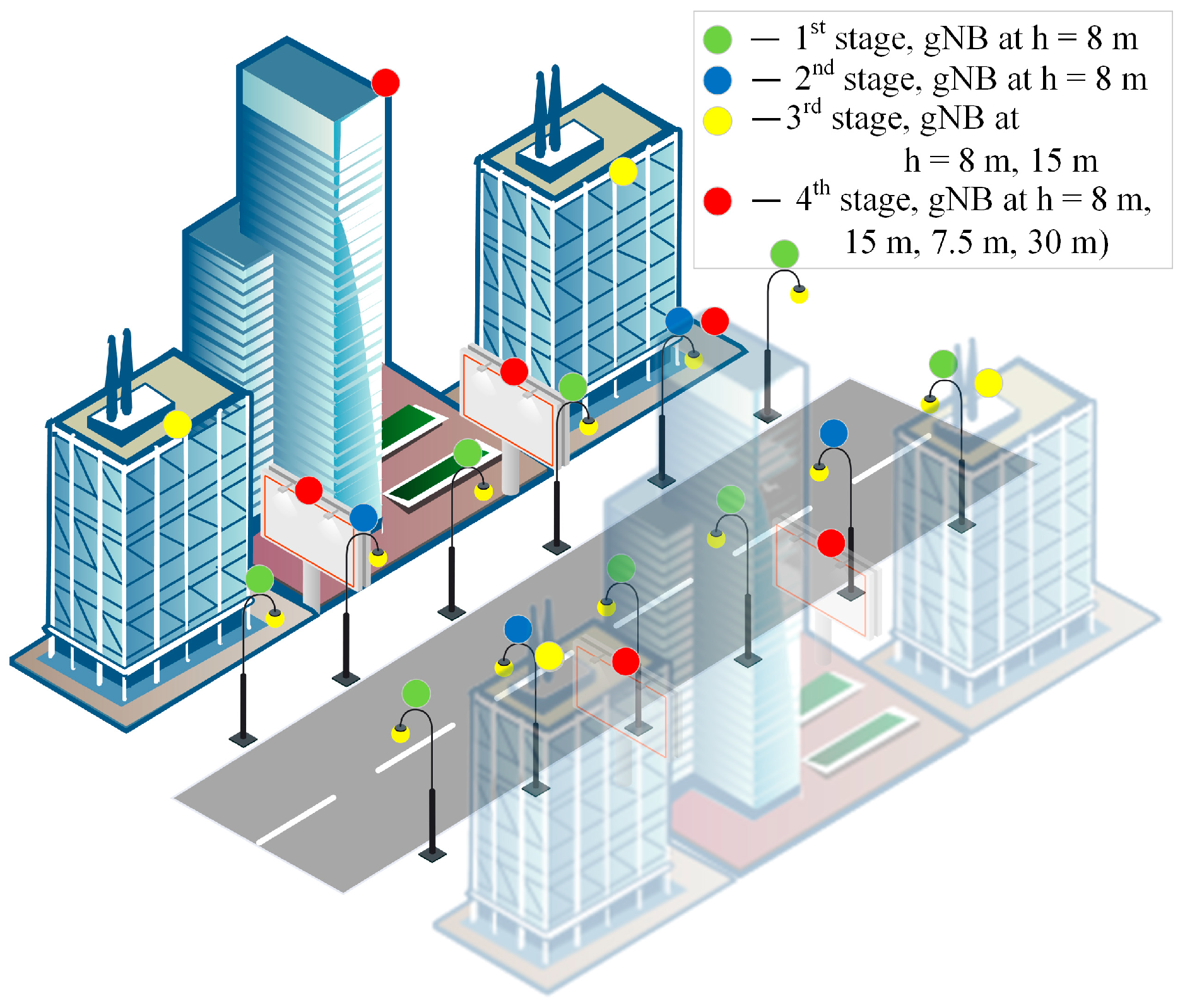
2.1. Ultra-Dense Network Positioning Service Area Scenario
2.2. Topology Search Using Dilution of Precision Criterion Background
2.3. Topology Search Using Dilution of Precision Criterion Problem Statement
3. Methods for Topology Search Using DOP Criteria in UDNs
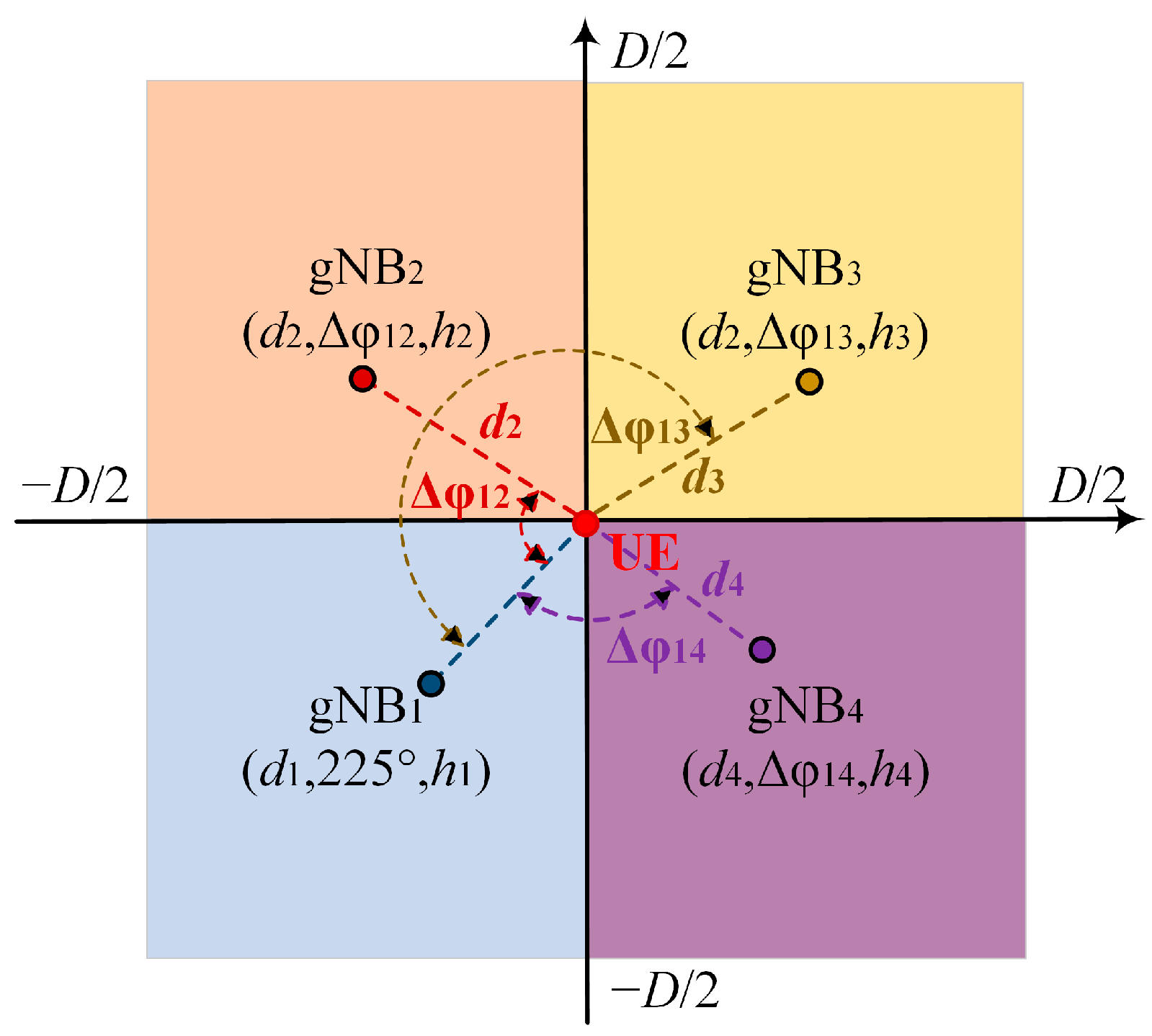
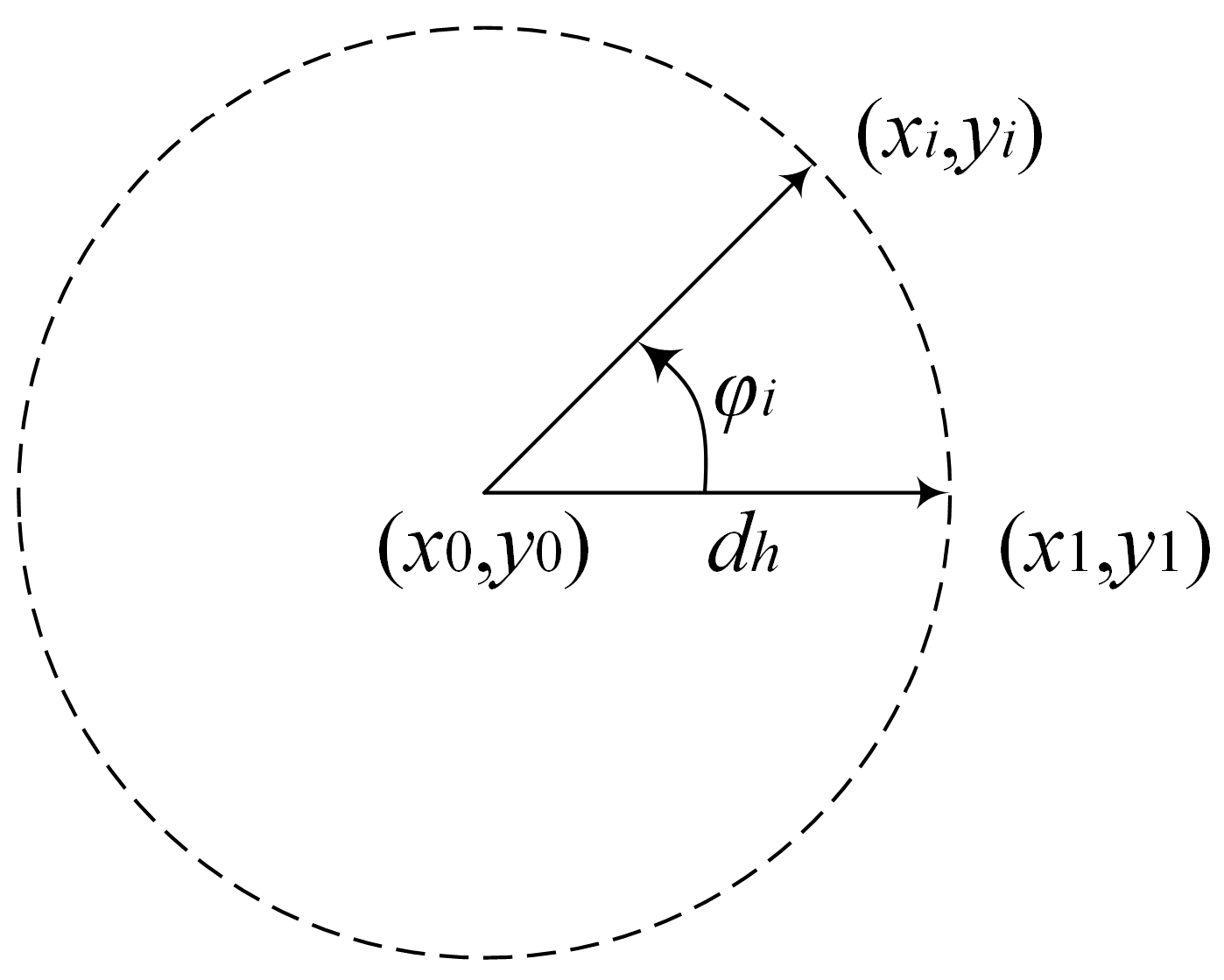
3.1. UE and gNB 3D Layout Geometry
3.2. Model for Primary Measurement Collection
3.3. Methods of Primary Measurement Processing
3.3.1. TOA Measurement Processing
3.3.2. TDOA Measurement Processing
3.3.3. AOA Measurement Processing
3.3.4. Combined TOA–AOA and TDOA–AOA Measurement Processing
3.4. Geometric Dilution of Precision Calculation
4. Models for Topology Search Using DOP Criterion in UDNs
4.1. Spatial Parameters for Topology Search Using DOP Criterion in UDNs
4.2. Procedures for Topology Search Using DOP Criterion in UDNs
4.3. Models for Dilution of Precision Factors Processing
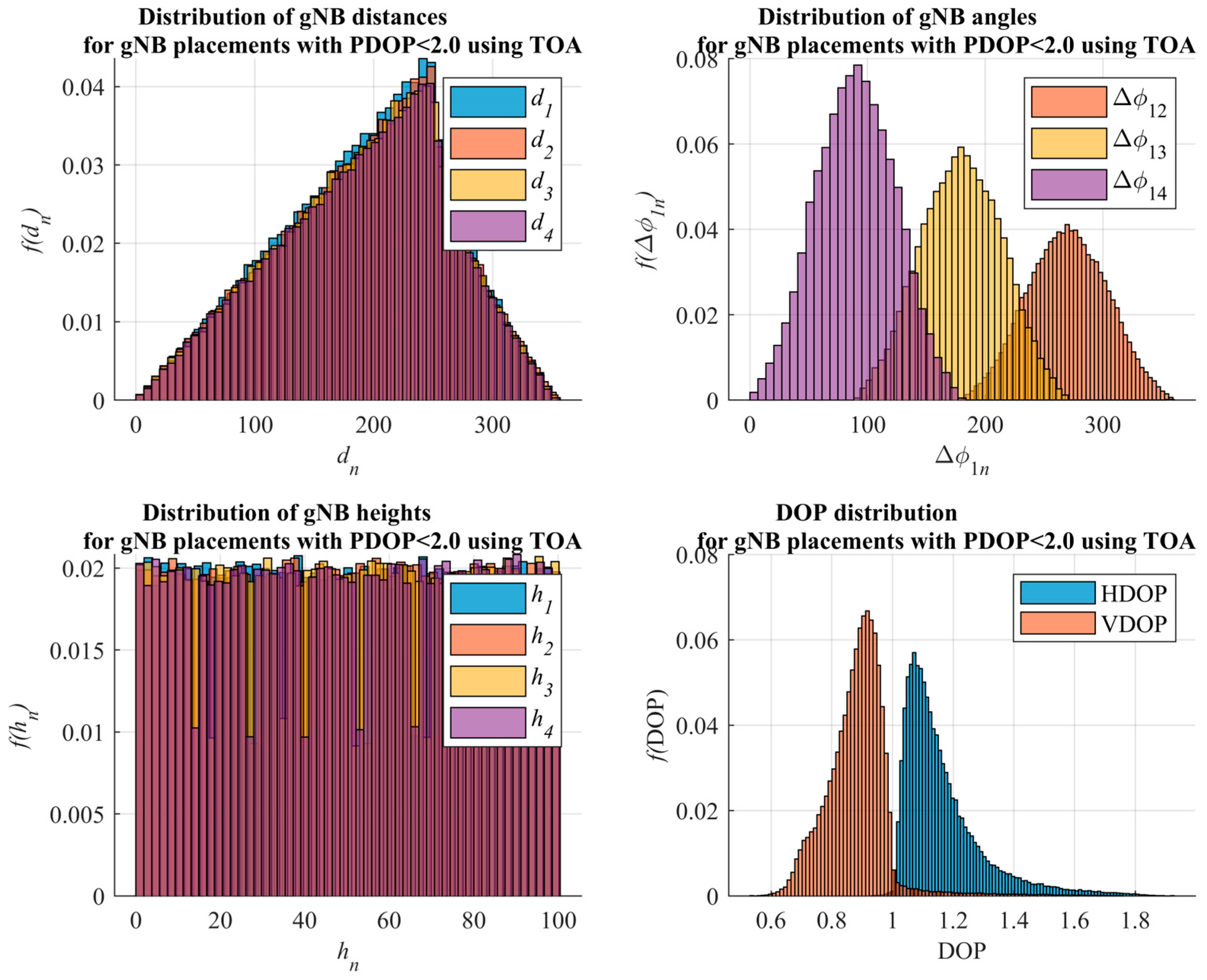
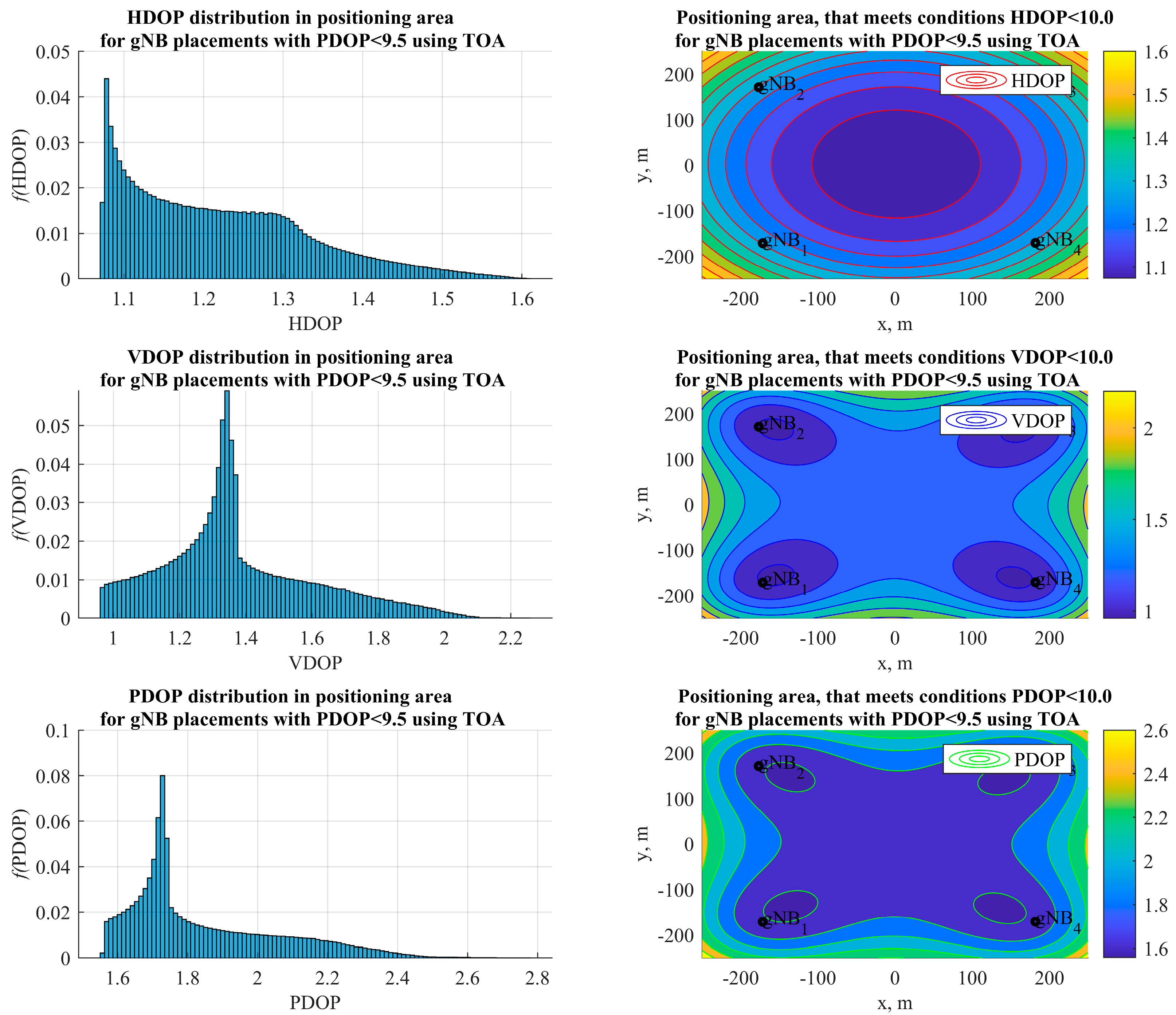
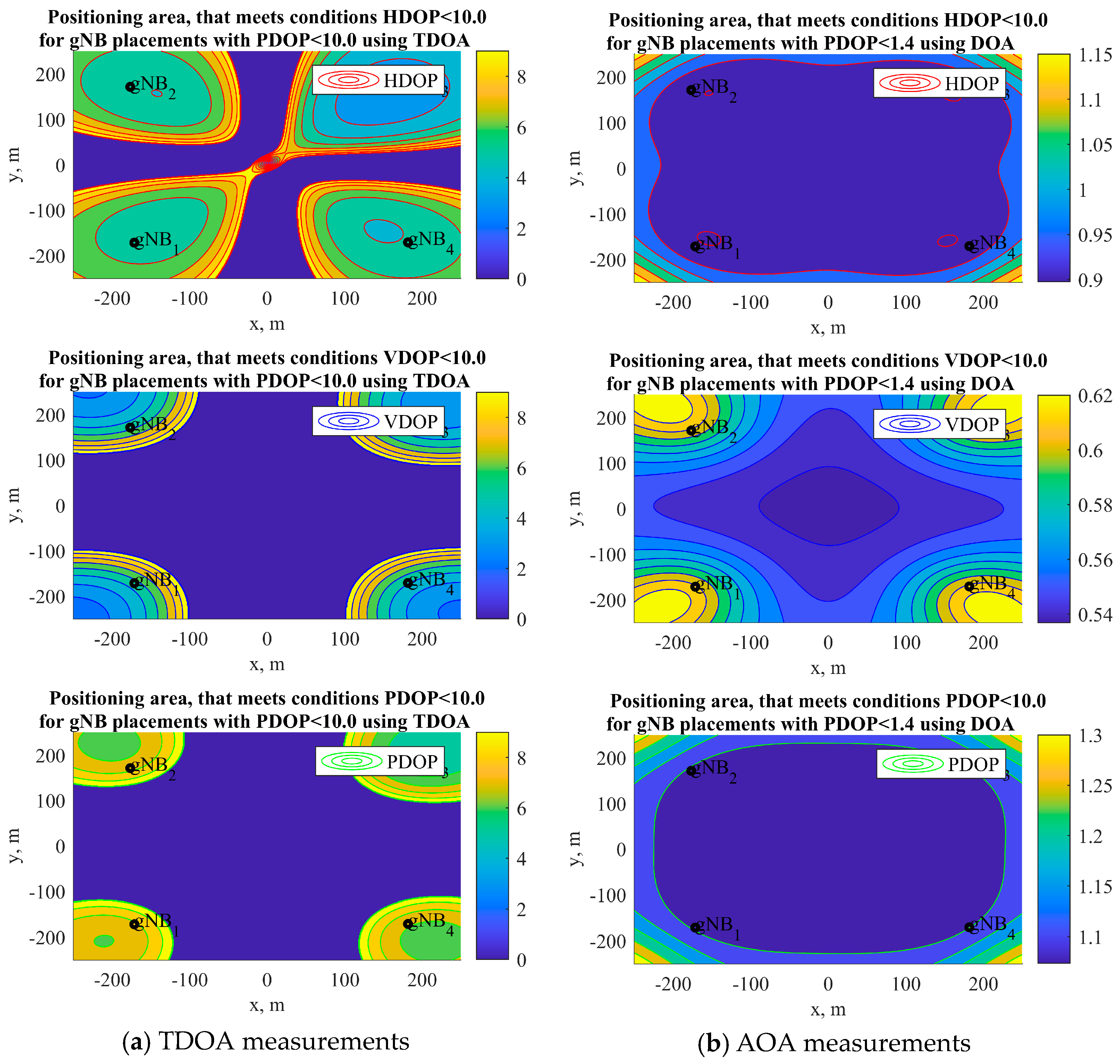
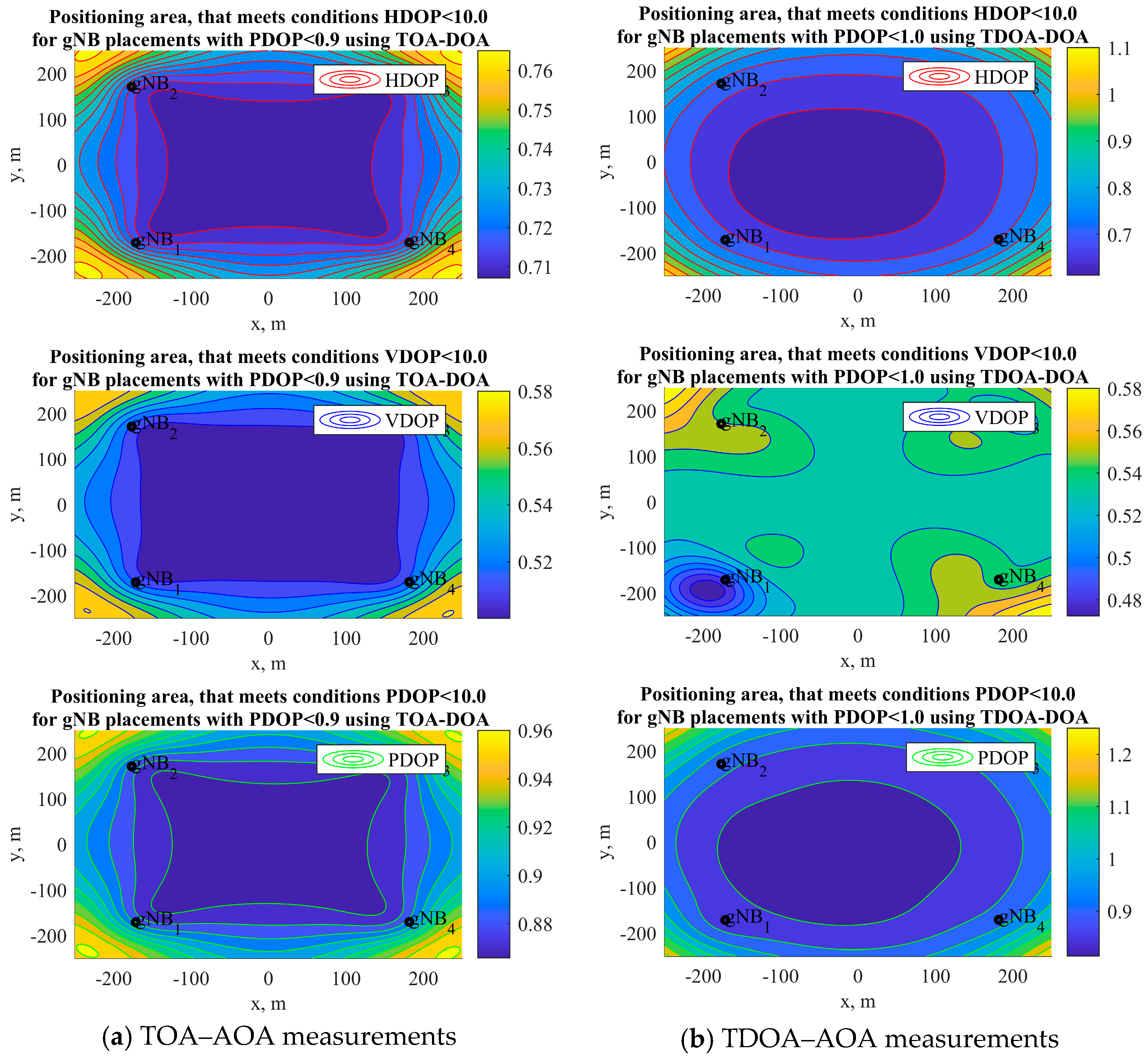
4.4. DOP for Topology of Four gNB Simulation Results Discussion
5. Algorithm for Topology Search Using DOP Criterion in UDN Formalization
5.1. Algorithm Restrictions
5.2. Algorithm Formalization
6. Algorithm for Topology Search Using DOP Criterion in UDN Simulation
6.1. Algorithm Initialization
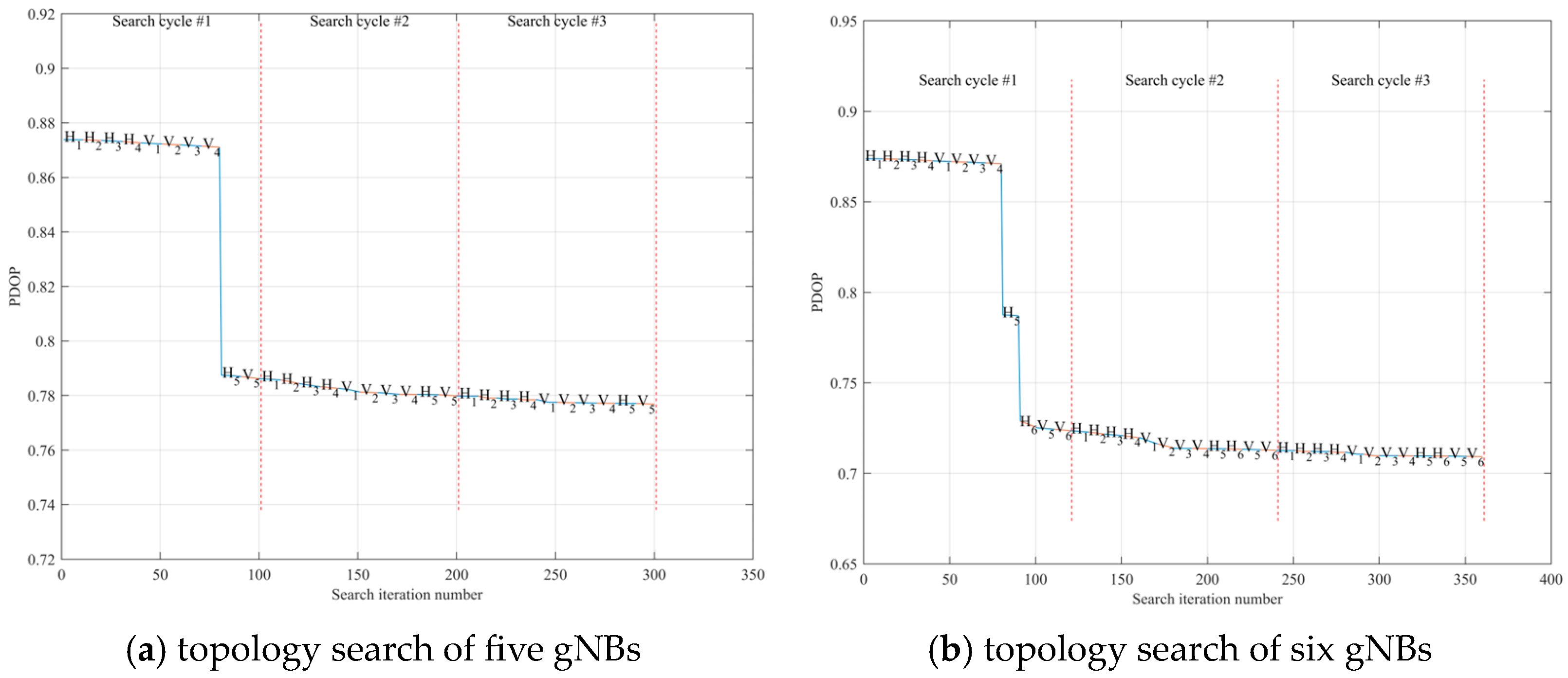
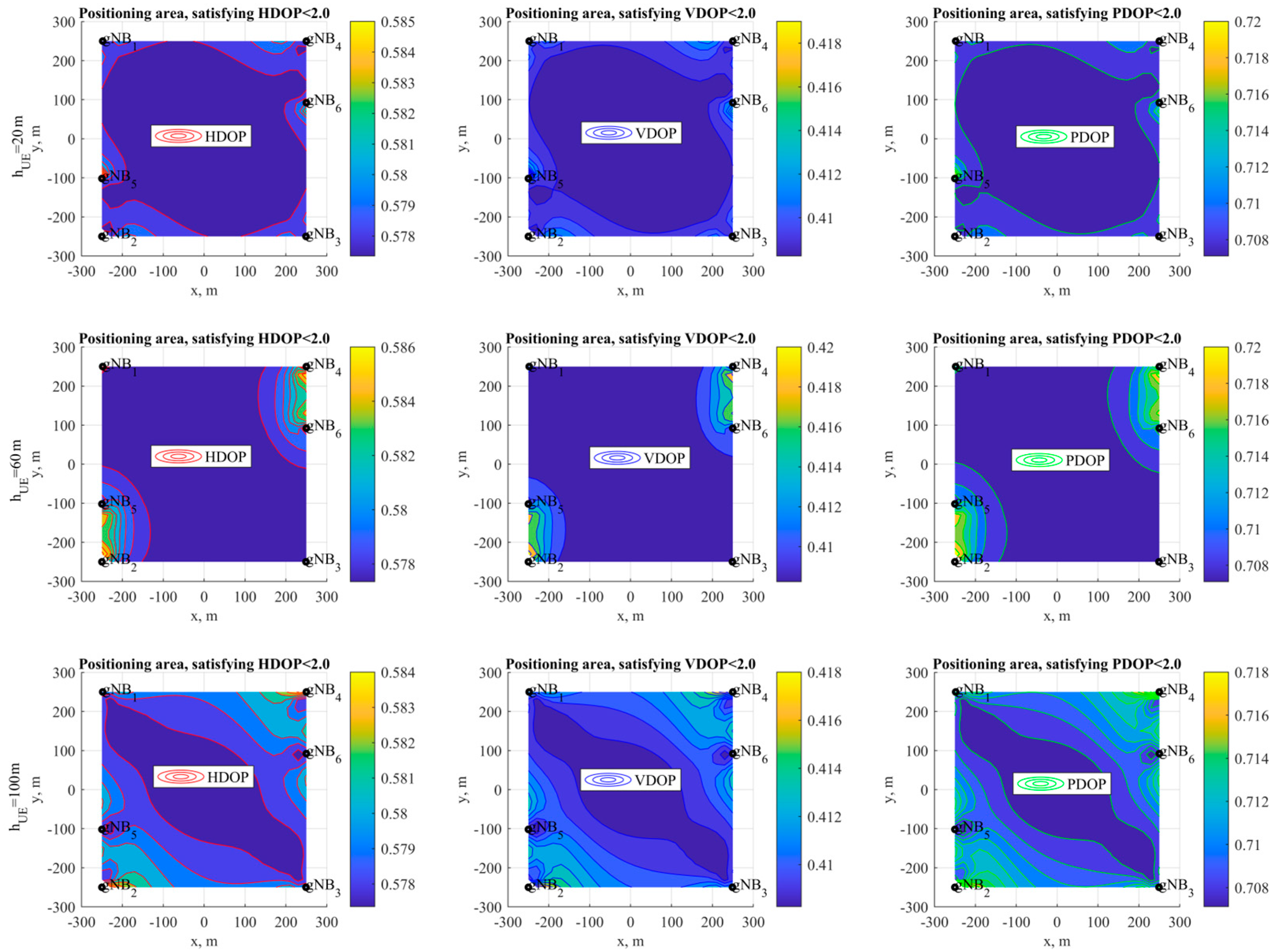
6.2. Algorithm Procedure Simulation Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kanhere, O.; Rappaport, T.S. Position Location for Futuristic Cellular Communications: 5G and Beyond. IEEE Commun. Mag. 2021, 59, 70–75. [Google Scholar] [CrossRef]
- Bartoletti, S.; Chiaraviglio, L.; Fortes, S.; Kennouche, T.E.; Solmaz, G.; Bernini, G.; Giustiniano, D.; Widmer, J.; Barco, R.; Siracusano, G.; et al. Location-based analytics in 5G and beyond. IEEE Commun. Mag. 2021, 59, 38–43. [Google Scholar] [CrossRef]
- Bartoletti, S.; Wymeersch, H.; Mach, T.; Brunnegård, O.; Giustiniano, D.; Hammarberg, P.; Keskin, M.F.; Lacruz, J.O.; Razavi, S.M.; Rönnblom, J.; et al. Positioning and sensing for vehicular safety applications in 5G and beyond. IEEE Commun. Mag. 2021, 59, 15–21. [Google Scholar] [CrossRef]
- Conti, A.; Morselli, F.; Liu, Z.; Bartoletti, S.; Mazuelas, S.; Lindsey, W.C.; Win, M.Z. Location awareness in beyond 5G networks. IEEE Commun. Mag. 2021, 59, 22–27. [Google Scholar] [CrossRef]
- De Lima, C.; Belot, D.; Berkvens, R.; Bourdoux, A.; Dardari, D.; Guillaud, M.; Isomursu, M.; Lohan, E.S.; Miao, Y.; Barreto, A.N.; et al. Convergent Communication, Sensing and Localization in 6G Systems: An Overview of Technologies, Opportunities and Challenges. IEEE Access 2021, 9, 26902–26925. [Google Scholar] [CrossRef]
- Bourdoux, A.; Barreto, A.N.; van Liempd, B.; de Lima, C.; Dardari, D.; Belot, D.; Lohan, E.S.; Seco-Granados, G.; Sarieddeen, H.; Wymeersch, H.; et al. 6G White Paper on Localization and Sensing. arXiv 2020, arXiv:2006.01779. Available online: https://arxiv.org/pdf/2006.01779.pdf (accessed on 27 March 2023).
- Mogyorósi, F.; Revisnyei, P.; Pašić, A.; Papp, Z.; Törös, I.; Varga, P.; Pašić, A. Positioning in 5G and 6G Networks—A Survey. Sensors 2022, 22, 4757. [Google Scholar] [CrossRef] [PubMed]
- Isaia, C.; Michaelides, M.P. A Review of Wireless Positioning Techniques and Technologies: From Smart Sensors to 6G. Signals 2023, 4, 90–136. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Trans. Veh. Technol. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Jia, X.; Liu, P.; Qi, W.; Liu, S.; Huang, Y.; Zheng, W.; Pan, M.; You, X. Link-Level Simulator for 5G Localization. arXiv 2022, arXiv:2212.12998. Available online: https://arxiv.org/pdf/2212.12998.pdf (accessed on 27 March 2023).
- Chen, H.; Sarieddeen, H.; Ballal, T.; Wymeersch, H.; Alouini, M.-S.; Al-Naffouri, T.Y. A Tutorial on Terahertz-Band Localization for 6G Communication Systems. IEEE Commun. Surv. Tutor. 2022, 24, 1780–1815. [Google Scholar] [CrossRef]
- Chen, H.; Keskin, M.F.; Aghdam, S.R.; Kim, H.; Lindberg, S.; Wolfgang, A.; Abrudan, T.E.; Eriksson, T.; Wymeersch, H. Modeling and Analysis of 6G Joint Localization and Communication under Hardware Impairments. arXiv 2023, arXiv:2301.01042. Available online: https://arxiv.org/pdf/2301.01042.pdf (accessed on 27 March 2023).
- Chen, H.; Ballal, T.; Eltayeb, M.E.; Al-Naffouri, T.Y. Antenna Selection in Switch-Based MIMO Arrays via DOA Threshold Region Approximation. IEEE Trans. Veh. Technol. 2022, 71, 12344–12349. [Google Scholar] [CrossRef]
- Chen, H.; Aghdam, S.R.; Keskin, M.F.; Wu, Y.; Lindberg, S.; Wolfgang, A.; Gustavsson, U.; Eriksson, T.; Wymeersch, H. MCRB-Based Performance Analysis of 6G Localization under Hardware Impairments. arXiv 2023, arXiv:2204.12788. Available online: https://arxiv.org/pdf/2204.12788.pdf (accessed on 27 March 2023).
- Liu, F.; Cui, Y.; Masouros, C.; Xu, J.; Han, T.X.; Eldar, Y.C.; Buzzi, S. Integrated Sensing and Communications: Toward Dual-Functional Wireless Networks for 6G and Beyond. IEEE J. Sel. Areas Commun. 2022, 40, 1728–1767. [Google Scholar] [CrossRef]
- Yildiz, O.; Khalili, A.; Erkip, E. Hybrid Beam Alignment for Multi-Path Channels: A Group Testing Viewpoint. In Proceedings of the 2022 56th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–2 November 2022; pp. 6–10. [Google Scholar] [CrossRef]
- Behravan, A.; Yajnanarayana, V.; Keskin, M.F.; Chen, H.; Shrestha, D.; Abrudan, T.E.; Svensson, T.; Schindhelm, K.; Wolfgang, A.; Lindberg, S.; et al. Positioning and Sensing in 6G: Gaps, Challenges, and Opportunities. IEEE Veh. Technol. Mag. 2023, 18, 40–48. [Google Scholar] [CrossRef]
- Mateos-Ramos, J.M.; Häger, C.; Keskin, M.F.; Magoarou, L.L.; Wymeersch, H. Model-Driven End-to-End Learning for Integrated Sensing and Communication. arXiv 2022, arXiv:2212.10211. Available online: https://arxiv.org/pdf/2212.10211.pdf (accessed on 27 March 2023).
- Rivetti, S.; Mateos-Ramos, J.M.; Wu, Y.; Song, J.; Keskin, M.F.; Yajnanarayana, V.; Häger, C.; Wymeersch, H. Spatial Signal Design for Positioning via End-to-End Learning. arXiv 2022, arXiv:2209.12818. Available online: https://arxiv.org/pdf/2209.12818.pdf (accessed on 27 March 2023). [CrossRef]
- Wymeersch, H.; Pärssinen, A.; Abrudan, T.E.; Wolfgang, A.; Haneda, K.; Sarajlic, M.; Leinonen, M.E.; Keskin, M.F.; Chen, H.; Lindberg, S.; et al. 6G Radio Requirements to Support Integrated Communication, Localization, and Sensing. In Proceedings of the 2022 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Grenoble, France, 7–10 June 2022; pp. 463–469. [Google Scholar] [CrossRef]
- Wymeersch, H.; Shrestha, D.; De Lima, C.M.; Yajnanarayana, V.; Richerzhagen, B.; Keskin, M.F.; Schindhelm, K.; Ramirez, A.; Wolfgang, A.; De Guzman, M.F.; et al. Integration of Communication and Sensing in 6G: A Joint Industrial and Academic Perspective. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Zheng, P.; Ballal, T.; Chen, H.; Wymeersch, H.; Al-Naffouri, T.Y. Localization Coverage Analysis of THz Communication Systems with a 3D Array. In Proceedings of the GLOBECOM 2022—2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 5378–5383. [Google Scholar] [CrossRef]
- Yajnanarayana, V.; Wymeersch, H. Multistatic Sensing of Passive Targets Using 6G Cellular Infrastructure. arXiv 2022, arXiv:2211.05340. Available online: https://arxiv.org/pdf/2211.05340.pdf (accessed on 27 March 2023).
- Paramonov, A.; Tonkikh, E.; Koucheryavy, A.; Tatarnikova, T.M. High Density Internet of Things Network Analysis. In Proceedings of the 20th International Conference, NEW2AN 2020, and 13th Conference, ruSMART 2020, St. Petersburg, Russia, 26–28 August 2020; pp. 307–316. [Google Scholar] [CrossRef]
- Yastrebova, A.; Kirichek, R.; Koucheryavy, Y.; Borodin, A.; Koucheryavy, A. Future Networks 2030: Architecture & Requirements. In Proceedings of the 2018 10th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Moscow, Russia, 5–9 November 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Fokin, G.; Lazarev, V. Location Accuracy of Radio Emission Sources for Beamforming in Ultra-Dense Radio Networks. In Proceedings of the 2019 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2019; pp. 9–12. [Google Scholar] [CrossRef]
- Lazarev, V.; Fokin, G.; Stepanets, I. Positioning for Location-Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2019 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 17–18 October 2019; pp. 136–139. [Google Scholar] [CrossRef]
- Fokin, G.; Lazarev, V. 3D Location Accuracy Estimation of Radio Emission Sources for Beamforming in Ultra-Dense Radio Networks. In Proceedings of the 2019 11th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Dublin, Ireland, 28–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fokin, G.; Bachevsky, S.; Sevidov, V. System Level Performance Evaluation of Location Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2020 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 15–16 October 2020; pp. 94–97. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P.; Barton, C.G. Global Navigation Satellite Systems, Inertial Navigation, and Integration, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; 608p. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: Hoboken, NJ, USA, 2001; 584p. [Google Scholar]
- Bensky, A. Wireless Positioning Technologies and Applications (GNSS Technology and Applications), 2nd ed.; Artech House: London, UK, 2016; 450p. [Google Scholar]
- Roth, J.D.; Tummala, M.; McEachen, J.C. Efficient System Geolocation Architecture in Next-Generation Cellular Networks. IEEE Syst. J. 2018, 12, 3414–3425. [Google Scholar] [CrossRef]
- Roth, J.D.; Tummala, M.; McEachen, J.C. Fundamental Implications for Location Accuracy in Ultra-Dense 5G Cellular Networks. IEEE Trans. Veh. Technol. 2019, 68, 1784–1795. [Google Scholar] [CrossRef]
- Elsawy, H.; Dai, W.; Alouini, M.; Win, M.Z. Base Station Ordering for Emergency Call Localization in Ultra-Dense Cellular Networks. IEEE Access 2018, 6, 301–315. [Google Scholar] [CrossRef]
- 3GPP TS 22.104. Service Requirements for Cyber-Physical Control Applications in Vertical Domains; Stage 1 (Release 18). V18.3.0 (2021-12). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3528 (accessed on 27 March 2023).
- 3GPP TS 22.261. Service Requirements for the 5G System; Stage 1 (Release 19). V19.1.0 (2022-12). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3107 (accessed on 27 March 2023).
- 3GPP TR 22.872. Study on Positioning Use Cases; Stage 1 (Release 16). V16.1.0 (2018-09). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3280 (accessed on 27 March 2023).
- 3GPP TS 38.305. NG Radio Access Network (NG-RAN); Stage 2 Functional Specification of User Equipment (UE) Positioning in NG-RAN (Release 17). V17.4.0 (2023-03). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3310 (accessed on 27 March 2023).
- 3GPP TR 38.855. Study on NR Positioning Support (Release 16). V16.0.0 (2019-03). Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3501 (accessed on 27 March 2023).
- Gazprom Arena. Available online: https://gazprom-arena.com/eng (accessed on 27 March 2023).
- Fokin, G.; Sevidov, V. Model for 5G UDN Positioning System Topology Search Using Dilution of Precision Criterion. In Proceedings of the 2021 International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 14–15 October 2021; pp. 32–36. [Google Scholar] [CrossRef]
- Fokin, G.; Sevidov, V. Topology Search Using Dilution of Precision Criterion for Enhanced 5G Positioning Service Area. In Proceedings of the 2021 13th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Brno, Czech Republic, 25–27 October 2021; pp. 131–136. [Google Scholar] [CrossRef]
- Lazarev, V.O.; Fokin, G.A. Positioning Performance Requirements Evaluation for Grid Model in Ultra-Dense Network Scenario. In Proceedings of the 2020 Systems of Signals Generating and Processing in the Field of on-Board Communications, Moscow, Russia, 19–20 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Fokin, G. Vehicles Tracking in 5G-V2X UDN Using Range and Bearing Measurements. In Proceedings of the 2021 IEEE Vehicular Networking Conference (VNC), Ulm, Germany, 10–12 November 2021; pp. 103–106. [Google Scholar] [CrossRef]
- Fokin, G.; Vladyko, A. Vehicles Tracking in 5G-V2X UDN using Range, Bearing and Inertial Measurements. In Proceedings of the 2021 13th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Brno, Czech Republic, 25–27 October 2021; pp. 137–142. [Google Scholar] [CrossRef]
- Fokin, G. Vehicle Positioning Requirements for Location-Aware Beamforming in 5G UDN. In Proceedings of the 2022 Intelligent Technologies and Electronic Devices in Vehicle and Road Transport Complex (TIRVED), Moscow, Russia, 10–11 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, J.; Liang, J.; Luo, S. Method and analysis of TOA-based localization in 5G ultra-dense networks with randomly distributed nodes. IEEE Access 2019, 7, 174986–175002. [Google Scholar] [CrossRef]
- Ash, J.N.; Moses, R.L. On optimal anchor node placement in sensor localization by optimization of subspace principal angles. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2289–2292. [Google Scholar] [CrossRef]
- Xhafa, A.; del Peral-Rosado, J.A.; López-Salcedo, J.A.; Seco-Granados, G. Evaluation of 5G Positioning Performance Based on UTDoA, AoA and Base-Station Selective Exclusion. Sensors 2022, 22, 101. [Google Scholar] [CrossRef] [PubMed]
- Posluk, M.; Ahlander, J.; Shrestha, D.; Razavi, S.M.; Lindmark, G.; Gunnarsson, F. 5G Deployment Strategies for High Positioning Accuracy in Indoor Environments. arXiv 2021, arXiv:2105.09584. Available online: https://arxiv.org/pdf/2105.09584.pdf (accessed on 27 March 2023).
- Deng, Z.; Wang, H.; Zheng, X.; Fu, X.; Yin, L.; Tang, S.; Yang, F. A Closed-Form Localization Algorithm and GDOP Analysis for Multiple TDOAs and Single TOA Based Hybrid Positioning. Appl. Sci. 2019, 9, 4935. [Google Scholar] [CrossRef]
- Roth, J.D.; Tummala, M.; Mceachen, J.C. A new probability density function for minimizing geometric dilution of precision in location-aware wireless communications. IEEE Access 2020, 8, 160461–160479. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, C.S.; Shou, H.N.; Sun, C.T. Dilution of Position calculation for Accuracy Improvement in Wireless Location Systems. Adv. Mat. Res. 2011, 204, 1036–1040. [Google Scholar] [CrossRef]
- Dempster, A.G. Dilution of precision in angle-of-arrival positioning systems. Electron. Lett. 2006, 42, 291–292. [Google Scholar] [CrossRef]
- Li, B.; Zhao, K.; Shen, X. Dilution of precision in positioning systems using both angle of arrival and time of arrival measurements. IEEE Access 2020, 8, 192506–192516. [Google Scholar] [CrossRef]
- Miao, S.; Dong, L.; Hou, J. Dynamic base stations selection method for passive location based on GDOP. PLoS ONE 2022, 17, e0272487. [Google Scholar] [CrossRef] [PubMed]
- Sharp, I.; Yu, K.; Guo, Y.J. GDOP analysis for positioning system design. IEEE Trans. Veh. Technol. 2009, 58, 3371–3382. [Google Scholar] [CrossRef]
- Li, F.; Tu, R.; Hong, J.; Zhang, S.; Liu, M.; Lu, X. Performance Analysis of BDS–5G Combined Precise Point Positioning. Remote Sens. 2022, 14, 3006. [Google Scholar] [CrossRef]
- Guo, W.; Deng, Y.; Guo, C.; Qi, S.; Wang, J. Performance improvement of 5G positioning utilizing multi-antenna angle measurements. Satell. Navig. 2022, 3, 17. [Google Scholar] [CrossRef]
- Levanon, N. Lowest GDOP in 2-D scenarios. IEE Radar Sonar Navig. 2000, 147, 149–155. [Google Scholar] [CrossRef]
- Stansfield, R.G. Statistical theory of DF fixing. J. Inst. Electr. Eng. Part IIIA Radiocommun. 1947, 94, 762–770. [Google Scholar] [CrossRef]
- Lee, H.B. A novel procedure for assessing the accuracy of hyperbolic multilateration systems. IEEE Trans Aerosp. Electron Syst. 1975, 1, 2–15. [Google Scholar] [CrossRef]
- Lee, H.B. Accuracy limitations of hyperbolic multilateration systems. IEEE Trans Aerosp. Electron. Syst. 1975, 1, 16–29. [Google Scholar] [CrossRef]
- Torrieri, D.J. Statistical Theory of Passive Location Systems. IEEE Trans Aerosp. Electron. Syst. 1984, 20, 183–198. [Google Scholar] [CrossRef]
- Massatt, P.; Rudnick, K. Geometric formulas for dilution of precision calculations. Navigation 1990, 37, 379–391. [Google Scholar] [CrossRef]
- Manolakis, D.E. Efficient solution and performance analysis of 3-D position estimation by trilateration. IEEE Trans Aerosp. Electron. Syst. 1996, 32, 1239–1248. [Google Scholar] [CrossRef]
- Shin, D.H.; Sung, T.K. Comparisons of error characteristics between TOA and TDOA positioning. IEEE Trans Aerosp. Electron. Syst. 2002, 38, 307–311. [Google Scholar] [CrossRef]
- Spirito, M.A. On the accuracy of cellular mobile station location estimation. IEEE Trans. Veh. 2001, 50, 674–685. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Li, B.; Dempster, A.G.; Wang, J. 3D DOPs for positioning applications using range measurements. Wirel. Sens. Netw. 2011, 3, 334. [Google Scholar] [CrossRef]
- Choi, H.H.; Jin, M.H.; Lim, D.W.; Lee, S.J.; Park, C. Dilution of Precision Relationship between Time Difference of Arrival and Time of Arrival Techniques with No Receiver Clock Bias. J. Electr. Eng. Technol. 2016, 11, 746–750. [Google Scholar] [CrossRef]
- Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area Simulator. Available online: https://github.com/grihafokin/Topology_search_using_DOP (accessed on 27 March 2023).

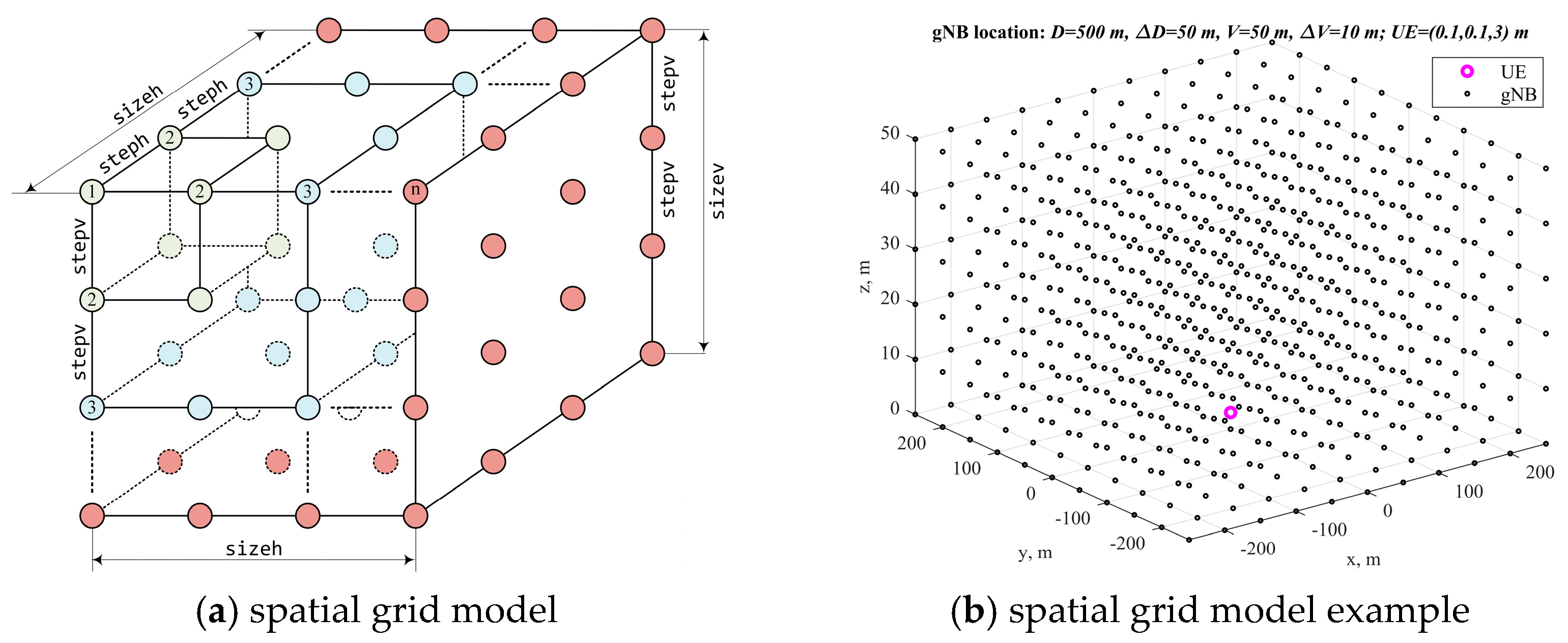

| Designation | Spatial Parameter Description |
|---|---|
| n | number of gNB base stations in a given region of space |
| sizeh | maximum length of gNB location area in horizontal plane (on xy plane) |
| steph | grid spacing of possible horizontal locations of gNBs (on the xy plane) |
| sizev | maximum height of the gNB location area in vertical plane (altitude z) |
| stepv | vertical grid spacing of possible gNB locations (in altitude z) |
| UEsizeh | maximum length of the UE location area in horizontal plane (on xy plane) |
| UEsteph | grid spacing of possible horizontal locations of UE (on the xy plane) |
| UEsizev | maximum height of the UE location area in vertical plane (altitude z) |
| UEstepv | grid spacing of possible vertical locations of UE (in altitude z) |
| dSizeHDefault | initial step for optimizing the position of gNB horizontally on xy plane |
| dSizeVDefault | initial step for optimizing the position of gNB vertically on altitude z |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fokin, G.; Koucheryavy, A. Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area. Mathematics 2023, 11, 2227. https://doi.org/10.3390/math11102227
Fokin G, Koucheryavy A. Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area. Mathematics. 2023; 11(10):2227. https://doi.org/10.3390/math11102227
Chicago/Turabian StyleFokin, Grigoriy, and Andrey Koucheryavy. 2023. "Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area" Mathematics 11, no. 10: 2227. https://doi.org/10.3390/math11102227
APA StyleFokin, G., & Koucheryavy, A. (2023). Algorithm for Topology Search Using Dilution of Precision Criterion in Ultra-Dense Network Positioning Service Area. Mathematics, 11(10), 2227. https://doi.org/10.3390/math11102227





