A Mini-Review on Recent Fractional Models for Agri-Food Problems
Abstract
:1. Introduction
- Are there fractional models to tackle agri-food problems? If so, which kind of fractional operators have been used?
- Has real-world data been employed along with such models?
2. Mathematical Models
3. Fractional Models
3.1. Review Methodology
| ((agri*) OR (food) OR (plant) OR (crop) OR (livestock) OR (fish)) AND (fractional) |
3.2. Caputo-Type Models
3.3. Other Fractional Models
4. Fractional Versus Non-Fractional
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Fractional Operators
References
- Yahya, N. Agricultural 4.0: Its implementation toward future sustainability. In Green Urea; Springer: Singapore, 2018; pp. 125–145. [Google Scholar]
- Saiz-Rubio, V.; Rovira-Más, F. From smart farming towards agriculture 5.0: A review on crop data management. Agronomy 2020, 10, 207. [Google Scholar] [CrossRef]
- Zhai, Z.; Martínez, J.F.; Beltran, V.; Martínez, N.L. Decision support systems for agriculture 4.0: Survey and challenges. Comput. Electron. Agric. 2020, 170, 105256. [Google Scholar] [CrossRef]
- Pardey, P.G.; Beddow, J.M.; Hurley, T.M.; Beatty, T.K.; Eidman, V.R. A bounds analysis of world food futures: Global agriculture through to 2050. Aust. J. Agric. Resour. Econ. 2014, 58, 571–589. [Google Scholar] [CrossRef]
- Pradhan, P.; Fischer, G.; van Velthuizen, H.; Reusser, D.E.; Kropp, J.P. Closing yield gaps: How sustainable can we be? PLoS ONE 2015, 10, e0129487. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Evaluation, Analysis, Parameterization, and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Pelak, N.; Revelli, R.; Porporato, A. A dynamical systems framework for crop models: Toward optimal fertilization and irrigation strategies under climatic variability. Ecol. Model. 2017, 365, 80–92. [Google Scholar] [CrossRef]
- Abraha, T.; Al Basir, F.; Obsu, L.L.; Torres, D.F. Farming awareness based optimum interventions for crop pest control. Math. Biosci. Eng. 2021, 18, 5364–5392. [Google Scholar] [CrossRef]
- Al Basir, F.; Ray, S. Modeling the transmission dynamics of plant viral disease using two routes of infection, nonlinear terms and incubation delay. Int. J. Biomath. 2022, 15, 2250032. [Google Scholar] [CrossRef]
- Uzair, M.; Tomasiello, S.; Loit, E.; Wei-Lin, J.C. Predicting the soil organic carbon by recent machine learning algorithms. In Proceedings of the 2022 IEEE Intl Conf on Dependable, Autonomic and Secure Computing, Intl Conf on Pervasive Intelligence and Computing, Intl Conf on Cloud and Big Data Computing, Intl Conf on Cyber Science and Technology Congress (DASC/PiCom/CBDCom/CyberSciTech), Falerna, Italy, 12–15 September 2022; pp. 1–7. [Google Scholar]
- Yogeswararao, G.; Malmathanraj, R.; Palanisamy, P. Fractional weighted nuclear norm based two dimensional linear discriminant features for cucumber leaf disease recognition. Multimed. Tools Appl. 2022, 81, 38735–38755. [Google Scholar] [CrossRef]
- Da Silva e Souza, G.; Gomes, E.G.; de Andrade Alves, E.R. Two-part fractional regression model with conditional FDH responses: An application to Brazilian agriculture. Ann. Oper. Res. 2020, 314, 393–409. [Google Scholar] [CrossRef]
- Ghoneim, M.S.; Gadallah, S.I.; Said, L.A.; Eltawil, A.M.; Radwan, A.G.; Madian, A.H. Plant stem tissue modeling and parameter identification using metaheuristic optimization algorithms. Sci. Rep. 2022, 12, 1–17. [Google Scholar] [CrossRef]
- Machado, J.A.; Lopes, A.M. On fractional-order characteristics of vegetable tissues and edible drinks. In Proceedings of the International Workshop on Advanced Theory and Applications of Fractional Calculus; Springer: Singapore, 2018; pp. 19–35. [Google Scholar]
- Birajdar, G.A. A Solution of Fractional Bio-Chemical Reaction Model by Adomian Decomposition Method. In Proceedings of the International Conference on Mathematics and Its Applications in Science and Engineering; Springer: Cham, Switzerland, 2022; pp. 179–189. [Google Scholar]
- Daudi, S.; Luboobi, L.; Kgosimore, M.; Kuznetsov, D.; Mushayabasa, S. A mathematical model for fall armyworm management on maize biomass. Adv. Differ. Equ. 2021, 2021, 1–27. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Ahmad, S.; Akgül, A. On Numerical Analysis of Bio-Ethanol Production Model with the Effect of Recycling and Death Rates under Fractal Fractional Operators with Three Different Kernels. Mathematics 2022, 10, 1102. [Google Scholar] [CrossRef]
- Mahmood, T.; ur Rahman, M.; Arfan, M.; Kayani, S.I.; Sun, M. Mathematical study of Algae as a bio-fertilizer using fractal–fractional dynamic model. Math. Comput. Simul. 2023, 203, 207–222. [Google Scholar] [CrossRef]
- Shaheen, A.; Sheng, J.; Arshad, S.; Defterli, O.; Xie, X.; Baleanu, D. A novel fractional grey model applied to the environmental assessment in Turkey. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050039. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel fractional grey Riccati model for carbon emission prediction. J. Clean. Prod. 2021, 282, 124471. [Google Scholar] [CrossRef]
- Ilhan, E.; Veeresha, P.; Baskonus, H.M. Fractional approach for a mathematical model of atmospheric dynamics of CO2 gas with an efficient method. Chaos Solitons Fractals 2021, 152, 111347. [Google Scholar] [CrossRef]
- Ya-kun, Z.; Bin, L.; Da-yu, P.; Peng, S.; Wen-chao, L.; Cheng, W.; Chun-jiang, Z. Estimation of Canopy Nitrogen Content of Soybean Crops Based on Fractional Differential Algorithm. Spectrosc. Spectr. Anal. 2018, 38, 3221–3230. [Google Scholar]
- Kaur, A.; Takhar, P.S.; Smith, D.M.; Mann, J.E.; Brashears, M.M. Fractional differential equations based modeling of microbial survival and growth curves: Model development and experimental validation. J. Food Sci. 2008, 73, E403–E414. [Google Scholar] [CrossRef]
- Adedje, K.E.; Barro, D. A Stochastic Approach to Modeling Food Pattern. Int. J. Math. Math. Sci. 2022, 2022, 9011873. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Yankson, E.; Opoku, A.A.; Adom-Konadu, A.; Acheampong, E.; Arthur, Y.D. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solitons Fractals 2022, 156, 111821. [Google Scholar] [CrossRef]
- Vu, H.; An, T.V.; Van Hoa, N. On the initial value problem for random fuzzy differential equations with Riemann-Liouville fractional derivative: Existence theory and analytical solution. J. Intell. Fuzzy Syst. 2019, 36, 6503–6520. [Google Scholar] [CrossRef]
- Filatova, D.V.; Orłowski, A.; Dicoussar, V. Estimating the time-varying parameters of SDE models by maximum principle. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014; pp. 401–406. [Google Scholar]
- Erjaee, G.; Ostadzad, M.; Okuguchi, K.; Rahimi, E. Fractional differential equations system for commercial fishing under predator-prey interaction. J. Appl. Nonlinear Dyn. 2013, 2, 409–417. [Google Scholar] [CrossRef]
- Shaw, P.K.; Kumar, S.; Momani, S.; Hadid, S. Dynamical analysis of fractional plant disease model with curative and preventive treatments. Chaos Solitons Fractals 2022, 164, 112705. [Google Scholar] [CrossRef]
- Abdullah, T.Q.; Huang, G.; Al-Sadi, W. A curative and preventive treatment fractional model for plant disease in Atangana–Baleanu derivative through Lagrange interpolation. Int. J. Biomath. 2022, 15, 2250052. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Wolle, G.A.; Tofik, M. Eco-epidemiological model and analysis of potato leaf roll virus using fractional differential equation. Arab J. Basic Appl. Sci. 2021, 28, 41–50. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Jleli, M. A numerical analysis for fractional model of the spread of pests in tea plants. Numer. Methods Partial Differ. Equ. 2022, 38, 540–565. [Google Scholar] [CrossRef]
- Singh, H. Jacobi collocation method for the fractional advection-dispersion equation arising in porous media. Numer. Methods Partial Differ. Equ. 2022, 38, 636–653. [Google Scholar] [CrossRef]
- Yu, C.; Wei, S.; Zhang, Y.; Zheng, Y.; Yu, Z.; Donahoe, R.; Wei, H. Quantifying colloid fate and transport through dense vegetation and soil systems using a particle-plugging tempered fractional-derivative model. J. Contam. Hydrol. 2019, 224, 103484. [Google Scholar] [CrossRef]
- Ramadas, M.; Ojha, R.; Govindaraju, R.S. Current and future challenges in groundwater. II: Water quality modeling. J. Hydrol. Eng. 2015, 20, A4014008. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Sze, K. A Novel Finite Element Method for a Class of Time Fractional Diffusion Equations. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; Volume 54808, pp. 369–376. [Google Scholar]
- Mehdinejadiani, B.; Naseri, A.A.; Jafari, H.; Ghanbarzadeh, A.; Baleanu, D. A mathematical model for simulation of a water table profile between two parallel subsurface drains using fractional derivatives. Comput. Math. Appl. 2013, 66, 785–794. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Timlin, D.; Rawls, W. Generalized Richards’ equation to simulate water transport in unsaturated soils. J. Hydrol. 2003, 272, 3–13. [Google Scholar] [CrossRef]
- Bohaienko, V.; Gladky, A.; Romashchenko, M.; Matiash, T. Identification of fractional water transport model with ψ-Caputo derivatives using particle swarm optimization algorithm. Appl. Math. Comput. 2021, 390, 125665. [Google Scholar] [CrossRef]
- Li, Y. Ecological balance model of effective utilization of agricultural water resources based on fractional differential equations. Appl. Math. Nonlinear Sci. 2021, 7, 371–378. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; PRISMA Group. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Ryba, A.; Lenzi, M.K. Monitoring Liquid-Liquid Mixtures Using Fractional Calculus and Image Analysis. Fractal Fract. 2018, 2, 11. [Google Scholar] [CrossRef]
- Romashchenko, M.I.; Bohaienko, V.O.; Matiash, T.V.; Kovalchuk, V.P.; Danylenko, I.I. Influence of evapotranspiration assessment on the accuracy of moisture transport modeling under the conditions of sprinkling irrigation in the south of Ukraine. Arch. Agron. Soil Sci. 2020, 66, 1424–1435. [Google Scholar] [CrossRef]
- Lamb, W.F.; Wiedmann, T.; Pongratz, J.; Andrew, R.; Crippa, M.; Olivier, J.G.; Wiedenhofer, D.; Mattioli, G.; Al Khourdajie, A.; House, J.; et al. A review of trends and drivers of greenhouse gas emissions by sector from 1990 to 2018. Environ. Res. Lett. 2021, 16, 073005. [Google Scholar] [CrossRef]
- Chu, M.X.; Tian, B.; Yin, H.M.; Chen, S.S.; Zhang, Z. Kink soliton solutions and bifurcation for a nonlinear space-fractional Kolmogorov–Petrovskii–Piskunov equation in circuitry, chemistry or biology. Mod. Phys. Lett. B 2019, 33, 1950372. [Google Scholar] [CrossRef]
- Kurganov, A.; Levy, D. A third-order semidiscrete central scheme for conservation laws and convection-diffusion equations. SIAM J. Sci. Comput. 2000, 22, 1461–1488. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. On the solution of a Riesz space-fractional nonlinear wave equation through an efficient and energy-invariant scheme. Int. J. Comput. Math. 2019, 96, 337–361. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macías-Díaz, J.E. A conservative scheme with optimal error estimates for a multidimensional space–fractional Gross–Pitaevskii equation. Int. J. Appl. Math. Comput. Sci. 2019, 29, 713–723. [Google Scholar] [CrossRef]
- Serna-Reyes, A.J.; Macías-Díaz, J.E. Theoretical analysis of a conservative finite-difference scheme to solve a Riesz space-fractional Gross–Pitaevskii system. J. Comput. Appl. Math. 2022, 404, 113413. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Zaslavsky, G.M. Conservation laws and Hamilton’s equations for systems with long-range interaction and memory. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1860–1878. [Google Scholar] [CrossRef]
- Tarasov, V.E. Continuous limit of discrete systems with long-range interaction. J. Phys. A Math. Gen. 2006, 39, 14895. [Google Scholar] [CrossRef]
- Zhang, T.; Xiong, L. Periodic motion for impulsive fractional functional differential equations with piecewise Caputo derivative. Appl. Math. Lett. 2020, 101, 106072. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Exponential Euler scheme of multi-delay Caputo–Fabrizio fractional-order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Kumar, P.; Baleanu, D.; Erturk, V.S.; Inc, M.; Govindaraj, V. A delayed plant disease model with Caputo fractional derivatives. Adv. Contin. Discret. Model. 2022, 2022, 1–22. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Zorica, D. Properties of the Caputo-Fabrizio fractional derivative and its distributional settings. Fract. Calc. Appl. Anal. 2018, 21, 29–44. [Google Scholar] [CrossRef]
- Owolabi, K.M. modeling and simulation of a dynamical system with the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2018, 133, 1–13. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
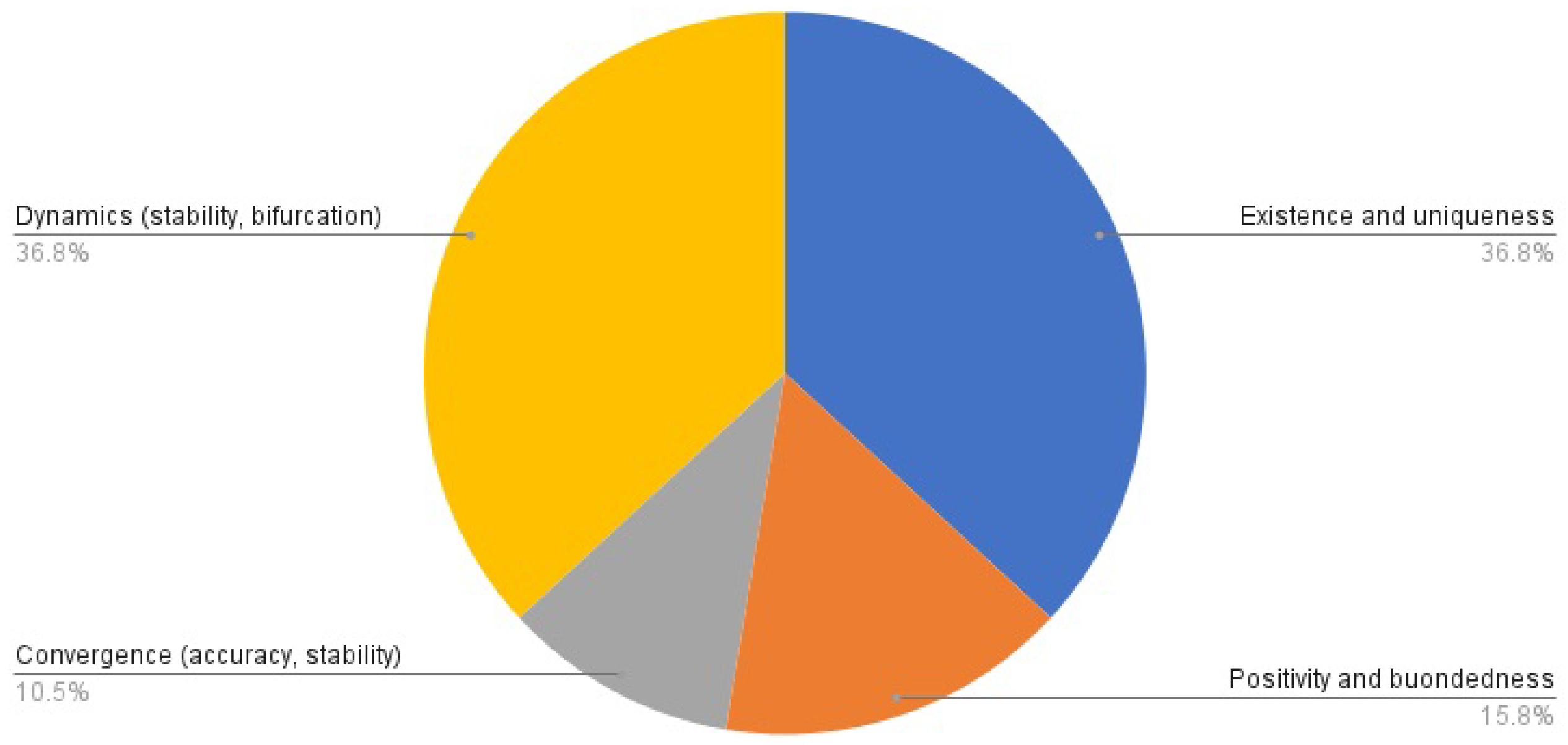
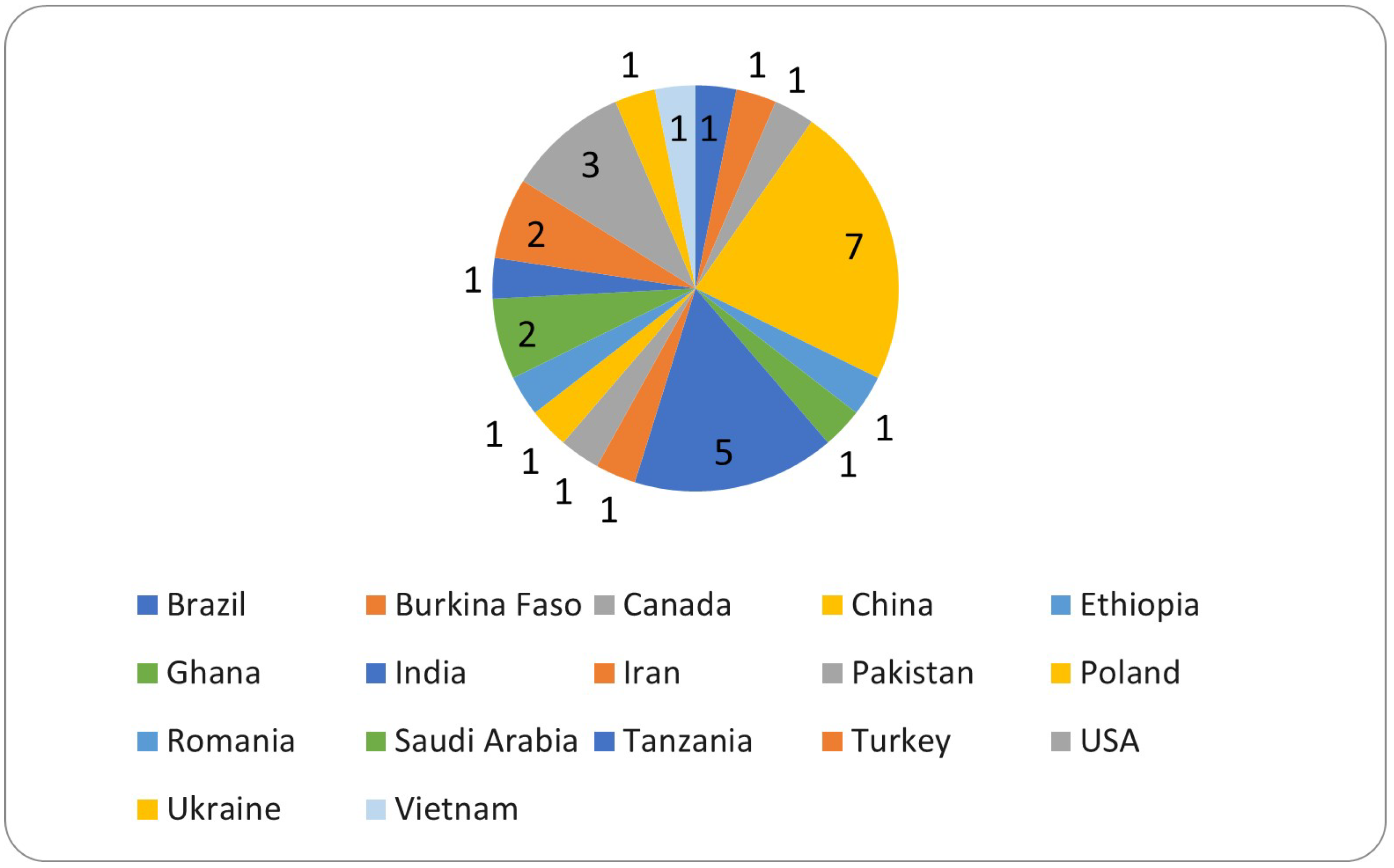

| Problems | Operators | References |
|---|---|---|
| Biomasses, biogases, and bio-fertilizers | C, CF, AB | [15,16,17,18] |
| Environmental issues (CO, nitrogen estimate) | C, CF, RL | [19,20,21,22] |
| Food science | RL | [23,24] |
| Livestock and fishery | C, CF, AB, RL | [25,26,27,28] |
| Plant diseases | C, CF, AB | [29,30,31,32] |
| Transportation of contaminants and water issues | C | [33,34,35,36,37,38,39,40] |
| Problems | Operators | References |
|---|---|---|
| CO emissions/dynamics | C, RL | [20,21] |
| Fishery | RL | [27] |
| Food science | RL | [23,24] |
| Soil moisture | C | [39] |
| Year | Number of Publications |
|---|---|
| 2003 | 1 |
| 2008 | 1 |
| 2012 | 1 |
| 2013 | 2 |
| 2014 | 1 |
| 2015 | 1 |
| 2018 | 1 |
| 2019 | 4 |
| 2020 | 1 |
| 2021 | 4 |
| 2022 | 10 |
| 2023 (April) | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasiello, S.; Macías-Díaz, J.E. A Mini-Review on Recent Fractional Models for Agri-Food Problems. Mathematics 2023, 11, 2316. https://doi.org/10.3390/math11102316
Tomasiello S, Macías-Díaz JE. A Mini-Review on Recent Fractional Models for Agri-Food Problems. Mathematics. 2023; 11(10):2316. https://doi.org/10.3390/math11102316
Chicago/Turabian StyleTomasiello, Stefania, and Jorge E. Macías-Díaz. 2023. "A Mini-Review on Recent Fractional Models for Agri-Food Problems" Mathematics 11, no. 10: 2316. https://doi.org/10.3390/math11102316
APA StyleTomasiello, S., & Macías-Díaz, J. E. (2023). A Mini-Review on Recent Fractional Models for Agri-Food Problems. Mathematics, 11(10), 2316. https://doi.org/10.3390/math11102316








