Quantile-Composited Feature Screening for Ultrahigh-Dimensional Data
Abstract
1. Introduction
2. A New Feature Screening Procedure
- (1)
- if and only if the Bernoulli variable and Y are independent, where is the indicator function;
- (2)
- for if Y and are independent.
- 1.
- If , follows the distribution with degrees of freedom [22].
- 2.
- is invariant to any monotonic transformation on predictors, because is free of the monotonic transformation on .
- 3.
- The computation of involves the integration of τ. We can calculate it by an approximate numerical method as
- 4.
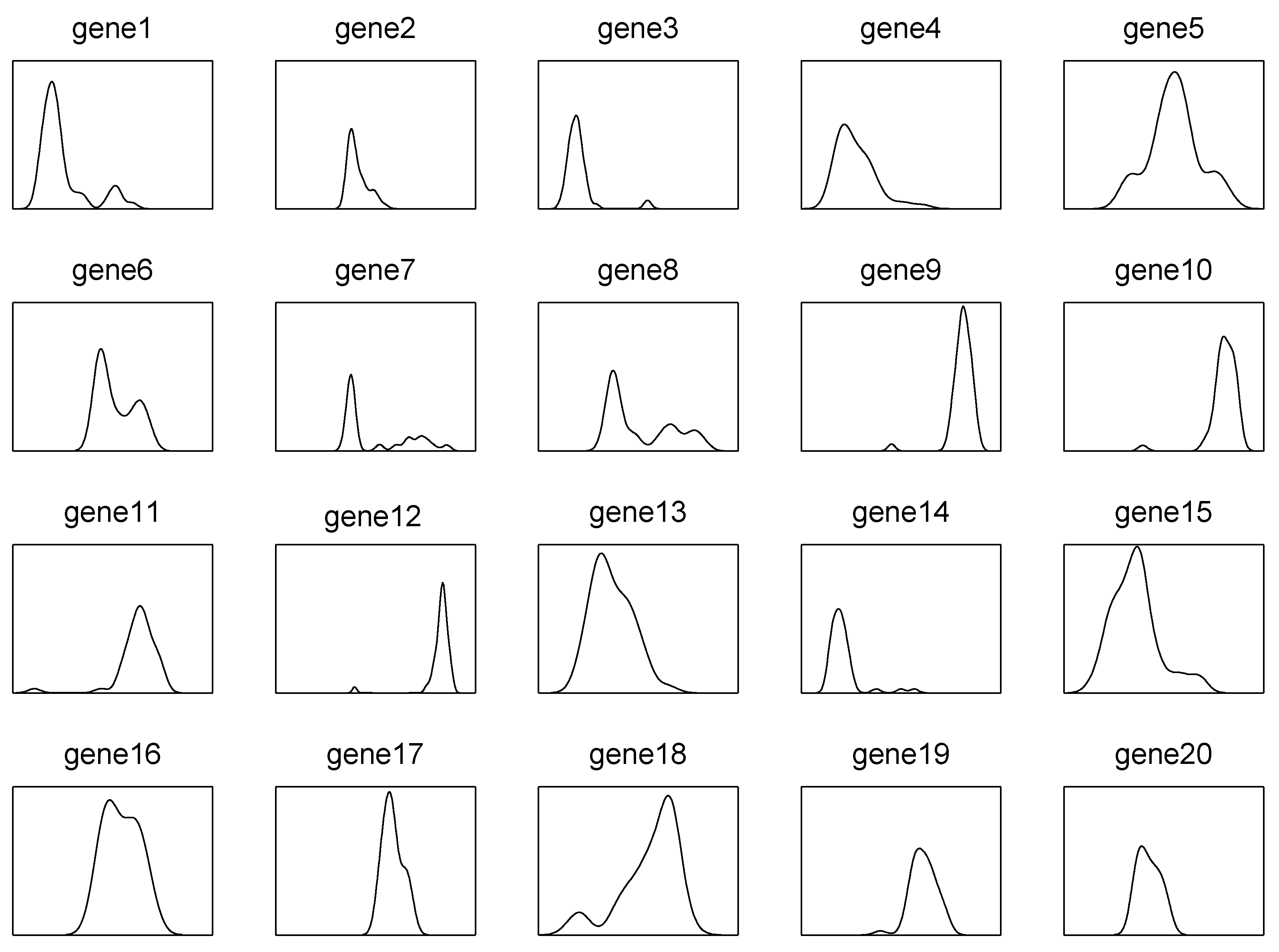
- The choice of s. Intuitively, a large s will make the approximation of integration more accurate. However, our method aims to efficiently separate the active predictors from the null ones, instead of getting an accurate estimate of . Figure 2 displays the density curves of marginal utilities of active and inactive predictors versus different choices of s with Example 2 in Section 3. It can be seen that the choice of s does not affect the distribution of either active predictors or inactive ones.
- 5.
- Figure 2 also shows that the gap between the indices of active predictors and inactive ones is clear, which means the proposed method is efficient at separating the influential predictors from the inactive ones well. Moreover, it can also be observed that the marginal utilities of active predictors are, with a smaller variance, comparable to those of inactive ones, which implies that the new method is sensitive to the active predictors.
2.1. Theoretical Properties
2.2. Extensions
3. Numerical Studies
3.1. General Settings
3.2. Monte Carlo Simulations
- Case 1.
- , and .
- Case 2.
- The same setup as Case 1, except that and .
- Case 3.
- for , and for , where represented a d-dimensional zero-valued vector.
- Case 4.
- The same setup as Case 1, except that .
- Case 1.
- ;
- Case 2.
- ;
- Case 3.
- ,
- Case 1.
- , and with ;
- Case 2.
- , , ;and with .
- 1.
- , where with and ;
- 2.
- , where , , , , where was independent of ;
- 3.
- , where was equal to if , 1 if , and 0 otherwise, and where with , and and were the first and third quartiles, respectively, of a standard normal distribution.
3.3. Real Data Analyses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Main Results
References
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Statist. Soc. B 2008, 70, 849–911. [Google Scholar] [CrossRef] [PubMed]
- Wang, H. Forward regression for ultra-high dimensional variable screening. J. Am. Statist. Assoc. 2009, 104, 1512–1524. [Google Scholar] [CrossRef]
- Chang, J.; Tang, C.; Wu, Y. Marginal empirical likelihood and sure independence feature screening. Ann. Statist. 2013, 41, 2123–2148. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Leng, C. High dimensional ordinary least squares projection for screening variables. J. R. Statist. Soc. B 2016, 78, 589–611. [Google Scholar] [CrossRef]
- Fan, J.; Feng, Y.; Song, R. Nonparametric independence screening in sparse ultrahigh dimensional additive models. J. Am. Statist. Assoc. 2011, 106, 544–557. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Ma, Y.; Dai, W. Nonparametric independence screening in sparse ultra-high-dimensional varying coefficient models. J. Am. Statist. Assoc. 2014, 109, 1270–1284. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Li, R.; Wu, R. Feature selection for varying coefficient models with ultrahigh-dimensional covariates. J. Am. Statist. Assoc. 2014, 109, 266–274. [Google Scholar] [CrossRef]
- Zhu, L.; Li, L.; Li, R.; Zhu, L. Model-free feature screening for ultrahigh-dimensional data. J. Am. Statist. Assoc. 2011, 106, 1464–1475. [Google Scholar] [CrossRef]
- Li, R.; Zhong, W.; Zhu, L. Feature screening via distance correlation learning. J. Am. Statist. Assoc. 2012, 107, 1129–1139. [Google Scholar] [CrossRef]
- He, X.; Wang, L.; Hong, H. Quantile-adaptive model-free variable screening for high-dimensional heterogeneous data. Ann. Statist. 2013, 41, 342–369. [Google Scholar] [CrossRef]
- Lin, L.; Sun, J.; Zhu, L. Nonparametric feature screening. Comput. Statist. Data Anal. 2013, 67, 162–174. [Google Scholar] [CrossRef]
- Lu, J.; Lin, L. Model-free conditional screening via conditional distance correlation. Statist. Pap. 2020, 61, 225–244. [Google Scholar] [CrossRef]
- Tong, Z.; Cai, Z.; Yang, S.; Li, R. Model-Free Conditional Feature Screening with FDR Control. J. Am. Statist. Assoc. 2002. [Google Scholar] [CrossRef]
- Guo, X.; Ren, H.; Zou, C.; Li, R. Threshold Selection in Feature Screening for Error Rate Control. J. Am. Statist. Assoc. 2022, 36, 1–13. [Google Scholar] [CrossRef]
- Zhong, W.; Qian, C.; Liu, W.; Zhu, L.; Li, R. Feature Screening for Interval-Valued Response with Application to Study Association between Posted Salary and Required Skills. J. Am. Statist. Assoc. 2023. [Google Scholar] [CrossRef]
- Fan, J.; Feng, Y.; Tong, X. A road to classification in high dimensional space: The regularized optimal affine discriminant. J. R. Statist. Soc. B 2012, 74, 745–771. [Google Scholar] [CrossRef]
- Huang, D.; Li, R.; Wang, H. Feature screening for ultrahigh dimensional categorical data with applications. J. Bus. Econ. Stat. 2014, 32, 237–244. [Google Scholar] [CrossRef]
- Pan, R.; Wang, H.; Li, R. Ultrahigh-dimensional multiclass linear discriminant analysis by pairwise sure independence screening. J. Am. Statist. Assoc. 2016, 111, 169–179. [Google Scholar] [CrossRef]
- Mai, Q.; Zou, H. The fused kolmogorov filter: A nonparametric model-free feature screening. Ann. Statist. 2015, 43, 1471–1497. [Google Scholar] [CrossRef]
- Cui, H.; Li, R.; Zhong, W. Model-free feature screening for ultrahigh dimensional discriminant analysis. J. Am. Statist. Assoc. 2015, 110, 630–641. [Google Scholar] [CrossRef]
- Xie, J.; Lin, Y.; Yan, X.; Tang, N. Category-Adaptive Variable Screening for Ultra-high Dimensional Heterogeneous Categorical Data. J. Am. Statist. Assoc. 2019, 36, 747–760. [Google Scholar] [CrossRef]
- Shao, J. Mathematical Statistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Meier, L.; van de Geer, S.; Buhlmann, P. High-Dimensional Additive Modeling. Ann. Statist. 2009, 37, 3779–3821. [Google Scholar] [CrossRef]
- Dettling, M. Bagboosting for tumor classification with gene expression data. Bioinformatics 2004, 20, 3583–3593. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.M.; Tibshirani, R. Penalized classification using fisher’s linear discriminant. J. R. Statist. Soc. B 2011, 73, 753–772. [Google Scholar] [CrossRef]
- Clemmensen, L.; Hastie, T.; Witten, D.; Ersbøll, B. Sparse discriminant analysis. Technometrics 2011, 53, 406–413. [Google Scholar] [CrossRef]

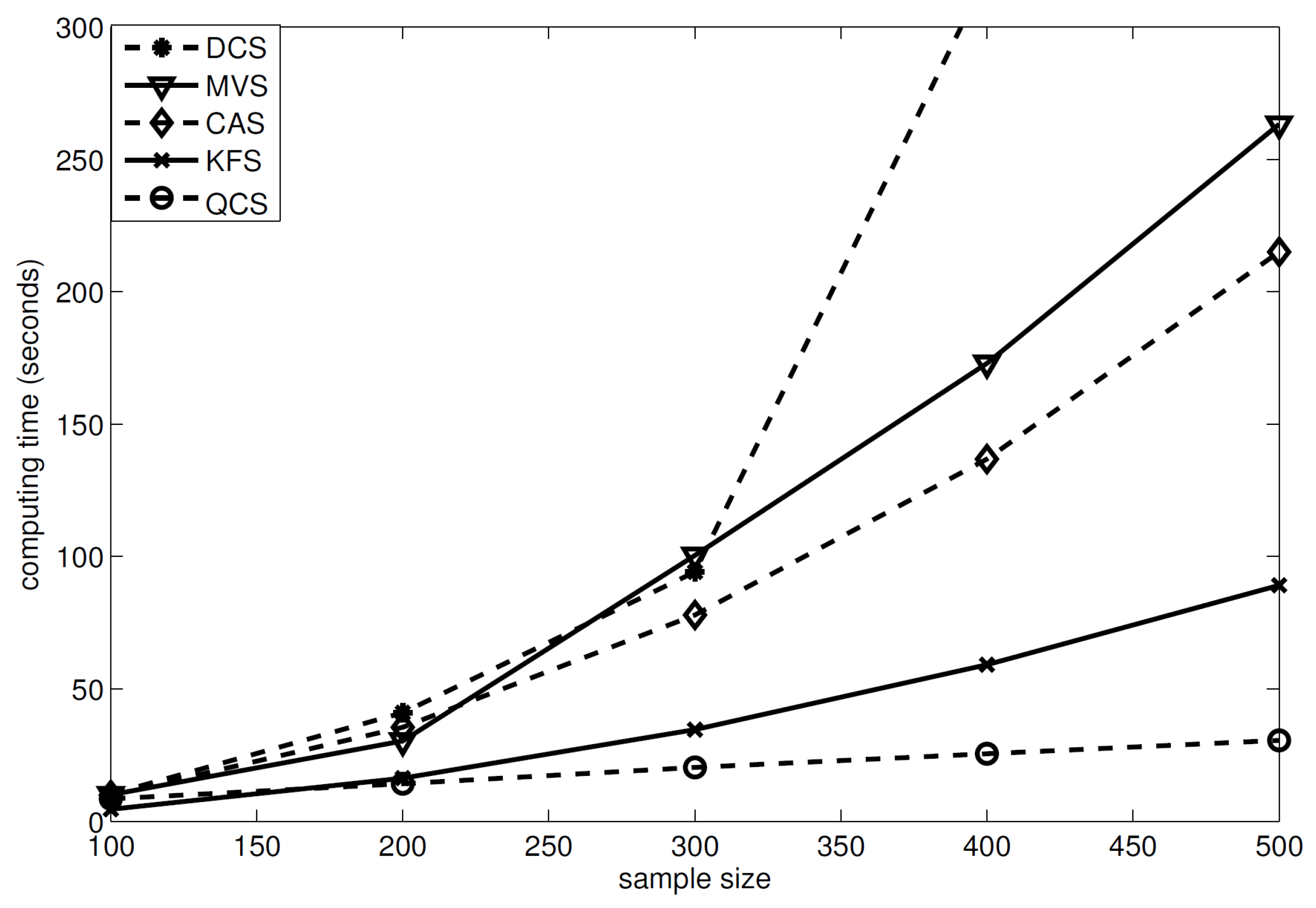
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MMS | IQR | EPR | MMS | IQR | EPR | |||||
| Case 1 | ||||||||||
| QCS | 2 | 1 | 12 | 94.2 | 97.3 | 2 | 2 | 21 | 91.2 | 95.4 |
| MVS | 2 | 1 | 6 | 97.1 | 98.6 | 2 | 1 | 16.5 | 93.4 | 97.0 |
| DCS | 7 | 5 | 14 | 86.4 | 98.0 | 20 | 13 | 44 | 12.0 | 65.2 |
| CAS | 2 | 0 | 5 | 97.5 | 98.9 | 2 | 1 | 15 | 92.1 | 95.9 |
| KFS | 2 | 2 | 16 | 91.2 | 96.1 | 2 | 3 | 29 | 86.2 | 93.1 |
| Case 2 | ||||||||||
| QCS | 2 | 2 | 23 | 90.7 | 94.7 | 3 | 4 | 34 | 85.8 | 92.6 |
| MVS | 2 | 1 | 15 | 91.6 | 96.0 | 2 | 2 | 22 | 90.4 | 93.7 |
| DCS | 7 | 6 | 23.5 | 78.8 | 94.8 | 22.5 | 19 | 62 | 13.3 | 56.1 |
| CAS | 2 | 1 | 16 | 93.3 | 96.0 | 2 | 3 | 24 | 90.1 | 93.2 |
| KFS | 3 | 4 | 35 | 85.0 | 91.1 | 3 | 5 | 53 | 83.0 | 90.2 |
| Case 3 | ||||||||||
| QCS | 8 | 0 | 3 | 98.8 | 99.3 | 8 | 0 | 10 | 98 | 99.3 |
| MVS | 8 | 2 | 15 | 96.4 | 98.3 | 8.5 | 3 | 45 | 92.3 | 96.0 |
| DCS | 68.5 | 31 | 126 | 0.2 | 41.2 | 190.5 | 103 | 334 | 0 | 0 |
| CAS | 8 | 0 | 2 | 99.7 | 99.9 | 8 | 1 | 6 | 98.2 | 98.9 |
| KFS | 9.5 | 4 | 21 | 96.0 | 99.2 | 11 | 7 | 43 | 90.0 | 96.3 |
| Case 4 | ||||||||||
| QCS | 8 | 0 | 11 | 96.9 | 98.7 | 8 | 2 | 24.5 | 94.9 | 97.0 |
| MVS | 9 | 4 | 39.5 | 92.6 | 96.0 | 11 | 14 | 84 | 83.5 | 92.0 |
| DCS | 91 | 63 | 270.5 | 0.0 | 19.2 | 272 | 213 | 630 | 0.0 | 0.0 |
| CAS | 8 | 1 | 6 | 98.4 | 99.4 | 9 | 4 | 19 | 93.1 | 96.3 |
| KFS | 12 | 10 | 47 | 86.6 | 96.2 | 14.5 | 20 | 98 | 77.0 | 91.6 |
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MMS | IQR | EPR | MMS | IQR | EPR | |||||
| Balanced response, | ||||||||||
| QCS | 20 | 0 | 1 | 100 | 100 | 20 | 0 | 1 | 99.2 | 100 |
| MVS | 20 | 0 | 0 | 100 | 100 | 20 | 0 | 1 | 99.5 | 100 |
| DCS | 33 | 8 | 19 | 74.0 | 99.7 | 68.5 | 21 | 58 | 0 | 66.3 |
| CAS | 20 | 0 | 0 | 100 | 100 | 20 | 0 | 0 | 100 | 100 |
| KFS | 20 | 0 | 2 | 100 | 100 | 20 | 1 | 6 | 99.2 | 100 |
| Imbalanced response, | ||||||||||
| QCS | 20 | 3 | 24 | 92.5 | 98.0 | 22 | 8 | 51 | 85.5 | 95.3 |
| MVS | 21 | 7 | 31 | 88.8 | 97.6 | 23 | 14 | 66 | 78.4 | 92.4 |
| DCS | 83 | 83 | 287 | 1.7 | 41.6 | 203.5 | 143 | 420 | 0 | 0.7 |
| CAS | 26 | 13 | 38 | 80.2 | 97.3 | 32 | 19 | 55 | 63.5 | 94.0 |
| KFS | 31 | 20 | 64 | 64.7 | 91.6 | 36 | 29 | 137 | 52.4 | 83.1 |
| Balanced response, | ||||||||||
| QCS | 20 | 0 | 1 | 100 | 100 | 20 | 0 | 2 | 99.2 | 100 |
| MVS | 20 | 0 | 1 | 100 | 100 | 20 | 0 | 3 | 99.2 | 100 |
| DCS | 61 | 16 | 56 | 0 | 80.4 | 159.5 | 50 | 162 | 0 | 0 |
| CAS | 20 | 0 | 0 | 100 | 100 | 20 | 0 | 1 | 100 | 100 |
| KFS | 20 | 2 | 8 | 96.8 | 100 | 21 | 2 | 17 | 95.1 | 98.8 |
| Imbalanced response, | ||||||||||
| QCS | 21 | 8 | 80 | 84.4 | 93.2 | 24 | 27 | 230 | 69.9 | 83.2 |
| MVS | 23 | 15 | 106 | 77.1 | 90.3 | 29 | 46 | 220 | 60.2 | 78.2 |
| DCS | 228.5 | 237 | 908 | 0 | 1.2 | 581 | 423 | 1148 | 0 | 0 |
| CAS | 37 | 34 | 109 | 50.9 | 81.7 | 57 | 62 | 161 | 20.5 | 63.3 |
| KFS | 48.5 | 56 | 257 | 36.6 | 69.2 | 68.5 | 80 | 306 | 19.1 | 54.8 |
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MMS | IQR | EPR | MMS | IQR | EPR | |||||
| Case 1 | ||||||||||
| QCS | 2 | 0 | 3 | 98.9 | 99.7 | 8 | 0 | 4 | 98.9 | 99.8 |
| MVS | 2 | 0 | 2 | 100 | 100 | 21 | 29 | 141 | 64.5 | 83.4 |
| DCS | 10 | 4.5 | 12 | 75.0 | 99.0 | 147.5 | 79 | 238 | 0 | 0 |
| CAS | 3 | 3 | 12.5 | 92.9 | 97.4 | 31 | 37.5 | 169.5 | 50.5 | 79.5 |
| KFS | 2 | 0 | 2 | 99.6 | 100 | 22 | 23 | 102 | 67.0 | 87.2 |
| Case 2 | ||||||||||
| QCS | 3 | 2 | 14 | 93.6 | 97.3 | 9 | 3 | 27.5 | 94.3 | 96.9 |
| MVS | 4 | 5 | 12.5 | 93.3 | 98.4 | 103 | 126.5 | 366 | 3.0 | 25.5 |
| DCS | 13 | 5 | 16 | 49.5 | 96.5 | 192.5 | 92 | 420 | 0 | 0 |
| CAS | 35 | 41 | 125 | 11.3 | 33.0 | 467 | 385 | 1014 | 0 | 0 |
| KFS | 2 | 2 | 11 | 95.0 | 97.6 | 103.5 | 108 | 344.5 | 8.0 | 28.4 |
| Case 3 | ||||||||||
| QCS | 6 | 10 | 44.5 | 74.5 | 87.6 | 13 | 16 | 86.5 | 78.1 | 89.7 |
| MVS | 12 | 13 | 49 | 52.1 | 79.4 | 346.5 | 277.5 | 841 | 0 | 0 |
| DCS | 15 | 8 | 21 | 28.7 | 88.2 | 271 | 153.5 | 545.5 | 0 | 0 |
| CAS | 297.5 | 207.5 | 550.5 | 0 | 0 | 1644 | 317 | 696.5 | 0 | 0 |
| KFS | 9 | 18 | 55 | 60.9 | 79.3 | 411 | 332.5 | 738 | 0 | 0 |
| Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MMS | IQR | EPR | MMS | IQR | EPR | |||||
| QCS | 12.5 | 15 | 112 | 77.7 | 88.3 | 12 | 12 | 101 | 81.6 | 90.4 |
| MVS | 13 | 18 | 165 | 75.2 | 84.8 | 12 | 14 | 143 | 76.6 | 88.1 |
| DCS | 13 | 18 | 177 | 76.0 | 85.6 | 18 | 37 | 210 | 65.1 | 80.0 |
| CAS | 12.5 | 13 | 153 | 78.1 | 87.1 | 31.5 | 46.0 | 172 | 47.2 | 72.8 |
| KFS | 21 | 36 | 281 | 62.2 | 78.1 | 32.5 | 53 | 230 | 48.0 | 70.4 |
| QCS | 10 | 15 | 137 | 85.6 | 92.2 | 10 | 12 | 49 | 92.0 | 95.2 |
| MVS | 10 | 15 | 150 | 85.3 | 92.4 | 10 | 12 | 67 | 90.1 | 94.4 |
| DCS | 10 | 15 | 133 | 84.7 | 91.2 | 11 | 23 | 112 | 79.0 | 88.6 |
| CAS | 10 | 14 | 106 | 85.2 | 92.8 | 14 | 30 | 136 | 72.6 | 83.6 |
| KFS | 12 | 24 | 139 | 79.2 | 88.5 | 13 | 34 | 174 | 72.8 | 82.8 |
| Method | MMS | IQR | EPR | |||
|---|---|---|---|---|---|---|
| Model 1 | QCS | 11 | 10 | 111 | 86.2 | 92.1 |
| MVS | 11.5 | 14 | 132 | 82.4 | 89.5 | |
| DCS | 957 | 713 | 1513 | 0.4 | 0.8 | |
| CAS | 30 | 78 | 338 | 56.7 | 71.2 | |
| KFS | 14 | 18 | 165 | 83.2 | 90.3 | |
| Model 2 | QCS | 4 | 1 | 7 | 98.1 | 100 |
| MVS | 4 | 1 | 9 | 98.0 | 100 | |
| DCS | 49 | 58 | 195 | 34.6 | 64.5 | |
| CAS | 6 | 10 | 35 | 92.9 | 98.3 | |
| KFS | 5 | 13 | 72 | 92.4 | 94.1 | |
| Model 3 | QCS | 6.5 | 14 | 109 | 88.7 | 94.2 |
| MVS | 7 | 16 | 114 | 86.4 | 90.8 | |
| DCS | 13 | 26 | 215 | 76.5 | 86.6 | |
| CAS | 17 | 54 | 258 | 60.8 | 78.9 | |
| KFS | 25 | 87 | 316 | 58.2 | 68.4 |
| Data | Method | No. of Training Errors | No. of Testing Errors | |||
|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | |||
| Leukemia | 16 | QCS-penLDA | 0.176 | 0.401 | 0.794 | 0.865 |
| MVS-penLDA | 0.166 | 0.383 | 0.828 | 0.864 | ||
| DCS-penLDA | 1.188 | 0.783 | 1.334 | 1.082 | ||
| CAS-penLDA | 0.140 | 0.353 | 0.814 | 0.867 | ||
| KFS-penLDA | 0.260 | 0.478 | 0.896 | 0.924 | ||
| 32 | QCS-penLDA | 0.152 | 0.359 | 0.670 | 0.813 | |
| MVS-penLDA | 0.130 | 0.336 | 0.696 | 0.808 | ||
| DCS-penLDA | 0.898 | 0.732 | 0.974 | 0.920 | ||
| CAS-penLDA | 0.128 | 0.334 | 0.682 | 0.801 | ||
| KFS-penLDA | 0.210 | 0.417 | 0.792 | 0.873 | ||
| SRBCT | 15 | QCS-penLDA | 0.100 | 0.319 | 0.574 | 0.818 |
| MVS-penLDA | 0.436 | 1.777 | 1.180 | 1.399 | ||
| DCS-penLDA | 1.366 | 2.753 | 1.740 | 1.701 | ||
| CAS-penLDA | 7.236 | 2.246 | 5.744 | 2.174 | ||
| KFS-penLDA | 2.850 | 1.665 | 2.852 | 1.744 | ||
| 30 | QCS-penLDA | 0.088 | 1.343 | 0.206 | 0.872 | |
| MVS-penLDA | 0.130 | 1.710 | 0.470 | 1.021 | ||
| DCS-penLDA | 0.320 | 2.693 | 0.604 | 1.458 | ||
| CAS-penLDA | 3.360 | 1.601 | 3.864 | 1.787 | ||
| KFS-penLDA | 0.594 | 0.831 | 0.860 | 0.964 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Lu, J. Quantile-Composited Feature Screening for Ultrahigh-Dimensional Data. Mathematics 2023, 11, 2398. https://doi.org/10.3390/math11102398
Chen S, Lu J. Quantile-Composited Feature Screening for Ultrahigh-Dimensional Data. Mathematics. 2023; 11(10):2398. https://doi.org/10.3390/math11102398
Chicago/Turabian StyleChen, Shuaishuai, and Jun Lu. 2023. "Quantile-Composited Feature Screening for Ultrahigh-Dimensional Data" Mathematics 11, no. 10: 2398. https://doi.org/10.3390/math11102398
APA StyleChen, S., & Lu, J. (2023). Quantile-Composited Feature Screening for Ultrahigh-Dimensional Data. Mathematics, 11(10), 2398. https://doi.org/10.3390/math11102398





