Swarm Robots Search for Multiple Targets Based on Historical Optimal Weighting Grey Wolf Optimization
Abstract
:1. Introduction
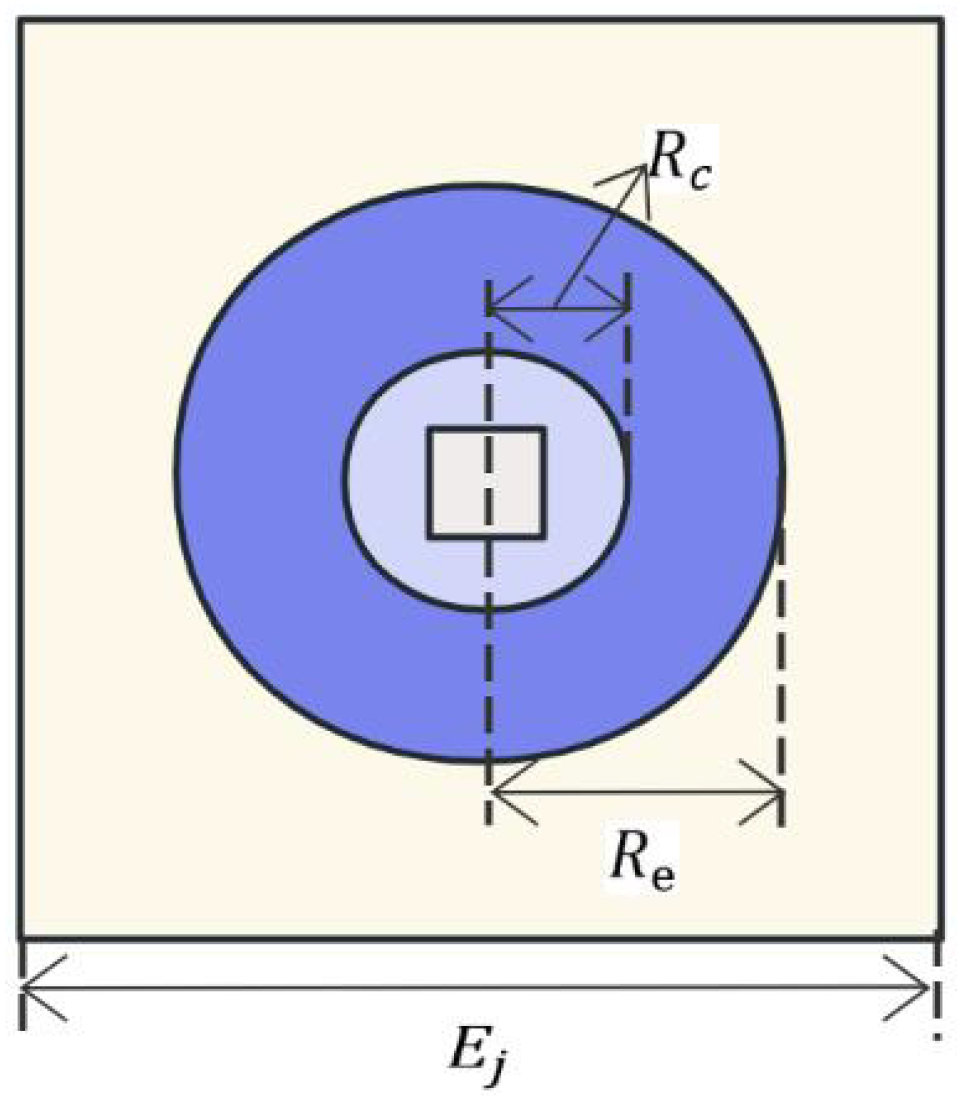
2. Problem Statement
3. Algorithm Statement
3.1. Grey Wolf Optimization Based on Historical Optimal Weight Estimation
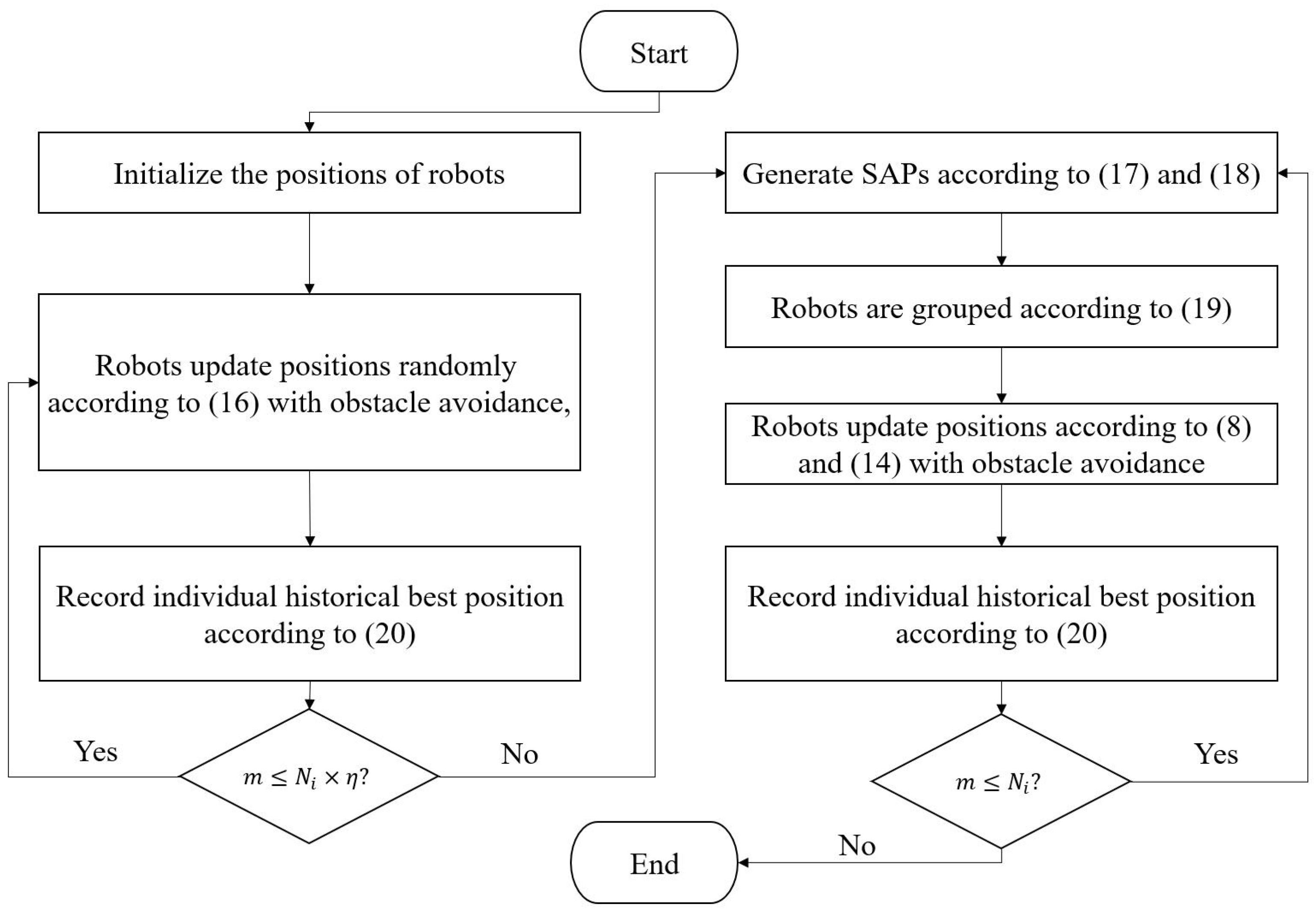
3.2. Random Walk Stage—First Stage
3.3. Dynamic Grouping Stage—Second Stage
3.3.1. Searching Auxiliary Points (SAPs) Generation
3.3.2. Dynamic Grouping and Searching
| Algorithm 1 Position update strategies in HOWGWO |
|
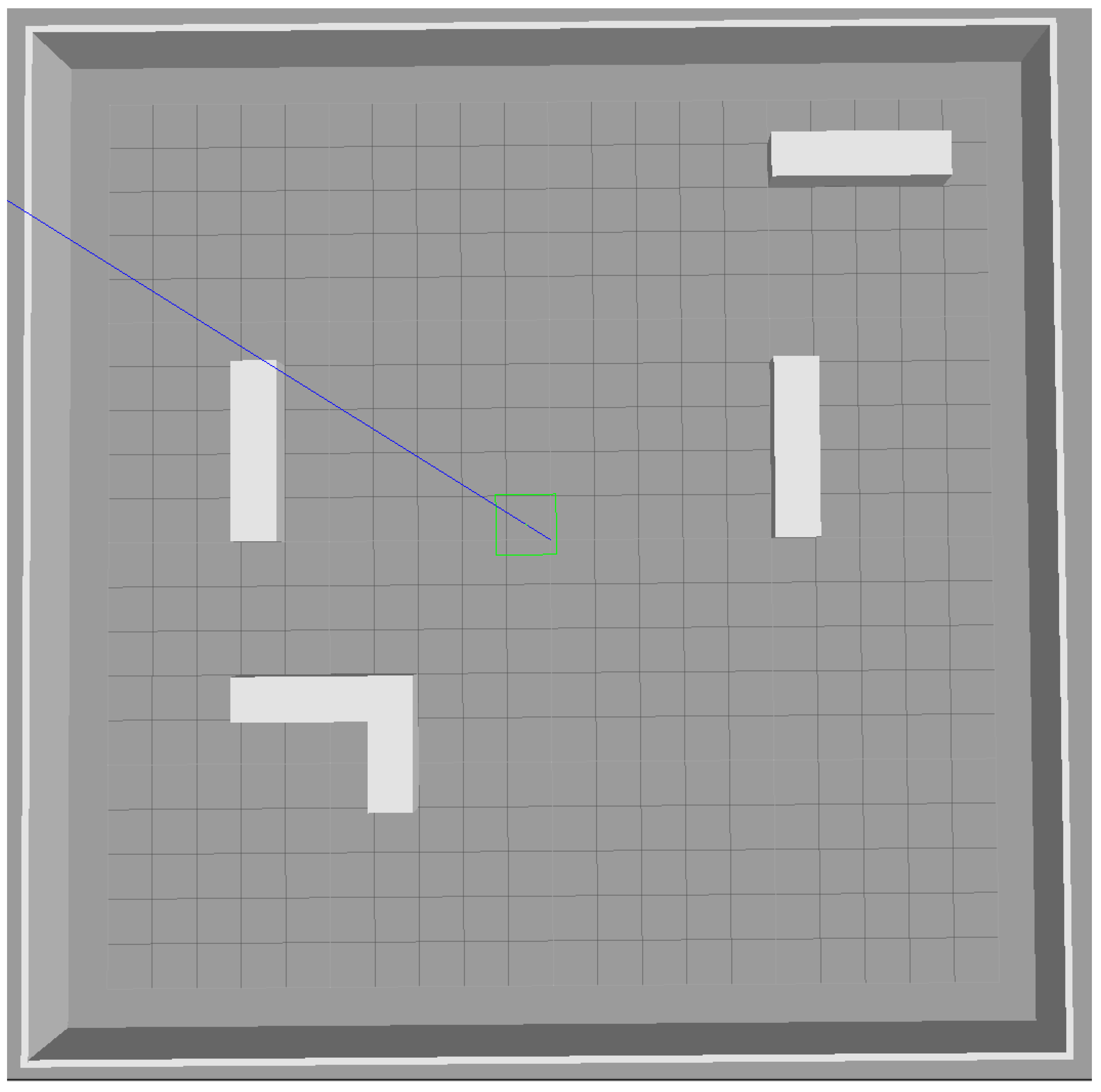
3.4. Obstacle Avoidance Strategy
3.5. Evaluation Index
4. Wilcoxson Rank Sum Test and Comparative Experiment
4.1. Wilcoxson Rank Sum Test
4.2. Experimental Environment
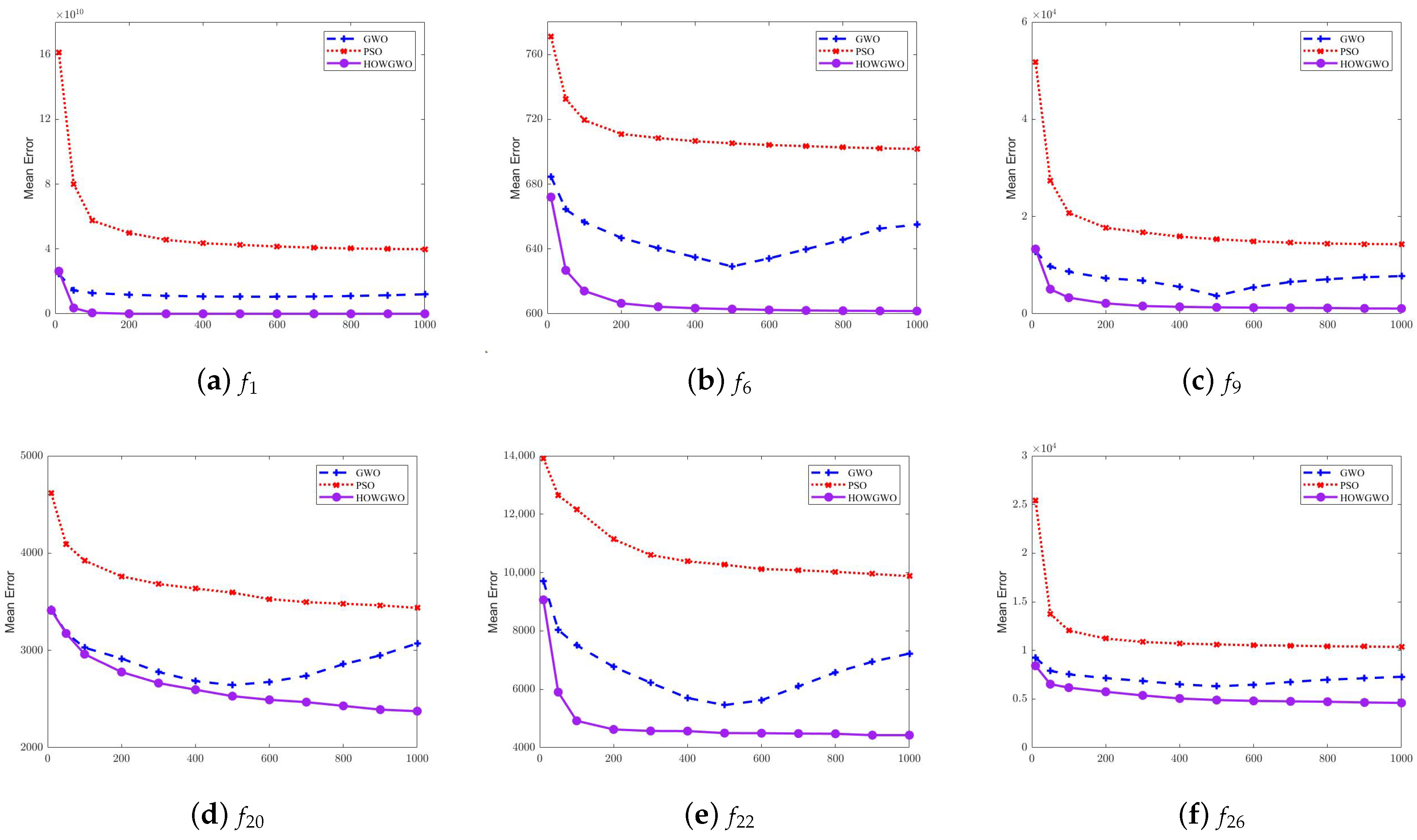
4.3. Results and Discussion
5. Simulation and Discussion of Results
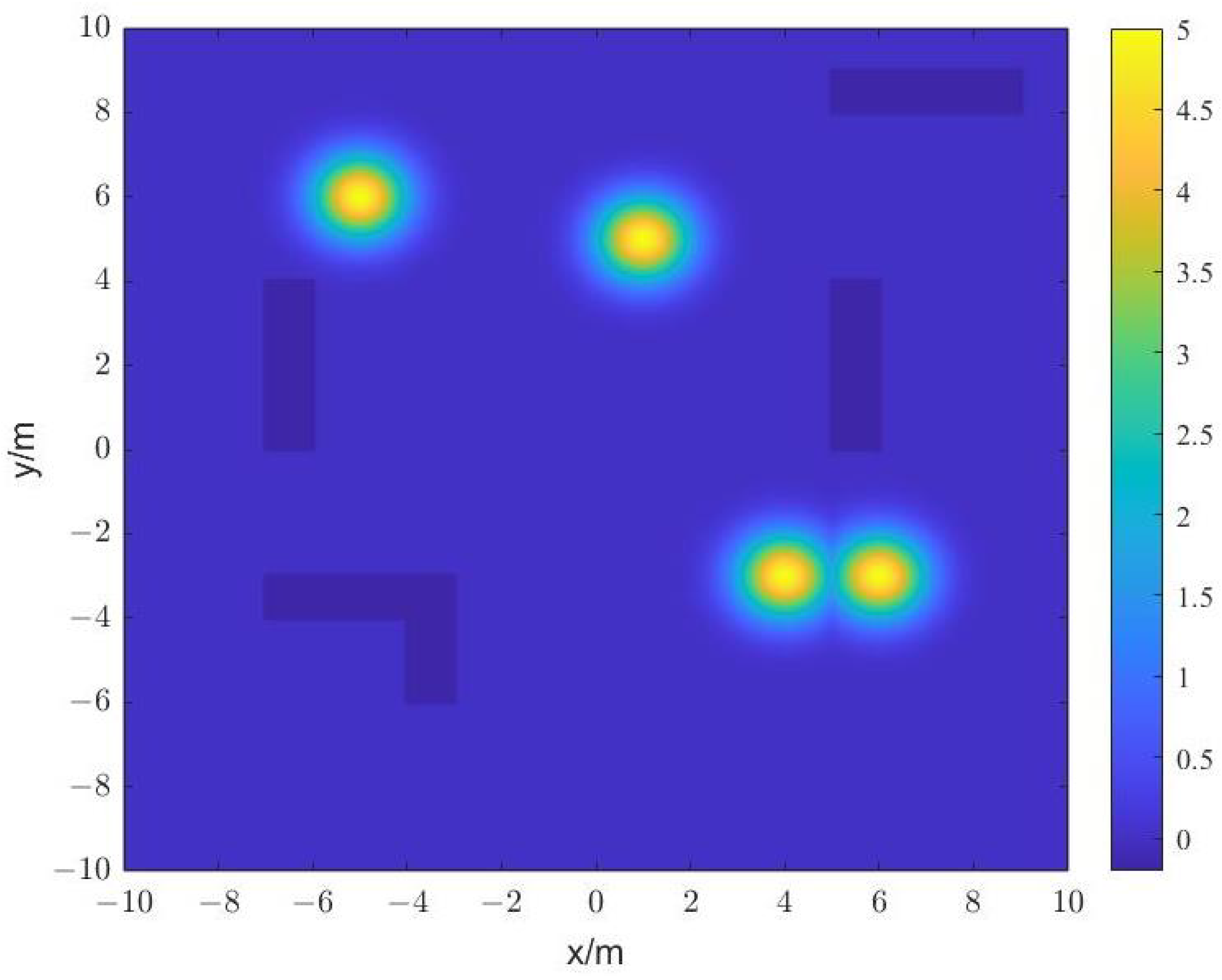
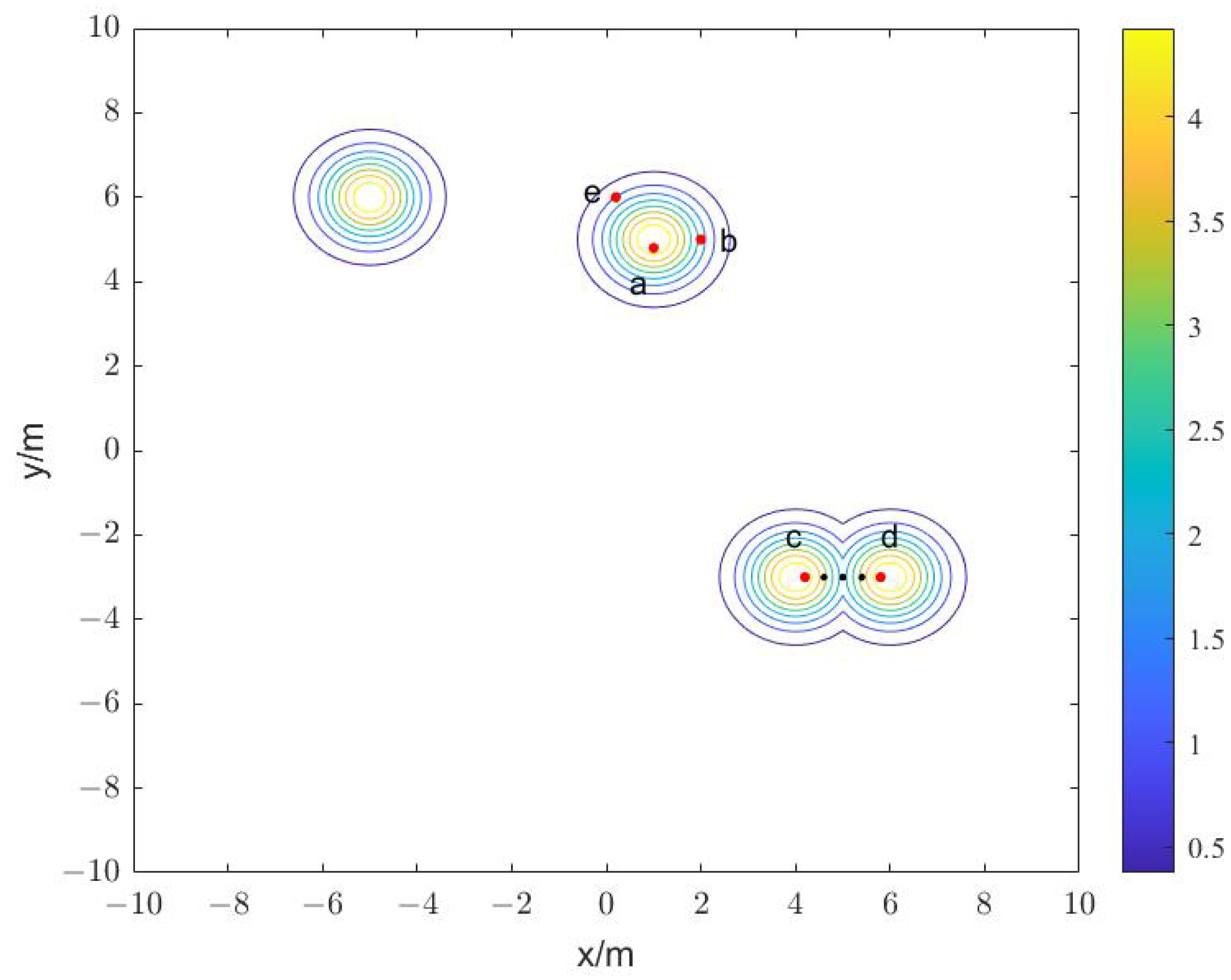
5.1. Description of Relevant Parameters and Objective Function
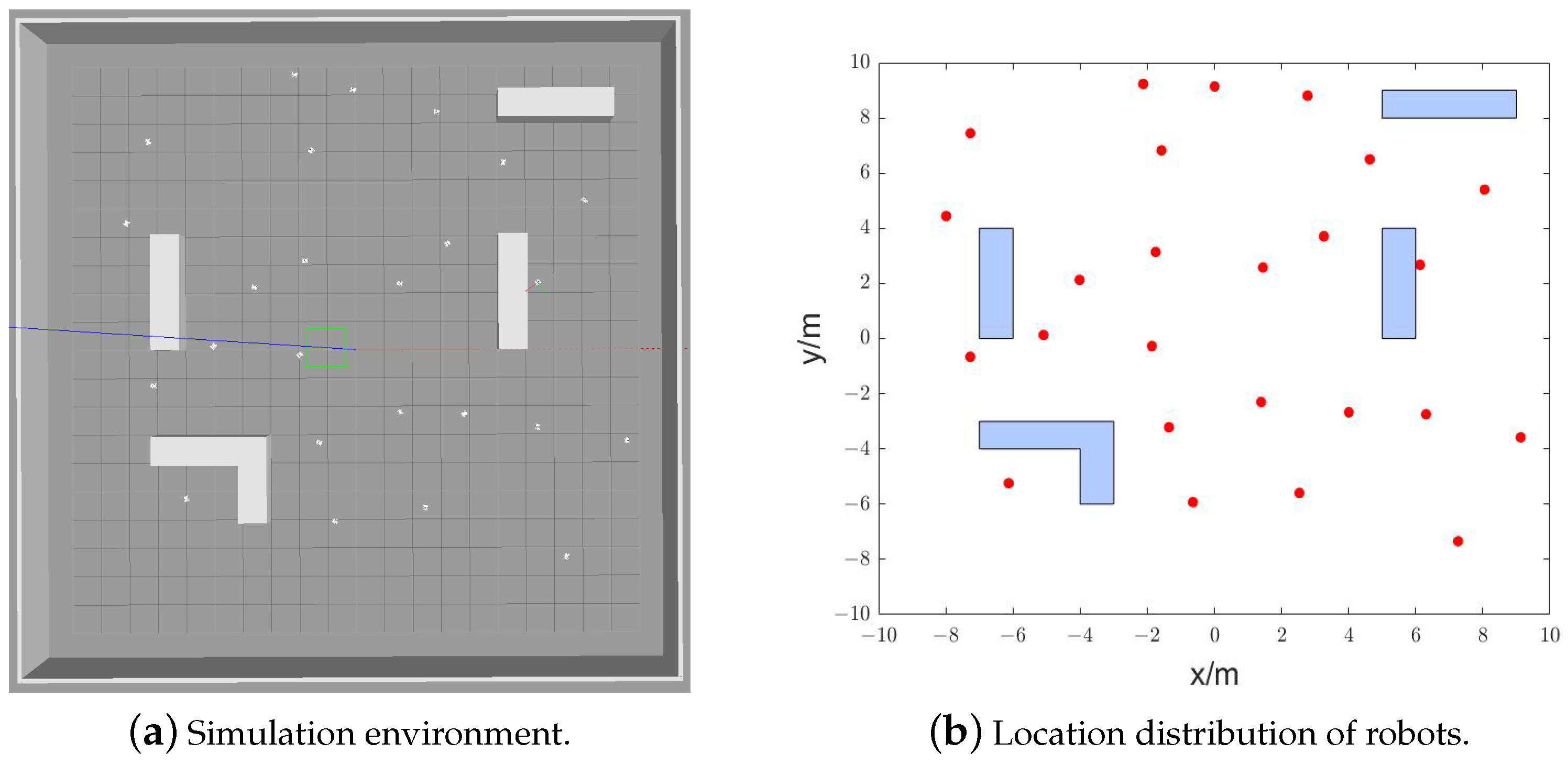
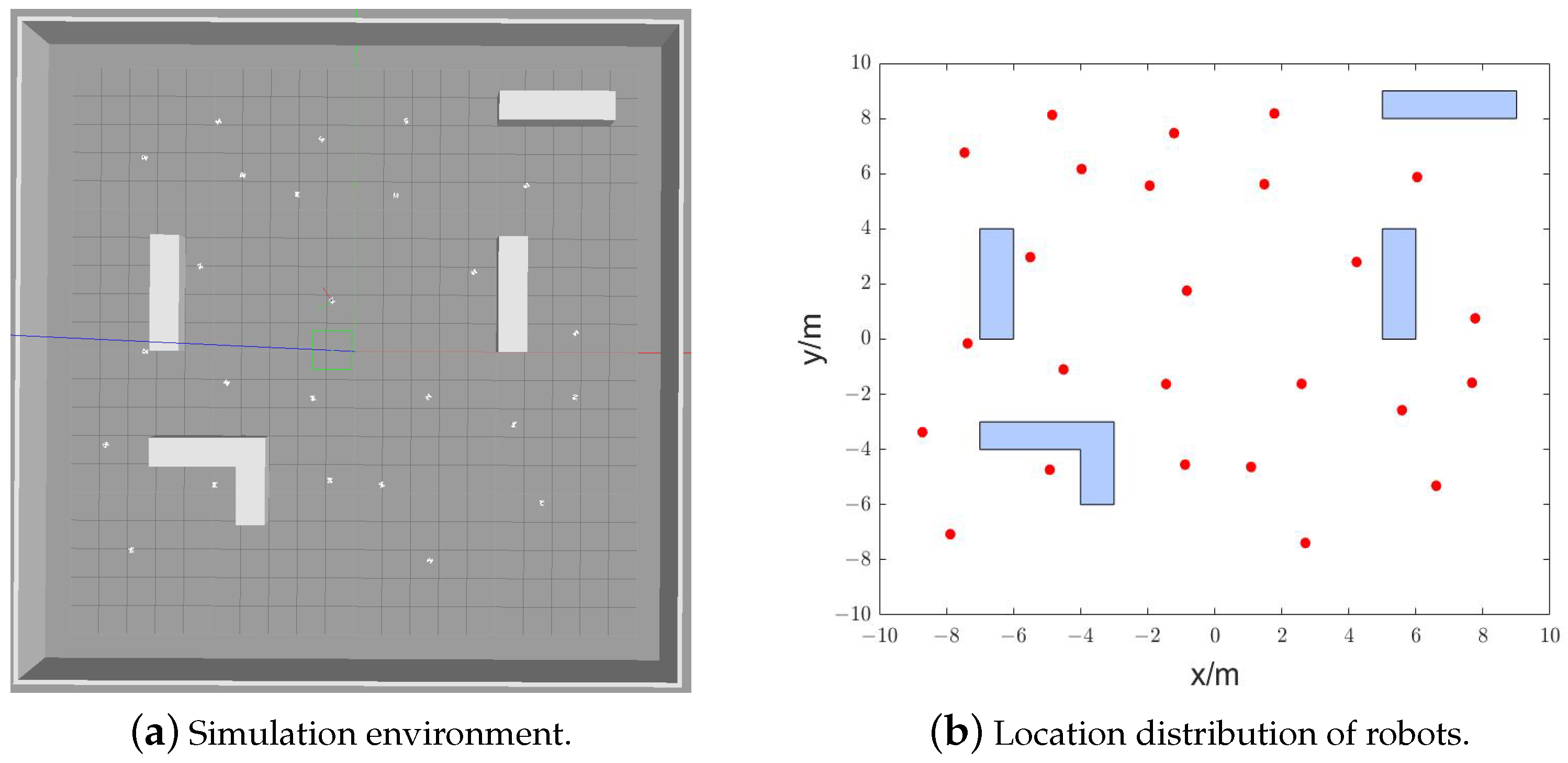
5.2. Search Process of Robots
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.R.; Wang, J.J.; Hou, X.W.; Fang, Z.R.; Du, J.; Ren, Y. Advance into ocean: From bionic monomer to swarm intelligence. Acta Electron. Sin. 2021, 49, 2458–2467. [Google Scholar]
- Prelec, D.; Seung, H.S.; McCoy, J. A solution to the single-question crowd wisdom problem. Nature 2017, 541, 532–535. [Google Scholar] [CrossRef]
- Berdahl, A.; Torney, C.J.; Ioannou, C.C.; Faria, J.J.; Couzin, I.D. Emergent sensing of complex environments by mobile animal groups. Science 2013, 339, 574–576. [Google Scholar] [CrossRef] [Green Version]
- Eiben, A.E.; Smith, J. From evolutionary computation to the evolution of things. Nature 2015, 521, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.X. Study on multiple mobile robots coordinated planning algorithms. Ph.D. Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Sharma, S.; Shukla, A.; Tiwari, R. Multi robot area exploration using nature inspired algorithm. Biol. Inspired Cogn. Archit. 2016, 18, 80–94. [Google Scholar] [CrossRef]
- Mehfuz, F. Recent implementations of autonomous robotics for space exploration. In Proceedings of the 2018 International Conference on Sustainable Energy, Electronics, and Computing Systems (SEEMS), Greater Noida, India, 26–27 October 2018; pp. 1–6. [Google Scholar]
- St-Onge, D.; Kaufmann, M.; Panerati, J.; Ramtoula, B.; Cao, Y.J.; Coffey, E.B.J.; Beltrame, G. Planetary exploration with robot teams: Implementing higher autonomy with swarm intelligence. IEEE Robot. Autom. Mag. 2020, 27, 159–168. [Google Scholar] [CrossRef]
- Duarte, M.; Gomes, J.; Costa, V.; Rodrigues, T.; Silva, F.; Lobo, V.; Marques, M.M.; Oliveira, S.M.; Christensen, A.L. Application of swarm robotics systems to marine environmental monitoring. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016; pp. 1–8. [Google Scholar]
- Pan, J.f.; Zi, B.; Wang, Z.Y.; Qian, S.; Wang, D.M. Real-time dynamic monitoring of a multi-robot cooperative spraying system. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 862–867. [Google Scholar]
- Elwin, M.L.; Freeman, R.A.; Lynch, K.M. Distributed environmental monitoring with finite element robots. IEEE Trans. Robot. 2020, 36, 380–398. [Google Scholar] [CrossRef]
- Bakhshipour, M.; Ghadi, M.J.; Namdari, F. Swarm robotics search & rescue: A novel artificial intelligence-inspired optimization approach. Appl. Soft Comput. 2017, 57, 708–726. [Google Scholar]
- Din, A.; Jabeen, M.; Zia, K.; Khalid, A.; Saini, D.K. Behavior-based swarm robotic search and rescue using fuzzy controller. Comput. Electr. Eng. 2018, 70, 53–65. [Google Scholar] [CrossRef]
- Cardona, G.A.; Calderon, J.M. Robot swarm navigation and victim detection using rendezvous consensus in search and rescue operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Ding, Y.S.; Jin, Y.C.; Hao, K.R. Self-organized swarm robot for target search and trapping inspired by bacterial chemotaxis. Robot. Auton. Syst. 2015, 72, 83–92. [Google Scholar] [CrossRef]
- Megalingam, R.K.; Nagalla, D.; Kiran, P.R.; Geesala, R.T.; Nigam, K. Swarm based autonomous landmine detecting robots. In Proceedings of the 2017 International Conference on Inventive Computing and Informatics (ICICI), Coimbatore, India, 23–24 November 2017; pp. 608–612. [Google Scholar]
- Tarapore, D.; Gross, R.; Zauner, K.-P. Sparse robot swarms: Moving swarms to real-world applications. Front. Robot. AI 2020, 57, 83. [Google Scholar] [CrossRef] [PubMed]
- Albiero, D.; Pontin Garcia, A.; Kiyoshi Umezu, C.; Leme de Paulo, R. Swarm robots in mechanized agricultural operations: A review about challenges for research. Comput. Electron. Agric. 2022, 193, 106608. [Google Scholar] [CrossRef]
- Senanayake, M.; Senthooran, I.; Barca, J.C.; Chung, H.; Kamruzzaman, J.; Murshed, M. Search and tracking algorithms for swarms of robots: A survey. Robot. Auton. Syst. 2016, 75, 422–434. [Google Scholar] [CrossRef]
- Prodhon, C. A hybrid evolutionary algorithm for the periodic location-routing problem. Eur. J. Oper. Res. 2011, 210, 204–212. [Google Scholar] [CrossRef]
- Zheng, Z.; Tan, Y. Group explosion strategy for searching multiple targets using swarm robotic. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 821–828. [Google Scholar]
- Liu, R.C.; Niu, X.; Jiao, L.C.; Ma, J.J. A multi-swarm particle swarm optimization with orthogonal learning for locating and tracking multiple optimization in dynamic environments. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 754–761. [Google Scholar]
- Dadgar, M.; Jafari, S.; Hamzeh, A. A PSO-based multi-robot cooperation method for target searching in unknown environments. Neurocomputing 2016, 177, 62–74. [Google Scholar] [CrossRef]
- Tang, H.W.; Sun, W.; Yu, H.S.; Lin, A.P.; Xue, M.; Song, Y.X. A novel hybrid algorithm based on PSO and FOA for target searching in unknown environments. Appl. Intell. 2019, 49, 2603–2622. [Google Scholar] [CrossRef]
- Zedadra, O.; Guerrieri, A.; Seridi, H. LFA: A Lévy Walk and Firefly-Based Search Algorithm: Application to Multi-Target Search and Multi-Robot Foraging. Big Data Cogn. Comput. 2022, 6, 22. [Google Scholar] [CrossRef]
- Ariyarit, A.; Kanazaki, M.; Bureerat, S. An Approach Combining an Efficient and Global Evolutionary Algorithm with a Gradient-Based Method for Airfoil Design Problems. Smart Sci. 2020, 8, 14–23. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Fatahi, A.; Mirjalili, S. MFO-SFR: An Enhanced Moth-Flame Optimization Algorithm Using an Effective Stagnation Finding and Replacing Strategy. Mathematics 2023, 11, 862. [Google Scholar] [CrossRef]
- Tang, Q.R.; Ding, L.; Yu, F.C.; Zhang, Y.; Li, Y.H.; Tu, H.B. Swarm robots search for multiple targets based on an improved grouping strategy. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 1943–1950. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Luo, K.P. Enhanced grey wolf optimizer with a model for dynamically estimating the location of the prey. Appl. Soft Comput. 2019, 77, 225–235. [Google Scholar] [CrossRef]




| Function | Range |
|---|---|
| Function | Mean Error—Original | Mean Error—Shifted | p-Value |
|---|---|---|---|
| Sphere | 0.9512 | ||
| Schwdfel 1.2 | 0.6894 | ||
| Rastrign | 0.2213 |
| Func. | GWO | PSO | EGWO | HOWGWO |
|---|---|---|---|---|
| 1 | ||||
| 2 | () | |||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 | ||||
| 15 | ||||
| 16 | ||||
| 17 | ||||
| 18 | ||||
| 19 | ||||
| 20 | ||||
| 21 | ||||
| 22 | ||||
| 23 | ||||
| 24 | ||||
| 25 | ||||
| 26 | ||||
| 27 | ||||
| 28 | ||||
| 29 | ||||
| 30 |
| Name | Description | Value |
|---|---|---|
| N | Sum of the Robots | 25 |
| Maximum Iterations | 100 | |
| Percentage Factor of Iterations | 0.4 | |
| Grouping Threshold | 0.09 | |
| Distance Threshold | 3 | |
| Search Range |
| N | Average of | ||||
|---|---|---|---|---|---|
| 25 | 100 | 0.2 | 0.09 | 94 | 0.55 |
| 25 | 100 | 0.4 | 0.09 | 98 | 0.47 |
| 25 | 100 | 0.6 | 0.09 | 100 | 0.53 |
| 25 | 100 | 0.8 | 0.09 | 96 | 0.65 |
| 25 | 100 | 0.9 | 0.09 | 88 | 2.29 |
| 25 | 80 | 0.2 | 0.09 | 90 | 0.46 |
| 25 | 80 | 0.4 | 0.09 | 94 | 0.50 |
| 25 | 80 | 0.6 | 0.09 | 100 | 0.58 |
| 25 | 80 | 0.8 | 0.09 | 94 | 0.94 |
| 25 | 80 | 0.9 | 0.09 | 76 | 2.10 |
| 25 | 50 | 0.2 | 0.09 | 88 | 0.79 |
| 25 | 50 | 0.4 | 0.09 | 92 | 0.53 |
| 25 | 50 | 0.6 | 0.09 | 96 | 0.44 |
| 25 | 50 | 0.8 | 0.09 | 88 | 2.27 |
| 25 | 50 | 0.9 | 0.09 | 64 | 3.17 |
| N | Average of | ||||
|---|---|---|---|---|---|
| 25 | 80 | 0.4 | 0.09 | 96 | 0.50 |
| 25 | 80 | 0.4 | 0.50 | 96 | 0.49 |
| 25 | 80 | 0.4 | 1.00 | 94 | 0.52 |
| 25 | 80 | 0.4 | 1.50 | 94 | 0.49 |
| 25 | 80 | 0.4 | 2.00 | 92 | 0.48 |
| 25 | 80 | 0.4 | 2.50 | 92 | 0.65 |
| 25 | 80 | 0.4 | 3.00 | 90 | 0.83 |
| 25 | 80 | 0.4 | 3.50 | 82 | 2.35 |
| 25 | 80 | 0.4 | 4.00 | 68 | 2.92 |
| N | |||||
|---|---|---|---|---|---|
| 25 | 80 | 0.1 | 0.09 | 92 | 24 |
| 25 | 80 | 0.2 | 0.09 | 92 | 14 |
| 25 | 80 | 0.3 | 0.09 | 96 | 30 |
| 25 | 80 | 0.4 | 0.09 | 96 | 32 |
| 25 | 80 | 0.4 | 0.20 | 98 | 24 |
| 25 | 80 | 0.4 | 0.30 | 92 | 18 |
| 25 | 80 | 0.4 | 0.40 | 94 | 20 |
| 25 | 80 | 0.4 | 0.50 | 92 | 26 |
| 20 | 80 | 0.4 | 0.09 | 92 | 22 |
| 30 | 80 | 0.4 | 0.09 | 98 | 40 |
| 35 | 80 | 0.4 | 0.09 | 98 | 60 |
| 40 | 80 | 0.4 | 0.09 | 100 | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Li, Y.; Zhang, Z. Swarm Robots Search for Multiple Targets Based on Historical Optimal Weighting Grey Wolf Optimization. Mathematics 2023, 11, 2630. https://doi.org/10.3390/math11122630
Zhu Q, Li Y, Zhang Z. Swarm Robots Search for Multiple Targets Based on Historical Optimal Weighting Grey Wolf Optimization. Mathematics. 2023; 11(12):2630. https://doi.org/10.3390/math11122630
Chicago/Turabian StyleZhu, Qian, Yongqing Li, and Zhen Zhang. 2023. "Swarm Robots Search for Multiple Targets Based on Historical Optimal Weighting Grey Wolf Optimization" Mathematics 11, no. 12: 2630. https://doi.org/10.3390/math11122630
APA StyleZhu, Q., Li, Y., & Zhang, Z. (2023). Swarm Robots Search for Multiple Targets Based on Historical Optimal Weighting Grey Wolf Optimization. Mathematics, 11(12), 2630. https://doi.org/10.3390/math11122630





