Dispatch for a Continuous-Time Microgrid Based on a Modified Differential Evolution Algorithm

Abstract

The carbon trading mechanism is proposed to remit global warming and it can be considered in a microgrid. There is a lack of continuous-time methods in a microgrid, so a continuous-time model is proposed and solved by differential evolution (DE) in this work. This research aims to create effective methods to obtain some useful results in a microgrid. Batteries, microturbines, and the exchange with the main grid are considered. Considering carbon trading, the objective function is the sum of a quadratic function and an absolute value function. In addition, a composite electricity price model has been put forward to conclude the common kinds of electricity prices. DE is utilized to solve the constrained optimization problems (COPs) proposed in this paper. A modified DE is raised in this work, which uses multiple mutation and selection strategies. In the case study, the proposed algorithm is compared with the other seven algorithms and the outperforming one is selected to compare two different types of electricity prices. The results show the proposed algorithm performs best. The Wilcoxon Signed Rank Test is also used to verify its significant superiority. The other result is that time-of-use pricing (ToUP) is economic in the off-peak period while inclining block rates (IBRs) are economic in the peak and shoulder periods. The composite electricity price model can be applied in social production and life. In addition, the proposed algorithm puts forward a new variety of DE and enriches the theory of DE.

1. Introduction

Global warming leads to the rising of sea levels and the reduction of biological diversity. To cope with climate change, many countries have taken action, such as the promulgation of the Kyoto Protocol and the Paris Agreement. In addition, in the 21st century, carbon neutrality may become the leading global environmental goal [1]. However, in some countries, power system carbon emissions are still at a high level. Carbon emission is one of the main causes of global warming. Carbon is the fuel of microgrides, so it is required for microgrids to reduce carbon emissions. Many kinds of energy have been considered to generate electricity, including solar energy [2], wind energy [3] and nuclear energy [4].

Now, a lot of researchers have studied the optimization problems in microgrids. These articles have various objectives. The aim of [2] is to minimize the electricity cost and the battery operational cost. In addition, Ref. [3] intends to optimize the energy cost, carbon trading cost, and operational cost. Gholian et al. [5] is to maximize the profit. However, nearly all existing works use discrete-time models. Though they are effective for some problems, they can only give approximate results in some specific time points. There are some kinds of electricity prices, such as the time-of-use pricing in [2,3] and critical peak pricing in [6,7]. The time-of-use pricing changes the price depending on the load and critical peak pricing is similar to time-of-use pricing. Nevertheless, there is a deficiency summary in the studies of microgrids.

For optimization, there are various methods to deal with them. In [8], simulated annealing (SA) is applied to cope with the optimization problem in a smart grid. Ref. [9] utilizes mixed-integer linear programming (MILP) and genetic algorithm (GA) to optimize the unit commitment and economic dispatch in microgrids.

Differential evolution is also an ideal method to solve optimization problems. DE proved to be one of the most successful evolutionary algorithms for solving global optimization problems over continuous space during the past two decades [10]. In addition, Ref. [2] applied DE in the optimal dispatch of microgrids and made a great effect. Therefore, it is applied in this work. It has many modified types, such as MADE [11], MSIQDE [12], EMMSIQDE [13], C²oDE [14], ANDE [15], MVDE [16], FSTDE [17], UDE [18] and AGDE [19]. Mohamed et al. combine novel mutation methods with fitness-adaptive DE and adaptive guided DE in [20] and [21], respectively. Ref. [22] uses a shift mechanism in adaptive multiple-elites-guided composite DE. Hadi et al. propose success history-based differential evolution with linear population size reduction and semi-parameter adaptation (LSHADE-SPA) in [23] and find that this algorithm is competitive among other algorithms. Furthermore, [24] combines DE with Convolutional Neural Networks (CNNs). Numerical experiments indicate this method is vigorously competitive with the other 12 methods and it has high accuracy. In terms of mutation, [25] introduces many kinds of mutation strategies. Mohamed et al. propose new mutation strategies in [10,26].They estimate the proposed methods by some numerical experiments and find the superiority of the proposed methods. Moreover, in [2], DE/rand/1 and DE/current-to-best/1 are used for mutation. These research works are based on theoretical analysis and the results of case studies. They use valid methods, interpreting and presenting the results effectively. The authors’ perspectives are even-handed and they make use of all usable data. Therefore, their arguments and conclusions are convincing, and these works contribute to an understanding of the subject in a significant way. Nonetheless, nearly no research considers continuous-time models and algorithms in the optimal dispatch of microgrids, so their consequences will inevitably have some errors or deviations when considering the time points they do not select.

A DE algorithm needs to consider the constraints. There are three common methods: add constraints when it is initialization; use if statement after mutation and crossover; add penalty terms. In addition, using constraint handling techniques in selection is also optional. To deal with constraints, [2] use stochastic ranking (SR) and superiority of feasible solutions (SF) when selecting.

This work aims to build a continuous-time model and process different kinds of electricity prices. Then, design an effective algorithm to solve it. According to the above present situation, carbon trading is considered in this paper to build a continuous-time optimization model on a convex set. Then, a modified DE is proposed. Compared with [2], it uses DE/pbest/1 and DE/current-to-best/1 in mutation, and uses stochastic ranking (SR) and ε-constraint (EC) in selection. After that, eight kinds of DE algorithms are compared and it shows that the proposed algorithm is better than other algorithms. The Wilcoxon Signed Rank Test also demonstrates this result. Then, this algorithm is applied to study different electricity prices. We find that ToUP is economic in the off-peak period, but IBRs are economic in peak time and shoulder time. The main contributions of this study are as follows.

• Different from these existing works, this paper uses a continuous-time optimization model and uses the integral of time to replace the summation in existing works. Then the model is converted to an equivalent form that is easier to address. Compared to the discrete-time model, the constraint-time model is closer to reality and can give precise results at arbitrary required time points;
• Composite electricity price model is raised in this work. In this model, 5 types of electricity prices in [5] are summarized and represented by one equation in this work, so that future works can use this model to represent nearly all common types of electricity prices. Furthermore, it can provide convenience when comparing different electricity prices in simulation experiments;
• The mutation and the selection strategies of the DE algorithm in [2] are modified in this study. The simulation experiments suggest the proposed algorithm achieves more ideal results than the other seven mentioned algorithms. It converges fast and avoids premature convergence.

The rest of this study is organized as follows. Section 2 introduces the continuous-time model used in this paper. The algorithms in this study are presented in Section 3. The case study is carried out in Section 4. Section 5 concludes this work.

2. Modeling

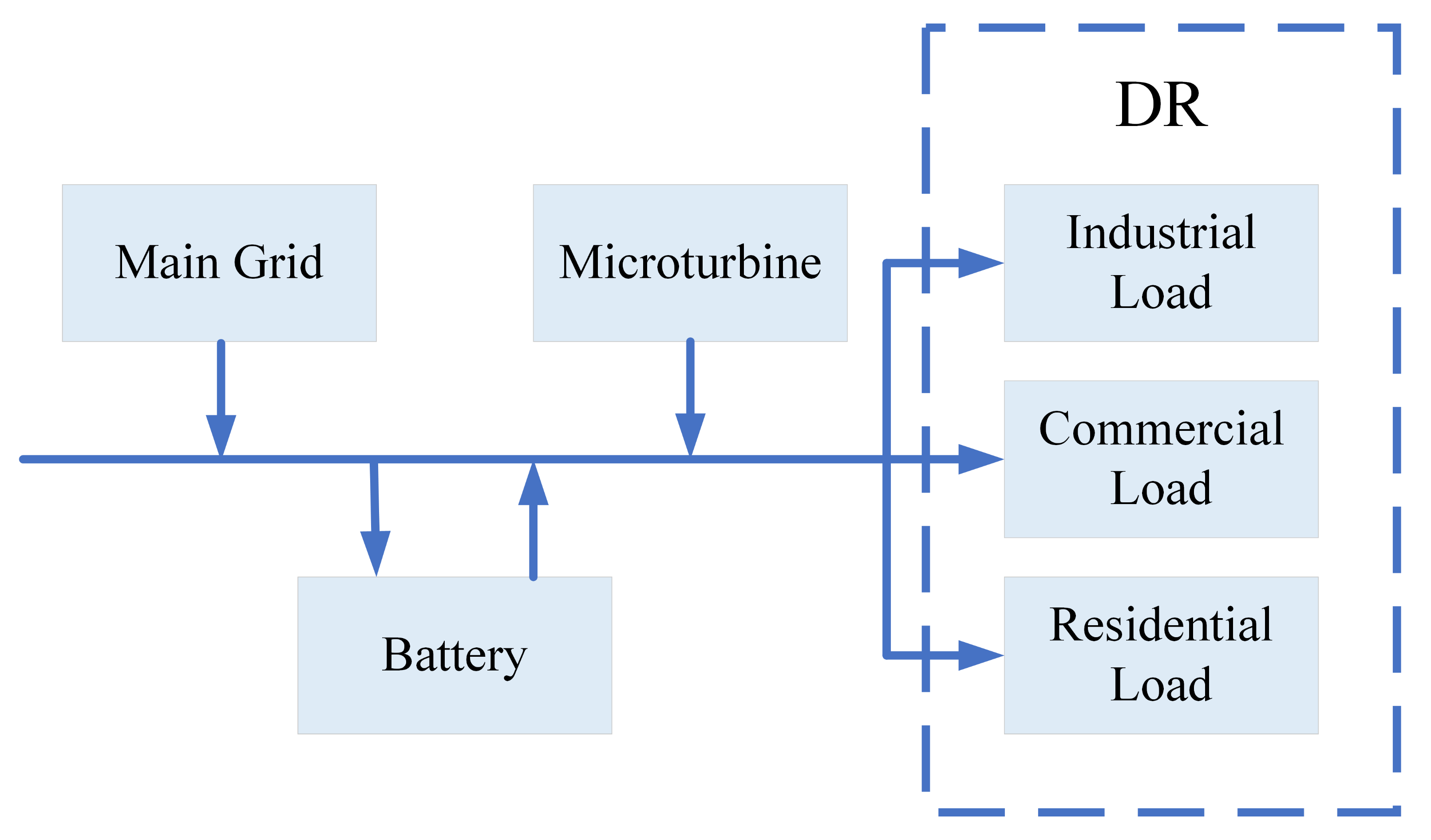
2.1. Structure of Microgrid

Microgrids are usually equipped with batteries, microturbines, photovoltaic power generations, and wind power generations. They also exchange electricity with the main grid. It is a process by which they obtain energy. In addition, microgrids sell excess energy to the main grid. There are three types of load, which are industrial load, commercial load, and residential load. Demand response (DR) means that customers change their loads according to the electricity price or incentive mechanism. Microgrids reduce pollution and they use renewable energy such as solar and wind [27]. In this study, we mainly consider batteries, microturbines, and the exchange with the main grid. The structure of this microgrid is represented in Figure 1.

2.2. Thermal Power Units Operation

The fuel of the thermal power units is natural gas in this paper. The cost of natural gas is quadratic function of units output [16,28].

$$C_g\left(t\right)=a{\left(P_g\left(t\right)\right)}^2+b{P}_g\left(t\right)+c$$

(1)

$$P_g^{min}\le P_g\left(t\right)\le P_g^{max},\forall t\in [0,T)$$

(2)

where $P_g\left(t\right)$ denotes the power output of the thermal power units at time t and $a,b,c$ denote the fuel cost coefficients; $P_g^{min}$ and $P_g^{max}$ denote the minimum and maximum of the thermal power units’ power output, respectively; in addition, T is the end point of time.

2.3. Electricity Purchase

According to [28], the cost of electricity sold to the main grid can be ignored to simplify the model. These are five kinds of prices of electricity that are introduced in [5]. They are day-ahead pricing (DAP), time-of-use pricing (ToUP), peak pricing (PP), inclining block rates (IBRs), and critical peak price (CPP) [5]. In this work, they can be concluded as (3).

$$C_{ele}\left(t\right)={\mathit{P}}_{\mathit{ele}}\left(t\right)·{\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$$

(3)

where ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ is a Riemann integrable vector function which respresents the power of purchasing electricity at time t. Different components of ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ mean different ranges of the power. In addition, ${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$ is also a Riemann integrable vector function, respresenting the price of electricity and its different components mean different prices. The “·” operator means the inner product of two vectors.

In fact, as for five kinds of electricity prices, DAP is shown in (4), which is the simplest form of electricity prices. ToUP is a type of DAP [5]. In addition, CPP is a type of ToUP and the quantity of purchasing electricity and the price of electricity both can be considered as piecewise functions which are both in three segments. PP can be written as (5) and it has one more term than DAP. Furthermore, IBRs are introduced in (6).

$$C_{ele}\left(t\right)=P_{ele}\left(t\right){\kappa }_1\left(t\right)$$

(4)

$$C_{ele}\left(t\right)=P_{ele}\left(t\right){\kappa }_1\left(t\right)+\frac{1}{T}\left(\underset{t}{max}{P}_{ele}\left(t\right)\right){\kappa }_{pd}$$

(5)

$$C_{ele}\left(t\right)=\left\{\begin{array}{c}{P}_{ele}\left(t\right){\kappa }_1\left(t\right),P_{ele}\left(t\right)\le p_0\left(t\right)\hfill \\ p_0\left(t\right){\kappa }_1\left(t\right)+\left(P_{ele}\left(t\right)-p_0\left(t\right)\right){\kappa }_2\left(t\right),P_{ele}\left(t\right)>p_0\left(t\right)\hfill \end{array}\right.$$

(6)

where $P_{ele}\left(t\right)$ is the power of purchasing electricity at time t and $p_0\left(t\right)$ is the threshold value at time t; ${\kappa }_1\left(t\right)$, ${\kappa }_2\left(t\right)$, ${\kappa }_{pd}$ and denote 3 kinds of electricity prices.

The quantity of purchasing electricity and the price of electricity for the first 3 kinds of electricity costs mentioned above are all one dimension, but for PP and IBRs, they become two dimensions. (5) can be written as (7).

$$C_{ele}\left(t\right)=\left({\kappa }_1\left(t\right),{\kappa }_{pd}\right)·\left(P_{ele}\left(t\right),\frac{\underset{t}{max}{P}_{ele}\left(t\right)}{T}\right)$$

(7)

where ${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$ is equal to $\left({\kappa }_1\left(t\right),{\kappa }_{pd}\right)$ and ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ is equal to $\left(P_{ele}\left(t\right),\frac{\underset{t}{max}{P}_{ele}\left(t\right)}{T}\right)$. (6) can be written as (8).

$$\begin{array}{cc}\hfill C_{ele}\left(t\right)& ={\kappa }_1\left(t\right)max\{P_{ele}\left(t\right),p_0\left(t\right)\}+{\kappa }_2\left(t\right)\epsilon \left(P_{ele}\left(t\right)-p_0\left(t\right)\right)\hfill \\ & ={\kappa }_1\left(t\right)\left(\frac{P_{ele}\left(t\right)+p_0\left(t\right)-|P_{ele}\left(t\right)-p_0\left(t\right)|}{2}\right)\hfill \\ & +{\kappa }_2\left(t\right)\epsilon \left(P_{ele}\left(t\right)-p_0\left(t\right)\right)\hfill \\ & =\left({\kappa }_1\left(t\right),{\kappa }_2\left(t\right)\right)·\left(\frac{P_{ele}\left(t\right)+p_0\left(t\right)-|P_{ele}\left(t\right)-p_0\left(t\right)|}{2},\right.\hfill \\ & \left.\epsilon (P_{ele}\left(t\right)-p_0\left(t\right))\right)\hfill \end{array}$$

(8)

where $\epsilon (·)$ denotes the step function, which is

$$\epsilon \left(x\right)=\left\{\begin{array}{cc}1,\hfill & x\ge 0\hfill \\ 0,\hfill & x<0.\hfill \end{array}\right.$$

(9)

In (8), ${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$ is equal to $\left({\kappa }_1\left(t\right),{\kappa }_2\left(t\right)\right)$ and ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ is equal to $\left(\frac{P_{ele}\left(t\right)+p_0\left(t\right)-|P_{ele}\left(t\right)-p_0\left(t\right)|}{2}\right.$, $\left.\epsilon \left(P_{ele}\left(t\right)-p_0\left(t\right)\right)\right)$. Therefore, the first component is the part of power which is less than $p_0\left(t\right)$, while the last component is the part of power which is more than $p_0\left(t\right)$. For the reason that ${\kappa }_1\left(t\right)<{\kappa }_2\left(t\right)$ for every t in $[0,T)$, it guarantees that the last component of ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ equals to 0 until the first component reaches its upper bound in the optimization problem without adding extra constraints. If there are three or more kinds of electricity prices, the analogous method can be used.

Furthermore, the power of purchasing electricity should also be limited to a specific range.

$$P_{ele,i}^{min}\le P_{ele,i}\left(t\right)\le P_{ele,i}^{max},\forall t\in [0,T),i=1,2,\dots ,n$$

(10)

where $P_{ele,i}^{min}$ and $P_{ele,i}^{max}$ denote the minimum and maximum of the ith component of ${\mathit{P}}_{\mathit{ele}}\left(t\right)$, respectively.

2.4. Carbon Emission

The carbon emission quota is judged by the provincial carbon emissions trading authority, issued and allowed to include carbon emissions trading enterprises within a specific period of carbon dioxide emissions. The carbon emission quota at time t can be calculated as

$$Q_1\left(t\right)=k_1{P}_g\left(t\right)$$

(11)

where $k_1$ is the carbon emission coefficient per unit power.

Thermal power units are the major resource of carbon emission. The actual carbon emission at time t can be calculated as

$$Q_2\left(t\right)=k_2{P}_g\left(t\right)$$

(12)

where $k_2$ is the carbon emission intensity per unit output.

The carbon trading cost is

$$\begin{array}{cc}\hfill C_{ca}& =k_{ca}{\int }_0^T\left(Q_2\left(t\right)-Q_1\left(t\right)\right)\mathrm{d}t\hfill \\ & =k_{ca}\left(k_2-k_1\right){\int }_0^T{P}_g\left(t\right)\mathrm{d}t\hfill \end{array}$$

(13)

where $k_{ca}$ is the carbon trading market price.

2.5. Battery Operation

The cost of the battery contains maintenance cost and depreciation cost.

$$C_b={\int }_0^T\left({\kappa }_b^m+{\kappa }_b^d\right)\left|P_b\left(t\right)\right|\mathrm{d}t$$

(14)

$$P_b^{min}\le P_b\left(t\right)\le P_b^{max},\forall t\in [0,T)$$

(15)

where ${\kappa }_b^m$ and ${\kappa }_b^d$ denote the maintenance price and depreciation price, respectively. $P_b\left(t\right)$ is the power of the battery at time t where $P_b\left(t\right)>0$ indicates discharging while $P_b\left(t\right)<0$ indicates charging. $P_b^{min}$ and $P_b^{max}$ denote the minimum and maximum of the battery’s power, respectively. $P_b^{min}$ is less than 0 while $P_b^{max}$ is more than 0.

2.6. Optimization Problem

The power researched in this work concludes the power output of the thermal power units, the power of purchasing electricity and the power of the battery.

$$P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)=P_l\left(t\right),\forall t\in [0,T)$$

(16)

where $P_{ele,i}\left(t\right)$ denotes the ith component of ${\mathit{P}}_{\mathit{ele}}\left(t\right)$; n denotes the dimension of ${\mathit{P}}_{\mathit{ele}}\left(t\right)$; $P_l\left(t\right)$ denotes the load at time t.

In conclusion, the optimization problem is expressed as

$$\begin{array}{c}minC=C_g+C_{ele}+C_{ca}+C_b+C_{fix}\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{P}_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)=P_l\left(t\right),\forall t\in [0,T)\hfill \\ P_g^{min}\le P_g\left(t\right)\le P_g^{max},\forall t\in [0,T)\hfill \\ P_{ele,i}^{min}\le P_{ele,i}\left(t\right)\le P_{ele,i}^{max},\forall t\in [0,T),i=1,2,\dots ,n\hfill \\ P_b^{min}\le P_b\left(t\right)\le P_b^{max},\forall t\in [0,T)\hfill \end{array}\right.\hfill \end{array}$$

(17)

where C is the total cost; $C_g$ denotes the cost of natural gas and $C_g={\int }_0^T{C}_g\left(t\right)\mathrm{d}t$; $C_{ele}$ denotes the cost of electricity bought from the main grid and $C_{ele}={\int }_0^T{C}_{ele}\left(t\right)\mathrm{d}t$; $C_{fix}$ denotes the fixed cost, which is the sum of other costs, including operating and maintenance costs, start-up and shut-down costs, and so on [28]. To be simplicity, $C_{fix}$ is regarded as a constant. Furthermore, $C_{fix}$ can equal to 0 without affecting the model.

To solve the optimization problem (17), we can solve (18) for all $t\in [0,T)$ at first, unless the electricity price is peak pricing. In the following article, it is assumed that prices are all not PP.

$$\begin{array}{c}\begin{array}{cc}\hfill minC\left(t\right)& =C_g\left(t\right)+C_{ele}\left(t\right)+k_{ca}(k_2-k_1)P_g\left(t\right)\hfill \\ & +\left({\kappa }_b^m+{\kappa }_b^d\right)\left|P_b\left(t\right)\right|\hfill \end{array}\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{P}_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)=P_l\left(t\right)\hfill \\ P_g^{min}\le P_g\left(t\right)\le P_g^{max}\hfill \\ P_{ele,i}^{min}\le P_{ele,i}\left(t\right)\le P_{ele,i}^{max},i=1,2,\dots ,n\hfill \\ P_b^{min}\le P_b\left(t\right)\le P_b^{max}\hfill \end{array}\right.\hfill \end{array}$$

(18)

where $C_{fix}$ is equal to 0. In fact, if (18)’s objective function reaches its minimum for every $t\in [0,T)$, (17)’s will also reach its minimum, so (18)’s solution is (17)’s solution.

In addition, optimizing (18) almost everywhere on $[0,T)$ is equivalent to optimizing (17). In fact, it is assumed that (17)’s objective function reaches its optimum $C_0$, but there is at least one period $\Delta t\subset [0,T)$ and $\Delta t$’s Lebesgue measure $m(\Delta t)>0$, such that the objective functions of (18) not reaches their optimum values. Let them reach their optimum values on $\Delta t$, the corresponding set of solution is S. Then, as to (17), replace the original solution on $\Delta t$ to S. After that, the objective function of (17) is small than before without breaking any constraints, so it is paradoxical. Therefore, (17)’s solution is also (18)’s solution on $[0,T)-T_0$, where $T_0$ is a subset of measure zero.

In (18), the objective function is the sum of a quadratic function and an absolute value function. In addition, the feasible region is a convex set.

Furthermore, $C\left(t\right)$ can be calculated as

$$C\left(t\right)=\tilde{a}{\left(P_g\left(t\right)\right)}^2+\tilde{b}{P}_g\left(t\right)+\tilde{c}+{\mathit{P}}_{\mathit{ele}}\left(t\right)·{\mathit{\kappa }}_{\mathit{ele}}\left(t\right)+\tilde{d}\left|P_b\left(t\right)\right|$$

(19)

where $\tilde{a}=a,\tilde{b}=\left[k_{ca}\left(k_2-k_1\right)+b\right],\tilde{c}=c,\tilde{d}={\kappa }_b^m+{\kappa }_b^d$.

3. Optimization Method

The main method used in this study is DE. This algorithm contains 4 main steps: initialization, mutation, crossover, and selection [13,14,25].

3.1. Initialization

The approximate range is given and an initial population is generated randomly within this range.

$$\begin{array}{c}{x}_{i,j,0}=rand\times \left(x_{max}-x_{min}\right)+x_{min},\\ i=1,2,\cdots ,d,j=1,2,\cdots ,np\end{array}$$

(20)

where $x_{i,j,0}$ is the ith component of the jth individual; rand is a uniformly distributed number in (0, 1). That is to say $rand\sim U(0,1)$, where $U(0,1)$ is uniform distribution in (0, 1). d denotes the dimension of the optimization problem and np denotes the number of individuals in the population.

3.2. Mutation

There are many ways to generate every dimension of the kth mutant individual $v_{i,j,k}$. The basic one is DE/rand/1:

$$v_{i,j,k}=x_{i,r_1^j,k}+F\times \left(x_{i,r_2^j,k}-x_{i,r_3^j,k}\right),i=1,2,\cdots ,d$$

(21)

where $x_{i,r_1^j,k}$, $x_{i,r_2^j,k}$ and $x_{i,r_3^j,k}$ are the ith components of the 3 individuals randomly selected from the population. In addition, $r_1^i,r_2^i,r_3^i$ and i are different from each other. F is the scaling factor, which is usually a constant in $[0,2]$. It affects the convergence rate. The higher the F is the more slowly the algorithm converges. However, F is no longer a constant in some study. In this work, different generations have different scaling factors. It is shown in (22).

$$F=F_0\times 2^{exp\left(1-\frac{gm}{gm+1-k}\right)}$$

(22)

where $F_0$ denotes the initial scaling factor; gm denotes the maximum number of generations.

Other population mutation methods are listed as follows.

DE/best/1:

$$v_{i,j,k}=x_{i,b,k}+F\times \left(x_{i,r_1^j,k}-x_{i,r_2^j,k}\right),i=1,2,\cdots ,d$$

(23)

DE/pbest/1:

$$v_{i,j,k}=x_{i,pb,k}+F\times \left(x_{i,r_1^i,k}-x_{i,r_2^i,k}\right),i=1,2,\cdots ,d$$

(24)

DE/current-to-best/1:

$$\begin{array}{c}{v}_{i,j,k}=x_{i,j,k}+F\times \left(x_{i,b,k}-x_{i,j,k}\right)+F\times \left(x_{i,r_1^i,k}-x_{i,r_2^j,k}\right),\\ i=1,2,\cdots ,d\end{array}$$

(25)

DE/current-to-pbest/1:

$$\begin{array}{c}{v}_{i,j,k}=x_{i,j,k}+F\times \left(x_{i,pb,k}-x_{i,j,k}\right)+F\times \left(x_{i,r_1^j,k}-x_{i,r_2^j,k}\right),\\ i=1,2,\cdots ,d\end{array}$$

(26)

where $x_{i,b,k}$ denotes the ith component of the best individual in the current population; $x_{i,pb,k}$ denotes the ith component of the individual randomly chosen from the top p individuals in the current population ($p\in (0,1]$) [25]. Compared to DE/best/1, DE/pbest/1 makes use of other good individuals imformation and avoid converging too early. In this work, $x_{i,b,k}$ and $x_{i,pb,k}$ are obtained based on the objective function value and the degree of constraint violation of the kth generation.

3.3. Crossover

Crossover is to improve the diversity of the population. There are two kinds of crossover methods. One is the binomial crossover. The other is the exponential crossover.

Binomial crossover:

$$u_{i,j,k}=\left\{\begin{array}{cc}{v}_{i,j,k},\hfill & j=j_{rand} \mathrm{or} rand\le CR\hfill \\ x_{i,j,k},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(27)

Exponential crossover:

$$u_{i,j,k}=\left\{\begin{array}{cc}{v}_{i,j,k},\hfill & \mathrm{from} j=j_{rand} \mathrm{while} rand\le CR\hfill \\ x_{i,j,k},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(28)

where $j_{rand}$ is an integer randomly selected from $[1,d]$; the crossover rate CR is a constant on $[0,1]$.

3.4. Selection

The process of selection is choosing the better individuals. In this study, the ways to estimate individuals are constraint handling methods, and they will be introduced in the next part.

$$\begin{array}{c}{x}_{i,j,k+1}=\left\{\begin{array}{cc}{u}_{i,j,k},\hfill & \mathrm{if} {\mathit{u}}_{j,k} \mathrm{is} \mathrm{better} \mathrm{than} {\mathit{x}}_{j,k}\hfill \\ x_{i,j,k},\hfill & \mathrm{otherwise}\hfill \end{array}\right.\\ i=1,2,\cdots ,d\end{array}$$

(29)

where ${\mathit{x}}_{j,k}$ denotes the jth individual of the kth generation; ${\mathit{u}}_{j,k}$ denotes the trial one (the one after crossover).

3.5. Constraint Handling Techniques

In optimization problems, constraint handling techniques are significant aspects. The no free lunch theorem [29] says that it is impossible that for each optimization problem, a single state-of-art constraint technique is better than all other techniques [30]. Therefore, two constraint handling techniques are introduced in this paper, which are stochastic ranking (SR) and ε-constraint (EC) [30].

There are two kinds of constraints for all kinds of constrained optimization problems, which are equality constraints and inequality constraints [31]. Therefore (18) is written as

$$\begin{array}{c}\begin{array}{c}\hfill minC\left(t\right)=\tilde{a}{\left(P_g\left(t\right)\right)}^2+\tilde{b}{P}_g\left(t\right)+\tilde{c}+{\mathit{P}}_{\mathit{ele}}\left(t\right)·{\mathit{\kappa }}_{\mathit{ele}}\left(t\right)+\tilde{d}\left|P_b\left(t\right)\right|\end{array}\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{P}_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)=0\hfill \\ -P_g\left(t\right)+P_g^{min}\le 0\hfill \\ P_g\left(t\right)-P_g^{max}\le 0\hfill \\ -P_{ele,i}\left(t\right)+P_{ele,i}^{min}\le 0,i=1,2,\dots ,n\hfill \\ P_{ele,i}\left(t\right)-P_{ele,i}^{max}\le 0,i=1,2,\dots ,n\hfill \\ -P_b\left(t\right)+P_b^{min}\le 0\hfill \\ P_b\left(t\right)-P_b^{max}\le 0.\hfill \end{array}\right.\hfill \end{array}$$

(30)

Refs. [14,30] introduces the degree of constraint violation. In this work, it is written as follow.

$$\begin{array}{cc}\hfill G& =max\left\{|P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)|-\delta ,0\right\}\hfill \\ & +max\left\{-P_g\left(t\right)+P_g^{min},0\right\}+max\left\{P_g\left(t\right)-P_g^{max},0\right\}\hfill \\ & +\sum _{i=1}^{n}max\left\{-P_{ele,i}\left(t\right)+P_{ele,i}^{min},0\right\}\hfill \\ & +\sum _{i=1}^{n}max\left\{P_{ele,i}\left(t\right)-P_{ele,i}^{max},0\right\}\hfill \\ & +max\left\{-P_b\left(t\right)+P_b^{min},0\right\}+max\left\{P_b\left(t\right)-P_b^{max},0\right\}\hfill \\ & =\frac{1}{2}\left(\right|P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)|-\delta \hfill \\ & +\left|\right|P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)|-\delta |\hfill \\ & -P_g\left(t\right)+P_g^{min}+|-P_g\left(t\right)+P_g^{min}|\hfill \\ & +P_g\left(t\right)-P_g^{max}+|P_g\left(t\right)-P_g^{max}|\hfill \\ & +\sum _{i=1}^n(-P_{ele,i}\left(t\right)+P_{ele,i}^{min}+|-P_{ele,i}\left(t\right)+P_{ele,i}^{min}\left|\right)\hfill \\ & +\sum _{i=1}^n(P_{ele,i}\left(t\right)-P_{ele,i}^{max}+|P_{ele,i}\left(t\right)-P_{ele,i}^{max}\left|\right)\hfill \\ & -P_b\left(t\right)+P_b^{min}+|-P_b\left(t\right)+P_b^{min}|\hfill \\ & +P_b\left(t\right)-P_b^{min}+|P_b\left(t\right)-P_b^{max}\left|\right)\hfill \\ & =\frac{1}{2}\left(\right|P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)|-\delta \hfill \\ & +\left|\right|P_g\left(t\right)+\sum _{i=1}^n{P}_{ele,i}\left(t\right)+P_b\left(t\right)-P_l\left(t\right)|-\delta |\hfill \\ & +P_g^{min}+|-P_g\left(t\right)+P_g^{min}|-P_g^{max}+|P_g\left(t\right)-P_g^{max}|\hfill \\ & +\sum _{i=1}^n(P_{ele,i}^{min}+|-P_{ele,i}\left(t\right)+P_{ele,i}^{min}\left|\right)+\hfill \\ & \sum _{i=1}^n(-P_{ele,i}^{max}+|P_{ele,i}\left(t\right)-P_{ele,i}^{max}\left|\right)\hfill \\ & +P_b^{min}+|-P_b\left(t\right)+P_b^{min}|-P_b^{min}+|P_b\left(t\right)-P_b^{max}\left|\right).\hfill \end{array}$$

(31)

3.6. Algorithm Procedure

The procedure of DE is represented in Algorithm 1. Its flowchart is in Figure 2. This work raises a mixed DE algorithm. The framework of it is shown in Figure 3.

Algorithm 1: Differential evolution algorithm.

Input:: gm, F0, np, CR, d Output: Optimal solution   Set k = 1;   Initiation: initialize a random population;   while k <= gm do     Generate a mutant population;     Generate a trial population;     Select the better individuals;     k = k + 1;   end while

The population is divided into two groups, like [2]. In this work, an individual contains the power of the battery at time t, thermal power units’ power output at time t and the power of purchasing electricity from the main grid at time t. ${\mathit{x}}_{j1,k}$ is an arbitrary individual in group 1, and ${\mathit{x}}_{j2,k}$ is an arbitrary individual in group 2. The algorithm uses DE/pbest/1 for ${\mathit{x}}_{j1,k}$, and uses DE/current-to-pbest/1 for ${\mathit{x}}_{j2,k}$. After that, all of the individuals experience binomial crossover. Then, ${\mathit{x}}_{j1,k+1}$ is obtained by SR, and ${\mathit{x}}_{j2,k+1}$ is obtained by EC. Finally, the minimal cost is obtained based on the objective function value and the degree of constraint violation of the last generation. Different from the algorithm in [2], the proposed algorithm processes the selection in larger groups in order to improve the quality of populations.

The main difference of this algorithm from the algorithm in [2] is in mutation. The algorithm in [2] uses DE/rand/1 for ${\mathit{x}}_{j1,k}$, and uses DE/current-to-best/ for ${\mathit{x}}_{j2,k}$. DE/rand/1 is one of the most common methods, but the algorithm usually explores slowly if the information of the best-so-far solution is not used in mutation [18].

In addition, the algorithm in [2] uses SR within $\{{\mathit{x}}_{j1,k},{\mathit{u}}_{j1,k},{\mathit{u}}_{j2,k}\}$ and uses SF within $\{{\mathit{x}}_{j2,k},{\mathit{u}}_{j1,k},{\mathit{u}}_{j2,k}\}$. EC is similar to SF, but EC views a solution as feasible if its degree of constraint violation is smaller than a given number [30]. Therefore, EC achieves a better tradeoff between the optimization of the objective function and the minimization of the degree of constraint violation compared to SF which attaches great importance to feasible solutions. EC used more information about infeasible solutions. Therefore, SF in [2] is replaced by EC in the proposed algorithm. Compared to [2], our paper involves more individuals for selection, which is more possible to select between individuals without consuming much computing time.

4. Case Study

4.1. Experiment Set Up

To obtain the fuel cost coefficients, after referring [32], a = 0.00324, b = 7.74, c = 240. In addition, [33] introduces a system with seven distributed generators. However, in this work, the generators are viewed as an entity, so the minimum and maximum thermal power units’ power are the sums of the ones in [33], which are equal to 0.05 MW and 0.33 MW, respectively. The carbon emission coefficient per unit power is 0.57 t/(MW·h) [3]. The carbon emission intensity per unit output is 0.61 t/(MW·h) [3]. The carbon trading market price is equal to 37 USD /t. The upper bound $x_{max}$ is set at 2.5 MW and the lower bound $x_{min}$ is set at 0 MW. To be simple, in this work, δ in the degree of constraint violation is equal to 0. The sampling range is one day and the sampling interval is set to 0.5 h. All programs are implemented with AMD Core R5-5600H [email protected] GHz.

The time-of-use electricity price is shown in

Table 1. Time-of-use pricing.

Period Type	Period	Electricity Price (USD/(MW·h))
Peak	09.00–12.00	103.11
	19.00–22.00
Shoulder	08.00–09.00	66.59
	12.00–19.00
	22.00–24.00
Off-peak	00.00–08.00	36.21

and Figure 4. In peak hours, the price is 103.11 USD/(MW·h). In addition, in shoulder hours, the price is 66.59 USD/(MW·h). Furthermore, in off-peak hours, the price reduces to 36.21 USD/(MW·h). It is evident that the electricity price fluctuates during the day. In this case, ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ and ${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$ are both one dimension. The range of purchasing power is

$$0\le P_{ele}\left(t\right)\le 2.2,\forall t\in [0,24).$$

(32)

In addition, here is another electricity price, which is inclining block rates. If the power of purchasing electricity is less than 1 MW, the price is 36.21 USD/(MW·h), or the excess part is 83.17 USD/(MW·h). ${\mathit{P}}_{\mathit{ele}}\left(t\right)$ and ${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)$ are both two dimensions vector functions.

$${\mathit{P}}_{\mathit{ele}}\left(t\right)=\left(\frac{P_{ele}\left(t\right)+1-|P_{ele}\left(t\right)-1|}{2},\epsilon (P_{ele}\left(t\right)-1)\right),$$

(33)

$${\mathit{\kappa }}_{\mathit{ele}}\left(t\right)=\left(36.21,83.17\right).$$

(34)

The range of purchasing power from the main grid is

$$0\le P_{ele,1}\left(t\right)\le 1,\forall t\in [0,24),$$

(35)

$$0\le P_{ele,2}\left(t\right)\le 1.2,\forall t\in [0,24).$$

(36)

The load can be found in [3]. To be simple, it is assessed that the load is a piecewise function. It is shown in Figure 5. In peak hours, it can be seen as a quadratic function, and be viewed as a constant function at other time, except 08.00–09.00.

$$P_l\left(t\right)=\left\{\begin{array}{cc}1.8,\hfill & 0\le t<8\hfill \\ 0.2t+0.2,\hfill & 8\le t<9\hfill \\ -0.2{(t-10.5)}^2+2.5,\hfill & 9\le t<12\hfill \\ 2,\hfill & 12\le t<19\hfill \\ -0.2{(t-20.5)}^2+2.5,\hfill & 19\le t<22\hfill \\ 2,\hfill & 22\le t<24.\hfill \end{array}\right.$$

(37)

We use the parameters of the battery in [28] with some modification, and they are shown in

Table 2. The parameters of the battery.

Parameters	Values
maintenance price ($/(MW·h))	13.08
depreciation price ($/(MW·h))	31.44
minimum power (MW)	−0.1
maximum power (MW)	0.1

.

To compare different algorithms, 3 representative experiment scenarios are selected. They are represented in

Table 3. The scenarios studied in the experiments.

Scenario	Period	Type of Electricity Price	Load (MW)
1	00.00–08.00	ToUP	1.8
2	12.00–19.00	ToUP	2
3	12.00–19.00	IBRs	2

.

Scenarios 1 and 2 use ToUP, so the cost of electricity is the product of real-valued functions. Scenario 3 uses IBRs electricity price, and the cost of electricity is the inner product of two vector functions that have two dimensions.

Some DE algorithms are listed in

Table 4. The design of the algorithms.

Number	Name	Mutation	Crossover	Selection	Time Complexity
1	PBS	DE/pbest/1	bin	SR	$O(gm\times np\times d)$
2	PBE	DE/pbest/1	bin	EC	$O(gm\times np\times d)$
3	CBS	DE/current -to-pbest/1	bin	SR	$O(gm\times np\times d)$
4	CBE	DE/current -to-pbest/1	bin	EC	$O(gm\times np\times d)$
5	RCBSE	DE/rand/1 + DE/current -to-best/1	bin	SR + EC	$O(gm\times np\times d)$
6	PCBSE	DE/pbest/1 + DE/current -to-pbest/1	bin	SR + EC	$O(gm\times np\times d)$
7	PEE	DE/pbest/1	exp	EC	$O(gm\times np\times d^2)$
8	PCESE	DE/pbest/1 + DE/current -to-pbest/1	exp	SR + EC	$O(gm\times np\times d^2)$

. The proposed algorithm (PCBSE) uses DE/pbest/1 and DE/current-to-pbest/1 for mutation, uses binomial crossover, and uses SR and EC for selection. To make comparisons, these 2 mutation strategies and 2 selection strategies are solely used in PBS, PBE, CBS, and CBE. RCBSE is similar to the algorithm in [2]. The main difference from the algorithm in [2] is that all parent vectors are involved in the selection to obtain the best vector more quickly. Six algorithms that used binomial crossover are studied at first. Ref. [34] says that exponential crossover has some weaknesses compared to binomial crossover. To verify this conclusion, two of the best algorithms used binomial crossover would be chosen to replace the crossover method with exponential crossover.

4.2. Simulation Results

In the comparison of algorithms, $gm,F_0,np,CR$ are taken as 10, 0.5, 100, 0.9, respectively. The results are shown in

Table 5. The comparison of the algorithms.

Algorithm	Scenario 1 ($/h)	Scenario 2 ($/h)	Scenario 3 ($/h)	Distance ($/h)	Rank
PBS	297.0841	350.9401	315.3181	15.8529	6
PBE	297.7589	350.6436	322.9923	8.3722	2
CBS	296.5217	350.6883	314.4773	16.6914	7
CBE	297.2674	350.2056	319.1222	12.1702	4
RCBSE	296.5088	353.0914	316.4333	14.7180	5
PCBSE	296.3159	352.5341	325.1002	6.0320	1
PEE	298.8343	349.2507	306.3789	25.0215	8
PCESE	296.8377	348.3407	321.7752	10.0592	3

.

In Table 5, the optimal values are the means of the results of several experiments. gm is lower than normal to distinguish different algorithms. When gm is large enough, the exact optimal value can be achieved, which is (296.2717, 352.0413, 331.1119). The distance is the Euclidean distance between the algorithm’s optimal value and the exact optimal value. The rank is based on the distance and a small rank means the algorithm is ideal. It is shown that the proposed algorithm is the best among these algorithms.

For the algorithms that used binomial crossover, PBE and PCBSE perform better. Although PBE is acceptable, PCBSE is the best one in the algorithms that used binomial crossover. The results also verify that no single method can perform well all the time.

After that, to study exponential crossover, the crossover methods of PBE and PCBSE are changed. They become PEE and 8, respectively. PEE and PCESE both perform not better than PBE and PCBSE, which verifies that binomial crossover is better than exponential crossover in this situation.

To make the differences between these algorithms clear, representative algorithms are visualized in scenario 2 whose decision variable is three dimensions, and scenario 3 whose decision variable is 4 dimensions. The decision variable in scenario 1 is also three dimensions, so it is similar to scenario 1. Figure 6 presents the situation in 3 dimensions. The algorithms are denoted by their numbers in Table 4. From the local amplification of it, which is in Figure 7, it shows that PCBSE converges the most quickly in them while algorithms 5, 7, and 8 perform not very well. Figure 8 presents the situation in four dimensions. When it comes to four dimensions, this phenomenon becomes much more obvious, so it is unnecessary to obtain the local amplification.

The convergence graph of the proposed algorithm shows in Figure 9. They are the three scenarios in one of our experiments. In Figure 9, the values of the objective function all fluctuate wildly within the first 50 generations. Then, they remain stable and do not vary in the end. This indicates that the proposed algorithm convergence ideally in all of the three scenarios.

To compare different electricity prices, gm is large enough to obtain exact solutions and other parameters do not change. Figure 10 demonstrates the cost at different kinds of electricity prices, which are obtained by PCBSE. The profiles of Figure 10 is like the profile of electricity load during a day. In off-peak time, the cost at ToUP is always lower than the one at IBRs electricity price. Nevertheless, the cost at ToUP is much higher than the one at IBRs in peak and shoulder periods.

Figure 11 and Figure 12 demonstrate the power of each piece of equipment at the two types of prices. The output of the thermal power unit keeps the maximum value both at ToUP and IBRs electricity price. At ToUP, the output of the battery is 0 MW during the off-peak time and maintains the maximum value at other times. However, at the IBRs, the output of the battery is 0.1 MW during the whole day. In fact, in (19), the quadratic coefficient is extremely small, so it can be ignored when cursorily estimating. After that, the equipment with a small coefficient in the objective function is preferred. Therefore, the thermal power unit always works with maximal power no matter what kind of electricity price is. Furthermore, at ToUP, part of the load of purchasing electricity converts to the load on the battery with the coefficient of purchasing electricity surpassing the one of the battery.

5. Discussion

Wilcoxon Signed Rank Test [35] is applied to display the significant superiority of the algorithm proposed in this work (PCBSE). It is compared with the second best algorithm (PBE) in

Table 6. Wilcoxon Signed Rank Test.

Sample	PBE	Distance	PCBSE	Distance	Difference	Rank
1	320.8570	10.2549	326.2325	4.8794	5.3754	4
2	319.1282	11.9837	333.2710	2.1591	9.8246	6
3	318.8662	12.2457	330.5337	0.5782	11.6674	7
4	314.2184	16.8935	328.6028	2.5091	14.3844	8
5	331.7966	0.6847	323.2957	7.8162	−7.1315	5
6	306.2662	24.8457	335.3584	4.2465	20.5992	10
7	328.3875	2.7244	331.4038	0.2919	2.4326	2
8	325.4941	5.6178	328.5918	2.5201	3.0977	3
9	308.4960	22.6159	324.2066	6.9053	15.7106	9
10	322.5186	8.5933	321.6220	9.4899	−0.8966	1

at first. The null hypothesis is PCBSE is not better than PBE, i.e., distance 2 ≤ distance 6 and the alternative hypothesis is PCBSE is better than PBE, i.e., distance 2 > distance 6.

$$H_0:\mathrm{distance} 2\le \mathrm{distance} 6 \mathrm{vs.} H_1:\mathrm{distance} 2>\mathrm{distance} 6$$

The samples are the results of 10 times experiments. The distance is the absolute value distance from the exact optimal value. Then, the differences between the two distances are calculated and ranked by their absolute values.

The Wilcoxon rank sum test statistic is 49, so the null hypothesis is rejected when the significance level equals 0.05. The Wilcoxon Signed Rank Test shows that PCBSE is significantly superior to PBE.

RCBSE uses the same mutation strategy as the algorithm proposed in [2]. They use DE/rand/1 and DE/current-to-best/1 in mutation. DE/best/1 is a mutation method that considers the best solution in the current population. Nonetheless, it might converge too early when solving some problems. To overcome this shortcoming, DE/pbest/1 uses the information of the top 100p% individuals ($p\in (0,1]$) to keep the diversity of the population. The difference between DE/current-to-best/1 and DE/current-to-pbest/1 is similar to the difference between DE/best/1 and DE/pbest/1. Therefore, the DE/rand/1 and DE/current-to-best/1 in [2] is replaced by DE/pbest/1 and DE/current-to-pbest/1, respectively in the proposed algorithm. Table 6 shows that PBE is not better than PCBSE, so PCBSE also has significant superiority compared with RCBSE, and so are other algorithms mentioned in Table 5.

Then, the stability and reliability of PCBSE are studied in

Table 7. Stability and Reliability Study.

Parameters	Values	Results
F0	0.3	352.0413
	0.5	352.0413
	0.7	352.0452
np	50	352.0413
	100	352.0413
	150	352.0414
CR	0.8	352.0415
	0.9	352.0413
	1	352.0413

. Scenario 2 is selected as an example. The results do not change obviously when $F_0$, np or CR has been changed. It means the algorithm does not depend on how the parameters are selected. However, Table 7 also shows the result is slightly sensitive to high $F_0$, so lower $F_0$ is recommended.

IBRs is economic in the off-peak period while ToUP is economic in other period. This is explained by the fact that that part of the electricity load is at a high electricity price during the off-peak period when the electricity price is IBRs. Therefore, the cost is higher. On the other hand, part of the electricity load is at low electricity price during the peak and shoulder period when using the IBRs, so the cost is lower.

These results can simplify further research on various types of demand response and continuous-time DE of this model.

6. Conclusions

This article successfully builds a continuous-time model of a microgrid, which contains batteries, microturbines, and the electricity exchange with the main grid. In addition, the carbon trading mechanism is taken into consideration to cope with climate change. The optimal model in this work is a minimization problem on a convex set. Furthermore, the composite electricity price model is implemented in the simulation experiments ideally. Modified differential evolution algorithms are proposed to solve this problem.

According to the simulation, the proposed DE algorithm outperforms other algorithms. This algorithm uses DE/pbest/1 and DE/current-to-pbest/1 mutation methods, binomial crossover method, stochastic ranking and ε-constraint selection methods.

For electricity prices, ToUP and IBRs electricity price are studied in this work. ToUP is economic in the off-peak period, and IBRs electricity price is economic in the peak period and the shoulder period.

The composite electricity price model can be used in social production and life. In addition, the proposed algorithm enriches the theory of DE and can be applied in future research.

Future work will consider various types of demand responses in this system and will propose a continuous-time differential evolution algorithm. In addition, the stability of high $F_0$ needs to strengthen.