Modelling Fractional Advection–Diffusion Processes via the Adomian Decomposition

Abstract

When treating geomaterials, fractional derivatives are used to model anomalous dispersion or diffusion phenomena that occur when the mass transport media are anisotropic, which is generally the case. Taking into account anomalous diffusion processes, a revised Fick’s diffusion law is to be considered, where the fractional derivative order physically reflects the heterogeneity of the soil medium in which the diffusion phenomena take place. The solutions of fractional partial differential equations can be computed by using the so-called semi-analytical methods that do not require any discretization and linearization in order to obtain accurate results, e.g., the Adomian Decomposition Method (ADM). Such a method is innovatively applied for overcoming the critical issue of geometric nonlinearities in coupled saturated porous media and the potentialities of the approach are studied, as well as findings discussed.

1. Introduction

Solute transport within porous media depends on various factors, including solvent and solute properties, fluid velocity field, and geometrical features, such as shape, size, porosity, and distribution of voids [1,2]; several phenomena can be affected, among which are transport of contaminants in soils [3,4], biomechanics problems (e.g., transport of nutrients in bones [5,6]), and intrusion of radioactive wastes within cemented materials [7]). If on one side the theoretical frameworks are well established [3,8,9,10,11,12,13], on the other hand, experimental tests show that solute concentration profiles deviate from the behavior based on the standard mass transport equation [14]. Again, when considering water flow in low-permeability porous media, a strong nonlinear relationship between water flux and hydraulic gradient should be considered, suggesting a non-Darcian flow. Hence, the fractional fashion is adopted to include memory effects that could not be captured by standard approaches [1,15]. In particular, converting the standard Advection–Diffusion Equation (ADE) into a Fractional Advection–Diffusion Equation (FRADE), both in space and time (SFRADE and TFRADE, respectively), was found to be efficient to predict non-Fickian dispersion processes.

Fractional and tempered fractional [16] differential equations lead to important developments in analytical methods for solving fractional ordinary and partial differential equations in recent times. They include, e.g., Laplace–Fourier transform techniques and the Green function approach [17], Lie symmetries theory, and group analysis [18,19,20,21]. However, analytical methods could fail, in particular when reactions terms are incorporated [22,23], or kernel non-singularities occur [24], and they have high computational efforts. As reported in [25], some numerical schemes have been developed for diffusion problems [26,27,28,29,30,31] and for advection–diffusion problems [32,33]. However, the stability and convergence of numerical schemes for fractional partial differential equations need further investigation.

A fractional derivative is a non-local operator; therefore, it is expected that the numerical and mathematical treatment involves information on the function further out the region close to the point in which the derivative is computed. In fact, as indicated in [34], different methods for the approximation of fractional derivatives can be used to achieve adequate results in finite differences schemes, considering various values of the fractional order (e.g., L1, L2, L2C, spline and spectral approximation, to name just a few). Alternatively, non-local problems, accounting for long-range interactions, can be treated via non-local integral models [35], and they can even combine time-fractional and space-nonlocal strategies [36].

These difficulties have led, in the past decade, to the formulation of innovative methodologies to obtain the required solutions, avoiding discretization and linearization, such as the Adomian Decomposition Method [37,38,39,40,41], homotopy perturbation method [42], He’s variational iteration method [43], the homotopy analysis method [44], the Galerkin method [45], and the collocation method [46]. Among these, the Adomian Decomposition Method (ADM), a semi-analytical method, acquired a prestigious position due to its effective and simple procedures for obtaining numerical solutions, still maintaining high accuracy solutions of a wide class of partial differential equations, linear or nonlinear, homogeneous or inhomogeneous, with constant coefficients or with variable coefficients, both integer and fractional [47,48].

More recently, within the framework of fractional calculus, which is the topic of the present work, the ADM has been used in different engineering fields, demonstrating high reliability and accuracy of the solution for nonlinear fractional differential equations [49,50,51,52,53,54]. Anyway, the ADM series-type solutions are to be approximated for numerical purposes; according to Jiao et al. [55,56], the main critical issue is the region and rate of convergence of the Adomian series solution that can be fast in a very small portion of domain and becomes wrong for wider ones. Furthermore, it is a semi-analytical method and, therefore, it requires specific assumptions regarding the continuity and integrability conditions of the functions involved. Anyway, the attainability of an enriched solution within a nonlinear field has been considered our priority at this stage.

Hence, the idea was to start from the novel formulation developed in [1], in which material and geometric nonlinearities have been only partly taken into account; particularly, it has been proved that, via a fractional approach, material heterogeneities can be reproduced, whereas other nonlinear sources are to be specifically treated. Correspondingly, the ADM was chosen, being that its structure is suitable to efficiently solve fractional equations with variable coefficients: such a feature has allowed us to reach novel closed-form solutions for SFRADE and TFRADE with variable advection and diffusion (SFRADE-T and TFRADE-T), thereby physically allowing us to include geometric nonlinearities within porous media behavior, as well as different initial conditions in order to obtain a more realistic description of anomalous percolations processes. It is to be recalled that just a temporal dependence of such coefficients is here considered, being that their spatial one is already included, thanks to the adoption of a fractional approach.

2. Preliminaries and Notations

There are various definitions for fractional derivatives and integrals in the literature. The three most frequently used definitions for the general fractional derivative are the Grünwald-Letnikov (GL), the Riemann-Liouville (RL), and the Caputo (C) definition [57,58].

The main adopted features of RL and C are briefly summarized below.

Definition 1. 

The Riemann-Liouville fractional integral operator of order $\alpha \ge 0$ of a function $f\left(t\right)$ is defined as:

$${{}_a{}^{RL}J}_t^{\alpha }\left[f\left(t\right)\right]=\frac{1}{\mathsf{\Gamma }\left(\mathsf{\alpha }\right)}{\int }_a^{t}f\left(\tau \right){\left(t-\tau \right)}^{\mathsf{\alpha }-1}d\tau ,$$

(1)

where; $\mathsf{\Gamma }$ is the (complete) gamma function. When $a=0$ (base point), and using convolution, it is possible to write:

$${{}_0{}^{RL}J}_t^{\alpha }\left[f\left(t\right)\right]=f\left(t\right)\ast {\mathsf{\Phi }}_p\left(t\right),$$

(2)

 in which:

$$\begin{array}{cc}{\mathsf{\Phi }}_p\left(t\right)=\left\{\begin{array}{cc}\frac{t^{p-1}}{\mathsf{\Gamma }\left(p\right)}& t>0,\\ 0& t\le 0;\end{array}\right.& \underset{p\to 0}{\lim }{\mathsf{\Phi }}_p\left(t\right)\end{array}=\delta \left(t\right).$$

(3)

Definition 2. 

The RL fractional derivative of order $p>0$ of a continuous function $f\left(t\right)$ is defined to be:

$$\begin{array}{ccc}{{}_a{}^{RL}D}_t^{p}f\left(t\right)=\frac{1}{\Gamma \left(k-p\right)}\frac{d^k}{d{t}^k}{\int }_a^t{\left(t-\tau \right)}^{k-p-1}f\left(\tau \right)d\tau ,& & k-1\le p<k,\end{array}$$

(4)

 with $k=\left[p\right]+1$ , and $\left[p\right]$ denotes the integer part of $p$

The RL derivative has some disadvantages when trying to model real-world phenomena with fractional differential equations. Therefore, a modified fractional differential operator ${{}_a{}^{C}D}_t^{\alpha }$ was proposed by Caputo [59].

Definition 3. 

The $\alpha$th Caputo fractional derivative of a continuous function $f\left(t\right)$ is defined as:

$$\begin{array}{ccc}{{}_a{}^{C}D}_t^{\alpha }f\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(n-\alpha \right)}{\int }_a^t\frac{f^{\left(n\right)}\left(\tau \right)d\tau }{{\left(t-\tau \right)}^{\alpha +1-n}},& & n-1<\alpha <n,\end{array}$$

(5)

where; $n\in \mathbb{N}$.

The partial Caputo derivative of $u(x,t)$ with respect to $t$ is defined as:

$${{}_a{}^{C}D}_t^{\alpha }u(x,t)=\frac{{\mathit{\partial }}^{\alpha }}{\mathit{\partial }{t}^{\alpha }}u(x,t)=\left\{\begin{array}{c}\begin{array}{cc}{{}_a{}^{RL}J}_t^{n-\alpha }\frac{{\mathit{\partial }}^n}{\mathit{\partial }{t}^n}u\left(x,t\right),& n-1<\alpha \le n,\end{array}\\ \begin{array}{cc}\frac{{\mathit{\partial }}^n}{\mathit{\partial }{t}^n}u\left(x,t\right),& \alpha =n\in \mathbb{N}\end{array}.\end{array}\right.$$

(6)

• Properties

Let $\alpha >0$, $\beta >0$, then:

$${{}_a{}^{RL}J}_t^{\alpha }{{}_a{}^{RL}J}_t^{\beta }f\left(t\right)={{}_a{}^{RL}J}_t^{\alpha +\beta }f\left(t\right),$$

(7)

$${{}_a{}^{RL}J}_t^{\alpha }{{}_a{}^{RL}J}_t^{\beta }f\left(t\right)={{}_a{}^{RL}J}_t^{\beta }{{}_a{}^{RL}J}_t^{\alpha }f\left(t\right),$$

(8)

$$\begin{array}{cc}{{}_a{}^{RL}J}_t^{\alpha }{{}_a{}^{C}D}_t^{\alpha }f\left(t\right)=f\left(t\right)-{\displaystyle \sum _{k=0}^{n-1}}{f}^{\left(k\right)}\left(a\right)\frac{{\left(t-a\right)}^k}{k!},& n-1<\alpha <n,\end{array}$$

(9)

$${{}_a{}^{C}D}_t^{\alpha }\left(t^p\right)=\left\{\begin{array}{cc}\frac{\mathsf{\Gamma }\left(p+1\right)}{\mathsf{\Gamma }\left(p-\alpha +1\right)}{t}^{p-\alpha },& n-1<\alpha <n,p>n-1,\\ 0,& p\in \mathbb{R},n-1<\alpha <n,p\le n-1,\end{array}\right.$$

(10)

$${{}_{-\infty }{}^{C}D}_t^{\alpha }\left(\mathrm{s}\mathrm{i}\mathrm{n}\left(t\right)\right)=\sin \left(t+\frac{\alpha \pi }{2}\right),$$

(11)

$${{}_{-\infty }{}^{C}D}_t^{\alpha }\left(\mathrm{c}\mathrm{o}\mathrm{s}\left(t\right)\right)=\cos \left(t+\frac{\alpha \pi }{2}\right),$$

(12)

$${{}_{-\infty }{}^{C}D}_t^{\alpha }\left(e^{\lambda t}\right)={\lambda }^{\alpha }{e}^{\lambda t}.$$

(13)

Proof of the properties (7)–(10) can be found in [58] and, using [34], it is straightforward to derive (11)–(13).

Definition 4. 

The Mittag-Leffler function involving one parameter is given by:

$$\begin{array}{ccc}{E}_{\mu }\left(t\right)={\displaystyle \sum _{j=0}^{+\infty }}\frac{t^j}{\mathsf{\Gamma }(j\mu +1)},& & t\in \mathbb{R}\end{array},\mu \in {\mathbb{R}}^{+}.$$

(14)

3. Basic Idea of the Adomian Decomposition Method

Let us consider a nonlinear differential equation of the type:

$$M_{t}u\left(x,t\right)+Nu\left(x,t\right)+Ru\left(x,t\right)=g\left(x,t\right),$$

(15)

where; $M_t$ represents the highest order time derivative with order $\alpha$, such that $n-1<\alpha <n$, which is assumed to be invertible, $R$ is the remaining linear operator grouping the lower derivatives, $N$ represents the nonlinear operator in the equation considered, and $g(x,t)$ is a known function. For the initial value problem, solving for $M_{t}u(x,t)$ and integrating $\left(15\right)$ by the operator $M_t^{-1}$ from $0$ to $t$ yields:

$$u\left(x,t\right)=\underset{{\phi }_0}{\underbrace{\sum _{k=0}^{n-1}{u}^{\left(k\right)}(x,0)\frac{t^k}{k!}}}+M_t^{-1}g\left(x,t\right)-M_t^{-1}Nu\left(x,t\right)-M_t^{-1}Ru\left(x,t\right).$$

(16)

The method is based on setting the solution in an infinite series in the form:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{u}_n(x,t),$$

(17)

additionally, the nonlinear operator can be decomposed as:

$$Nu\left(x,t\right)=\sum _{n=0}^{\infty }{A}_n\left(u_0+u_1+\cdots u_n\right)=A_0+A_1+\cdots A_n,$$

(18)

where; $A_n$ are called Adomian polynomials, which are defined by:

$$\begin{array}{ccc}{A}_n=\frac{1}{n!}\frac{d^n}{d{\lambda }^n}{\left[N\left({\displaystyle \sum _{n=0}^n}{\lambda }^i{u}_i\right)\right]}_{\lambda =0},& & n=\mathrm{0,1},2,\cdots ,\end{array}$$

(19)

so, the components can be determined, recursively, as:

$$\begin{array}{ccc}\begin{array}{c}{u}_0={\phi }_0+M_t^{-1}g\left(x,t\right),\\ u_{n+1}=-M_t^{-1}N{u}_n\left(x,t\right)-M_t^{-1}R{u}_n\left(x,t\right),\end{array}& & n=\mathrm{0,1},2,\cdots .\end{array}$$

(20)

4. Physical Interpretation: Anomalous Advection Diffusion–Reaction Processes within Saturated Multiphase Porous Media

A fractional model, suitable for describing advection–diffusion–reaction processes within deformable saturated porous media in finite strains [1], based on the modified mixture theory [60], is here briefly recalled being the starting point for the proposed approach. By concentrating only on the transport equation for the contaminant, the final expression takes the form:

$$\frac{\mathit{\partial }\stackrel{-}{C}}{\mathit{\partial }t}+\stackrel{-}{u}\frac{\mathit{\partial }\stackrel{-}{C}}{\mathit{\partial }x}+\stackrel{-}{Y}\stackrel{-}{C}-\stackrel{-}{K}{\left(-∆\right)}^{\frac{\alpha }{2}}\stackrel{-}{C}=0,$$

(21)

with

$$\begin{array}{ccc}\stackrel{-}{u}=\frac{\phi {\rho }_{w}k}{(1-\phi )J({\rho }_s{K}_d-1)\mu }\frac{\mathit{\partial }p}{\mathit{\partial }x},& \stackrel{-}{Y}=\frac{{\stackrel{-}{Q}}_f+(J+\phi {\rho }_w)\frac{k}{\mu }\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}}{(1-\phi )J({\rho }_s{K}_d-1)},& \stackrel{-}{K}=\frac{\phi D}{J^2(1-\phi )({\rho }_s{K}_d-1)},\end{array}$$

(22)

where; $\stackrel{-}{C}=C{Q}_f$ with $C$ concentration of solute and $Q_f$ being the flow discharge, $\phi$ is the porosity, ${\rho }_w$ and ${\rho }_s$ are the density of fluid and solid, respectively, $k$ is the (isotropic) permeability constant, $\mu$ is the viscosity, $p$ is the pore pressure, $J=\det \left(\mathbf{F}\right)>0$ with $\mathbf{F}(\mathbf{X},t)$ is the deformation gradient of the solid skeleton, $K_d$ is the contaminant partitioning coefficient, $D$ is the diffusion constant, and ${\stackrel{-}{Q}}_f$ is a complex function of all the previous parameters.

For a complete description of the coupled model, wherein (21) is a part, the reader is referred to [1,61].

Coefficients $\stackrel{-}{u}=\stackrel{-}{u}\left(x,t\right),\stackrel{-}{Y}=\stackrel{-}{Y}\left(x,t\right),\stackrel{-}{K}=\stackrel{-}{K}\left(x,t\right),$ previously considered as constants as a simplifying assumption, are here treated as effectively space–time functions, thereby adding an additional source of nonlinearity (together with the material one) to the problem.

5. The Fractional Advection–Diffusion Equation Model and Its Solution by ADM

The solution of FRADE via ADM, in both space and time (STFRADE) with constant diffusion and advection terms, has already been obtained in [62]. As stated, exclusively a temporal dependence for these functions has been considered here in order to model $\stackrel{-}{u}$ and $\stackrel{-}{K}$ in (21), being that the heterogeneity of the medium has already been caught via the fractional approach.

In the following, different initial conditions have been implemented, whereas source terms are not included in this discussion.

Let us consider the following one-dimensional space–time fractional differential equation (STFRADE-T) with initial conditions:

$$\begin{array}{cc}\left\{\begin{array}{c}\frac{{\mathit{\partial }}^{\alpha }u}{\mathit{\partial }{t}^{\alpha }}+h\left(t\right)\frac{{\mathit{\partial }}^{\beta }u}{\mathit{\partial }{x}^{\beta }}=g\left(t\right)\frac{{\mathit{\partial }}^{\gamma }u}{\mathit{\partial }{x}^{\gamma }}\\ u\left(x,0\right)=f\left(x\right)\end{array}\right.,& \begin{array}{c}0<\alpha \le 1,\\ 0<\beta \le 1,\\ 1<\gamma \le 2,\end{array}\end{array}$$

(23)

which can also be written in the following way:

$$D_t^{\alpha }u\left(x,t\right)+h\left(t\right)D_x^{\beta }u\left(x,t\right)=g\left(t\right)D_x^{\gamma }u\left(x,t\right),$$

(24)

where; the differential operators are defined as:

$$\begin{array}{ccc}{D}_t^{\alpha }=\frac{{\mathit{\partial }}^{\alpha }}{\mathit{\partial }{t}^{\alpha }},& D_x^{\beta }=\frac{{\mathit{\partial }}^{\beta }}{\mathit{\partial }{x}^{\beta }},& D_x^{\gamma }=\frac{{\mathit{\partial }}^{\gamma }}{\mathit{\partial }{x}^{\gamma }}\end{array},$$

(25)

additionally, when applying to both sides the Riemann-Liouville integral expressed by $D_t^{-\alpha }\left(·\right)=J_t^{\alpha }(·)$ with the property 9, we obtain:

$$D_t^{-\alpha }{D}_t^{\alpha }u\left(x,t\right)=D_t^{-\alpha }\left\{g\left(t\right)D_x^{\gamma }u\left(x,t\right)\right\}-D_t^{-\alpha }\left\{h\left(t\right)D_x^{\beta }u\left(x,t\right)\right\},$$

(26)

$$u\left(x,t\right)=u\left(x,0\right)+J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }u\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }u\left(x,t\right)\right\}.$$

(27)

It is important to emphasize that we have omitted the left subscript and superscript relative to base point $a$ and the type of differintegral considered in order to make the mathematical passages more readable. However, it is implied that, when dealing with fractional derivatives, the Caputo derivative type is used, and different base points are chosen, depending on the functions involved, and when dealing with fractional integrals, the Riemann-Liouville type with base point $a=0$ is adopted.

Using the ADM hypothesis, the following can be observed:

$$\sum _{n=0}^{\mathrm{\infty }}{u}_n\left(x,t\right)=u\left(x,0\right)+J_t^{\alpha }\left\{g(t)D_x^{\gamma }\left(\sum _{n=0}^{\mathrm{\infty }}{u}_n\left(x,t\right)\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }\left(\sum _{n=0}^{\mathrm{\infty }}{u}_n\left(x,t\right)\right)\right\},$$

(28)

from which the recursive algorithm is deduced:

$$\left\{\begin{array}{cc}\begin{array}{c}{u}_0\left(x,t\right)=u\left(x,0\right)=f\left(x\right),\\ u_{n+1}\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_n\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_n\left(x,t\right)\right\},\end{array}& n=\mathrm{0,1},2,\cdots +\mathrm{\infty }\end{array}.\right.$$

(29)

It is to be highlighted that, once the $u_0\left(x,t\right)$ component is defined, the remaining ones can be completely determined and, consequently, the series solution is entirely determined.

In the following, a novel compact symbolic notation is introduced, allowing for shortening of the required recursive operations.

Definition 5. 

$\mathfrak{D}$ is called a DIRECTION MATRIX, whose lines indicate the “direction” to be respected for the sequence of functions that are involved in the temporal fractional integration. $\mathfrak{D}\in {\mathcal{M}}_{\left[D_{p,n}^{\prime }=p^n,n\right]}$ , where $D_{p,n}^{\prime }=p^n$ with $n\in \mathbb{N}$ defines the dispositions with repetition of $p$ elements of class $n$. In this context, $p=2$ is $g\left(t\right)$ and $h\left(t\right)$ , so $D_{2,n}^{\prime }=2^n$.

$$\begin{array}{cccc}{\mathfrak{D}}_{\left[2^1,1\right]}=\left[\begin{array}{c}g\\ h\end{array}\right],& {\mathfrak{D}}_{\left[2^2,2\right]}=\left[\begin{array}{cc}g& g\\ g& h\\ h& g\\ h& h\end{array}\right],& {\mathfrak{D}}_{\left[2^3,3\right]}=\left[\begin{array}{ccc}g& g& g\\ g& g& h\\ g& h& g\\ h& g& g\\ g& h& h\\ h& g& h\\ h& h& g\\ h& h& h\end{array}\right],& \cdots .\end{array}$$

(30)

Therefore, one can construct a specific direction matrix for every natural number $n\in \mathbb{N}$. The order of the rows and columns is not fundamental in the formation of the matrix $\mathfrak{D}$, and any movement of them does not change its meaning, and then it is not unique. However, as reported below, it is to be specifically structured to correctly and compactly represent the reached solution.

Definition 6. 

A submatrix of $\mathfrak{D}$, where each row contains a number of functions, $g\left(t\right)$, is equal to $(n-j)$, and a number of $h\left(t\right)$ is equal to $j$, which is a dummy index that goes from $0$ to $n$ , is defined as:

$${\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}.$$

(31)

In order to better understand the listed symbolic representations, let us consider the already explicitly expressed cases for $n=\mathrm{1,2},3$ (30), where the different submatrices ${\mathfrak{D}}^{\mathbf{\prime }}$ are defined for every $n$ and for each direction matrix.

$$\begin{array}{c}\begin{array}{cc}{\mathfrak{D}}_{\left[2^1,1\right]}=\left\{\begin{array}{ccc}{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}1\\ 0\end{array}\right)=\mathrm{1,1}\right]}\right|}_{1g}^{0h}& \to & \left[g\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}1\\ 1\end{array}\right)=\mathrm{1,1}\right]}\right|}_{0g}^{1h}& \to & \left[h\right]\end{array}\right.,& {\mathfrak{D}}_{\left[2^3,3\right]}=\left\{\begin{array}{ccc}{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}2\\ 0\end{array}\right)=\mathrm{1,2}\right]}\right|}_{2g}^{0h}& \to & \left[\begin{array}{cc}g& g\end{array}\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}2\\ 1\end{array}\right)=\mathrm{2,2}\right]}\right|}_{1g}^{1h}& \to & \left[\begin{array}{cc}g& h\\ h& g\end{array}\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}2\\ 2\end{array}\right)=\mathrm{1,2}\right]}\right|}_{0g}^{2h}& \to & \left[\begin{array}{cc}h& h\end{array}\right]\end{array}\right.\end{array}\\ {\mathfrak{D}}_{\left[2^3,3\right]}=\left\{\begin{array}{ccc}{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}3\\ 0\end{array}\right)=\mathrm{1,3}\right]}\right|}_{3g}^{0h}& \to & \left[\begin{array}{ccc}g& g& g\end{array}\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}3\\ 1\end{array}\right)=\mathrm{3,3}\right]}\right|}_{2g}^{1h}& \to & \left[\begin{array}{ccc}g& g& h\\ g& h& g\\ h& g& g\end{array}\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}3\\ 2\end{array}\right)=\mathrm{3,3}\right]}\right|}_{1g}^{2h}& \to & \left[\begin{array}{ccc}g& h& h\\ h& g& h\\ h& h& g\end{array}\right]\\ {\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}3\\ 3\end{array}\right)=\mathrm{1,3}\right]}\right|}_{0g}^{3h}& \to & \left[\begin{array}{ccc}h& h& h\end{array}\right]\end{array}\right.\end{array}$$

(32)

and so on.

Therefore, the matrix $\mathfrak{D}$ can be considered as a block matrix or partitioned matrix, whose blocks are the submatrices ${\mathfrak{D}}^{\mathbf{\prime }}$. One can change the position of the single blocks and nothing changes, since $\mathfrak{D}$ is not unique, as said before. Movements of single rows inside the blocks are also allowed.

Definition 7. 

By considering a vector of $n$ functions of the type:

$${\mathbf{M}}_{[1,n]}={\left(f_1\left(t\right),f_2\left(t\right),\cdots ,f_n\left(t\right)\right)}^{\mathrm{T}}$$

(33)

Then, ${{}_0{}^{RL\mathbf{M}}\mathbb{J}}_t^{n\alpha }\left(t\right)$ is the Riemann-Liouville fractional integral term, defined as follow:

$${{}_0{}^{RL\mathbf{M}}\mathbb{J}}_t^{n\alpha }\left(t\right)=J_t^{\alpha }\left[f_1\left(t\right)J_t^{\alpha }\left[f_2\left(t\right)\cdots J_t^{\alpha }{f}_n\left(t\right)\right]\right]$$

(34)

where; $n\alpha$ notes that the operator $\mathbb{J}$ are formed by $n$ fractional integrals $J_t^{\alpha }$ of order $\alpha$.

Definition 8. 

By considering ${\mathit{N}}_{[m,n]}$ a matrix of $m\times n$ functions, then ${{}_0{}^{RL\mathit{N}}\mathbb{J}}_t^{n\alpha }\left(t\right)$ is the Riemann-Liouville fractional integral term, defined as follow:

$${{}_0{}^{RL\mathbf{N}}\mathbb{J}}_t^{n\alpha }\left(t\right)={{}_0{}^{RL\mathbf{N}[1,n]}\mathbb{J}}_t^{n\alpha }\left(t\right)+{{}_0{}^{RL\mathbf{N}[2,n]}\mathbb{J}}_t^{n\alpha }\left(t\right)+\cdots +{{}_0{}^{RL\mathbf{N}\left[m,n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)=\sum _{l=1}^m{{}_0{}^{RL\mathbf{N}\left[l,n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right).$$

(35)

By adopting:

$${\mathbf{N}}_{[m,n]}={\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}$$

(36)

then:

$$\begin{gathered} {{}_0{}^{RL\left\{{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}\right\}}\mathbb{J}}_t^{n\alpha }\left(t\right) \\ ={{}_0{}^{RL{\mathfrak{D}}^{\mathbf{\prime }}\left[1,n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)+{{}_0{}^{RL{\mathfrak{D}}^{\mathbf{\prime }}\left[2,n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)+\cdots +{{}_0{}^{RL{\mathfrak{D}}^{\mathbf{\prime }}\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)=\sum _{l=1}^{\left(\begin{array}{c}n\\ j\end{array}\right)}{{}_0{}^{RL{\mathfrak{D}}^{\mathbf{\prime }}\left[l,n\right]}\mathbb{J}}_t^{n\alpha }\left(t\right), \end{gathered}$$

(37)

where; $0$ and $t$ are the bounds of the fractional integral.

By recalling the definitions above we can calculate some components, reported in

Table 1. Some components as of the ADM series solution.

$u_0\left(x,t\right)=u\left(x,0\right)=f\left(x\right),$

$u_1\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_0\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_0\left(x,t\right)\right\}={{}_0{}^{RL\left[g\right]}\mathbb{J}}_t^{\alpha }\left(t\right)·D_x^{\gamma }f\left(x\right)-{{}_0{}^{RL\left[h\right]}\mathbb{J}}_t^{\alpha }\left(t\right)·D_x^{\beta }f\left(x\right),$

$\begin{array}{c}{u}_2\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_1\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_1\left(x,t\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={{}_0{}^{RL\left[g,g\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)·D_x^{2\gamma }f\left(x\right)-D_x^{\beta +\gamma }f\left(x\right)·\left[{{}_0{}^{RL\left[g,h\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)\right]+{{}_0{}^{RL\left[h,h\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)·D_x^{2\beta }f\left(x\right),\hfill \end{array}$

$\begin{array}{c}{u}_3\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_2\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_2\left(x,t\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=D_x^{3\gamma }f\left(x\right)·{{}_0{}^{RL\left[g,g,g\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)-D_x^{2\gamma +\beta }f\left(x\right)·\left[{{}_0{}^{RL\left[g,g,h\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)\right]+D_x^{\gamma +2\beta }f\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left[{{}_0{}^{RL\left[g,h,h\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)\right]-D_x^{3\beta }f\left(x\right)·{{}_0{}^{RL\left[h,h,h\right]}\mathbb{J}}_t^{3\alpha }\left(t\right),\hfill \end{array}$

$\begin{array}{c}{u}_4\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_3\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_3\left(x,t\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=D_x^{4\gamma }f\left(x\right)·{{}_0{}^{RL\left[g,g,g,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)-D_x^{3\gamma +\beta }f\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left[{{}_0{}^{RL\left[g,g,g,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[g,g,h,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)\right]+D_x^{2\gamma +2\beta }f\left(x\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left[{{}_0{}^{RL\left[g,g,h,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,h,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-D_x^{\gamma +3\beta }f\left(x\right)·\left[{{}_0{}^{RL\left[g,h,h,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,h,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)\right]+D_x^{4\beta }f\left(x\right)·{{}_0{}^{RL\left[h,h,h,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right),\hfill \end{array}$

$$\begin{gathered} u_5\left(x,t\right)=J_t^{\alpha }\left\{g\left(t\right)D_x^{\gamma }{u}_4\left(x,t\right)\right\}-J_t^{\alpha }\left\{h\left(t\right)D_x^{\beta }{u}_4\left(x,t\right)\right\} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=D_x^{5\gamma }f\left(x\right)·{{}_0{}^{RL\left[g,g,g,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)-D_x^{4\gamma +\beta }f\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left[{{}_0{}^{RL\left[g,g,g,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,g,g,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,g,h,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+D_x^{3\gamma +2\beta }f\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·{[{}_0{}^{RL\left[g,g,g,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,g,h,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,g,h,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{{}_0{}^{RL\left[g,h,h,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-D_x^{2\gamma +3\beta }f\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·{[{}_0{}^{RL\left[g,g,h,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,g,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,h,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[g,h,h,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,g,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{{}_0{}^{RL\left[h,g,h,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,h,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+D_x^{\gamma +4\beta }f\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}·\left[{{}_0{}^{RL\left[g,h,h,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,g,h,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,g,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,h,g,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)+{{}_0{}^{RL\left[h,h,h,h,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-D_x^{5\beta }f\left(x\right)·{{}_0{}^{RL\left[h,h,h,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right), \end{gathered}$$

$⋮$

.

The $u_n$ components by using Definition 8 are formulated in

Table 2. Same components as Table 1 in compact form.

$u_1\left(x,t\right)={{}_0{}^{RL\left[g\right]}\mathbb{J}}_t^{\alpha }\left(t\right)·D_x^{\gamma }f\left(x\right)-{{}_0{}^{RL\left[h\right]}\mathbb{J}}_t^{\alpha }\left(t\right)·D_x^{\beta }f\left(x\right),$

$u_2\left(x,t\right)=$ ${{}_0{}^{RL\left[g,g\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)·D_x^{2\gamma }f\left(x\right)-{{}_0{}^{RL\begin{array}{c}\left[g,h\right]\\ \left[h,g\right]\end{array}}\mathbb{J}}_t^{2\alpha }\left(t\right)·D_x^{\beta +\gamma }f\left(x\right)+{{}_0{}^{RL\left[h,h\right]}\mathbb{J}}_t^{2\alpha }\left(t\right)·D_x^{2\beta }f\left(x\right),$

$u_3\left(x,t\right)=$ ${{}_0{}^{RL\left[g,g,g\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)·D_x^{3\gamma }f\left(x\right)-{{}_0{}^{RL\begin{array}{c}\left[g,g,h\right]\\ \left[g,h,g\right]\\ \left[h,g,g\right]\end{array}}\mathbb{J}}_t^{3\alpha }\left(t\right)·D_x^{2\gamma +\beta }f\left(x\right)+{{}_0{}^{RL\begin{array}{c}\left[g,h,h\right]\\ \left[h,g,h\right]\\ \left[h,h,g\right]\end{array}}\mathbb{J}}_t^{3\alpha }\left(t\right)·D_x^{2\gamma +\beta }-{{}_0{}^{RL\left[h,h,h\right]}\mathbb{J}}_t^{3\alpha }\left(t\right)·D_x^{3\beta }f\left(x\right),$

$u_4\left(x,t\right)=$ $$\begin{gathered} {{}_0{}^{RL\left[g,g,g,g\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)·D_x^{4\gamma }f\left(x\right)-{{}_0{}^{RL\begin{array}{c}\left[g,g,g,h\right]\\ \left[g,g,h,g\right]\\ \left[g,h,g,g\right]\\ \left[h,g,g,g\right]\end{array}}\mathbb{J}}_t^{4\alpha }\left(t\right)·D_x^{3\gamma +\beta }f\left(x\right)+{{}_0{}^{RL\begin{array}{c}\left[g,g,h,h\right]\\ \left[g,h,g,h\right]\\ \left[g,h,h,g\right]\\ \left[h,g,g,h\right]\\ \left[h,g,h,g\right]\\ \left[h,h,g,g\right]\end{array}}\mathbb{J}}_t^{4\alpha }\left(t\right)·D_x^{2\gamma +2\beta }f\left(x\right)-{{}_0{}^{RL\begin{array}{c}\left[g,h,h,h\right]\\ \left[h,g,h,h\right]\\ \left[h,h,g,h\right]\\ \left[h,h,h,g\right]\end{array}}\mathbb{J}}_t^{4\alpha }\left(t\right)·D_x^{\gamma +3\beta }f\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{{}_0{}^{RL\left[h,h,h,h\right]}\mathbb{J}}_t^{4\alpha }\left(t\right)·D_x^{4\beta }f\left(x\right), \end{gathered}$$

$u_5\left(x,t\right)=$ ${{}_0{}^{RL\left[g,g,g,g,g\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{5\gamma }f\left(x\right)-{{}_0{}^{RL\begin{array}{c}\left[g,g,g,g,h\right]\\ \left[g,g,g,h,g\right]\\ \left[g,g,h,g,g\right]\\ \left[g,h,g,g,g\right]\\ \left[h,g,g,g,g\right]\end{array}}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{4\gamma +\beta }f\left(x\right)+{{}_0{}^{RL\begin{array}{c}\left[g,g,g,h,h\right]\\ \left[g,g,h,g,h\right]\\ \left[g,g,h,h,g\right]\\ \left[g,h,g,g,h\right]\\ \left[g,h,g,h,g\right]\\ \left[g,h,h,g,g\right]\\ \left[h,g,g,g,h\right]\\ \left[h,g,g,h,g\right]\\ \left[h,g,h,g,g\right]\\ \left[h,h,g,g,g\right]\end{array}}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{3\gamma +2\beta }f\left(x\right)$ $-{{}_0{}^{RL\begin{array}{c}\left[g,g,h,h,h\right]\\ \left[g,h,g,h,h\right]\\ \left[g,h,h,g,h\right]\\ \left[g,h,h,h,g\right]\\ [h,g,g,h,h]\\ [h,g,h,g,h]\\ [h,g,h,h,g]\\ [h,h,g,g,h]\\ [h,h,g,h,g]\\ [h,h,h,g,g]\end{array}}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{2\gamma +3\beta }f\left(x\right)+{{}_0{}^{RL\begin{array}{c}\left[g,h,h,h,h\right]\\ \left[h,g,h,h,h\right]\\ \left[h,h,g,h,h\right]\\ \left[h,h,h,g,h\right]\\ [h,h,h,h,g]\end{array}}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{\gamma +4\beta }f\left(x\right){{}_0{}^{RL\left[h,h,h,h,h\right]}\mathbb{J}}_t^{5\alpha }\left(t\right)·D_x^{5\beta }f\left(x\right)$,

$⋮$

.

By considering the calculated components, it is possible to determine the general term:

$$u_n\left(x,t\right)={\sum }_{j=0}^n{\left(-1\right)}^j\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f\left(x\right)·\left({{}_0{}^{RL\left\{{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}\right\}}\mathbb{J}}_t^{n\alpha }\left(t\right)\right).$$

(38)

It is evident that, also, the fractional order of the fractional Caputo derivative is linked with the submatrices ${\mathfrak{D}}^{\mathbf{\prime }}$. From (23) indeed, one can note that $h\left(t\right)$ is the function associated with the Caputo fractional derivative of order $\beta$, and $g\left(t\right)$ is associated with the Caputo fractional derivative of order $\gamma$. Each fractional derivative of order $\left(n-j\right)\gamma +j\beta$ is referred to a specific ${\mathfrak{D}}^{\mathbf{\prime }}$ as follow:

$${\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g\to \left(n-j\right)\gamma }^{jh\to j\beta }\to D_x^{\left(n-j\right)\gamma +j\beta }.$$

(39)

Explicit developments are given in Appendix A.

From these considerations, it is evident that, in order to do not affect the ADM expression of the solution, correct pairs of fractional derivatives and submatrices ${\mathfrak{D}}^{\mathbf{\prime }}$ have to be considered. Furthermore, since the term $\mathbb{J}$ implies a summation of fractional integrals, one can change the rows inside a block, and the solution does not change.

Thus, via ADM decomposition:

$$u\left(x,t\right)={\sum }_{n=0}^{\infty }{u}_n\left(x,t\right)={\sum }_{n=0}^{\infty }\left\{{\sum }_{j=0}^n{\left(-1\right)}^j\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f(x)·\left({{}_0{}^{RL\left\{{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}\right\}}\mathbb{J}}_t^{n\alpha }(t)\right)\right\}.$$

(40)

It is highlighted that the terms necessary for the calculation of the ADM components grow exponentially, being referred to the number of simple dispositions with repetition of $p$ elements of class $n$.

6. Calibration

Cherrualt indicates some necessary conditions in order to qualify the convergence of ADM by adopting the fix point theorem for functional equations [63,64,65,66]. Further indications can be deduced in [67,68,69], also for integral equations, where ADM became one of the most prestigious methods for the second kind of Volterra integrodifferential equation [70,71]. In [72], it is shown that ADM can be used efficiently in reaction–convection–diffusion partial differential equations, as in [73], where the convergence of ADM for initial value problems is treated. Other applications for convergence of the method can be found in [74].

In this paragraph, the formulation of [62] has been chosen as reference for calibration, where an ADM solution for fractional Advection–Diffusion Equations with constant advective and diffusive coefficients has been found.

Definition 9. 

The operator ${{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }$ is defined as below:

$${{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)=J_t^{\alpha }\left(g\left(t\right)·{{}_0{}^{RL\left[\left(n-1\right)g\right]}\mathbb{J}}_t^{\left(n-1\right)\alpha }\left(t\right)\right)=\underset{n}{\underbrace{J_t^{\alpha }\left[g\left(t\right)J_t^{\alpha }\left[g\left(t\right)J_t^{\alpha }g\left(t\right)\right]\right]\cdots }},$$

(41)

where; $J_t^{\alpha }$ is the RL fractional integral.

Using the latter definition, if it is posed that $h\left(t\right)=g\left(t\right)$, which results in:

$${{}_0{}^{RL\left\{{\left.{{\mathfrak{D}}^{\mathbf{\prime }}}_{\left[\left(\begin{array}{c}n\\ j\end{array}\right),n\right]}\right|}_{\left(n-j\right)g}^{jh}\right\}}\mathbb{J}}_t^{n\alpha }\left(t\right)\stackrel{h\left(t\right)=g\left(t\right)}{\overbrace{\to }}\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left({{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)\right),$$

(42)

This is the case because all ${\mathfrak{D}}^{\mathbf{\prime }}$ matrices become equal to each other. Details are reported in Appendix B.

So, the general term is:

$$u_n\left(x,t\right)=\left({{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)\right)·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f\left(x\right).$$

(43)

If $g\left(t\right)=1$, then:

$${{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)=\underset{n}{\underbrace{J_t^{\alpha }\left(1\right)\cdots J_t^{\alpha }\left(1\right)J_t^{\alpha }\left(1\right)}}=\frac{t^{n\alpha }}{\mathsf{\Gamma }\left(n\alpha +1\right)},$$

(44)

Hence, the general ADM solution with these assumptions is:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{u}_n\left(x,t\right)=\sum _{n=0}^{\infty }\left\{\frac{t^{n\alpha }}{\mathsf{\Gamma }\left(n\alpha +1\right)}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f(x)\right\},$$

(45)

which can be rearranged considering the binomial formula, hence:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }\left[\frac{t^{n\alpha }}{\mathsf{\Gamma }\left(n\alpha +1\right)}{\left(D_x^{\gamma }-D_x^{\beta }\right)}^n\right]f\left(x\right)=\sum _{n=0}^{\infty }\left[\frac{{\left(t^{\alpha }\left(D_x^{\gamma }-D_x^{\beta }\right)\right)}^n}{\mathsf{\Gamma }\left(n\alpha +1\right)}\right]f(x)=E_{\alpha }\left[t^{\alpha }\left(D_x^{\gamma }-D_x^{\beta }\right)\right]f(x),$$

(46)

where Definition 4 of the Mittag-Leffler function has been used.

Equation (46) emphasizes that the proposed model, with the assumptions explained above, perfectly matches with the formulation deduced in [62], with $\mu =1$ being $\mu$ the ratio between diffusive and advective terms considered as constants. Thereby, it can be intended as a particular case of the proposed results, deduced from the general ADM decomposition (40).

It is important to notice that, if $\alpha =1$, the RL fractional integral becomes the standard Riemann integral, here below defined as ${{}_0{}^{\left[ng\right]}\mathbb{I}}_t^n\left(t\right)$:

$${{}_0{}^{RL\left[ng\right]}\mathbb{J}}_t^{n\alpha }\left(t\right)={{}_0{}^{\left[ng\right]}\mathbb{I}}_t^n\left(t\right)={\int }_0^t\left(g\left(t\right)·{{}_0{}^{\left[\left(n-1\right)g\right]}\mathbb{I}}_t^{\left(n-1\right)}\left(t\right)\right)dt={\int }_0^{t}g\left(t\right)\left({\int }_0^{t}g\left(t\right)\left({\int }_0^{t}g\left(t\right)\dots dt\right)dt\right)dt,$$

(47)

Additionally, if $g\left(t\right)=1$, then:

$${}_0{}^{\left[ng\right]}\mathbb{J}{}_t^n\left(t\right)={\int }_0^{t}1\cdots {\int }_0^{t}1{\int }_0^{t}1\underset{n}{\underbrace{dtdt\cdots dt}}=\frac{t^n}{\Gamma \left(n+1\right)}=\frac{t^n}{n!},$$

(48)

leading to the following general solution:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{u}_n\left(x,t\right)=\sum _{n=0}^{\infty }\left\{\frac{t^n}{n!}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f(x)\right\},$$

(49)

Additionally, for the standard Advection–Diffusion Equation with $\beta =1$ and $\gamma =2$, the following is observed:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{u}_n\left(x,t\right)=\sum _{n=0}^{\infty }\left\{\frac{t^n}{n!}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left[D_x^{\left(2n-j\right)}\right]f(x)\right\}.$$

(50)

7. Numerical Implementation

Consider SFRADE-T with convection and advection terms equal to $g\left(t\right)$ and an initial condition:

$$\begin{array}{cc}\left\{\begin{array}{c}\frac{\mathit{\partial }u}{\mathit{\partial }t}+g\left(t\right)\frac{{\mathit{\partial }}^{\beta }u}{\mathit{\partial }{x}^{\beta }}=g\left(t\right)\frac{{\mathit{\partial }}^{\gamma }u}{\mathit{\partial }{x}^{\gamma }}\\ u\left(x,0\right)=f\left(x\right)\end{array},\right.& \begin{array}{c}0<\alpha \le 1,\\ 0<\beta \le 1,\\ 1<\gamma \le 2,\end{array}\end{array}$$

(51)

Additionally, the ADM solution assumes the form:

$$u\left(x,t\right)=\sum _{n=0}^{\infty }{u}_n\left(x,t\right)=\sum _{n=0}^{\infty }\left\{{{}_0{}^{\left[ng\right]}\mathbb{I}}_t^n(t)·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\left[D_x^{\left(n-j\right)\gamma +j\beta }\right]f(x)\right\}.$$

(52)

By considering different types of initial conditions, it is possible to determine the fractional derivative components in the decomposition (52) by using the properties (9)–(13), as reported in

Table 3. Fractional derivatives of the considered initial conditions.

$f\left(x\right)$
$x^{\delta }$	${{}_0{}^{C}D}_x^{\left(n-j\right)\gamma +j\beta }$	$\frac{\mathsf{\Gamma }\left(\delta +1\right){·x}^{\delta -\left[\left(n-j\right)\gamma +j\beta \right]}}{\mathsf{\Gamma }\left(\delta +1-\left[\left(n-j\right)\gamma +j\beta \right]\right)}$
$\sin \left(x\right)$	${{}_{-\infty }{}^{C}D}_x^{\left(n-j\right)\gamma +j\beta }$	$\sin \left(x+\frac{\left[\left(n-j\right)\gamma +j\beta \right]\pi }{2}\right)$
$\cos \left(x\right)$	${{}_{-\infty }{}^{C}D}_x^{\left(n-j\right)\gamma +j\beta }$	$\cos \left(x+\frac{\left[\left(n-j\right)\gamma +j\beta \right]\pi }{2}\right)$
$e^{ax}$	${{}_{-\infty }{}^{C}D}_x^{\left(n-j\right)\gamma +j\beta }$	$a^{\left(n-j\right)\gamma +j\beta }·e^{ax}$

.

This is presented to mention that all the considered initial conditions are sufficiently derivable in their domain in a fractional sense. Moreover, the expression of the differintegral is explicitly known for specific base points and for any fractional derivation order.

The integral terms assume the form as reported in

Table 4. Recursive temporal Riemann integration terms in ADM decomposition.

$g\left(t\right)$	${{}_0{}^{\left[ng\right]}\mathbb{I}}_t^n\left(t\right)$
$t^{\omega }$	$\frac{t^{n\left(\omega +1\right)}}{n!{\left(\omega +1\right)}^n}$
$\cosh \left(t\right)$	$\frac{{\sinh }^n\left(t\right)}{n!}$
$\cos \left(t\right)$	$\frac{{\sin }^n\left(t\right)}{n!}$
$\sin \left(t\right)$	${\left(\frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T}\right)}_{(1,n+1)}·{\left(\mathfrak{I}\right)}_{(n+1,n+1)}·{\mathbf{C}\mathbf{O}\mathbf{S}}_{(n+\mathrm{1,1})}$
$\sinh \left(t\right)$	${\left(\frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T}\right)}_{(1,n+1)}·{\left(\mathfrak{I}\right)}_{(n+1,n+1)}·{\mathbf{C}\mathbf{O}\mathbf{S}\mathbf{H}}_{(n+\mathrm{1,1})}$
$e^t$	${\left(\frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T}\right)}_{(1,n+1)}·{\left(\mathfrak{I}\right)}_{(n+1,n+1)}·{\mathbf{E}\mathbf{X}\mathbf{P}}_{(n+\mathrm{1,1})}$

for different kinds of temporal functions.

With

$$\mathfrak{I}={\left(\begin{array}{cccccc}+1& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0\\ 0& 0& \ddots & 0& 0& 0\\ 0& 0& 0& a_{lm}& 0& 0\\ 0& 0& 0& 0& \ddots & 0\\ 0& 0& 0& 0& 0& {\left(-1\right)}^{m+1}\end{array}\right)}_{(n+1,n+1)},$$

(53)

$$\begin{array}{ccc}\mathbf{C}\mathbf{O}\mathbf{S}=\left(\begin{array}{c}1\\ \cos t\\ {\cos }^{2}t\\ ⋮\\ {\cos }^{\left(n-1\right)}t\\ {\cos }^{n}t\end{array}\right),& \mathbf{C}\mathbf{O}\mathbf{S}\mathbf{H}=\left(\begin{array}{c}{\cosh }^{n}t\\ {\cosh }^{\left(n-1\right)}t\\ {\cosh }^{\left(n-2\right)}t\\ ⋮\\ \cosh t\\ 1\end{array}\right),& \mathbf{E}\mathbf{X}\mathbf{P}=\left(\begin{array}{c}{e}^{n·t}\\ e^{\left(n-1\right)·t}\\ e^{\left(n-2\right)·t}\\ ⋮\\ e^t\\ 1\end{array}\right),\end{array}$$

(54)

$$\begin{array}{cc}\mathbb{A}=\left(\begin{array}{c}n!\\ \left(n-1\right)!\\ \left(n-2\right)!\\ ⋮\\ 2!\\ 1!\\ 0!\end{array}\right),& \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}=\left(\begin{array}{c}0!\\ 1!\\ 2!\\ ⋮\\ (n-2)!\\ (n-1)!\\ n!\end{array}\right),\end{array}$$

(55)

$$\begin{gathered} \mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}=\mathbb{A}{\left(\mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right)}^T= \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left(\begin{array}{cccccc}n!0!& n!1!& n!2!& \cdots & n!\left(n-1\right)!& n!n!\\ \left(n-1\right)!0!& \left(n-1\right)!1!& \left(n-1\right)!2!& \cdots & \left(n-1\right)!\left(n-1\right)!& \left(n-1\right)!n!\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 1!0!& 1!1!& 1!2!& \cdots & 1!\left(n-1\right)!& 1!n!\\ 0!0!& 0!1!& 0!2!& \cdots & 0!\left(n-1\right)!& 0!n!\end{array}\right), \end{gathered}$$

(56)

$$\begin{gathered} \frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left[\begin{array}{ccccccc}\frac{1}{n!0!}& \frac{1}{\left(n-1\right)!1!}& \frac{1}{\left(n-2\right)!2!}& \cdots & \frac{1}{2!\left(n-2\right)!}& \frac{1}{1!\left(n-1\right)!}& \frac{1}{0!n!}\end{array}\right], \end{gathered}$$

(57)

where; $1.$ denotes that the operation/is referred component per component, as shown above. See Appendix C for detailed calculations of ${{}_0{}^{\left[ng\right]}\mathbb{I}}_t^n\left(t\right)$.

The assumption of taking such expressions for the diffusion coefficient is based on the fact that, even in the hypothesis that the scalar function $K\left(t\right)$ is linked to other functional relations, it is, however, possible to derive an approximation of $K\left(t\right)$ as a linear combination of these basic functions. The possibility of superimposing the results is a fundamental characteristic of having innovatively applied the ADM to SFRADE-T equations, thus allowing for the consideration of any advective–diffusive parameter, as well as correspondingly giving generality to the obtained results.

In the following, a graphical representation of some solutions expressed by the terms calculated above (via Matlab R2022b) is illustrated, where different kind of differential equations have been compared, both fractional and integer, subjected to the same initial conditions $u\left(x,0\right)=f\left(x\right)$ and $0<\alpha \le 1,0<\beta \le 1,1<\gamma \le 2$ (

Table 5. Types of equations considered when $0<\alpha \le 1,0<\beta \le 1,1<\gamma \le 2$.

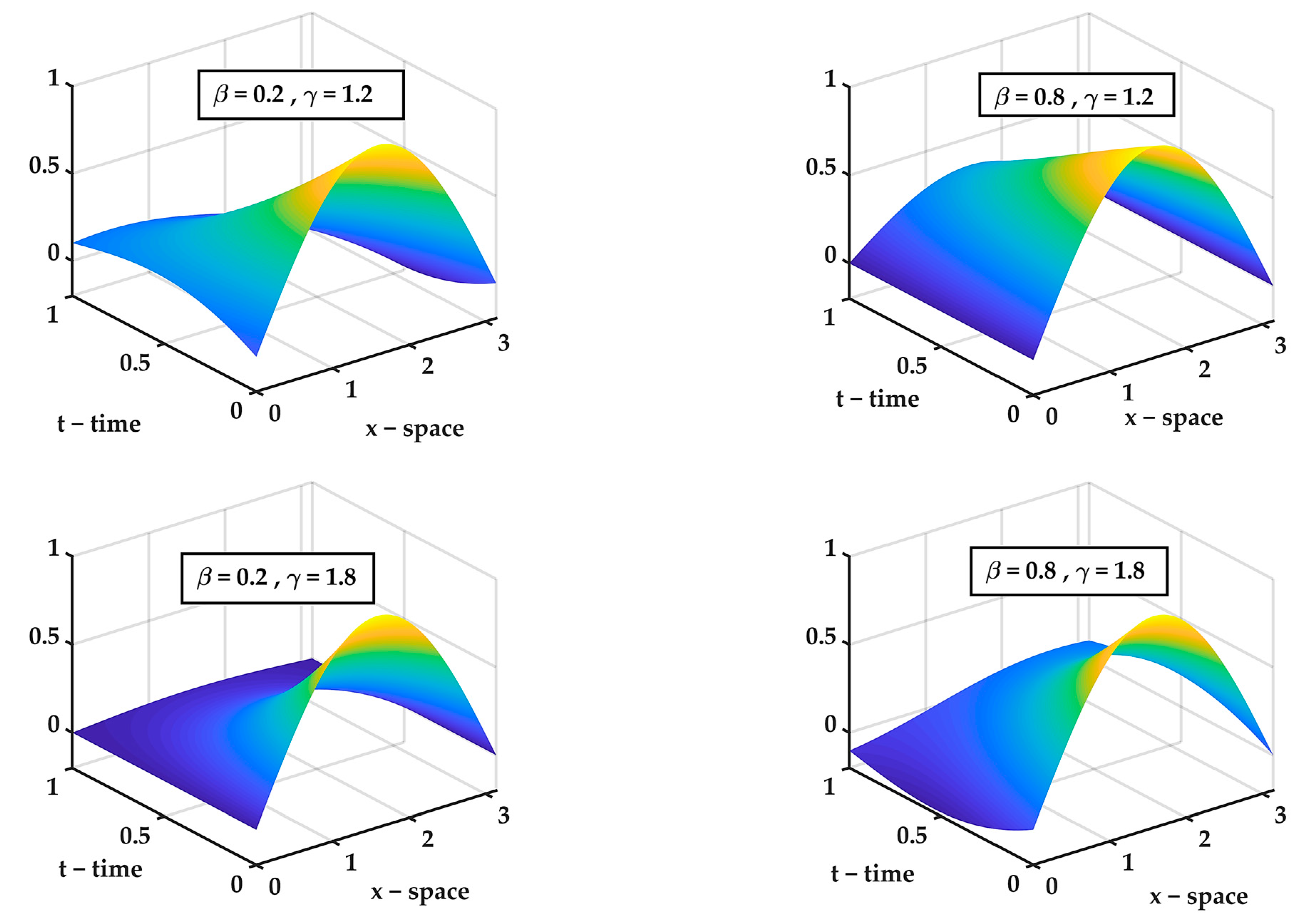
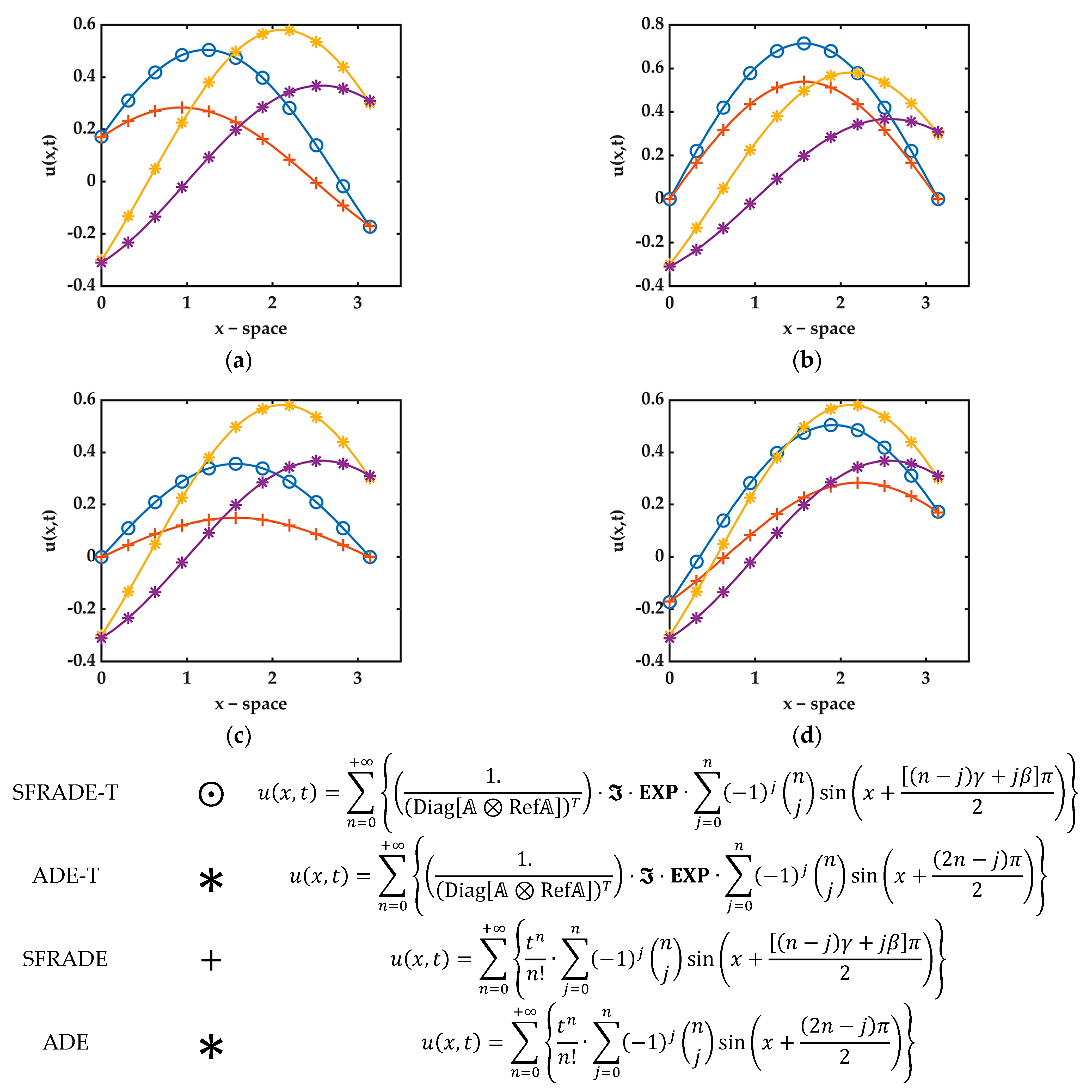
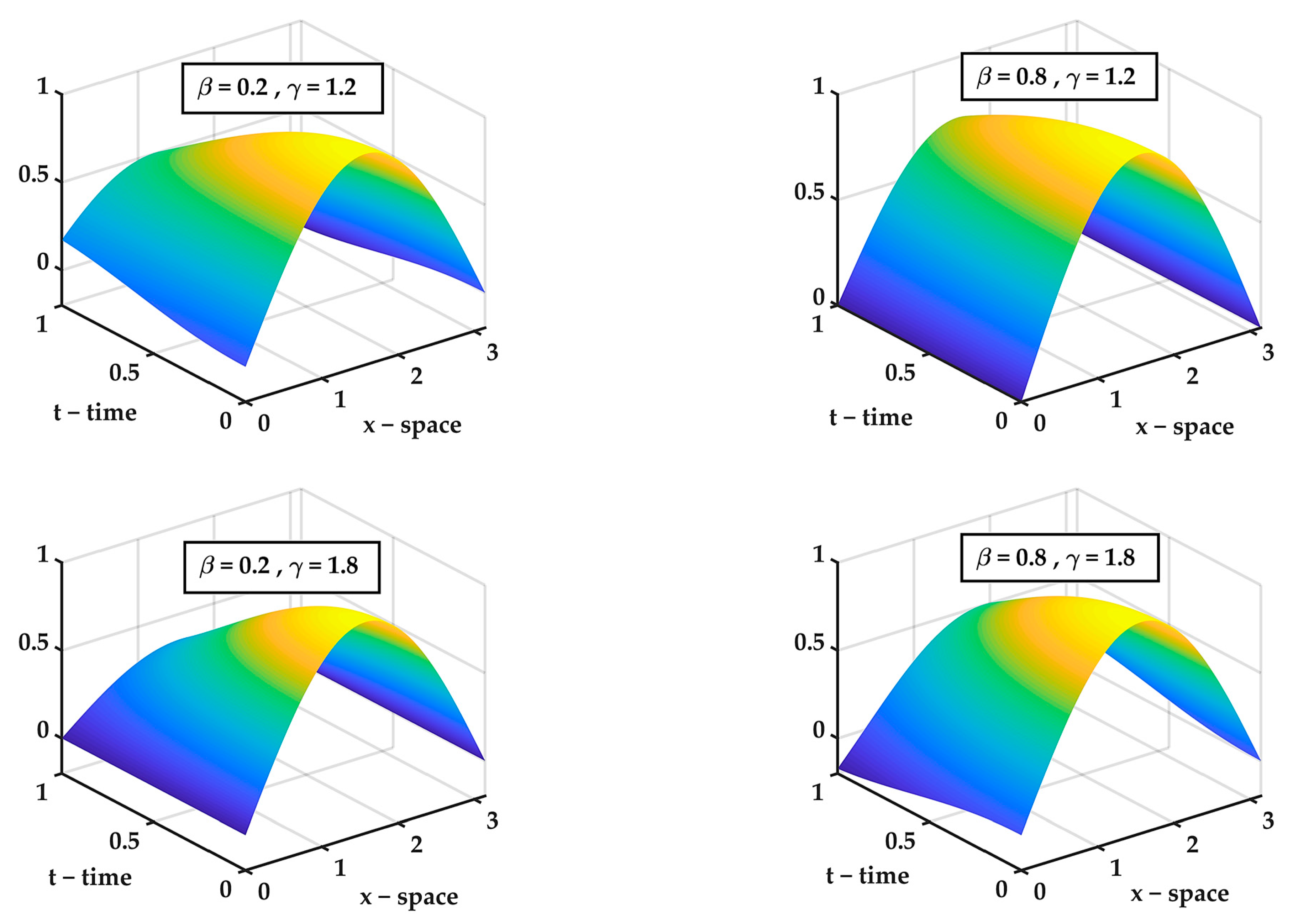
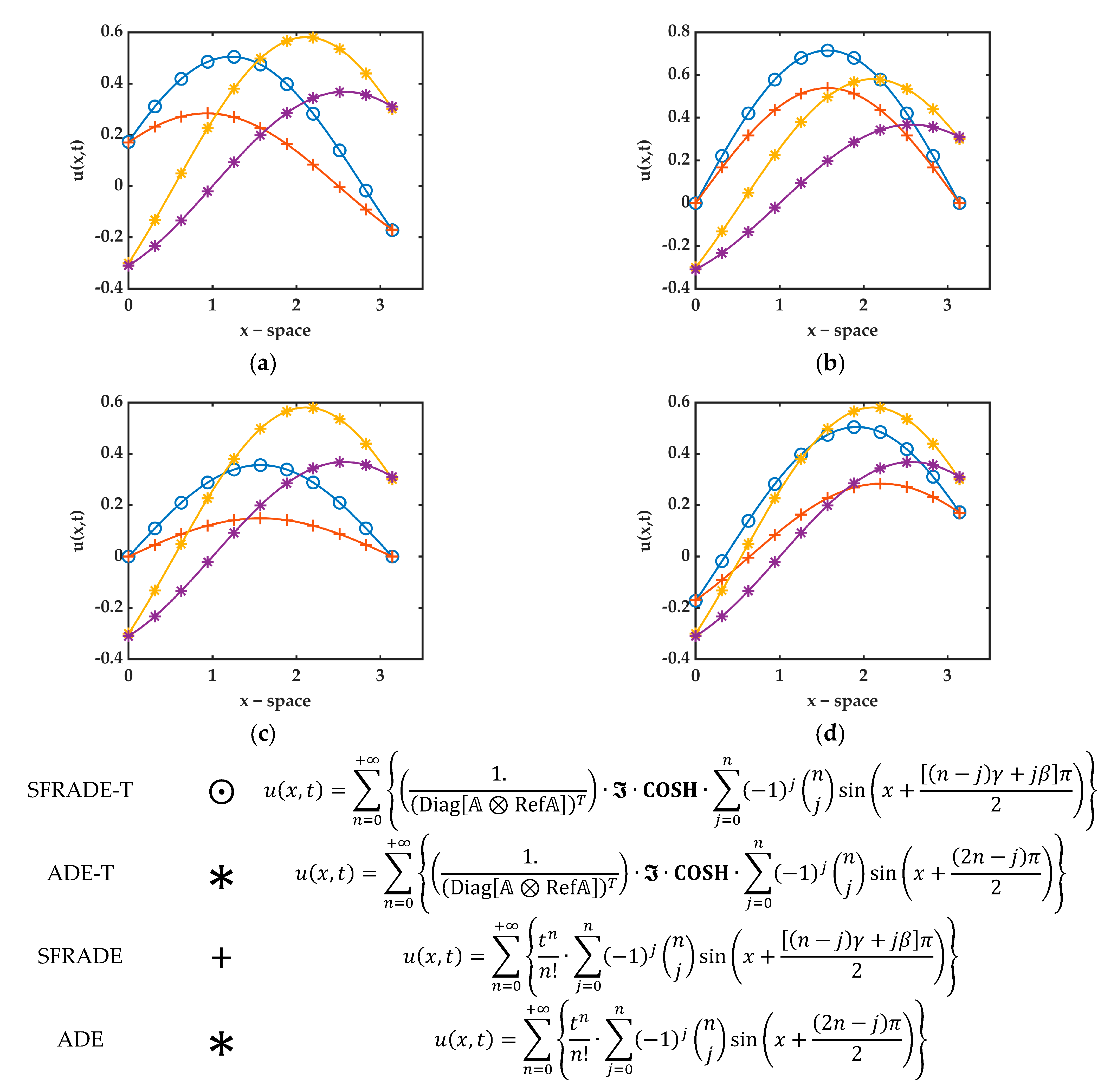
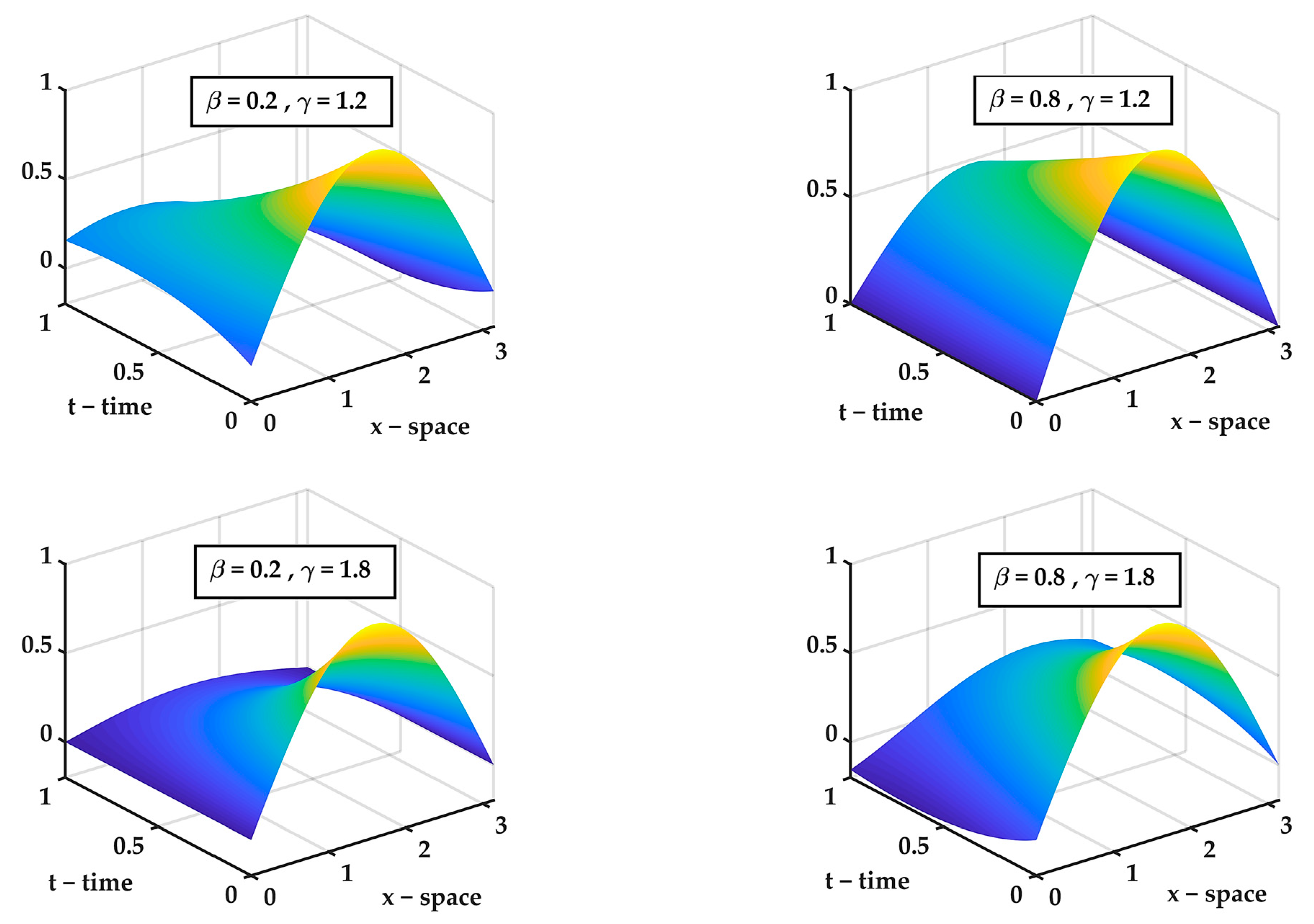
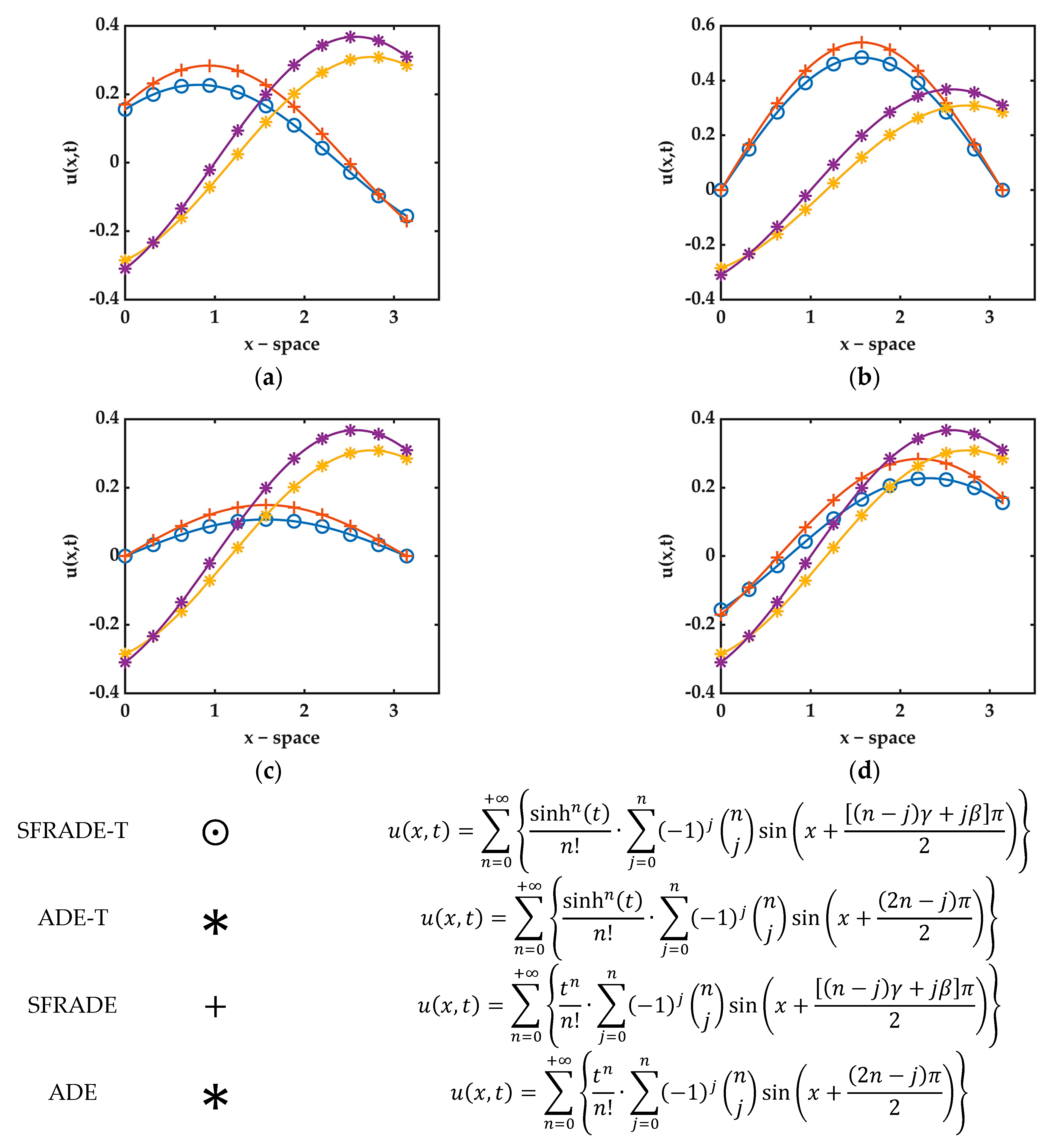
ADE	Advection–Diffusion Equation	$\frac{\mathit{\partial }u}{\mathit{\partial }t}+\frac{\mathit{\partial }u}{\mathit{\partial }x}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}$
ADE-T	Advection–Diffusion Equation-Time dependent advective and diffusive terms	$\frac{\mathit{\partial }u}{\mathit{\partial }t}+g\left(t\right)\frac{\mathit{\partial }u}{\mathit{\partial }x}=g\left(t\right)\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}$
SFRADE	Space FRactional Advection–Diffusion Equation	$\frac{\mathit{\partial }u}{\mathit{\partial }t}+\frac{{\mathit{\partial }}^{\beta }u}{\mathit{\partial }{x}^{\beta }}=\frac{{\mathit{\partial }}^{\gamma }u}{\mathit{\partial }{x}^{\gamma }}$
SFRADE-T	Space FRactional Advection–Diffusion Equation-Time dependent advective and diffusive terms	$\frac{\mathit{\partial }u}{\mathit{\partial }t}+g\left(t\right)\frac{{\mathit{\partial }}^{\beta }u}{\mathit{\partial }{x}^{\beta }}=g\left(t\right)\frac{{\mathit{\partial }}^{\gamma }u}{\mathit{\partial }{x}^{\gamma }}$

).

• $\mathit{g}\left(\mathit{t}\right)={\mathit{e}}^{\mathit{t}},\mathit{f}\left(\mathit{x}\right)=\mathbf{s}\mathbf{i}\mathbf{n}\left(\mathit{x}\right)$

The ADM solution for (52) is given by (Figure 1 and Figure 2):

$$u\left(x,t\right)=\sum _{n=0}^{+\infty }\left\{\left(\frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T}\right)\cdot \mathfrak{I}\cdot \mathbf{E}\mathbf{X}\mathbf{P}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\sin \left(x+\frac{\left[\left(n-j\right)\gamma +j\beta \right]\pi }{2}\right)\right\}.$$

(58)

• $\mathit{g}\left(\mathit{t}\right)=\mathbf{s}\mathbf{i}\mathbf{n}\mathbf{h}\left(\mathit{t}\right),\mathit{f}\left(\mathit{x}\right)=\mathbf{s}\mathbf{i}\mathbf{n}\left(\mathit{x}\right)$

The ADM solution for (52) is given by (Figure 3 and Figure 4):

$$u\left(x,t\right)=\sum _{n=0}^{+\infty }\left\{\left(\frac{1.}{{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{g}\left[\mathbb{A}\otimes \mathrm{R}\mathrm{e}\mathrm{f}\mathbb{A}\right]\right)}^T}\right)·\mathfrak{I}·\mathbf{C}\mathbf{O}\mathbf{S}\mathbf{H}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\sin \left(x+\frac{\left[\left(n-j\right)\gamma +j\beta \right]\pi }{2}\right)\right\}.$$

(59)

• $\mathit{g}\left(\mathit{t}\right)=\mathbf{c}\mathbf{o}\mathbf{s}\mathbf{h}\left(\mathit{t}\right),\mathit{f}\left(\mathit{x}\right)=\mathbf{s}\mathbf{i}\mathbf{n}\left(\mathit{x}\right)$

The ADM solution for (52) is given by (Figure 5 and Figure 6):

$$u\left(x,t\right)=\sum _{n=0}^{+\infty }\left\{\frac{{\sinh }^n\left(t\right)}{n!}·\sum _{j=0}^n{\left(-1\right)}^j\left(\genfrac{}{}{0pt}{}{n}{j}\right)\sin \left(x+\frac{\left[\left(n-j\right)\gamma +j\beta \right]\pi }{2}\right)\right\}.$$

(60)

By examining the results, the nonlocality of the fractional derivatives emerges, and it appears to affect the solution, influencing both the shape and the global diffusion velocity. Particularly, relating the influence of the fractional order for diffusion and advective terms, it is possible to deduce a similar general trend: by increasing the value of the advective order $\beta$, the slope of the surfaces decreases, indicating that the solution profiles assume higher values with a decrease in the diffusion velocity. On the other hand, the higher the $\gamma$ value, the more the slope of the surfaces increases, deducing an increase in the diffusion rate. This means that the typical delayed behavior of the fractional regime response is mainly due to the fractional Laplacian (fractional second order derivative in one dimensions), rather than to the time dependence of the diffusion and advection terms.

In fact, looking at Figure 2, comparing ADE/SFRADE and ADE-T/SFRADE-T, it is possible to notice that the concentration profiles referred to fractional differential problems show a delay in the sinusoidal waves. This is the typical behavior of fractional solutions compared to integer ones, as said before.

In order to observe the effect of the temporal functions used to model advective and diffusion coefficients, ADE/ADE-T and SFRADE/SFRADE-T are considered. In both cases, the concentration profiles with temporal diffusive and advective terms assume lower values than the respective profiles equipped with constant terms, which consists in a delay in the response, so demonstrating to enhance the behavior evidenced when taking constant coefficients. The same phenomenon appears (Figure 6) with $g\left(t\right)=\cosh \left(t\right)$. Differently, if now $g\left(t\right)=\sinh \left(t\right)$ with same initial condition (Figure 4), an opposite trend is shown, where the concentration profiles with temporal advective and diffusion terms exhibit higher values than the non-temporal standard solutions.

Correspondingly, it is evidenced that, when accounting for geometric nonlinearities within saturated porous media, the fractional model does not give a single and unique solution, being the behavior driven by the temporal functions adopted to model $\stackrel{-}{u}$ and $\stackrel{-}{K}$ in (21): different trends can be derived, not attributable to a general character, as in the case of standard fractional approaches. Such a finding suggests that small strains (i.e., constant diffusivity) could overpredict concentrations profiles, even when a material heterogeneity is included, in comparison with the large strains solution. Hence, the necessity of a deeper analysis of the phenomenon, made evident by the inclusion of fractional operators treated via ADM, is established and it is being subject of a future work.

8. Conclusions

A series of Adomian decomposition solutions of space–time Fractional Advection-Diffusion Equations, focusing on the temporal dependence of the advective and diffusion terms, has been here presented. The diffusion and advection coefficients are modelled by space–time scalar functions, leading to a more complex mathematical structure that physically takes into account variable permeability throughout the domain due to a strain-dependent permeability tensor. The ADM has been revealed to be computationally efficient, avoiding linearization and discretization problems, via the Caputo derivative definition. Particularly, a novel general formulation for differential problems, equipped with different time scalar functions as coefficients, has been derived. The time fractional differential order derivative is replaced by an integer one, so the Riemann-Liouville fractional integral becomes the standard Riemann integral, and the same function for advective and diffusion terms is selected. The crucial result resides on the time-dependence of advective and diffusion terms influencing the general behavior. Hence, apart from an ad-hoc symbolic representation for compactly expressing the recursive structure of the resulting advective-diffusive terms, the novelty resides in applying the ADM to overcome the critical issue of geometric nonlinearities when dealing with modeling transport phenomena within porous media, physically represented by variable advection and diffusion coefficients within fractional transport equations. Correspondingly, the ADM, generally used for standard fractional equations, has been found to efficiently treat such nonlinear sources, reducing the problem to the superposition of different solutions. Again, thanks to such a novel application, even new results have been reached indicating that the long tail effect typical of the fractional contribution would not give a unique effect when modeling porous media behavior in large strains. Particularly, concentration profiles can be under- or over-estimated when compared to the small strain-non fractional ones. Such an observation, which could be easily attained via the adoption of the ADM, gives promising suggestions for a further understanding of the phenomenon.