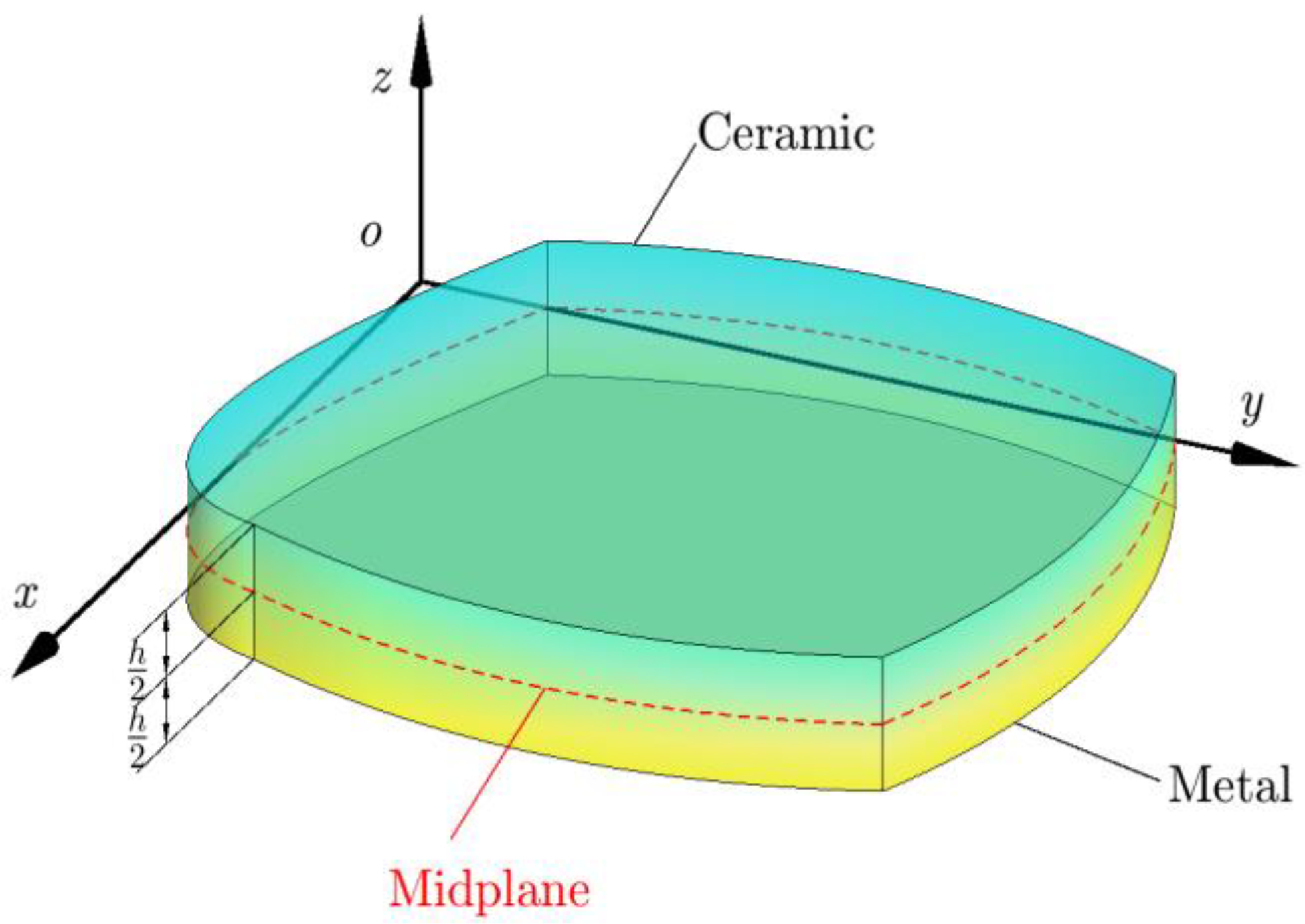
1. Introduction
Functionally graded materials (FGMs) are multiphase composite materials characterized by the variation in composition and structure over volume, resulting in their thermodynamic and physical properties also exhibiting gradient changes across the volume. This unique characteristic enables FGMs to possess tailored and optimized properties to meet specific engineering requirements. Due to their exceptional mechanical strength, thermal shock resistance, and high-temperature durability, among other qualities, FGMs are widely applicable in diverse fields, including aerospace equipment, electronic devices, automotive engines, chemical components, and medical equipment [
1,
2].
The mechanical analysis of functionally graded material (FGM) plates has attracted significant attention from researchers [
3,
4,
5]. The classical plate theory (CPT) [
4], based on the Kirchhoff–Love assumptions, is commonly employed to analyze thin FGM plates. Nevertheless, its applicability to moderately thick FGM plates may produce less accurate results. The first-order shear deformation theory (FSDT) [
4], which takes the shear effect into account, is therefore developed to improve the CPT. However, a shear correction factor (SCF) is necessary to modify the calculation of shear stresses, and determining the appropriate value of SCF can be challenging as it varies between different problems. Additionally, FSDT is susceptible to the shear-locking problem when the thickness to length ratio becomes very small. Numerous types of higher-order shear deformation theories (HSDTs) [
4] have been developed to elucidate the nonlinear, parabolic changes in transverse shear stresses throughout the thickness, thereby obviating the need to calculate the SCF. HSDTs can be categorized into models based on polynomial shape functions, such as the third-order shear deformation theory (TSDT) [
6], the fifth-order shear deformation theory [
7], and the nth-order shear deformation theory [
8]. Alternatively, there are models based on nonpolynomial shape functions, such as trigonometric HSDTs [
9,
10,
11,
12], exponential HSDTs [
13,
14], hyperbolic HSDTs [
15,
16,
17,
18], and hybrid HSDTs [
19,
20,
21]. Traction-free boundary conditions on the top and bottom surfaces are automatically satisfied in these HSDTs, and the displacement and stress results obtained from HSDTs are also more accurate than those obtained from CPT and FSDT.
Carrera et al. [
22] demonstrated the significance of the thickness stretching effect on the response analysis of FGM plates and shells. Through multiple comparative studies, they found that considering the thickness stretching effect is crucial in the computation of moderately thick FGM plates and shells. Furthermore, they discovered that in the case of sandwich structures, including thin plates and shells, the thickness stretching effect must be taken into account. Quasi-three-dimensional (3D) theories are HSDTs with high-order variations throughout the thickness for the transverse displacement [
4]. By accounting for higher-order variations in both in-plane and transverse displacements, the quasi-3D theory takes into account the shear deformation effect and the thickness stretching effect. Generally, Carrera’s unified formulation (CUF) proposed by Carrera [
23] and extended by Demasi [
24] is commonly used for implementing quasi-3D theories. Numerous quasi-3D theories have been proposed in the literature. Zenkour [
25] developed a quasi-3D theory for FGM plates using trigonometric functions. Matsunaga [
26,
27] constructed a quasi-3D theory by expanding in-plane and transverse displacements using power series. Ferreira et al. [
28] employed CUF to develop a sinusoidal quasi-3D shear deformation theory. Neves and Ferreira et al. [
29,
30] conducted similar work using hyperbolic or hybrid functions instead of sinusoidal functions. Mantari and Soares et al. [
19] introduced a general formulation that allows for deriving various quasi-3D theories using polynomials, trigonometric, or hybrid functions. They [
31,
32] optimized the number of unknowns in tangential-based quasi-3D shear deformation theories by separating transverse displacement into bending and shear compohnents, requiring only four unknowns to describe the unknown displacement field model. Thai and Kim et al. [
33] developed a quasi-3D theory with five unknowns using sinusoidal functions, where the transverse displacement is divided into bending, shear, and stretching parts. Following a similar approach, Thai et al. [
16], Hebali et al. [
17], Bessaim et al. [
34], and Bennoun et al. [
35] employed hyperbolic functions to construct quasi-3D theories. At the same time, Belabed et al. [
36] and Mantari et al. [
20,
21] used combined exponential and hyperbolic functions and combined exponential and trigonometric functions to develop quasi-3D theories. Quasi-3D theories, as modifications of HSDTs, typically yield more accurate results in response analysis compared to conventional HSDTs.
The free vibration analysis of FGM plates based on quasi-3D shear deformation theories has been extensively discussed. Talha and Singh [
37] designed a nine-node C
0 continuous isoparametric element with 13 degrees of freedom per node based on quasi-3D theory. They investigated the influence of aspect ratio, thickness ratio, volume fraction index, and boundary conditions on the bending and free vibration responses of FGM plates. Matsunaga [
26,
27] considered the effects of transverse shear and normal stresses, as well as rotational inertia on the natural frequencies and buckling stress of FGM plates and shallow shells. Thai and Choi [
38] studied the free vibration of FGM plates on a Pasternak foundation using a new quasi-3D shear deformation theory with only four unknowns. Hebali et al. [
17] analyzed the bending and free vibration of FGM plates using a novel hyperbolic quasi-3D theory. Abualnour et al. [
39] developed a new trigonometric quasi-3D theory to analyze the vibration problems of FGM plates, where the displacement field includes undetermined integral terms. Mantari et al. [
20,
21] investigated the free vibration analysis of FGM plates resting on elastic foundations by using a generalized quasi-3D hybrid-type higher-order shear deformation theory (HSDT). The significant feature of this formulation is that it considers only five unknowns instead of six unknowns in the well-known trigonometric plate theory (TPT). Zenkour and Sobhy [
40] utilized quasi-3D theory to analyze the statics, buckling, and free vibration of simply supported sandwich plates. Li et al. [
41] employed a new quasi-3D theory to analyze the free vibration of simply supported FGM plates. This new quasi-3D theory introduces two reformulated transverse shear strain functions to describe the distribution of transverse shear strains along the plate thickness. Additionally, using an undetermined integral format of displacement field enhances computational efficiency. Shahsavari et al. [
42] presented a novel quasi-3D hyperbolic theory for the free vibration analysis of FGM porous plates resting on elastic foundations. A comprehensive parametric study is carried out to consider the effects of porosity fraction index, stiffness of foundation parameters, and volume fraction index on the frequencies of imperfect FGM plates. Hai Van et al. [
43] investigated the free vibration of nonuniform-thickness 2D-FGM sandwich porous plates using a quasi-3D theory. The findings revealed that the mechanical behaviors of the porous sandwich plates are significantly affected by the hygrothermal environment, the boundary conditions, and the patterns of porosity. Jafari and Kiani [
44] obtained a free vibration response of composite plates which are reinforced with graphene platelets using a quasi-3D plate model. Pham et al. [
45] proposed the free vibration response from bi-directional FGM rectangular plates in the fluid medium based on a quasi-3D plate theory. Kaddari et al. [
46] investigated a new quasi-3D hyperbolic shear deformation theory to discuss the statics and free vibration of FGM porous plates resting on elastic foundations. The influences of the porosity parameter, power-law index, aspect ratio, thickness ratio, and the foundation parameters on the vibration of porous FGM plate are considered. Daikh and Zenkour [
47] studied the free vibration of porous FGM sandwich plates using a new and simple higher-order shear deformation theory. The effect of porosity, sandwich plate geometry, and heterogeneity parameters on the FGM sandwich plate’s free vibration was investigated.
As previously stated, considerable focus has been on analyzing the free vibration of FGM plates. It is worth noting that in numerical analysis, HSDTs generally require C
1 continuity, which can be easily achieved through the isogeometric method. Isogeometric analysis (IGA), introduced by Hughes et al. [
48], aims to seamlessly integrate finite element analysis (FEA) with computer-aided design (CAD). By directly employing the widely used nonuniform rational B-splines (NURBS) basis functions from CAD software in FEA, IGA methods exhibit notable advantages, primarily due to their ability to accurately represent geometric shapes. NURBS basis functions can precisely describe the geometry of the research object, even with relatively sparse mesh discretization, thereby ensuring high numerical accuracy. Moreover, NURBS-based IGA offers flexibility in satisfying arbitrary order continuity requirements, which proves challenging in conventional FEA. Consequently, IGA methods have found extensive application in analyzing FGM plates.
This paper presents a novel quasi-3D theory called the spectral deformation formulation (SDF) [
49,
50], where the unknown displacement field is expanded as a unique form using the Chebyshev series. Similar to CUF, this theory exhibits hierarchical refinement capability, enabling a perfect match with the 3D elasticity solution. Additionally, the SDF is an extension of CPT, thus naturally avoiding the shear-locking problem. Consequently, this theory is applicable to both thin and thick plates while maintaining high accuracy [
50]. This study analyzes the free vibration of FGM plates by incorporating this theory with IGA methods. Numerical results are compared with existing literature, demonstrating the reliability and accuracy of this quasi-3D theory in the analysis of free vibration in FGM plates.
The paper is organized as follows.
Section 2 describes the FGM plate model and the quasi-3D deformation theory based on the SDF. The governing equations are derived using the d’Alembert principle and the principle of virtual work, followed by discretization using NURBS.
Section 3 presents relevant numerical examples and discussions.
Section 4 provides the corresponding conclusions.
4. Conclusions
In the classical plate theory (CPT), there is no independent variable for the angles of rotation, which naturally avoids the shear-locking phenomenon. The spectral displacement formulation (SDF) is an extension of the CPT and naturally possesses the advantage of avoiding shear locking. Chebyshev polynomials offer several advantages, such as orthogonality and spectral convergence, which make them well suited for approximating complex functions with high accuracy using a small number of terms. Combining the Chebyshev polynomials and complete 3D elasticity constitutive equations ensures the high precision of the SDF. Isogeometric analysis (IGA) is incorporated to analyze the free vibrations of functionally graded material (FGM) plates with complex geometries and different boundary conditions.
Numerical examples involving various types of plates, such as square plates, circular plates, square plates with complicated cutouts, and L-shaped plates with multiple holes, have been utilized to validate the effectiveness of the SDF-based IGA method in analyzing FGM plates. The results demonstrate that the proposed method accurately calculates the free vibrations of both thick and thin plates. The investigations in this study have also highlighted the significant influences of thickness and boundary conditions on the natural frequencies of the plates. Additionally, the gradient index of the FGM plates has been shown to affect the natural frequencies. These findings further emphasize the importance of considering these factors in the design and analysis of FGM plates.
With its demonstrated accuracy, the proposed SDF-based IGA method offers a practical and efficient approach for predicting the natural frequencies and mode shapes of FGM plates. Future research can expand upon this method by considering additional factors such as porosity, voids, and microstructural defects, as they may impact the vibrational behavior of FGM plates. Furthermore, generalizing this method to analyze nonlinear, forced vibrations, and other dynamic behaviors of FGM plates can provide valuable insights for designing and optimizing structures in various engineering applications.