Positive Periodic Solution for Neutral-Type Integral Differential Equation Arising in Epidemic Model
Abstract
1. Introduction
- (1)
- We extend the scope of the parameter a from to with and obtain sufficient conditions for the existence of a positive periodic solution to Equations (1) and (2).
- (2)
- We innovatively use Mawhin’s continuation theorem to study the existence of positive periodic solutions for Equations (1) and (2).
2. Preliminaries
- (1)
- (2)
- (3)
- (1)
- (2)
- (3)
- (1)
- (2)
- (3)
- ,
- ()
- with .
- ()
- There exist positive constants and such that:and
- ()
- There exist positive constants c and M such that:
- ()
- There exist positive constants c and M such that:
3. Positive Periodic Solution for Equation (1)
4. Positive Periodic Solution for Equation (2)
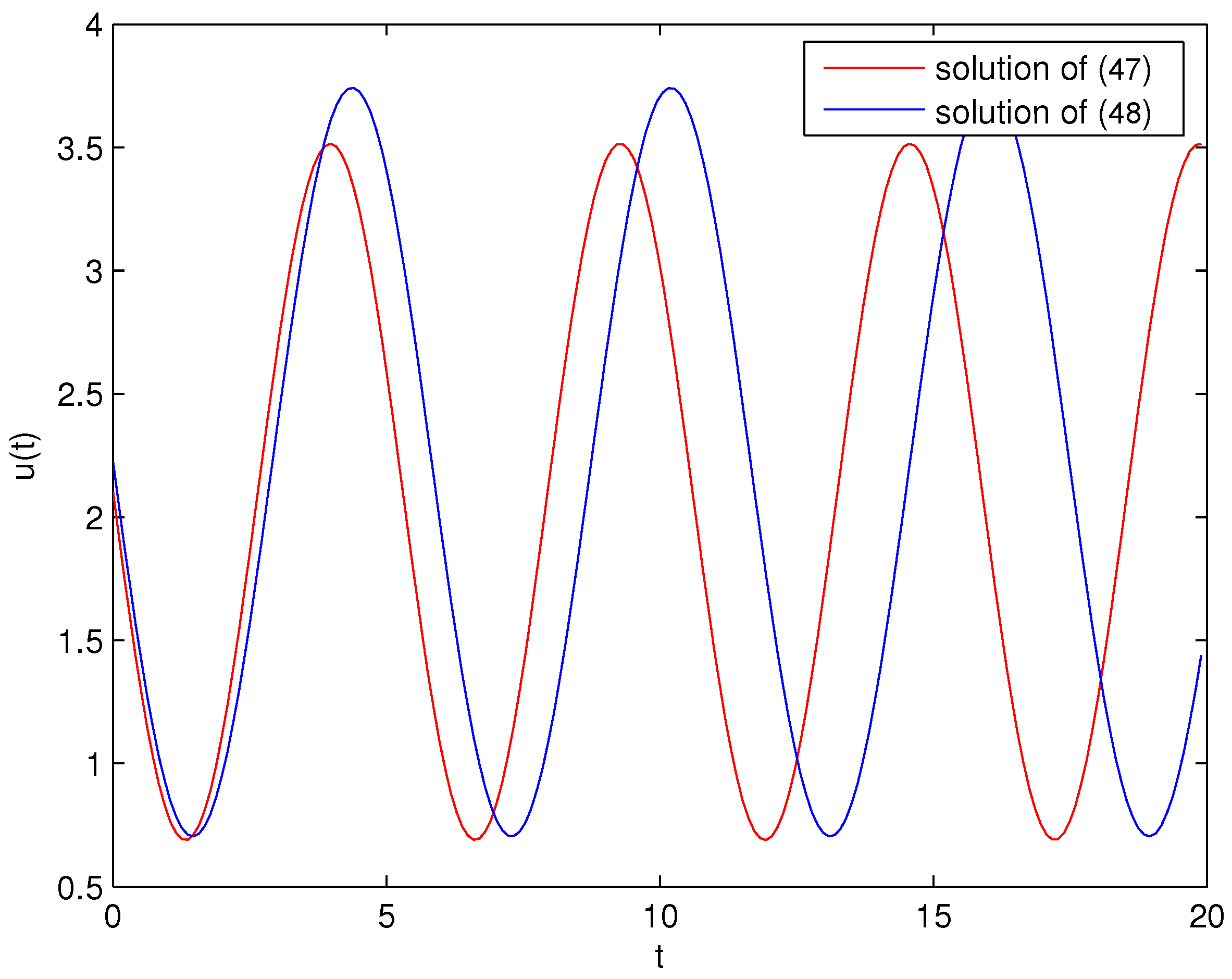
5. Examples
6. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fink, A.; Gatica, J. Positive almost periodic solutions of some delay integral equations. J. Differ. Equ. 1990, 83, 166–178. [Google Scholar] [CrossRef]
- Ait Dads, E.; Ezzinbi, K. Existence of positive pseudo almost periodic solution for a class of functional equations arising in epidemic problems. Cybern. Syst. Anal. 1994, 30, 133–144. [Google Scholar] [CrossRef]
- Ezzinbi, K.; Hachimi, M.A. Existence of positive almost periodic solutions of functional equations via Hilberts projective metric. Nonlinear Anal. 1996, 26, 1169–1176. [Google Scholar] [CrossRef]
- Long, W.; Ding, H. Positive almost automorphic solutions for some nonlinear delay integral equations. Electron. J. Differ. Equ. 2008, 57, 1–8. [Google Scholar]
- Torrejón, R. Positive almost periodic solutions of a nonlinear integral equation from the theory of epidemics. J. Math. Anal. Appl. 1991, 156, 510–534. [Google Scholar] [CrossRef]
- Ding, H.; Chen, Y.; N’Guérékata, G. Existence of positive pseudo almost periodic solutions to a class of neutral integral equations. Nonlinear Anal. 2011, 74, 7356–7364. [Google Scholar] [CrossRef]
- Ding, H.; Liang, J.; Xiao, T. Positive almost automorphic solutions for a class of nonlinear delay integral equations. Appl. Anal. 2009, 88, 231–242. [Google Scholar] [CrossRef]
- Kikina, L.; Kikina, K. Positive almost automorphic solutions for some nonlinear integral equations. Int. J. Math. Anal. 2011, 5, 1459–1467. [Google Scholar]
- Torrejón, R. Positive almost periodic solutions of a state-dependent delay nonlinear integral equation. Nonlinear Anal. 1993, 22, 1383–1416. [Google Scholar] [CrossRef]
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of epidemic systems with Neumann boundary value under delayed impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Y.; Guan, Y.; Li, W. Stability analysis of multi-point boundary conditions for fractional differential equation with non-instantaneous integral impulse. Math. Biosci. Eng. 2023, 20, 7020–7041. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhu, Q. Stabilization of stochastic highly nonlinear delay systems with neutral term. IEEE Trans. Autom. Control 2023, 68, 2544–2551. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L. Practical exponential stability of impulsive stochastic food chain system with time-varying delays. Mathematics 2023, 11, 147. [Google Scholar] [CrossRef]
- Xia, M.; Liu, L.; Fang, J.; Zhang, Y. Stability analysis for a class of stochastic differential equations with impulses. Mathematics 2023, 11, 1541. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, L.; Tang, J.; Rao, Y.; Fan, H.; Zhu, J. Hybrid impulsive pinning control for mean square Synchronization of uncertain multi-link complex networks with stochastic characteristics and hybrid delays. Mathematics 2023, 11, 1697. [Google Scholar] [CrossRef]
- Fu, X.; Zhu, Q. Stability of nonlinear impulsive stochastic systems with Markovian switching under generalized average dwell time condition. Sci. China Inf. Sci. 2018, 61, 112211. [Google Scholar] [CrossRef]
- Zhu, Q. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans. Autom. Control 2019, 64, 3764–3771. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Jiao, F.; Mai, H.; Chen, H.; Lin, R. Generalized Halanay inequalities and relative application to time-delay dynamical systems. Mathematics 2023, 11, 1940. [Google Scholar] [CrossRef]
- Ding, H.; Liang, J.; N’Guérékata, G.; Xiao, T. Existence of positive almost automorphic solutions to neutral nonlinear integral equations. Nonlinear Anal. 2008, 69, 1188–1199. [Google Scholar] [CrossRef]
- Ezzinbi, K.; Hachimi, M.A. Periodic solutions for nonlinear neutral delay intrgro-differential equations. Electron. J. Differ. Equ. 2015, 100, 1–9. [Google Scholar]
- Zhang, M. Periodic solution of linear and quasilinear neutral functional differential equations. J. Math. Anal. Appl. 1995, 189, 378–392. [Google Scholar] [CrossRef]
- Lu, S.; Ge, W. Existence of periodic solutions for a kind of second order neutral functional differential equation. Appl. Math. Comput. 2004, 157, 433–448. [Google Scholar] [CrossRef]
- Xin, Y.; Chen, Z. Neutral operator with variable parameter and third-order neutral differential equation. Adv. Differ. Equ. 2014, 2014, 273. [Google Scholar] [CrossRef]
- Gaines, R.; Mawhin, J. Coincidence Degree and Nonlinear Differential Equations; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Nussbaum, R. A periodicity threshold theorem for some nonlinear integral equations. SIAM J. Math. Anal. 1978, 9, 356–376. [Google Scholar] [CrossRef]
- Dads, E. Existence Of positive almost periodic or ergodic solutions for some neutral nonlinear integral equations. Differ. Integral Equ. 2009, 22, 1075–1096. [Google Scholar]
- Cooke, K.; Kaplan, J. A periodicity threshold theorem for epidemics and population growth. Math. Biosci. 1976, 31, 87–104. [Google Scholar] [CrossRef]
- Ardjouni, A.; Djoudi, A. Existence of periodic solutions for nonlinear neutral dynamic equations with variable delay on a time scale. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3061–3069. [Google Scholar] [CrossRef]
- Cheung, W.; Ren, J.; Han, W. Positive periodic solution of second-order neutral functional differential equations. Nonlinear Anal. TMA 2009, 71, 3948–3955. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z. Two periodic solutions of second-order neutral functional differential equations. J. Math. Anal. Appl. 2007, 329, 677–689. [Google Scholar] [CrossRef]
- Wang, Q.; Dai, B. Three periodic solutions of nonlinear neutral functional differential equations. Nonlinear Anal. Real World Appl. 2008, 9, 977–984. [Google Scholar] [CrossRef]
- Ren, S.; Siegmund, S.; Chen, Y. Positive periodic solutions for third-order nonlinear differential equations. Electron. J. Differ. Equ. 2011, 2011, 66. [Google Scholar]
- Hale, J. Theory of Functional Differential Equations; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Krasnoselskii, M. Positive Solution of Operator Equation; Noordhoff: Groningen, The Netherlands, 1964. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Wang, X.; Cheng, X.; Du, B.; Zhao, Y. Positive Periodic Solution for Neutral-Type Integral Differential Equation Arising in Epidemic Model. Mathematics 2023, 11, 2701. https://doi.org/10.3390/math11122701
Yang Q, Wang X, Cheng X, Du B, Zhao Y. Positive Periodic Solution for Neutral-Type Integral Differential Equation Arising in Epidemic Model. Mathematics. 2023; 11(12):2701. https://doi.org/10.3390/math11122701
Chicago/Turabian StyleYang, Qing, Xiaojing Wang, Xiwang Cheng, Bo Du, and Yuxiao Zhao. 2023. "Positive Periodic Solution for Neutral-Type Integral Differential Equation Arising in Epidemic Model" Mathematics 11, no. 12: 2701. https://doi.org/10.3390/math11122701
APA StyleYang, Q., Wang, X., Cheng, X., Du, B., & Zhao, Y. (2023). Positive Periodic Solution for Neutral-Type Integral Differential Equation Arising in Epidemic Model. Mathematics, 11(12), 2701. https://doi.org/10.3390/math11122701





