Solving the (2+1)-Dimensional Derivative Toda Equation
Abstract
:1. Introduction
2. Modified Toda Lattice Equation Related to New Spectral Problem
3. -Soliton Solutions for the Modified Toda Lattice Equation
4. (2+1)-Dimensional Derivative Toda Equation
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Kdv | Kortewegde Vries |
| TL | Toda lattice |
| TTL | two-dimensional Toda lattice |
References
- Fuchssteiner, B. Application of Hereditary Symmetries to Nonlinear Evolution equations. Nonlinear Anal. 1979, 3, 849–862. [Google Scholar] [CrossRef] [Green Version]
- Hirota, R.; Satsuma, J. A Variety of Nonlinear Network Equations Generated from the Bäcklund Transformation for the Toda latticee. Prog. Theor. Phys. Suppl. 1976, 59, 64–100. [Google Scholar] [CrossRef] [Green Version]
- Bogoyavlensky, O.I. On perturbations of the periodic toda latticee. Commun. Math. Phys. 1976, 51, 201–209. [Google Scholar] [CrossRef]
- Leznov, A.N.; Saveliev, M.V. Representation of zero curvature for the system of nonlinear partial differential equations xα,z,z = exp(kx)α and its integrability. Lett. Math. Phys. 1979, 3, 489–494. [Google Scholar] [CrossRef]
- Mikhailov, A.V.; Olshanetsky, M.A.; Perelomov, A.M. Two-Dimensional Generalized Toda Lattice. Commun. Math. Phys. 1981, 79, 473–488. [Google Scholar] [CrossRef]
- Girardello, L.; Sciuto, S. Inverse scattering-like problem for supersymmetric models. Phys. Lett. 1978, 77, 267–269. [Google Scholar] [CrossRef] [Green Version]
- Chaichian, M.; Kulish, P. On the method of inverse scattering problem and B icklund transformations for supersymmetric equations. Phys. Lett. 1978, 78, 413–416. [Google Scholar] [CrossRef]
- Inami, T.; Kanno, H. Lie superalgebraic approach to super Toda lattice and generalized super KdV equations. Commun. Math. Phys. 1991, 136, 519–542. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the KdV equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1981. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Gu, C.; Hu, H.; Zhou, Z. Darboux Transformations in Integrable Systems: Theory and Their Applications to Geometry; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Olver, P. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Bluman, G.; Anco, S. Symmetry and Integration Methods in Differential Equations; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Miura, R.M. Bäcklund Transformations, the Inverse Scattering Method, Solitons and Their Applications; Miura, R.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1976. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Novikov, S.P.; Manakov, S.V.; Pitaevskii, L.P.; Zakharov, V.E. Theory of Solitons. The Inverse Scattering Method; Nauka: Moscow, Russia, 1980. [Google Scholar]
- Belokolos, E.D.; Bobenko, A.I.; Enolskii, V.Z.; Its, A.R.; Matveev, V.B. Algebro-Geometric Approach to Nonlinear Integrable Equations; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Cao, C.; Yang, X. A (2+1)-dimensional derivative Toda equation in the context of the Kaup-Newell spectral problem. J. Phys. A Math. Theor. 2008, 41, 19. [Google Scholar] [CrossRef]
- Fan, F.C.; Wen, X.Y. A generalized integrable lattice hierarchy associated with the Toda and modified Toda lattice equations: Hamiltonian representation, soliton solutions. Wave Motion 2021, 103, 102727. [Google Scholar] [CrossRef]
- Yuan, C.L.; Wen, X.Y. Integrability, discrete kink multi-soliton solutions on an inclined plane background and dynamics in the modified exponential Toda lattice equation. Nonlinear Dyn. 2021, 105, 643–669. [Google Scholar] [CrossRef]
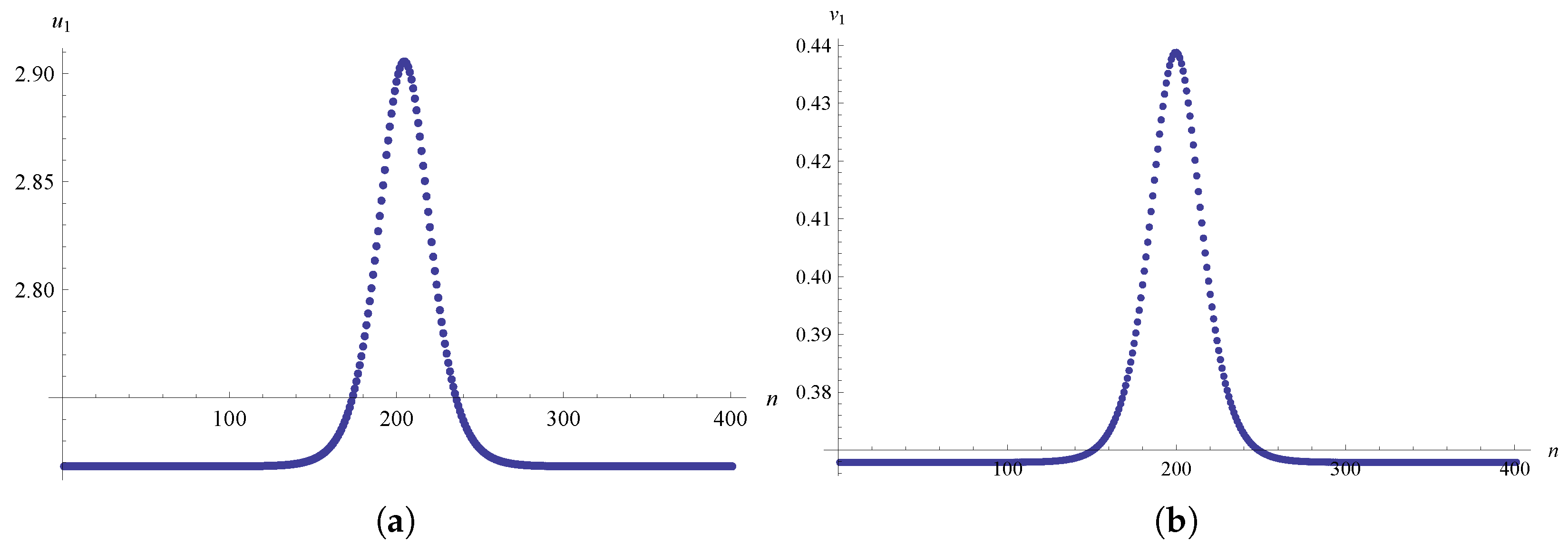
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.-Y.; Wang, F.-H. Solving the (2+1)-Dimensional Derivative Toda Equation. Mathematics 2023, 11, 2845. https://doi.org/10.3390/math11132845
Zhu X-Y, Wang F-H. Solving the (2+1)-Dimensional Derivative Toda Equation. Mathematics. 2023; 11(13):2845. https://doi.org/10.3390/math11132845
Chicago/Turabian StyleZhu, Xiao-Ying, and Feng-He Wang. 2023. "Solving the (2+1)-Dimensional Derivative Toda Equation" Mathematics 11, no. 13: 2845. https://doi.org/10.3390/math11132845



