Numerical Solution of Thermal Phenomena in Welding Problems

Abstract

We present a novel finite element method to solve the thermal variables in welding problems. The mathematical model is based on the enthalpy formulation of the energy conservation law, which is simultaneously valid for the solid, liquid, and mushy regions. Both isothermal and non-isothermal melting models are considered to relate the enthalpy with the temperature. Quadratic triangular elements with local anisotropic mesh adaptation are employed for the space discretization of the governing equation, and a second-order backward differentiation formula is employed for the time discretization. The resulting non-linear discretized system is solved with a simple Newton algorithm with two versions: the $\theta$-Newton algorithm, which considers the temperature as the main unknown variable, as in most works in the literature, and the h-Newton algorithm, which considers the enthalpy, which is the main novelty of the present work. Then, we show via numerical experiments that the h-Newton method is robust and converges well to the solution, both for isothermal and non-isothermal melting. However, the $\theta$-method can only be applied to the case of non-isothermal melting and converges only for a sufficiently large melting temperature range or sufficiently small time step. Numerical experiments also confirm that the method is able to adequately capture the discontinuities or sharp variations in the solution without the need for any kind of numerical dissipation.

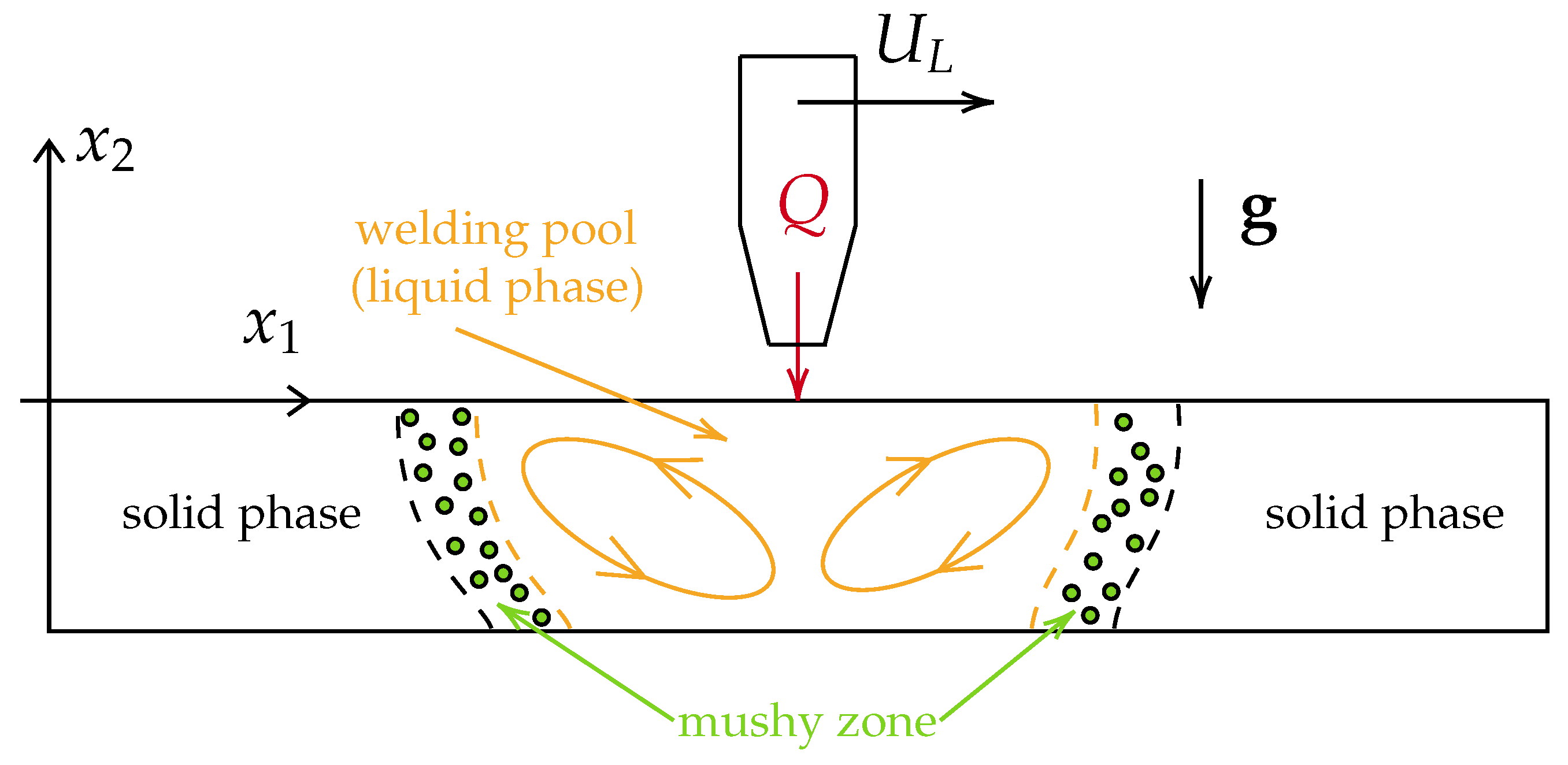
1. Introduction

Welding is one of the most important industrial processes employed to join parts of complex structures due to its versatility, economic cost and technological advantages. Welding involves applying powerful heat sources, which is the principal reason for the appearance of sophisticated phenomena, such as undesirable residual stresses, deformations, porous, internal, and external cracks, and micro-defects that affect the mechanical properties of the welded metals. Due to the complexity of the process, numerical tools for the thermo-mechanical analysis of the physical variables involved are essential in order to develop new welding technologies and techniques [1].

A simplification of the welding process is characterized schematically in Figure 1. A moving heat source is applied to a solid metal plate so as to increase its temperature. When the melting temperature of the material is reached, the solid begins to melt and some areas of the plate become liquid. If the heat source continues its action, the temperature also increases in the liquid zone. In the presence of gravity, this can generate buoyancy forces, which lead to the movement of the fluid. Moreover, in this problem, the presence of a transient zone where the two phases coexist is usual. Atthey [2] was the first who observed this region by numerical calculations, and he called it the ‘mushy region’, a name widely used now. When the heat source goes out, the mushy and liquid zones solidify again.

The thermal welding process with phase change leads to the so-called two-phase Stefan problem [3]. This process is governed in the whole domain by an enthalpy formulation of the energy conservation equation [4,5,6], which relates time changes in enthalpy, h, with space changes in temperature, T. The conservation equation must be complemented with a constitutive relation between h and T, which depends on the considered model. In the case of pure metals, the transition between solid and liquid phases takes place at a constant temperature $T_F$ (isothermal melting model). However, in alloys, which are composed of metals with different melting temperatures, the transition occurs at a range of $[T_F,T_F+\Delta T]$ (non-isothermal melting model) [7].

Many methods in the literature, such as [8,9,10,11,12,13,14,15], consider a non-isothermal melting model, express h and other variables as a function of T, and solve the energy conservation equation in terms of the temperature. These are called temperature-based methods or effective specific heat methods. Their main drawback is that they cannot be applied to the isothermal melting model because some variables, such as the enthalpy or the liquid mass fraction, may take different values for the melting temperature $T_F$. As a remedy, enthalpy-based methods [16,17,18] pose the energy conservation equation in terms of the enthalpy, which always defines univocally the state (temperature and liquid mass fraction are single-valued functions of enthalpy) of the metal irrespective of the melting model.

In both isothermal and non-isothermal cases, the energy conservation equation is highly non-linear and usually has no analytical solution. Thus, some numerical methods are needed. For instance, the element-free Galerkin [19] and Petrov–Galerkin [20] methods, the finite volume method [8], and the finite element method [21] are employed for space–time discretization, whereas Newton-type methods [16,21] and the Bermúdez–Moreno algorithm [17,18] are employed as non-linear solvers.

In this work, we develop a finite element method to solve the energy conservation equation with phase change that governs welding problems. The non-linear discretized equations are solved with two versions of a Newton method. The first one, called the $\theta$-Newton algorithm, solves the energy equation considering the temperature as the main unknown variable, as conducted in most of the literature; see, e.g., [8,9,13,19,20,21]. The second one, called the h-Newton method, is the main contribution of this work and solves the energy equation considering the enthalpy as the main unknown variable [16,17,18]. The h-Newton algorithm presented here iterates directly in the enthalpy variable, and, hence, it is more simple to implement than other enthalpy-based methods, such as the Bermúdez–Moreno algorithm [17,18] (which requires to fine-tune some parameters and to compute a regularization operator) and the method by Nedjar [16] (which iterates in the temperature variable with a damped Newton iteration). We also prove via numerical experiments that the h-Newton method is much better numerically conditioned than the $\theta$-Newton method, both for isothermal and non-isothermal melting.

For the space discretization of the energy equation, we consider quadratic polynomials, reaching $\mathcal{O}\left({\mathrm{h}}^3\right)$ convergence rates for regular solutions, with $\mathrm{h}$ the mesh size. For the time discretization, we employ a BDF2 formula, reaching $\mathcal{O}(\Delta t^2)$ convergence rates, with $\Delta t$ the time step, thus improving the $\mathcal{O}(\Delta t)$ convergence rates—equivalent to an implicit Euler scheme—of previous works present in the literature. Furthermore, we employ anisotropic mesh adaptation techniques [22] in order to capture the discontinuities or sharp changes in the state variables with better accuracy.

The layout of the paper is as follows. After this introduction, Section 2 presents the mathematical formulation of the problem based on the energy conservation equation. Models valid for isothermal and non-isothermal phase-change processes are derived. This section finishes introducing the dimensionless formulation of the problem as well as the most relevant non-dimensional parameters. Section 3 describes the numerical method to solve the governing equation based on the finite element method as space discretization and the BDF2 scheme as time discretization. This is presented in a local adaptative framework based on anisotropic triangles. To solve the non-linear discretized problem, we present the $\mathcal{X}$-Newton algorithm, with $\mathcal{X}$ being h—enthalpy—or $\theta$—temperature—depending on the main unknown (dimensionless) variable considered. Finally, in Section 4, we present the numerical results to analyze the main features of the isothermal and non-isothermal models for the mushy region, as well as the convergence of the $\mathcal{X}$-Newton algorithm.

2. Governing Equations

In this section, we present the equations that govern the welding phenomenon described in the introduction and shown schematically in Figure 1. Recall that there are three regions in the metal plate: solid, liquid, and mushy zone (where solid and liquid phases coexist). As basic hypotheses of the model, we assume:

• Constant density $\rho$ at the three regions, as in [13].
• The intensity of the convective currents in the liquid zone is negligible; i.e., the velocity $\mathbf{v}\sim \mathbf{0}$ at each material point. That is, we consider problems at low Grashof number limit $\mathrm{Gr}\to 0$, so there is no motion caused by the buoyancy forces. Otherwise, mass and momentum equations for the fluid motion would need to be considered.
• Radiation and evaporation are not considered in this study.
• The equations of elasticity—which take into account deformations and stresses in the material—and electromagnetism—which model the effect of the laser-arc heat source—are not considered in this study.
• The specific heat coefficient and the thermal conductivity depend on the state of the material but not on the temperature. Nevertheless, the present method can be easily extended to the more realistic case of temperature-dependent thermal coefficients; see Remark 3.

Under these assumptions, the metal plate is governed by the the energy conservation equation [16,18], without convective terms:

$$\rho \frac{\partial h}{\partial t}=\nabla ·(\lambda \nabla T)+Q,\mathrm{in}\mathsf{\Omega },$$

(1)

where h is the enthalpy per unit mass, T is the temperature, $\lambda$ is the thermal conductivity, Q is a volumetric heat source, and $\mathsf{\Omega }$ is the (fixed) domain occupied by the plate. We assume that the heat source Q is produced by a hybrid laser-arc source, which is able to internally heat the material due to the Joule effect [8,9]. The initial condition corresponds to a fully solid state at ambient temperature $T=T_0$, and Dirichlet and Robin boundary conditions are defined on ${\mathsf{\Gamma }}_D$ and ${\mathsf{\Gamma }}_R$, respectively (with $\partial \mathsf{\Omega }={\mathsf{\Gamma }}_D\bigcup {\mathsf{\Gamma }}_R$):

$$T=T_0\mathrm{on}{\mathsf{\Gamma }}_D,\mathrm{and}-\lambda \frac{\partial T}{\partial \mathrm{n}}=\alpha (T-T_0)\mathrm{on}{\mathsf{\Gamma }}_R,$$

(2)

where $\alpha$ is a convective coefficient and $\partial /\partial \mathrm{n}$ is the normal derivative.

The enthalpy depends on the temperature and on the liquid mass fraction, $Y_L$, in such a way that $dh=cdT+H_{F}d{Y}_L$, where c is the specific heat capacity and $H_F$ is the latent heat of fusion. For pure metals, melting takes place in welding processes at a constant temperature $T_F$. In the case of constant values for the latent heat of fusion, $H_F$, and for the specific heat coefficients at the solid and liquid regions, $c_S$ and $c_L$, respectively, the relation between enthalpy and temperature is given by

$$h\in h\left(T\right)=\left\{\begin{array}{cc}{\displaystyle c_S(T-T_0),}\hfill & T<T_F,\hfill \\ {\displaystyle [h_S,h_L],}\hfill & T=T_F,\hfill \\ {\displaystyle h_L+c_L(T-T_F),}\hfill & T>T_F,\hfill \end{array}\right.$$

(3)

with $h_S=c_S(T_F-T_0)$ and $h_L=h_S+H_F$ the enthalpies of the solid and liquid regions at the melting temperature $T_F$, respectively. Note the choice $h\left(T_0\right)=0$. Above, the notation $h\in [h_S,h_L]$ means that h may take any value in this interval. That is, the function $h\left(T\right)$ is multi-valued at $T=T_F$, and, hence, the state of the metal is not univocally defined by the temperature. This makes it impossible to numerically solve (1) and (2) with isothermal model (3) in terms of the temperature. However, the inverse function $T=T\left(h\right)$ is single-valued; hence, it is possible to solve these equations in terms of the enthalpy.

On the other hand, many references assume that the material is an alloy, a mixture of metals with different melting temperatures, and therefore the phase change takes place in a range of temperatures $[T_F,T_F+\Delta T]$. In these non-isothermal melting processes, the enthalpy can be written as a single-valued function in terms of the temperature, i.e., $dh=[c+H_{F}d{Y}_L/dT]dT$, or shortly as $dh=c_{\mathrm{eff}}dT$, where $c_{\mathrm{eff}}=c+H_{F}d{Y}_L/dT$ is the effective heat capacity, which includes the heat released during the melting process; see, e.g., [8,9,13]. In this paper, we consider:

$$h=h\left(T\right)=\left\{\begin{array}{cc}{\displaystyle c_S(T-T_0),}\hfill & T\le T_F,\hfill \\ {\displaystyle h_S+\frac{H_F}{\Delta T}(T-T_F),}\hfill & T_F<T<T_F+\Delta T,\hfill \\ {\displaystyle h_L+c_L(T-T_F),}\hfill & T\ge T_F.\hfill \end{array}\right.$$

(4)

Note that $h(T_F+\Delta T)=h\left(T_F\right)+H_F$, so non-isothermal melting model (4) requires the same energy as isothermal melting model (3) for the change in phase, and both models are equivalent if $\Delta T=0$. Now, the enthalpy is a single-valued function of the temperature, so, in principle, this model makes possible to employ this variable to solve Equations (1) and (2), as conducted in many research papers. Nevertheless, we can see that the temperature variation required for the change in phase may be small, whereas the enthalpy variation is not. This makes Equations (1) and (2) numerically better conditioned when solved by setting the enthalpy as main unknown variable than by setting the temperature, as will be shown in the numerical experiments.

Whenever we employ models (3) or (4), the thermal conductivity takes the form:

$$\lambda =\lambda \left(T\right)=\left\{\begin{array}{cc}{\displaystyle {\lambda }_S,}\hfill & T\le T_F,\hfill \\ {\displaystyle {\lambda }_S+({\lambda }_L-{\lambda }_S)\frac{T-T_F}{\Delta T},}\hfill & T_F<T<T_F+\Delta T,\hfill \\ {\displaystyle {\lambda }_L,}\hfill & T\ge T_F+\Delta T,\hfill \end{array}\right.$$

(5)

making the diffusion term in (1) non-linear. To manipulate this non-linearity, we use Kirchhoff transformation [23], which consists of defining a new variable u such that

$$du=\lambda \left(T\right)dT,u\left(T_0\right)=0.$$

(6)

In that case, (1) and (2) read:

$$\rho {\displaystyle \frac{\partial h}{\partial t}}=\Delta u+Q\mathrm{in}\mathsf{\Omega },$$

(7)

$$T{|}_{t=0}=T_0\mathrm{in}\mathsf{\Omega },$$

(8)

$$T=T_0\mathrm{on}{\mathsf{\Gamma }}_D,$$

(9)

$$-{\displaystyle \frac{\partial u}{\partial n}}=\alpha (T-T_0)\mathrm{on}{\mathsf{\Gamma }}_R.$$

(10)

Remark 1. 

For physical reasons, T is continuous in Ω, and, hence, so is Kirchhoff’s variable u. On the other hand, due to the changes in phase, h, λ, and $Y_L$ may present discontinuities (isothermal melting model) or very sharp variations (non-isothermal melting model).

Non-Dimensional Formulation

To have a better understanding of the physical phenomenon, it is always convenient to formulate the problem in a non-dimensional form. In this way, we can evaluate the order of magnitude of each term in the equations and see which are the relevant (non-dimensional) parameters that characterize the problem. The non-dimensional variables are denoted with the asterisk (${}^{*}$) symbol and defined as

$$\left\{\begin{array}{c}{\displaystyle {\mathbf{x}}^{*}=\frac{\mathbf{x}}{L_0},t^{*}=\frac{U_0}{L_0}t,}\hfill \\ \\ {\displaystyle \theta =\frac{T-T_0}{T_F-T_0},u^{*}=\frac{u}{{\lambda }_S(T_F-T_0)},h^{*}=\frac{h}{c_S(T_F-T_0)},Q^{*}=\frac{Q{L}_0}{\rho c_S(T_F-T_0)U_0},}\hfill \end{array}\right.$$

(11)

where $L_0$ is a characteristic length (i.e., that of the longest boundary) and $U_0$ is a characteristic velocity (i.e., that of the moving source). With the definitions established in (11), (7)–(10) are written in the following dimensionless form:

$$\begin{array}{cccc}\hfill {\displaystyle \frac{\partial h^{*}}{\partial t^{*}}}& ={\displaystyle \frac{1}{\mathrm{Pe}}}{\Delta }^{*}{u}^{*}+Q^{*}\hfill & & \mathrm{in}\mathsf{\Omega },\hfill \end{array}$$

(12)

$$\begin{array}{cccc}\hfill \theta {|}_{t^{*}=0}& =0\hfill & & \mathrm{in}\mathsf{\Omega },\hfill \end{array}$$

(13)

$$\begin{array}{cccc}\hfill \theta & =0\hfill & & \mathrm{on}{\mathsf{\Gamma }}_D,\hfill \end{array}$$

(14)

$$\begin{array}{cccc}\hfill -{\displaystyle \frac{\partial u^{*}}{\partial {\mathrm{n}}^{*}}}& =\mathrm{Nu}\theta \hfill & & \mathrm{on}{\mathsf{\Gamma }}_R,\hfill \end{array}$$

(15)

where the Péclet and Nusselt numbers are defined as

$$\mathrm{Pe}=\frac{\rho c_S{L}_0{U}_0}{{\lambda }_S},\mathrm{Nu}=\frac{\alpha L_0}{{\lambda }_S}.$$

(16)

Two more dimensionless numbers have transcendental importance in thermal processes involving a change in phase: the Stefan number, Ste, defined as the ratio of the sensible heat and latent heat at solid, and the dimensionless temperature width, $\Delta T^{*}$, at which the phase change takes place; that is:

$$\mathrm{Ste}=\frac{c_S(T_F-T_0)}{H_F},\Delta T^{*}=\frac{\Delta T}{T_F-T_0}.$$

(17)

With the definitions above and (4) and (5), the (dimensionless) enthalpy, $h^{*}$, and Kirchhoff variable, $u^{*}$, read in terms of $\theta$ as

$$h^{*}\left(\theta \right),u^{*}\left(\theta \right)=\left\{\begin{array}{ccc}\theta ,\hfill & \theta ,\hfill & \theta \le 1,\hfill \\ 1+\frac{\theta -1}{\mathrm{Ste}\Delta T^{*}},\hfill & 1+\left(\theta -1\right)\left[1+\frac{\frac{{\lambda }_L}{{\lambda }_S}-1}{2\Delta T^{*}}(\theta -1)\right],\hfill & 1<\theta <1+\Delta T^{*},\hfill \\ \left(1+\frac{1}{\mathrm{Ste}}\right)+\frac{c_L}{c_S}\left(\theta -1-\Delta T^{*}\right),\hfill & \frac{{\lambda }_L}{{\lambda }_S}\left(\theta -1\right)+1-\frac{\Delta T^{*}}{2}\left(\frac{{\lambda }_L}{{\lambda }_S}-1\right),\hfill & \theta \ge 1+\Delta T^{*}.\hfill \end{array}\right.$$

(18)

We note that expressions in (18) are valid for isothermal and non-isothermal phase change processes, but, in the first case (in which $\Delta T^{*}=0$), the definition of $h^{*}(\theta$) degenerates into a multi-valued function. However, the inverse of the enthalpy function, $\theta \left(h^{*}\right)$, can be easily defined, and, therefore, also $u^{*}\left(h^{*}\right)$. The corresponding expressions are given by:

$$\theta \left(h^{*}\right),u^{*}\left(h^{*}\right)=\left\{\begin{array}{ccc}{h}^{*},\hfill & h^{*},\hfill & h^{*}\le 1,\hfill \\ 1+\mathrm{Ste}\Delta T^{*}\left(h^{*}-1\right),\hfill & 1+\mathrm{Ste}\Delta T^{*}\left(h^{*}-1\right)\left[1+\frac{\frac{{\lambda }_L}{{\lambda }_S}-1}{2}\mathrm{Ste}\left(h^{*}-1\right)\right],\hfill & 1<h^{*}<1+\frac{1}{\mathrm{Ste}},\hfill \\ \left(h^{*}-1-\frac{1}{\mathrm{Ste}}\right)\frac{c_S}{c_L}+1+\Delta T^{*},\hfill & 1+\frac{\Delta T^{*}}{2}\left(\frac{{\lambda }_L}{{\lambda }_S}+1\right)+\frac{{\lambda }_L}{{\lambda }_S}\frac{c_S}{c_L}\left(h^{*}-1-\frac{1}{\mathrm{Ste}}\right),\hfill & h^{*}\ge 1+\frac{1}{\mathrm{Ste}}.\hfill \end{array}\right.$$

(19)

Now, the expressions in (19) do not degenerate; i.e., the functions $\theta \left(h^{*}\right)$ and $u^{*}\left(h^{*}\right)$ are single-valued even if $\Delta T^{*}=0$. This property makes non-linear (12) numerically better conditioned when solved (via, e.g., a Newton method) considering the enthalpy as main unknown variable.

Moreover, the mass fraction of liquid $Y_L$ can also be defined in terms of the enthalpy and does not depend on $\Delta T^{*}$. Although it does not appear in this formulation, it can be used to visualize the free surfaces that separate the mushy region from the solid phase ($Y_L=0$) and the mushy region from the liquid phase ($Y_L=1$).

$$Y_L\left(h^{*}\right)=\left\{\begin{array}{cc}{\displaystyle 0,}\hfill & {\displaystyle h^{*}\le 1,}\hfill \\ {\displaystyle (h^{*}-1)\mathrm{Ste},}\hfill & {\displaystyle 1<h^{*}<1+\frac{1}{\mathrm{Ste}},}\hfill \\ {\displaystyle 1,}\hfill & {\displaystyle h^{*}\ge 1+\frac{1}{\mathrm{Ste}}.}\hfill \end{array}\right.$$

(20)

The expression above is valid for isothermal and non-isothermal phase-change processes.

From now on, we drop the asterisk (${}^{*}$) symbol so as not to overload the notation, and all the variables that appear will be dimensionless unless otherwise stated.

It should be pointed out that the present thermal model also applies when there is a thermal shock. For that purpose, the heat source must be described by means of a hyperbolic tangent or a similar mathematical function in order to force a sudden change in the temperature. However, in order to find the mechanical stresses due to thermal effects and strain, it would be necessary to complement the thermal model with the equations of elasticity.

3. Numerical Discretization of the Problem

Once the mathematical model has been formulated, we design an algorithm based on a second-order time-marching scheme in combination with second-order local adaptative finite element discretization in space. More specifically, we first split the time interval of integration $[0,t_f]$ into subintervals $[t_{n-1},t_n]$ of constant length $\Delta t=t_n-t_{n-1}$. Then, we discretize (12) with a BDF2 formula:

$${\displaystyle \frac{3h^n-4h^{n-1}+h^{n-2}}{2\Delta t}}={\displaystyle \frac{1}{\mathrm{Pe}}}\Delta u^n+Q^n,\mathrm{in}\mathsf{\Omega },$$

(21)

for $n=2,\dots ,N_t$, with $N_t\Delta t=t_f$. At each time level $t^n$, the domain $\mathsf{\Omega }$ is partitioned into a triangular mesh ${\mathbb{T}}_h^n$, to which we associate the conforming finite element space

$$V_{h0}^n=\{{\phi }_h\in C^0\left({\mathbb{R}}^2\right):{\phi }_h{|}_K\in P_2\left(K\right),\forall K\in {\mathbb{T}}_h^n\mathrm{and}{\phi }_h{|}_{{\mathsf{\Gamma }}_D}=0\},$$

(22)

where $P_2\left(K\right)$ is the space of quadratic polynomials on an element K. That is, $V_{h0}^n$ is the space of continuous and quadratic polynomials (defined piecewise at the mesh elements) that vanish at the Dirichlet boundary ${\mathsf{\Gamma }}_D$. Note from (14) and (18) that h, $\theta$, and u also vanish at ${\mathsf{\Gamma }}_D$. Hence, we can approximate these variables as

$$h_h^n\left(\mathbf{x}\right)=\sum _{i=1}^{N^n}{h}_i^n{\phi }_i\left(\mathbf{x}\right),{\theta }_h^n\left(\mathbf{x}\right)=\sum _{i=1}^{N^n}{\theta }_i^n{\phi }_i\left(\mathbf{x}\right),\mathrm{and}{u}_h^n\left(\mathbf{x}\right)=\sum _{i=1}^{N^n}{u}_i^n{\phi }_i\left(\mathbf{x}\right),$$

(23)

where $N^n$ is the number of mesh nodes (excluding those at ${\mathsf{\Gamma }}_D$), $h_i^n$, ${\theta }_i^n$, and $u_i^n$ are the values of $h^n$, ${\theta }^n$, and $u^n$ at these nodes, and ${\phi }_i\left(\mathbf{x}\right)$ are the corresponding Lagrangian basis functions.

With the considerations above, (21) reads in weak form as

$$\begin{array}{cc}\hfill & 3{\int }_{\mathsf{\Omega }}{h}_h^n{\phi }_{h}d\mathrm{x}+\frac{2\Delta t}{\mathrm{Pe}}{\int }_{\mathsf{\Omega }}\nabla u_h^n·\nabla {\phi }_{h}d\mathrm{x}+\frac{2\Delta t\mathrm{Nu}}{\mathrm{Pe}}{\int }_{{\mathsf{\Gamma }}_R}{\theta }_h^n{\phi }_{h}d\mathrm{s}=\hfill \\ & ={\int }_{\mathsf{\Omega }}2\Delta t{Q}^n{\phi }_{h}d\mathrm{x}+{\int }_{\mathsf{\Omega }}(4h_h^{n-1}-h_h^{n-2}){\phi }_{h}d\mathrm{x},\forall {\phi }_h\in V_{h0}^n.\hfill \end{array}$$

(24)

(24) can be rewritten in matrix form to simplify the notation:

$${\displaystyle 3\mathbf{M}{\mathbf{h}}^n+\frac{2\Delta t}{\mathrm{Pe}}\mathbf{K}{\mathbf{u}}^n+\frac{2\Delta t\mathrm{Nu}}{\mathrm{Pe}}{\mathbf{M}}_{{\mathsf{\Gamma }}_R}{\theta }^n={\mathbf{f}}^n,}$$

(25)

where the bold variables are vectors or matrices whose elements are defined by:

$$\begin{array}{cc}\hfill & M_{ij}={({\phi }_i,{\phi }_j)}_{\mathsf{\Omega }},K_{ij}={(\nabla {\phi }_i,\nabla {\phi }_j)}_{\mathsf{\Omega }},M_{{\mathsf{\Gamma }}_{R}ij}={({\phi }_i,{\phi }_j)}_{{\mathsf{\Gamma }}_R}\hfill \\ & f_i^n={(2\Delta t{Q}^n+4h_h^{n-1}-h_h^{n-2},{\phi }_i)}_{\mathsf{\Omega }},\hfill \end{array}$$

(26)

and with $(·,·)$ the standard scalar product in the $L^2$ norm. Note that, due to the introduction of Kirchhoff’s variable (6), the stiffness matrix is constant (whenever the mesh remains fixed), which greatly simplifies the solution algorithm.

3.1. The $\mathcal{X}$-Newton Algorithm

System (25) defines a non-linear problem due to the relations between the unknown variables of the problem $h_i^n$, ${\theta }_i^n$, and $u_i^n$. To approach its resolution, here, we have employed a Newton algorithm. We consider two versions of the latter. In the first one, the $\theta$-Newton algorithm, we set the (nodal) temperatures ${\theta }_i^n$ as main unknowns and evaluate $h_i^n$ and $u_i^n$ via (18). In the second, the h-Newton algorithm, we set the (nodal) enthalpies $h_i^n$ as main unknowns and evaluate ${\theta }_i^n$ and $u_i^n$ via (19). As both versions are formally identical, we introduce an abstract variable $\mathcal{X}$, which denotes $\theta$ or h depending on the case, and we call the method the $\mathcal{X}$-Newton algorithm.

Let ${\mathcal{X}}_k^n$ denote the vector of unknowns at the kth iteration. The residual and Jacobian of (25) are:

$$\begin{array}{cc}\hfill {\mathbf{b}}_k^n& =3\mathbf{M}{\mathbf{h}}_k^n+\frac{2\Delta t}{\mathrm{Pe}}\mathbf{K}{\mathbf{u}}_k^n+\frac{2\Delta t\mathrm{Nu}}{\mathrm{Pe}}{\mathbf{M}}_{{\mathsf{\Gamma }}_R}{\mathit{\theta }}_k^n-{\mathbf{f}}^n,\hfill \\ \hfill {\mathbf{J}}_k^n& =3\mathbf{M}{\mathbf{D}}_k^h+\frac{2\Delta t}{\mathrm{Pe}}\mathbf{K}{\mathbf{D}}_k^u+\frac{2\Delta t\mathrm{Nu}}{\mathrm{Pe}}{\mathbf{M}}_{{\mathsf{\Gamma }}_R}{\mathbf{D}}_k^{\theta }.\hfill \end{array}$$

where $h_{k,i}^n=h\left({\mathcal{X}}_{k,i}^n\right)$, ${\theta }_{k,i}^n=\theta \left({\mathcal{X}}_{k,i}^n\right)$, $u_{k,i}^n=u\left({\mathcal{X}}_{k,i}^n\right)$ are evaluated via (18) or (19); ${\mathbf{D}}_k^{\varphi }$ (with $\varphi$ denoting h, $\theta$, or u) is the diagonal matrix

$$D_{k,ij}^{\varphi }={\left.\frac{d\varphi }{d\mathcal{X}}\right|}_{{\mathcal{X}}_{k,i}^n}{\delta }_{ij},$$

(27)

${\delta }_{ij}$ is the Kronecker delta, and the derivatives $d\varphi /d\mathcal{X}$ are easily computed from expressions (18) or (19). Then, the value of ${\mathcal{X}}_{k+1}^n$ at the next iteration $k+1$ is given by solving

$${\mathbf{J}}_k^n\Delta {\mathcal{X}}_{k+1}^n=-{\mathbf{b}}_k^n,{\mathcal{X}}_{k+1}^n={\mathcal{X}}_k^n+\Delta {\mathcal{X}}_{k+1}^n.$$

The iterations are stopped when the norm of $\Delta {\mathcal{X}}_{k+1}^n$ is under a tolerance of ${10}^{-10}$.

Remark 2. 

The Jacobian has to be evaluated at each iteration. However, since the finite element matrices $\mathbf{M}$, $\mathbf{K}$, ${\mathbf{M}}_{{\mathsf{\Gamma }}_R}$ are constant, and only the diagonal matrices ${\mathbf{D}}_k^{\varphi }$ need to be recomputed, this is not an expensive operation.

Remark 3. 

Relations (19) are built upon the major assumption that the specific heat and thermal conductivity do not depend on the temperature. However, in more realistic cases, this assumption is not true, and there is no analytical expression for the relations $\theta \left(h\right)$ and $u\left(h\right)$ required by the h-Newton method. Instead, one disposes of analytical (non-linear) expressions for $h\left(\theta \right)$ and $u\left(\theta \right)$, e.g., the NASA polynomials [24]. In these cases, it is straightforward to obtain θ from h (and hence also u from h) by solving the equation $h=h\left(\theta \right)$, e.g., with the aid of a Newton algorithm. Since the function $h\left(\theta \right)$ is piecewise monotone and smooth, the cost of this operation should be negligible. On the other hand, the matrices ${\mathbf{D}}_k^{\theta }$ and ${\mathbf{D}}_k^u$ defined by (27) can be readily calculated in the h-Newton algorithm as

$$D_{k,ij}^{\theta }={\left.\frac{d\theta }{dh}\right|}_{h_{k,i}^n}{\delta }_{ij}={\left[{\left.\frac{dh}{d\theta }\right|}_{{\theta }_{k,i}^n}\right]}^{-1}{\delta }_{ij},\mathrm{and}{D}_{k,ij}^u={\left.\frac{du}{dh}\right|}_{h_{k,i}^n}{\delta }_{ij}={\left.\frac{du}{d\theta }\right|}_{{\theta }_{k,i}^n}{\left[{\left.\frac{dh}{d\theta }\right|}_{{\theta }_{k,i}^n}\right]}^{-1}{\delta }_{ij}.$$

We note that, although there is no analytical expression, the function $\theta \left(h\right)$ is single-valued, and, therefore, ${\left.d\theta /dh\right|}_{h_{k,i}^n}={\left[{\left.dh/d\theta \right|}_{{\theta }_{k,i}^n}\right]}^{-1}$ is finite.

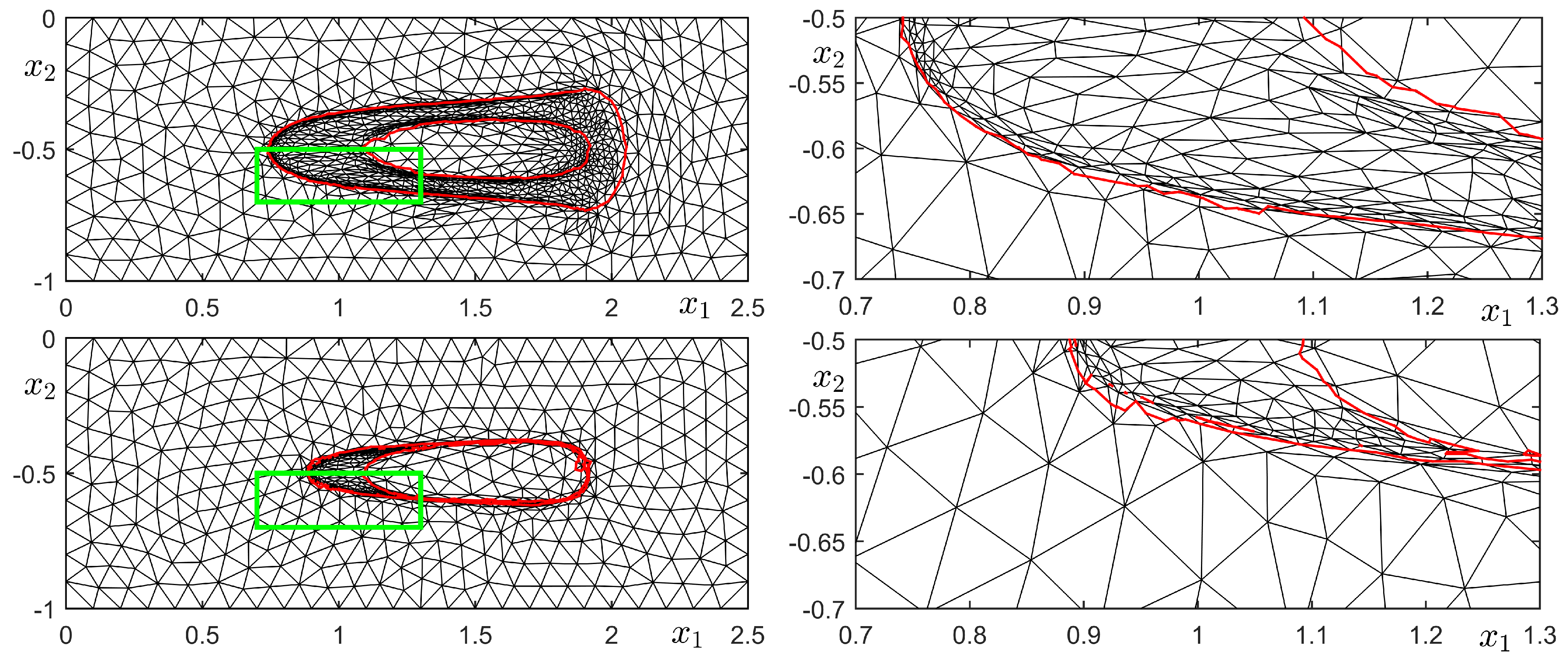
3.2. Mesh Refinement

To conclude with the section dedicated to the discretization and numerical resolution of the equations, we provide a brief description of the local anisotropic mesh refinement technique employed here; the reader is referred to [22] for more details. With this technique, we define at each time level $t^n$ a mesh triangulation ${\mathbb{T}}_h^n$ so that the solution is computed within a given accuracy employing the minimum possible number of degrees of freedom (mesh nodes).

As shown in Figure 2, an anisotropic element K can be defined by the semiaxes lengths ${\lambda }_{1,K}\ge {\lambda }_{2,K}$ of the circumscribed ellipse E, and by the corresponding orthogonal directions ${\mathbf{r}}_{1,K}$ and ${\mathbf{r}}_{2,K}$. The element size is $\left|K\right|=3\sqrt{3}/4{\lambda }_{1,K}{\lambda }_{2,K}$, and the aspect ratio is defined as $s_K={\lambda }_{1,K}/{\lambda }_{2,K}$. In order to employ an automatic mesh generator, we must define a metric tensor ${\mathbf{M}}_K$ such that

$${\mathbf{M}}_K={\left({\displaystyle \frac{|\widehat{K}|}{\left|K\right|}}\right)}^2{\mathbf{R}}_K{\mathbf{S}}_K^{-1}{\mathbf{R}}_K^T,$$

(28)

with ${\mathbf{R}}_K=\left\{{\mathbf{r}}_{1,K},{\mathbf{r}}_{2,K}\right\}$, ${\mathbf{S}}_K=\mathrm{diag}\left\{s_K,1/s_k\right\}$ and $|\widehat{K}|$ the size of the generated element when ${\mathbf{M}}_K$ is the unity tensor. The latter parameter depends on the specific mesh generator; in this work, we employ BAMG [25], for which $|\widehat{K}|=\sqrt{3}/4$.

The optimal orientation ${\mathbf{R}}_K^{*}$ and shape ${\mathbf{S}}_K^{*}$ of the element K can be computed from the Hessian matrix ${\mathbf{H}}_K$ of the solution $h_h^n$. More specifically, if $g_{i,K}$ are the eigenvalues (with $|g_{1,K}|<|g_{2,K}|$) and ${\mathbf{l}}_{i,K}$ are the corresponding eigenvectors, we obtain:

$$s_K^{*}={\left(|g_{2,K}|/|g_{1,K}|\right)}^{1/2},{\mathbf{r}}_{i,K}^{*}={\mathbf{l}}_{i,K},\mathrm{for}i=1,2.$$

(29)

Finally, the optimal size $\left|K^{*}\right|$ for each element K is computed so as to minimize the number of mesh elements under a condition of the form ${\eta }^n={\left({\sum }_K{\left({\eta }_K^n\right)}^2\right)}^{1/2}\le \mathrm{Tol}$, where ${\eta }_K$ is an estimation of the error on K. In particular,

$${\eta }_K^n={\left({\int }_K{\left[h^n-{\mathsf{\Pi }}_{h1}{h}^n\right]}^{2}d\mathrm{x}\right)}^{1/2},$$

(30)

with ${\mathsf{\Pi }}_{h1}{h}^n$ being the continuous, piecewise linear interpolation of $h^n$ at the mesh vertices, and

$$\left|K^{*}\right|=\left|K\right|{\left(\frac{{\mathrm{Tol}}^2}{{\displaystyle \sum _{K\in {\mathbb{T}}_h^n}{\left({\eta }_K^n\right)}^{1/2}}}\right)}^{1/3}{\left({\eta }_K^n\right)}^{-1/2}.$$

(31)

The variables $|K^{*}|$, ${\mathbf{R}}_K^{*}$, and ${\mathbf{S}}_K^{*}$ define a metric tensor ${\mathbf{M}}^{*}$ via Equation (28), which is sent to BAMG [25] to generate a new mesh ${\mathbb{T}}_h^{n*}$.

Hence, at each time level $t^n$, we have a solution computed on ${\mathbb{T}}_h^n$ with an estimated error ${\eta }^n$ and a new (more optimal) mesh ${\mathbb{T}}_h^{n*}$. If ${\eta }^n>\mathrm{Tol}$, we set ${\mathbb{T}}_h^n={\mathbb{T}}_h^{n*}$ and recompute the solution at $t^n$. Otherwise, we accept the solution at time $t_n$ and set ${\mathbb{T}}_h^{n+1}={\mathbb{T}}_h^{n*}$. In practice, if the time step size is moderate, the solution computed at $t^n$ is seldom rejected, and thus the CPU time does not increase substantially with the present local mesh adaptation algorithm.

Remark 4. 

It is not strictly necessary to adapt the mesh at each iteration. Indeed, some authors prefer to keep the mesh fixed until the time step is rejected because the space error is higher than the tolerance. However, we prefer to update the mesh at each time level in order to have a better tracking of the borders of the phase-change region. Furthermore, the number of rejected time steps is smaller if the mesh is updated at each time level.

4. Results

In this section, we show the results of several numerical experiments to address the performance of the present method. All the tests were carried out on an i7-8700 CPU computer with 16GB DDR3 RAM @1.3 GHz and Ubuntu 20.02.4 LTS operative system using C programming language.

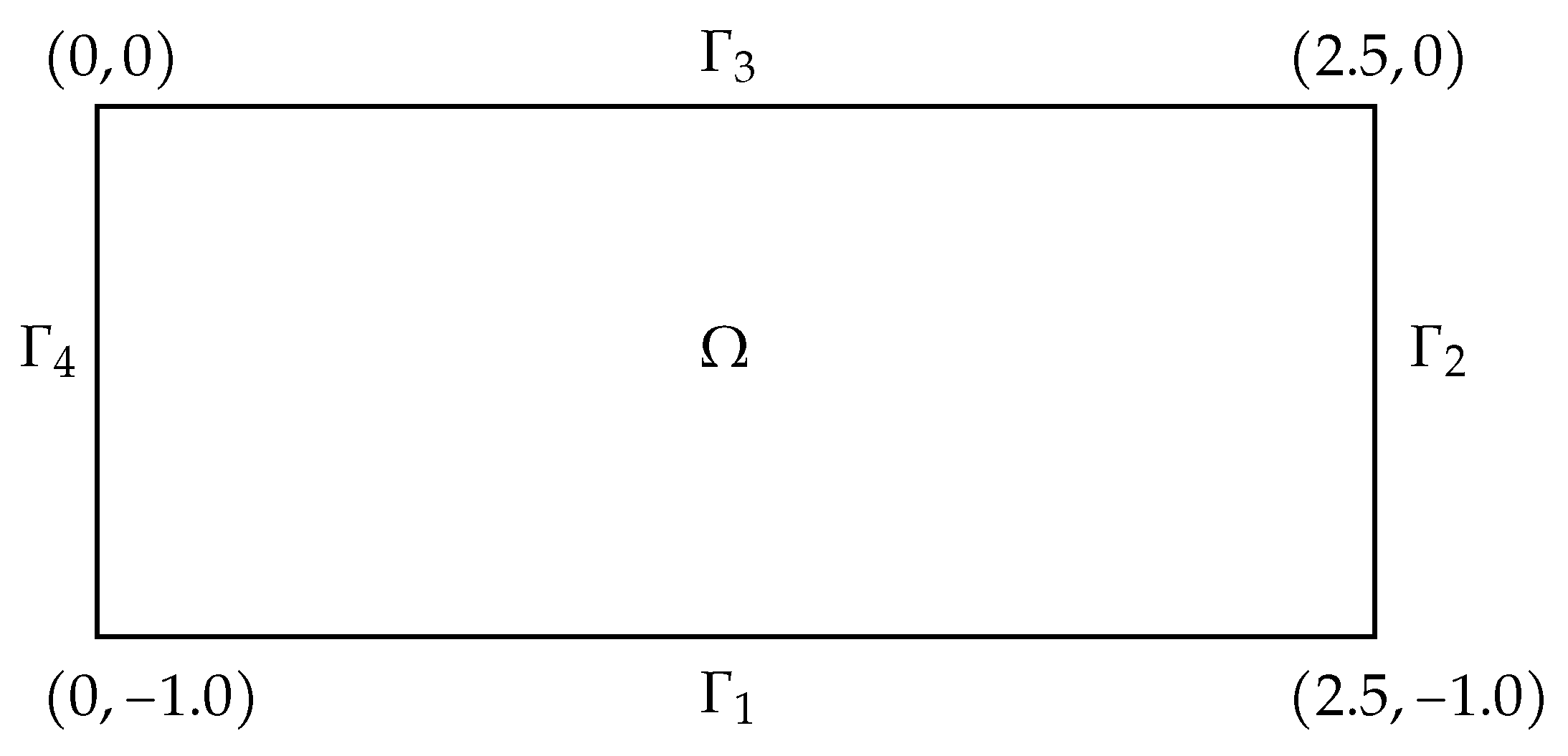
4.1. Test I: Convergence and Computational Cost Analysis

The first test is employed to verify that the numerical solution is correct and to analyze the convergence properties and the computational cost of the method. The test is defined by the domain ${[-1/2,1/2]}^2$, a heat source of the form

$$Q(\mathbf{x},t)={\displaystyle \frac{A}{t_0}}{e}^{-t/t_0}cos\left(\pi x_1\right)+{\displaystyle \frac{A{\pi }^2}{\mathrm{Pe}}}(1-e^{-t/t_0})cos\left(\pi x_1\right),$$

with $A=1.5$ and $t_0=0.5$, initial condition $h=0$, homogeneous Dirichlet conditions $h=0$ at $x_1=\pm 1/2$, homogeneous Neumann conditions $du/d{x}_2=0$ at $x_2=\pm 1/2$, and the dimensionless parameters

$$\mathrm{Ste}=0.5,\mathrm{Pe}=20,c_S/c_L=0.75,{\lambda }_S/{\lambda }_L=1.5.$$

Here, we employ the h-Newton solver.

We show in Appendix A that, for $t<t_m:=t_{0}ln(A/(A-1))\simeq 0.55$, the whole metal is in solid state and the solution is

$$h(\mathbf{x},t)=A\left(1-e^{-t/t_0}\right)cos\left(\pi x_1\right).$$

Furthermore, for $t\to +\infty$, the metal is at a steady state in which there exists (i) a pure solid region, defined by $|x_1|>x_{LS}:=arccos(1/A)/\pi$, where the solution is

$$h(\mathbf{x},t)=Acos\left(\pi x_1\right),$$

(32)

and (ii) a pure liquid region, defined by $|x_1|<x_{LS}$, where the solution is

$$h(\mathbf{x},t)={\displaystyle \frac{A}{\beta }}cos\left(\pi x_1\right)+1+{\displaystyle \frac{1}{\mathrm{Ste}}}-{\displaystyle \frac{1}{\beta }},$$

(33)

with $\beta =\left({\lambda }_L{c}_S\right)/\left({\lambda }_S{c}_L\right)$.

Figure 3 shows the numerical solution for several instants of time. As can be seen, the agreement with the theoretical solution at the fully solid state is very good. Then, a phase change appears and the solution evolves into a steady state solution. For large t, we see that the numerical solution agrees again very well with the theoretical steady state solution, not only for the values of the solution but also for the position of the phase front.

On the other hand, Figure 4 (left) shows the convergence of the $L^2$ error between the theoretical and numerical solution, $e_{L^2}$, with respect to the mesh size, defined as $\mathrm{h}:=\sqrt{\left|\mathsf{\Omega }\right|/\mathrm{NE}}$, with $\mathrm{NE}$ the number of elements. The error is evaluated at $t=0.5<t_m$, when the solution is smooth yet. Here, we use a uniform mesh and a time step $\Delta t=0.001$. As can be seen, we obtain the expected $\mathcal{O}\left({\mathrm{h}}^3\right)$ convergence rate.

Similarly, Figure 4 (right) illustrates the dependence of the $L^2$ error on the time step. Here, we set a space tolerance $\mathrm{Tol}=0.1$. We can verify that the expected $\mathcal{O}(\Delta t^2)$ convergence rate is achieved.

Finally, Figure 5 shows the evolution of the number of elements and of the accumulated CPU time with respect to the solved instant of time t. Here, we employ different mesh adaptation tolerances and a time step $\Delta t=0.001$. As can be seen, the number of elements increases slowly since $t=0$. At $t=t_m$, melting starts to take place and the number of elements starts to increase more quickly. Finally, for $t\gtrsim 1.3$, the evolution of the phase front is more stable and the number of elements remains constant. Since the number of elements increases until $t\gtrsim 1.3$, so does the time needed to solve each instant of time. We can verify this point by observing the slope of the curve of the accumulated CPU time.

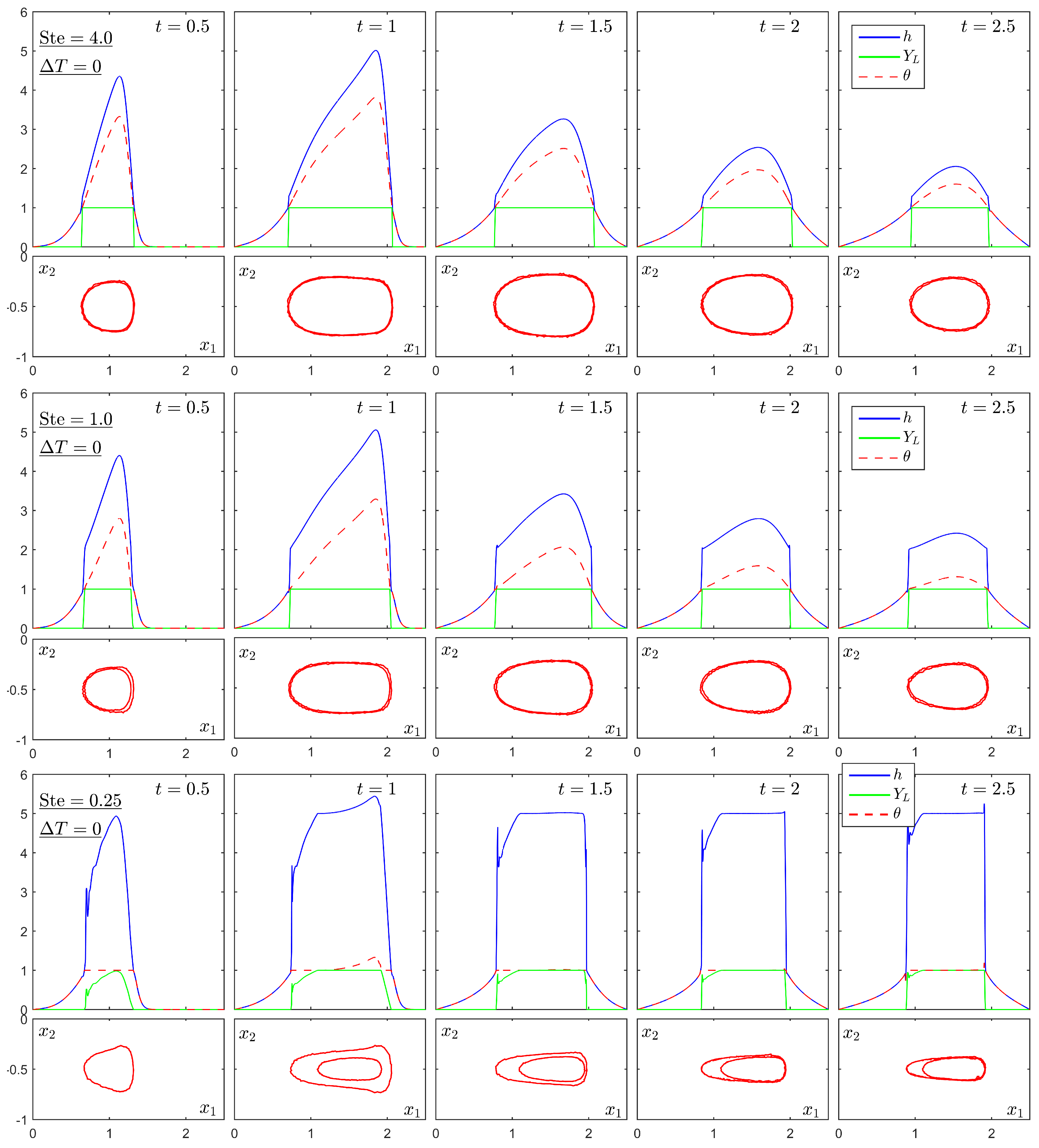
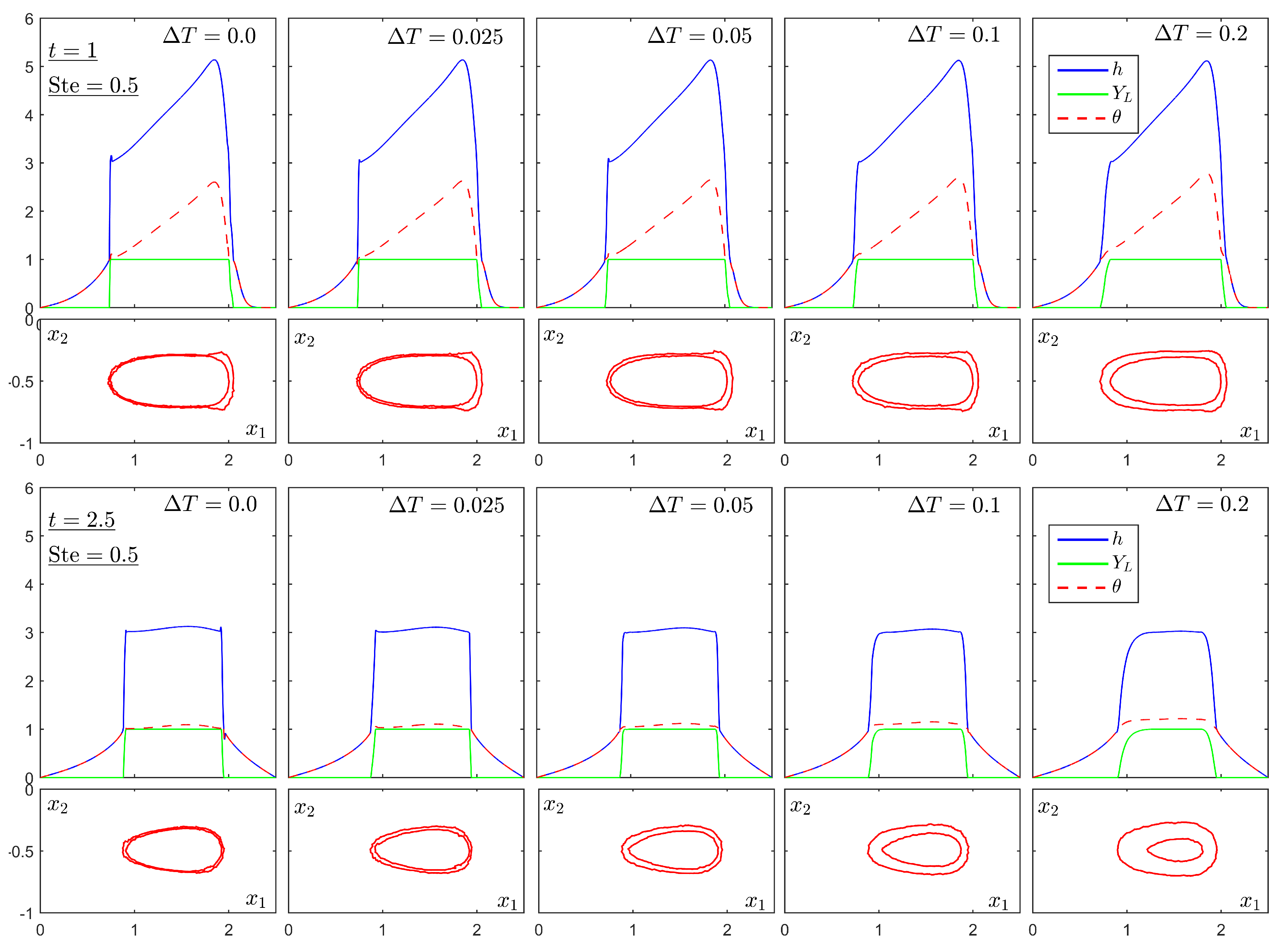
4.2. Test II: Gaussian-Type Heat Source

To evaluate the two numerical strategies (the $\theta$-Newton method or the h-Newton method, depending on the considered unknown) in the resolution of the welding problem, we present an example defined by the rectangular domain $\mathsf{\Omega }=[0,2.5]\times [-1,0]$, with boundary $\partial \mathsf{\Omega }\equiv {\mathsf{\Gamma }}_1\cup {\mathsf{\Gamma }}_2\cup {\mathsf{\Gamma }}_3\cup {\mathsf{\Gamma }}_4$, as can be seen in Figure 6. We consider an initial condition $\theta =0$, Dirichlet boundary conditions on ${\mathsf{\Gamma }}_D\equiv {\mathsf{\Gamma }}_1\cup {\mathsf{\Gamma }}_2\cup {\mathsf{\Gamma }}_4$, where the temperature is set to the ambient one, and a Robin condition on ${\mathsf{\Gamma }}_R\equiv {\mathsf{\Gamma }}_3$, where there is a loss of heat by convection; recall Equations (13)–(15). The numerical integration will take place for $0\le t\le 2.5$ with $\Delta t=0.01$.

With the heat source Q, we take a Gaussian-type function moving from left to right at a constant velocity $v^0$. Furthermore, to obtain more valuable information on the physical process under study, we consider that the heat source only acts up to the instant $t=1.0$ so as to analyze the behavior of the system with ($0<t\le 1$) and without ($1<t\le 2.5$) a heat source:

$$Q(x_1,x_2,t)=\left\{\begin{array}{cc}{\displaystyle Q^{0}exp\left(-100{\left(x_1-\left(x_1^0+v^{0}t\right)\right)}^2-25{\left(x_2-x_2^0\right)}^2\right)\left(1-e^{-5t}\right),}\hfill & 0\le t\le 1,\hfill \\ \\ {\displaystyle 0,}\hfill & 1<t\le 2.5,\hfill \end{array}\right.$$

(34)

with $Q^0=50.0$, $v^0=1.5$, $x_1^0=0.5$, and $x_2^0=-0.5$.

Finally, the values of dimensionless parameters are computed from the physical magnitudes of [8,9]:

$$\mathrm{Pe}=20,\mathrm{Nu}=10,c_S/c_L=0.75,{\lambda }_S/{\lambda }_L=1.5.$$

(35)

Figure 7 shows the solution for different values of the Stefan number at three different instants of time. Here, we employ isothermal melting model (3). The upper panels represent the thermodynamic variables (enthalpy h, temperature $\theta$, and mass fraction of liquid $Y_L$) at the line $x_2=-0.5$, whereas the bottom panels show the border between the pure solid and pure liquid zones ($Y_L=0$ and $Y_L=1$, respectively).

As can be seen in the Figure 7, the mushy region is negligible when the Stefan number is large. However, as the latter decreases, the mushy region becomes more relevant and the method must be more accurate to capture it. This is due to the fact that a smaller Stefan number implies a larger $h_L-h_S$; i.e., more energy is needed for the phase change. As a consequence, for the same heat source and the same time level—i.e., same energy transferred to the material—the proportion of the material that is yet in phase change state is larger. In all cases, after the heat source goes out at $t=1$, the mushy region tends to disappear and the transition between solid and liquid becomes a discontinuity for the enthalpy variable. At the discontinuity, the material is at the melting temperature, so the jump in the enthalpy equals $h_L-h_S=1/\mathrm{Ste}$, as can be verified in the figure.

Furthermore, Figure 8 shows the evolution of the mesh for the case $\mathrm{Ste}=0.25$ considered before. We can see that, due to the use of anisotropic mesh adaptation techniques, the elements are refined at the border of the mushy region, which is the region at which the variations in the solution are more noticeable, and also that they are aligned with the latter.

On the other hand, Figure 9 considers a fixed Stefan number $\mathrm{Ste}=0.5$ and non-isothermal melting model (4) with different values for the temperature width $\Delta T$. We can see that, as $\Delta T$ increases, the solution smooths out (especially in the enthalpy variable h and liquid mass fraction $Y_L$) and the mushy region becomes larger. This is to be expected since, for a continuous temperature field, it is impossible to have a discontinuity in the enthalpy with the non-isothermal melting model. Indeed, for the same range of temperatures, the variation in the enthalpy is less abrupt for larger $\Delta T$, hence the fact that the enthalpy smooths out with this parameter. Moreover, when the heat source is not applied (i.e., from $t=1$ to $t=2.5$), the size of the mushy region increases, something that is opposite to the physics of the problem for $\Delta T=0$, shown in Figure 7, where an abrupt transition between the solid and liquid zone tends to appear when time goes on. Apart from the physical insights of the results, we are interested in proving that solving for the enthalpy (i.e., the h-Newton method) is more robust than solving for the temperature (i.e., the $\theta$-method). For that purpose, Figure 10 shows a convergence study of the $\theta$-method for different values of $\mathrm{Ste}$, $\Delta t$, and $\Delta T$. More specifically, it shows for which cases the $\theta$-method is able to obtain a solution and for which ones it fails. It is interesting to see that, for sufficiently large melting temperature width $\Delta T$, the method converges irrespective of the time step. This threshold $\Delta T$ increases with $1/\mathrm{Ste}$, i.e., with the enthalpy variation between liquid and solid states. For smaller $\Delta T$, the time step $\Delta t$ has to be sufficiently small; otherwise, the method fails to converge. It seems that the maximum $\Delta t$ is approximately proportional to $\Delta T$. Hence, for this particular problem and boundary conditions, the convergence criterion for the $\theta$-method can be summarized as

$$\Delta T\gtrsim min\left({\displaystyle \frac{1}{3\mathrm{Ste}}},10\Delta t\right).$$

(36)

For other problems, we may expect to find a qualitatively similar convergence criterion.

Conversely, the h-Newton converged for all the cases shown in Figure 10. This proves numerically that solving for the enthalpy is more robust than solving for the temperature. This a consequence of the fact that relations (18) are ill-conditioned for temperatures close to the melting range, in the sense that small variations in $\theta$ may cause large variations in the enthalpy, and, hence, convergence is more difficult. The slope of the curve $h\left(\theta \right)$ at the melting temperature range is proportional to $1/(\Delta T\mathrm{Ste})$, and, thus, convergence is more difficult when $\Delta T$ and/or $\mathrm{Ste}$ are smaller, as can be verified in the figure. On the contrary, relations (19) are always well conditioned irrespective of $\Delta T$ and $1/\mathrm{Ste}$, making convergence much easier when solving for the enthalpy.

Finally, it must be pointed out that, although there are some spurious oscillations, the discontinuities in the solutions shown in previous figures are well captured without the need of any kind of artificial viscosity.

5. Conclusions

This paper presents a novel finite element method to solve the thermal variables in welding problems. For this purpose, we start from the enthalpy formulation of the energy conservation equation, which is valid at the whole domain and allows to implicitly track the phase interfaces through the enthalpy variable. Both isothermal and non-isothermal melting models are considered as constitutive equations. The energy equation is discretized with quadratic polynomials in space and a BDF2 formula in time, which is more accurate than the first-order schemes employed by previous works in the literature. Local anisotropic mesh adaptation is also considered. The non-linear discretized equations are solved with a Newton method in two ways: (i) considering the temperature as the main unknown ($\theta$-Newton method), as in most papers, and (ii) considering the enthalpy as the main unknown (h-Newton method).

The above-mentioned h-Newton is the main novelty of this work. It allows to consider both isothermal and non-isothermal melting models, it is more simple to implement than other enthalpy-based methods, such as [16,17,18], and it is more robust than the usual temperature-based methods. Indeed, numerical experiments show that the h-Newton method converges to the solution in all the cases considered in our numerical experiments. However, the temperature-based $\theta$-Newton method works only for non-isothermal melting and fails unless the time step is sufficiently small or the melting temperature range $\Delta T$ is sufficiently large. Hence, we prove numerically that considering the enthalpy as the main unknown is a much better choice from the numerical point of view.

Numerical experiments also show that the method converges as expected with the mesh and time step sizes, and that the method is able to adequately capture the discontinuities or sharp variations in the enthalpy and liquid mass fraction without the use of any kind of numerical dissipation.