Abstract
Role-based access control (RBAC) is a widely adopted security model that provides a flexible and scalable approach for managing permissions in various domains. One of the critical challenges in RBAC is the efficient assignment of roles to users while minimizing the number of roles involved. This article presents a novel role minimization optimization algorithm (RMOA) based on the concept lattice factor to address this challenge. The proposed RMOA leverages the concept lattice, a mathematical structure derived from formal concept analysis, to model and analyze the relationships between roles, permissions, and users in an RBAC system. By representing the RBAC system as a concept lattice, the algorithm captures the inherent hierarchy and dependencies among roles and identifies the optimal role assignment configuration. The RMOA operates in two phases: the first phase focuses on constructing the concept lattice from the RBAC system’s role–permission–user relations, while the second phase performs an optimization process to minimize the number of roles required for the access control. It determines the concept lattice factor using the concept lattice interval to discover the minimum set of roles. The optimization process considers both the user–role assignments and the permission–role assignments, ensuring that access requirements are met while reducing role proliferation. Experimental evaluations conducted on diverse RBAC datasets demonstrate the effectiveness of the proposed algorithm. The RMOA achieves significant reductions in the number of roles compared to existing role minimization approaches, while preserving the required access permissions for users. The algorithm’s efficiency is also validated by its ability to handle large-scale RBAC systems within reasonable computational time.
MSC:
68T30; 68T09
1. Introduction
Role-based access control (RBAC) is a widely used security model that provides a structured approach to managing permissions in various domains [1]. In RBAC systems, users are assigned roles, and roles are associated with specific permissions. However, one of the major challenges in RBAC is the efficient assignment of roles to users while minimizing the number of roles (the role mining problem (RMP)) involved.
The proliferation of roles in an RBAC system can lead to administrative complexities, increased maintenance efforts, and potential security vulnerabilities. Therefore, there is a need for effective algorithms that can optimize the role assignment process, reducing the number of roles while ensuring that access requirements are met.
The research field of role minimization optimization algorithms based on the concept lattice factor is still relatively limited but growing. The concept of role minimization in RBAC systems has garnered attention due to the challenges posed by role proliferation and its impact on system complexity and security.
Several studies have explored different approaches for role minimization in RBAC systems [2]. Traditional methods often rely on heuristics, graph-based algorithms, or mathematical optimization techniques. However, these approaches may face limitations in terms of computational complexity, scalability, and the ability to handle large-scale RBAC systems.
The introduction of the concept lattice factor as a basis for role minimization algorithms has opened up new possibilities for more efficient and effective solutions. The concept lattice, derived from formal concept analysis, provides a structured framework to capture the relationships between roles, permissions, and users [3]. By leveraging the concept lattice factor, we aim to develop algorithms that can exploit the inherent hierarchy and dependencies among roles to minimize their number.
2. Related Work
Krra et al. [4] summarized and categorized many methods in recent years to approximate the optimal solutions for role generation and role allocation in access control systems, such as role mining, dynamic user–role assignments, and role refinement.
Role mining was first proposed based on initial clustering of users who were assigned the same privileges [5]. Basic-RMP [6] finds the fewest set of roles from the user rights assignments and provides the user with the role assignments along with the permissions.
Role mining algorithms partially automate the construction of an RBAC policy from an ACL (access control lists) policy and possibly other information, reducing the cost of migration to RBAC [7]. Xu and Stoller [8] proposed algorithms for role mining. The algorithms can easily be used to optimize a variety of policy quality metrics, including metrics based on policy size, metrics based on interpretability of the roles with respect to user attribute data, and compound metrics that consider size and interpretability.
The researchers found that obtaining a workable set of roles to optimize user access mapping to the role mining problem (RMP) is the well-known (NP-hard) problem. Polynomial time approximation algorithms such as greedy and random methods can be used to obtain a feasible set roles. For example, Basic-RMP maps to minimal tiling problems [6] (where each tile corresponds to a role), minimal biclique coverage [9] (where each role corresponds to biclique), and set cover problems [10] (where each subset corresponds to a role). In edge-RMP [11], work has been carried out to minimize the administrative burden by optimizing user–role and permission–role assignments. Since Basic-RMP and Edge RMP prove to be NP hard, a greedy and approximate algorithm is proposed to optimize the edges (i.e., user–role assignments (UR) and permission–role assignments (PR)) in RBAC. Ene et al. [12] also introduced fast graph reductions that allow recovery of the solution from the solution to a problem on a smaller input graph.
An unsupervised role mining method called fast miner [13] is based on permission set enumeration of predefined constraints. The Simple Role Mining Algorithm [14] is a heuristic-based solution for approximating the best set of characters. The user with the fewest privileges will be the initial entry for the role set. This process of selecting the minimum number of permissions is carried out gradually after the individual user’s tasks are completed. It maintains subsequent updates to the role set by eliminating roles acquired as a federation of other roles that have been inserted into the role set. Li et al. [15] used operations and resources of permissions as the functional information in role mining algorithm, role mining with functional features (FMiner), to reduce composite roles. The HP Role Minimization Algorithm [7] and Weighted Structure Complexity Optimization [16] are exact variants of RMP because the set of roles is highly compatible with the permissions assigned to users. The process of mining roles is also included in the RBAC extension model, such as Temporary RBAC and Generalized Temporary RBAC. This is known as Temporal RMP [17]. Here, role assignments to users and permissions are enabled only for a set of time intervals. In the constrained role miner [18], the proposed role mining algorithm conforms to various constraints to optimize the role assignment to users and permissions.
When the only information is user–permission relation, roles are discovered whose semantic meaning is based on formal concept lattices [19]. They argue that the theory of formal concept analysis provides a solid theoretical foundation for mining roles from user permission relation. A dyadic formal context from the triadic security context represents role-based access permission and performs attribute exploration from formal concept analysis (FCA) [20,21]. An FCA construction, by introducing the enrichment of an incidence relation by a set of intervals in a formal context, investigated the approach for lattice-generating interval relations on the context side [22].
The existing algorithms mainly group permissions or users, but for role mining, both users and permissions need to be grouped, so it is necessary to find more effective methods for role mining.
3. Preliminaries
RBAC is an access control model that organizes user permissions based on roles. It simplifies access control management by grouping users with similar access requirements into roles, and then assigning permissions to those roles.
In this paper, we follow the basic definitions in NIST standard, which is the most widely known formal description of the RBAC model.
The RBAC model contains the following components:
User: An individual or entity that interacts with the system and requires access to resources. Users are assigned roles that define their access rights.
Role: A defined set of permissions that represents a specific job function, responsibility, or level of authority within an organization. Roles are associated with users to determine their access privileges.
Permission: The rights or actions that users are authorized to perform on resources. Permissions are assigned to roles and determine what actions users can take within the system.
User–Role Assignment: The process of associating users with roles based on their job responsibilities, functions, or other attributes. User–role assignments define the roles that each user is authorized to fulfill.
Role–Permission Assignment: The process of associating permissions with roles. Role–permission assignments specify the actions that users in a particular role are authorized to perform on resources [23].
The following definitions formalize the above discussion.
U, R, P (users, roles, and permissions).
UR ⊂ U × R: a many-to-many user to role assignment relation.
RP ⊂ R × P: a many-to-many role to permission assignment relation.
UP ⊂ U × P: a many-to-many users to permission assignment relation.
Pers (r) = {p ∈ P|(r, P) ∈ RP}: the permission set owned by role r.
PERS (R) = {p ∈ P|r∈R, (r, P) ∈ RP}: the permission set owned by the role set R.
Given m users, n permissions, and k roles, the user–role mapping can be represented as an m × k Boolean matrix, where aij in cell ij indicates the assignment of role j to user i. Similarly, the role–permission mapping can be represented as a k × n Boolean matrix, where a 1 in cell ij indicates the assignment of permission j to role i. Finally, the user–permission mapping can be represented as an m × n Boolean matrix, where aij in cell ij indicates the assignment of permission j to user i.
Definition 1.
Role Mining Problem: Given an m × n access control matrix, UP is decomposed into sizes of m × k and k × n two matrices UR and RP, and k is the smallest among all possible matrix decompositions.
Definition 2.
A formal context or a dyadic context K is a triple (X, Y, I), where X, called the universe of discourse, is a nonempty and finite set of objects, Y is a nonempty finite set of attributes, and I ⊆ X × Y is a binary relation between X and Y.
Definition 3.
For a formal context K, operators ↑: 2X→2Y and ↓: 2Y→2X are defined for every A ⊆ X and B ⊆ Y by A↑ = {y ∈ Y/ for each x ∈ A:<x,y> ∈ I} and B↓ = {x ∈ X/ for each y ∈ B:<x,y>I}. The operators ↑ and ↓ are known as concept-forming operators.
Definition 4.
A formal concept of the context K = (X, Y, I) is a pair (A, B) of A ⊆ X and B ⊆ Y, such that A↑ = B and B↓ = A.
We call A extent and B intent of the concept (A, B). Formal concepts are naturally ordered by partial order “≤” using a subconcept–superconcept relation, such that, for any two formal concepts (A1, B1) and (A2, B2), (A1, B1) ≤ (A2, B2) if and only if A1 ⊆ A2 and B2 ⊆ B1. The objects and attributes are dual in nature, which forms a Galois connection. This connection exhibits closure relation among objects and attributes such that, from any set of formal objects, one can identify all the attributes that they have in common.
Definition 5.
The collection of all formal concepts of the context K = (X, Y, I) equipped with subconcept–superconcept partial ordering ≤ is called a concept lattice L(K).
According to the definitions of RBAC, a formal context K = (U, P, IA) corresponds to an access control matrix, where U is the user set, P is the permission set, and IA represents UP. For u ∈ U, p ∈ P, (u, p) ∈ IA, it indicates that user u has permission p. Therefore, Table 1 can be used to represent the formal context under the RBAC model.

Table 1.
An example of RBAC formal context.
4. Proposed Methodology
On the concept lattice, since all possible roles can be mined and the concepts and roles correspond one-to-one, the problem of solving the minimum set of roles on the access control matrix UP in the role mining problem can be equivalent to solving the minimum set of role concepts generated by the concept lattice.
Definition 6.
Minimum Role Concept Set: Let K = (U, P, IA), and Sm be a set of concepts in the concept lattice L(K) generated by the formal context. If Sm satisfies the following two conditions, it is called the minimum role concept set on the access control context K.
Condition 1: The permissions owned by each user in the access control context K can be represented by the union of the intents of several concepts in the concept set Sm.
Condition 2 The number of concepts in the concept set Sm is the smallest.
In the following discussion, we will no longer distinguish between the general formal context and the access control context, and both will be represented by K.
Definition 7.
For formal concepts (A1, B1),(A2, B2) ∈ L(K), the subset [(A1, B1),(A2, B2)] = {(A, B) ∈ L(K)|(A1, B1) ≤ (A, B) ≤ (A2, B2)} is called the interval in L(K) bounded by (A1, B1) and (A2, B2).
Furthermore, for A ⊆ X and B ⊆ Y, let γ(A) = (A↑↓, A↑) and μ(B) = (B↓, B↓↑), i.e., γ(A) and μ(B) are the least formal concept in L(K) whose extent includes A and the greatest one whose intent includes B. γ({i}) and μ({j}), denoted simply by γ(i) and μ(j), are called the object and attribute concept determined by i ∈ X and j ∈ Y, respectively. We denote [A, B] = [γ(A),μ(B)]. Clearly, every interval in L(K) is of this form. Of particular importance are the intervals of the form Iij = [γ(i),μ(j)].
Definition 8.
Assuming that the concept lattice L(K) with formal context K = (X, Y, I) has an interval set E = {e1, e2, …, en}, then the factor of L(K) is a subset G = {(A, B)|A ⊆ X, B ⊆ Y}, where (A, B) ∈ L(K) is a formal concept. For any (A, B), (A’, B’) ∈ L(K), (A, B) ∈ ei, (A’, B’) ∈ ej that satisfies ei ⊆ ej, then (A, B) must be a formal concept in G.
Theorem 1.
If the concept lattice interval Iij is nonempty and is minimal with respect to ⊆, then Iij is the concept lattice factor.
Proof.
Note that Iij ⊆ Ii′j′ iff γ(i) ≤ γ(i′) and μ(j) ≤ μ(j′) iff {i}↑ ⊆ {i′}↑ and {j}↓ ⊆ {j′}↓ and that a nonempty Iij is minimal with respect to ⊆ if it does not contain any other Ii′j′, i.e., Iij = Ii′j′ whenever Iij ⊆ Ii′j′ for every I′, j′. □
Theorem 2.
In the formal context K = (U, P, IA), the concept lattice factor is the minimum role concept set.
Proof.
We prove that the concept lattice factor satisfies two conditions for the minimum role concept set. (1) According to definition 8, concept lattice factors are concepts included in the minimum interval, so all concepts in context K = (U, P, IA) can be represented by their union of the intents; (2) According to Theorem 1, the concept lattice factor, which is minimal with respect to ⊆, satisfies Condition 2. □
Theorem 1 and Theorem 2 indicate that the optimal set of roles can be determined by determining the concept lattice factor in context K = (U, P, IA).
We can first calculate all intervals of the context K = (U, P, IA) using the algorithm (Algorithm 1) in reference [24].
| Algorithm 1 ComputeIntervals [24]. |
| Input: Boolean matrix IA |
| Output: Set G ⊆ (𝓔(IA)) |
| 1 𝓔 ← 𝓔(IA); U ← {(i,j)|𝓔ij = 1}; G ← while U ≠ ∅ do |
| 2 D ← ∅; s ← 0 |
| 3 while exists jD with |((D∪{j})↓𝓔)↑IA↓IA×((D∪{j})↓𝓔↑𝓔)↓IA↑IA ∩ U|>s do |
| 4 select j which maximizes |((D∪{j})↓𝓔)↑I↓I×((D∪{j})↓𝓔↑𝓔)↓I↑I ∩ U| |
| 5 D ← (D∪{j})↓𝓔↑𝓔; C ← (D∪{j})↓𝓔 |
| 6 s ← |C↑I↓I×D↓I↑I ∩ U| |
| 7 end |
| 8 add (C, D) to G |
| 9 U ← U − C↑I↓I × D↓I↑I |
| 10 end |
| 11 return G |
For IA ∈ {0,1}n×m, we denote by 𝓔(IA) the n × m Boolean matrix given by (𝓔(IA))ij = 1 iff IAij is nonempty and minimal with respect to ⊆. G is a collection of possibly overlapping groups of essential 1s, i.e., 1s in 𝓔(IA).
The concept lattice interval is actually a set of several formal concepts, so we can use a double loop to check whether each set si is a subset of other sets sj in G = {s1 si, sj, sn}. If so, then si is not the set we are looking for; otherwise, si may be the set we are looking for. Then, for each possible set si, we need to check if it is a subset of other sets. If si is a subset of other sets, then it is not the set we are looking for; otherwise, si may be one of the sets we are looking for. Finally, for each possible set si, we need to check whether it is the smallest set, that is, whether there is a set smaller than si that can also be a subset of other sets.
Specifically, the algorithm can be implemented as follows (Algorithm 2):
| Algorithm 2 Finding the minimum role concept set algorithm. |
| Input: Concept lattice interval G |
| Output: Minimum role concept set Rs |
| 1. Initialize an empty collection result Rs, representing the final result set. |
| 2. is_ subset = 0 //Initialize a Boolean variable is_ subset is false, indicating whether si is a subset of other sets. |
| 3. For each set sj and si, proceed as follows: |
| 4. If i = j, skip this loop. |
| 5. If si ⊆ sj, |
| 6. Then set is_ subset = 1 |
| 7. jumps out of the loop. |
| 8. If si is not a subset of any set |
| 9. then si is added to the result set result Rs. |
| 10. For each set si and sj, proceed as follows: |
| 11. is_minimal = 1 //Initialize a Boolean variable is_minimal is true, indicating whether si is the minimum set. |
| 12. If i = j, skip this loop. |
| 13. If si ⊆ sj |
| 14. then is_minimal = 0 |
| 15. exit the loop. |
| 16. If si is the smallest set, add si to the result set result Rs. |
| 17. Returns the result set result Rs. |
5. An Illustrative Example
To demonstrate the effectiveness of our algorithm, we used the example electronic medical record system in reference [25] as a context instance for role mining and semantic assignment, thereby generating role states with semantic meaning and hierarchical structure.
In this example, user positions are divided into two categories: ordinary positions and management positions. Ordinary positions include registrar (1), surgeon (2), physician (3), gynecologist (4), nurse (5), and pharmacist (6). The management positions include surgical director (7), internal medicine director (8), gynecological director (9), medical department head (10), chief nurse (11), pharmacy director (12), and dean (13). Based on the reading and writing of information in various scenarios and authorized operations for various functions, the permissions used in the system are listed as follows: reading patient basic information (a), writing patient basic information (b), reading hospitalization information (c), writing hospitalization information (d), reading history records (e), reading diagnostic information (f), reading prescriptions (g), reading nurse reports (h), writing internal medicine history records (i), writing surgical history records (j), writing gynecological history records (k), writing internal medicine diagnostic information (l) Write surgical diagnosis information (m), gynecological diagnosis information (n), internal medicine prescription (o), surgical prescription (p), gynecological prescription (q), nurse report (r), physician authorization (s), surgeon authorization (t), gynecologist authorization (u), pharmacist authorization (v), nurse authorization (w). The attributes used in the department and functional information system are as follows: internal medicine (A), surgery (B), gynecology (C), medication (D), registration (E), diagnosis (F), nursing (G), and director (H). The entire system has 13 types of users, 23 types of permissions, and 8 types of attributes. The corresponding relationship between each type of user and permissions is listed in Table 2, and the attributes owned by each type of user are listed in Table 3.

Table 2.
User–permission relationship.

Table 3.
User–attribute relationship.
Step 1: Construct a user permission concept lattice based on the user permission relationships provided in Table 2, mapping it to candidate role states, as shown in Figure 1.
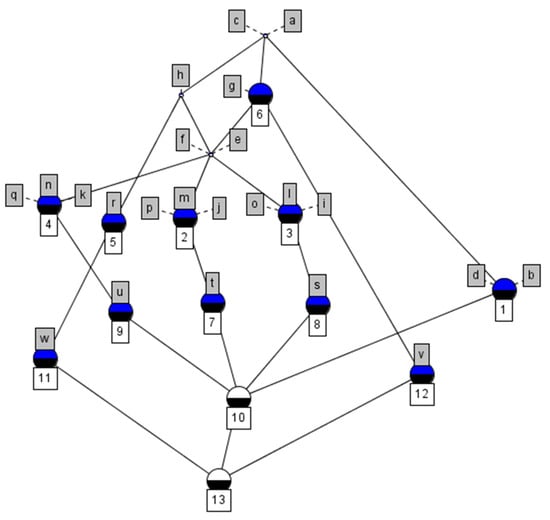
Figure 1.
The corresponding role concept lattice in Table 2.
Step 2: Determine Iji based on aij = 1 and use the algorithm to determine the concept lattice factor. Establish a correspondence between concepts and reduced concepts to obtain the candidate role states for reduction, as shown in Figure 2.
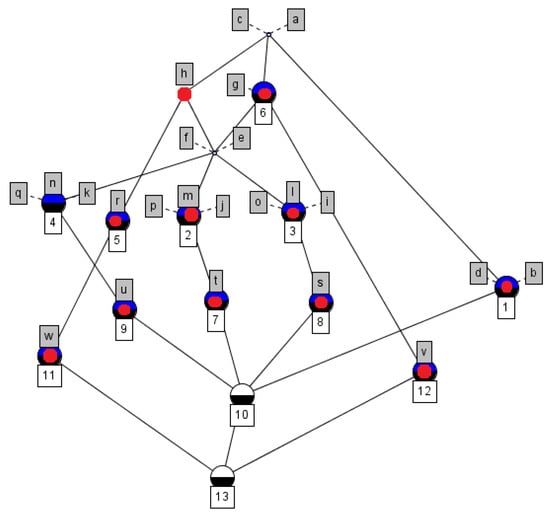
Figure 2.
The corresponding role concept lattice factor (nodes marked in red) in Table 2.
For example, s3i = I3i = [({3,8,10,13},{a,c,e,f,g,h,i,l,o})], s3e = I3e = [({3,8,10,13},{a,c,e,f,g,h,i,l,o}), ({2,3,7,8,9,10,13},{a,c,e,f,g,h})], s3i ⊆ s3e, s3i is a concept lattice factor. All concept lattice factors are marked in red in Figure 2.
Step 3: Generate a user attribute concept set based on the user attribute relationships provided in Table 3, and sort the generated concept set based on the number of users and permissions to obtain an ordered user attribute concept set.
Step 4: In the concept set, for the extension of the corresponding concept for each role, search for its closest expression in order from top to bottom, and assign semantic meaning to each role.
Figure 3 and Figure 4 show the original and minimum roles of the electronic medical record system, respectively.
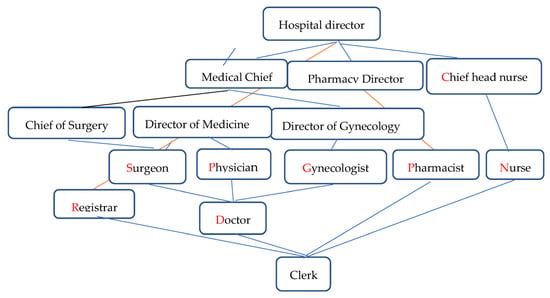
Figure 3.
Original position of the electronic medical record system.
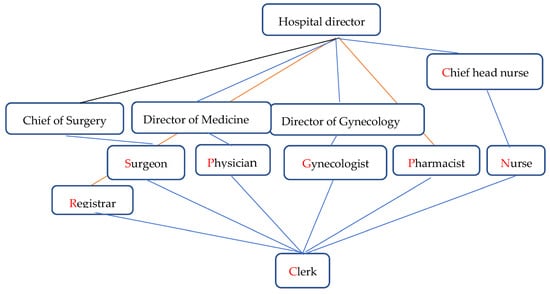
Figure 4.
Minimum role concept lattice of the electronic medical record system.
The role structure mining algorithm in this article has a simple hierarchy and requires fewer allocation relationships to be added. At the same time, the algorithm in this article uses the nearest neighbor expression of user attributes to assign semantic meaning to roles, which is more accurate than assigning semantic meaning to roles based on their permissions, user functions in the system, and actual positions in reference [25].
6. Experimental Results
We conducted an experimental study to evaluate our proposed method. The ideal method for evaluating the accuracy of role mining is to use real-world user permission data. However, obtaining such data is extremely difficult, especially those containing complete RBAC states. Therefore, most role mining algorithms use synthesized user permission data as input for evaluation [26]. Similarly, we prepared our input dataset based on the template in reference [27].
To evaluate the performance of our algorithm, we implement the algorithm by Java and run the program on the synthetic dataset. Our experimental platform is a personnel computer with an Intel(R) Core(TM) i5 CPU and 16 GB memory.
In this study, we conducted experiments and analysis on five different datasets, as shown in Table 4. We used the program shown in Algorithm 3 [28] to prepare the dataset. Firstly, we defined a set of roles based on the above template. Then we created multiple users and randomly assigned them to each role, specifying the maximum number of users for any given role. Then, we set user–permissions based on the roles assigned to each user in the study.
| Algorithm 3 Data preparation algorithm. |
| Input: 𝑅 ← 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜 𝑓 𝑟𝑜𝑙𝑒𝑠; |
| 𝑈 ← 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜 𝑓 𝑢𝑠𝑒𝑟𝑠; |
| 𝑃 ← 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜 𝑓 𝑝𝑒𝑟𝑚𝑖𝑠𝑠𝑖𝑜𝑛𝑠; |
| 𝑈 𝑅 ← 𝑖𝑛𝑖𝑡𝑖𝑎𝑙𝑖𝑧𝑒 𝑎𝑡 𝑧𝑒𝑟𝑜; |
| 𝑅𝑃 ← 𝑖𝑛𝑖𝑡𝑖𝑎𝑙𝑖𝑧𝑒 𝑎𝑐𝑐𝑜𝑟𝑑𝑖𝑛𝑔 𝑡𝑜 𝑡h𝑒 𝑡𝑒𝑚𝑝𝑙𝑎𝑡𝑒; |
| Output: Dataset |
| 1. 𝑛𝑢𝑚𝑏𝑒𝑟𝑈 𝑠𝑒𝑟𝑠𝑃𝑒𝑟𝑅𝑜𝑙𝑒 ← 𝐷𝑖𝑠𝑡𝐹𝑢𝑛𝑐𝑡𝑖𝑜𝑛(𝑈, 𝑅); |
| 2. for 𝑘 ← 1 to 𝑅 do |
| 3. 𝑛𝑢𝑚𝑏𝑒𝑟𝑈𝑠𝑒𝑟𝑠 ← 𝑛𝑢𝑚𝑏𝑒𝑟𝑈𝑠𝑒𝑟𝑠𝑃𝑒𝑟𝑅𝑜𝑙𝑒 [𝑘]; |
| 4. for 𝑖 ← 1 to 𝑛𝑢𝑚𝑏𝑒𝑟𝑈𝑠𝑒𝑟𝑠 do |
| 5. 𝑢𝑠𝑒𝑟 ← 𝑅𝑎𝑛𝑑 (𝑈); |
| 6. 𝑈𝑅𝑢𝑠𝑒𝑟,𝑘 ← 1; |
| 7. end for |
| 8. end for |

Table 4.
Synthesized user permission data.
Our goal is to achieve a 100% reconstruction rate. Figure 5 illustrates the number of original roles used for preparing the datasets against the number of extracted roles. The number of original roles and extracted roles are indicated by red and blue bars, respectively. Notably, the number of extracted roles among different datasets is close to the number of original roles, indicating that our approach is very close to the optimal solution. More specifically, the number of extracted roles is identical to the number of original roles for Dataset1, i.e., the small-scale dataset. For large datasets, the number of extracted roles is slightly lower than the original number. This is because the concept lattice factor completely eliminates concepts that can be a union of the intents.
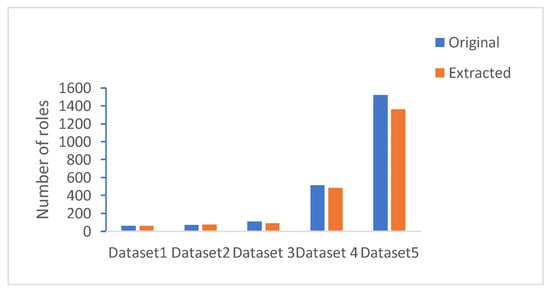
Figure 5.
Comparison between original roles and extracted roles.
Time Complexity
Consider first Algorithm 1. It first computes 𝓔(IA), which may be performed in time O(n2m2), since it suffices to repeat for every of the nm entries of IA the test and since the test may be performed in time O(nm). Inside this loop, the most critical is the number of executions of the innermost cycle. The most expensive in that cycle is computing ((D∪{j})↓𝓔 ↑𝓔)↓IA↑IA, which takes time O(nm). The outer cycles proceed at most m times since no more than m attributes may eventually be added when extending the rectangle under construction. Within the jth execution of the outer cycle, the inner cycle is executed at most m + 1 − j times, since this is the number of remaining candidate attributes for extending the so-far computed rectangle <C,D>. Hence, the innermost cycle is executed times, along with the at most O(nm) steps within each execution of the innermost cycle. Since max(n,m)≤, the time for ComputeIntervals itself is O(n2m2)+ O(nm3) = O(nm3). .
After Algorithm 1, Algorithm 2 executes at most O(nm+nm) times the loop 3–9 within which it executes at most nm times. To sum up, all algorithms have a polynomial upper bound of time complexity, namely, O(nm3).
Our role minimization optimization algorithm is based on the concept lattice factor, which is the formal context matrix factorization. A good factorization algorithm computes a factorization of the input matrix IA using a reasonably small number of factors in such a way that the first factors have a reasonably good coverage, i.e., they explain a large portion of data. For this purpose, Radim et al. [24] employed the following function of and , representing the coverage quality of the first l factors delivered by the particular algorithm: . They compared the factorization algorithms. For all datasets, it has the highest coverage by the first few factors, providing the best, almost exact factorizations.
7. Conclusions and Future Work
This paper proposes to use operations and resources of the permissions as the function information in role mining and presents a new role mining approach that could reduce composite roles. Our algorithm has two main processes. Firstly, we generate the initial RBAC state that each permission only belongs to a role using formal concept analysis. Secondly, we optimize this RBAC state based on concept lattice factor considering both the user–role assignments and the permission–role assignments, ensuring that access requirements are met while reducing role proliferation.
The algorithm demonstrates effectiveness in handling various optimization tasks by reducing the dimensionality of the problem through concept lattice factorization. By identifying and utilizing the inherent relationships and dependencies among variables, it can efficiently explore the solution space and converge towards optimal or near-optimal solutions.
Our approach is purely data-driven, as all performance metrics are directly associated with the inherent features of the dataset. With this approach, we can quickly set the right goal for role mining before actually running any role mining algorithms.
However, there are areas for further improvement and future work. Firstly, the algorithm’s performance could be evaluated and compared against existing state-of-the-art optimization algorithms to assess its competitiveness and scalability. Additionally, conducting comprehensive experimental studies on various benchmark problems and real-world applications would help validate its effectiveness and generalizability.
Furthermore, exploring ways to enhance the algorithm’s robustness to handle noisy or uncertain data would be valuable. Investigating the algorithm’s behavior on large-scale problems and developing strategies to scale it up effectively would also be beneficial.
Overall, the role minimization optimization by concept lattice factor presents a novel approach to optimization that shows promise [29]. Continued research and development could lead to further advancements, making it a valuable tool for solving complex optimization problems in various domains.
Author Contributions
Conceptualization, Q.W. and T.W.; methodology, Q.W.; software, T.W.; validation, T.W.; formal analysis, Q.W.; resources, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the public welfare industry project of Zhejiang Science and Technology Department (LGG18F020012).
Data Availability Statement
The data used for this experiment are available in public repository. The detailed information about the data are provided in the result analysis section.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jaeger, T.; Xiaolan, Z. Policy Management Using Access Control Spaces. Int. J. ACM Trans. 2003, 6, 327–364. [Google Scholar] [CrossRef]
- Mitra, B.; Sural, S.; Vaidya, J.; Atluri, V. A Survey of Role Mining. ACM Comput. Surv. 2016, 48, 1–37. [Google Scholar] [CrossRef]
- Mario, F.; Joachim, M.B.; David, B. On the Definition of Role Mining. In Proceedings of the ACM Symposium on Access Control Models and Technologies, Pittsburgh, PA, USA, 9–11 June 2010. [Google Scholar]
- Krra, R.R.; Ashalatha, N.; Indranil, G.R.; Yogachandran, R.; Muttukrishnan, R. Role recommender-RBAC: Optimizing user-role assignments in RBAC. Comput. Commun. 2021, 166, 140–153. [Google Scholar]
- Jurgen, S.; Ulrike, S. Role mining with ORCA. In Proceedings of the 10th ACM Symposium on Access Control Models and Technologies, Stockholm, Sweden, 1–3 June 2005. [Google Scholar]
- Jaideep, V.; Vijayalakshmi, A.; Qi, G. The role mining problem: Finding a minimal descriptive set of roles. In Proceedings of the 12th ACM Symposium on Access Control Models and Technologies, Sophia Antipolis, France, 20–22 June 2007. [Google Scholar]
- Hamid, N.A.; Ahmad, R.; Rahayu, S. Recent Trends in Role Mining Algorithms for Role-Based Access Control: A Systematic Review. World Appl. Sci. J. 2017, 35, 1054–1058. [Google Scholar]
- Xu, Z.; Stoller, S.D. Algorithms for mining meaningful roles. In Proceedings of the 17th ACM symposium on Access Control Models and Technologies, Newark, NJ, USA, 20–22 June 2012; pp. 57–66. [Google Scholar]
- Alina, E. Biclique Covers of Bipartite Graphs: The Minimum Biclique Cover and Edge Concentration Problems; Princeton University: Princeton, NJ, USA, 2007. [Google Scholar]
- Huang, H.; Shang, F.; Liu, J.; Du, H. Handling least privilege problem and role mining in RBAC. J. Comb. Optim. 2015, 30, 63–68. [Google Scholar] [CrossRef]
- Jaideep, V.; Vijayalakshmi, A.; Qi, G.; Haibing, L. Edge-RMP: Minimizing administrative assignments for role-based access control. J. Comput. Secur. 2009, 17, 211–235. [Google Scholar]
- Ene, A.; Horne, W.; Milosavljevic, N.; Rao, P.; Schreiber, R.; Tarjan, R.E. Fast exact and heuristic methods for role minimization problems. In Proceedings of the 13th ACM Symposium on Access Control Models and Technologies (SACMAT 2008), Estes Part, CO, USA, 11–13 June 2008. [Google Scholar]
- Vaidya, J.; Atluri, V.; Warner, J.; Guo, Q. Role engineering via prioritized subset enumeration. IEEE Trans. Dependable Secur. Comput. 2010, 7, 300–314. [Google Scholar] [CrossRef]
- Carlo, B.; Stelvio, C. A simple role mining algorithm. In Proceedings of the 25th ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010. [Google Scholar]
- Li, R.; Wang, W.; Ma, X.; Gu, X.; Wen, K. Mining roles using attributes of permissions. Int. J. Innov. Comput. Inf. Control 2012, 8, 7909–7923. [Google Scholar]
- Ian, M.; Hong, C.; Tiancheng, L.; Qihua, W.; Ninghui, L.; Elisa, B.; Seraphin, C.; Jorge, L. Mining roles with multiple objectives. ACM Trans. Inf. Syst. Secur. 2010, 13, 1–35. [Google Scholar]
- Mitra, B.; Sural, S.; Atluri, V.; Vaidya, J. Toward mining of temporal roles. In Proceedings of the 27th International Conference on Data and Applications Security and Privacy, Newark, NJ, USA, 15–17 July 2013. [Google Scholar]
- Ye, W.; Li, R.; Gu, X.; Li, Y.; Wen, K. Role mining using answer set programming. Futur. Gener. Comput. Syst. 2016, 55, 336–343. [Google Scholar] [CrossRef]
- Molloy, I.; Chen, H.; Li, T.; Wang, Q.; Li, N.; Bertino, E.; Calo, S.; Lobo, J. Mining roles with semantic meanings. In Proceedings of the Symposium on Sacmat, Estes Park, CO, USA, 11–13 June 2008. [Google Scholar]
- Kumar, C.A. Designing role-based access control using formal concept analysis. Secur. Commun. Netw. 2013, 6, 373–383. [Google Scholar] [CrossRef]
- Chen, B.; Qiu, J.D.; Chen, M.M. Designing Access Control Policy Using Formal Concept Analysis. Appl. Mech. Mater. 2014, 602–605, 3822–3825. [Google Scholar]
- Koyda, M.; Stumme, G. Factorizing Lattices by Interval Relations. Int. J. Approx. Reason. 2023, 157, 70–87. [Google Scholar] [CrossRef]
- Haibing, L.; Jaideep, V.; Vijayalakshmi, A. An optimization framework for role mining. J. Comput. Secur. 2014, 22, 1–31. [Google Scholar]
- Belohlavek, R.; Trnecka, M. From-below approximations in Boolean matrix factorization: Geometry and new algorithm. J. Comput. Syst. Sci. 2015, 81, 1678–1697. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.L.; Han, D.J.; Shen, X.J. Theory and algorithm for roles minimization problem in RBAC based on concept lattice. Acta Electron. Sin. 2014, 42, 2371–2378. (In Chinese) [Google Scholar]
- Ian, M.; Ninghui, L.; Tiancheng, L.; Ziqing, M.; Qihua, W.; Jorge, L. Evaluating role mining algorithms. In Proceedings of the 14th ACM Symposium on Access Control Models and Technologies, Stresa, Italy, 3–5 June 2009. [Google Scholar]
- Scott, S.; Ping, Y.; Ramakrishnan, C.R.; Mikhail, G. Efficient policy analysis for administrative role based access control. In ACM Conference on Computer and Communication Security, CCS; ACM Press: Alexandria, WV, USA, 2007. [Google Scholar]
- Abolfathi, M.; Raghebi, Z.; Jafarian, H.; Banaei-Kashani, F. A Scalable Role Mining Approach for Large Organizations. In Proceedings of the 2021 ACM Workshop on Security and Privacy Analytics, Virtual Event, USA, 28 April 2021; ACM Press: Alexandria, WV, USA, 2021. [Google Scholar]
- Blundo, C.; Cimato, S.; Siniscalchi, L. Role Mining Heuristics for Permission-Role-Usage Cardinality Constraints. Comput. J. 2022, 65, 1386–1411. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).