Parallel Selector for Feature Reduction

Abstract

In the field of rough set, feature reduction is a hot topic. Up to now, to better guide the explorations of this topic, various devices regarding feature reduction have been developed. Nevertheless, some challenges regarding these devices should not be ignored: (1) the viewpoint provided by a fixed measure is underabundant; (2) the final reduct based on single constraint is sometimes powerless to data perturbation; (3) the efficiency in deriving the final reduct is inferior. In this study, to improve the effectiveness and efficiency of feature reduction algorithms, a novel framework named parallel selector for feature reduction is reported. Firstly, the granularity of raw features is quantitatively characterized. Secondly, based on these granularity values, the raw features are sorted. Thirdly, the reordered features are evaluated again. Finally, following these two evaluations, the reordered features are divided into groups, and the features satisfying given constraints are parallel selected. Our framework can not only guide a relatively stable feature sequencing if data perturbation occurs but can also reduce time consumption for feature reduction. The experimental results over 25 UCI data sets with four different ratios of noisy labels demonstrated the superiority of our framework through a comparison with eight state-of-the-art algorithms.

1. Introduction

In the real world, data play the role of recording abundant information from objects. Thus, an open issue is how to effectively obtain valuable information from high-dimensional data.

Thus far, based on different deep learning models, various popular feature selection devices with respect to this issue have been provided. For instance, Gui et al. [1] proposed a neural network-based feature selection architecture by employing attention and learning modules, which aimed to improve the computation complexity and stability on noisy data. Li et al. [2] proposed a two-step nonparametric approach by combining the strengths of both neural networks and feature screening, which aimed to overcome the challenging problems if feature selection occurs in high-dimension, low-sample-size data. Chen et al. [3] proposed a deep learning-based method, which aimed to select important features for high-dimensional and low-sample size data. Xiao et al. [4] reported a federated learning system with enhanced feature selection, which aimed to produce high recognition accuracy to wearable sensor-based human activity recognition. In addition, based on probability theory, some classical mathematical models were also used to obtain a qualified feature subset. For example, the Bayesian model was employed in mixture model training and feature selection [5]. The trace of the conditional covariance operator was also used to perform feature selection [6].

Currently, in rough set theory [7,8,9,10], feature reduction [11,12,13,14,15,16,17] is drawing considerable attention in regard to this topic by virtue of its high efficiency in alleviating the case of overfitting [18,19], reducing the complexity of learners [20,21,22], and so on. It has been widely employed in general data preprocessing [23] because of its typical advantage in that redundant features can be removed from data without influencing the structure of raw features. A key point of traditional feature reduction devices is the search strategy. With an extensive review, most of the accepted search strategies employed in previous devices can be categorized into the following three fundamental aspects.

• Forward searching. The core of such a phase is to discriminate appropriate features in each iteration and add them into a feature subset named the reduct pool. The specific process of one popular forward search strategy named forward greedy searching (FGS) [24,25,26,27,28,29,30] is a follows: (1) given a predefined constraint, each feature is evaluated by a measure [31,32,33,34], and the most qualified feature is selected; (2) the selected feature is added into a reduct pool; (3) if the constraint is satisfied, the search process is terminated. Obviously, the most effective feature in each iteration constitutes the final feature subset.
• Backward searching. The core of such a phase is to discriminate those features with inferior quality and remove them from the raw features. The specific process of one popular backward searching named backward greedy searching (BGS) [35,36] is as follows: (1) given a predefined constraint, each object in raw feature is evaluated by a measure, and those unqualified features are selected; (2) selected features from raw features are removed; (3) if the constraint is satisfied by the remaining features, the search process is terminated.
• Random searching. The core of such a phase is to randomly select qualified features from candidate features and add them into a reduct pool. The specific process of one classic random searching strategy is named simulated annealing (SA) [37,38] is as follows: (1) for given a predefined constraint, a randomly generated binary sequence is used to picture features (“1” indicates the corresponding feature is selected; “0” indicates the corresponding feature is not selected; the number of binary digits represents the number of raw features.); (2) multiple random changes are exerted upon the sequence, the corresponding fitness values are recorded, i.e., the selected features are evaluated; (3) the sequence turns into a new state with the highest fitness value; (4), (2), and (3) are executed iteratively until the given constraint is satisfied.

Obviously, there mainly exist three limitations regarding the previous feature reduction algorithms. (1) Lack of diverse evaluations. The evaluation originating from different measures may have a disparity; that is, the features selected in single measure are likely to be ineffective when evaluated by some other measures with different semantic explanations. (2) Lack of stable selection. The previous selected feature(s) based on single constraint may seriously mislead the subsequent selection if data perturbation occurs. (3) Lack of efficient selection. For each iteration, all candidate features are required to be evaluated; thus, the time consumption tends to be unsatisfactory with the increasing of feature dimensions.

Based on these three limitations discussed above, a novel framework named parallel selector for feature reduction is reported in the context of this paper. Compared with previous research, our framework mainly consists of three differences: (1) more viewpoints for evaluating features are introduced; that is, different measures are employed for acquiring more qualified features; (2) data perturbation exerts no obvious effect on our framework because the constraints related to different measures are employed and a stable feature sequence sorted by granularity values also works; (3) the iterative selection process is abandoned and replaced by a parallel selection mechanism, through which the efficiency of deriving a final reduct is then improved.

Significantly, the detailed calculation process of our framework should also be plainly expressed. Firstly, to reveal the distinguishing ability of different features over samples, the granularity of feature is combined with our framework; that is, the granularity values of all features are calculated respectively. Secondly, based on the obtained granularity values, all features are sorted. Note that a smaller granularity value means that a corresponding feature could make samples more distinguishable. Thirdly, another measure is used to evaluate the importance of the reordered features. Fourthly, features are divided into groups by considering their comprehensive performance. Finally, the qualified features are parallel selected from these groups according to the required constraints. Immediately, a few distinct advantages emerge from such a framework.

• Providing diverse viewpoints for feature evaluation. In most existing search strategies, the richness of the measure is hard to take into account; that is, the importance of candidate features generated from single measure is usually deemed to be sufficient, e.g., the final reduct of greedy-based forward searching algorithm which was proposed by Hu et al. [39] is derived from a measure named dependency and a corresponding constraint. From this point of view, the selected feature subset may be unqualified if another independent measure is used to evaluate the importance of features. However, in our framework, different measures are employed for evaluating features; thus, more comprehensive evaluations about features can then be obtained. In view of this, our framework is then more effective than are previous feature reduction strategies.
• Improving data stability for feature reduction. In previous studies, the reduct pool is composed of the qualified features selected from each iteration, which indicates the reduct pool is iteratively updated. Thus, it should be pointed out that for each iteration, all features that have been added into the reduct pool are involved in the next evaluation, e.g., the construction of final feature subset in feature reduction strategy proposed by Yang et al. [40] is affected by the selected features. From this point of view, if data perturbation occurs, the selected features will mislead subsequent selection. However, in our framework, each feature is weighted by its granularity value and a feature sequence is then obtained, which is relatively stable in the face of data perturbation.
• Accelerating searching process for feature reduction. In most search strategies for selecting features, e.g., heuristic algorithm and backward greedy algorithm, all iterative features should be evaluated for characterizing their importance. However, the redundancy of evaluation is inevitable in the iteration. This will bring extra time consumption if selection occurs in higher dimensional data. However, in our framework, according to different measures, the process of feature evaluation should be respectively carried out only once. Moreover, the introduction of a grouping mechanism makes it possible to select qualified features in parallel.

In summary, the main contributions regarding our framework are listed as follows: (1) a diverse evaluation mechanism is designed, which can produce different viewpoints for evaluating features; (2) granularity is used for not only evaluating features but also for providing the stability of the selection results if data perturbation occurs; (3) an efficient parallel selection mechanism is developed to accelerate the process of deriving a final reduct; (4) a novel feature reduction framework is reported, which can be combined with various existing feature reduction strategies to improve the quality of their final reduct.

The remainder of this paper is organized as follows. Section 2 provides the reviews of some basic concepts concerning feature reduction. Section 3 details basic contents of our framework and elaborates its application regarding feature reduction. The results of comparative experiments and the corresponding analysis are reported in Section 4. Finally, conclusions and future prospects are outlined in Section 5.

2. Preliminaries

2.1. Neighborhood Rough Set

In rough set field, a decision system can be represented by a pair such that $\mathcal{DS}=⟨U,AT\cup \left\{d\right\}⟩$. $U=\left\{x_i\right|1\le i\le n\}$ is a nonempty set of samples, $AT=\left\{a_k\right|1\le k\le m\}$ is a nonempty set of conditional features, and d is a specific feature which aims to unlock the labels of samples. Particularly, the set of all distinguished labels in $\mathcal{DS}$ is $L=\left\{l_p\right|1\le p\le q\}(q\ge 2)$. $\forall x_i\in U$, $d\left(x_i\right)\in L$ represents the label of sample $x_i$.

Given a decision system $\mathcal{DS}$, assume that a classification task is considered, an equivalence relation over U can be established with d such that $\mathrm{IND}\left(d\right)=\{(x_i,x_j)\in U^2|d\left(x_i\right)=d\left(x_j\right)\}$. Immediately, U is separated into a set of disjoint blocks such that $U/\mathrm{IND}\left(d\right)=\{X_1,X_2,\dots ,X_q\}$. $\forall X_p\in U/\mathrm{IND}\left(d\right)$; it is the p-th decision class that contains all samples with label $l_p$. This process is considered to be the information granulation in the field of granular computing [41,42,43,44].

Nevertheless, equivalence relation may be powerless to perform information granulation if conditional features are introduced, mainly because continuous values instead of categorical values are frequently recorded over such type of features. In view of this, various substitutions have been proposed. For instance, fuzzy relation [45,46] induced by kernel function and neighborhood relation [47,48] based on distance function are two widely accepted devices. Both of them are equipped with an advantage of performing information granulation in respect to different scales. The parameter used in these two binary relations is the key to offering multiple scales. Given a decision system $\mathcal{DS}$, $\delta$ is a radius such that $\delta \ge 0$, $\forall A\subseteq AT$, and a neighborhood relation over A is

$${\delta }_A=\{(x_i,x_j)\in U^2|{\Delta }_A(x_i,x_j)\le \delta \},$$

(1)

in which ${\Delta }_A(x_i,x_j)$ is a distance between $x_i$ and $x_j$ over A.

A higher value of $\delta$ will produce a large-sized neighborhood. Conversely, a smaller value of $\delta$ will generate a small-sized neighborhood. The detailed formulation of neighborhood is then given by ${\delta }_A\left(x_i\right)=\{x_j\in U|(x_i,x_j)\in {\delta }_A\}$.

In the field of rough set, one of the important tasks is to approximate the objective by the result of information granulation. Generally speaking, the objectives which should be approximated are decision classes in $U/IND\left(d\right)$. The details of lower and upper approximations which are based on the neighborhood are then shown in the following. Given a decision system $\mathcal{DS}$ and a radius $\delta \ge 0$, $\forall A\subseteq AT$, $\forall l_p\in L$, $X_p$ is the p-th decision class related to label $l_p$, and neighborhood lower and upper approximations of $X_p$ are

$$\begin{array}{cc}\hfill & {\underline{\delta }}_A\left(X_p\right)=\{x_i\in U|\delta \left(x_i\right)\subseteq X_p\},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & {\overline{\delta }}_A\left(X_p\right)=\{x_i\in U|\delta \left(x_i\right)\cap X_p\ne \varnothing \}.\hfill \end{array}$$

(3)

Following the above definition, it is not difficult to present the following approximations related to the specific feature d. Given a decision system $\mathcal{DS}$ and a radius $\delta \ge 0$, $\forall A\subseteq AT$, and the neighborhood lower and upper approximations of d are

$$\begin{array}{cc}\hfill & {\underline{\delta }}_A\left(d\right)=\bigcup _{p=1}^q{\underline{\delta }}_A\left(X_p\right),\hfill \end{array}$$

(4)

$$\begin{array}{cc}& {\overline{\delta }}_A\left(d\right)=\bigcup _{p=1}^q{\overline{\delta }}_A\left(X_p\right).\hfill \end{array}$$

(5)

2.2. Neighborhood-Based Measures

2.2.1. Granularity

Information granules with adjustable granularity are becoming one of the most genuine goals of data transformation due to two fundamental reasons: (1) fitting granularity-based granular computing leads to processing that is less time-demanding when dealing with detailed numeric problems; (2) information granules with fitted granularity have emerged as a sound conceptual and algorithmic vehicle because of their way of offering a more overall view of the data to support an appropriate level of abstraction aligned with the nature of specific problems. Thus, granularity has becomes a significant concept, and various models regarding it can be developed and utilized.

Given a pair $S=⟨U,R⟩$ in which U is a finite nonempty set of samples, and R is a binary relation over U, $\forall x_i\in U$, the R-related set [34] of $x_i$ is

$$\begin{array}{c}\hfill R\left(x_i\right)=\{x_j\in U:(x_i,x_j)\in R\}.\end{array}$$

(6)

Given a pair $S=⟨U,R⟩$, the granularity [49] related to R can be defined as

$$\begin{array}{c}\hfill G_R\left(U\right)=\frac{{\sum }_{x_i\in U}\left|R\right(x_i\left)\right|}{|U{|}^2},\end{array}$$

(7)

in which $\left|X\right|$ is the cardinality of set X.

Following Equation (7), it is not difficult to see that $0\le G_R\left(U\right)\le 1$. Without loss of generality, the binary relation R can be regarded as one of the most intuitive representations of information granulation over U. The granularity corresponding to the binary relation R then plainly reveals the discriminability of the information granulation results (all R-correlation sets). A smaller $G_R\left(U\right)$ value contains fewer ordered pairs, which means R becomes more discriminative; that is, most samples in U can be distinguished from each other.

Note that ${\delta }_A$ mentioned in Equation (1) is also supposed to be a kind of binary relation, which furnishes the possibility of proposing the following concept of granularity based on neighborhood relation. Given a decision system $\mathcal{DS}$ and a radius $\delta \ge 0$, $\forall A\subseteq AT$, the ${\delta }_A$ based granularity can be defined as follows:

$$\begin{array}{c}\hfill G_{\delta }(A,U)=\frac{{\sum }_{x_i\in U}|{\delta }_A\left(x_i\right)|}{|U{|}^2}.\end{array}$$

(8)

Granularity characterizes the inherent performance of information granulation from the perspective of the distinguishability of features. However, it should be emphasized that the labels of samples do not participate in the process of feature evaluation, which may bring some potential limitations to subsequent learning tasks. In view of this, a classical measure called conditional entropy can be considered.

2.2.2. Conditional Entropy

The conditional entropy is another important measure corresponding to neighborhood rough set, which can characterize the discriminating performance of $\forall A\subseteq AT$ with respect to d. Thus far, various forms of conditional entropy [50,51,52,53] have been proposed in respect to different requirements. A special form which is widely used is shown below.

Given a decision system $\mathcal{DS}$, $\forall A\subseteq AT$, $\delta$ is a radius such that $\delta \ge 0$, and the conditional entropy [54] of d with respect to A is defined as follows:

$$\begin{array}{c}\hfill C{E}_{\delta }(A,d)=-\frac{1}{U}\sum _{x_i\in U}|{\delta }_A\left(x_i\right)\cap {\left[x_i\right]}_d|·\log \frac{|{\delta }_A\left(x_i\right)\cap {\left[x_i\right]}_d|}{|{\delta }_A\left(x_i\right)|}.\end{array}$$

(9)

Obviously, $0\le C{E}_{\delta }(A,d)\le \left|U\right|/e$ holds. A lower value of conditional entropy represents a better discrimination performance of A. Immediately, $\forall A,B\subseteq AT$. Supposing $A\subseteq B$, we then have $C{E}_{\delta }(A,d)\ge C{E}_{\delta }(B,d)$; that is, the conditional entropy monotonously decreases with the increasing scale of A.

2.3. Feature Reduction

In the field of rough set, one of the most significant tasks is to abandon redundant or irrelevant conditional features, which can be considered to be feature reduction. Various measures have been utilized to construct corresponding constraints with respect to different requirements [55,56], with various feature reduction approaches subsequently being explored. A general form of feature reduction presented by Yao et al. [57] is introduced as follows.

Given a decision system $\mathcal{DS}$, $\forall A\subseteq AT$, $\delta$ is a radius such that $\delta \ge 0$, ${\mathcal{C}}_{\rho }$-constraint is a constraint based on the measure $\subset$ which is related to radius $\delta$, and A is referred to as a ${\mathcal{C}}_{\rho }$-based qualified feature subset (${\mathcal{C}}_{\rho }$-reduct) if and only if the following conditions are satisfied:

• A meets the ${\mathcal{C}}_{\rho }$-constraint;
• $\forall B\subseteq A$, B does not meet the ${\mathcal{C}}_{\rho }$-constraint.

It is not difficult to observe that A is actually a optimal and minimal subset of $AT$ and satisfies the ${\mathcal{C}}_{\rho }$-constraint. For the purpose of achieving such a subset, various search strategies have been proposed. For example, an efficient searching strategy named forward greedy searching is widely accepted, whose core process is to evaluate all candidate features and select qualified features according to some measure and corresponding constraint. Based on such a strategy, it is possible for us to determine which feature should be added into or removed from A. For achieving more details about forward greedy searching strategy, the readers can refer to [58].

3. The Construction of a Parallel Selector for Feature Reduction

3.1. Isotonic Regression

In the field of statistical analysis, isotonic regression [59,60] has become a typical topic of statistical inference. For instance, concerning the medical clinical trial, it can be assumed that as the dose of a drug increases, so to does its efficacy and toxicity. However, the estimation of the ratio of patient toxicity at each dose level may be inaccurate; that is, the probability of toxicity at the corresponding dose level may not be a nondecreasing function with respect to the dose level, which will prevent the statistically observation of the average reaction of patients with the increase in drug dosage. In view of this, isotonic regression can then be employed in revealing the variation rule of clinical data. Generally, given a nonempty and finite set $\theta =\{{\theta }_1,{\theta }_2,\dots ,{\theta }_m\}$, an ordering relation “⪯” over $\theta$ can be defined as follows.

The ordering relation “⪯” is considered as a total-order over $\theta$ if and only if the following entries are satisfied:

• Reflexivity: ${\theta }_i⪯{\theta }_i(1\le i\le m)$.
• Transitivity: ${\theta }_j⪯{\theta }_k$, ${\theta }_i⪯{\theta }_j(1\le i\le j\le k\le m)$.
• Antisymmetry: $\forall {\theta }_i,{\theta }_j\in \theta$, if ${\theta }_i⪯{\theta }_j$ and ${\theta }_j⪯{\theta }_i$, then ${\theta }_i={\theta }_j$.
• Comparability: $\forall {\theta }_i,{\theta }_j\in \theta$, we always have ${\theta }_i⪯{\theta }_j$ or ${\theta }_j⪯{\theta }_i$.

Without loss of generality, the ordering relation “⪰” can be defined in similar way. Specifically, if ordering relation “⪯” or “⪰” with respect to $\theta$ satisfies reflexivity, transitivity, and Antisymmetry only, they will be considered as a semiorder. Now we take “⪯” into discussion. Suppose that $\Theta =\{\theta ={({\theta }_1,{\theta }_2,\dots ,{\theta }_m)}^T\in R^m|{\theta }_1⪯{\theta }_2⪯\dots ⪯{\theta }_m\}$, the definition of isotonic function can then be obtained as follows.

Given a function $Y={(Y_1,Y_2,\dots ,Y_m)}^T$ such that $Y_k=Y\left({\theta }_k\right)$ which is based on $\Theta =\{\theta ={({\theta }_1,{\theta }_2,\dots ,{\theta }_m)}^T\in R^m|{\theta }_1⪯{\theta }_2⪯\dots ⪯{\theta }_m\}$; if we have $Y_1⪯Y_2⪯\dots ⪯Y_m$, then Y is called an isotonic function according to the ordering relation “⪯” over $\Theta$.

Let ${\Theta }_{all}$ represent all isotonic functions over $\Theta$ such that ${\Theta }_{all}=\{X\in R^m|X_1⪯X_2⪯\dots ⪯X_m\}$, then we can obtain the following definition of isotonic regression.

Given a function $Y={(Y_1,Y_2,\dots ,Y_m)}^T$, $X^{*}={({X_1}^{*},{X_2}^{*},\dots ,{X_m}^{*})}^T$ is the isotonic regression of Y if it satisfies

$$\begin{array}{c}\hfill \sum _{k=1}^m{w}_k{(Y_k-{X_k}^{*})}^2=\min \sum _{k=1}^m{w}_k{(Y_k-X_k)}^2,\end{array}$$

(10)

in which $w={(w_1,w_2,\dots ,w_m)}^T$ is the weight coefficient and $0\le w_k\le 1$.

Following Equation (10), we can observe that $X^{*}$, i.e., solutions of isotonic regression, can be viewed as the projection of Y onto ${\Theta }_{all}$ when given the inner product ${\displaystyle \sum _{k=1}^m}{w}_k{X}_k{Y}_k$. Immediately, an open problem about how to find such a projection is then intuitively revealed. Thus far, various algorithms [61,62] have been proposed to address such issue, the pool adjacent violators algorithm (PAVA) proposed by Ayer et al. [62] is considered to be the most widely utilized version under the situation of total order. The following Algorithm 1 gives us a detailed process of PAVA for obtaining the $X^{*}$ shown in Equation (10).    

Algorithm 1: Pool adjacent violators algorithm (PAVA).

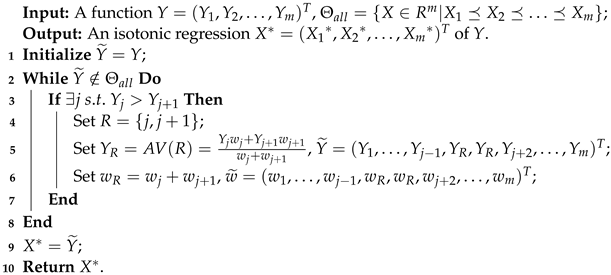For the process of updating values in Algorithm 1, it is not difficult to observe that each $Y_j$ should be considered for value correction. In the worst case, if all elements of Y need to be corrected, it follows that the time complexity of Algorithm 1 is $\mathcal{O}\left(m\right)$. To further facilitate the understanding of the above process, an example will be presented.

Example 1. 

Let us introduce the statistical model through a medical example.

1.

Suppose the dosage in a kind of animal is gradually increased such that

$${\theta }_1⪯{\theta }_2⪯\dots ⪯{\theta }_r.$$

(11)

N animals are tested corresponding to dosage ${\theta }_k(1\le k\le r)$, and ${\dot{X}}_{kj}$ means the reaction of the j-th animal regarding the dosage ${\theta }_k$ such that

$${\dot{X}}_{kj}=\left\{\begin{array}{cc}1,\hfill & active\hfill \\ 0,\hfill & inactive\hfill \end{array}\right..$$

(12)

${\widehat{P}}_k$ means that the active proportion at the dosage is ${\theta }_k$, which is usually estimated from sample proportion such that

$${\widehat{P}}_k=\frac{1}{N}\sum _{j=1}^N{\dot{X}}_{kj}.$$

(13)

2.

Following Equation (11), suppose that $P={(P_1,P_2,\dots ,P_r)}^T$ has the same order such that

$$P_1⪯P_2⪯\dots ⪯P_r.$$

(14)

$N{\widehat{P}}_k$ follows binomial distribution and the likelihood function of P is

$$\prod _{k=1}^r{P}_k^{N{\widehat{P}}_k}{(1-P_k)}^{N(1-{\widehat{P}}_k)}.$$

(15)

Note that when Equation (15) takes Equation (14) as a constraint, Equation (15) can obtain the maximum, i.e., the maximum likelihood estimation(MLE) of P can be obtained. In view of this, ${\widehat{P}}_k$ should have the same order as does Equation (14). If ${\widehat{P}}_k$ does not satisfy Equation (14), ${\widehat{P}}_k$ and ${\widehat{P}}_{k+1}$ should be merged as

$${\widehat{P}}_k={\widehat{P}}_{k+1}=(N_k{\widehat{P}}_k+N_{k+1}{\widehat{P}}_{k+1})/(N_k+N_{k+1}).$$

(16)

3.

To give a further explanation, suppose $r=5$; the specific calculation process is shown in Table 1.

Table 1. A specific calculation process.

k	1	2		3	4	5
$n_k$	25	14		10	20	22
${\widehat{P}}_k$	0.4	0.5		0.6	0.3	0.5
${n_k}^{\left(1\right)}$	39			30		22
${{\widehat{P}}_k}^{\left(1\right)}$	0.436			0.4		0.5
${n_k}^{\left(2\right)}$	39			52
${{\widehat{P}}_k}^{\left(2\right)}$	0.436			0.442

According to Table 1, we know that ${\widehat{P}}_k$ does not satisfy Equation (14), and so then we have

(a) 

$0.436=(25\times 0.4+14\times 0.5)/(25+14)$;

(b) 

$0.442=(30\times 0.4+22\times 0.5)/(30+22)$.

Due to $0.436⪯0.442$, we have ${{\widehat{P}}_1}^{\left(1\right)}={{\widehat{P}}_2}^{\left(1\right)}=0.436$, ${{\widehat{P}}_3}^{\left(2\right)}={{\widehat{P}}_4}^{\left(2\right)}={{\widehat{P}}_5}^{\left(2\right)}=0.442$; that is, $P_1=P_2=0.436$, $P_3=P_4=P_5=0.442$, and so Equation (14) holds, which facilitates the general statistical analysis of the medicine’s effects.

3.2. Isotonic Regression-Based Numerical Correction

It should be emphasized that isotonic regression can be understood as a kind of general framework, which has been demonstrated to be valuable not only in providing inexpensive technical supports for data analysis in the medical field but also in bringing new motivation to other research in the academic community. Correspondingly, by reviewing the relevant contents of two feature measures mentioned in Section 2.2, we find the following: although two measures have been specifically introduced, the statistical correlation between them still lacks explanation. Therefore, an interesting idea is then naturally guided: Can we explore and analyze the statistical laws between these two measures by means of isotonic regression? Moreover, it is not difficult to realize this kind of analysis.

Given a decision system $\mathcal{DS}$, $AT=\left\{a_k\right|1\le k\le m\}$, and $\delta$ is a radius such that $\delta \ge 0$, $\forall a_k\in AT$, we then have $\delta$-based granularity $G_{\delta }(a_k,U)$ and conditional entropy $C{E}_{\delta }(a_k,d)$. Now, we sort conditional features in ascending order by following their values of granularity such that $Gra=\{G={(G_1,G_2,\dots ,G_m)}^T\in R^m|G_1⪯G_2⪯\dots ⪯G_m\}$. In particular, a conditional entropy-based function $Gce={(C{E}_1,C{E}_2,\dots ,C{E}_m)}^T$ according to the same feature order of $Gra$ can be obtained.

Definition 1. 

Given a function $Gce={(C{E}_1,C{E}_2,\dots ,C{E}_m)}^T$ such that $C{E}_k=Gce\left(G_k\right)$ which is based on $Gra=\{G={(G_1,G_2,\dots ,G_m)}^T\in R^m|G_1⪯G_2⪯\dots ⪯G_m\}$, if we have $C{E}_1⪯C{E}_2⪯\dots ⪯C{E}_m$ or $C{E}_1⪰C{E}_2⪰\dots ⪰C{E}_m$, then $Gce$ is called an isotonic function according to the ordering relation“⪯” over $Gra$.

$Gr{a}_{all}$ is employed in representing all isotonic functions over $Gra$ such that $Gr{a}_{all}=\{X\in R^m|X_1⪯X_2⪯\dots ⪯X_{m}or{X}_1⪰X_2⪰\dots ⪰X_m\}$. Likewise, we can obtain the following definition.

Definition 2. 

Given a function $Gce={(C{E}_1,C{E}_2,\dots ,C{E}_m)}^T$, $Gc{e}^{*}={(Gc{e}_1^{*},Gc{e}_2^{*},\dots ,Gc{e}_m^{*})}^T$$\in Gr{a}_{all}$, is the isotonic regression of $(Gce,w)$ if it satisfies

$$\begin{array}{c}\hfill \sum _{k=1}^m{w}_k{(C{E}_k-Gc{e}_k^{*})}^2=\min \sum _{k=1}^m{w}_k{(C{E}_k-X_k)}^2,\end{array}$$

(17)

where $w={(w_1,w_2,\dots ,w_m)}^T$ is the weight coefficient, $0\le w_k\le 1$.

Similarly, we can still apply the PAVA shown in Section 3.1 to calculate $Gc{e}^{*}$, which can be denoted by Algorithm 2.

Algorithm 2: Pool Adjacent Violators Algorithm for Feature Measure (PAVA_FM).

Following the process of Algorithm 2, the time complexity of Algorithm 2 is similar to that of Algorithm 1, i.e., $\mathcal{O}\left(m\right)$. Specifically, the time complexity of Algorithm 2 can also be written as $\mathcal{O}\left(\right|AT\left|\right)$ because m represents the number of raw features.

3.3. Isotonic Regression-Based Parallel Selection

By reviewing what has been discussed of traditional feature reduction algorithms, we can observe that all candidate features should be evaluated in the process of selecting qualified features, which result in a redundant evaluation process. Additionally, although various measures have been explored and corresponding constraints can be constructed, the fact that the single viewpoint of evaluation is underabundant and the reducts derived by single constraint are relatively unstable should not be forgetting. Rather, how to explore the relevant resolution with respect to the above issues becomes significantly urgent. In view of this, motivated by Section 3.2, we introduce the framework for feature reduction.

• Calculate the granularity of each conditional feature in turn, sort these features in ascending order by granularity value, and record the original location index of sorted features.
• Based on 1, calculate the conditional entropy of each sorted feature according to the recorded location index.
• Based on 2, obtain the isotonic regression of conditional entropy according to Definitions (12) and (13). Inspired by Example 1, we group features through updated conditional entropy; that is, features with the same value of conditional entropy are placed into one group. Assume that the number of groups is $N_g\in [1,m]$, and m is the number of raw features.
• Based on 3, when $N_g$ becomes too large, i.e., $N_g$ approaches m, the grouping mechanism is obviously meaningless. To prevent this from happening, we propose a mechanism to reduce the number of groups. That is, to begin with $Grou{p}_1$, calculate D-value ${DV}_i(1\le i\le N_g-1)$ between $Grou{p}_i$ and $Grou{p}_{i+1}$ (the value of a group means the corrected value of the conditional entropy of features in the group arrived via isotonic regression), obtain the sum of all D-values such that ${DV}_{sum}={DV}_1+\dots +{DV}_i+\dots +{DV}_{N_g-1}$, and calculate the mean D-value $Mea{n}_D$ of ${DV}_{sum}$. To begin with $Grou{p}_1$ again, if ${DV}_i<Mea{n}_D$, merge $Grou{p}_i$ with $Grou{p}_{i+1}$.

The main contributions of the above framework are as follows: (1) different measures can be combined in the form of grouping and (2) a parallel selection mechanism to select features is provided. Furthermore, the related reduction strategy is called isotonic regression-based fast feature reduction (IRFFR), and the process of IRFFR is a follows: (1) from $Grou{p}_1$ to $Grou{p}_{N_g/2}$, select features with the minimum of granularity in each group and put them into a reduct pool; (2) from group $Grou{p}_{N_g/2+1}$ to $Grou{p}_{N_g}$, select features with the minimum of original conditional entropy in each group and put them into a reduct pool.

Based on the above discussion, further details of IRFFR are shown in Algorithm 3.

Algorithm 3: Isotonic Regression-based Fast Feature Reduction (IRFFR).

Obviously, different from what occurs in the greedy-based forward searching strategy, the raw features are added in groups. Notably, IRFFR offers a pattern of parallel selection which can reduce corresponding time consumption greatly.

The time complexity of IRFFR mainly comprises three components: obtaining the isotonic regression feature sequence and dividing features into groups in Steps 2 to 6; in the worst case, all features in $AT$ are required to be queried, and then the scanning times for feature sorting is $\left|AT\right|+\left(\right|AT-1\left|\right)+\left(\right|AT-2\left|\right)+\dots +1$, i.e., $\frac{\left|AT\right|·\left(\right|AT|-1)}{2}$, the time complexity of such a phase is $\mathcal{O}\left({\left|AT\right|}^2\right)$, where $AT$ is raw conditional features over $DS$. Updating the number of groups in Steps 7 to 21, in the worst case, considering $N_g<\left|AT\right|$ holds, the time complexity of such a phase can be ignored. Selecting feature from groups in Steps 22–27 requires $N_{gnew}$ times ($N_{gnew}<\left|AT\right|$), and the time complexity of such a phase can also be ignored. Therefore, in general, the time complexity of IRFFR is $\mathcal{O}\left(m^2\right)$. It is worth noting that the time complexity of the forward greedy searching strategy is $\mathcal{O}(n^2·m^2)$ [16]. From this point of view, the efficiency of feature reduction can be improved.

Example 2. 

The following example of data which contains 12 samples and 11 features is given to further explain Algorithm 3; all samples are classified into four categories by d (see Table 2).

Table 2. A Toy Data.

	${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_5$	${\mathit{f}}_6$	${\mathit{f}}_7$	${\mathit{f}}_8$	${\mathit{f}}_9$	${\mathit{f}}_{10}$	${\mathit{f}}_{11}$	d
$x_1$	0.3305	0.4533	0.0240	0.0260	0.1378	0.0486	0.1105	0.1906	0.4186	0.2415	0.2608	$l_1$
$x_2$	0.3388	0.3466	0.0361	0.0153	0.0996	0.0486	0.1220	0.1791	0.4496	0.1348	0.2028	$l_1$
$x_3$	0.3057	0.2800	0.2168	0.0843	0.1029	0.0555	0.2211	0.2060	0.4883	0.3258	0.3623	$l_1$
$x_4$	0.3305	0.1400	0.1746	0.0391	0.0581	0.1388	0.2557	0.0852	0.4031	0.0730	0.5072	$l_1$
$x_5$	0.3223	0.2333	0.6024	0.2967	0.0382	0.1423	0.3640	0.1987	0.4418	0.1573	0.5797	$l_2$
$x_6$	0.3057	0.1667	0.1686	0.0659	0.0548	0.0694	0.3433	0.1299	0.4961	0.1966	0.4202	$l_2$
$x_7$	0.3305	0.3333	0.0120	0.0214	0.1063	0.0277	0.0276	0.1868	0.4961	0.1966	0.2173	$l_3$
$x_8$	0.3884	0.1333	0.3373	0.0184	0.1378	0.1180	0.2235	0.1887	0.4496	0.2977	0.3623	$l_3$
$x_9$	0.2314	0.0533	0.2409	0.0138	0.0581	0.1631	0.3156	0.0788	0.6356	0.1685	0.6376	$l_3$
$x_{10}$	0.1983	0.3866	0.2891	0.0092	0.0332	0.0972	0.1589	0.0402	0.4728	0.0955	0.6956	$l_4$
$x_{11}$	0.2479	0.1200	0.2530	0.0168	0.0664	0.1388	0.2672	0.1135	0.5813	0.1460	0.3623	$l_4$
$x_{12}$	0.2148	0.1600	0.2108	0.0644	0.0348	0.1145	0.2188	0.0788	0.4961	0.2134	0.6521	$l_4$

1.

For each feature, we have $G_{\delta }(f_1,U)=0.0667$, $G_{\delta }(f_2,U)=0.6583$, $G_{\delta }(f_3,U)=0.3655$, $G_{\delta }(f_4,U)=0.0679$, $G_{\delta }(f_5,U)=0.0417$, $G_{\delta }(f_6,U)=0.1917$, $G_{\delta }(f_7,U)=0.3155$, $G_{\delta }(f_8,U)=0.2155$, $G_{\delta }(f_9,U)=0.1750$, $G_{\delta }(f_{10},U)=0.5083$, $G_{\delta }(f_{11},U)=0.4917$.

2.

Sort features in ascending order such that $G_1=G_{\delta }(f_5,U)$, $G_2=G_{\delta }(f_1,U)$, $G_3=G_{\delta }(f_4,U)$, $G_4=G_{\delta }(f_9,U)$, $G_5=G_{\delta }(f_6,U)$, $G_6=G_{\delta }(f_8,U)$, $G_7=G_{\delta }(f_7,U)$, $G_8=G_{\delta }(f_3,U)$, $G_9=G_{\delta }(f_{11},U)$, $G_{10}=G_{\delta }(f_{10},U)$, $G_{11}=G_{\delta }(f_2,U)$.

3.

Calculate the corresponding conditional entropy such that $C{E}_1=2.8666$, $C{E}_2=2.1805$, $C{E}_3=3.1327$, $C{E}_4=2.4333$, $C{E}_5=2.3917$, $C{E}_6=2.0387$, $C{E}_7=1.3463$, $C{E}_8=1.2591$, $C{E}_9=0.9972$, $C{E}_{10}=1.7841$, $C{E}_{11}=1.1557$.

4.

The isotonic regression of $Gce$ is $Gc{e}^{*}={(2.8666,2.6566,2.6566,2.4125,2.4125,1.6925,1.6925,1.3468,1.3468,1.3468,1.1557)}^T$, then $Grou{p}_1=\left\{f_5\right\}$, $Grou{p}_2=\{f_1,f_4\}$, $Grou{p}_3=\{f_9,f_6\}$, $Grou{p}_4=\{f_8,f_7,f_{10}\}$, $Grou{p}_5=\{f_3,f_{11}\}$, $Grou{p}_6=\left\{f_2\right\}$.

5.

$D{V}_1=0.21$, $D{V}_2=0.2441$, $D{V}_3=0.72$, $D{V}_4=0.3457$, $D{V}_5=0.1911$, $Mea{n}_D=0.3422$, we then have $Grou{p}_{new1}=\{f_5,f_1,f_4\}$, $Grou{p}_{new2}=\{f_9,f_6\}$, $Grou{p}_{new3}=\{f_8,f_7,f_{10}\}$, $Grou{p}_{new4}=\{f_3,f_{11},f_2\}$.

6.

For $Grou{p}_{new1}\to Grou{p}_{new2}$, we put $f_5$ and $f_9$ into a reduct pool; for $Grou{p}_{new3}\to Grou{p}_{new4}$, we put $f_{10}$ and $f_2$ into a reduct pool. That is, we have the final reduct $\{f_2,f_5,f_9,f_{10}\}$.

4. Experiments

4.1. Datasets

To demonstrate the effectiveness of our proposed framework for feature reduction, the 25 UCI data sets were used to conduct the experiments. The following Table 3 shows the details of these data sets.

Table 3. Data description.

ID	Datasets	# Samples	# Features	# Labels	Domain	Feature Type
1	Breast Cancer Wisconsin (Diagnostic)	569	32	2	Life	Real
2	Cardiotocography	2126	21	10	Medicine	Real
3	Contraceptive Method	1473	9	3	Life	Integer & Real
4	Diabetic Retinopathy Debrecen	1151	19	2	Biology	Integer & Real
5	Forest Type Mapping	523	27	4	Geography	Integer & Real
6	Ionosphere	351	34	2	Physical	Integer & Real
7	Libras Movement	360	90	15	N/A	Real
8	LSVT Voice Rehabilitation	126	309	2	Life	Real
9	Musk (Version 1)	476	168	2	Physical	Integer
10	Parkinson Multiple Sound Recording	1208	26	2	Medicine	Real
11	Pen-Based Recognition of Handwritten Digits	10,992	16	10	Computer	Integer
12	QSAR Biodegradation	1055	41	2	Biology	Integer & Real
13	Quality Assessment of Digital Colposcopies	287	62	2	Life	Real
14	Sonar	208	60	2	Physics	Real
15	SPECTF Heart	267	44	2	Biology	Real
16	Statlog (Image Segmentation)	2310	18	7	Geography	Real
17	Statlog (Vehicle Silhouettes)	846	18	4	Physical	Integer
18	Steel Plates Faults	1941	33	2	Physical	Integer & Real
19	Synthetic Control Chart Time Series	600	60	6	N/A	Real
20	Twonorm	7400	20	2	Historical	Real
21	Urban Land Cover	675	147	9	Geography	Real
22	Wall-Following Robot Navigation	5456	24	4	Computer	Real
23	Website Phishing	1353	10	2	Computer	Integer
24	Wine Quality	6497	11	7	Physical	Real
25	Wireless Indoor Localization	2000	7	4	Computer	Real

During the experiments, each dataset participates in the calculation in the form of a two-dimensional table. Specifically, the “rows” of these tables represent “samples”, and the number of rows reveals how many samples participate in the calculation; the “columns” of these tables represent different features of samples, and the number of columns reveals how many features a sample has.

It is worth noting that in practical applications, data perturbation is sometimes inevitable. Therefore, when data perturbation occurs, it is necessary to investigate immunity of the proposed algorithm. In our experiments, the label noise is used to generate data perturbation. Specifically, the perturbated labels are used to inject into raw labels, and if the perturbation ratio is given as $\beta \%$, the injection is realized by randomly selecting $\beta \%$ number of samples and injecting white Gaussian noise(WGN) [63] into their labels. It should be emphasized that excessive WGN ratio of raw labels will lead to the data losing their original semantics. From this point of view, the experimental results may be meaningless. Thus, in the following experiments, to better observe the performance of our proposed algorithm in response to the increasing noise ratio of raw labels, we conduct 4 WGN ratios such that $10\%$, $20\%$, $30\%$ and $40\%$.

4.2. Experimental Configuration

In the context of this experiment, the neighborhood rough set is constructed by 20 different neighborhood radii such that $\delta =0.02,0.04,\dots ,0.4$. Moreover, 10-fold cross-validation [64] is applied to the calculation of each reduct, whose details are as follows: (1) each data set is randomly partitioned into two groups with the same size of samples, with the first group being regarded as the testing samples and the second group being regarded as the training samples; (2) the set of training samples is further partitioned into 10 groups with the same size such that $U_1,U_2,\dots ,U_{10}$, and for the first round of computation, $U_2,U_3,\dots ,U_{10}$ is combined such that $U_2\cup U_3\cup \dots \cup U_{10}$, which is used to derive reduct, with derived reduct then being used to predict the labels of testing samples; …; for the last round of computation, $U_1\cup U_2\cup \dots \cup U_9$ is used to derive the reduct. In the same way, the derived reduct is used to predict the labels of the testing samples.

All experiments were carried out on a personal computer with Windows 10 and an Intel Core i9-10885H CPU (2.40 GHz) with 16.00 GB memory. The programming language used was MATLAB R2017b.

4.3. The First Group of Experiments

In the first group of experiments, to perform IRFFR, Algorithm 3 is employed in conducting the final reducts. Based on the final reducts, we verifies the effectiveness of our IRFFR by comparing it with six state-of-art feature reduction methods from three aspects: classification accuracy, classification stability, and elapsed time. It is worth noting that the comparative method “Ensemble Selector for Attribute Reduction (ESAR)” is based on the ensemble [65] framework. The comparative methods are as follows:

• Knowledge Change Rate(KCR) [33].
• Forward Greedy Searching(FGS) [39].
• Self Information(SI) [32].
• Attribute Group(AG) [66].
• Ensemble Selector for Attribute Reduction(ESAR) [40].
• Novel Fitness Evaluation-based Feature Reduction(NFEFR) [67].

4.3.1. Comparison of Classification Accuracy

The index called classification accuracy was employed to measure the classification performance of the seven algorithms. Two classic classifiers named KNN (K-nearest neighbor, K = 3) [68], CART (classification and regression tree) [69], and SVM (support vector machine) [70] were employed to reflect the classification performance. Generally, given a decision system $\mathcal{DS}$, assuming that the set U is divided into z (Note that as 10-folds cross-validation was employed in this experiment, $z=10$ holds) groups which are disjointed and with the same size, i.e., $U_1,\dots ,U_{\tau },\dots ,U_z$ ($1\le \tau \le z$). The classification accuracy related to reduct $re{d}_{\tau }$ ($re{d}_{\tau }$ is the reduct derived over $U-U_{\tau }$) which is

$$Ac{c}_{re{d}_{\tau }}=\frac{\left|\right\{x\in re{d}_{\tau }|Pr{e}_{re{d}_{\tau }}\left(x\right)=d\left(x\right)\}|}{|U_{\tau }|},$$

(18)

in which $Pr{e}_{re{d}_{\tau }}\left(x\right)$ is the predicted label of x through employing reduct $re{d}_{\tau }$.

The mean values of the classification accuracies are the radar charts shown in Figure 1, Figure 2 and Figure 3, in which four different colors are used to represent four different ratios of noisy labels.

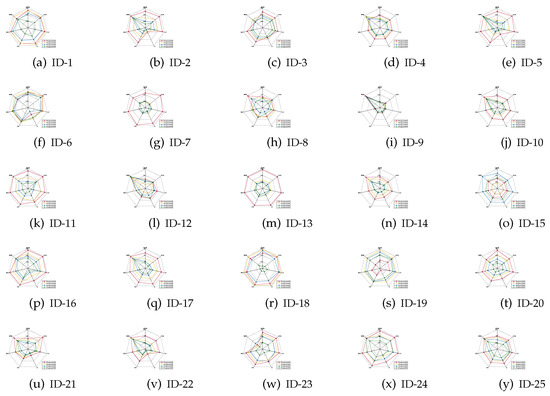
Figure 1. Classification accuracies (KNN).

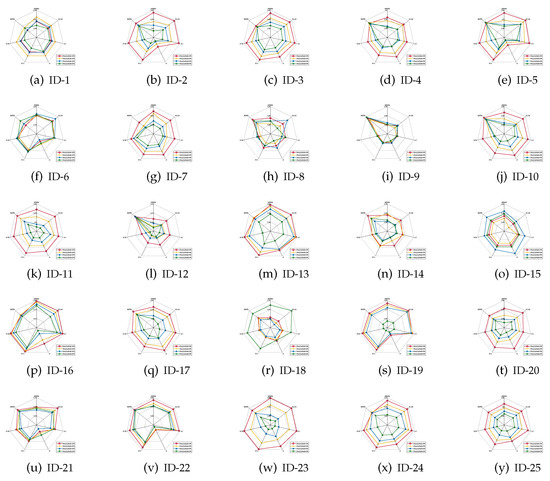
Figure 2. Classification accuracies (CART).

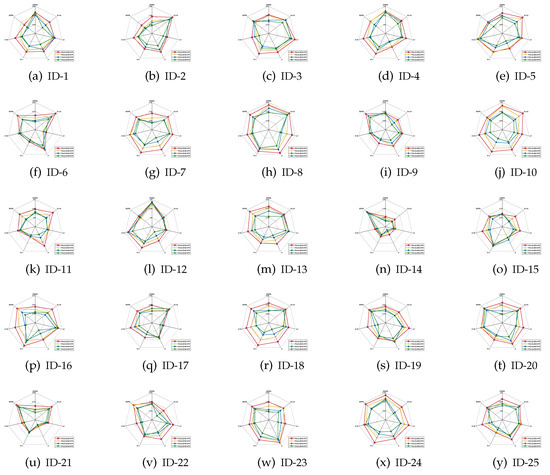
Figure 3. Classification accuracies (SVM).

Based on the specific experimental results expressed by Figure 1, Figure 2 and Figure 3, the following becomes apparent.

• For most of data sets, no matter which ratio of label noise is injected into the raw data, compared with six popular algorithms, the predictions generated through the reducts derived by our IRFFR possess superiorities. The essential reason is that the feature sequence regarding granularity is helpful for selecting out more stable features. In the example of “Parkinson Multiple Sound Recording” (ID-10, Figure 1j)’, all classification accuracies of IRFFR over four label noise ratios are greater than 0.6; in contrast, when the label noise ratio reaches 20%, 30%, and 40%, all classification accuracies of the six comparative algorithms are less than 0.6. Moreover, for some data sets, no matter which classifier is adopted, the classification accuracies regarding our IRFFR are greatly superior to the six comparative algorithms. The essential reason is that diverse evaluations do bring more qualified features out. With the example of “QSAR Biodegradation” (ID-12, Figure 1l and Figure 2l)’, in KNN, all classification accuracies of IRFFR are greater than 0.66 over four label noise ratios; in contrast, the classification accuracies of all comparative algorithms are less than 0.66 over these noise ratios. In CART, all classification accuracies of IRFFR are greater than 0.67 over four label noise ratios; in contrast, the classification accuracies of all comparative algorithms are less than 0.67 over these noise ratios. In SVM, with “Sonar” (ID-14, Figure 3n) as an example, all classification accuracies of IRFFR are greater than 0.76 over four label noise ratios; in contrast, the classification accuracies of all comparative algorithms are around 0.68 over these noise ratios. Therefore, it can be observed that our IRFFR can derive the reducts with outstanding classification accuracy.
• For most data sets, a higher label noise ratio led to a negative impact on the classification accuracies of all seven algorithms. In other words, with the increase in the label noise ratio ($\beta$ increases from 10 to 40), the classification accuracies of all seven algorithms show a significant decrease, which can be seen in Figure 1, Figure 2 and Figure 3. With “Twonorm” (ID-20, Figure 1t and Figure 2t)’ as an example, the increase of $\beta$ does discriminate the stripes with different colors. However, it should be noted that for some data sets, such as “LSVT Voice Rehabilitation” (ID-8, Figure 1h and Figure 2h) and “SPECTF Heart” (ID-15, Figure 1o and Figure 2o) and “QSAR Biodegradation” (ID-12, Figure 3l, the changes in these figures are quite unexpected, which can be attributed to a higher label noise ratio leading to the lower stability of the classification results. Furthermore, for some data sets, such as “Diabetic Retinopathy Debrecen” (ID-4, Figure 1d and Figure 2d)’, “Parkinson Multiple Sound Recording” (ID-10, Figure 1j, Figure 2j and Figure 3j)’, and “Statlog” (Vehicle Silhouettes) (ID-17, Figure 1q and Figure 2q)’, the increasing label noise ratio does not have a significant effect on the classification accuracies of our IRFFR. In other words, compared with other algorithms, our IRFFR has a better antinoise ability.

4.3.2. Comparison of Classification Stability

In this subsection, the classification stability [40] is discussed, which was obtained over different classification results with respect to all seven algorithms. Similar to the classification accuracy, all experimental results are based on the CART, KNN, and SVM classifiers. Given a decision system $\mathcal{DS}$, suppose that the set U is divided into z (10-folds cross-validation is employed; S thus, $z=10$) groups which are disjoint and with the same size such that $U_1,\dots ,U_{\tau },\dots ,U_z$ ($1\le \tau \le z$). Then, the classification stability related to reduct $re{d}_{\tau }$ ($re{d}_{\tau }$ is the reduct derived over $U-U_{\tau }$), which is

$$Sta{b}_{classification}=\frac{2}{z·(z-1)}\sum _{\tau =1}^{z-1}\sum _{{\tau }^{\prime }=\tau +1}^{z}Exa(re{d}_{\tau },re{d}_{{\tau }^{\prime }}),$$

(19)

in which $Exa(re{d}_{\tau },re{d}_{{\tau }^{\prime }})$ represents the agreement of the classification results and can be defined based on Table 4.

Table 4. Joint distribution of classification results.

	${\mathit{Pre}}_{{\mathit{red}}_{\mathit{\tau }}}\left(\mathit{x}\right)=\mathit{d}\left(\mathit{x}\right)$	${\mathit{Pre}}_{{\mathit{red}}_{\mathit{\tau }}}\left(\mathit{x}\right)\ne \mathit{d}\left(\mathit{x}\right)$
$Pr{e}_{re{d}_{\tau }^{\prime }}\left(x\right)=d\left(x\right)$	${\psi }_1$	${\psi }_2$
$Pr{e}_{re{d}_{\tau }^{\prime }}\left(x\right)\ne d\left(x\right)$	${\psi }_3$	${\psi }_4$

In Table 4, $Pr{e}_{re{d}_{\tau }}\left(x\right)$ means the predicted label of x obtained by $re{d}_{\tau }$. ${\psi }_1$, ${\psi }_2$, ${\psi }_3$, and ${\psi }_4$ represents the number of samples meeting the corresponding conditions in Table 4. Following this, $Exa(re{d}_{\tau },re{d}_{{\tau }^{\prime }})$ is

$$Exa(re{d}_{\tau },re{d}_{{\tau }^{\prime }})=\frac{{\psi }_1+{\psi }_4}{{\psi }_1+{\psi }_2+{\psi }_3+{\psi }_4}.$$

(20)

It should be emphasized that the index of classification stability describes the degree of deviation of the predicted labels if data perturbation occurs. A higher value of classification stability indicates that the predicted labels are more stable, i.e., the corresponding reduct has better quality. As for what follows, the mean values of the classification stabilities are shown in Figure 4, Figure 5 and Figure 6.

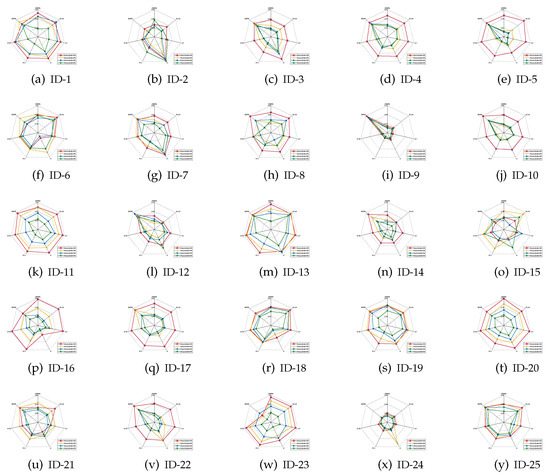
Figure 4. Classification stabilities (KNN).

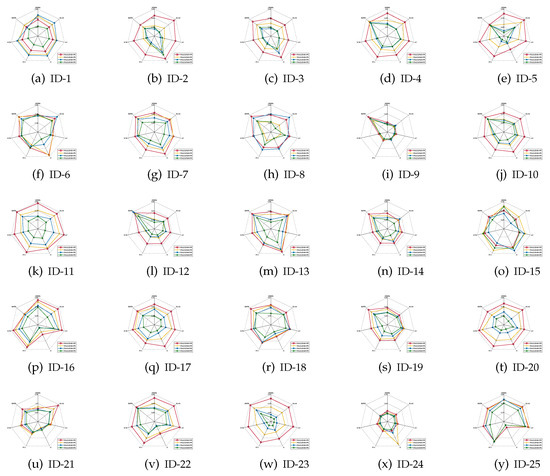
Figure 5. Classification stabilities (CART).

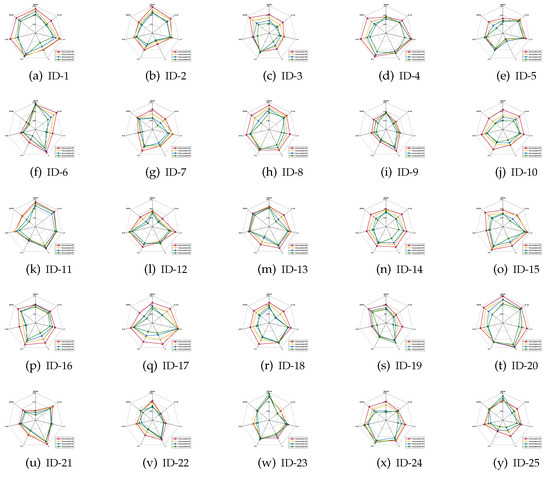
Figure 6. Classification stabilities (SVM).

Based on the experimental results reported in Figure 4, Figure 5 and Figure 6, it is not difficult to conclude the following.

• For most of data sets, regardless of which ratio of label noise was injected into raw data, compared with six popular algorithms, the classification stabilities of the reducts derived by our IRFFR were not the greatest out-performers in SVM; rather, the classification stabilities in KNN and CART were superior. Especially, for some data sets, the predictions conducted by the reducts of our IRRFR obtained absolute dominance. With “Musk” (Version 1)(ID-9, Figure 4i and Figure 5i) as an example, regarding KNN and CART, the classification stabilities of our IRFFR are respectively greater than 0.66 and 0.65; S in contrast, the classification stabilities of the six comparative algorithms are only around 0.56 and 0.58. Therefore, it can be observed that by introducing the new grouping mechanism proposed in Section 3.3, from the viewpoint of both stability and accuracy, our IRFFR is effective in improving the classification performance.
• Following Figure 4 and Figure 5, similar to the classification accuracy, we can also observe that a higher ratio does have a negative impact on the classification stability. Moreover, the classification stability regarding our IRFFR has superior antinoise ability that is similar to that of the classification accuracy. With “Parkinson Multiple Sound Recording” (ID-10, Figure 4j and Figure 5j)” and “QSAR Biodegradation” (ID-12, Figure 4l and Figure 5l)” as examples, although the increasing ratio of label noise was injected into the raw data, the classification stabilities corresponding to our IRFFR over four different label noise ratios do not show dramatic change.

4.3.3. Comparison of Elapsed Time

In this section, the elapsed time for deriving reducts by employing different approaches are compared. The detailed results are shown in the following Table 5 and Table 6. The bold texts indicate the optimal method for each row.

Table 5. The elapsed time of deriving reducts (noisy label ratio of 10% and 20%)(s).

$\mathit{\beta }$	ID	IRFFR	KCR	FGS	SI	AG	ESAR	NFEFR
$\beta =10$	1	0.0536	0.7782	0.7163	0.4309	0.1933	0.2366	4.3213
	2	0.3441	28.8755	12.1876	9.9088	3.2336	3.7912	37.8901
	3	0.0688	0.9308	1.0216	0.4289	0.2293	0.2286	2.9642
	4	0.0937	1.7850	2.1746	0.7978	0.4394	0.4718	9.2432
	5	0.0285	1.1619	0.6590	0.7516	0.2087	0.2622	2.8259
	6	0.0207	0.3110	0.2639	0.4131	0.0776	0.1074	1.4439
	7	0.0877	1.3412	0.9288	1.6358	0.3757	0.4650	13.4194
	8	0.0692	0.9497	0.9542	0.7542	0.2887	0.3210	10.4971
	9	0.1662	3.3097	3.0787	2.2836	0.8185	0.9544	56.8696
	10	0.1316	2.8113	3.0106	1.3394	0.6109	0.7706	16.3750
	11	25.2519	251.1537	4083.2167	139.3251	80.3628	111.3182	864.9137
	12	0.1582	3.7813	4.2592	1.7390	0.8326	0.9802	28.2335
	13	0.0176	0.3975	0.3412	0.4415	0.1302	0.1509	1.8344
	14	0.0205	0.3544	0.3153	0.3123	0.0845	0.1121	1.4849
	15	0.0199	0.3656	0.3079	0.1735	0.0912	0.1174	1.6289
	16	0.3597	37.4184	9.7542	5.0382	2.6134	2.8379	26.8831
	17	0.0506	1.5741	0.9303	0.5577	0.2569	0.3081	3.6622
	18	0.1344	11.4536	7.1114	4.7126	2.3747	4.1211	22.7714
	19	0.2144	16.1564	3.1614	3.8465	2.4617	5.1545	49.2311
	20	18.5196	174.6279	838.6248	88.3156	56.7514	77.2156	557.3168
	21	0.3085	20.2897	5.9909	5.2205	2.8539	4.6020	76.5475
	22	2.7307	83.4015	167.8977	39.8466	11.0354	14.2905	263.3195
	23	0.0608	0.5849	0.8442	0.2917	0.1719	0.1667	2.9786
	24	2.5880	59.9067	148.2454	19.2041	9.1134	10.0511	98.9501
	25	0.1248	1.7158	2.4156	0.9829	0.5993	0.4756	8.1322
	AVE	2.0649	28.2174	255.9365	13.1501	7.0484	9.5804	86.5495
$\beta =20$	1	0.0452	0.5909	0.5424	0.3048	0.1488	0.1932	3.3916
	2	0.3431	26.1039	11.0641	9.6548	3.0425	3.5674	35.6682
	3	0.0694	0.9199	1.0003	0.4512	0.2255	0.2217	2.8017
	4	0.0931	1.6936	2.0875	0.7222	0.4199	0.4312	9.0950
	5	0.0292	0.8807	0.5102	0.7246	0.1662	0.2043	2.2947
	6	0.0202	0.2956	0.2449	0.4147	0.0696	0.0979	1.3670
	7	0.0736	1.3963	0.8492	1.4892	0.2840	0.3811	12.5079
	8	0.0661	0.9041	0.8549	0.7762	0.2701	0.2983	9.9450
	9	0.1650	3.2286	2.9890	2.4350	0.7940	0.9160	55.3699
	10	0.1308	2.2509	2.4461	1.1042	0.5276	0.6114	13.6189
	11	17.5276	268.2813	4033.1561	142.8134	83.4129	121.3421	871.3185
	12	0.1641	3.2625	3.6797	1.2514	0.7245	0.8604	25.0494
	13	0.0028	0.4147	0.2734	0.3857	0.1075	0.0635	1.9477
	14	0.0199	0.3360	0.3026	0.3273	0.0778	0.0989	1.4706
	15	0.0196	0.3436	0.2994	0.1520	0.0831	0.1029	1.5284
	16	0.3666	17.2910	9.8411	6.2131	2.5054	2.6535	26.5666
	17	0.0515	1.5593	0.9236	0.5482	0.2309	0.2957	3.5708
	18	0.1348	11.4658	7.0604	4.6848	2.3096	4.0948	22.8890
	19	0.2138	16.2287	3.0204	3.7783	2.3523	5.1122	48.4254
	20	12.1955	170.1989	1922.1891	80.7466	51.5930	70.7186	558.6663
	21	0.3085	19.9418	6.2093	12.2543	2.8679	4.2509	77.9080
	22	2.7500	78.1211	152.9137	40.2533	11.8096	13.1762	242.1188
	23	0.0629	0.5696	0.8556	0.2918	0.1695	0.1671	2.8427
	24	4.1455	81.0404	165.8189	29.7028	13.0710	14.3930	159.9506
	25	0.1127	1.6159	2.3784	0.9381	0.5337	0.4157	7.8566
	AVE	1.5645	28.3574	253.2604	13.6967	7.1119	9.7867	87.9268

Table 6. The elapsed time of deriving reducts (noisy label ratio of 30% and 40%)(s).

$\mathit{\beta }$	ID	IRFFR	KCR	FGS	SI	AG	ESAR	NFEFR
$\beta =30$	1	0.0474	0.5990	0.5494	0.2736	0.1360	0.1867	3.5187
	2	0.3374	25.0034	10.6129	9.8791	2.8190	3.4207	32.9282
	3	0.0684	0.8996	0.9426	0.4494	0.2200	0.2126	2.6851
	4	0.0966	1.6500	2.0918	0.7303	0.3952	0.3970	8.8716
	5	0.0293	0.8955	0.5394	0.7472	0.1550	0.2005	2.2598
	6	0.0211	0.3043	0.2611	0.4264	0.0737	0.1026	1.3970
	7	0.0732	1.4337	0.7981	1.4789	0.2350	0.2868	12.3809
	8	0.0715	0.9460	0.9289	0.3575	0.2745	0.3130	10.0617
	9	0.1746	3.3834	3.1107	2.7393	0.8036	0.9633	57.5430
	10	0.1319	2.1473	2.3723	0.9770	0.4789	0.5942	13.1255
	11	16.1564	267.4983	4023.1564	138.4983	80.9853	119.2531	870.4638
	12	0.1642	3.1912	3.5769	1.3367	0.6314	0.8159	24.4300
	13	0.0059	0.3292	0.2229	0.3393	0.0179	0.0344	2.0627
	14	0.0200	0.3218	0.2730	0.3349	0.0755	0.0935	1.3827
	15	0.0206	0.3401	0.2887	0.1474	0.0741	0.0956	1.4982
	16	0.3571	16.8586	10.0374	6.8824	2.4172	2.5327	26.8768
	17	0.0519	1.4422	0.8571	0.5823	0.2200	0.2771	3.3948
	18	0.1372	11.3884	7.0711	4.6152	2.1914	4.1006	22.8787
	19	0.2055	16.1867	2.9679	3.6706	2.2534	5.1159	47.4915
	20	10.4985	168.6851	1901.9933	81.5166	58.6844	75.3100	540.0020
	21	0.3095	19.8291	6.4364	5.2514	2.7627	3.7103	81.5410
	22	2.8341	76.7897	152.5695	42.3649	9.9306	12.9020	237.2487
	23	0.0586	0.5311	0.8019	0.2688	0.1635	0.1563	2.5599
	24	4.3277	80.8440	171.6118	29.1230	13.0709	14.2647	161.9921
	25	0.1000	1.6625	2.2242	0.8286	0.4491	0.4181	8.1859
	AVE	1.4519	28.1264	252.2518	13.3528	7.1807	9.8303	87.0712
$\beta =40$	1	0.0477	0.5750	0.5143	0.2659	0.1271	0.1733	3.2591
	2	0.3416	24.3643	10.4060	9.7229	2.6469	3.3132	32.6536
	3	0.0692	0.8752	0.9655	0.4341	0.2196	0.2125	2.6402
	4	0.0936	1.5387	1.9316	0.6998	0.3433	0.3651	8.2427
	5	0.0297	0.8927	0.5093	0.7516	0.1552	0.2040	2.2548
	6	0.0201	0.2853	0.2343	0.3221	0.0634	0.0856	1.3058
	7	0.0591	1.3633	0.7513	1.4581	0.2067	0.1697	12.6555
	8	0.0678	0.8898	0.8115	0.3315	0.2606	0.2894	9.5256
	9	0.1871	3.4483	3.3549	2.6639	0.8415	0.9867	59.1489
	10	0.1420	2.2963	2.5092	0.9748	0.4825	0.6393	13.6530
	11	19.5612	277.1566	4057.2135	144.2356	80.9851	119.3544	871.1983
	12	0.1814	3.1453	3.5566	1.3475	0.5905	0.8007	23.6727
	13	0.0029	0.3144	0.1955	0.2347	0.0045	0.0695	2.0031
	14	0.0227	0.3232	0.2736	0.3419	0.0745	0.0939	1.3458
	15	0.0196	0.3147	0.2692	0.1352	0.0718	0.0885	1.4129
	16	0.5885	23.7795	18.6242	10.0813	3.3244	3.6619	45.9315
	17	0.0497	1.4368	0.8528	0.5397	0.2122	0.2552	3.3861
	18	0.1255	11.4535	6.9874	4.6026	2.1267	4.1127	23.1883
	19	0.1944	16.1517	2.9665	3.5403	2.2440	5.0574	46.6051
	20	9.7851	160.5344	1855.4531	78.2101	59.5111	71.1651	520.6933
	21	0.3118	18.6813	6.1723	5.1530	2.6032	3.3897	76.1348
	22	2.7809	73.5303	151.6155	41.7967	8.9678	12.0370	232.5254
	23	0.0588	0.5055	0.8270	0.2831	0.1672	0.1566	2.3377
	24	4.3872	80.4337	172.5754	30.0218	13.4168	14.1845	167.2978
	25	0.0908	1.6617	2.2339	0.7634	0.4651	0.3579	7.0799
	AVE	1.5687	28.2381	252.0722	13.5565	7.2045	9.6490	86.8061

With a deep investigation of Table 5 and Table 6, it is not difficult to arrive at the following conclusions.

• The time consumption for selecting features by our IRFFR was much less than that of all the comparative algorithms. The essential reason is that IRFFR can reduce the searching space for candidate features, which indicates that our IRFFR has superior efficiency. With the “Wine quality” (ID-24, Table 5)” data set as an example, if $\beta =10$, the time consumption to obtain the reducts of IRFFR, KCR, FGS, SI, AG, ESAR, and NFEFR are 2.5880, 59.9067, 1480.2454, 19.2041, 9.1134, 10.0511, and 98.9501 s, respectively. Our IRFFR requires only 2.5880 s.
• It should be pointed out that for IRFFR and FGS, the time consumption has the largest difference. With “Pen-Based Recognition of Handwritten Digits” (ID-11) as an example, the elapsed time of our IRFFR over four different noisy label ratios are 25.2519, 17.5276, 16.1564, and 19.5612 s respectively; in contrast, the elapsed time of the FGS over four different noisy label ratios are 1083.2167, 4033.1561, 4023.1564, and 4057.2135 s, respectively. Therefore, the mechanism of parallel selection can significantly improve the efficiency in selecting features.
• With the increase in the label noise ratio, the elapsed time of seven different algorithms express different change tendencies. For example, when $\beta$ increases from 10 to 20, all elapsed time according to seven algorithms over the data set of “Breast Cancer Wisconsin” (Diagnostic) (ID-1) show a downward tendency. However, when $\beta$ is 30, the case is quite different, as is the case when $\beta$ is 40. That is, some algorithms require more time for reduct construction. In addition, we can observe that for the average elapsed time, the change of six comparative algorithms is gradual. On the contrary, the elapsed time of our IRFFR shows a clear descending trend. Therefore, the increase in the noisy label ratio does not significantly affect the time consumption of our IRFFR.

To further show the superiority of our IRFFR, the values of speed-up ratio are further presented in Table 7 and Table 8.

Table 7. The speed-up ratio related to the elapsed time of obtaining reducts (noisy label ratios of 10% and 20%).

$\mathit{\beta }$	ID	IRFFR & KCR	IRFFR & FGS	IRFFR & SI	IRFFR & AG	IRFFR & ESAR	IRFFR & NFEFR
$\beta =10$	1	0.9311	0.9252	0.8756	0.7227	0.7735	0.9876
	2	0.9881	0.9718	0.9653	0.8936	0.9092	0.9909
	3	0.9261	0.9327	0.8396	0.7000	0.6990	0.9768
	4	0.9475	0.9569	0.8826	0.7868	0.8014	0.9899
	5	0.9755	0.9568	0.9621	0.8634	0.8913	0.9899
	6	0.9334	0.9216	0.9499	0.7332	0.8073	0.9857
	7	0.9346	0.9056	0.9464	0.7666	0.8114	0.9935
	8	0.9271	0.9275	0.9082	0.7603	0.7844	0.9934
	9	0.9498	0.9460	0.9272	0.7969	0.8259	0.9971
	10	0.9532	0.9563	0.9017	0.7846	0.8292	0.9920
	11	0.8995	0.9938	0.8188	0.6858	0.7732	0.9708
	12	0.9582	0.9629	0.9090	0.8100	0.8386	0.9944
	13	0.9557	0.9484	0.9601	0.8648	0.8834	0.9904
	14	0.9422	0.9350	0.9344	0.7574	0.8171	0.9862
	15	0.9456	0.9354	0.8853	0.7818	0.8305	0.9878
	16	0.9904	0.9631	0.9286	0.8624	0.8733	0.9866
	17	0.9679	0.9456	0.9093	0.8030	0.8358	0.9862
	18	0.9883	0.9811	0.9715	0.9434	0.9674	0.9941
	19	0.9867	0.9322	0.9443	0.9129	0.9584	0.9956
	20	0.8939	0.9904	0.7903	0.6737	0.7602	0.9668
	21	0.9848	0.9485	0.9409	0.8919	0.9330	0.9960
	22	0.9673	0.9837	0.9315	0.7526	0.8089	0.9896
	23	0.8961	0.9280	0.7916	0.6463	0.6353	0.9796
	24	0.9568	0.9983	0.8652	0.7160	0.7425	0.9738
	25	0.9273	0.9483	0.8730	0.7918	0.7376	0.9847
	AVE	0.9491	0.9518	0.9045	0.7881	0.8211	0.9872
$\beta =20$	1	0.9235	0.9167	0.8517	0.6962	0.7660	0.9867
	2	0.9869	0.9690	0.9645	0.8872	0.9038	0.9904
	3	0.9246	0.9306	0.8462	0.6922	0.6870	0.9752
	4	0.9450	0.9554	0.8711	0.7783	0.7841	0.9898
	5	0.9668	0.9428	0.9597	0.8243	0.8571	0.9873
	6	0.9317	0.9175	0.9513	0.7098	0.7937	0.9852
	7	0.9473	0.9133	0.9506	0.7408	0.8069	0.9941
	8	0.9269	0.9227	0.9148	0.7553	0.7784	0.9934
	9	0.9489	0.9448	0.9322	0.7922	0.8199	0.9970
	10	0.9419	0.9465	0.8815	0.7521	0.7861	0.9904
	11	0.9347	0.9957	0.8773	0.7899	0.8556	0.9799
	12	0.9497	0.9554	0.8689	0.7735	0.8093	0.9934
	13	0.9932	0.9898	0.9927	0.9740	0.9559	0.9986
	14	0.9408	0.9342	0.9392	0.7442	0.7988	0.9865
	15	0.9430	0.9345	0.8711	0.7641	0.8095	0.9872
	16	0.9788	0.9627	0.9410	0.8537	0.8618	0.9862
	17	0.9670	0.9442	0.9061	0.7770	0.8258	0.9856
	18	0.9882	0.9809	0.9712	0.9416	0.9671	0.9941
	19	0.9868	0.9292	0.9434	0.9091	0.9582	0.9956
	20	0.9283	0.9937	0.8490	0.7636	0.8275	0.9782
	21	0.9845	0.9503	0.9748	0.8924	0.9274	0.9960
	22	0.9648	0.9820	0.9317	0.7671	0.7913	0.9886
	23	0.8896	0.9265	0.7844	0.6289	0.6236	0.9779
	24	0.9488	0.9750	0.8604	0.6828	0.7120	0.9741
	25	0.9303	0.9526	0.8799	0.7888	0.7289	0.9857
	AVE	0.9509	0.9506	0.9086	0.7872	0.8174	0.9879

Table 8. The speed-up ratio related to the elapsed time of obtaining reducts (noisy label ratios of 30% and 40%).

$\mathit{\beta }$	ID	IRFFR & KCR	IRFFR & FGS	IRFFR & SI	IRFFR & AG	IRFFR & ESAR	IRFFR & NFEFR
$\beta =30$	1	0.9209	0.9137	0.8268	0.6515	0.7461	0.9865
	2	0.9865	0.9682	0.9658	0.8803	0.9014	0.9898
	3	0.9240	0.9274	0.8478	0.6891	0.6783	0.9745
	4	0.9415	0.9538	0.8677	0.7556	0.7567	0.9891
	5	0.9673	0.9457	0.9608	0.8110	0.8539	0.9870
	6	0.9307	0.9192	0.9505	0.7137	0.7943	0.9849
	7	0.9489	0.9083	0.9505	0.6885	0.7448	0.9941
	8	0.9244	0.9230	0.8000	0.7395	0.7716	0.9929
	9	0.9484	0.9439	0.9363	0.7827	0.8187	0.9970
	10	0.9386	0.9444	0.8650	0.7246	0.7780	0.9900
	11	0.9396	0.9960	0.8833	0.8005	0.8645	0.9814
	12	0.9485	0.9541	0.8772	0.7399	0.7987	0.9933
	13	0.9821	0.9735	0.9826	0.6704	0.8285	0.9971
	14	0.9378	0.9267	0.9403	0.7351	0.7861	0.9855
	15	0.9394	0.9286	0.8602	0.7220	0.7845	0.9863
	16	0.9788	0.9644	0.9481	0.8523	0.8590	0.9867
	17	0.9640	0.9394	0.9109	0.7641	0.8127	0.9847
	18	0.9880	0.9806	0.9703	0.9374	0.9665	0.9940
	19	0.9873	0.9308	0.9440	0.9088	0.9598	0.9957
	20	0.9378	0.9945	0.8712	0.8211	0.8606	0.9806
	21	0.9844	0.9519	0.9411	0.8880	0.9166	0.9962
	22	0.9631	0.9814	0.9331	0.7146	0.7803	0.9881
	23	0.8897	0.9269	0.7820	0.6416	0.6251	0.9771
	24	0.9465	0.9748	0.8514	0.6689	0.6966	0.9733
	25	0.9398	0.9550	0.8793	0.7773	0.7608	0.9878
	AVE	0.9503	0.9491	0.9018	0.7631	0.8058	0.9877
$\beta =40$	1	0.9170	0.9073	0.8206	0.6247	0.7248	0.9854
	2	0.9860	0.9672	0.9649	0.8709	0.8969	0.9895
	3	0.9209	0.9283	0.8406	0.6849	0.6744	0.9738
	4	0.9392	0.9515	0.8662	0.7274	0.7436	0.9886
	5	0.9667	0.9417	0.9605	0.8086	0.8544	0.9868
	6	0.9295	0.9142	0.9376	0.6830	0.7652	0.9846
	7	0.9566	0.9213	0.9595	0.7141	0.6517	0.9953
	8	0.9238	0.9165	0.7955	0.7398	0.7657	0.9929
	9	0.9457	0.9442	0.9298	0.7777	0.8104	0.9968
	10	0.9382	0.9434	0.8543	0.7057	0.7779	0.9896
	11	0.9294	0.9952	0.8644	0.7585	0.8361	0.9775
	12	0.9423	0.9490	0.8654	0.6928	0.7734	0.9923
	13	0.9908	0.9852	0.9876	0.3556	0.9583	0.9986
	14	0.9298	0.9170	0.9336	0.6953	0.7583	0.9831
	15	0.9377	0.9272	0.8550	0.7270	0.7785	0.9861
	16	0.9753	0.9684	0.9416	0.8230	0.8393	0.9872
	17	0.9654	0.9417	0.9079	0.7658	0.8053	0.9853
	18	0.9890	0.9820	0.9727	0.9410	0.9695	0.9946
	19	0.9880	0.9345	0.9451	0.9134	0.9616	0.9958
	20	0.9390	0.9947	0.8749	0.8356	0.8625	0.9812
	21	0.9833	0.9495	0.9395	0.8802	0.9080	0.9959
	22	0.9622	0.9817	0.9335	0.6899	0.7690	0.9880
	23	0.8837	0.9289	0.7923	0.6483	0.6245	0.9748
	24	0.9455	0.9746	0.8539	0.6730	0.6907	0.9738
	25	0.9454	0.9594	0.8811	0.8048	0.7463	0.9872
	AVE	0.9492	0.9490	0.8991	0.7416	0.7978	0.9874

Following Table 7 and Table 8, it is not difficult to observe that in the comparison with the other six famous devices, not only are all the values of speed-up ratio with respect to four different noisy labels over 25 data sets much higher than 35%, but all average values of the speed-up ratio exceed 45%. Therefore, our IRFFR does possess the ability to accelerate the process of deriving reducts. Moreover, the Wilcoxon signed rank test [71] was also used to compare the algorithms. As can be analyzed from the experimental results, the p-values derived from our IRFFR and other six devices are all $8.8574\times {10}^{-5}$ please use scientific notations throughout the text. which are obviously far less than 0.05. In addition, it can be reasonably conjectured that there exists a tremendous difference between our IRFFR and the other six state-of-the-art devices in terms of efficiency; therefore, the obtained p-values reach the lower bound of Matlab.

On the whole, the conclusion of that our proposed IRFFR does possess a significant advantage in time efficiency as seen by comparison with the other six algorithms can finally be obtained.

4.4. The Second Group of Experiments

In the second group of experiments, to verify the performance of IRFFR, two famous accelerators regarding feature reduction were employed to a conduct a comparison with our framework.

• Quick Random Sampling for Attribute Reduction (QRSAR) [58].
• Dissimilarity-Based Searching for Attribute Reduction (DBSAR) [72].

4.4.1. Comparison of Elapsed Time

In this section, the elapsed time derived from all feature reduction algorithms are compared. Table 9, Table 10 and Table 11 show the mean values of the different elapsed time obtained over 25 datasets.

Table 9. The elapsed time of deriving reducts (label noise ratio of 10% to 20%)(s).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.0628	0.1769	0.3337	0.0521	0.1324	0.2892
2	0.3614	2.4125	2.9180	0.3407	2.6281	2.7269
3	0.0560	0.1306	0.2900	0.1177	0.1268	0.2862
4	0.0928	0.2987	0.5697	0.1453	0.3036	0.5502
5	0.0616	0.1744	0.3232	0.0565	0.1917	0.1507
6	0.0510	0.1712	0.1932	0.0155	0.1640	0.1852
7	0.4165	1.6451	1.2564	0.3827	1.6113	1.2226
8	0.0752	0.2814	0.3545	0.0802	0.1643	0.3359
9	0.1561	0.6201	1.2469	0.2057	0.5956	1.2224
10	0.1343	0.4787	0.8931	0.1300	0.3954	0.8098
11	16.2186	76.8057	99.5899	17.5167	51.8558	125.6400
12	0.1499	0.6312	0.8640	0.2179	0.5231	0.7559
13	0.3156	1.2615	1.0561	0.3887	1.3346	1.1292
14	0.0362	0.0771	0.0891	0.0242	0.0852	0.0824
15	0.0203	0.0790	0.1890	0.0543	0.0953	0.1809
16	0.3712	2.2313	3.0115	0.3655	2.1233	2.9035
17	0.0496	0.2182	0.3856	0.0741	0.1922	0.3596
18	1.2015	3.1645	2.9131	1.1425	3.1055	2.8541
19	0.2156	0.9115	1.2198	0.2294	0.9253	1.2336
20	11.7702	50.6085	78.1043	12.2331	35.4501	72.9459
21	0.3213	2.6717	2.6661	0.3802	2.6857	2.6801
22	2.7791	10.0723	17.7285	2.7587	6.8465	18.5027
23	0.0747	0.1382	0.5356	0.1073	0.1358	0.5332
24	2.5812	8.5460	9.7298	4.2021	12.5036	13.6874
25	0.1252	0.6667	0.5871	0.1928	0.7343	0.6547
AVE	1.5079	6.5789	10.0019	1.6566	4.9964	10.0769

Table 10. The elapsed time of deriving reducts (label noise ratio of 30% to 40%)(s).

ID	$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.0887	0.1196	0.2764	0.0733	0.1107	0.2675
2	0.4025	2.4046	2.5034	0.4111	2.2325	2.3313
3	0.0982	0.1213	0.2807	0.0790	0.1209	0.2803
4	0.1327	0.2789	0.5255	0.0807	0.2270	0.4736
5	0.1023	0.1805	0.1395	0.0339	0.1807	0.1397
6	0.0708	0.1681	0.1893	0.0255	0.1578	0.1790
7	0.3220	1.5506	1.1619	0.3736	1.6022	1.2135
8	0.1098	0.1687	0.3403	0.0920	0.1548	0.3264
9	0.2361	0.6052	1.2320	0.1684	0.6431	1.2699
10	0.1998	0.3467	0.7611	0.2117	0.3503	0.7647
11	16.2165	49.4282	123.2124	19.5709	49.428	123.2122
12	0.2431	0.4300	0.6628	0.1811	0.3891	0.6219
13	0.2893	1.2352	1.0298	0.2976	1.2435	1.0381
14	0.0301	0.0829	0.0801	0.0120	0.0819	0.0791
15	0.0907	0.0863	0.1719	0.0242	0.0840	0.1696
16	0.3899	2.0351	2.8153	0.6680	2.9423	3.7225
17	0.0894	0.1813	0.3487	0.0802	0.1735	0.3409
18	1.1215	3.0845	2.8331	1.0330	2.9960	2.7446
19	0.2395	0.9354	1.2437	0.2970	0.9929	1.3012
20	10.5013	42.5415	80.0373	9.7713	43.3682	80.8640
21	0.3760	2.5805	2.5749	0.3225	2.4210	2.4154
22	2.8621	4.9675	16.6237	2.7941	4.0047	15.6609
23	0.1231	0.1298	0.5272	0.1149	0.1335	0.5309
24	4.4067	12.5035	13.6873	4.3774	12.8494	14.0332
25	0.1370	0.6785	0.5989	0.0373	0.5788	0.4992
AVE	1.5552	5.0738	10.1543	1.6452	5.0987	10.1792

Table 11. The speed-up ratio related to the elapsed time of obtaining reducts (label noise ratios of 10% to 40%).

ID	$\mathit{\beta }=10$		$\mathit{\beta }=20$		$\mathit{\beta }=30$		$\mathit{\beta }=40$
	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR
1	0.6450	0.8118	0.6065	0.8198	0.2584	0.6791	0.3379	0.7260
2	0.8502	0.8761	0.8704	0.8751	0.8326	0.8392	0.8159	0.8237
3	0.5712	0.8069	0.0718	0.5887	0.1904	0.6502	0.3466	0.7182
4	0.6893	0.8371	0.5214	0.7359	0.5242	0.7475	0.6445	0.8296
5	0.6468	0.8094	0.7053	0.6251	0.4332	0.2667	0.8124	0.7573
6	0.7021	0.7360	0.9055	0.9163	0.5788	0.6260	0.8384	0.8575
7	0.7468	0.6685	0.7625	0.6870	0.7923	0.7229	0.7668	0.6921
8	0.7328	0.7879	0.5119	0.7612	0.3491	0.6773	0.4057	0.7181
9	0.7483	0.8748	0.6546	0.8317	0.6099	0.8084	0.7381	0.8674
10	0.7194	0.8496	0.6712	0.8395	0.4237	0.7375	0.3957	0.7232
11	0.7888	0.8371	0.6622	0.8606	0.6719	0.8684	0.6041	0.8412
12	0.7625	0.8265	0.5834	0.7117	0.4347	0.6332	0.5346	0.7088
13	0.7498	0.7012	0.7088	0.6558	0.7658	0.7191	0.7607	0.7133
14	0.5305	0.5937	0.7160	0.7063	0.6369	0.6242	0.8535	0.8483
15	0.7430	0.8926	0.4302	0.6998	-0.0510	0.4724	0.7119	0.8573
16	0.8336	0.8767	0.8279	0.8741	0.8084	0.8615	0.7730	0.8206
17	0.7727	0.8714	0.6145	0.7939	0.5069	0.7436	0.5378	0.7647
18	0.6203	0.5876	0.6321	0.5997	0.6364	0.6041	0.6552	0.6236
19	0.7635	0.8232	0.7521	0.8140	0.7440	0.8074	0.7009	0.7717
20	0.7674	0.8493	0.6549	0.8323	0.7532	0.8688	0.7747	0.8792
21	0.8797	0.8795	0.8584	0.8581	0.8543	0.8540	0.8668	0.8665
22	0.7241	0.8432	0.5971	0.8509	0.4238	0.8278	0.3023	0.8216
23	0.4595	0.8605	0.2099	0.7988	0.0516	0.7665	0.1393	0.7836
24	0.6980	0.7347	0.6639	0.6930	0.6476	0.6780	0.6593	0.6881
25	0.8122	0.7867	0.7374	0.7055	0.7981	0.7712	0.9356	0.9253
AVE	0.7183	0.8009	0.6372	0.7654	0.5470	0.7142	0.6365	0.7851

With an in-depth analysis of Table 9, Table 10 and Table 11, it is not difficult to obtain the following conclusions.

• Compared with those of other advanced accelerators, the time consumptions for deriving the final reduct of our IRFFR were considerably superior, meaning the mechanism of grouping and parallel selection does improve the efficiency of selecting features. In other words, our IRFFR substantially reduces the time needed to complete the process of selecting features. With the data set “Pen-Based Recognition of Handwritten Digits” (ID-11)’ as an example, when $\beta =10$, the elapsed time of the three algorithms are 16.2186, 76.8057, and 99.5899 s, respectively. Moreover, regarding three other ratios ($\beta =20,30,40$), the elapsed time also shows great differences.
• With the examples of both IRFFR and QRSAR, the change of ratio does not bring distinct oscillation to the elapsed time of our IRFFR. The essential reason for this is that the mechanism of the diverse evaluation is especially significant for the selection of more qualified features if data perturbation occurs. However, this mechanism does not exist in QRSAR, which may results in some abnormal changes to QRSAR. For instance, when $\beta$ changes from 10 to 30, the elapsed times of QRSAR for “Twonorm” (ID-20) are 50.6085, 35.4501, and 42.5415 s, respectively.
• Although our IRFFR is not faster than the two comparative algorithms in all cases, the speed-up ratios related to elapsed time of IRFFR are all higher than 40%. This is mainly because IRFFR selects the qualified features in parallel; that is, IRFFR places the optimal feature at a specific location in each group, and the final feature subset is then derived. From this point of view, QRSAR and DBSAR are more complicated than IRFFR.

4.4.2. Comparison of Classification Performances

In this section, the classification performances of the selected features with respect to three feature reduction approaches are examined. The classification accuracies and classification stabilities are recorded Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17. Note that the classifiers are KNN, CART and SVM.

Table 12. The KNN classification accuracies (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8984	0.9154	0.9159	0.9201	0.9267	0.9146	0.8873	0.9036	0.8983	0.9005	0.8534	0.8503
2	0.5501	0.5261	0.5121	0.5074	0.4144	0.3927	0.5128	0.3497	0.3291	0.4840	0.3137	0.2751
3	0.4033	0.4306	0.4301	0.4186	0.4274	0.4175	0.4018	0.4122	0.4119	0.4111	0.4032	0.4044
4	0.5665	0.5544	0.5522	0.5884	0.5373	0.5389	0.5674	0.5280	0.5278	0.5866	0.5318	0.5328
5	0.7421	0.5516	0.7401	0.7361	0.6795	0.6357	0.7532	0.4725	0.5476	0.7540	0.7548	0.7990
6	0.7598	0.7820	0.8308	0.8183	0.7805	0.7424	0.7696	0.7526	0.6507	0.7341	0.7700	0.7345
7	0.8310	0.8218	0.8049	0.8437	0.7850	0.8500	0.8250	0.7843	0.7817	0.8008	0.7680	0.7418
8	0.7437	0.6897	0.6815	0.7133	0.7121	0.7347	0.6609	0.6917	0.6419	0.6685	0.6529	0.6795
9	0.7744	0.7813	0.7625	0.7334	0.5849	0.5724	0.7508	0.5855	0.5752	0.7346	0.5795	0.5710
10	0.6341	0.5945	0.6430	0.6212	0.5462	0.5431	0.6099	0.5423	0.5382	0.6058	0.5368	0.5221
11	0.8011	0.7988	0.7850	0.7015	0.7145	0.7102	0.6632	0.6988	0.6712	0.6742	0.6868	0.6403
12	0.7030	0.7480	0.6999	0.7134	0.7204	0.7451	0.6183	0.6276	0.6098	0.6156	0.6197	0.6387
13	0.8812	0.9022	0.9154	0.7901	0.6404	0.8611	0.7761	0.5783	0.8488	0.7156	0.5718	0.7685
14	0.6848	0.6552	0.6911	0.6485	0.6145	0.6403	0.5652	0.5658	0.5765	0.5880	0.5652	0.5815
15	0.7295	0.7178	0.7161	0.6886	0.6898	0.6832	0.8041	0.7733	0.7710	0.7401	0.7302	0.7368
16	0.7604	0.7071	0.8358	0.7618	0.5641	0.7149	0.7507	0.4432	0.6725	0.7028	0.6866	0.5991
17	0.5907	0.5639	0.5359	0.5712	0.4740	0.4804	0.5463	0.4162	0.4126	0.5170	0.3825	0.3773
18	0.8365	0.8294	0.8161	0.7814	0.7880	0.8224	0.7617	0.7663	0.7525	0.7296	0.7260	0.7261
19	0.6563	0.5959	0.6340	0.6178	0.5803	0.5793	0.6512	0.6603	0.6346	0.6139	0.5507	0.5957
20	0.8316	0.8810	0.8454	0.7988	0.8270	0.8136	0.7780	0.7733	0.7790	0.7280	0.7302	0.7080
21	0.6058	0.5030	0.5375	0.5569	0.4856	0.5661	0.5326	0.4416	0.4872	0.5525	0.4675	0.4905
22	0.8116	0.7351	0.7132	0.7684	0.6447	0.5109	0.7592	0.5665	0.4491	0.7631	0.5315	0.4636
23	0.7651	0.8704	0.8718	0.7461	0.8495	0.8511	0.7865	0.8207	0.8284	0.7315	0.7624	0.7642
24	0.4354	0.4409	0.4165	0.4023	0.4147	0.4177	0.4351	0.4063	0.4100	0.4118	0.3814	0.3787
25	0.5829	0.5779	0.5905	0.5994	0.5422	0.5770	0.5889	0.5420	0.5282	0.5715	0.5187	0.5205
AVE	0.7032	0.6870	0.6991	0.6819	0.6377	0.6526	0.6702	0.6041	0.6133	0.6534	0.6030	0.6040
		↑ 2.36%	↑ 0.59%		↑ 6.93%	↑ 4.49%	↑ 10.94%	↑ 9.28%		↑ 8.36%	↑ 8.18%

↑ indicates that the performance of IRFFR is better than the comparative method; ↓ indicates that the performance of IRFFR is worse than the comparative method.

Table 13. The CART classification accuracies (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8908	0.9094	0.9093	0.9083	0.9300	0.9291	0.8913	0.9114	0.9109	0.8643	0.8928	0.8923
2	0.5899	0.6323	0.6239	0.5484	0.5141	0.4942	0.5528	0.4352	0.4446	0.5281	0.4028	0.3634
3	0.4204	0.4401	0.4409	0.4153	0.4275	0.4282	0.4140	0.4158	0.4121	0.4150	0.4035	0.4037
4	0.5799	0.5662	0.5736	0.5836	0.5507	0.5650	0.5742	0.5296	0.5351	0.5820	0.5231	0.5368
5	0.7590	0.5812	0.7893	0.7493	0.5441	0.7317	0.7240	0.5185	0.6637	0.6696	0.5104	0.6359
6	0.7658	0.7955	0.8170	0.7850	0.8038	0.7455	0.7844	0.8016	0.7091	0.8193	0.7953	0.7384
7	0.8318	0.8156	0.8011	0.8398	0.7809	0.8453	0.8194	0.7817	0.7823	0.7994	0.7626	0.7423
8	0.7201	0.6749	0.6731	0.6801	0.6513	0.6363	0.6893	0.7129	0.6539	0.7069	0.6281	0.6575
9	0.7366	0.6295	0.6567	0.7185	0.6281	0.6322	0.6451	0.6415	0.6363	0.6252	0.6314	0.6366
10	0.6012	0.6112	0.6117	0.5946	0.5666	0.5621	0.6113	0.5594	0.5400	0.5654	0.5488	0.5247
11	0.9166	0.9256	0.9102	0.9006	0.8560	0.8610	0.8571	0.7974	0.8082	0.8144	0.7624	0.7833
12	0.7132	0.6553	0.6413	0.6522	0.6107	0.5783	0.6179	0.6023	0.5736	0.5563	0.5632	0.5613
13	0.7820	0.8960	0.9116	0.7862	0.6363	0.8564	0.7705	0.5757	0.8494	0.7142	0.5664	0.7690
14	0.7277	0.6499	0.6496	0.6917	0.6028	0.6542	0.6514	0.5672	0.5884	0.6892	0.5709	0.5962
15	0.7216	0.7117	0.7180	0.7056	0.7004	0.7024	0.7716	0.7604	0.7884	0.7325	0.7174	0.7316
16	0.7921	0.7614	0.9191	0.8102	0.6893	0.8852	0.7900	0.5658	0.8819	0.7682	0.5040	0.8148
17	0.6467	0.6397	0.6025	0.6146	0.6026	0.6013	0.5996	0.5247	0.5267	0.6030	0.5174	0.4734
18	0.8073	0.8232	0.8123	0.7775	0.7839	0.8177	0.7561	0.7637	0.7531	0.7282	0.7206	0.7266
19	0.6571	0.5897	0.6302	0.6139	0.5762	0.5746	0.6456	0.6577	0.6352	0.6125	0.5453	0.5962
20	0.8971	0.8971	0.9324	0.8644	0.8441	0.8512	0.8534	0.8136	0.8469	0.8370	0.7874	0.8169
21	0.7123	0.6362	0.6697	0.6873	0.6256	0.7017	0.6811	0.5990	0.6578	0.6905	0.6185	0.6744
22	0.9135	0.9410	0.9261	0.8936	0.8827	0.5917	0.9024	0.8516	0.5419	0.8940	0.8120	0.5406
23	0.8041	0.8348	0.8350	0.7710	0.7751	0.7730	0.7639	0.6853	0.6863	0.7071	0.6416	0.6545
24	0.4675	0.4959	0.4760	0.4711	0.4752	0.4781	0.4665	0.4553	0.4565	0.4425	0.4204	0.4246
25	0.5837	0.5717	0.5867	0.5955	0.5381	0.5723	0.5833	0.5394	0.5288	0.5701	0.5133	0.5210
AVE	0.7215	0.7074	0.7247	0.7063	0.6638	0.6827	0.6967	0.6427	0.6564	0.6774	0.6144	0.6326
		↑ 1.99%	↓ 0.044%		↑ 6.40%	↑ 3.46%		↑ 8.40%	↑ 6.14%		↑ 10.25%	↑ 7.08%

Table 14. The SVM classification accuracies (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8872	0.8960	0.8917	0.9058	0.9212	0.9208	0.8802	0.9207	0.9230	0.8686	0.8607	0.8559
2	0.6241	0.6475	0.6552	0.6073	0.5848	0.5800	0.5855	0.5512	0.5536	0.5872	0.5614	0.5597
3	0.6080	0.5873	0.5904	0.5909	0.5718	0.5714	0.5570	0.5408	0.5402	0.5687	0.5408	0.5402
4	0.5699	0.5634	0.5738	0.5819	0.5318	0.5605	0.5658	0.5152	0.5089	0.5627	0.5057	0.5033
5	0.7480	0.8147	0.7952	0.7378	0.6509	0.7189	0.7320	0.6439	0.6334	0.7375	0.6283	0.6016
6	0.8180	0.8073	0.7882	0.8262	0.7746	0.8335	0.8019	0.7575	0.7624	0.7920	0.7550	0.7246
7	0.6433	0.5814	0.6173	0.6003	0.5699	0.5628	0.6281	0.6335	0.6153	0.6051	0.5377	0.5785
8	0.6932	0.5833	0.5794	0.6532	0.5757	0.5717	0.6728	0.5660	0.5647	0.6751	0.5622	0.5598
9	0.6020	0.5812	0.5822	0.5882	0.5405	0.5346	0.5804	0.5322	0.5261	0.5852	0.5242	0.5032
10	0.8327	0.8337	0.8188	0.8035	0.7915	0.7828	0.7777	0.7478	0.7516	0.7213	0.7064	0.6955
11	0.6703	0.5880	0.5996	0.6688	0.5526	0.5399	0.6851	0.5485	0.5236	0.6288	0.5221	0.5029
12	0.6580	0.5853	0.6048	0.6433	0.5753	0.5826	0.6134	0.5825	0.5634	0.6095	0.5304	0.5376
13	0.7323	0.7129	0.7330	0.7289	0.7503	0.7456	0.7238	0.7380	0.7595	0.7077	0.7145	0.7400
14	0.7682	0.8877	0.8987	0.7726	0.6300	0.8446	0.7530	0.5515	0.8295	0.7068	0.5588	0.7513
15	0.6738	0.6666	0.6748	0.6704	0.6309	0.6469	0.6199	0.5754	0.5959	0.6198	0.5558	0.5551
16	0.7935	0.8149	0.7994	0.7639	0.7776	0.8059	0.7386	0.7395	0.7332	0.7208	0.7130	0.7089
17	0.7112	0.6052	0.6568	0.6895	0.6647	0.7209	0.6790	0.6418	0.6721	0.6646	0.6360	0.6697
18	0.8704	0.8736	0.7496	0.8465	0.8284	0.7322	0.8496	0.7779	0.6261	0.8449	0.7292	0.6319
19	0.8529	0.8105	0.8169	0.7975	0.7029	0.6985	0.7501	0.6029	0.5987	0.6764	0.5628	0.5568
20	0.5760	0.5869	0.5908	0.5814	0.5824	0.5875	0.5757	0.5683	0.5773	0.5687	0.5691	0.5638
21	0.8175	0.8125	0.7906	0.8274	0.7796	0.8336	0.8075	0.7628	0.7680	0.7933	0.7564	0.7304
22	0.7677	0.8929	0.9011	0.7738	0.6350	0.8447	0.7586	0.5568	0.8351	0.7081	0.5602	0.7571
23	0.7930	0.8201	0.8018	0.7651	0.7826	0.8060	0.7442	0.7448	0.7388	0.7221	0.7144	0.7147
24	0.6428	0.5866	0.6197	0.6015	0.5749	0.5629	0.6337	0.6388	0.6209	0.6064	0.5391	0.5843
25	0.5694	0.5686	0.5762	0.5831	0.5368	0.5606	0.5714	0.5205	0.5145	0.5640	0.5071	0.5091
AVE	0.7169	0.7083	0.7082	0.7044	0.6607	0.6860	0.6914	0.6383	0.6535	0.6738	0.6141	0.6254
		↑ 1.21%	↑ 1.23%		↑ 6.61%	↑ 2.68%		↑ 8.32%	↑ 5.80%		↑ 9.72%	↑ 7.74%

Table 15. The KNN classification stabilities (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8929	0.9085	0.9102	0.9109	0.8883	0.8886	0.8765	0.9045	0.8912	0.8931	0.8359	0.8229
2	0.6087	0.6048	0.6071	0.5933	0.5820	0.5891	0.5803	0.5947	0.6007	0.5796	0.6090	0.6326
3	0.6276	0.6029	0.6024	0.6227	0.5750	0.5738	0.6028	0.5524	0.5529	0.6145	0.5479	0.5456
4	0.6010	0.5895	0.5926	0.5854	0.5275	0.5373	0.5876	0.5312	0.5285	0.5787	0.5196	0.5267
5	0.7518	0.7038	0.7572	0.7199	0.6240	0.6156	0.7238	0.6067	0.5555	0.7254	0.5926	0.5493
6	0.7677	0.8002	0.8724	0.8584	0.7930	0.8462	0.7683	0.7670	0.6680	0.7984	0.7730	0.8045
7	0.8289	0.8161	0.7987	0.8370	0.7811	0.8417	0.8212	0.7808	0.7795	0.7985	0.7592	0.7410
8	0.6849	0.6621	0.6435	0.6329	0.6013	0.5775	0.6401	0.6385	0.5951	0.5637	0.6001	0.6031
9	0.7439	0.5455	0.5457	0.7173	0.5295	0.5146	0.7197	0.5228	0.5239	0.6905	0.5342	0.5323
10	0.6563	0.5962	0.5965	0.6047	0.5253	0.5199	0.6048	0.5294	0.5336	0.6103	0.5362	0.5316
11	0.8885	0.8821	0.8747	0.8543	0.8360	0.8402	0.8029	0.7763	0.7802	0.7620	0.7358	0.7104
12	0.6780	0.5965	0.6353	0.6822	0.5932	0.5798	0.7045	0.6114	0.5967	0.6641	0.5874	0.6669
13	0.7791	0.8965	0.9092	0.7834	0.6365	0.8528	0.7723	0.5748	0.8466	0.7133	0.5630	0.7677
14	0.7231	0.6345	0.6262	0.6751	0.5848	0.5667	0.6023	0.5946	0.5608	0.6129	0.5606	0.5369
15	0.7484	0.7578	0.7640	0.7664	0.7445	0.7480	0.7764	0.7904	0.7524	0.7593	0.7555	0.7999
16	0.7515	0.8297	0.6526	0.7305	0.5816	0.6990	0.7127	0.5836	0.6686	0.6517	0.6020	0.6273
17	0.6455	0.6265	0.6379	0.6449	0.5729	0.5611	0.5997	0.5572	0.5680	0.5950	0.5469	0.5591
18	0.8044	0.8237	0.8099	0.7747	0.7841	0.8141	0.7579	0.7628	0.7503	0.7273	0.7172	0.7253
19	0.6542	0.5902	0.6278	0.6111	0.5764	0.5710	0.6474	0.6568	0.6324	0.6116	0.5419	0.5949
20	0.7396	0.7443	0.7758	0.7018	0.7365	0.7153	0.6890	0.6889	0.6862	0.6579	0.6501	0.6387
21	0.6368	0.5674	0.5895	0.6404	0.6129	0.6069	0.6018	0.5789	0.5707	0.6165	0.5866	0.5777
22	0.7666	0.7081	0.7152	0.7128	0.6171	0.7126	0.7065	0.5834	0.6013	0.7095	0.5654	0.6123
23	0.7397	0.8793	0.8779	0.7265	0.8417	0.8491	0.7737	0.7879	0.7981	0.6763	0.7230	0.7206
24	0.5792	0.5884	0.5910	0.5823	0.5742	0.5765	0.5811	0.5715	0.5737	0.5759	0.5791	0.5851
25	0.5808	0.5722	0.5843	0.5927	0.5383	0.5687	0.5851	0.5385	0.5260	0.5692	0.5099	0.5197
AVE	0.7152	0.7011	0.7039	0.7025	0.6503	0.6706	0.6895	0.6434	0.6456	0.6702	0.6213	0.6373
		↑ 2.01%	↑ 1.61%		↑ 8.03%	↑ 4.76%		↑ 7.17%	↑ 6.82%		↑ 7.87%	↑ 5.16%

Table 16. The CART classification stabilities (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8916	0.8967	0.8887	0.9044	0.9202	0.9195	0.8846	0.9257	0.9256	0.8712	0.8643	0.8637
2	0.6285	0.6482	0.6522	0.6059	0.5838	0.5787	0.5899	0.5562	0.5562	0.5898	0.5650	0.5675
3	0.6124	0.5880	0.5874	0.5895	0.5708	0.5701	0.5614	0.5458	0.5428	0.5713	0.5444	0.5480
4	0.5743	0.5641	0.5708	0.5805	0.5308	0.5592	0.5702	0.5202	0.5115	0.5653	0.5093	0.5111
5	0.7524	0.8154	0.7922	0.7364	0.6499	0.7176	0.7364	0.6489	0.6360	0.7401	0.6319	0.6094
6	0.8224	0.8080	0.7852	0.8248	0.7736	0.8322	0.8063	0.7625	0.7650	0.7946	0.7586	0.7324
7	0.8219	0.8132	0.7876	0.8260	0.7786	0.8323	0.8119	0.7678	0.7706	0.7959	0.7600	0.7382
8	0.6477	0.5821	0.6143	0.5989	0.5689	0.5615	0.6325	0.6385	0.6179	0.6077	0.5413	0.5863
9	0.6976	0.5840	0.5764	0.6518	0.5747	0.5704	0.6772	0.5710	0.5673	0.6777	0.5658	0.5676
10	0.6064	0.5819	0.5792	0.5868	0.5395	0.5333	0.5848	0.5372	0.5287	0.5878	0.5278	0.5110
11	0.8371	0.8344	0.8158	0.8021	0.7905	0.7815	0.7821	0.7528	0.7542	0.7239	0.7100	0.7033
12	0.6747	0.5887	0.5966	0.6674	0.5516	0.5386	0.6895	0.5535	0.5262	0.6314	0.5257	0.5107
13	0.7721	0.8936	0.8981	0.7724	0.6340	0.8434	0.7630	0.5618	0.8377	0.7107	0.5638	0.7649
14	0.6624	0.5860	0.6018	0.6419	0.5743	0.5813	0.6178	0.5875	0.5660	0.6121	0.5340	0.5454
15	0.7367	0.7136	0.7300	0.7275	0.7493	0.7443	0.7282	0.7430	0.7621	0.7103	0.7181	0.7478
16	0.7726	0.8884	0.8957	0.7712	0.6290	0.8433	0.7574	0.5565	0.8321	0.7094	0.5624	0.7591
17	0.6782	0.6673	0.6718	0.6690	0.6299	0.6456	0.6243	0.5804	0.5985	0.6224	0.5594	0.5629
18	0.7974	0.8208	0.7988	0.7637	0.7816	0.8047	0.7486	0.7498	0.7414	0.7247	0.7180	0.7225
19	0.6472	0.5873	0.6167	0.6001	0.5739	0.5616	0.6381	0.6438	0.6235	0.6090	0.5427	0.5921
20	0.7979	0.8156	0.7964	0.7625	0.7766	0.8046	0.7430	0.7445	0.7358	0.7234	0.7166	0.7167
21	0.7156	0.6059	0.6538	0.6881	0.6637	0.7196	0.6834	0.6468	0.6747	0.6672	0.6396	0.6775
22	0.8748	0.8743	0.7466	0.8451	0.8274	0.7309	0.8540	0.7829	0.6287	0.8475	0.7328	0.6397
23	0.8573	0.8112	0.8139	0.7961	0.7019	0.6972	0.7545	0.6079	0.6013	0.6790	0.5664	0.5646
24	0.5804	0.5876	0.5878	0.5800	0.5814	0.5862	0.5801	0.5733	0.5799	0.5713	0.5727	0.5716
25	0.5738	0.5693	0.5732	0.5817	0.5358	0.5593	0.5758	0.5255	0.5171	0.5666	0.5107	0.5169
AVE	0.7213	0.7090	0.7052	0.7030	0.6597	0.6847	0.6958	0.6434	0.6560	0.6764	0.6177	0.6332
		↑ 1.73%	↑ 2.28%		↑ 6.56%	↑ 2.67%		↑ 8.14%	↑ 6.07%		↑ 9.50%	↑ 6.82%

Table 17. The SVM classification stabilities (label noise ratio of 10% to 40%).

ID	$\mathit{\beta }=10$			$\mathit{\beta }=20$			$\mathit{\beta }=30$			$\mathit{\beta }=40$
	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR	IRFFR	QRSAR	DBSAR
1	0.8908	0.9170	0.9150	0.9070	0.9380	0.9259	0.8924	0.9123	0.9117	0.8616	0.8939	0.8957
2	0.5899	0.6399	0.6296	0.5471	0.5221	0.4910	0.5539	0.4361	0.4454	0.5254	0.4039	0.3668
3	0.4204	0.4477	0.4466	0.4140	0.4355	0.4250	0.4151	0.4167	0.4129	0.4123	0.4046	0.4071
4	0.5799	0.5738	0.5793	0.5823	0.5587	0.5618	0.5753	0.5305	0.5359	0.5793	0.5242	0.5402
5	0.7590	0.5888	0.7950	0.7480	0.5521	0.7285	0.7251	0.5194	0.6645	0.6669	0.5115	0.6393
6	0.7658	0.8031	0.8227	0.7837	0.8118	0.7423	0.7855	0.8025	0.7099	0.8166	0.7964	0.7418
7	0.7201	0.6825	0.6788	0.6788	0.6593	0.6331	0.6904	0.7138	0.6547	0.7042	0.6292	0.6609
8	0.7366	0.6371	0.6624	0.7172	0.6361	0.6290	0.6462	0.6424	0.6371	0.6225	0.6325	0.6400
9	0.6012	0.6188	0.6174	0.5933	0.5746	0.5589	0.6124	0.5603	0.5408	0.5627	0.5499	0.5281
10	0.9166	0.9332	0.9159	0.8993	0.8640	0.8578	0.8582	0.7983	0.8090	0.8117	0.7635	0.7867
11	0.7132	0.6629	0.6470	0.6509	0.6187	0.5751	0.6190	0.6032	0.5744	0.5536	0.5643	0.5647
12	0.7277	0.6575	0.6553	0.6904	0.6108	0.6510	0.6525	0.5681	0.5892	0.6865	0.5720	0.5996
13	0.7216	0.7193	0.7237	0.7043	0.7084	0.6992	0.7727	0.7613	0.7892	0.7298	0.7185	0.7350
14	0.7921	0.7690	0.9248	0.8089	0.6973	0.8820	0.7911	0.5667	0.8827	0.7655	0.5051	0.8182
15	0.6467	0.6473	0.6082	0.6133	0.6106	0.5981	0.6007	0.5256	0.5275	0.6003	0.5185	0.4768
16	0.8971	0.9047	0.9381	0.8631	0.8521	0.8480	0.8545	0.8145	0.8477	0.8343	0.7885	0.8203
17	0.7123	0.6438	0.6754	0.6860	0.6336	0.6985	0.6822	0.5999	0.6586	0.6878	0.6196	0.6778
18	0.9135	0.9486	0.9318	0.8923	0.8907	0.5885	0.9035	0.8525	0.5427	0.8913	0.8131	0.5440
19	0.8041	0.8424	0.8407	0.7697	0.7831	0.7698	0.7650	0.6862	0.6871	0.7044	0.6427	0.6579
20	0.4675	0.5035	0.4817	0.4698	0.4832	0.4749	0.4676	0.4562	0.4573	0.4398	0.4215	0.4280
21	0.8318	0.8232	0.8068	0.8385	0.7889	0.8421	0.8205	0.7826	0.7831	0.7967	0.7637	0.7457
22	0.7820	0.9036	0.9173	0.7849	0.6443	0.8532	0.7716	0.5766	0.8502	0.7115	0.5675	0.7724
23	0.8073	0.8308	0.8180	0.7762	0.7919	0.8145	0.7572	0.7646	0.7539	0.7255	0.7217	0.7300
24	0.6571	0.5973	0.6359	0.6126	0.5842	0.5714	0.6467	0.6586	0.6360	0.6098	0.5464	0.5996
25	0.5837	0.5793	0.5924	0.5942	0.5461	0.5691	0.5844	0.5403	0.5296	0.5674	0.5144	0.5244
AVE	0.7215	0.7150	0.7304	0.7050	0.6718	0.6795	0.6978	0.6435	0.6572	0.6747	0.6155	0.6360
		↑ 0.91%	↑ 1.22%		↑ 4.94%	↑ 3.75%		↑ 8.44%	↑ 6.18%		↑ 9.62%	↑ 6.08%

Observing Table 12, Table 13, Table 14, Table 15, Table 16 and Table 17, it is not difficult to draw the following conclusions.

• Compared with QRSAR and DBSAR, when $\beta =10$, in KNN, our IRFFR achieves slightly superior rising rates of classification accuracy such that 2.36% and 0.59% (see Table 12). With the increase of $\beta$, the advantage of our IRFFR is gradually revealed. For instance, when $\beta =20$, regarding the KNN classifier, the rising rates of classification accuracy with respect to the comparative algorithms are 6.93% and 4.49%, respectively, which shows a significant increase. The essential reason is that the granularity has been introduced into our framework, the corresponding feature sequence is achieved, and the final subset is then relatively stable. Although the rising rates of QRSAR and DBSAR are slightly lower when $\beta$ increases from 30 to 40, compared with the case of lower ratio of $\beta$, i.e., $\beta =10$, our IRFFR does yield great success.
• Different from classification accuracy, regardless of which label noise ratio is injected and which classifier employed, the classification stabilities of our IRFFR show steady improvement (see Table 15, Table 16 and Table 17). Specifically, if $\beta =40$, concerning all three classifiers, all rising rates of average classification stabilities exceed 5.0 %. Such an improvement is especially significant in a higher label noise ratio because diverse evaluation is helpful for deriving a more stable reduct, and our IRFFR can then posses a better classification performance if data perturbation occurs.

In addition, Table 18 and Table 19 show the counts of wins, ties, and losses regarding the classification stabilities and accuracies in the different classifiers. As has been reported in in [73], the number of wins in s the datasets obeys the normal distribution $N(\frac{s}{2},\frac{\sqrt{s}}{2})$ under the null hypothesis in the sign test for a given learning algorithm. We assert that the IRFFR is significantly better than are those under the significance level $\alpha$, when the number of wins is at least $\frac{s}{2}+Z_{\frac{\alpha }{2}}\times \frac{\sqrt{s}}{2}$. In our experiments, $s=25$, $\alpha =0.1$, then $\frac{s}{2}+Z_{\frac{\alpha }{2}}\times \frac{\sqrt{s}}{2}\approx 17$. This implies that our IRFFR will achieve statistical superiority if the number of wins and ties over 25 datasets reaches 17.

Table 18. Counts of wins, ties, and losses regarding the classification stabilities.

Win/Tie/Loss	$\mathit{\beta }=10$		$\mathit{\beta }=20$		$\mathit{\beta }=30$		$\mathit{\beta }=40$
	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR
KNN	(16/0/9)	(15/0/10)	(22/0/3)	(20/0/5)	(19/0/6)	(21/0/4)	(21/0/4)	(17/0/8)
CART	(17/0/8)	(19/0/6)	(20/0/5)	(15/0/10)	(19/0/6)	(21/0/4)	(23/0/2)	(20/0/5)
SVM	(12/0/13)	(10/0/15)	(18/0/7)	(16/0/9)	(19/0/6)	(21/0/4)	(22/0/3)	(18/0/7)

Table 19. Counts of wins, ties and losses regarding classification accuracies.

Win/Tie/Loss	$\mathit{\beta }=10$		$\mathit{\beta }=20$		$\mathit{\beta }=30$		$\mathit{\beta }=40$
	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR	IRFFR vs. QRSAR	IRFFR vs. DBSAR
KNN	(16/0/9)	(15/0/10)	(16/0/9)	(15/0/10)	(16/0/9)	(18/0/7)	(19/0/6)	(19/0/6)
CART	(13/1/11)	(11/0/14)	(19/0/6)	(16/0/9)	(19/0/6)	(21/0/4)	(22/0/3)	(20/0/5)
SVM	(15/0/10)	(13/0/12)	(20/0/5)	(15/0/10)	(19/0/6)	(20/0/5)	(23/0/2)	(21/0/4)

Considering the above discussions, we can clearly conclude that our IRFFR can not only accelerate the process of deriving reducts but can also provide qualified reducts with better classification performance.

5. Conclusions

In this study, considering the predictable shortcomings of the application of a single feature measure, we developed a novel parallel selector which includes the following: (1) the evaluation of features from diverse viewpoints and (2) a reliable paradigm which can be used for improving the effectiveness and efficiency of final selected features. Therefore, the additive time consumption with respect to incremental evaluation is then reduced. Different from previous devices which only consider single measure-based constraints for deriving qualified reducts, our selector pays considerable attention to the pattern of fusing different measures for attaining reducts with better generalization performance. Furthermore, It is worth emphasizing that our new selector can be seen as an effective framework which can be easily combined with other recent measures and other acceleration strategies. The results of the persuasive experiments and the corresponding analysis strongly prove the superiority of our selector.

Many follow-up comparison studies can be proposed on the basis of our strategy, with the items warranting further exploration being the following.

• It should not be ignored that the problems caused by multilabeling have aroused extensive discussion in the academic community. Therefore, it is urgent to further introduce the proposed method to dimension reduction problems with multilabel distributed data sets.
• The type of data perturbation considered in this paper involves only the aspect of the label. Therefore, can simulate other data perturbation forms, such as injecting feature noise [74], to make the proposed algorithm more robust.