Greenhouse Micro-Climate Prediction Based on Fixed Sensor Placements: A Machine Learning Approach
Abstract
:1. Introduction
2. Review of Related Works
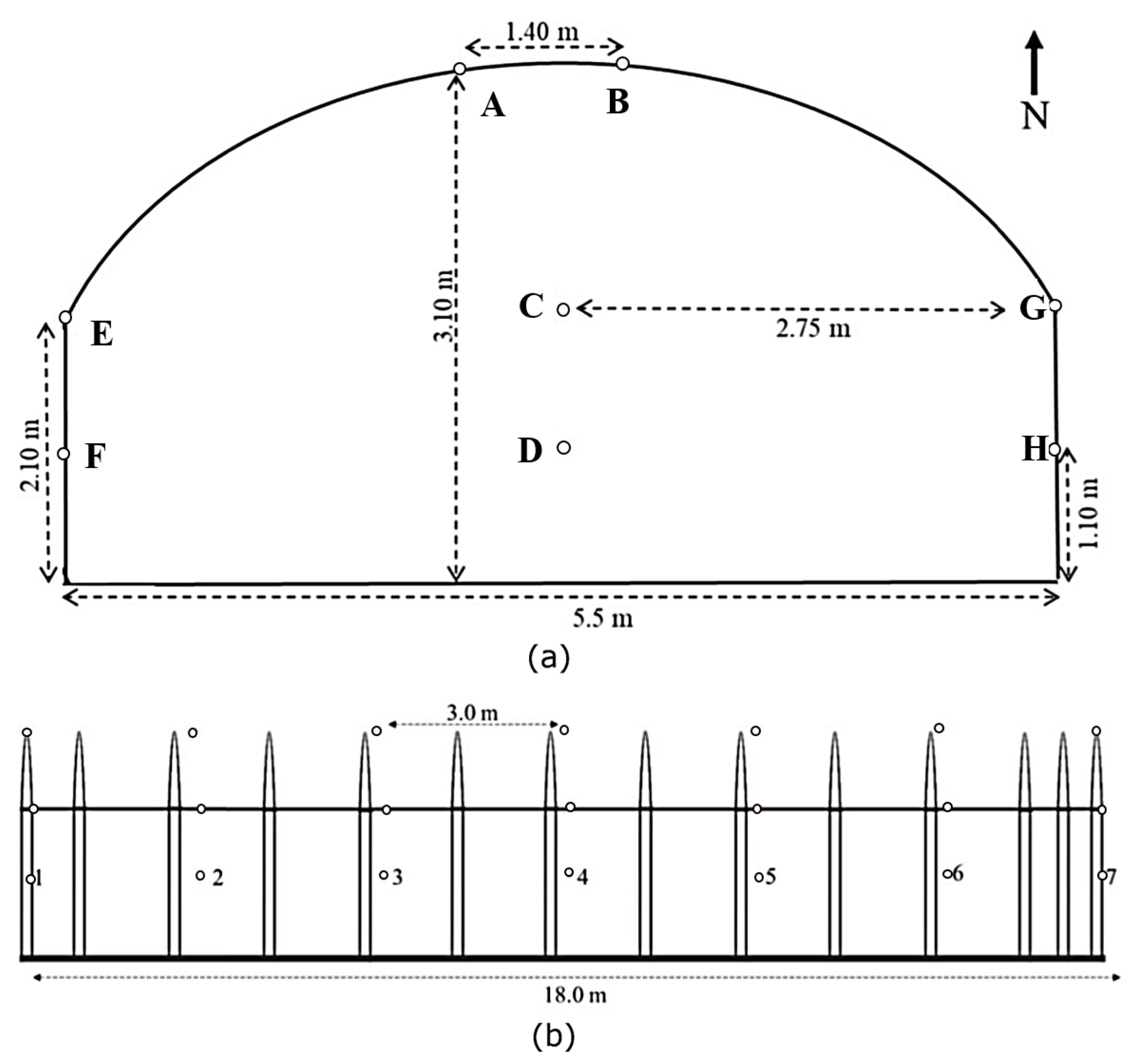
3. Data Description and Pre-Processing
4. Methodology
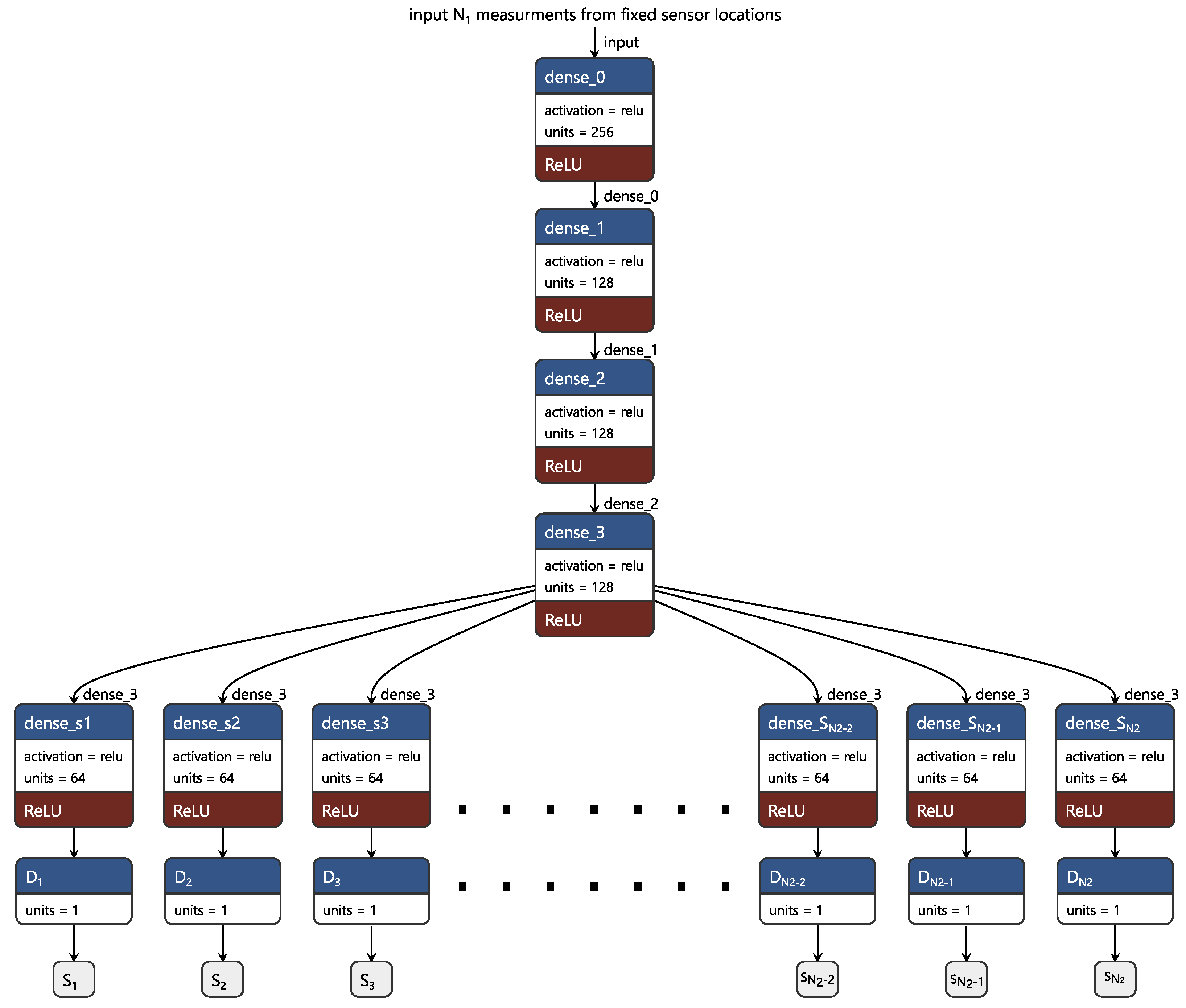
4.1. Dense Neural Network (DNN)-Based Regression Model
4.2. Evaluation Metrics
5. Results and Discussion
5.1. Temperature and Humidity Prediction RMSE
5.2. Correlation Coefficients
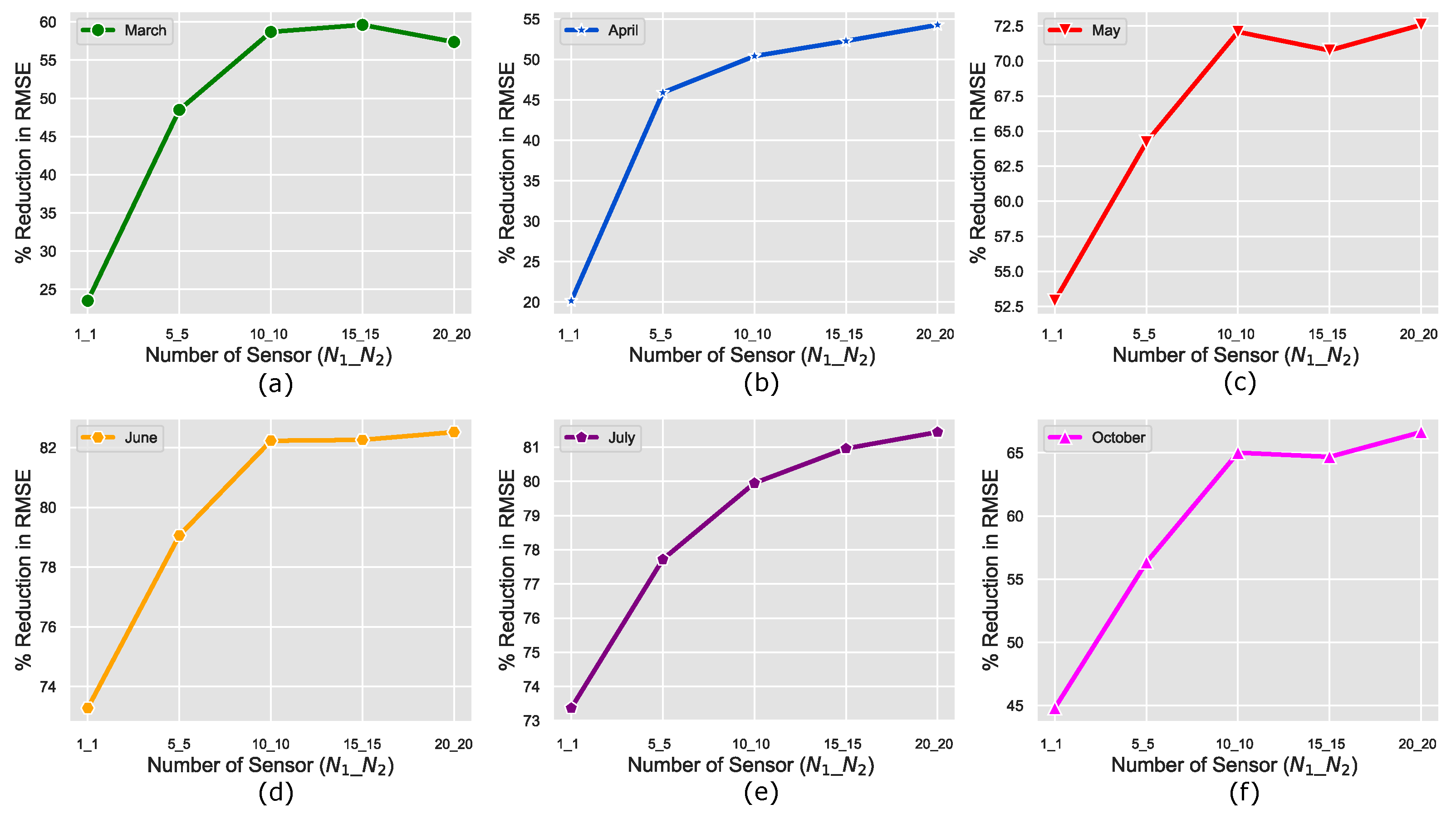
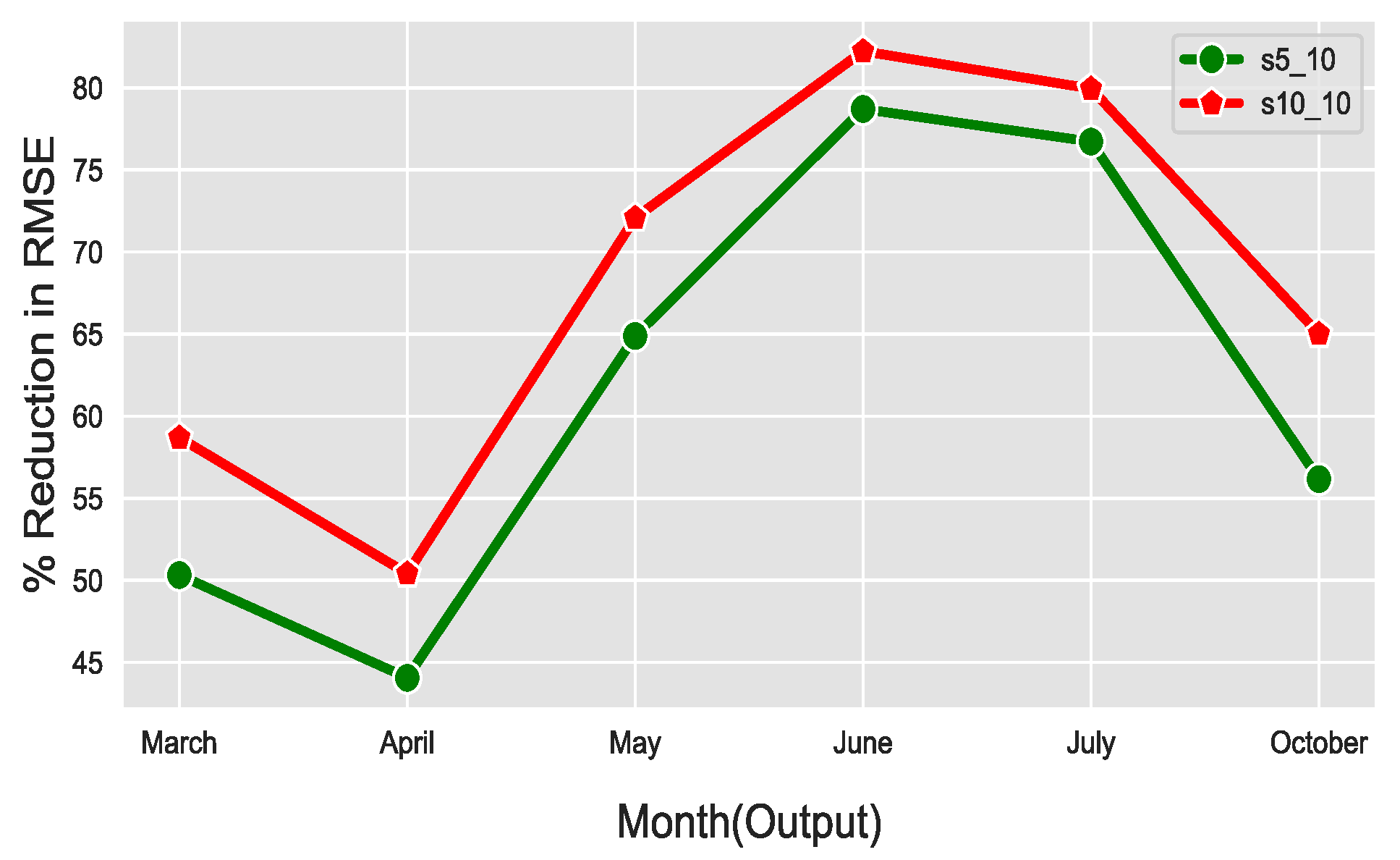
5.3. Effect of Number of Fixed Sensor Locations on the Prediction Accuracy of DNN Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Godde, C.; Mason-D’Croz, D.; Mayberry, D.; Thornton, P.; Herrero, M. Impacts of climate change on the livestock food supply chain; a review of the evidence. Glob. Food Secur. 2021, 28, 100488. [Google Scholar] [CrossRef] [PubMed]
- Kumar, L.; Chhogyel, N.; Gopalakrishnan, T.; Hasan, M.K.; Jayasinghe, S.L.; Kariyawasam, C.S.; Kogo, B.K.; Ratnayake, S. Chapter 4—Climate change and future of agri-food production. In Future Foods; Bhat, R., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 49–79. [Google Scholar] [CrossRef]
- Reddy, P.P. Sustainable Crop Protection under Protected Cultivation; Springer: Singapore, 2016. [Google Scholar]
- Zhang, W.; Xia Dou, Z.; He, P.; Ju, X.; Powlson, D.S.; Chadwick, D.R.; Norse, D.; Lu, Y.; Zhang, Y.; Wu, L.; et al. New technologies reduce greenhouse gas emissions from nitrogenous fertilizer in China. Proc. Natl. Acad. Sci. USA 2013, 110, 8375–8380. [Google Scholar] [CrossRef] [PubMed]
- Research and Markets. Agricultural Films Market by Type (LLDPE, LDPE, Reclaim, EVA, HDPE), Application ((Greenhouse Films (Classic Greenhouse, Macro Tunnels), Silage Films (Silage Stretch Wraps), and Mulch Films (Transparent, Clear Mulches)), and Region—Global Forecast to 2028. 2022. Available online: https://www.marketsandmarkets.com/Market-Reports/agricultural-mulch-films-market-741.html. (accessed on 4 July 2022).
- Zeng, S.; Hu, H.; Xu, L.; Li, G. Nonlinear Adaptive PID Control for Greenhouse Environment Based on RBF Network. Sensors 2012, 12, 5328–5348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahata, K.; Miura, H. Effects of Growth Period and Air Temperature on the Position of the Inflorescence on the Stem of Tomato Plants. Hortic. J. 2017, 86, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Syed, A.M.; Hachem, C. Review of Construction, Geometry, Heating, Ventilation, and Air-Conditioning, and Indoor Climate Requirements of Agricultural Greenhouses. J. Biosyst. Eng. 2019, 23, 18–27. [Google Scholar] [CrossRef]
- Singh, V.K. Prediction of Greenhouse Micro-Climate Using Artificial Neural Network. Appl. Ecol. Environ. Res. 2017, 15, 767–778. [Google Scholar] [CrossRef]
- Vox, G.; Teitel, M.; Pardossi, A.; Minuto, A.; Tinivella, F.; Schettini, E. Sustainable Greenhouse Systems. In Sustainable Agriculture: Technology, Planning and Management; Nova Science Publishers, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Harjunowibowo, D.; Ding, Y.; Omer, S.; Riffat, S. Recent Active Technologies of Greenhouse Systems—A Comprehensive Review. Bulg. J. Agric. Sci. 2018, 24, 158–170. [Google Scholar]
- Bhujel, A.; Basak, J.K.; Khan, F.; Arulmozhi, E.; Jaihuni, M.; Sihalath, T.; Lee, D.; Park, J.; Kim, H.T. Sensor Systems for Greenhouse Microclimate Monitoring and Control: A Review. J. Biosyst. Eng. 2020, 45, 341–361. [Google Scholar] [CrossRef]
- Fen-FangHe, C.M. Modeling greenhouse air humidity by means of artificial neural network and principal component analysis. Comput. Eng. Agric. 2010, 71, 9–23. [Google Scholar]
- Yeon Lee, S.; Bok Lee, I.; Hyeon Yeo, U.; Woo Kim, R.; Gyu Kim, J. Optimal sensor placement for monitoring and controlling greenhouse internal environments. Biosyst. Eng. 2019, 188, 190–206. [Google Scholar] [CrossRef]
- Kubrusly, C.S.; Malebranche, H. Sensors and controllers location in distributed systems—A survey. Automatica 1985, 21, 117–128. [Google Scholar] [CrossRef]
- Alonso, A.A.; Kevrekidis, I.G.; Banga, J.R.; Frouzakis, C.E. Optimal sensor location and reduced order observer design for distributed process systems. Comput. Chem. Eng. 2004, 28, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Yi, T.; Li, H.; Gu, M. Optimal Sensor Placement for Health Monitoring of High-Rise Structure Based on Genetic Algorithm. Math. Probl. Eng. 2011, 2011, 395101. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Gao, W.; Sun, Y.; Xu, M. Optimal sensor placement for spatial lattice structure based on genetic algorithms. J. Sound Vib. 2008, 317, 175–189. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Hussain, K.; Zhu, W.; Shaban, H.; Hassaballah, M. Optimal Sink Node Placement in Large Scale Wireless Sensor Networks Based on Harris’ Hawk Optimization Algorithm. IEEE Access 2020, 8, 19381–19397. [Google Scholar] [CrossRef]
- Castro-Triguero, R.; Murugan, S.; Gallego, R.; Friswell, M.I. Robustness of optimal sensor placement under parametric uncertainty. Mech. Syst. Signal Process. 2013, 41, 268–287. [Google Scholar] [CrossRef]
- Sun, Y.; Halgamuge, S. Minimum-Cost Heterogeneous Node Placement in Wireless Sensor Networks. IEEE Access 2019, 7, 14847–14858. [Google Scholar] [CrossRef]
- Duan, R.; Lin, Y.; Feng, T. Optimal Sensor Placement Based on System Reliability Criterion Under Epistemic Uncertainty. IEEE Access 2018, 6, 57061–57072. [Google Scholar] [CrossRef]
- Flynn, E.B.; Todd, M.D. A Bayesian approach to optimal sensor placement for structural health monitoring with application to active sensing. Mech. Syst. Signal Process. 2010, 24, 891–903. [Google Scholar] [CrossRef]
- Wu, H.; Li, Q.; Zhu, H.; Han, X.; Li, Y.; Yang, B. Directional sensor placement in vegetable greenhouse for maximizing target coverage without occlusion. Wirel. Netw. 2020, 26, 4677–4687. [Google Scholar] [CrossRef]
- Uyeh, D.D.; Bassey, B.I.; Mallipeddi, R.; Asem-Hiablie, S.; Amaizu, M.; Woo, S.; Ha, Y.S.; Park, T. A Reinforcement Learning Approach for Optimal Placement of Sensors in Protected Cultivation Systems. IEEE Access 2021, 9, 100781–100800. [Google Scholar] [CrossRef]
- Ajani, O.S.; Aboyeji, E.; Mallipeddi, R.; Dooyum Uyeh, D.; Ha, Y.; Park, T. A genetic programming-based optimal sensor placement for greenhouse monitoring and control. Front. Plant Sci. 2023, 14, 1152036. [Google Scholar] [CrossRef] [PubMed]
- Uyeh, D.D.; Iyiola, O.; Mallipeddi, R.; Asem-Hiablie, S.; Amaizu, M.; Ha, Y.; Park, T. Grid Search for Lowest Root Mean Squared Error in Predicting Optimal Sensor Location in Protected Cultivation Systems. Front. Plant Sci. 2022, 13, 920284. [Google Scholar] [CrossRef] [PubMed]
- Körner, O.; Aaslyng, J.M.; Andreassen, A.U.; Holst, N. Microclimate Prediction for Dynamic Greenhouse Climate Control. HortScience 2007, 42, 272–279. [Google Scholar] [CrossRef] [Green Version]
- Petrakis, T.; Kavga, A.; Thomopoulos, V.; Argiriou, A.A. Neural Network Model for Greenhouse Microclimate Predictions. Agriculture 2022, 12, 780. [Google Scholar] [CrossRef]
- Liu, Q.; Jin, D.; Shen, J.; Fu, Z.; Linge, N. A WSN-based prediction model of microclimate in a greenhouse using extreme learning approaches. In Proceedings of the 2016 18th International Conference on Advanced Communication Technology (ICACT), PyeongChang, Republic of Korea, 31 January–3 February 2016; pp. 730–735. [Google Scholar] [CrossRef]
- Singh, M.C.; Singh, J.; Singh, K. Development of a microclimate model for prediction of temperatures inside a naturally ventilated greenhouse under cucumber crop in soilless media. Comput. Electron. Agric. 2018, 154, 227–238. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Chakir, S.; Bekraoui, A.; Zemmouri, E.M.; Majdoubi, H.; Mouqallid, M. Prediction of Olive Cuttings Greenhouse Microclimate Under Mediterranean Climate Using Artificial Neural Networks. In Digital Technologies and Applications, Proceedings of the Digital Technologies and Applications, Fez, Morocco, 28–30 January 2022; Motahhir, S., Bossoufi, B., Eds.; Springer: Cham, Switzerland, 2022; pp. 63–69. [Google Scholar]

| Rank | Optimal Locations | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| February | March | April | May | June | July | October | ||||||||
| T | RH | T | RH | T | RH | T | RH | T | RH | T | RH | T | RH | |
| 1 | E3 | B4 | G1 | D6 | A4 | E4 | D1 | B2 | E7 | E2 | B4 | D3 | A4 | E4 |
| 2 | F7 | F5 | C7 | G6 | E7 | D2 | B2 | A3 | C7 | E6 | D5 | B6 | E7 | D2 |
| 3 | D1 | A1 | B6 | C4 | F7 | E3 | F5 | F6 | F6 | B2 | G7 | C3 | F7 | E3 |
| 4 | D7 | C1 | A3 | A2 | A1 | A2 | C1 | F7 | D7 | F7 | G6 | D6 | A1 | A2 |
| 5 | E2 | C5 | D1 | D3 | E6 | E6 | D7 | G6 | G1 | H3 | E1 | D7 | E6 | E6 |
| 6 | C4 | F2 | E2 | E6 | D2 | E5 | A7 | E3 | E1 | G6 | E7 | F5 | D2 | E5 |
| 7 | H2 | F3 | D2 | E1 | F6 | A4 | C5 | B4 | G7 | H1 | D7 | A3 | F6 | A4 |
| 8 | E7 | H5 | B3 | F4 | G7 | D3 | F2 | H1 | B2 | B1 | G1 | C2 | G7 | D3 |
| 9 | G1 | E2 | C1 | B4 | G6 | A5 | F3 | B1 | A2 | A6 | F7 | F4 | G6 | A5 |
| 10 | E1 | F1 | E1 | A5 | D6 | F2 | A3 | D7 | E3 | E4 | A1 | G3 | D6 | F2 |
| Predicted Month | Temperature Data | Humidity Data | ||||
|---|---|---|---|---|---|---|
| Train | Test | Validate | Train | Test | Validate | |
| March | 16,711 | 5223 | 4178 | 16,252 | 5080 | 4064 |
| April | 16,283 | 5089 | 4071 | 16,516 | 5162 | 4130 |
| May | 16,639 | 5200 | 4160 | 16,343 | 5108 | 4086 |
| June | 15,264 | 4771 | 3816 | 15,270 | 4772 | 3818 |
| July | 14,954 | 4674 | 3739 | 15,160 | 4738 | 3791 |
| October | 15,549 | 4860 | 3888 | 16,031 | 5010 | 4008 |
| Predicted Month | RMSE | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | |
| March | 3.4313 | 4.486 | 23.5 | 2.2177 | 4.3059 | 48.49 | 1.7744 | 4.295 | 58.69 | 1.7274 | 4.27676 | 59.61 | 1.813 | 4.253 | 57.37 |
| April | 3.769 | 4.7207 | 20.16 | 2.8217 | 5.2158 | 45.9 | 2.4798 | 5.0001 | 50.41 | 2.3984 | 5.0265 | 52.28 | 2.2835 | 4.9931 | 54.27 |
| May | 4.879 | 10.3591 | 52.9 | 3.6129 | 10.0993 | 64.22 | 2.8061 | 10.051 | 72.08 | 2.9978 | 10.2512 | 70.76 | 2.8256 | 10.3058 | 72.58 |
| June | 4.5209 | 16.91844 | 73.28 | 3.4017 | 16.2493 | 79.06 | 2.9317 | 16.4949 | 82.23 | 2.8681 | 16.1764 | 82.26 | 2.8209 | 16.1334 | 82.52 |
| July | 3.555 | 13.3485 | 73.37 | 3.0707 | 13.7859 | 77.72 | 2.7632 | 13.7796 | 79.95 | 2.5978 | 13.6444 | 80.96 | 2.528 | 13.6213 | 81.44 |
| October | 3.9781 | 7.2066 | 44.8 | 3.2783 | 7.5076 | 56.33 | 2.6372 | 7.5388 | 65.01 | 2.6396 | 7.4724 | 64.68 | 2.4957 | 7.4801 | 66.64 |
| Predicted Month | RMSE | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | DNN Model | W/O DNN Model | RMSE Reduction (%) | |
| March | 14.2951 | 16.6314 | 14.05 | 12.0131 | 16.1924 | 25.81 | 10.5982 | 16.1097 | 34.21 | 10.7687 | 16.13353 | 33.25 | 10.4168 | 16.0724 | 35.19 |
| April | 14.1778 | 22.7773 | 37.75 | 12.7681 | 22.8833 | 44.2 | 13.0693 | 22.18422 | 41.09 | 10.5447 | 21.63 | 51.25 | 10.8462 | 21.8471 | 50.35 |
| May | 17.6504 | 26.2172 | 32.68 | 17.0076 | 26.8919 | 36.76 | 15.3399 | 26.9629 | 43.11 | 14.4252 | 26.359 | 45.27 | 13.81256 | 26.35056 | 47.82 |
| June | 15.5105 | 32.1841 | 51.81 | 14.0204 | 32.4554 | 56.8 | 13.6979 | 32.4173 | 57.75 | 13.28 | 32.1747 | 58.73 | 13.4313 | 32.08896 | 58.14 |
| July | 11.7474 | 24.05563 | 51.17 | 11.77418 | 24.092 | 51.13 | 10.9207 | 24.2066 | 54.89 | 10.4535 | 23.9932 | 56.43 | 10.61337 | 23.9488 | 55.68 |
| October | 14.1119 | 23.4509 | 39.82 | 13.0888 | 23.126 | 43.4 | 12.363 | 23.1641 | 46.63 | 12.677 | 23.6228 | 46.34 | 12.6537 | 23.714 | 46.64 |
| Predicted Month | Correlation Coefficients | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | Humidity | Temperature | Humidity | Temperature | Humidity | Temperature | Humidity | Temperature | Humidity | |
| March | 0.87 | 0.85 | 0.93 | 0.93 | 0.96 | 0.94 | 0.96 | 0.94 | 0.95 | 0.95 |
| April | 0.82 | 0.89 | 0.92 | 0.91 | 0.95 | 0.93 | 0.95 | 0.95 | 0.95 | 0.94 |
| May | 0.69 | 0.76 | 0.82 | 0.78 | 0.89 | 0.82 | 0.89 | 0.84 | 0.9 | 0.86 |
| June | 0.79 | 0.76 | 0.87 | 0.80 | 0.92 | 0.81 | 0.92 | 0.82 | 0.91 | 0.82 |
| July | 0.56 | 0.66 | 0.78 | 0.72 | 0.82 | 0.75 | 0.85 | 0.79 | 0.84 | 0.78 |
| October | 0.73 | 0.8 | 0.85 | 0.83 | 0.911 | 0.84 | 0.92 | 0.84 | 0.92 | 0.84 |
| Predicted Month | RMSE | ||
|---|---|---|---|
| DNN Model | DNN Model | W/O DNN Model | |
| March | 2.1337 | 1.7744 | 4.295 |
| April | 2.811 | 2.4798 | 5.0001 |
| May | 3.5302 | 2.8061 | 10.051 |
| June | 3.5121 | 2.9317 | 16.4949 |
| July | 3.2077 | 2.7632 | 13.7796 |
| October | 3.305 | 2.6372 | 7.5388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajani, O.S.; Usigbe, M.J.; Aboyeji, E.; Uyeh, D.D.; Ha, Y.; Park, T.; Mallipeddi, R. Greenhouse Micro-Climate Prediction Based on Fixed Sensor Placements: A Machine Learning Approach. Mathematics 2023, 11, 3052. https://doi.org/10.3390/math11143052
Ajani OS, Usigbe MJ, Aboyeji E, Uyeh DD, Ha Y, Park T, Mallipeddi R. Greenhouse Micro-Climate Prediction Based on Fixed Sensor Placements: A Machine Learning Approach. Mathematics. 2023; 11(14):3052. https://doi.org/10.3390/math11143052
Chicago/Turabian StyleAjani, Oladayo S., Member Joy Usigbe, Esther Aboyeji, Daniel Dooyum Uyeh, Yushin Ha, Tusan Park, and Rammohan Mallipeddi. 2023. "Greenhouse Micro-Climate Prediction Based on Fixed Sensor Placements: A Machine Learning Approach" Mathematics 11, no. 14: 3052. https://doi.org/10.3390/math11143052
APA StyleAjani, O. S., Usigbe, M. J., Aboyeji, E., Uyeh, D. D., Ha, Y., Park, T., & Mallipeddi, R. (2023). Greenhouse Micro-Climate Prediction Based on Fixed Sensor Placements: A Machine Learning Approach. Mathematics, 11(14), 3052. https://doi.org/10.3390/math11143052








