Two-Grid Method for a Fully Discrete Mixed Finite Element Solution of the Time-Dependent Schrödinger Equation

Abstract

We study the backward Euler fully discrete mixed finite element method for the time-dependent Schrödinger equation; the error result of the mixed finite element solution is obtained in the $L^2$-norm with order $O(\tau +h^{k+1})$. Then, a two-grid method is presented with a backward Euler fully discrete scheme. Using this method, we solve the original problem on a much coarser grid and solve elliptic equations on a fine grid. In addition, the error of the two-grid solution is also obtained in the $L^2$-norm with order $O(\tau +h^{k+1}+H^{k+2})$. The numerical experiment is provided to demonstrate the efficiency of the algorithm.

1. Introduction

There have been many studies on numerical methods for the Schrödinger equation, e.g., see [1,2,3] for finite difference methods, [4,5,6,7] for finite element methods, [8,9] for mixed finite element methods, and [10,11,12,13] for other methods. Liao et al. [2] proposed a fourth-order compact difference scheme for two-dimensional linear Schrödinger equations with periodic boundary conditions. Li et al. [6] studied a fast linearized conservative finite element method for solving the strongly coupled nonlinear fractional Schrödinger equations. Liu et al. [8] discussed an $H^1$-Galerkin mixed finite element method for a linear Schrödinger equation. Bao et al. [10] studied the performance of time-splitting spectral approximations for nonlinear Schrödinger equations in semiclassical regimes.

In this paper, we consider the following initial value problem of the linear Schrödinger equation

$$\left\{\begin{array}{ccc}i{u}_t(x,y,t)=-\Delta u(x,y,t)+\Psi (x,y)u(x,y,t)+f(x,y,t),\hfill & \hfill & (x,y)\in \Omega ,t\in (0,T],\hfill \\ u(x,y,t)=0,\hfill & \hfill & (x,y)\in \partial \Omega ,t\in (0,T],\hfill \\ u(x,y,0)=u_0(x,y),\hfill & \hfill & (x,y)\in \Omega ,\hfill \end{array}\right.$$

(1)

where $\Delta$ is the Laplacian operator, $i=\sqrt{-1}$ is the complex unit, and T is a constant. $\Omega \subset {\mathbb{R}}^2$ is a convex polygonal domain; $u(x,y,t)$, $u_0(x,y)$, and $f(x,y,t)$ are complex-valued; and $\Psi (x,y)$ is non-negative bounded and real-valued.

The two-grid finite element method was firstly proposed by Xu in [14,15]. In recent years, there are many studies on the two-grid method, e.g., for elliptic equations [16,17], parabolic equations [18,19,20,21], reaction–diffusion equations [22,23], and others [24,25,26]. The two-grid method is also used to solve the Schrödinger equation [27,28,29,30,31]. Jin et al. [29] firstly proposed a two-grid finite element method for solving coupled partial differential equations, such as the time-independent linear Schrödinger equation. Wu [30] developed the two-grid mixed finite element schemes for solving nonlinear Schrödinger equations. In [31], we studied the semi-discrete mixed finite element scheme and constructed a two-grid algorithm for the linear Schrödinger equation.

The current paper is the extension of [31]. We propose a fully discrete scheme that uses a mixed finite element method in space with the backward Euler method in time for the linear Schrödinger Equation (1); we obtain error results of mixed finite element solution in the $L^2$-norm with order $O(\tau +h^{k+1})$. Next, we propose a two-grid algorithm of a fully discrete mixed finite element with the backward Euler scheme, and we obtain the errors of the two-grid solution in the $L^2$-norm with order $O(\tau +h^{k+1}+H^{k+2})$.

The rest of the paper is organized as follows. Some notation and projection operators are presented in Section 2. In Section 3, we provide the fully discrete mixed finite element with the backward Euler scheme and provide the error analysis. In Section 4, we construct a two-grid fully discrete mixed finite element algorithm. In Section 5, a numerical example is provided to verify the results of the theoretical analysis. Finally, the conclusions are drawn in Section 6. Throughout this paper, $\tau$ is the constant denoting the time step, and $h,H$ are the constants denoting the mesh size in space; C denotes a generic positive constant, which is independent of $\tau ,h,$ and H and may vary with the context.

2. Notation and Preliminaries

Let $L^p(\Omega )$ for $p\ge 1$ denote the standard Banach space defined on $\Omega$. We shall use $W^{m,p}(\Omega )$ to denote the standard Sobolev space of complex-valued measurable functions defined on $\Omega$ with the norm ${\parallel \varphi \parallel }_{m,p}^p={\sum }_{\left|\alpha \right|\le m}{\parallel D^{\alpha }\varphi \parallel }_{L^p(\Omega )}^p$. We also set $W_0^{m,p}(\Omega )=\{v\in W^{m,p}(\Omega ):v{|}_{\partial \Omega }=0\}.$ For $p=2$, we denote $H^m(\Omega )=W^{m,2}(\Omega )$, $H_0^m(\Omega )=W_0^{m,2}(\Omega )$, and ${\parallel ·\parallel }_m={\parallel ·\parallel }_{m,2}$, $\parallel ·\parallel ={\parallel ·\parallel }_{0,2}$. Furthermore, let ${\left(L^2(\Omega )\right)}^2$ be the space of two-dimensional vectors that have all components in $L^2(\Omega )$ with its usual norm of $\parallel ·\parallel$.

For any $u(x,y),v(x,y)\in L^2(\Omega )$ (or ${\left(L^2(\Omega )\right)}^2$), the inner product $(u,v)$ is defined with

$$(u,v)={\int }_{\Omega }u(x,y)\overline{v}(x,y)dxdy,$$

where $\overline{v}(x,y)$ denotes the complex conjugate of $v(x,y)$.

Furthermore, for any complex-valued function $u(x,y)=u_R(x,y)+i{u}_I(x,y)$, let

$${\parallel u\parallel }_{m,p}=(\parallel u_R{\parallel }_{m,p}^p+\parallel u_I{{\parallel }_{m,p}^p)}^{\frac{1}{p}}.$$

In addition, let

$$\begin{array}{cc}\hfill & W=L^2(\Omega ),\hfill \\ \hfill & V=H(div;\Omega )=\{v\in {\left(L^2(\Omega )\right)}^2:\nabla ·v\in L^2(\Omega )\},\hfill \\ \hfill & V^0=\{v\in {\left(L^2(\Omega )\right)}^2:\nabla ·v\in L^2(\Omega ),v·n{|}_{\partial \Omega }=0\}.\hfill \end{array}$$

Let ${\Gamma }_h$ be a quasi-uniform triangular partition of $\Omega$; the partition step is h. We form $V_h$ and $W_h$, which are discrete subspaces of V and W, using standard mixed finite element spaces such as the RT spaces RT${}_k$ [32] and the Brezzi–Douglas–Marini spaces BDM${}_k$ [33].

For any $u(x,y)\in L^2(\Omega )$ and $\phi (x,y)\in {\left(L^2(\Omega )\right)}^2$, the $L^2$ projection $P_{h}u\in W_h$ and $P_h\phi \in V_h$ can be defined by

$$\begin{array}{cc}\hfill & (u,w_h)=(P_{h}u,w_h),\forall w_h\in W_h,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & (\phi ,v_h)=(P_h\phi ,v_h),\forall v_h\in V_h.\hfill \end{array}$$

(3)

Then, according to [33,34], for the function $\phi (x,y)\in W^{k+1,p}(\Omega )$ (or ${\left(W^{k+1,p}(\Omega )\right)}^2$), when $2\le p<\infty$, the $P_h$ projection has the properties

$$\begin{array}{cc}\hfill & \parallel P_h{\phi \parallel }_{0,p}\le C{\parallel \phi \parallel }_{0,p},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \parallel \phi -P_h{\phi \parallel }_{0,p}\le C{h}^r{\parallel \phi \parallel }_{r,p},1\le r\le k+1.\hfill \end{array}$$

(5)

The mixed elliptic projection $(R_{h}u,R_h\overrightarrow{q})\in W_h\times V_h$ is defined by

$$\begin{array}{cccc}\hfill & i(u_t,w_h)=-(\nabla ·R_h\overrightarrow{q},w_h)+(\Psi u,w_h)+(f,w_h),\hfill & \hfill & \forall w_h\in W_h,\hfill \end{array}$$

(6)

$$\begin{array}{cccc}\hfill & (R_h\overrightarrow{q},v_h)+(R_{h}u,\nabla ·v_h)=0,\hfill & \hfill & \forall v_h\in V_h.\hfill \end{array}$$

(7)

Let $\overrightarrow{q}=\nabla u$; the weak solution $(u,\overrightarrow{q})\in W\times V$ of problem (1) is defined by

$$\begin{array}{cccc}\hfill & i(u_t,w)=-(\nabla ·\overrightarrow{q},w)+(\Psi u,w)+(f,w),\hfill & \hfill & \forall w\in W,\hfill \end{array}$$

(8)

$$\begin{array}{cccc}\hfill & (\overrightarrow{q},v)+(u,\nabla ·v)=0,\hfill & \hfill & \forall v\in V.\hfill \end{array}$$

(9)

The semi-discrete mixed finite element solution $(u_h,{\overrightarrow{q}}_h)\in W_h\times V_h\subset W\times V$ of Equations (8) and (9) is defined by

$$\begin{array}{cccc}\hfill & i(u_{ht},w_h)=-(\nabla ·{\overrightarrow{q}}_h,w_h)+(\Psi u_h,w_h)+(f,w_h),\hfill & \hfill & \forall w_h\in W_h,\hfill \end{array}$$

(10)

$$\begin{array}{cccc}\hfill & ({\overrightarrow{q}}_h,v_h)+(u_h,\nabla ·v_h)=0,\hfill & \hfill & \forall v_h\in V_h.\hfill \end{array}$$

(11)

Lemma 1

([31]). Let $(u,\overrightarrow{q})\in W\times V$ be the solution that is satisfied in Equations (8) and (9), and let $(R_{h}u,R_h\overrightarrow{q})\in W_h\times V_h$ be the solution defined in Equations (6) and (7); when $2\le p<\infty$, there are the following error estimations

$$\begin{array}{cc}\hfill & \parallel \overrightarrow{q}-R_h\overrightarrow{q}{\parallel }_{0,p}+\parallel {(\overrightarrow{q}-R_h\overrightarrow{q})}_t{\parallel }_{0,p}\le C{h}^{k+1}(\parallel \overrightarrow{q}{\parallel }_{k+1,p}+\parallel {\overrightarrow{q}}_t{\parallel }_{k+1,p}),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \parallel \nabla ·(\overrightarrow{q}-R_h\overrightarrow{q}){\parallel }_{0,p}+\parallel \nabla ·{(\overrightarrow{q}-R_h\overrightarrow{q})}_t{\parallel }_{0,p}\le C{h}^k(\parallel \overrightarrow{q}{\parallel }_{k+1,p}+\parallel {\overrightarrow{q}}_t{\parallel }_{k+1,p}).\hfill \end{array}$$

(13)

Lemma 2

([31]). Let $(u,\overrightarrow{q})\in W\times V$ be the solution satisfied in (8) and (9), and let $(R_{h}u,R_h\overrightarrow{q})\in W_h\times V_h$ be the solution defined in (6) and (7); when $2\le p<\infty ,1\le r\le k+1$, there are the following error estimations

$$\begin{array}{c}\parallel P_{h}u-R_h{u\parallel }_{0,p}+\parallel {(P_{h}u-R_{h}u)}_t{\parallel }_{0,p}+{\parallel {(P_{h}u-R_{h}u)}_{tt}\parallel }_{0,p}\\ \le C{h}^{r+1}{(\parallel u\parallel }_{r+1,p}+\parallel u_t{\parallel }_{r+1,p}+\parallel u_{tt}{\parallel }_{r+1,p}),\end{array}$$

(14)

$$\begin{array}{c}\parallel u-R_h{u\parallel }_{0,p}+\parallel {(u-R_{h}u)}_t{\parallel }_{0,p}+{\parallel {(u-R_{h}u)}_{tt}\parallel }_{0,p}\\ \le C{h}^r{(\parallel u\parallel }_{r,p}+\parallel u_t{\parallel }_{r,p}+\parallel u_{tt}{\parallel }_{r,p}).\end{array}$$

(15)

3. Error Analysis for the Backward Euler Fully Discrete Scheme

Let $\tau =\frac{T}{N}$ be the time step, where N be a positive integer. We also let $t_j=j\tau$, $j=1,2,\dots ,N$ be the time nodes. To simplify notation, we use $u^j$ instead of the function $u(x,y,t_j)$. For the function series $u^j(x,y),j=0,1,\dots ,N$, let

$$\begin{array}{c}\hfill {\partial }_t{u}^j=\frac{1}{\tau }(u^j(x,y)-u^{j-1}(x,y)).\end{array}$$

Then, we can define the fully discrete mixed finite element solution $(u_h^n,{\overrightarrow{q_{}}}_h^n)\in W_h\times V_h,1\le n\le N$ of Equations (8) and (9), satisfying the backward Euler scheme

$$\begin{array}{cccc}\hfill & i({\partial }_t{u}_h^n,w_h)=-(\nabla ·{\overrightarrow{q_{}}}_h^n,w_h)+(\Psi u_h^n,w_h)+(f^n,w_h),\hfill & \hfill & \forall w_h\in W_h,\hfill \end{array}$$

(16)

$$\begin{array}{cccc}\hfill & ({\overrightarrow{q_{}}}_h^n,v_h)+(u_h^n,\nabla ·v_h)=0,\hfill & \hfill & \forall v_h\in V_h.\hfill \end{array}$$

(17)

We rewrite Equations (6) and (7) for time $t=t_n,1\le n\le N$; that is:

$$\begin{array}{cccc}\hfill & i(u_t^n,w_h)=-(\nabla ·R_h{\overrightarrow{q_{}}}^n,w_h)+(\Psi u^n,w_h)+(f^n,w_h),\hfill & \hfill & \forall w_h\in W_h,\hfill \end{array}$$

(18)

$$\begin{array}{cccc}\hfill & (R_h{\overrightarrow{q_{}}}^n,v_h)+(R_h{u}^n,\nabla ·v_h)=0,\hfill & \hfill & \forall v_h\in V_h.\hfill \end{array}$$

(19)

Lemma 3.

Let $(u_h^n,{\overrightarrow{q_{}}}_h^n)\in W_h\times V_h$ be the solution satisfied in Equations (16) and (17), and let $(R_h{u}^n,R_h{\overrightarrow{q_{}}}^n)\in W_h\times V_h$ be the solution defined in Equations (18) and (19); when $u_h^0=R_{h}u(·,0)$, there are the following error estimates

$$\begin{array}{cc}\hfill & \parallel R_h{u}^n-u_h^n\parallel +\parallel R_h{\overrightarrow{q_{}}}^n-{\overrightarrow{q_{}}}_h^n\parallel \le C(\tau +h^{k+2}),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \parallel (R_h{u}^n-u_h^n)-(R_h{u}^{n-1}-u_h^{n-1})\parallel \le C\tau (\tau +h^{k+2}).\hfill \end{array}$$

(21)

Proof. 

Let

$$\begin{array}{cc}\hfill & u^n-u_h^n=(u^n-R_h{u}^n)+(R_h{u}^n-u_h^n)={\epsilon }^n+{\theta }^n,\hfill \\ \hfill & {\overrightarrow{q_{}}}^n-{\overrightarrow{q_{}}}_h^n=({\overrightarrow{q_{}}}^n-R_h{\overrightarrow{q_{}}}^n)+(R_h{\overrightarrow{q_{}}}^n-{\overrightarrow{q_{}}}_h^n)={\sigma }^n+{\rho }^n,\hfill \end{array}$$

then, subtracting (16) and (17) from (18) and (19), respectively, we can obtain

$$\begin{array}{cc}\hfill & i({\partial }_t{\theta }^n,w_h)=i({\partial }_t{R}_h{u}^n-u_t^n,w_h)-(\nabla ·{\rho }^n,w_h)+(\Psi {\epsilon }^n,w_h)+(\Psi {\theta }^n,w_h),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & ({\rho }^n,v_h)+({\theta }^n,\nabla ·v_h)=0.\hfill \end{array}$$

(23)

By taking $w_h={\theta }^n$ in (22) and $v_h={\rho }^n$ in (23) and then adding these two equations, we have

$$\begin{array}{cc}\hfill i({\partial }_t{\theta }^n,{\theta }^n)& +({\rho }^n,{\rho }^n)+2Re\left\{(\nabla ·{\rho }^n,{\theta }^n)\right\}\hfill \\ \hfill & =i({\partial }_t{R}_h{u}^n-u_t^n,{\theta }^n)+(\Psi {\epsilon }^n,{\theta }^n)+(\Psi {\theta }^n,{\theta }^n),\hfill \end{array}$$

(24)

comparing the imaginary parts of (24) gives

$$\begin{array}{cc}\hfill Re\left\{({\partial }_t{\theta }^n,{\theta }^n)\right\}& =Re\{({\partial }_t{R}_h{u}^n-u_t^n,{\theta }^n)+(\Psi {\epsilon }^n,{\theta }^n)\}\hfill \\ \hfill & \le |({\partial }_t{R}_h{u}^n-u_t^n,{\theta }^n)|+|(\Psi {\epsilon }^n,{\theta }^n)|\hfill \\ \hfill & \le |({\partial }_t{u}^n-u_t^n,{\theta }^n)|+|({\partial }_t{\epsilon }^n,{\theta }^n)|+|(\Psi {\epsilon }^n,{\theta }^n)|\hfill \\ \hfill & =:E_1+E_2+E_3,\hfill \end{array}$$

(25)

where combining (2) and (14) gives

$$\begin{array}{cc}\hfill E_1& =\left|\left(\frac{1}{\tau }{\int }_{t_{n-1}}^{t_n}(t-t_{n-1})u_{tt}(·,t)dt,{\theta }^n\right)\right|\hfill \\ \hfill & \le \parallel {\theta }^n\parallel {\int }_{t_{n-1}}^{t_n}\parallel u_{tt}(·,t)\parallel dt\hfill \\ \hfill & \le C\tau \parallel {\theta }^n\parallel ,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill E_2& =|({\partial }_t(u^n-P_h{u}^n),{\theta }^n)+({\partial }_t(P_h{u}^n-R_h{u}^n),{\theta }^n)|\hfill \\ \hfill & =\left|\right({\partial }_t(P_h{u}^n-R_h{u}^n),{\theta }^n\left)\right|\hfill \\ \hfill & \le \frac{1}{\tau }\parallel {\theta }^n\parallel {\int }_{t_{n-1}}^{t_n}\parallel {(P_{h}u-R_{h}u)}_t(·,t)\parallel dt\hfill \\ \hfill & \le C{h}^{k+2}\parallel {\theta }^n\parallel ,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill E_3& \le C|(u^n-P_h{u}^n,{\theta }^n)+(P_h{u}^n-R_h{u}^n,{\theta }^n)|\hfill \\ \hfill & \le C\left|\right(P_h{u}^n-R_h{u}^n,{\theta }^n\left)\right|\hfill \\ \hfill & \le C{h}^{k+2}\parallel {\theta }^n\parallel .\hfill \end{array}$$

(28)

In addition, noticing that

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\theta }^n,{\theta }^n)\right\}=\frac{1}{2\tau }(\parallel {\theta }^n{\parallel }^2-\parallel {\theta }^{n-1}{\parallel }^2+\parallel {\theta }^n-{\theta }^{n-1}{\parallel }^2),\end{array}$$

(29)

it follows from (25)–(29) that

$$\begin{array}{c}\hfill \frac{1}{2\tau }(\parallel {\theta }^n{\parallel }^2-\parallel {\theta }^{n-1}{\parallel }^2)\le C(\tau +h^{k+2})\parallel {\theta }^n\parallel ,\end{array}$$

(30)

that is,

$$\begin{array}{c}\hfill \parallel {\theta }^n{\parallel }^2-\parallel {\theta }^{n-1}{\parallel }^2\le C\tau ({\tau }^2+h^{2k+4})+\tau {\parallel {\theta }^n\parallel }^2.\end{array}$$

(31)

To any integer $1\le m\le N$, by summing up for n from 2 to m in (31), we have

$$\begin{array}{c}\hfill \parallel {\theta }^m{\parallel }^2-\parallel {\theta }^0{\parallel }^2\le C{\tau }^2+C{h}^{2k+4}+\tau \sum _{n=1}^m{\parallel {\theta }^n\parallel }^2,\end{array}$$

(32)

noticing that

$$\begin{array}{c}\hfill {\theta }^0=u_h^0-R_{h}u(·,0)=0,\end{array}$$

(33)

and by substituting (33) into (32), when $\tau <1$, using Gronwall inequality gives

$$\begin{array}{c}\hfill \parallel {\theta }^m\parallel \le C\tau +C{h}^{k+2}.\end{array}$$

(34)

Let

$$\begin{array}{c}\hfill {\alpha }^n={\partial }_t{\theta }^n,{\beta }^n={\partial }_t{R}_h{u}^n.\end{array}$$

(35)

By replacing n with $n-1$ in (22) and (23), we can see that

$$\begin{array}{cc}\hfill & i({\partial }_t{\theta }^{n-1},w_h)=i({\partial }_t{R}_h{u}^{n-1}-u_t^{n-1},w_h)-(\nabla ·{\rho }^{n-1},w_h)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +(\Psi {\epsilon }^{n-1},w_h)+(\Psi {\theta }^{n-1},w_h),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & ({\rho }^{n-1},v_h)+({\theta }^{n-1},\nabla ·v_h)=0,\hfill \end{array}$$

(37)

and by subtracting (36) and (37) from (22) and (23) and dividing them by $\tau$, respectively, we have

$$\begin{array}{cc}\hfill & i({\partial }_t{\alpha }^n,w_h)=i({\partial }_t{\beta }^n-{\partial }_t{u}_t^n,w_h)-(\nabla ·{\partial }_t{\rho }^n,w_h)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +(\Psi {\partial }_t{\epsilon }^n,w_h)+(\Psi {\alpha }^n,w_h),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & ({\partial }_t{\rho }^n,v_h)+({\alpha }^n,\nabla ·v_h)=0.\hfill \end{array}$$

(39)

By taking $w_h={\alpha }^n$ in (38) and $v_h={\partial }_t{\rho }^n$ in (39) and then adding these two equations, we can obtain

$$\begin{array}{cc}\hfill i({\partial }_t{\alpha }^n,{\alpha }^n)+({\partial }_t{\rho }^n,{\partial }_t{\rho }^n)& =i({\partial }_t{\beta }^n-{\partial }_t{u}_t^n,{\alpha }^n)+2Re\left\{(\nabla ·{\partial }_t{\rho }^n,{\alpha }^n)\right\}\hfill \\ \hfill & +(\Psi {\partial }_t{\epsilon }^n,{\alpha }^n)+(\Psi {\alpha }^n,{\alpha }^n),\hfill \end{array}$$

(40)

where comparing the imaginary parts of (40) yields

$$\begin{array}{cc}\hfill Re\left\{({\partial }_t{\alpha }^n,{\alpha }^n)\right\}& =Re\left\{({\partial }_t{\beta }^n-{\partial }_t{u}_t^n,{\alpha }^n)\right\}-Im\left\{(\Psi {\partial }_t{\epsilon }^n,{\alpha }^n)\right\}\hfill \\ \hfill & \le |({\partial }_t{\beta }^n-{\partial }_t{u}_t^n,{\alpha }^n)|+|(\Psi {\partial }_t{\epsilon }^n,{\alpha }^n)|,\hfill \\ \hfill & \le \frac{1}{\tau }|({\partial }_t{\epsilon }^n-{\partial }_t{\epsilon }^{n-1}),{\alpha }^n\left)\right|+\frac{1}{\tau }\left|(({\partial }_t{u}^n-u_t^n)-({\partial }_t{u}^{n-1}-u_t^{n-1}),{\alpha }^n)\right|\hfill \\ \hfill & +\left|\right(\Psi {\partial }_t{\epsilon }^n,{\alpha }^n\left)\right|,\hfill \\ \hfill & =:F_1+F_2+F_3,\hfill \end{array}$$

(41)

combining (14) gives

$$\begin{array}{cc}\hfill F_1& =\frac{1}{\tau }\left|({\partial }_t(P_h{u}^n-R_h{u}^n)-{\partial }_t(P_h{u}^{n-1}-R_h{u}^{n-1}),{\alpha }^n)\right|\hfill \\ \hfill & =\frac{1}{{\tau }^2}\left|\left({\int }_{t_{n-1}}^{t_n}{(P_{h}u-R_{h}u)}_t(·,t)dt-{\int }_{t_{n-2}}^{t_{n-1}}{(P_{h}u-R_{h}u)}_t(·,t)dt,{\alpha }^n\right)\right|\hfill \\ \hfill & \le C\frac{1}{\tau }\parallel {\alpha }^n\parallel {\int }_{t_{n-2}}^{t_n}\parallel {(P_{h}u-R_{h}u)}_{tt}(·,t)\parallel dt\hfill \\ \hfill & \le C{h}^{k+2}\parallel {\alpha }^n\parallel .\hfill \end{array}$$

(42)

In addition,

$$\begin{array}{cc}\hfill F_2& =\frac{1}{{\tau }^2}\left|\left({\int }_{t_{n-1}}^{t_n}(t-t_{n-1})u_{tt}(·,t)dt-{\int }_{t_{n-2}}^{t_{n-1}}(t-t_{n-2})u_{tt}(·,t)dt,{\alpha }^n\right)\right|\hfill \\ \hfill & =\frac{1}{{\tau }^2}\left|\left(O\left(\tau \right)\left({\int }_{t_{n-1}}^{t_n}-{\int }_{t_{n-2}}^{t_{n-1}}\right)\parallel u_{tt}(·,t)\parallel dt,{\alpha }^n\right)\right|\hfill \\ \hfill & \le C\parallel {\alpha }^n\parallel {\int }_{t_{n-2}}^{t_n}\parallel u_{ttt}(·,t)\parallel dt\hfill \\ \hfill & \le C\tau \parallel {\alpha }^n\parallel ,\hfill \end{array}$$

(43)

and combining (15) yields

$$\begin{array}{c}\hfill F_3\le C|\frac{1}{\tau }({\int }_{t_{n-1}}^{t_n}{\epsilon }_t(·,t)dt,{\alpha }^n){\displaystyle |}\hspace{0.17em}\le C\parallel {\epsilon }_t(·,t)\parallel \parallel {\alpha }^n\parallel \le C{h}^{k+2}\parallel {\alpha }^n\parallel ,\end{array}$$

(44)

where it follows from (41)–(44) that

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\alpha }^n,{\alpha }^n)\right\}\le C(\tau +h^{k+2})\parallel {\alpha }^n\parallel .\end{array}$$

(45)

Noticing that

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\alpha }^n,{\alpha }^n)\right\}=\frac{1}{2\tau }(\parallel {\alpha }^n{\parallel }^2-\parallel {\alpha }^{n-1}{\parallel }^2+\parallel {\alpha }^n-{\alpha }^{n-1}{\parallel }^2),\end{array}$$

(46)

from (45) and (46), we have

$$\begin{array}{c}\hfill \parallel {\alpha }^n{\parallel }^2-\parallel {\alpha }^{n-1}{\parallel }^2\le C\tau (\tau +h^{k+2})\parallel {\alpha }^n\parallel ,\end{array}$$

that is,

$$\begin{array}{c}\hfill \parallel {\alpha }^n{\parallel }^2-\parallel {\alpha }^{n-1}{\parallel }^2\le C\tau ({\tau }^2+h^{2k+4}+\parallel {\alpha }^n{\parallel }^2).\end{array}$$

(47)

To any integer $1\le m\le N$, by summing up for n from 2 to m in (47), we get

$$\begin{array}{c}\hfill \parallel {\alpha }^m{\parallel }^2-\parallel {\alpha }^1{\parallel }^2\le C{\tau }^2+C{h}^{2k+4}+\tau \sum _{n=1}^m{\parallel {\alpha }^n\parallel }^2.\end{array}$$

(48)

By taking $n=1$ in (30) and combining (33), we have

$$\begin{array}{c}\hfill \parallel {\alpha }^1\parallel =\parallel \frac{{\theta }^1}{\tau }\parallel \le C(\tau +h^{k+2}),\end{array}$$

(49)

and by substituting (49) into (48), when $\tau <1$, using Gronwall inequality gives

$$\begin{array}{c}\hfill \parallel {\alpha }^m\parallel \le C(\tau +h^{k+2}).\end{array}$$

(50)

Therefore, (21) follows from (50) and (35).

By taking $w_h={\partial }_t{\theta }^n$ in (22) and $v_h={\rho }^n$ in (23) and then subtracting (23) from (22), we have

$$\begin{array}{cc}\hfill & i({\partial }_t{\theta }^n,{\partial }_t{\theta }^n)-({\partial }_t{\rho }^n,{\rho }^n)+2iIm\left\{(\nabla ·{\rho }^n,{\partial }_t{\theta }^n)\right\}\hfill \\ \hfill & =i({\partial }_t{R}_h{u}^n-u_t^n,{\partial }_t{\theta }^n)+(\Psi {\epsilon }^n,{\partial }_t{\theta }^n)+(\Psi {\theta }^n,{\partial }_t{\theta }^n).\hfill \end{array}$$

(51)

Comparing the real parts of (51), we can see that

$$\begin{array}{cc}\hfill Re\left\{({\partial }_t{\rho }^n,{\rho }^n)\right\}& =Im\left\{({\partial }_t{R}_h{u}^n-u_t^n,{\partial }_t{\theta }^n)\right\}+Re\{(\Psi {\epsilon }^n,{\partial }_t{\theta }^n)+(\Psi {\theta }^n,{\partial }_t{\theta }^n)\}\hfill \\ \hfill & \le |({\partial }_t{R}_h{u}^n-u_t^n,{\partial }_t{\theta }^n)|+|(\Psi {\epsilon }^n,{\partial }_t{\theta }^n)|+|(\Psi {\theta }^n,{\partial }_t{\theta }^n)|.\hfill \end{array}$$

(52)

Similar to the derivation of (25), we can get

$$\begin{array}{c}\hfill |({\partial }_t{R}_h{u}^n-u_t^n,{\partial }_t{\theta }^n)|+|(\Psi {\epsilon }^n,{\partial }_t{\theta }^n)|\le C(\tau +h^{k+2})\parallel {\partial }_t{\theta }^n\parallel ,\end{array}$$

(53)

where combining (52) and (53) gives

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\rho }^n,{\rho }^n)\right\}\le C(\tau +h^{k+2})\parallel {\partial }_t{\theta }^n\parallel +C\parallel {\theta }^n\parallel \parallel {\partial }_t{\theta }^n\parallel ,\end{array}$$

(54)

and from (34), (50) and (54), we have

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\rho }^n,{\rho }^n)\right\}\le C({\tau }^2+h^{2k+4}).\end{array}$$

(55)

We notice that

$$\begin{array}{c}\hfill Re\left\{({\partial }_t{\rho }^n,{\rho }^n)\right\}=\frac{1}{2\tau }(\parallel {\rho }^n{\parallel }^2-\parallel {\rho }^{n-1}{\parallel }^2+\parallel {\rho }^n-{\rho }^{n-1}{\parallel }^2),\end{array}$$

(56)

from (55) and (56), we have

$$\begin{array}{c}\hfill \parallel {\rho }^n{\parallel }^2-{\parallel {\rho }^{n-1}\parallel }^2\le C\tau ({\tau }^2+h^{2k+4}).\end{array}$$

(57)

Noticing that

$$\begin{array}{c}\hfill {\rho }^0={\overrightarrow{q_{}}}_h^0-R_h\overrightarrow{q}(·,0)=\nabla {\theta }^0=0.\end{array}$$

(58)

To any integer $1\le m\le N$, by summing up for n from 1 to m in (57) and combining (58), we can obtain

$$\begin{array}{c}\hfill \parallel {\rho }^m{\parallel }^2\le C({\tau }^2+h^{2k+4}),\end{array}$$

that is,

$$\begin{array}{c}\hfill \parallel {\rho }^m\parallel \le C(\tau +h^{k+2}).\end{array}$$

(59)

Therefore, (20) follows from (34) and (59). ☐

In addition, by combining (12) and (15) with (20) and triangle inequality, we can obtain the following result:

Theorem 1.

Let $(u,\overrightarrow{q})\in W\times V$ be the solution satisfied in Equations (8) and (9) and $(u_h^n,{\overrightarrow{q_{}}}_h^n)\in W_h\times V_h$ be the solution defined in Equations (16) and (17); when $u_h^0=R_{h}u(·,0)$, there is

$$\begin{array}{cc}\hfill & \parallel u^n-u_h^n\parallel +\parallel {\overrightarrow{q_{}}}^n-{\overrightarrow{q_{}}}_h^n\parallel \le C(\tau +h^{k+1}).\hfill \end{array}$$

(60)

4. Error Analysis for the Two-Grid Algorithm

We construct a two-grid algorithm of the fully discrete mixed finite element with the backward Euler scheme for Equations (8) and (9). Let ${\Gamma }_h$ be a quasi-uniform triangular partition of $\Omega$. $W_h\times V_h$ is the corresponding mixed finite element space. ${\Gamma }_H$ is a coarser quasi-uniform triangular partition of $\Omega$ with mesh size $H>>h$, and $W_H\times V_H\subset W_h\times V_h$ is the mixed finite element space defined on ${\Gamma }_H$. Thus, solving the Schrödinger equation on a fine grid is reduced to solving the original problem on a much coarser grid and the decoupled equations on the fine grid. See Algorithm 1.

Algorithm 1: Fully discrete two-grid mixed finite element scheme

Step 1: Find $(u_H^n,{\overrightarrow{q_{}}}_H^n)\in W_H\times V_H,1\le n\le N$ to satisfy the coupled equations on the coarse grid ${\Gamma }_H$. $$\begin{array}{cccc}\hfill & i(u_{Ht}^n,w_H)=-(\nabla ·{\overrightarrow{q_{}}}_H^n,w_H)+(\Psi u_H^n,w_H)+(f^n,w_H),\hfill & \hfill & \forall w_H\in W_H,\hfill \end{array}$$ (61) $$\begin{array}{cccc}\hfill & ({\overrightarrow{q_{}}}_H^n,v_H)+(u_H^n,\nabla ·v_H)=0,\hfill & \hfill & \forall v_H\in V_H.\hfill \end{array}$$ (62) Step 2: Find $(U_h^n,{\overrightarrow{Q}}_h^n)\in W_h\times V_h,1\le n\le N$ to satisfy the decoupled equations on the fine grid ${\Gamma }_h$. $$\begin{array}{cccc}\hfill & (\nabla ·{\overrightarrow{Q}}_h^n,w_h)-(\Psi u_h^n,w_h)=-i({\partial }_t{u}_H^n,w_h)+(f^n,w_h),\hfill & \hfill & \forall w_h\in W_h,\hfill \end{array}$$ (63) $$\begin{array}{cccc}\hfill & ({\overrightarrow{Q}}_h^n,v_h)+(U_h^n,\nabla ·v_h)=0,\hfill & \hfill & \forall v_h\in V_h.\hfill \end{array}$$ (64)

Lemma 4.

Let $(R_h{u}^n,R_h{\overrightarrow{q_{}}}^n)\in W_h\times V_h$ be the solution defined in Equations (18) and (19), and let $(U_h^n,{\overrightarrow{Q}}_h^n)\in W_h\times V_h$ be the solution defined in Equations (63) and (64); when $U_h^0=R_{h}u(·,0)$, there is the following error estimate

$$\begin{array}{c}\hfill \parallel R_h{u}^n-U_h^n\parallel +\parallel R_h{\overrightarrow{q_{}}}^n-{\overrightarrow{Q}}_h^n\parallel \le C(\tau +h^{k+1}+H^{k+2}).\end{array}$$

(65)

Proof. 

Let

$$\begin{array}{cc}\hfill & u^n-U_h^n=(u^n-R_h{u}^n)+(R_h{u}^n-U_h^n)={\epsilon }^n+{\xi }^n,\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill & {\overrightarrow{q_{}}}^n-{\overrightarrow{Q}}_h^n=({\overrightarrow{q_{}}}^n-R_h{\overrightarrow{q_{}}}^n)+(R_h{\overrightarrow{q_{}}}^n-{\overrightarrow{Q}}_h^n)={\sigma }^n+{\eta }^n;\hfill \end{array}$$

(67)

by subtracting (63) and (64) from (18) and (19), we have

$$\begin{array}{cc}\hfill & (\nabla ·{\eta }^n,w_h)-(\Psi {\xi }^n,w_h)=-i(u_t^n-{\partial }_t{u}_H^n,w_h)+(\Psi {\epsilon }^n,w_h),\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill & ({\eta }^n,v_h)+({\xi }^n,\nabla ·v_h)=0.\hfill \end{array}$$

(69)

By taking $w_h={\xi }^n$ in (68) and $v_h={\eta }^n$ in (69) and then subtracting (68) from (69), we have

$$\begin{array}{c}\hfill ({\eta }^n,{\eta }^n)+(\Psi {\xi }^n,{\xi }^n)=i(u_t^n-{\partial }_t{u}_H^n,{\xi }^n)-(\Psi {\epsilon }^n,{\xi }^n),\end{array}$$

(70)

that is,

$$\begin{array}{c}\hfill |({\eta }^n,{\eta }^n)+(\Psi {\xi }^n,{\xi }^n)|\le |(u_t^n-{\partial }_t{u}_H^n,{\xi }^n)|+|(\Psi {\epsilon }^n,{\xi }^n)|,\end{array}$$

(71)

thus,

$$\begin{array}{cc}\hfill \parallel {\eta }^n{\parallel }^2+C_0{\parallel {\xi }^n\parallel }^2& \le \parallel u_t^n-{\partial }_t{u}_H^n\parallel \parallel {\xi }^n\parallel +C\parallel {\epsilon }^n\parallel \parallel {\xi }^n\parallel \hfill \\ \hfill & \le C\parallel u_t^n-{\partial }_t{u}_H^n{\parallel }^2+C\parallel {\epsilon }^n{\parallel }^2+C_1{\parallel {\xi }^n\parallel }^2,\hfill \end{array}$$

(72)

where $C_0\le |\Psi |$ is a positive constant and $C_1$ is a small enough positive constant. Then, from (72), we obtain

$$\begin{array}{cc}\hfill \parallel {\eta }^n{\parallel }^2+{\parallel {\xi }^n\parallel }^2& \le C\parallel u_t^n-{\partial }_t{u}_H^n{\parallel }^2+C{\parallel {\epsilon }^n\parallel }^2\hfill \\ \hfill & \le C\parallel u_t^n-{\partial }_t{R}_h{u}^n{\parallel }^2+C\parallel {\partial }_t(R_h{u}^n-u_H^n){\parallel }^2+C{\parallel {\epsilon }^n\parallel }^2.\hfill \end{array}$$

(73)

Combining (15) gives

$$\begin{array}{cc}\hfill \parallel u_t^n-{\partial }_t{R}_h{u}^n\parallel & \le \parallel u_t^n-{\partial }_t{u}^n\parallel +\parallel {\partial }_t(u^n-R_h{u}^n)\parallel \hfill \\ \hfill & \le \frac{1}{\tau }\left(\parallel {\int }_{t_{n-1}}^{t_n}(t-t_{n-1})u_{tt}(·,t)dt\parallel +\parallel {\int }_{t_{n-1}}^{t_n}{(u-R_{h}u)}_t(·,t)dt\parallel \right)\hfill \\ \hfill & \le C(\tau +h^{k+1}),\hfill \end{array}$$

(74)

it follows from (21) that

$$\begin{array}{c}\hfill \parallel {\partial }_t(R_h{u}^n-u_H^n)\parallel \le C(\tau +H^{k+2}),\end{array}$$

(75)

from (15) and (73)–(75), we have

$$\begin{array}{c}\hfill \parallel {\eta }^n{\parallel }^2+{\parallel {\xi }^n\parallel }^2\le C({\tau }^2+h^{2k+2}+H^{2k+4}).\end{array}$$

(76)

The proof is completed. ☐

Therefore, by combining (12) and (15) with (65) and triangle inequality, we can obtain the following result.

Theme 1

Let$(u,\overrightarrow{q})\in W\times V$be the solution satisfied in Equations (8) and (9) and$(U_h^n,{\overrightarrow{Q}}_h^n)\in W_h\times V_h$be the solution defined in Equations (63) and (64); when$U_h^0=R_{h}u(·,0)$, there is

$$\begin{array}{c}\hfill \parallel u^n-U_h^n\parallel +\parallel {\overrightarrow{q_{}}}^n-{\overrightarrow{Q}}_h^n\parallel \le C(\tau +h^{k+1}+H^{k+2}).\end{array}$$

(77)

5. Numerical Examples

Now, we present a numerical example to confirm the efficiency of the two-grid algorithm. All simulations are carried out using MATLAB R2011a on a Windows server with an Intel Core i5-8265 processor featuring 8 GB of RAM and a 1.60 GHz CPU.

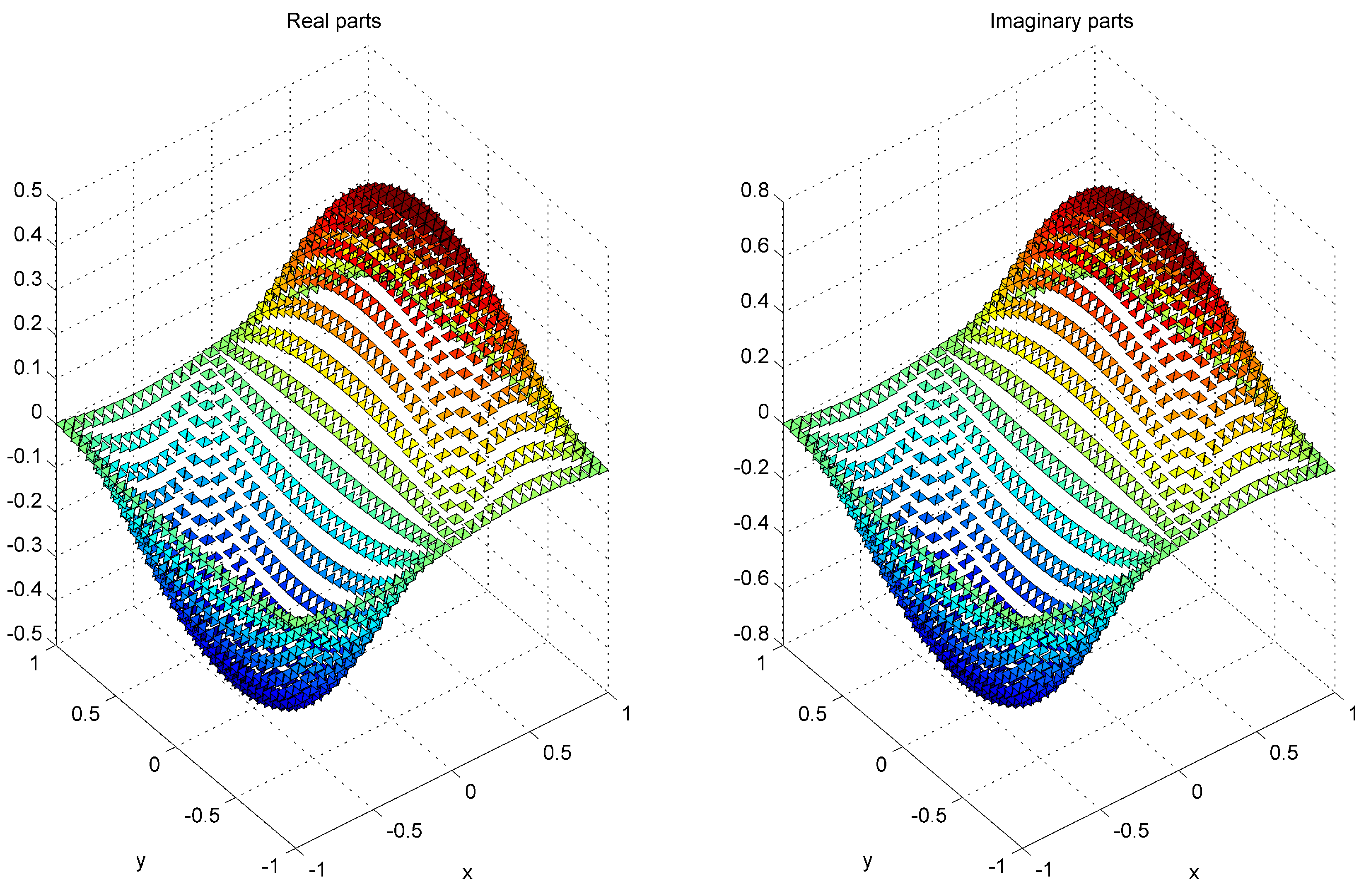
Example 1.

We consider the linear Schrödinger equation

$$\left\{\begin{array}{cc}i{u}_t(x,y,t)=-\Delta u(x,y,t)+u(x,y,t)+f(x,y,t),\hfill & (x,y)\in \Omega ,t\in (0,1],\hfill \\ u(x,y,t)=0,\hfill & (x,y)\in \partial \Omega ,t\in (0,1],\hfill \\ u(x,y,0)=u_0(x,y),\hfill & (x,y)\in \Omega ,\hfill \end{array}\right.$$

where $\Omega =[-1,1]\times [-1,1]$ and $f(x,y,t)$ satisfies the exact solution

$$u(x,y,t)=e^{it}sin\left(\pi x\right)sin(1-y^2).$$

Let ${\Gamma }_H$ and ${\Gamma }_h$ be the quasi-uniform triangular partition of $\Omega$ with the mesh sizes satisfying $h=H^2$, respectively. The Schrödinger equation is solved in the RT${}_0$ space, and $(u_h^n,{\overrightarrow{q}}_h^n)$ is the fully discrete mixed finite element solution with a backward Euler scheme in time. The two-grid solution $(U_h^n,{\overrightarrow{Q}}_h^n)$ is obtained by the algorithm in Section 4. The errors are computed by varying H and h with the time step $\tau ={10}^{-3}$; the results in

Table 1. Errors of the MFEM solution at t = 0.1.

h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/4$	$1.9676\times {10}^{-1}$	/	$7.1287\times {10}^{-1}$	/	0.34
$1/16$	$4.7371\times {10}^{-2}$	4.1536	$1.7072\times {10}^{-1}$	4.1757	3.91
$1/64$	$1.1813\times {10}^{-2}$	4.0101	$4.2566\times {10}^{-2}$	4.0107	102
$1/256$	$2.9529\times {10}^{-3}$	4.0005	$1.0641\times {10}^{-2}$	4.0002	3282

,

Table 2. Errors of the TGM solution at t = 0.1.

H	h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{U}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{Q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/2$	$1/4$	$2.8318\times {10}^{-1}$	/	$1.0980\times {10}^{-0}$	/	0.21
$1/4$	$1/16$	$7.6063\times {10}^{-2}$	3.7230	$2.9112\times {10}^{-1}$	3.7716	0.37
$1/8$	$1/64$	$1.9486\times {10}^{-2}$	3.9035	$7.4161\times {10}^{-2}$	3.9255	1.79
$1/16$	$1/256$	$4.9191\times {10}^{-3}$	3.9613	$1.8703\times {10}^{-2}$	3.9652	45.91

,

Table 3. Errors of the MFEM solution at t = 0.2.

h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/4$	$1.9710\times {10}^{-1}$	/	$7.1062\times {10}^{-1}$	/	0.52
$1/16$	$4.7377\times {10}^{-2}$	4.1602	$1.7072\times {10}^{-1}$	4.1625	7.65
$1/64$	$1.1812\times {10}^{-2}$	4.0109	$4.2565\times {10}^{-2}$	4.0108	201
$1/256$	$2.9532\times {10}^{-3}$	3.9997	$1.0642\times {10}^{-2}$	3.9997	6382

,

Table 4. Errors of the TGM solution at t = 0.2.

H	h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{U}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{Q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/2$	$1/4$	$2.8624\times {10}^{-1}$	/	$1.0772\times {10}^{-0}$	/	0.25
$1/4$	$1/16$	$7.7307\times {10}^{-2}$	3.7026	$2.8812\times {10}^{-1}$	3.7387	0.49
$1/8$	$1/64$	$1.9796\times {10}^{-2}$	3.9052	$7.3489\times {10}^{-1}$	3.9206	2.38
$1/16$	$1/256$	$4.9853\times {10}^{-3}$	3.9709	$1.8499\times {10}^{-2}$	3.9726	49.79

,

Table 5. Errors of the MFEM solution at t = 0.5.

h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/4$	$1.9534\times {10}^{-1}$	/	$7.0124\times {10}^{-1}$	/	1.09
$1/16$	$4.7349\times {10}^{-2}$	4.1255	$1.7057\times {10}^{-1}$	4.1112	18.61
$1/64$	$1.1812\times {10}^{-2}$	4.0086	$4.2563\times {10}^{-2}$	4.0075	512
$1/256$	$2.9527\times {10}^{-3}$	4.0004	$1.0640\times {10}^{-2}$	4.0003	15272

,

Table 6. Errors of the TGM solution at t = 0.5.

H	h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{U}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{Q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/2$	$1/4$	$2.6776\times {10}^{-1}$	/	$9.8898\times {10}^{-1}$	/	0.39
$1/4$	$1/16$	$7.2388\times {10}^{-2}$	3.6990	$2.6511\times {10}^{-1}$	3.7305	0.95
$1/8$	$1/64$	$1.8530\times {10}^{-2}$	3.9065	$6.7713\times {10}^{-2}$	3.9152	4.48
$1/16$	$1/256$	$4.6739\times {10}^{-3}$	3.9646	$1.7069\times {10}^{-2}$	3.9670	62.89

,

Table 7. Errors of the MFEM solution at t = 1.0.

h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/4$	$1.9486\times {10}^{-1}$	/	$6.9750\times {10}^{-1}$	/	2.05
$1/16$	$4.7342\times {10}^{-2}$	4.1160	$1.7052\times {10}^{-1}$	4.0904	36.89
$1/64$	$1.1812\times {10}^{-2}$	4.0080	$4.2563\times {10}^{-2}$	4.0063	1003
$1/256$	$2.9530\times {10}^{-3}$	4.0000	$1.0641\times {10}^{-2}$	3.9999	30357

and

Table 8. Errors of the TGM solution at t = 1.0.

H	h	$\parallel {\mathit{u}}^{\mathit{n}}-{\mathit{U}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	$\parallel {\overrightarrow{\mathit{q}}}^{\mathit{n}}-{\overrightarrow{\mathit{Q}}}_{\mathit{h}}^{\mathit{n}}\parallel$	Rate	CPU/s
$1/2$	$1/4$	$2.6601\times {10}^{-1}$	/	$9.6420\times {10}^{-1}$	/	0.67
$1/4$	$1/16$	$7.1831\times {10}^{-2}$	3.7033	$2.5897\times {10}^{-1}$	3.7232	1.71
$1/8$	$1/64$	$1.8373\times {10}^{-2}$	3.9096	$6.6237\times {10}^{-2}$	3.9097	7.69
$1/16$	$1/256$	$4.6362\times {10}^{-3}$	3.9629	$1.6712\times {10}^{-2}$	3.9634	77.12

coincide with the theoretical analysis. In addition, the two-grid method is more efficient than the standard mixed finite element method with respect to CPU cost. The profiles of the exact solution, mixed finite element solution, and two-grid solution at $t=1.0$ are plotted in Figure 1, Figure 2 and Figure 3, respectively.

6. Conclusions

In this paper, we have considered a time-dependent linear Schrödinger equation using the mixed finite element method. We presented a backward Euler fully discrete mixed finite element scheme and constructed a two-grid mixed finite element algorithm. A numerical example was provided to partly verify the theoretical result. In the future, we shall study the two-grid mixed finite method for two-dimensional time-dependent nonlinear Schrödinger equations.