Color Image Encryption Algorithm Based on Cross-Spiral Transformation and Zone Diffusion

Abstract

Due to their rich information, color images are frequently utilized in many different industries, but the network’s security in handling their delivery of images must be taken into account. To improve the security and efficiency of color images, this paper proposed a color image encryption algorithm based on cross-spiral transformation and zone diffusion. The proposed algorithm is based on Chen’s system and the piecewise linear chaotic map, and uses the chaotic sequences generated by them for related operations. Firstly, the R, G and B planes are extracted, and the spiral starting point of each plane is randomly selected by the chaotic sequence to implement the cross-spiral transformation. Secondly, the bit-level image matrix is constructed by the scrambled image matrix, and the bit-level chaotic matrix is constructed by the chaotic sequence. Finally, the three-dimensional matrix is divided into four zones by a dividing line, and partition diffusion is carried out to obtain the encrypted image. Simulation results and algorithm analyses indicate that the proposed algorithm has superior performance and can resist a wide range of attacks.

1. Introduction

With the rise of emerging technologies, people have realized the rapid information transmission in Internet. Digital images have a significant role in communication, the medical industry, the military, and other fields as vital carriers of multimedia communications. However, the convenience brought by new technologies is accompanied by the risk of information leakage, which poses a threat to the development of the country, society, and individuals. In March 2022, Samsung Electronics was attacked by a hacker group, resulting in the leakage of a large amount of the company’s confidential data. That same month, the anonymous hacking group released a database of food giant Nestlé on its Twitter account, exfiltrating about 10 GB of sensitive data, including company emails, passwords, and data related to business customers. The consequences and losses caused by these information breaches are immeasurable. Therefore, the secure transmission of information is an urgent problem. As a result, both in theory and in practice, the protection of digital image information becomes crucial. Encrypting the plain image is the most common method.

Traditional encryption algorithms are mainly designed for protecting the security of text information, such as the advanced encryption standard [1], data encryption standard [2], and international data encryption algorithm [3]. However, due to the high redundancy and strong correlation of images, there are some drawbacks to encrypt the image by the traditional encryption algorithms, such as the low encryption efficiency and weak security [4,5]. With the wide application of digital images, these traditional encryption algorithms are obviously no longer applicable, so it is necessary to study the encryption algorithm suitable for digital images to ensure the secure and efficient transmission of images.

The encrypted image is obtained through the encryption algorithm with the encryption key. The encrypted image is transmitted to the recipient through the communication channel, and the key is transmitted through the secure channel. After the recipient finally obtains the encrypted image, the decryption algorithm and the decryption key are used to decrypt the encrypted image to obtain the plain images. During the image transmission, even if the encrypted image is attacked, it is difficult for the attacker to obtain the real information of the plain image without the decryption algorithm and decryption key. Most of the image encryption algorithms are designed based on the scrambling and diffusion operations, and the decryption algorithm is the inverse process of the encryption algorithm.

Most image encryption algorithms cover roughly two parts. The first part is the method design of generating chaotic sequences. The generation of chaotic sequences depends on chaotic systems and keys, and complex chaotic systems and excellent key-generated methods always make encryption algorithms more secure. The chaotic system is a nonlinear phenomenon with the characteristics of initial sensitivity, unpredictability, ergodicity, etc. [6]. It is very consistent with the concepts in cryptographic algorithms. Most of the current image encryption algorithms are based on chaotic theory [7,8,9]. Therefore, it is necessary to select a chaotic system with excellent performance and design a reasonable random sequence generation method. Fridrich firstly used chaotic theory in 1998 to change the positions of image pixels to achieve the purpose of encrypting images [10]. Wang et al. used the improved one-dimensional (1D) Logistic map to scramble the pixel position [11]. Naskar P. K. et al. used the Logistic map for diffusion [12]. Many scholars propose a 1D chaotic system. In addition, some experts and scholars use high-dimensional chaotic systems to encrypt images. Chen applied the Lorentz chaotic system to image encryption [13]. Luo et al. proposed a hybrid system [14].

The second part is the structural design of the encryption algorithm. The scrambling-diffusion mechanism is the framework of typical image encryption. The scrambling operation can change the pixel positions of the plain image to reduce the correlation of adjacent pixels. The classical scrambling methods include the spiral transformation [15], Zigzag transformation [16], Arnold transformation [17], magic square transformation [18], and Latin square transformation, etc. [19]. Among them, the magic square transformation and the Latin square transformation are complex. Arnold has a short conversion period and low efficiency. The Zigzag transformation has the disadvantages of the unchanged position of the first and last elements before and after the transformation and a single scanning starting point. Compared with the above transformations, the spiral transformation has the advantages of simple transformation and low time complexity, so the spiral transformation is selected to realize the chaotic process in our algorithm. Xian et al. proposed a novel chaotic image encryption algorithm based on the spiral transformation [15]. Tang et al. designed a double helix transformation that effectively shuffles the pixels of image blocks [20]. Yuan et al. devised a bit-level spiral-filling method that scans pixels with odd and even lines successively [21]. Wang et al. constructed a two-way spiral transformation. For the R, G, and B planes of color images, the left half of the region is scanned clockwise spirally, and then the right half of the area is counterclockwise. The scrambling effect of the proposed bidirectional spiral transformation is significantly better than that of the traditional spiral transformation [22]. Thangaraja et al. designed a randomly selectable starting point of the spiral based on the chaotic map and used this helical transformation to scramble the plain image in a clockwise direction [23]. Xiao et al. screwed the image in pixel blocks, and its starting position, orientation and direction were all controlled by the chaotic sequences [24]. Huang et al. firstly performed a clockwise or counterclockwise spiral transformation within the block on the image and then performed the spiral transformation between the blocks to achieve scrambling of the image [7]. Wang et al. designed a dynamic spiral scrambling algorithm to dynamically combine the chaotic sequence with the plain image to change the pixel value of the plain image. Experimental simulation analysis showed that the algorithm can resist various common attacks. However the non-square image needs to be filled, and there may be blank information after decryption [25]. Liu et al. proposed the RSA algorithm to protect the structural parameters and geometric size of the structured spiral phase mask and the security of the JTC cryptosystem, which can be enhanced simultaneously [26]. Xian et al. proposed a novel chaotic image encryption algorithm with a spiral transformation-based fractal sorting matrix [27]. Xu et al. proposed a robust image encryption algorithm combining a new chaotic system and discrete cosine transformation. The spatial image is scrambled by the spiral transformation, and then the diffusion operation is performed to obtain the encrypted image [28]. Wang et al. designed a dynamic spiral block scrambling to encrypt the sparse matrix generated by performing discrete wavelet transformation (DWT) on the plain image. Then, the encrypted image is compressed and quantified to obtain the noise-like cipher image [29].

The diffusion operation can modify the pixel values of an image to improve the ability of statistical attacks. The scrambled image is still difficult to resist statistical attacks, and the security is not strong enough. Therefore, the further diffusion operation on the image is necessary. Diffusion methods processes generally include the exclusive OR (XOR) operation diffusion and additive mode diffusion. To further strengthen the diffusion method, Huang et al. carried out the XOR diffusion of the three components of the color image by a cyclic shift of the row and column, respectively [30]. Zhu et al. constructed an improved two-dimensional (2D) diffusion structure that extends slight variations of the plain image to the entire encrypted image [31]. The diffusion process can also be divided into pixel-level diffusion and bit-level diffusion from the study of particle size. Bit-level image encryption causes both the positions and pixel values in the image matrix to change. Wang et al. devised a snake-like pixel-level diffusion method. The chaotic image is XOR from left to right, the row elements move in a circular manner, and then the columns of the image are XOR from right to left in a serpentine order, and the column elements move in a circular manner [32]. Xu et al. designed a bit-level mutual diffusion technique, which can achieve the ideal effect in just one round [33]. Wang et al. designed cross-plane diffusion rule based on the bit-level level and combined it with the S-box to replace half a pixel. The algorithm design is ingenious, and the secure factor is high [34].

At present, many encryption algorithms for color images have been proposed in academia. Wang et al. innovated a chaotic system and applied it to color images in combination with new deterministic scrambling and XOR diffusion [35]. Zhang et al. combined the three channels of color images into a 2D matrix. They used a chaotic index to scramble the pixel positions and use the DNA dynamic coding operation to obtain color-encrypted images [36]. Liu et al. used Arnold transformation to shuffle the pixels of R, G, and B components, and then they spread the pixel values with the help of chaotic sequences [37].

However, the current color image encryption algorithm still has shortcomings. For examples, the partial scrambling algorithm has an obvious horizontal correlation [38], and many algorithms only repeat the grayscale image encryption algorithm in the three components, R, G, and B, when encrypting color images, ignoring the high correlation among the R, G, and B components [36]. Therefore, on the basis of breaking the strong correlation between the components of color images and making full use of the characteristics of color images, it is necessary to propose an effective color image encryption algorithm for solving the problem of weak security and low efficiency. An image encryption algorithm based on cross-spiral transformation and zone segmentation is proposed in this paper. Firstly, to increase the key space and improve the key sensitivity, the hash value of the plaintext color image and six external parameters are utilized as the key in the key generation stage. Secondly, a cross-spiral transformation with arbitrary starting points is established by combining the features of color images, and the cross-spiral transformation of the three components is performed by the constructed index matrix. Thirdly, the scrambled image is decomposed into 8-bit planes, which are redivided into four zones. The bitwise XOR operations are performed in different directions for each zone to obtain the cipher image. Finally, in the simulation and performance testing stage, several metrics demonstrate that the proposed algorithm is highly resistant to brute-force, statistical, robustness, and chosen-plaintext attacks.

The main contributions of this paper are described as follows, (1) Color image encryption algorithm based on cross-spiral transformation and zone diffusion is proposed. (2) The cross-spiral transformation is designed, which is not only suitable for any spiral starting point in the matrix but also breaks the strong correlation between the components of the color image. (3) The zone segmentation is designed, which can spread to three planes at the same time. The operation based on the bit level can make the desirable diffusion effect better.

The rest of this paper is arranged as follows. Section 2 describes the theoretical principles. Section 3 proposes a new color image encryption algorithm based on cross-spiral transformation and zone segmentation. Section 4 carries out some experiments. The experimental analyses are provided in Section 5. Section 6 draws the conclusions and outlooks.

2. Theoretical Principles

2.1. Color Image Encryption Algorithm

Vivid color images are widely used in various fields. The color image can be broken down into three components: red, blue, and green. They are arranged in a certain order and can be regarded as a three-dimensional (3D) matrix, as shown in Figure 1. All three components are integers ranging from 0 to 255. each pixel contains information about these three colors, and their proportions determine the color of the pixel.

There are two main ideas for existing color image encryption algorithms.

(1)

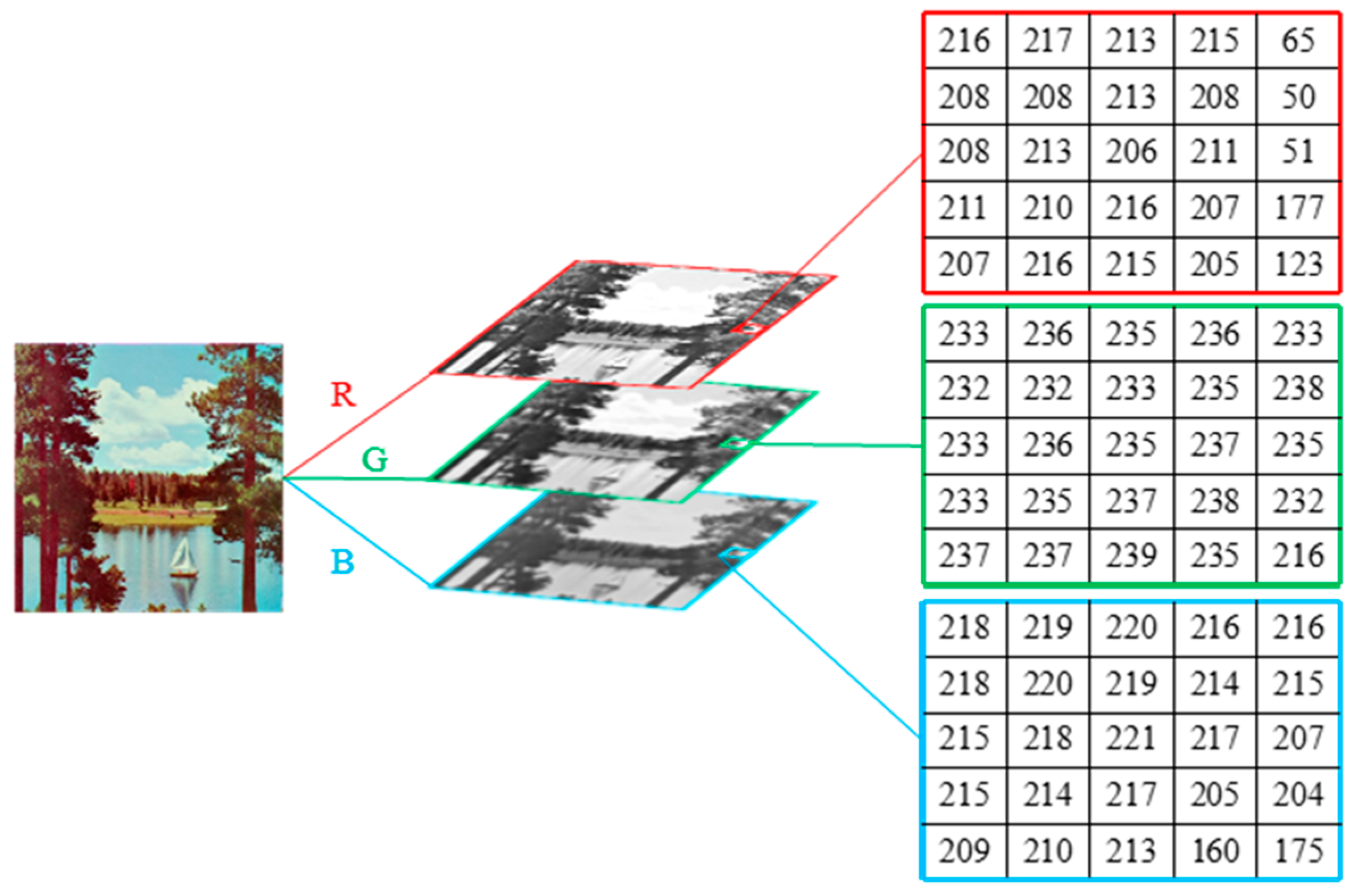
The three channels are encrypted independently. Firstly, the three components, R, G, and B, of the color image are decomposed, as shown in Figure 2. Secondly, the same algorithm is used for the three channels and encrypted separately in the form of grayscale images. Finally, the grayscale ciphertext images of the three components are combined in their original order to form the final color ciphertext image. This line of thinking does not take into account the high correlation between the R, G, and B components, resulting in color images being slightly less defensive against attacks.

(2)

The three channels are encrypted in the form of grayscale images as a whole. Firstly, the three channels, R, G, and B, of the color image are decomposed, as shown in Figure 3. Secondly, the three channels are first stitched into a large grayscale image. Finally, the whole is encrypted in the form of a grayscale image to obtain a ciphertext image. This line of thinking would ignore the characteristics of color images.

2.2. Traditional Spiral Transformation

The traditional spiral transformation is a classic method of transforming the position of pixels and can scan all pixels in the image in a spiral manner at a given spiral start and direction to complete the scrambling process [15]. As shown in Figure 4, the upper-right corner is used as the starting point to scramble the image. The matrix elements are changed following the arrow trajectory, which converts the spiral matrix into a vector of length 25. The two matrices of 5 × 5 shown are illustrated to represent the matrices before and after the spiral transformation, respectively.

2.3. Cross Spiral Transformation

On the basis of the traditional spiral transformation, the, R, G, and B components and chaotic sequences of color images are combined to propose a new cross spiral transformation. The detailed steps are as described follows.

Step 1: Selecting the transformation starting points.

According to the chaotic sequence, the starting points are randomly selected in the three components: R, G, and B.

Step 2: Arbitrary points spiral transformation.

Although the traditional spiral transformation operation is efficient, it can only process square matrices, and the scrambling effect is undesirable. Therefore, an arbitrary points spiral transformation is designed to solve the problems of limited image size and weak scrambling effect. The specific transformation process is shown in Figure 5. Elements in the matrix are scanned clockwise from the selected scan starting point from the inside to the outside until the traversal is complete. The scanned elements are stored sequentially in a 2D matrix to obtain the scrambled matrix.

In the R, G, and B components, the selected starting points are used to carry out a clockwise arbitrary points spiral transformation, and the scrambled R, G, and B components can be obtained.

Step 3: Cross-scrambling operation.

Three chaotic matrices, whose elements are 1, 2, or 3, are used to further scramble pixel position. The pixels in the scrambled R, G, and B components are selected, in turn, to obtain three new matrices and reconstitute a 3D matrix. If the element of the chaos matrix is 1, it means that the element on the R component is selected. If the element of the chaos matrix is 2, it means that the element on the G component is selected. If the elements of the chaos matrix are 3, it means that the elements on the B component are selected.

Taking an example with a 5 × 5 × 3 matrix, the specific transformation process of the cross-spiral transformation can be seen in Figure 6.

Firstly, arbitrary points spiral transformations are performed in the R, G, and B components in the 5 × 5 × 3 matrix. Secondly, the chaotic matrix is used to realize cross-scrambling operations. Finally, the new R, G, and B components are combined to obtain a scrambled matrix.

2.4. Chen’s Chaotic System

Chen’s chaotic system has the complex dynamic behavior, and its chaotic sequences are random and unpredictable. Chen’s chaotic system is defined by [39]:

$$\left\{\begin{array}{l}\dot{x}=a(y-x)\\ \dot{y}=(c-a)x-xz+cy,\\ \dot{z}=xy-bz\end{array}\right.$$

(1)

where x, y, and z are state variables and a, b, and c are control parameters. This system behaves as a chaotic characteristic when a = 35, b = 3, and $20\le c\le 28.4$ [39,40]. The chaotic attractor is shown in Figure 7. It can be seen that the chaotic system has excellent traversability when c = 28. Figure 8 shows a time series plot of Chen’s map. Chen’s map has uniform distribution and excellent traversability, which can provide a good random sequence for the encrypting of images.

2.5. Piecewise Linear Chaotic Map

The piecewise linear chaotic map (PWLCM), as one of the common 1D chaotic systems, meets the characteristics of transversality and simplicity. The PWLCM is defined by [41]

$$s_{n+1}=f(s_n, p)=\left\{\begin{array}{ll}{s}_n/p,& 0<s_n<p\\ (s_n-p)/(0.5-p),& p\le s_n<0.5,\\ f(1-s_n, p),& 0.5\le s_n<1\end{array}\right.$$

(2)

where state variables are $s_n\in (0, 1)$ and control parameters are $p\in (0, 0.5)$. Figure 9 shows the bifurcation diagram of the PWLM.

2.6. Zone Segmentation

The pixel values can be changed by the diffusion operation. If the bit-level diffusion method is reasonably designed, a better diffusion effect will be achieved to affect the entire image, and there will only be minor changes in the plain image. To improve the security of the proposed image encryption algorithm, this paper designs a bit-level zone segmentation method. Zone segmentation is an important part of the bit-level diffusion method. The main purpose is to divide the 3D image matrix into four zones, and each zone selects different diffusion methods to change the pixel values and enhance the diffusion effect.

A color image with a size of m × n × 3, and any pixel of the R, G, and B components, can be represented as having 8 bits. Therefore, a color image can be viewed as a 3D matrix, like Figure 10. Segmentation is performed by selecting a dividing line, which then divides the bit image matrix into four zones based on the chosen dividing line. The detailed steps for zone segmentation are described as follows.

Step 1: Bit-plane decomposition.

The plain color image is I with a size of m × n × 3. It is decomposed into m × n × 24-bit planes. Therefore, I can be viewed as a 3D matrix T with a size of m × n × 24.

Step 2: Selecting the dividing line.

The dividing line dpx $\in$ {1, 2, …, m} on the x-axis and the dividing line dpy $\in$ {1, 2, …, n} on the y-axis are randomly selected by the chaotic sequence.

Step 3: 3D matrix segmentation.

According to the two dividing lines dpx and dpy, the 3D matrix T is decomposed into four zones: Z₁, Z₂, Z₃, and Z₄.

3. Algorithm Description

The proposed algorithm in this paper is composed of three stages, i.e., key generation, encryption process, and decryption process.

3.1. Key Generation

The SHA-256 of the plain color image and external parameters are used to generate the control parameters and initial values of Chen’s chaotic system and the PWLCM. The detailed steps to generate the key are described as follows.

Step 1: Dividing the hash value.

The hash value K of the plain color image is decomposed into 32 segments with an 8-bit length:

$$K=k_1, k_2, \dots , k_{32}.$$

(3)

Step 2: Calculating intermediate parameters.

The six intermediate parameters are generated by:

$$\left\{\begin{array}{l}{h}_1=floor\left({\displaystyle \sum _{i=1}^6{\delta }_i}+\frac{(k_1+k_3+k_5+k_7+k_9+k_{11})}{\max (k_1,k_3,k_5,k_7,k_9,k_{11})}\right)\begin{array}{ll}& \end{array}\\ h_2=floor\left({\displaystyle \sum _{i=1}^2{\delta }_i}+h_1+\frac{(k_2+k_4+k_6+k_8+k_{10}+k_{12})}{\max (k_2,k_4,k_6,k_8,k_{10},k_{12})}\right)\\ h_3=floor\left({\displaystyle \sum _{i=1}^3{\delta }_i}+{\displaystyle \sum _{i=1}^2{h}_i}+\frac{(k_{13}+k_{15}+k_{17}+k_{19}+k_{21})}{\max (k_{13},k_{15},k_{17},k_{19},k_{21})}\right)\\ h_4=floor\left({\displaystyle \sum _{i=1}^4{\delta }_i}+{\displaystyle \sum _{i=1}^3{h}_i}+\frac{(k_{14}+k_{16}+k_{18}+k_{20}+k_{22})}{\max (k_{14},k_{16},k_{18},k_{20},k_{22})}\right)\\ h_5=floor\left({\displaystyle \sum _{i=1}^5{\delta }_i}+{\displaystyle \sum _{i=1}^4{h}_i}+\frac{(k_{23}+k_{25}+k_{27}+k_{29}+k_{31})}{\max (k_{23},k_{25},k_{27},k_{29},k_{31})}\right)\\ h_6=floor\left({\displaystyle \sum _{i=1}^6{\delta }_i}+{\displaystyle \sum _{i=1}^5{h}_i}+\frac{(k_{24}+k_{26}+k_{28}+k_{30}+k_{32})}{\max (k_{24},k_{26},k_{28},k_{30},k_{32})}\right)\end{array}\right.,$$

(4)

where floor(·) is the rounding toward negative infinity function, max(·) means the maximum value in all numbers, and δ₁, δ₂, δ₃, δ₄, δ₅, and δ₆ are the external parameters.

Step 3: Generating initial values and control parameters.

Six intermediate parameters can be used to calculate the control parameter c and initial values x₀, y₀, and z₀ of Chen’s chaotic system and the control parameter p and initial value s₀ of the PWLCM. These initial values and control parameters are generated by:

$$\left\{\begin{array}{l}{x}_0=\left(\left(h_1\oplus h_2\oplus h_3\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1\\ y_0=\left(\left(h_2\oplus h_3\oplus h_4\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1\\ z_0=\left(\left(h_3\oplus h_4\oplus h_5\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1\\ s_0=\left(\left(h_4\oplus h_5\oplus h_6\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1\\ p=\left(h_2+h_4+h_6\right)\mathrm{mod}0.4+0.1\begin{array}{l}\end{array}\begin{array}{l}\end{array}\\ c=floor\left(\left(h_1+h_3+h_5\right)\mathrm{mod}8.4\right)+20\end{array}\right.,$$

(5)

where ⊕ indicates XOR operation, and mod(·) denotes the modulus operation after division.

3.2. Encryption Process

The proposed algorithm uses the classical permutation-diffusion framework. In the scrambling stage, the chaotic sequence is used to select the spiral starting points of the three planes of R, G, and B in the color image, and then cross-spiral transformation is used to change the color image pixel position of each component to solve the problem of the strong correlation between pixels. In the diffusion stage, the chaotic sequence is used to randomly determine the two dividing lines, and then the bit-level zone segmentation is used to enhance the resistance to data statistical attacks. The encryption diagram is described in Figure 11. The specific steps are shown as follows.

Step 1: Inputting the color image.

Let the plain color image be I, whose size is m × n × 3. Its R, G, and B components, IR, IG, and IB, are matrices with sizes of m × n.

Step 2: Generating chaotic sequences.

This step uses the control parameter c and the initial values x₀, y₀, and z₀ of Chen’s chaotic system defined in Section 2.4. Three chaotic sequences, L₁, L₂, and L₃, with lengths of mn, can be obtained after iterating 1000 + mn times according to Equation (1) and discarding the first 1000 values. Similarly, using the control parameter p and the initial values s₀ of the PWLCM defined in Section 2.5, the chaotic sequence S with a length of 3 mn + 8 can be obtained after iterating 1008 + 3 mn times according to Equation (2) and discarding the first 1000 values.

Step 3: Chaotic sequence processing.

L₁, L₂, and L₃ are processed by:

$$H_1(i)=\left\{\begin{array}{l}1,\begin{array}{l}\end{array}{L}_1(i)>L_2(i)\\ -1,\begin{array}{l}\end{array}{L}_1(i)\le L_2(i)\end{array}\right.,\begin{array}{l}\end{array}i=1, 2, \cdots , mn,$$

(6)

$$H_2(i)=floor\left(\left(L_1(i)\times {10}^{14}\right)\mathrm{mod}2\right)+1,\begin{array}{l}\end{array}i=1, 2, \cdots , mn,$$

(7)

$$H_3(i)=floor\left(\left(L_2(i)\times {10}^{14}\right)\mathrm{mod}2\right)+1,\begin{array}{l}\end{array}i=1, 2, \cdots , mn,$$

(8)

where H₁, H₂, and H₃ are the intermediate sequences used to generate the index matrices.

Step 4: Generating index matrices.

L₃, H₁, H₂, and H₃ are processed by:

$$A_1(i)=floor\left(\left(L_3(i)\times {10}^{14}\right)\mathrm{mod}3\right)+1,\begin{array}{l}\end{array}i=1,2,\cdots ,mn,$$

(9)

$$A_2(i)=\left\{\begin{array}{l}{H}_1(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=1\\ H_2(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=3\\ H_3(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=2\end{array}\right.,\begin{array}{l} i=1, 2, \cdots , mn\end{array},$$

(10)

$$A_3(i)=\left\{\begin{array}{l}1,\begin{array}{l}\end{array}\left(A_1(i)=2\&A_2(i)=3\right)\left|\right|\left(A_1(i)=3\&A_2(i)=2\right)\\ 2,\begin{array}{l}\end{array}\left(A_1(i)=1\&A_2(i)=3\right)\left|\right|\left(A_1(i)=3\&A_2(i)=1\right)\\ 3,\begin{array}{l}\end{array}\left(A_1(i)=1\&A_2(i)=2\right)\left|\right|\left(A_1(i)=2\&A_2(i)=1\right)\end{array}\right.,\begin{array}{l}\end{array}i=1, 2, \cdots , mn,$$

(11)

where A₁, A₂, and A₃ index sequences with a size of mn. A₁, A₂, and A₃ are reshaped into three new 2D chaotic matrices, X₁, X₂, and X₃, with lengths of m × n to select the pixels of R, G, and B. The specific selection rules are described as follows.

(1)

If the value of the index matrix X₁, X₂, and X₃ is 1, it means that the pixel of the R component is selected;

(2)

If the value of the index matrix X₁, X₂, and X₃ is 2, it means that the pixel of the G component is selected;

(3)

If the value of the index matrix X₁, X₂, and X₃ is 3, it means that the pixel of the B component is selected.

Step 5: Cross-spiral transformation.

The starting point of the spiral transformation of the three planes of R, G, and B is calculated according to the first six values of the chaotic sequence S. The specific formula is designed by:

$$s{p}_i=floor\left(\left(S(i)\times {10}^{14}\right)\mathrm{mod}256\right),\begin{array}{l}\end{array}i=1,2,\cdots ,6,$$

(12)

where sp_i (i = 1, 2, …, 6) represents the coordinates of the spiral transformation starting in the three planes of R, G, and B. The starting point in the R plane is (sp₁, sp₂). The starting point in the G plane is (sp₃, sp₄). The starting point in the B plane is (sp₅, sp₆).

The cross-spiral transformation is achieved in IR, IG, and IB to obtain three scrambled matrices, P₁, P₂, and P₃ with a size of mn, using sp_i, X₁, X₂, and X₃.

Step 6: Zone segmentation.

Each pixel value of P₁, P₂, and P₃ is converted from a decimal to 8-bit binary to obtain three binary matrices, Q₁, Q_2, and Q₃, with sizes of mn × 8. Q₁, Q_2, and Q₃ are reshaped into a 3D image matrix Q with a size of m × n × 24.

S is calculated to obtain X with a length of 3 mn, and X is converted into a binary 3D chaotic matrix B with a size of m × n × 24.

$$X(i)=floor\left(\left(S(i)\times {10}^{14}\right)\mathrm{mod}256\right),\begin{array}{l}\end{array}i=9,10,\cdots ,3mn+9.$$

(13)

S is used to select the dividing lines x = dpx on the x-axis and y = dpy on the y axis; they are calculated by:

$$\left\{\begin{array}{l}dpx=\left(floor\left(S(7)\times {10}^{14}\right)\right)\mathrm{mod}m\\ dpy=\left(floor\left(S(8)\times {10}^{14}\right)\right)\mathrm{mod}n\end{array}\right.,$$

(14)

where dpx $\in$ (1, m), dpy $\in$ (1, n), dpx, and dpy are used as the two dividing lines to divide Q and E. They are divided into four areas: Z₁, Z₂, Z₃, and Z₄.

Step 7: Zone diffusion.

Row by row or column by column XOR operations are performed on each zone Q and E to obtain a 3D matrix W with a size of m × n × 24. The specific process of zone diffusion is designed by Z₁ zone diffusion, Z₂ zone diffusion, Z₃ zone diffusion, and Z₄ zone diffusion.

(1)

Z₁ zone diffusion:

$$\left\{\begin{array}{ll}W(i,j,z)=Q(i,j,z)\oplus Q(i+1,j,z)\oplus E(i,j,z),& i=dpx+1, dpx+2, \dots , m-1\\ W(i,j,z)=Q(i,j,z)\oplus E(i,j,z),& i=m\end{array}\right.,$$

(15)

(2)

Z₂ zone diffusion:

$$\left\{\begin{array}{ll}W(i,j,z)=Q(i,j,z)\oplus E(i,j,z),& j=dpy+1\\ W(i,j,z)=Q(i,j,z)\oplus Q(i,j-1,z)\oplus E(i,j,z),& j=dpy+2, dpy+3, \dots , n\end{array}\right.,$$

(16)

where i = dpx + 1, dpx + 2, …, m, and z = 1, 2, …, 24.

(3)

Z₃ zone diffusion:

$$\left\{\begin{array}{ll}W(i,j,z)=Q(i,j,z)\oplus Q(i,j,z+1)\oplus E(i,j,z),& z=1, 2, \dots , 23\\ W(i,j,z)=Q(i,j,z)\oplus E(i,j,z),& z=24\end{array}\right.,$$

(17)

where i = 1, 2, …, dpx, y = dpy +1, and dpy + 2, …, n.

(4)

Z₄ zone diffusion:

$$\left\{\begin{array}{ll}W(i,j,z)=Q(i,j,z)\oplus Q(i,j+1,z)\oplus E(i,j,z),& j=1, 2, \dots , dpy-1\\ W(i,j,z)=Q(i,j,z)\oplus E(i,j,z),& j=dpy\end{array}\right.,$$

(18)

where i = 1, 2, …, dpx and z = 1, 2, …, 24.

Step 8: Generating the encrypted image.

W is reshaped into a matrix with a size of 3 mn × 8, and the matrix is converted to a decimal sequence U with a length of 3 mn. U reshaped the encrypted image C with a size of m × n × 3. Algorithm 1 shows the encryption process.

Algorithm 1: Encryption process.

Input: Plain color image I, h1, h2, h3, h4, h5 and h6 Output: Encryption image C 1: $x_0=\left(\left(h_1\oplus h_2\oplus h_3\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1$ 2: $y_0=\left(\left(h_2\oplus h_3\oplus h_4\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1$ 3: $z_0=\left(\left(h_3\oplus h_4\oplus h_5\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1$ 4: $s_0=\left(\left(h_4\oplus h_5\oplus h_6\right)/{\displaystyle \sum _{i=1}^6{h}_i}\right)\mathrm{mod}1$ 5: $p=\left(h_2+h_4+h_6\right)\mathrm{mod}0.4+0.1$ 6: $c=floor\left(\left(h_1+h_3+h_5\right)\mathrm{mod}8.4\right)+20$ 7: L1, L2, L3= Chen (x0, y0, z0, 1000 + 1: 1000 + m × n) 8: for t = 1 to mn do: 9: $H_1(i)=\left\{\begin{array}{l}1,\begin{array}{l}\end{array}{L}_1(i)>L_2(i)\\ -1,\begin{array}{l}\end{array}{L}_1(i)\le L_2(i)\end{array}\right.$ 10: $H_2(i)=floor\left(\left(L_1(i)\times {10}^{14}\right)\mathrm{mod}2\right)+1$ 11: $H_3(i)=floor\left(\left(L_2(i)\times {10}^{14}\right)\mathrm{mod}2\right)+1$ 12: $A_1(i)=floor\left(\left(L_3(i)\times {10}^{14}\right)\mathrm{mod}3\right)+1$ 13: $A_2(i)=\left\{\begin{array}{l}{H}_1(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=1\\ H_2(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=3\\ H_3(i)+A_1(i),\begin{array}{l}\end{array}{A}_1(i)=2\end{array}\right.$ 14: $A_3(i)=\left\{\begin{array}{l}1,\begin{array}{l}\end{array}\left(A_1(i)=2\&A_2(i)=3\right)\left|\right|\left(A_1(i)=3\&A_2(i)=2\right)\\ 2,\begin{array}{l}\end{array}\left(A_1(i)=1\&A_2(i)=3\right)\left|\right|\left(A_1(i)=3\&A_2(i)=1\right)\\ 3,\begin{array}{l}\end{array}\left(A_1(i)=1\&A_2(i)=2\right)\left|\right|\left(A_1(i)=2\&A_2(i)=1\right)\end{array}\right.$ 15: end for 16: X1 = reshape (A1, m, n) 17: X2 = reshape (A2, m, n) 18: X3 = reshape (A3, m, n) 19: when X1 = 1, X2 = 1, X3 = 1, R component is selected 20: when X1 = 2, X2 = 2, X3 = 2, G component is selected 21: when X1 = 3, X2 = 3, X3 = 3, B component is selected 22: for t = 1 to 3 do: 23: Pt= Cross spiral transform (I(:, :, t)) 24 : Qt = dec2bin(Pt) 25 : C( :, :, t) = Zone diffusion Qt 26 : Et = C( :, :, t) 27 : end for

3.3. Decryption Process

Each part of the proposed algorithm is reversible, and the encrypted image can be decrypted to obtain the correct plain image by the correct decryption key and the reverse operations of the encrypted process. The decryption diagram is shown in Figure 12.

4. Simulation Experiments and Results

The encryption algorithm is run in Matlab R2018b. The hardware environment is a 2.8 GHz CPU processor and 8 GB of memory. The software environment is a 64-bit Windows 10 operating system. The keys are hash value K of the plain color image and the external parameters δ₁ = 20, δ₂ = 0.4, δ₃ = 12, δ₄ = 130, δ₅ = 256, and δ₆ = 1.6. The plain images are converted into encrypted images through the proposed algorithm. We tested 50 images, 16 of which are shown in Figure 13. They are from the University of Southern California SIPI image database (http://sipi.usc.edu/database (accessed on 5 April 2023)) [42]. Figure 13a–p shows that sixteen color images from the database: Tree, Jelly beans, Couple, and Female are 256 × 256 × 3. Baboon, House, Peppers, and Airplane are 512 × 512 × 3. Sailboat has a size of 489 × 281 × 3 and Splash has a size of 377 × 467 × 3. Richmond, Foster City, Oakland, San Diego, Shreveport, and Stockton are 1024 × 1024 × 3. In Figure 14a–p, the encrypted images are displayed. The encryption images can be effectively restored using the decryption procedure, as shown in Figure 15a–p.

5. Algorithm Analyses

5.1. Key Space Analysis

It is known that the key space is one of the important indicators to measure the security of the algorithms. The larger the key space, the stronger the resistance to brute force attacks. When the key size made by the algorithm exceeds 2¹⁰⁰, it can be considered to have the conditions to resist brute force attacks, and the algorithm is secure [43]. The keys are hash value K of the plain color image and the external parameters δ₁ = 20, δ₂ = 0.4, δ₃ = 12, δ₄ = 130, δ₅ = 256, and δ₆ = 1.6. The key space is 10^{14 × 6} × 2²⁵⁶ ≈ 10¹⁶¹, and it is much larger than the minimum key space required. The comparisons of the proposed algorithm with the key space of other algorithms is shown in

Table 1. Key space analysis.

Algorithm	Proposed	Ref. [44]	Ref. [45]	Ref. [46]	Ref. [47]
Key space	10161	10135	1056	10128	1090

. The results show that compared with the existing algorithms, the proposed algorithm has better resistance to brute-force attacks.

5.2. Key Sensitivity Analysis

Analyzing the key sensitivity is a crucial indicator for confirming the algorithm. Key sensitivity refers to the impact of small changes in keys in the same encryption algorithm on producing results [48]. The stronger the key sensitivity, the greater the difference between the obtained result and the result obtained by the original key under a slight change in the key, and the higher the security of the algorithm. If the encrypted image is decrypted with two different keys. The decrypted results should be completely different. Figure 16a draws the image decrypted of a Baboon with the correct key. Figure 16b–d depicts the encrypted image of the Baboon using the incorrect key. These decrypted images have no visible connection to one another.

The distinction between the two results is displayed in

Table 2. Difference between decryption results from slightly modified keys.

Figure	Decrypted Key	Pixel Difference Ratios
Figure 13a	the correct key	0.0%
Figure 13b	δ1 + 10−14	99.7421%
Figure 13c	δ3 + 10−14	99.6357%
Figure 13d	δ5 + 10−14	99.2297%

. The suggested keys are, consequently, sensitive.

5.3. Information Entropy Analysis

Information entropy is a key factor in measuring cryptographic algorithms. The information entropy increases with better random performance [49]. Its mathematical equation is:

$$H(I)={\displaystyle \sum _{i=0}^{255}p(m_i)}{\log }_2\frac{1}{p(m_i)},$$

(19)

where p(m_i) denotes the pixel gray level m_i.

Therefore, encryption algorithms should be designed with the entropy value as high as possible.

Table 3. Information entropy values.

Algorithm	Images	Entropy of Plain Images			Entropy of Encrypted Images
		R	G	B	R	G	B
Proposed	Baboon	7.7066	7.4752	7.7522	7.9993	7.9991	7.9993
	House	7.4156	7.2294	7.4353	7.9993	7.9992	7.9993
	Sailboat	7.1927	7.5641	7.3057	7.9741	7.9746	7.9745
	Splash	6.3093	6.9206	5.9263	7.9990	7.9990	7.9988
	Average	7.1560	7.2973	7.1048	7.9929	7.9929	7.9929
Ref. [22]	Baboon	7.7066	7.4752	7.7522	7.9970	7.9974	7.9975
Ref. [44]	Baboon	7.7066	7.4752	7.7522	7.9970	7.9973	7.9973
Ref. [45]	Baboon	7.7066	7.4752	7.7522	7.9992	7.9994	7.9992
Ref. [46]	Baboon	7.7066	7.4752	7.7522	7.9972	7.9973	7.9974

draws the entropy values of plain images and corresponding encrypted images. The data show that the entropy values of the encrypted images of the proposed algorithm are very close to the expected value of 8 and have an advantage over other algorithms, which means that the statistical information of the plain images is successfully hidden. It can be confirmed that the proposed algorithm has a strong anti-entropy attack ability.

In addition, local information entropy was introduced into the experiment to assess the randomness of local images.

Table 4. Test results of local information entropy of the color-encrypted images.

Color Encrypted Images	Components	Local Information Entropy		Pass/File
		Test Values	Average Values
Baboon	R	7.9020	7.9021	Passed
	G	7.9023		Passed
	B	7.9021		Passed
House	R	7.9026	7.8026	Passed
	G	7.9028		Passed
	B	7.9024		Passed
Sailboat	R	7.9026	7.9028	Passed
	G	7.9030		Passed
	B	7.9028		Passed
Splash	R	7.9025	7.9022	Passed
	G	7.9021		Passed
	B	7.9022		Passed

shows the local information entropy of the color-encrypted images of the proposed algorithm. It can be seen that the local information entropy of the encrypted images is in the ideal value (7.9019, 7.9030), which indicates that the proposed algorithm cannot only encrypt the color image, but also have good randomness in the local image.

5.4. Histogram Analysis

The histogram, also known as the mass distribution map, represents the frequency of pixel values when analyzing the image and reflects the distribution of pixel values in the image [50]. Ideally, the histograms of the original image are not evenly distributed, and the pixel values of encrypted images occur almost identically; that is, the histograms are evenly distributed. Figure 17 shows that the histograms of the encrypted image are relatively evenly distributed. Therefore, the proposed algorithm can disrupt the image’s pixel distribution.

5.5. Differential Attack Analysis

Differential attack analysis tests the plaintext sensitivity of the algorithm aim to encrypt two original images with the same key that are only slightly different [51]. Two encrypted images can be obtained. A great algorithm should result in the ciphertext images having larger changes than before. The Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) can test the capability of a differential attack. The ideal values of the NPCR and UACI are about 99.61% and 33.46%, respectively [52].

Both the specific values can be obtained by [53]:

$$NPCR=\frac{1}{m\times n}\times {\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{m}D(i,j)}}\times 100\%,$$

(20)

$$UACI=\frac{1}{255\times m\times n}\times {\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\left|C(i,j)-C^{\prime }(i,j)\right|\times 100\%,}}$$

(21)

where C (i, j) is the unmodified plain image, and $C^{\prime }(i,j)$ and C (i, j) only have a one-pixel difference.

$$D(i,j)=\left\{\begin{array}{l}0 C(i,j)=C^{\prime }(i,j)\\ 1 C(i,j)\ne C^{\prime }(i,j)\end{array}\right..$$

(22)

The results are close to the ideal values, as shown in

Table 5. The NPCR and UACI values of the color-encrypted images.

Algorithms	Images	NPCR (%)			UACI (%)
		R	G	B	R	G	B
Proposed	Baboon	99.61	99.61	99.60	33.42	33.41	33.43
	House	99.59	99.61	99.61	33.41	33.42	33.44
	Sailboat	99.64	99.60	99.60	33.47	33.51	33.50
	Splash	99.62	99.62	99.60	33.50	33.64	33.51
Ref. [22]	Baboon	99.62	99.62	99.63	33.57	33.37	33.63
Ref. [44]	Baboon	99.61	99.55	99.60	33.45	33.41	33.28
Ref. [45]	Sailboat	99.59	99.62	99.60	33.47	33.46	33.48
Ref. [46]	Baboon	99.65	99.64	99.62	33.26	33.64	33.33

, and they show the proposed algorithm defends against differential attacks.

5.6. Correlation of Adjacent Pixels

Image transformation has a high degree of data redundancy. To prevent an attacker from analyzing the correlation of the adjacent pixels, the cipher image pixels should be as uncorrelated as possible [54]. That is, the coefficient should be close to the ideal value of 0. It is defined by:

$$D(x)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{(x_i-E(x))}^2},$$

(23)

$$r_{x,y}=\frac{E((x-E(x))(y-E(y)))}{\sqrt{D(x)D(y)}},$$

(24)

$$E(x)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i},$$

(25)

where x and y are the values of the adjacent pixels and D(x) and E(x) are the variance and mathematical expectation of x, respectively. The calculated results are revealed in

Table 6. Correlation coefficients of the plain images and corresponding encrypted images.

Images	Channel	Plain Images			Encrypted Images
		Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
Baboon	R	0.9227	0.8597	0.8476	0.0004	−0.0003	0.00272
	G	0.8656	0.7578	0.7260	0.0038	0.0009	0.0042
	B	0.9070	0.8776	0.8357	−0.0010	0.0001	−0.0013
House	R	0.9543	0.9532	0.9184	−0.0025	−0.0013	−0.0006
	G	0.9339	0.9279	0.8771	0.0028	−0.0015	0.0019
	B	0.9751	0.9591	0.9356	0.0021	0.001	−0.0010
Sailboat	R	0.9415	0.9365	0.9203	0.0100	0.0359	0.0407
	G	0.9678	0.9664	0.9523	0.0162	0.0484	0.0510
	B	0.9691	0.9702	0.9511	0.0485	0.0810	0.1786
Splash	R	0.9883	0.9942	0.9862	0.0031	−0.0027	−0.0023
	G	0.9883	0.9877	0.9804	−0.0052	−0.0008	0.0019
	B	0.9864	0.9842	0.9753	0.0037	0.0021	−0.0008

and

Table 7. Comparisons of the correlation coefficients with other algorithms.

Images	Algorithms	Channel	Directions
			Horizontal	Vertical	Diagonal
Encrypted images of the Baboon	Proposed	R	0.0004	−0.0003	0.0027
		G	0.0038	0.0009	0.0042
		B	−0.0010	0.0001	−0.0013
	Ref. [22]	R	−0.0017	−0.0007	0.0015
		G	0.0028	0.0039	0.0015
		B	0.0041	0.0061	0.0025
	Ref. [44]	R	0.0033	−0.0013	−0.0009
		G	0.0001	0.0020	−0.0012
		B	0.0000	0.0000	0.0004
	Ref. [45]	R	−0.0023	0.0014	0.0155
		G	−0.0115	−0.0178	0.0044
		B	0.0066	−0.0089	−0.0132
	Ref. [46]	R	−0.0036	−0.0109	−0.0052
		G	−0.0008	0.0070	0.0095
		B	−0.0009	0.0082	−0.0113

. Figure 18a–c, Figure 19a–c and Figure 20a–c show correlation maps of the plain color image Baboon and encrypted images of R, G, and B in three directions, respectively. It can be shown that the pixel correlation of the images before encryption is very high, and the pixel encrypted is uniform, and has a very low correlation. Figure 18d–f, Figure 19d–f and Figure 20d–f show that the plain images have a great large correlation, and the encrypted image of the proposed algorithm has a low correlation.

5.7. Occlusion Attack Analysis

To evaluate the robustness of resisting occlusion attacks [55], 10%, 25%, and 50% of Peppers images are deleted, as drawn in Figure 21a–c. The decryption images are drawn in Figure 21d–f. We can clearly see that the decrypted images are almost the same as the plain images. Therefore, the proposed algorithm can resist data cropping attacks.

5.8. Chosen-Plaintext Attack

This is example 1 of an equation:

In an encryption system, the attack is very threatening to the encryption system. Therefore, an image encryption system must have enough strength to resist the attack analysis [56]. The result in Figure 22 indicates the encrypted images for three special images, i.e., the all-white image, all-black image, all-purple image. Therefore, the plain image features are corrupted. The proposed algorithm is reliable.

5.9. Randomness Test

The NIST test includes 15 tests [57]. The p-values of each test are calculated, and they should be greater than 0.01 in the test. The encrypted image of the Baboon is tested. A total of 100 repeat tests each have about 6.3 million bits.

Table 8. The NIST test.

Test	p-Values	Pass/File
Random excursions variant test	0.9921	Passed
Frequency test	0.7652	Passed
Frequency test within a block	0.0975	Passed
Runs test	0.8743	Passed
Test for the longest run of the ones in a block	0.0871	Passed
Binary matrix rank test	0.4563	Passed
Discrete Fourier transform test	0.7611	Passed
Non-overlapping template matching test	0.2187	Passed
Overlapping template matching test	0.3125	Passed
Maurer’s “Universal Statistical” test	0.5692	Passed
Linear complexity test	0.1143	Passed
Serial test	0.3217	Passed
Approximate entropy test	0.5689	Passed
Cumulative sums test	0.4303	Passed
Random excursions test	0.7615	Passed

shows the NIST test results of the Baboon, and we can find that the encrypted image of the Baboon has passed all the random tests. Therefore, the encryption effect of the proposed algorithm is excellent.

5.10. Encryption Time and Computational Complexity Analysis

The proposed algorithm is suitable for color images of any size, and its computational complexity depends on the size of the plain image. Firstly, in the chaotic sequence generation stage, the complexity of the sequence generated by Chen’s map, and the PWLCM map is about O(3 × m × n). Secondly, in the scrambling stage, it is mainly reflected in the cross-spiral transformation of the three planes of the color image, and its complexity is O(m × n). Finally, in the diffusion stage, it is mainly reflected in the bit-level partitioned diffusion, and its complexity is O(8 × m × n). In summary, the total complexity of the proposed algorithm is about O(m × n). Therefore, the higher the resolution of the image, the higher the complexity.

The encrypted time is a parameter that affects the feasibility of an encryption algorithm. Efficiency becomes especially important when encryption systems reach a certain level of security. In the experiment, color images sizes of 256 × 256 × 3 and 512 × 512 × 3 were tested several times, and their average was calculated.

Table 9. Computational complexity and encryption time analysis.

Algorithms	Size	Resolution	Time	Simulation Software
Proposed	256 × 256 × 3	256 × 256	0.5 s	MATLAB
	512 × 512 × 3	512 × 512	1.7 s
	1024 × 1024 × 3	1024 × 1024	3.1 s
Ref. [22]	256 × 256 × 3	256 × 256	1.1 s	MATLAB
Ref. [44]	512 × 512 × 3	512 × 512	2.5 s	MATLAB
Ref. [45]	512 × 512 × 3	512 × 512	2.1 s	MATLAB
Ref. [46]	512 × 512 × 3	512 × 512	1.7 s	MATLAB
Ref. [58]	512 × 512	512 × 512	5.78 s	FPGA
Ref. [59]	512 × 512 × 3	512 × 512	5.18 s	FPGA

shows the computational complexity and encrypted time with other algorithms under the same image. It can be seen that the larger the plain image size, the higher the computational complexity of the proposed algorithm, and the encryption speed of the proposed algorithm is relatively fast and not inferior to other algorithms. Therefore, the proposed algorithm is efficient and suitable for real-world scenarios of image transmission.

6. Conclusions and Outlooks

To improve efficiency and security, this paper designs a cross-spiral transformation and partition diffusion and proposes a new color image encryption algorithm. On the one hand, with the help of the characteristics of color images, the cross-spiral transformation is constructed; that is, the pixel values of the R, G, and B planes are randomly exchanged by the index matrix to change pixel position. On the other hand, the zone diffusion operation is used to change the pixel values, and high security is obtained. After analysis, it is found that the histogram of the encrypted image shows that the pixel distribution is uniform, the information entropy is close to the theoretical value, the key space is sufficient to resist brute force attacks, and the encryption speed is fast. It can be confirmed that the proposed algorithm can successfully encrypt color images with high security and effectively resist various illegal attacks. These analyses indicate the superiority of the proposed algorithm.

However, with the large-scale application of color images in various fields, the proposed color image encryption algorithms are only suitable for single-color images of any size. Multiple color image encryption algorithms will be studied to ensure their secure and efficient transmission in the future.