Dynamical Behaviors in a Stage-Structured Model with a Birth Pulse
Abstract
:1. Introduction
2. Single-Species Population Model with Stage Structure
3. Existence and Stability of Equilibria
- (i)
- and ⇔ and ;
- (ii)
- and ⇔ and ;
- (iii)
- and (or and ) ⇔.
- (iv)
- are complex and ⇔ and .
- 1.
- E is a sink if and only if
- 2.
- E is a source if and only if
- 3.
- E is a saddle if and only if
- 4.
- E is non-hyperbolic if one of the following conditions is true:
- (1)
- and ;
- (2)
- and .
4. Bifurcation Analysis
4.1. Transcritical Bifurcation at E
4.2. Flip Bifurcation at E
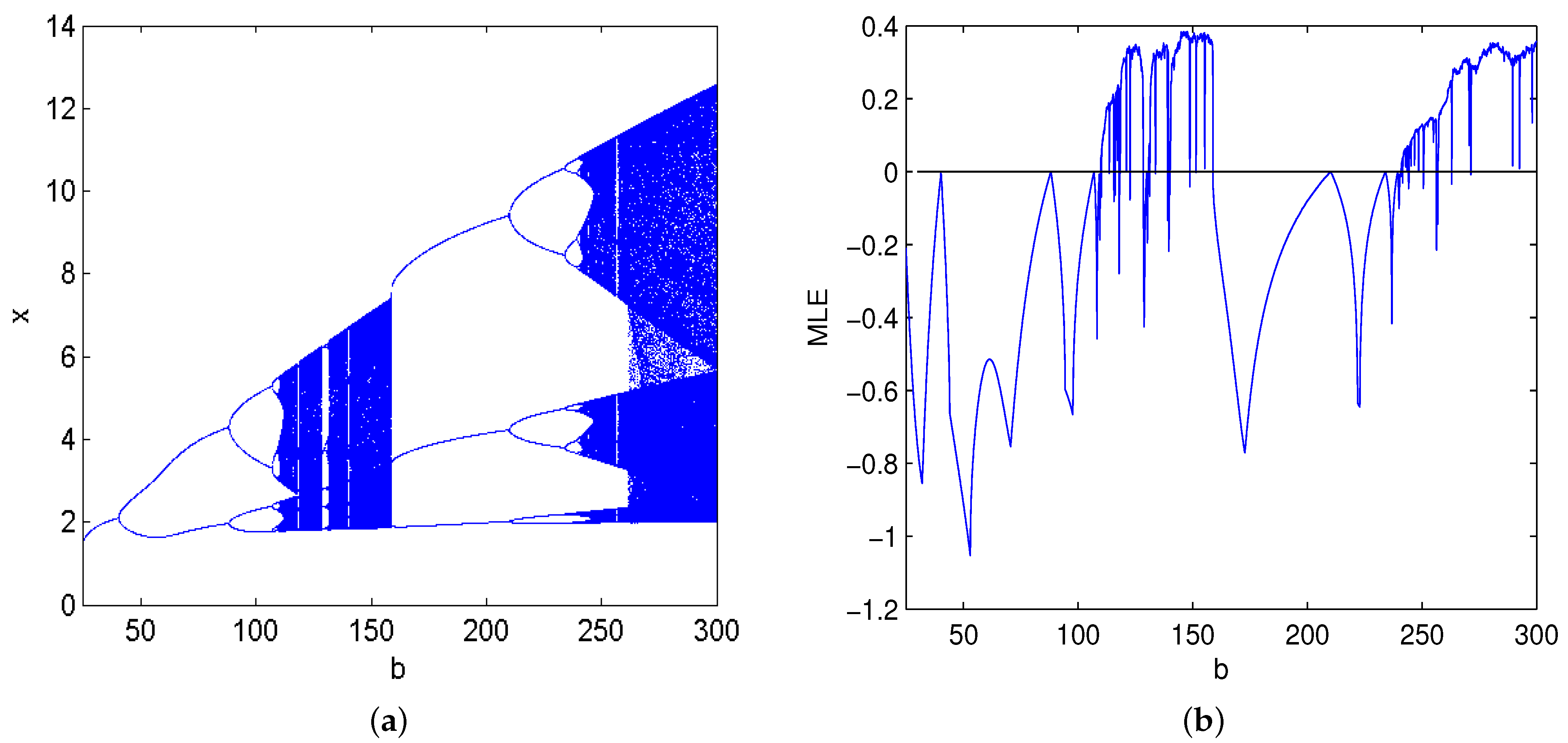
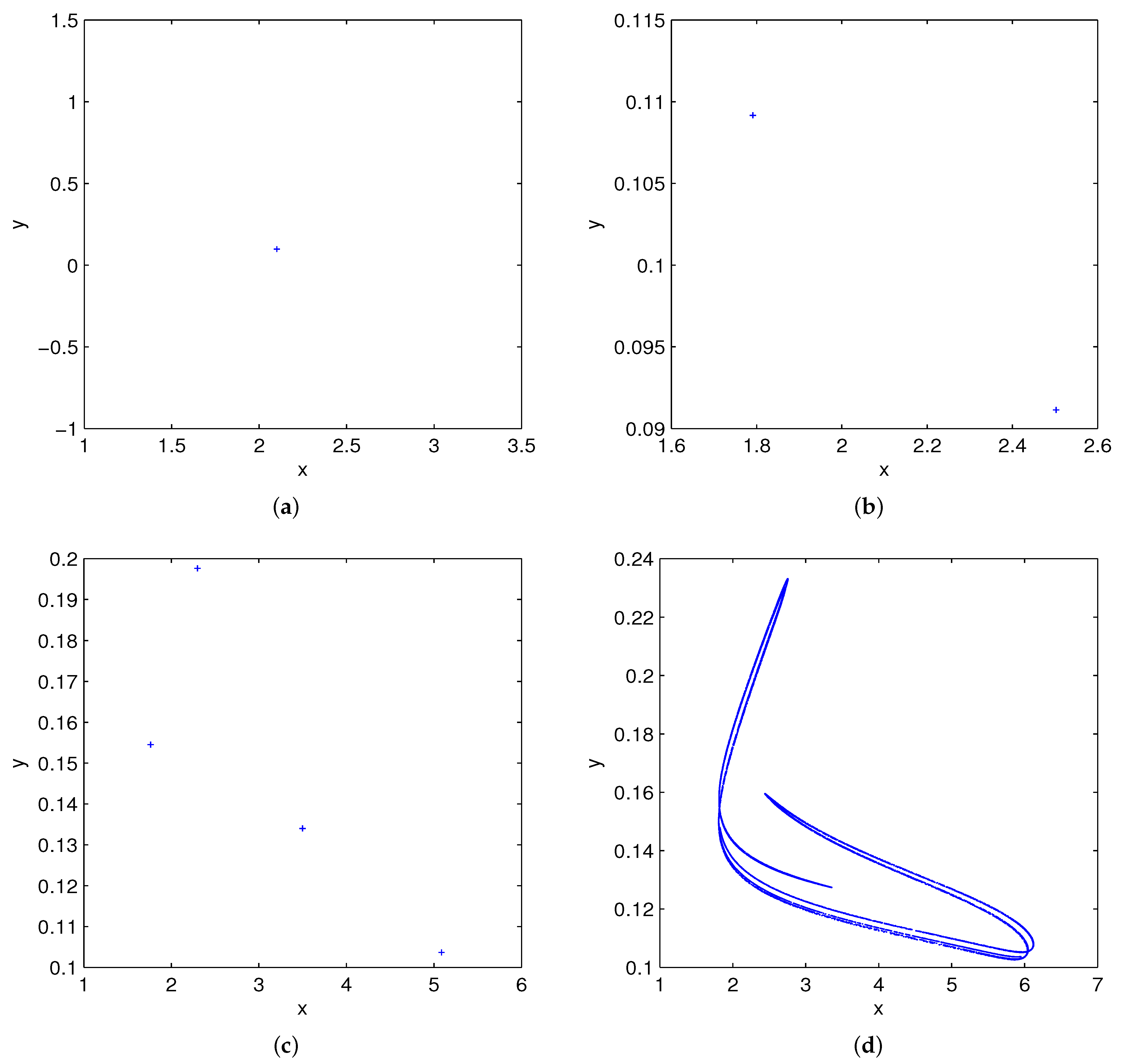
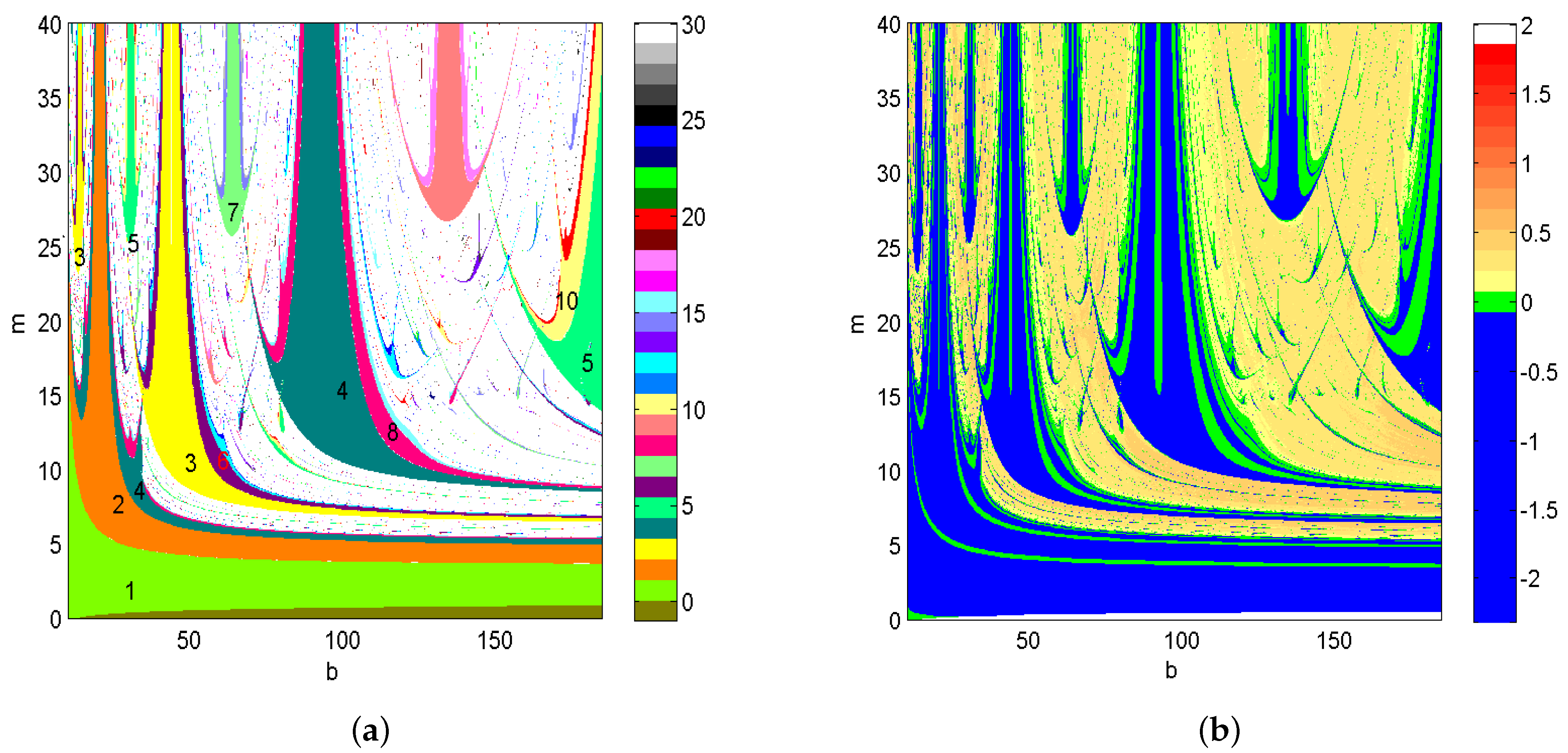
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, S.Y.; Chen, L.S. The effect of seasonal harvesting on stage-structured population models. J. Math. Biol. 2003, 48, 357–374. [Google Scholar] [CrossRef]
- Battistelli, C.; Baringo, L.; Conejo, A. Optimal energy management of small electric energy systems including V2G facillities and renewable energy sources. Electr. Pow. Syst. Res. 2012, 92, 50–59. [Google Scholar] [CrossRef]
- Murty, V.V.; Kumar, A. Optimal energy managemet and technoeconomic analysis in microgrid with hybrid renewable energy source. J. Mod. Power. Syst. Clean Energy 2020, 8, 929–940. [Google Scholar] [CrossRef]
- Kesavan, T.; Lakshmi, K. Optimization of a renewable energy source-based virtual power plant for electrical energy management in an unbalanced distribution network. Sustainability 2022, 14, 11129. [Google Scholar] [CrossRef]
- Ben Miled, S.; Kebir, A.; Hbid, M.L. Mathematical Modeling Describing the Effect of Fishing and Dispersion on Hermaphrodite Population Dynamics. Int. Rev. Red. Cross 2010, 5, 159–179. [Google Scholar] [CrossRef]
- Arino, O.; Hbid, M.L.; Bravo de la Parra, R. A mathematical model of growth of population of fish in the larval stage: Density-dependence effects. Math. Biosci. 1998, 150, 1–20. [Google Scholar] [CrossRef]
- Gao, S.J.; Chen, L.S. The effect of seasonal harvesting on a single-species discrete population model with stage structure and birth pulses. Chaos Solitons Fract. 2005, 24, 1013–1023. [Google Scholar] [CrossRef]
- Liu, J.L.; Zhang, T.L. Global dynamics of a stage-structured hantavirus infection model with seasonality. Nonlinear. Anal. 2021, 26, 21–40. [Google Scholar] [CrossRef]
- Soudijin, F.H.; de Roos, A.M. Approximation of a physiologically structured population model with seasonal reproduction by a stage-structured biomass mdel. Theor. Ecol. 2017, 10, 73–90. [Google Scholar] [CrossRef]
- Kaul, S.K.; Liu, X.Z. Generalized variation of parameters and stability of impulsive system. Nonlinear. Anal. 2000, 40, 295–307. [Google Scholar] [CrossRef]
- Raheem, A. Oscillation criteria for impulsive partial fractional differential equations. Comput. Math. Appl. 2017, 107, 17–21. [Google Scholar] [CrossRef]
- Church, K.E.M. Eigenvalues and delay differential equations: Periodic coefficients, impulses and rigorous numerics. J. Dyn. Diff. Equ. 2021, 33, 2173–2252. [Google Scholar] [CrossRef]
- Xia, M.L.; Liu, L.N.; Fang, J.Y.; Zhang, Y.C. Stability analysis for a class of stochastic differential equations with impulses. Mathematics 2023, 11, 1542. [Google Scholar] [CrossRef]
- Feketa, P.; Klinshov, V.; Lucken, L. A survey on the modeling of hybrid behaviors: How to account for impulsive jumps properly. Commun. Nonlinear Sci. 2021, 103, 105955. [Google Scholar] [CrossRef]
- Milman, V.D.; Myshkis, A.D. On the stability of motion in the presence of impulses. Sib. Math. J. 1960, 1, 233–237. [Google Scholar]
- Bainov, D.D.; Minchev, E.; Nakagawa, K. Asymptotic behaviour of solutions of impulsive semilinear parabolic equations. Nonlinear Anal. 1997, 30, 2725–2734. [Google Scholar] [CrossRef]
- Liu, X.N.; Chen, L.S. Global dynamics of the periodic logistic system with periodic impulsive perturbations. J. Math. Anal. Appl. 2004, 289, 279–291. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Liu, B.; Feng, W. Dynamics of a birth-pulse single-species model with restricted toxin input and pulse harvesting. Discret. Dyn. Nat. Soc. 2010, 2010, 142534. [Google Scholar] [CrossRef] [Green Version]
- Samoilenko, A.M.; Perestyuk, A.A. Impulsive Differential Equations; World Scientific: Singapore, 1995. [Google Scholar]
- Hernández, E.; O’Regan, D. On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 2013, 141, 1641–1649. [Google Scholar]
- Lindner, F.; Schilling, R.L. Weak order for the discretization of the stochastic heat equation driven by impulsive noise. Potential. Anal. 2013, 38, 345–379. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Wu, R.C. Bifurcation and patterns analysis for a spatiotemporal discrete Gierer-Meinhart system. Mathematics 2022, 10, 243. [Google Scholar] [CrossRef]
- Gao, S.J.; Chen, L.S.; Sun, L.H. Optimal pulse fishing policy in stage-structured models with birth pulses. Chaos Solitons Fract. 2005, 25, 1209–1219. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory, 2nd ed.; Springer: New York, NY, USA, 1988. [Google Scholar]
- Liu, X.J.; Liu, Y.; Chu, Y.D. Bifurcation and chaos in a host-parasitoid model with a lower bound for the host. Adv. Differ. Equ. 2018, 2018, 31. [Google Scholar] [CrossRef] [Green Version]
- Yousef, A.; Yousef, F.B. Bifurcation and stability analysis of a system of fractional-order differential equations for a plant-herbivore model with Allee effect. Mathematics 2019, 7, 454. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Sharma, V.S. Bifurcations and chaos control in a discrete-time prey-predator model with Holling type-II functional response and prey huge. J. Comput. Appl. Math. 2023, 418, 114666. [Google Scholar] [CrossRef]
- Tang, S.Y.; Chen, L.S. Chaos in functional response host-parasitoid ecosystem models. Chaos Solitons Fract. 2002, 13, 875–884. [Google Scholar] [CrossRef]
- Lv, S.J.; Zhao, M. The dynamic complexity of a host-parasitoid model with a lower bound for the host. Chaos Solitons Fract. 2008, 36, 911–919. [Google Scholar] [CrossRef]
- Magnitskii, N.A. Universal bifurcation chaos theory and its new applications. Mathematics 2023, 11, 2536. [Google Scholar] [CrossRef]
- Rao, X.B.; Chu, Y.D.; Zhang, J.G.; Gao, J.S. Complex mode-locking oscillations and Stern-Brocot derivation tree in a CSTR reaction with impulsive perturbations. Chaos 2020, 30, 113117. [Google Scholar] [CrossRef]
- Klapcsik, K.; Varga, R.; Hegeds, F. Bi-parameter topology of subharmonics of an asymmetric bubble oscillator at high dissipation rate. Nonlinear Dyn. 2018, 94, 2373–2389. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Guo, L.; Liu, X. Dynamical Behaviors in a Stage-Structured Model with a Birth Pulse. Mathematics 2023, 11, 3321. https://doi.org/10.3390/math11153321
Liu Y, Guo L, Liu X. Dynamical Behaviors in a Stage-Structured Model with a Birth Pulse. Mathematics. 2023; 11(15):3321. https://doi.org/10.3390/math11153321
Chicago/Turabian StyleLiu, Yun, Lifeng Guo, and Xijuan Liu. 2023. "Dynamical Behaviors in a Stage-Structured Model with a Birth Pulse" Mathematics 11, no. 15: 3321. https://doi.org/10.3390/math11153321



