Lithium-Ion Battery Modeling and State of Charge Prediction Based on Fractional-Order Calculus
Abstract
:1. Introduction
2. Fractional-Order Modeling of Lithium-Ion Batteries
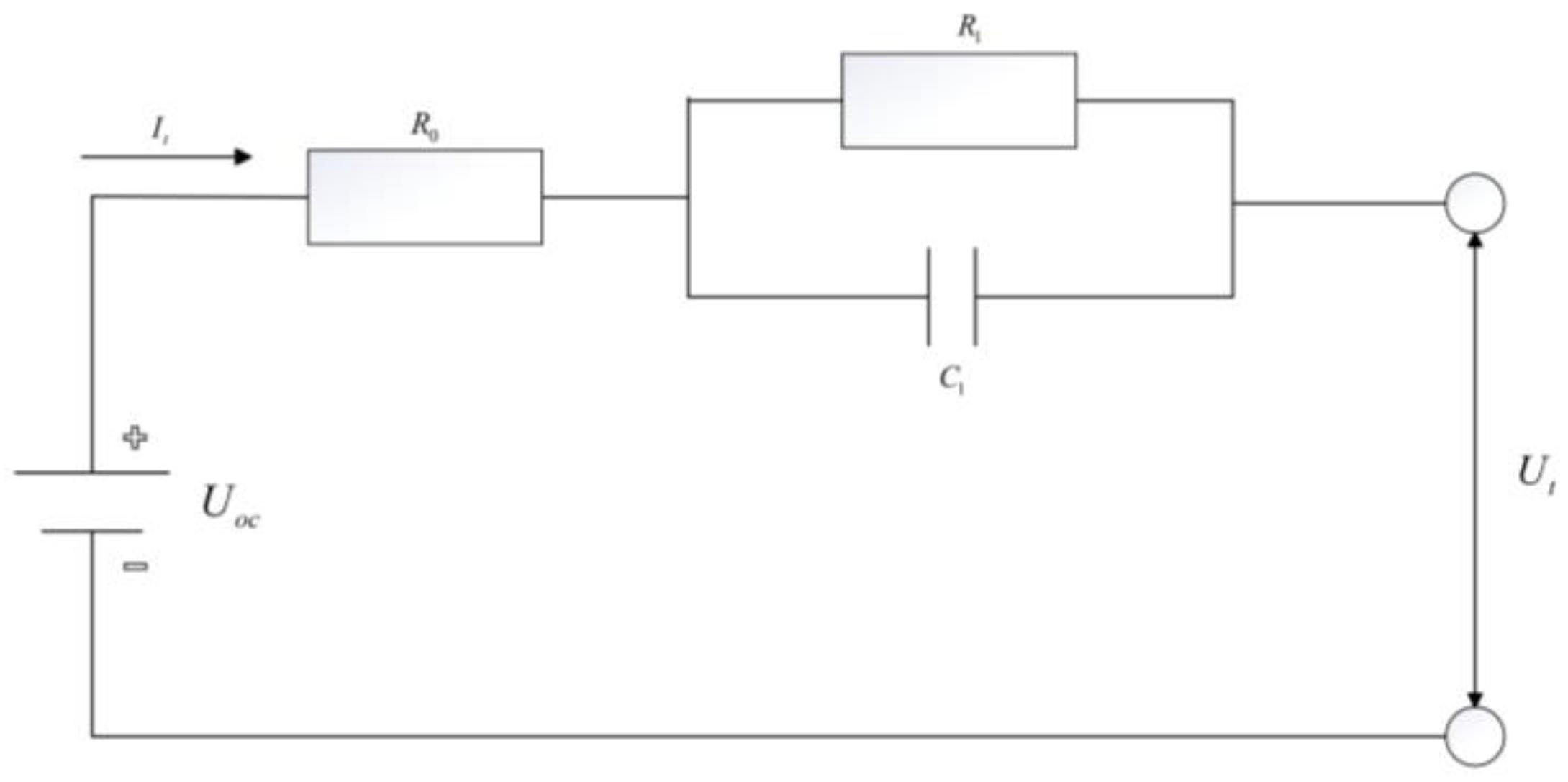
2.1. Thevenin Equivalent Circuit Model
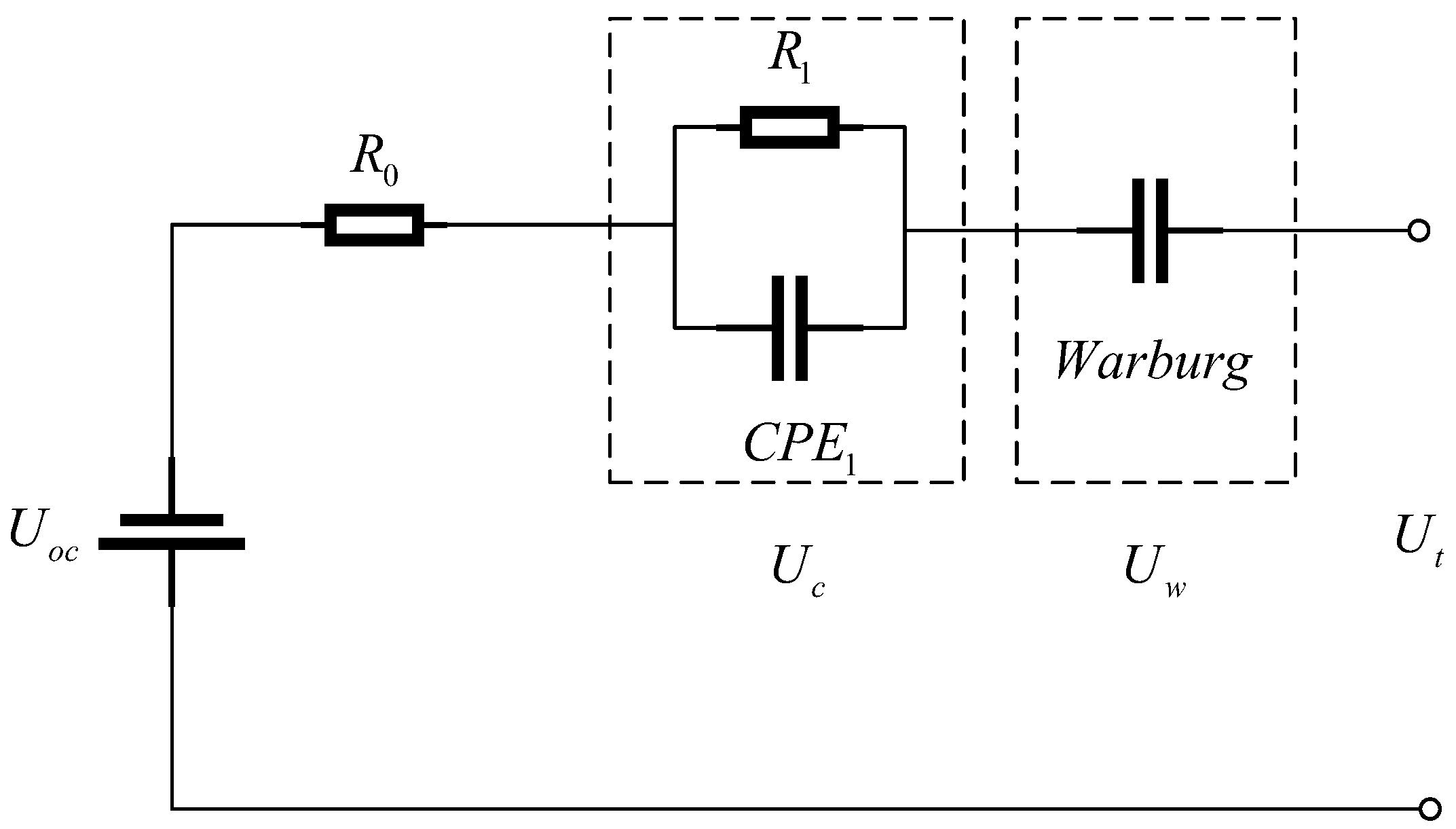
2.2. Fractional Calculus Modeling
2.2.1. Fractional-Order Calculus Definition
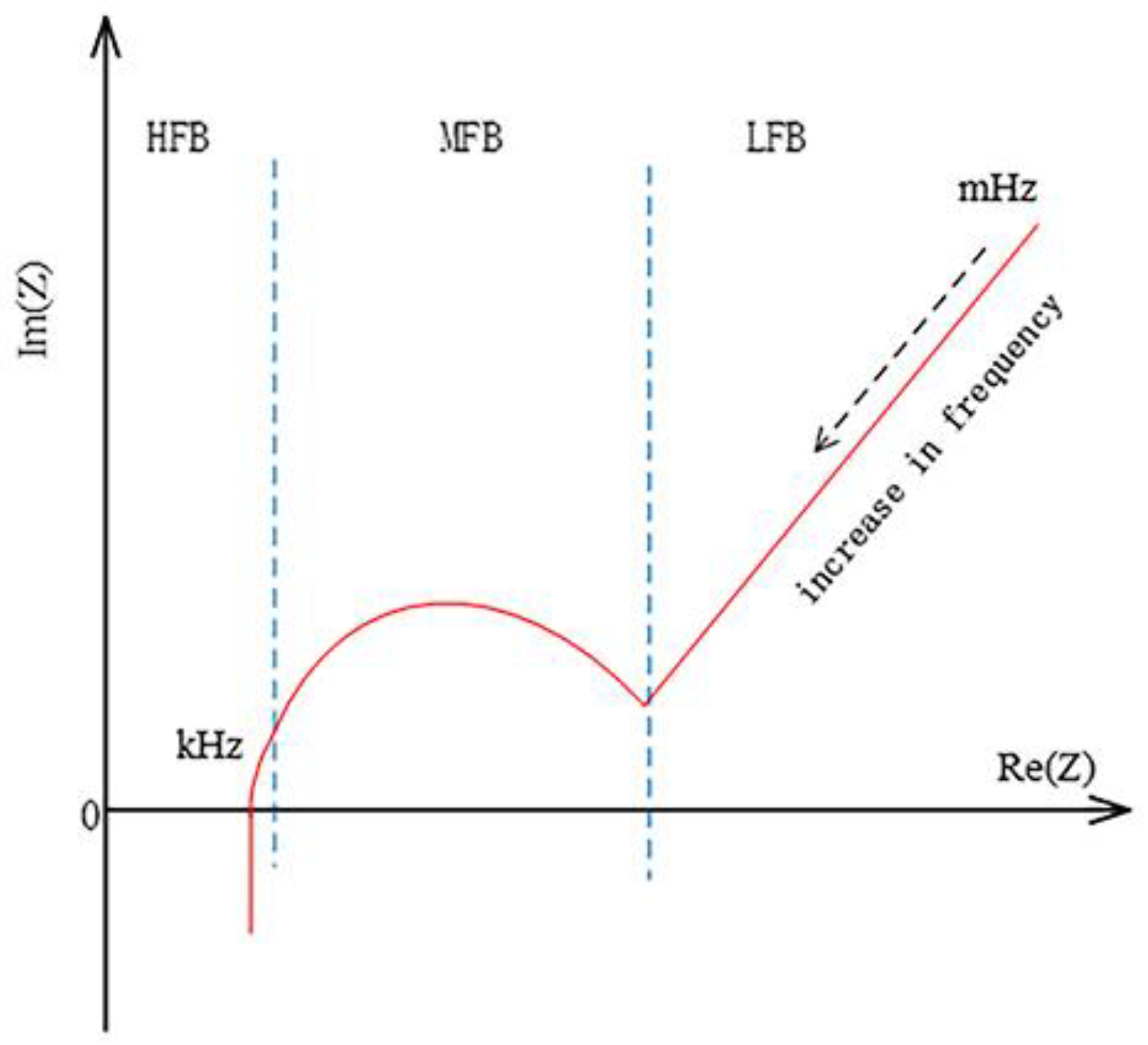
2.2.2. Fractional-Order Impedance Model
2.3. Parameter Identification
- (1)
- Identification of parameters , , , ,
- (2)
- Identification of parameter
3. SOC Prediction Based on the Fractional-Order Extended Kalman Filter
- (1)
- Initialization
- (2)
- Time update
- (3)
- Measurement update
4. Experiment Results
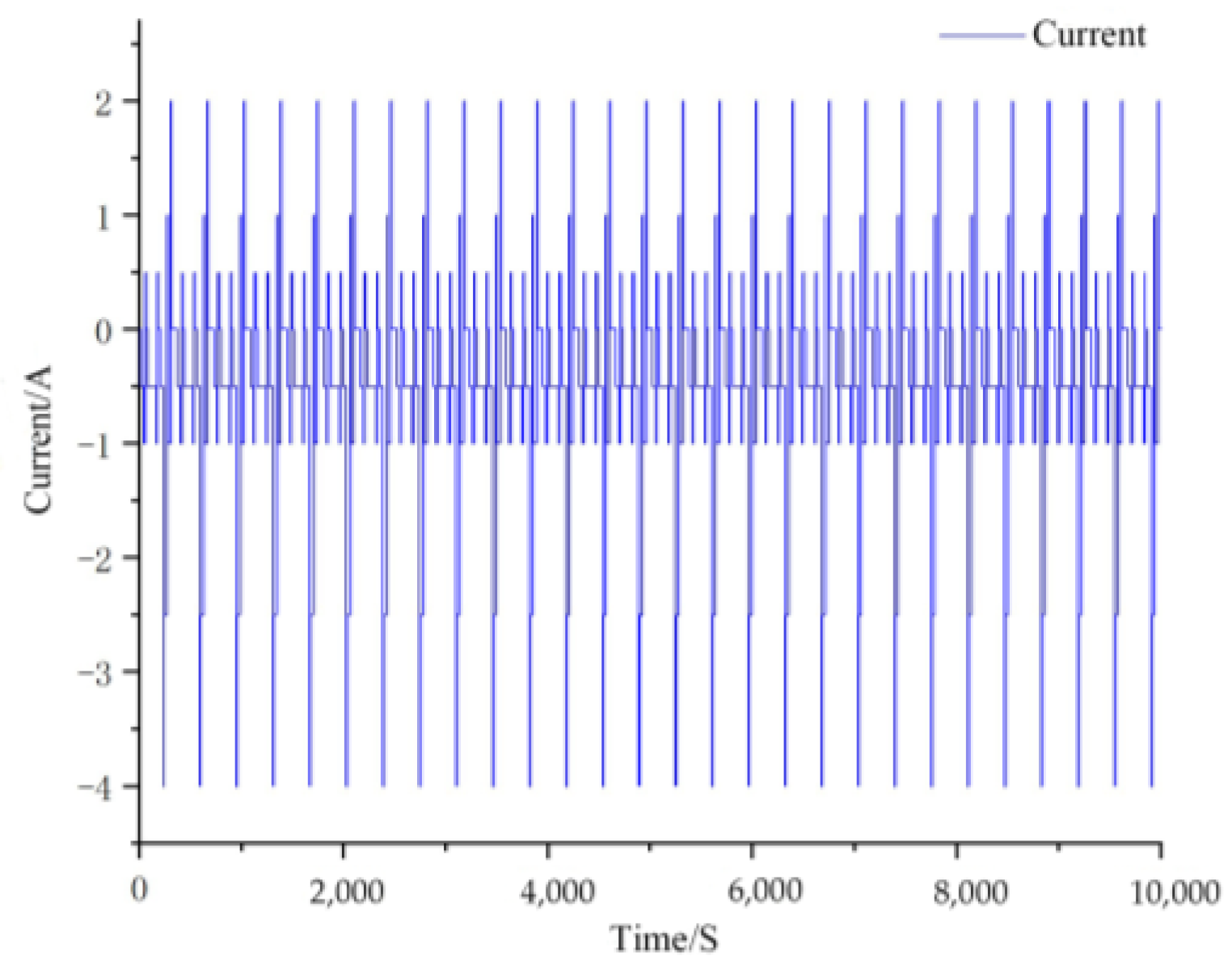
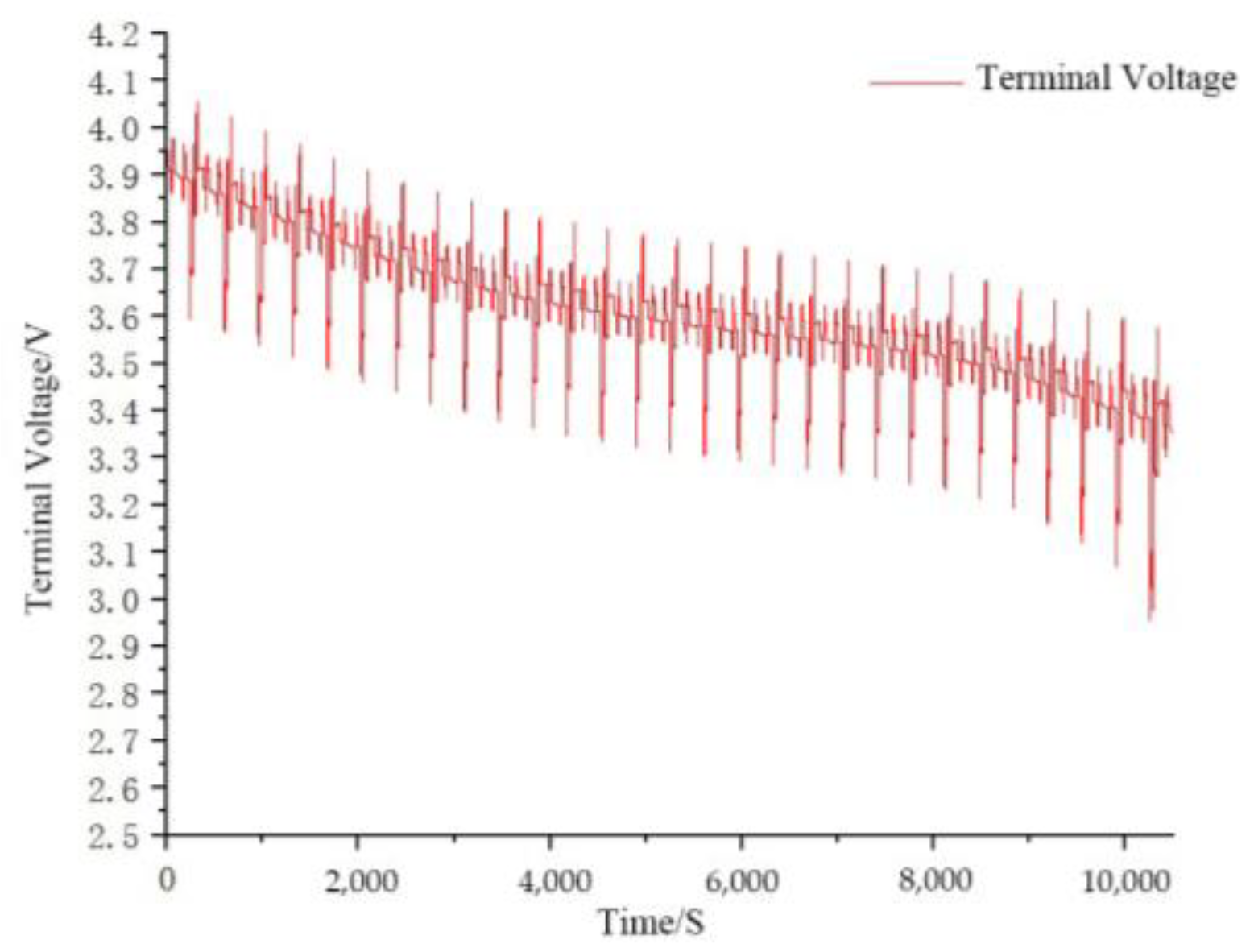
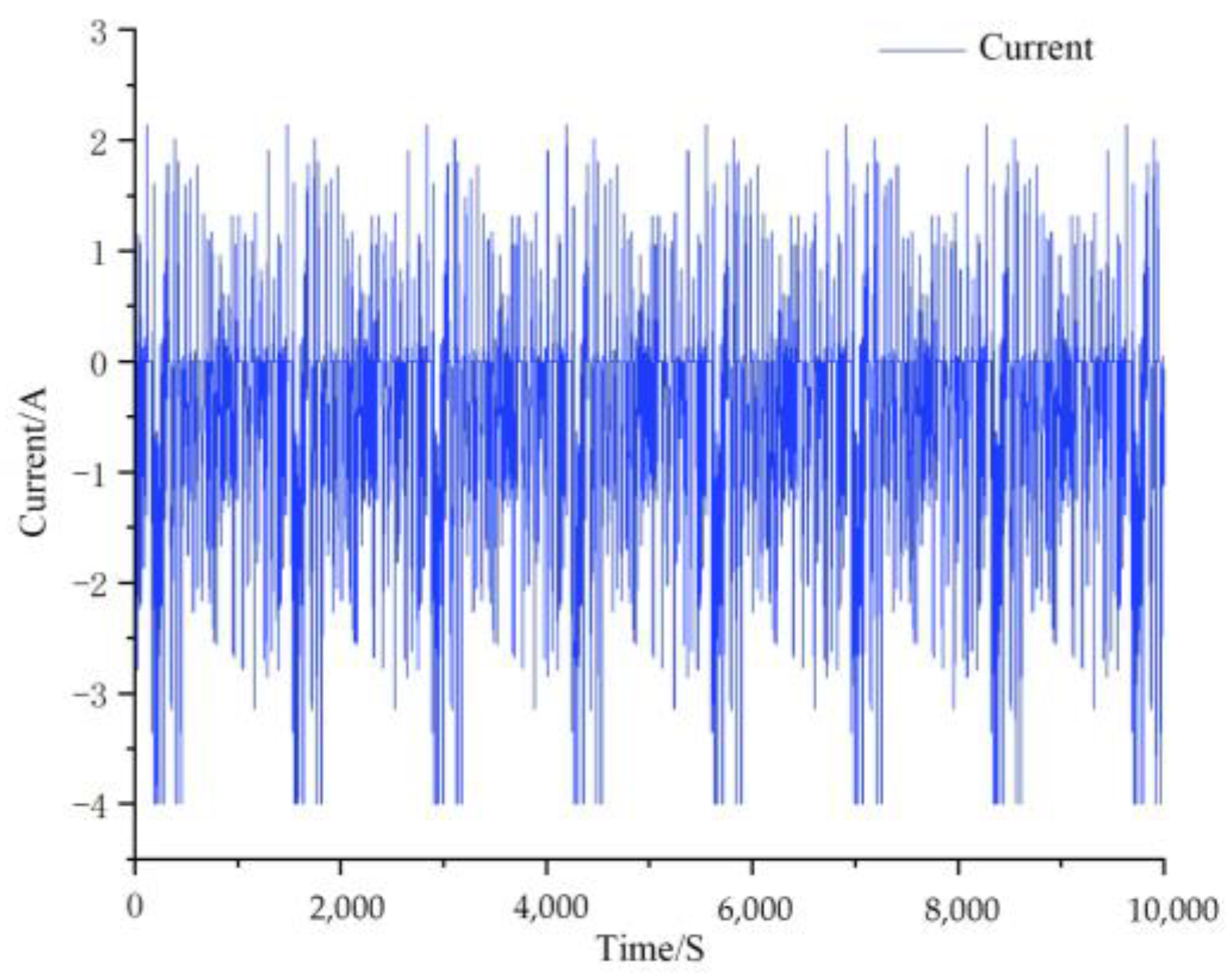
4.1. Data Acquisition
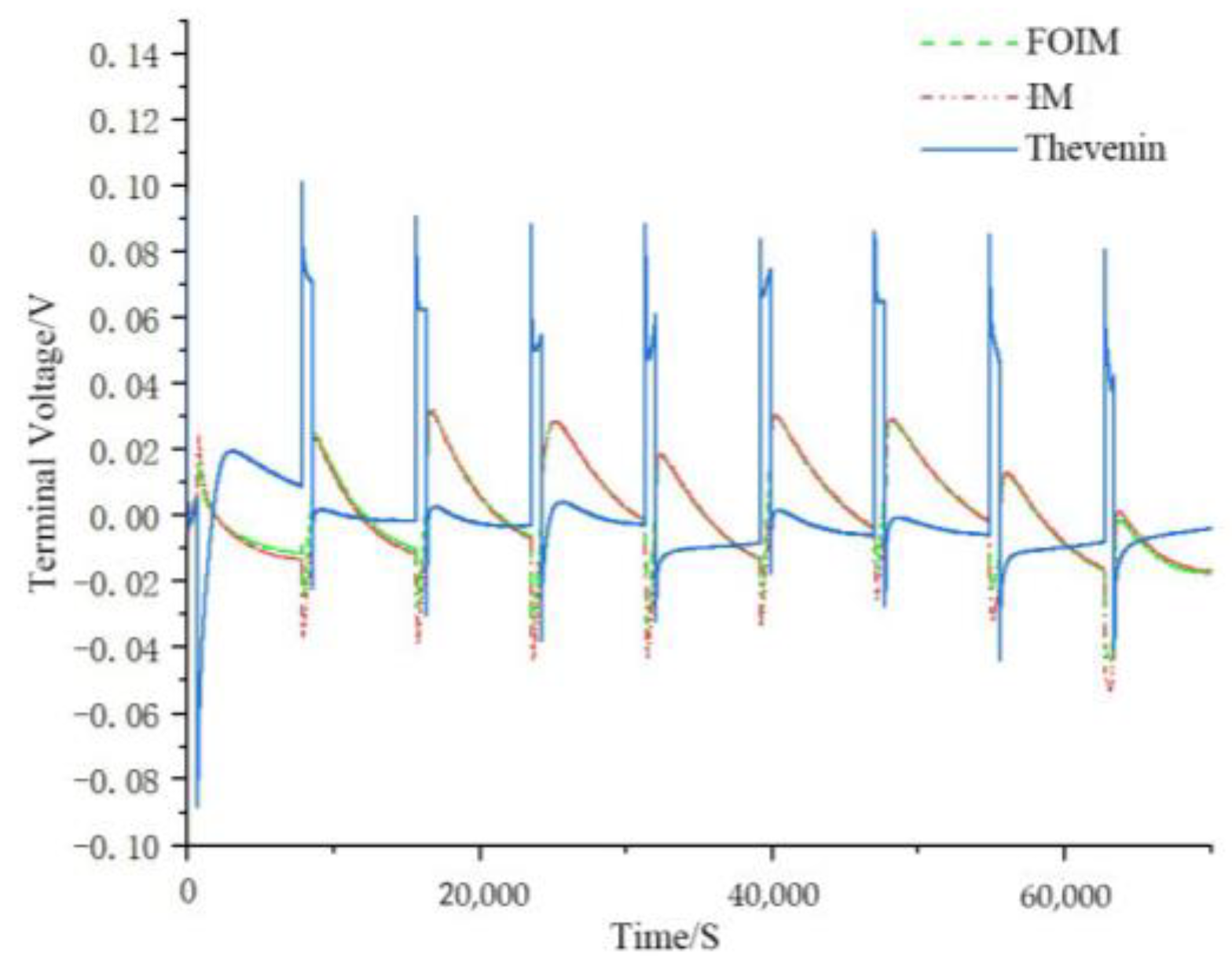
4.2. Battery Model Verification
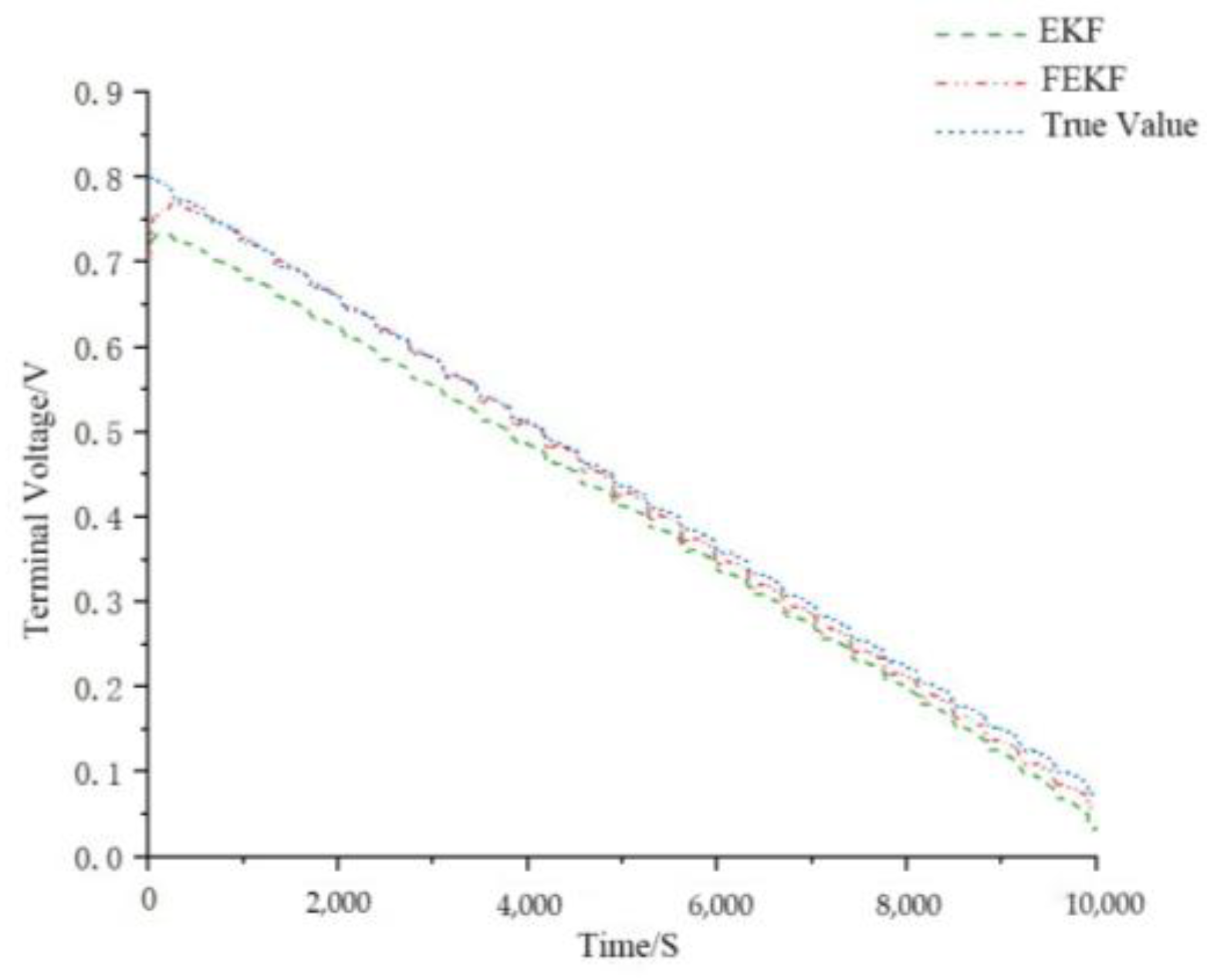
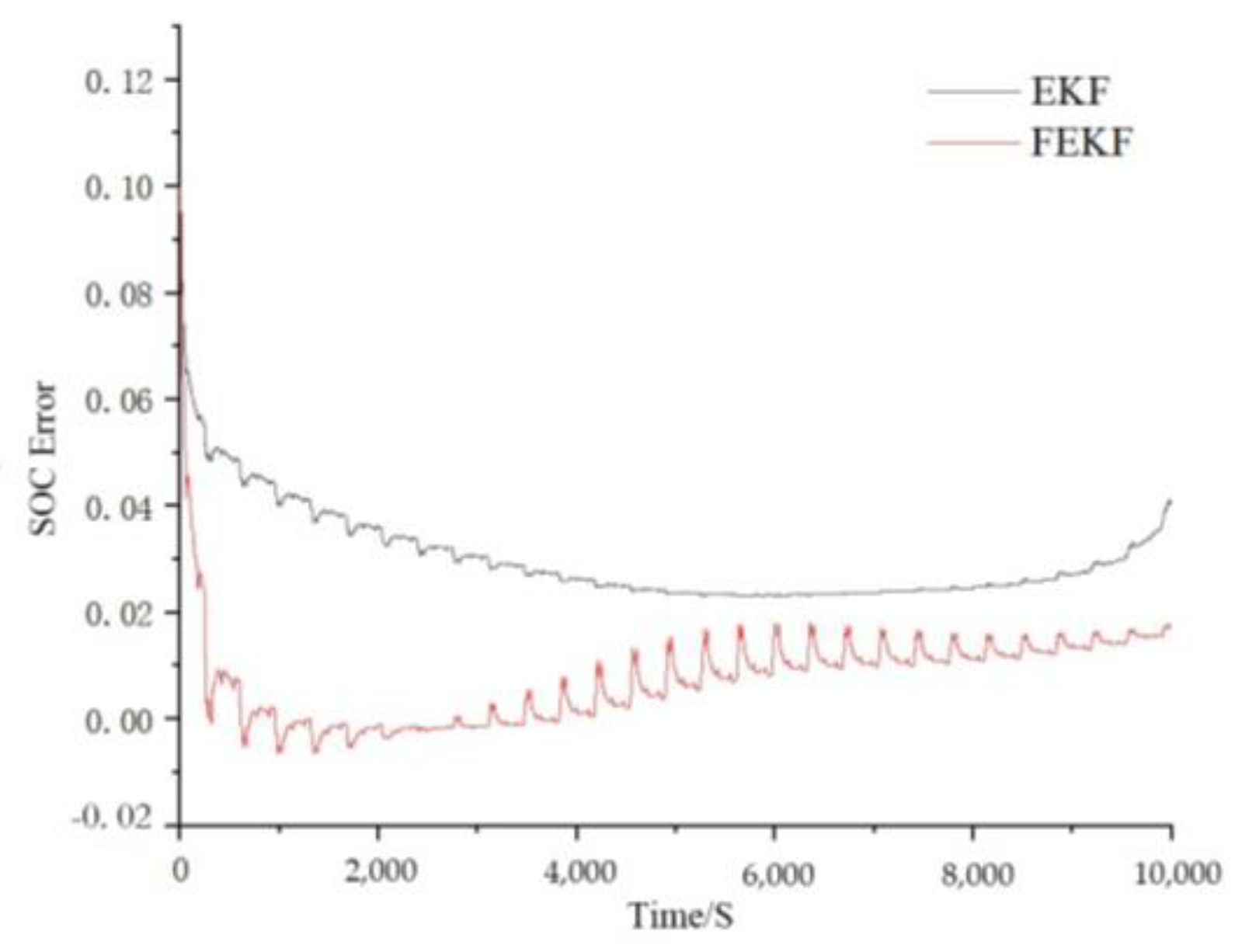
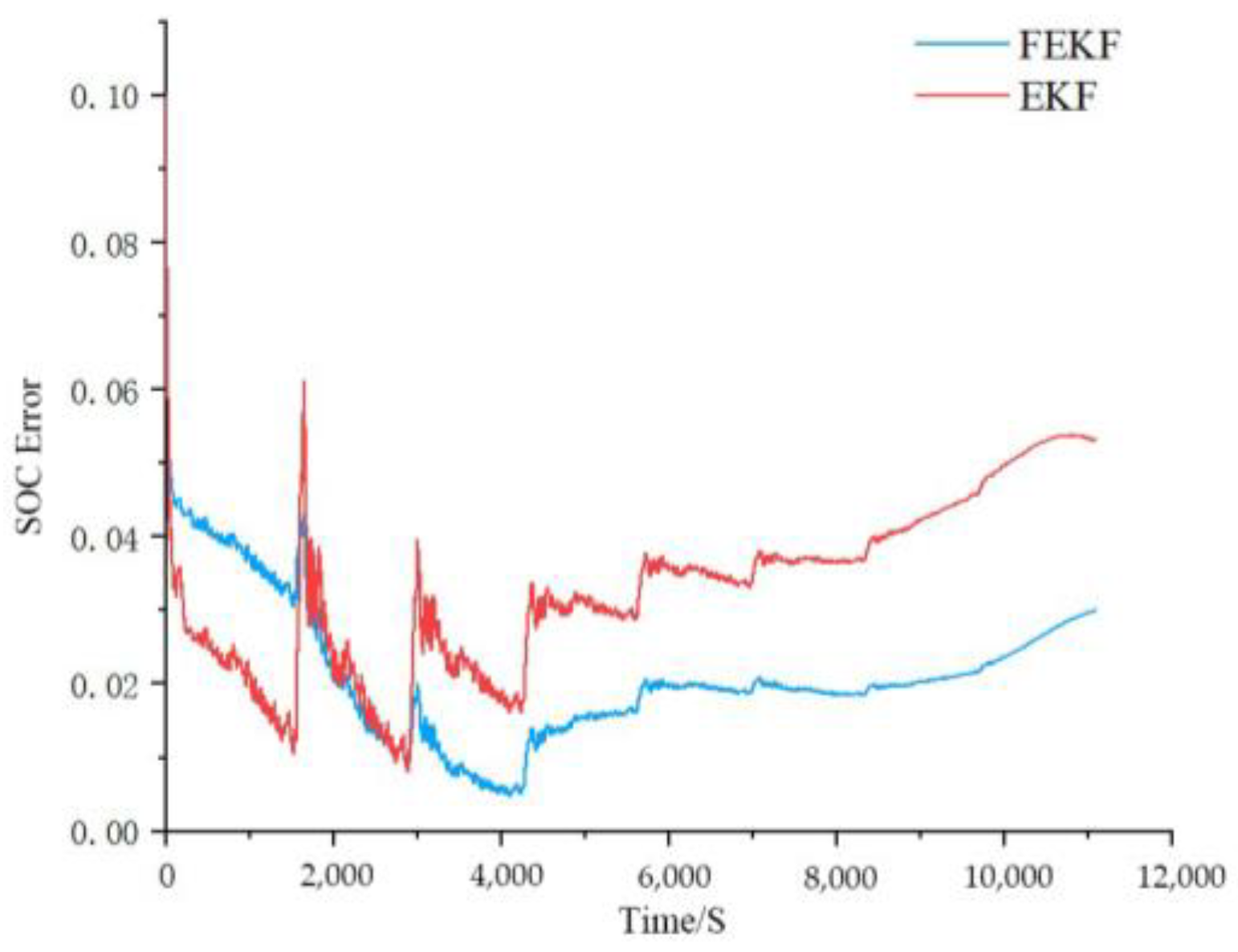
4.3. SOC Prediction and Analysis of Lithium-Ion Batteries
4.3.1. DST Working Condition Simulation Verification
4.3.2. FUDS Working Condition Simulation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martinez, C.M.; Hu, X.S.; Cao, D.P.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Ma, J.; Su, W.; Dou, R.; Lin, H. Estimation method of charging state of electric vehicle power battery in full life cycle based on adaptive regression Extended Kalman filter. Trans. China Electrotech. Soc. 2020, 35, 698–707. [Google Scholar]
- Lv, J.; Song, W.; Feng, Z. Design and implementation of battery management system. Batteries 2019, 49, 499–501. [Google Scholar]
- Wang, Z.; Wang, Q.; Liu, P.; Zhang, Z. A review of power battery health state estimation methods driven by Big data. J. Mech. Eng. 2023, 59, 151–168. [Google Scholar]
- Wang, Y.; Zuo, X. Estimation methods of state of charge of lithium-ion batteries and their application scenarios. Autom. Electr. Power Syst. 2022, 46, 193–207. [Google Scholar]
- Tian, Y.; Li, D.; Tian, J.D.; Xia, B.Z. State of charge estimation of lithium-ion batteries using an optimal adaptive gain nonlinear observer. Electrochim. Acta 2017, 225, 225–234. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium-Sulphur. Renew. Sust. Energy. Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wang, T.; Du, C.; Min, F.; Lu, T.; Zhang, Y.; Yan, L.; Xie, J.; Yin, G. A review of lithium-ion battery models. Energy Storage Sci. Technol. 2019, 8, 58–64. [Google Scholar]
- Gopaluni, R.B.; Braatz, R.D. State of Charge Estimation in Li-ion Batteries Using an Isothermal Pseudo Two-Dimensional Model. IFAC Proc. Vol. 2013, 46, 135–140. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef] [Green Version]
- Di Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-Ion Battery State of Charge and Critical Surface Charge Estimation Using an Electrochemical Model-Based Extended Kalman Filter. J. Dyn. Syst. Meas. Control 2010, 132, 061302. [Google Scholar] [CrossRef]
- Gao, R.; Lv, Z.; Zhao, S.; Huang, X. Estimation of lithium-ion battery health status based on electrochemical model. J. Beijing Univ. Technol. 2022, 42, 791–797. [Google Scholar]
- Xie, C.; Fei, Y.; Zeng, C.; Fang, W. State estimation of vehicle-mounted lithium ion batteries based on untracked particle filter. Trans. China Electrotech. Soc. 2018, 33, 3958–3964. [Google Scholar]
- Li, W.; Liu, W.; Deng, Y. Estimation of charged state of lithium-ion batteries based on Extended Kalman filter. China Mech. Eng. 2020, 31, 321–327+343. [Google Scholar]
- Wang, P.; Gong, Q.; Cheng, Z.; Zhang, J. SOC Estimation method for lithium-ion batteries based on AUKF. Automot. Eng. 2022, 44, 1080–1087. [Google Scholar]
- Zhang, X.; Yao, M.; Song, R.; Cui, J. Joint estimation of SOC and SOH for lithium-ion batteries based on AEKPF algorithm. J. Jiangsu Univ. (Nat. Sci. Ed.) 2022, 43, 24–31. [Google Scholar]
- Qiao, J.L.; Wang, S.L.; Yu, C.M.; Yang, X.; Fernandez, C. A chaotic firefly-Particle filtering method of dynamic migration modeling for the state-of-charge and state-of-health co-estimation of a lithium-ion battery performance. Energy 2023, 263, 126164. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Volume I Background and Theory Volume II Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zelenyi, L.M.; Milovanov, A.V. Fractal topology and strange kinetics: From percolation theory to problems in cosmic electrodynamics. Phys. Uspekhi 2004, 47, 749–788. [Google Scholar] [CrossRef]
- Metzler, R.J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A. Math. Gen. 2004, 37, R161. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations [electronic resource]: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng. 2013, 2013, 553–563. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. Higher Education Press: Beijing, China, 2011. [Google Scholar]
- Wang, B. Modeling and State Estimation of Lithium-Ion Batteries Based on Fractional Order Theory. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Sun, G.; Ren, J.; Cheng, L.; Zhu, Y.; Wei, Z.; Zang, H. Estimation of charged state of lithium iron phosphate batteries based on fractional impedance model. Autom. Electr. Power Syst. 2018, 42, 57–63. [Google Scholar]
- Center for Advanced Life Cycle Engineering, University of Maryland. Battery Research Data. Available online: https://calce.umd.edu/data (accessed on 10 March 2021).
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Xu, J.; Pei, L.; Xu, B.; Wu, G.; Zhu, C. Battery equivalent circuit model analysis based on simulation comparison. Electr. Meas. Instrum. 2017, 54, 6. [Google Scholar]
- Wang, Y.; Zhao, Y.; Hua, D.; An, R. State estimation method of lithium battery based on second-order equivalent circuit model. Energy Sav. 2022, 41, 38–42. [Google Scholar]
- Guo, X.; Gao, Y.; Si, Y.; Liu, Z.; Xu, X. Research on equivalent circuit model of power battery. Sens. Microsyst. 2022, 41, 4. [Google Scholar]





| Parameter | ||||||
|---|---|---|---|---|---|---|
| FOIM | 0.998 | 0.982 | 0.2452 Ω | 15,879 F | 526,190 Ω | 0.2129 Ω |
| IM | 0.995 | - | 0.2834 Ω | 18,527 F | - | 0.2129 Ω |
| Thevenin model | - | - | 0.3521 Ω | 25,413 F | - | 0.2129 Ω |
| Model | FOIM | IM | Thevenin |
|---|---|---|---|
| Root mean square error | 0.0139 V | 0.0152 V | 0.0195 V |
| Conditions | EKF | FEKF |
|---|---|---|
| DST | 0.0352 | 0.0121 |
| FUDS | 0.0348 | 0.0233 |
| Conditions | EKF | FEKF |
|---|---|---|
| DST | 0.042 | 0.020 |
| FUDS | 0.060 | 0.045 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, X.; Yang, K.; Wang, Z. Lithium-Ion Battery Modeling and State of Charge Prediction Based on Fractional-Order Calculus. Mathematics 2023, 11, 3401. https://doi.org/10.3390/math11153401
Zhang X, Li X, Yang K, Wang Z. Lithium-Ion Battery Modeling and State of Charge Prediction Based on Fractional-Order Calculus. Mathematics. 2023; 11(15):3401. https://doi.org/10.3390/math11153401
Chicago/Turabian StyleZhang, Xinfeng, Xiangjun Li, Kaikai Yang, and Zhongyi Wang. 2023. "Lithium-Ion Battery Modeling and State of Charge Prediction Based on Fractional-Order Calculus" Mathematics 11, no. 15: 3401. https://doi.org/10.3390/math11153401
APA StyleZhang, X., Li, X., Yang, K., & Wang, Z. (2023). Lithium-Ion Battery Modeling and State of Charge Prediction Based on Fractional-Order Calculus. Mathematics, 11(15), 3401. https://doi.org/10.3390/math11153401








