A Symbolic Approach to Discrete Structural Optimization Using Quantum Annealing
Abstract
:1. Introduction
2. Background on QUBO and Ising Formulations
3. Problem Description
4. Method
4.1. General Concept
- Using the expression for the truss cross-sectional area, the element stiffness matrices of the truss members can also be written in terms of the qubit variables.
- Using the FEM assembly procedure, the symbolic global stiffness matrix of the entire truss structure can be assembled from each of the element stiffness matrices.
- Proceed as normal with the FEM analysis, taking into account of the boundary conditions and applied loads. By inverting the symbolic global stiffness matrix, and multiplying this inverse matrix with the load vector, a symbolic vector of nodal displacements can be obtained.
- Using the symbolic vector of nodal displacements and the known initial length of every truss element, symbolic expressions for the strains of the truss elements can be set up.
- By multiplying the symbolic expressions of the truss strains with the Young’s modulus, symbolic expressions for the truss stresses are obtained.
- The symbolic expressions for the truss stresses will be used to construct an objective function for which the minimum solution encodes the optimal choice of cross-sectional area for every truss element in the structure.
- The symbolic objective function will be transformed into a QUBO format, then sent to D-Wave to find the minimum solution.
4.2. Symbolic Finite Element Method
4.2.1. Finding Expressions for Nodal Displacement
4.2.2. Finding Expressions for Strain
4.2.3. Expressions for Stress
4.3. Development of an Objective Function
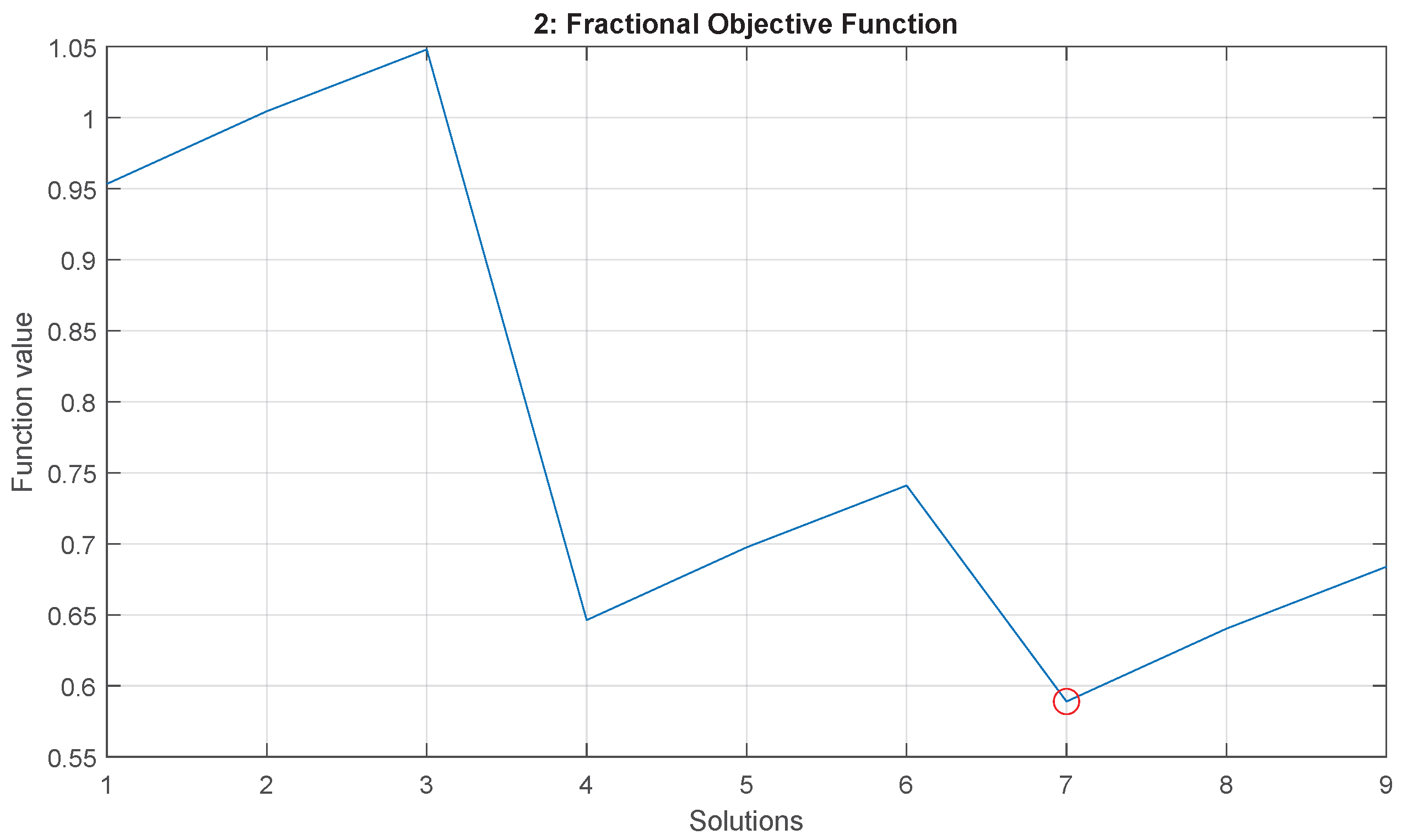
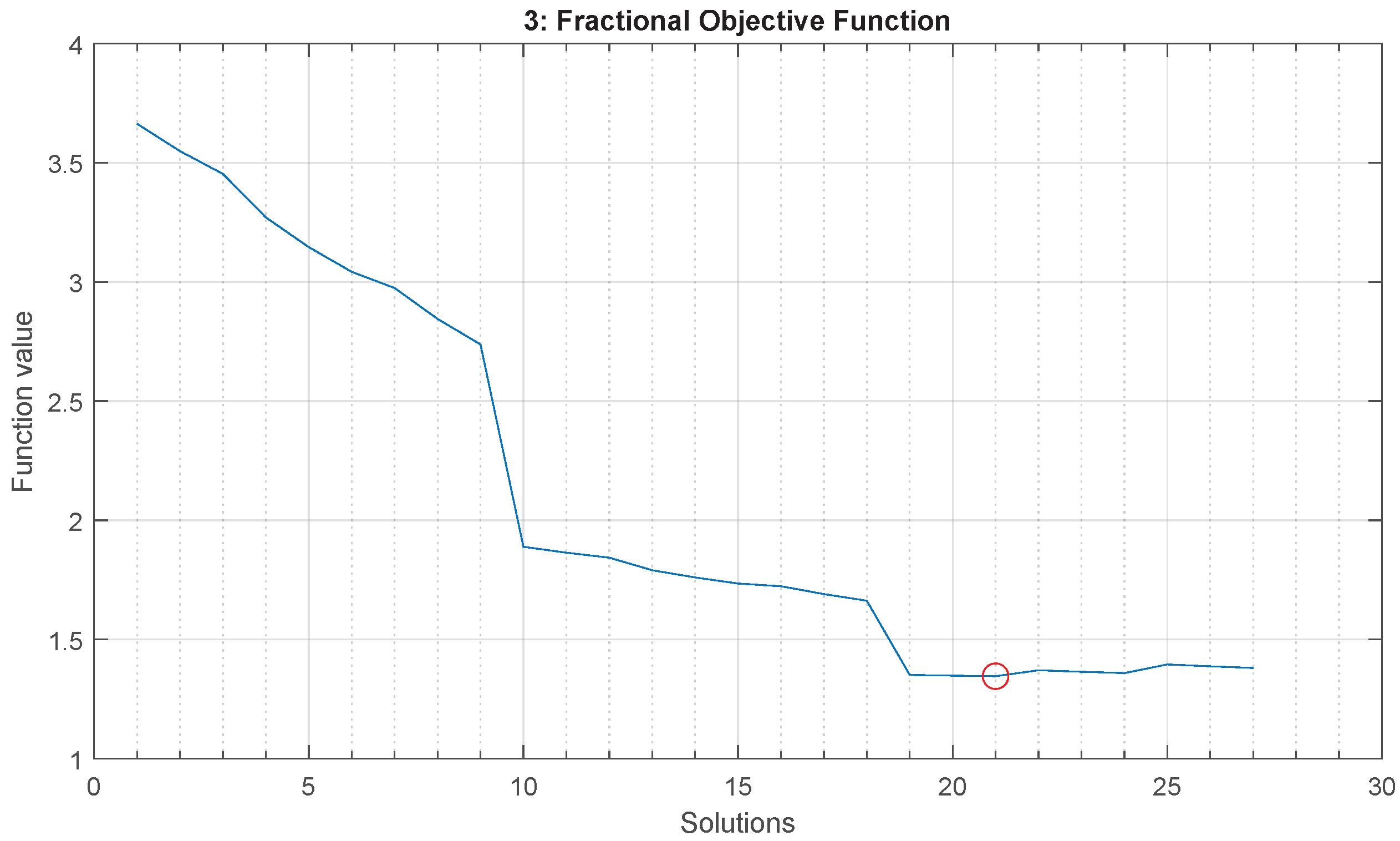
4.3.1. Fractional Objective Function
- Two-truss problem: minimum at solution number 7,
- Three-truss problem: minimum at solution number 21,
- Four-truss problem: minimum at solution number 7,
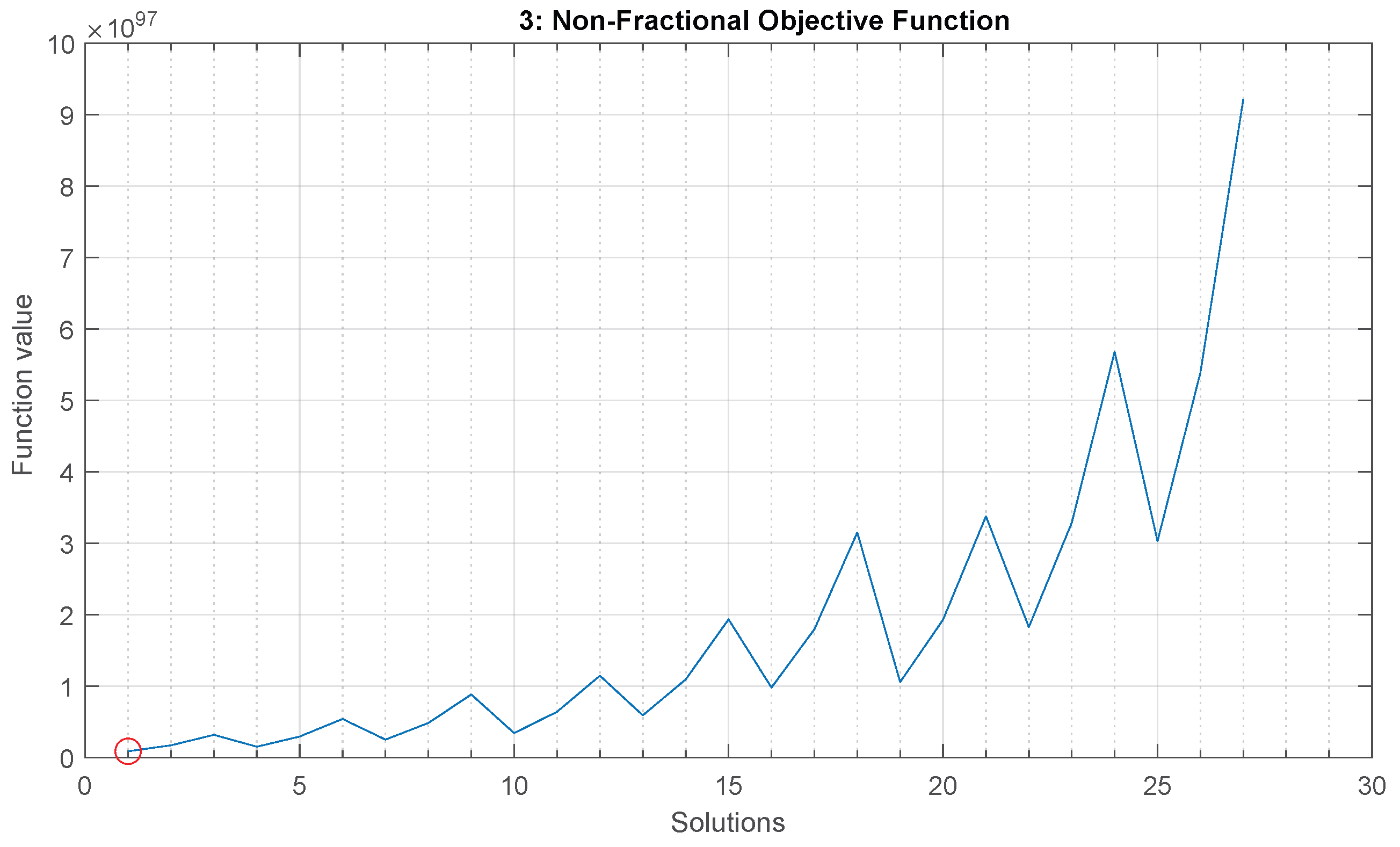
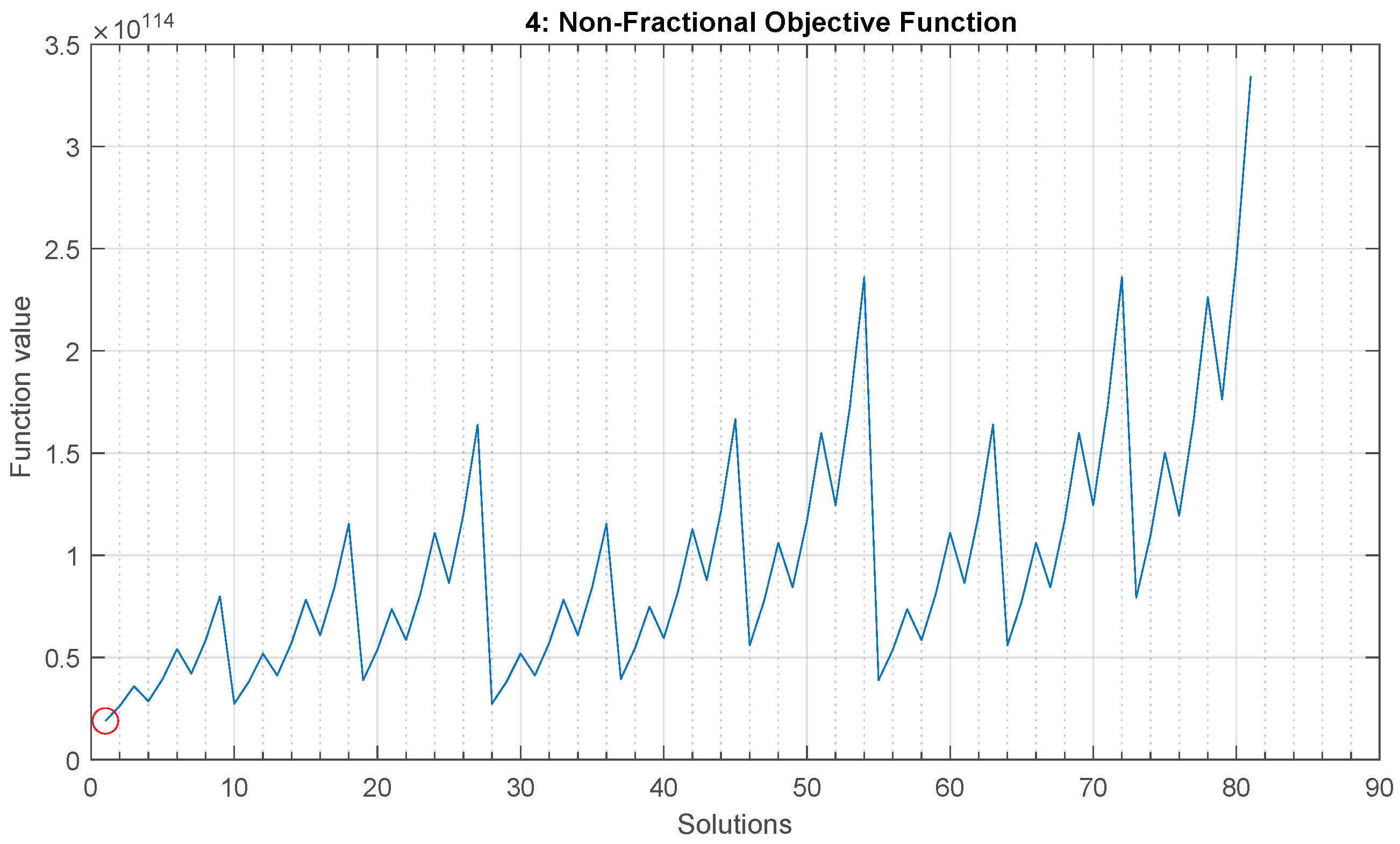
4.3.2. Non-Fractional Objective Function
- Two-truss problem: minimum at solution number 7,
- Three-truss problem: minimum at solution number 1,
- Four-truss problem: minimum at solution number 1,
4.4. Iterative Non-Fractional Approximations to the Fractional Objective Function
4.5. Objective Function Processing to Yield a QUBO Problem
4.5.1. High-Order Truncation
4.5.2. Linear Scaling
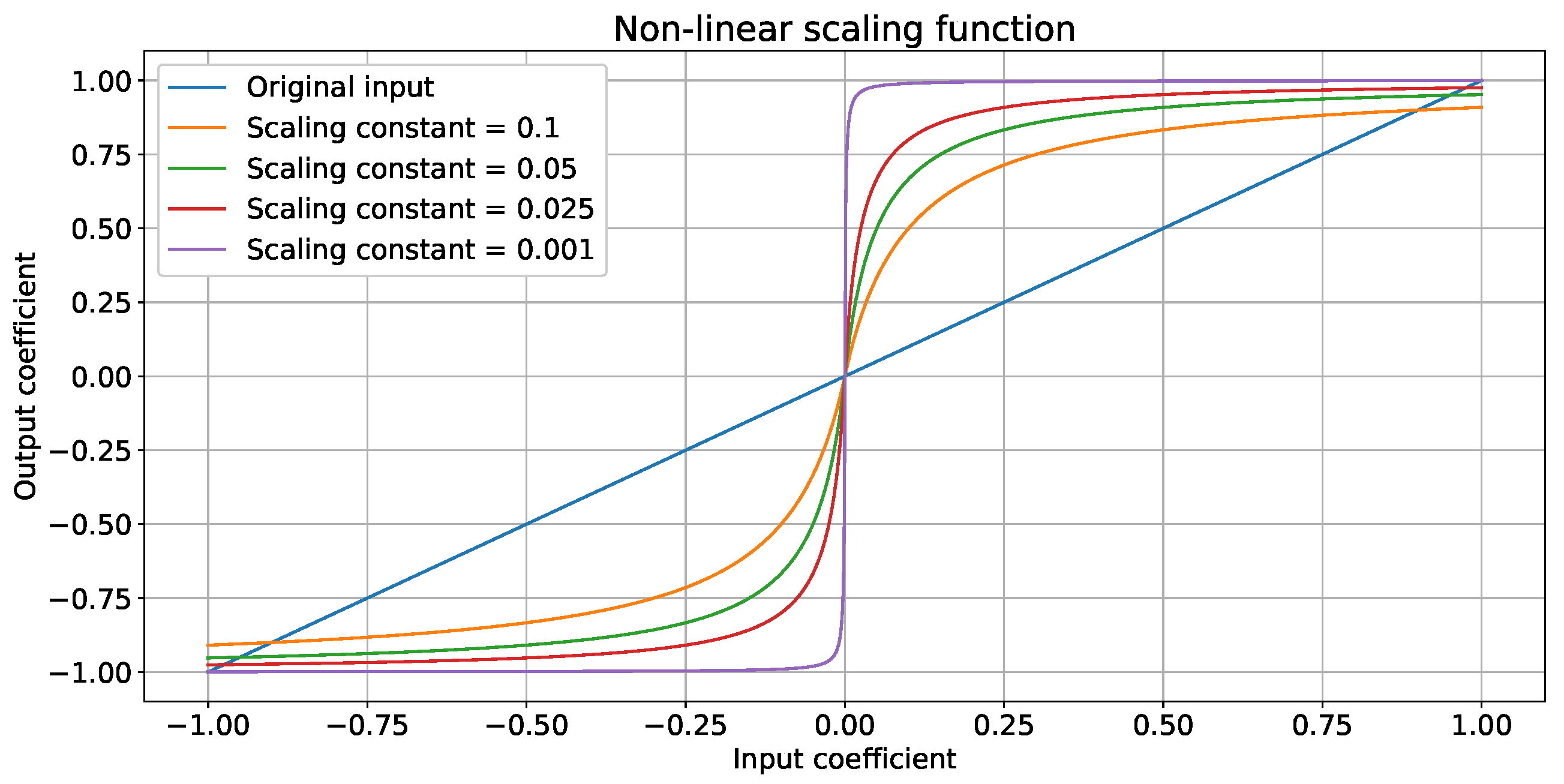
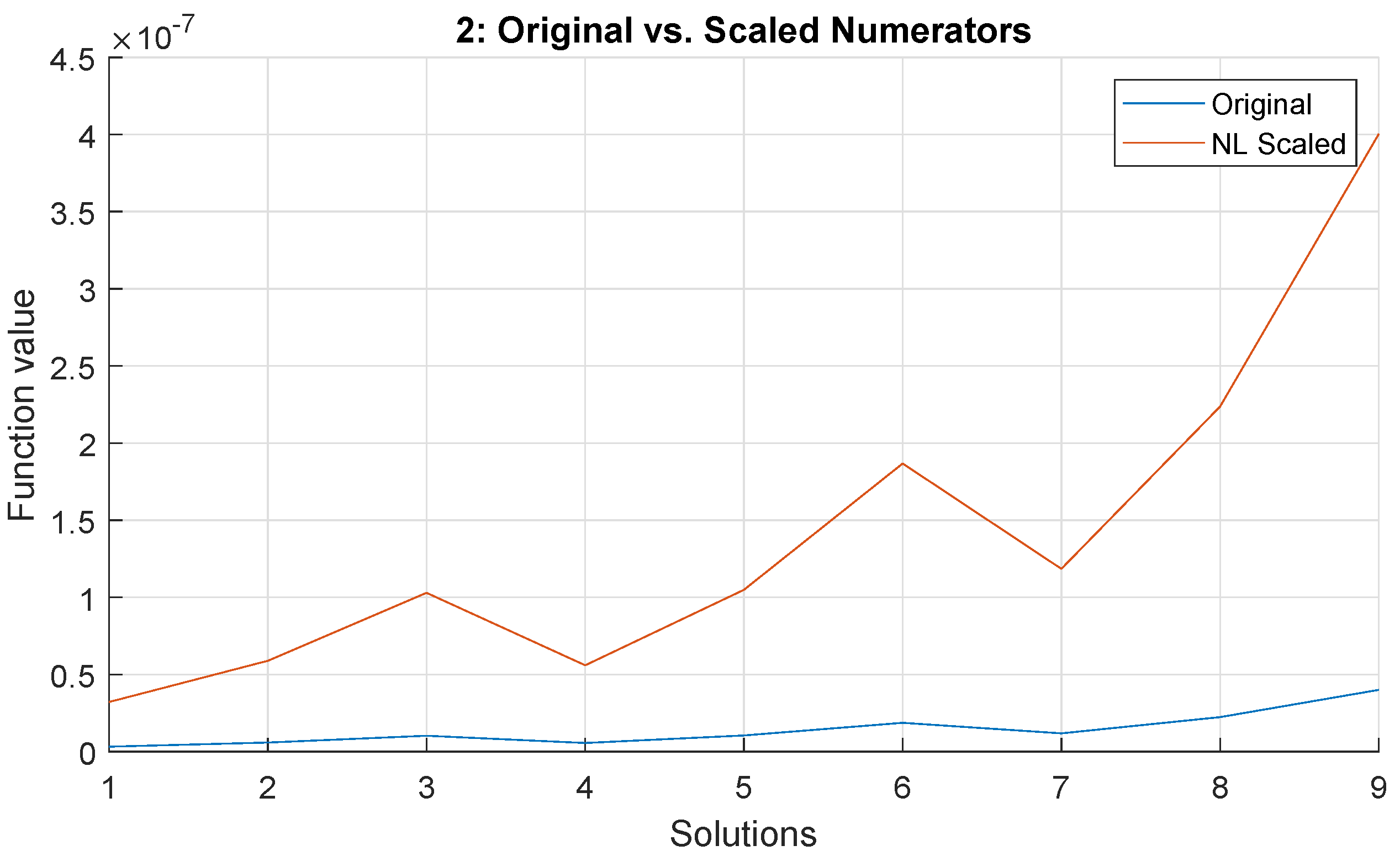
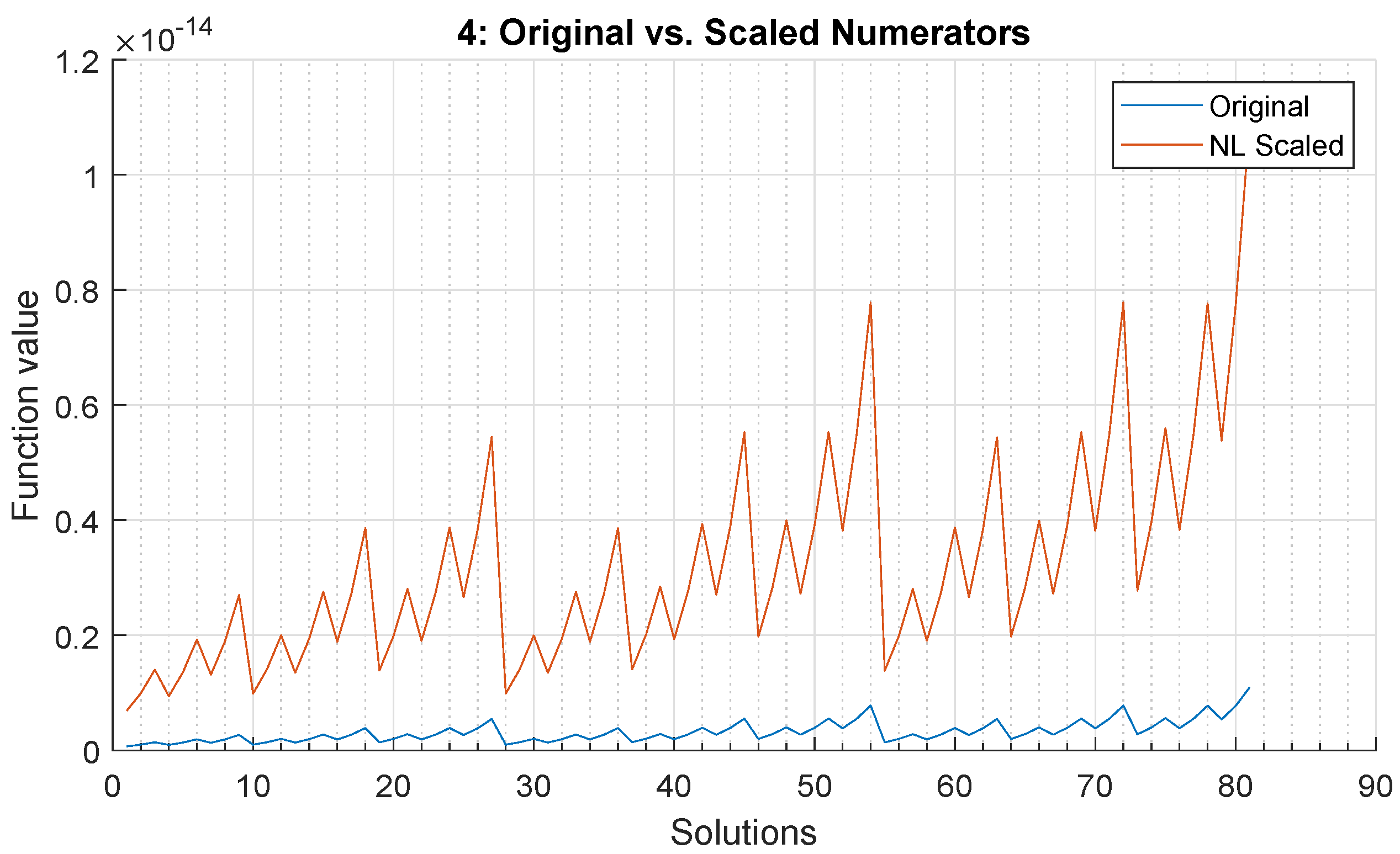
4.5.3. Non-Linear Scaling
4.5.4. Truncation of Insignificant Terms
4.5.5. Unary Constraint
4.5.6. Quadratization
4.6. Parameter Tuning
- Iterative solving procedure
- -
- Maximum number of iterations allowed
- -
- Iteration convergence threshold
- Objective function processing
- -
- Highest order terms allowed
- -
- Linear scaling magnitude
- -
- Non-linear scaling strength
- -
- Precision truncation magnitude
- -
- Unary constraint strength
- -
- Quadratization strength
- Quantum annealing
- -
- Number of reads
- -
- Chain strength
5. Results
5.1. Overview of Analyses Performed
5.2. Results: Two-Truss Problem
- With number of reads = 16
- -
- Average total time = 19.52 s. Standard deviation = 5.10 s.
- -
- Average QPU time = 59,176 μs. Standard deviation = 15,061 μs.
- With number of reads = 64
- -
- Average total time = 19.06 s. Standard deviation = 0.21 s.
- -
- Average QPU time = 118,207 μs. Standard deviation = 10.7 μs.
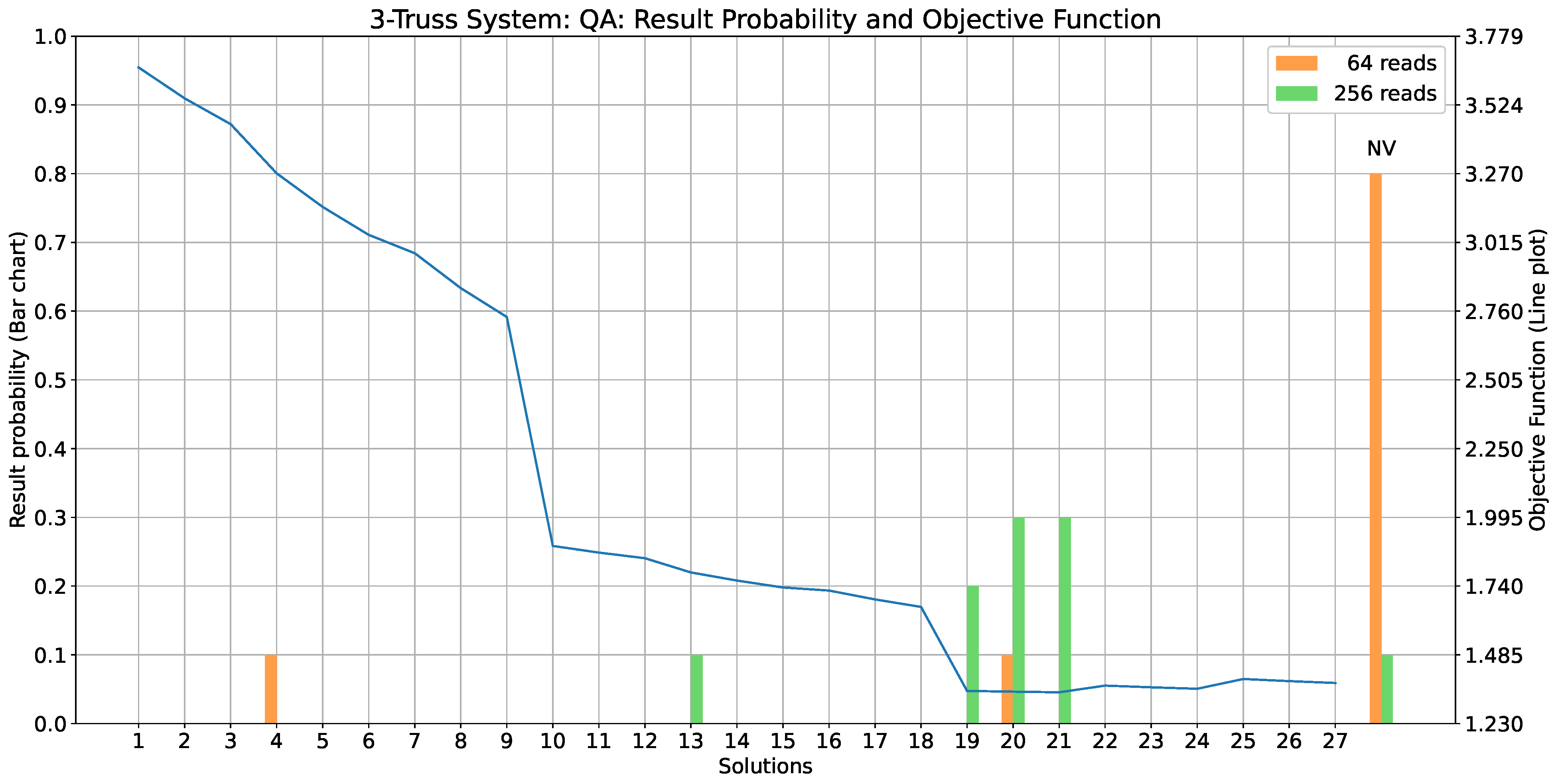
5.3. Results: Three-Truss Problem
- With number of reads = 64
- -
- Average total time = 98.7 s. Standard deviation = 37.5 s.
- -
- Average QPU time = 337,477 μs. Standard deviation = 117,808 μs.
- With number of reads = 256
- -
- Average total time = 48.8 s. Standard deviation = 20.6 s.
- -
- Average QPU time = 558,414 μs. Standard deviation = 244,331 μs.
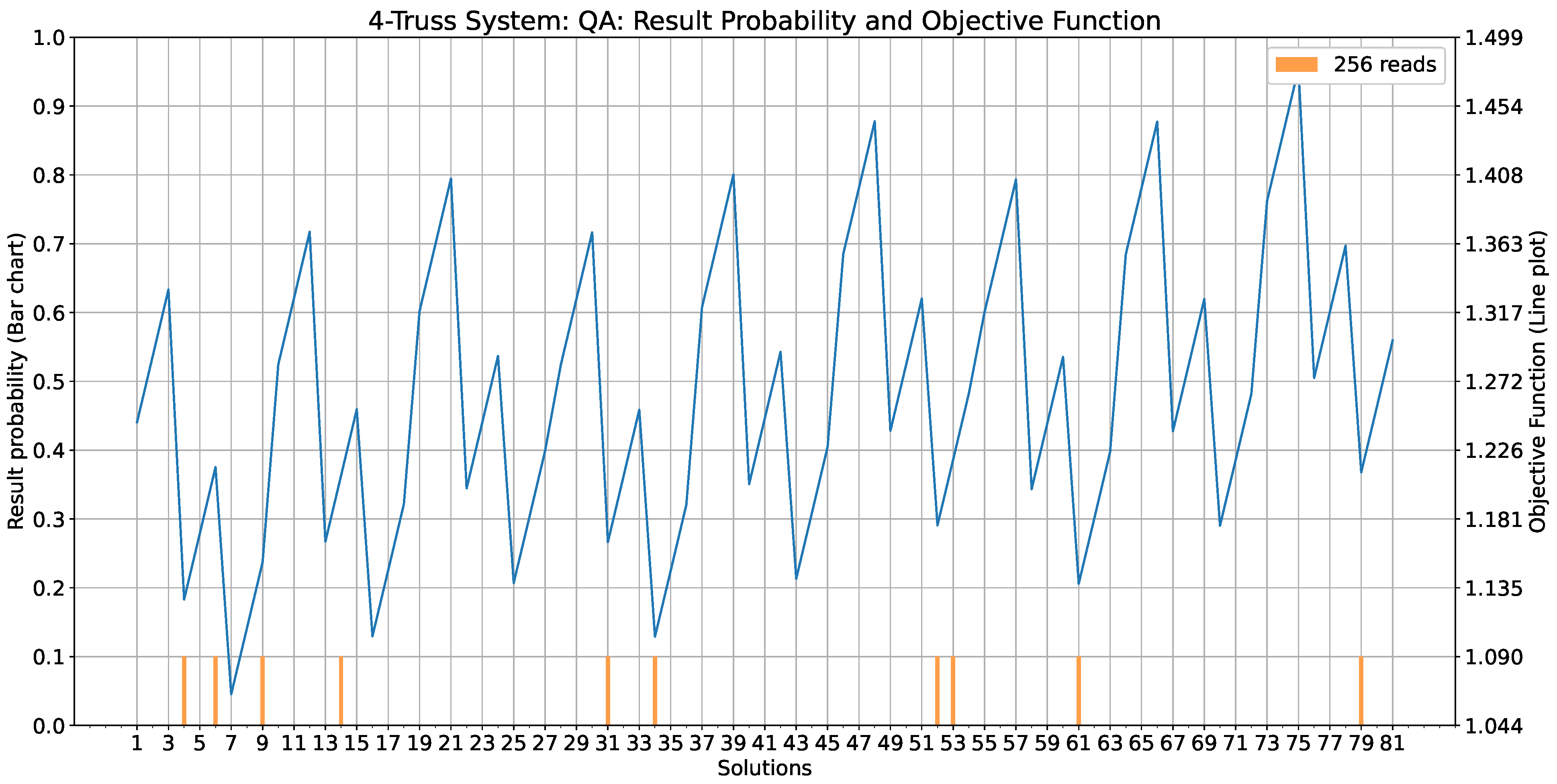
5.4. Results: Four-Truss Problem
- With number of reads = 256
- -
- Average total time = 437 s. Standard deviation = 39.0 s.
- -
- Average QPU time = 1,280,156 μs. Standard deviation = 251,109 μs.
6. Conclusions
6.1. Symbolic Finite Element Method
6.2. Fractional Objective Function
6.3. Quantum Annealing
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOAJ | Directory of open access journals |
| FEM | Finite element method |
| GPQC | General-purpose quantum computer |
| MDPI | Multidisciplinary Digital Publishing Institute |
| QA | Quantum annealer |
| QPU | Quantum processing unit |
| QUBO | Quadratic unconstrained binary optimization |
| SA | Simulated annealing |
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef] [Green Version]
- Montanaro, A. Quantum algorithms: An overview. npj Quantum Inf. 2016, 2, 15023. [Google Scholar] [CrossRef]
- Kadowaki, T.; Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 1998, 58, 5355–5363. [Google Scholar] [CrossRef] [Green Version]
- Morita, S.; Nishimori, H. Mathematical foundation of quantum annealing. J. Math. Phys. 2008, 49, 125210. [Google Scholar] [CrossRef] [Green Version]
- Santoro, G.E.; Martoňák, R.; Tosatti, E.; Car, R. Theory of Quantum Annealing of an Ising Spin Glass. Science 2002, 295, 2427–2430. [Google Scholar] [CrossRef] [Green Version]
- Denchev, V.S.; Boixo, S.; Isakov, S.V.; Ding, N.; Babbush, R.; Smelyanskiy, V.; Martinis, J.; Neven, H. What is the Computational Value of Finite-Range Tunneling? Phys. Rev. X 2016, 6, 031015. [Google Scholar] [CrossRef] [Green Version]
- Rajak, A.; Suzuki, S.; Dutta, A.; Chakrabarti, B.K. Quantum annealing: An overview. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2023, 381, 20210417. [Google Scholar] [CrossRef]
- D-Wave Systems Inc. Getting Started with the D-Wave System: User Manual; D-Wave Systems Inc.: Burnaby, BC, Canada, 2020. [Google Scholar]
- Zheng, Y.; Song, C.; Chen, M.C.; Xia, B.; Liu, W.; Guo, Q.; Zhang, L.; Xu, D.; Deng, H.; Huang, K.; et al. Solving Systems of Linear Equations with a Superconducting Quantum Processor. Phys. Rev. Lett. 2017, 118, 210504. [Google Scholar] [CrossRef] [Green Version]
- Neukart, F.; Compostella, G.; Seidel, C.; von Dollen, D.; Yarkoni, S.; Parney, B. Traffic flow optimization using a quantum annealer. arXiv 2017, arXiv:1708.01625. [Google Scholar] [CrossRef] [Green Version]
- Van Vreumingen, D.; Neukart, F.; Von Dollen, D.; Othmer, C.; Hartmann, M.; Voigt, A.C.; Bäck, T. Quantum-assisted finite-element design optimization. arXiv 2019, arXiv:1908.03947. [Google Scholar]
- Stollenwerk, T.; O’Gorman, B.; Venturelli, D.; Mandrà, S.; Rodionova, O.; Ng, H.; Sridhar, B.; Rieffel, E.G.; Biswas, R. Quantum Annealing Applied to De-Conflicting Optimal Trajectories for Air Traffic Management. IEEE Trans. Intell. Transp. Syst. 2019, 21, 285–297. [Google Scholar] [CrossRef] [Green Version]
- Dukalski, M.; Rovetta, D.; van der Linde, S.; Möller, M.; Neumann, N.; Phillipson, F. Quantum computer-assisted global optimization in geophysics illustrated with stack-power maximization for refraction residual statics estimation. Geophysics 2023, 88, V75–V91. [Google Scholar] [CrossRef]
- Ye, Z.; Qian, X.; Pan, W. Quantum Topology Optimization via Quantum Annealing. IEEE Trans. Quantum Eng. 2023, 4, 1–15. [Google Scholar] [CrossRef]
- Lee, D.; Shon, S.; Lee, S.; Ha, J. Size and Topology Optimization of Truss Structures Using Quantum-Based HS Algorithm. Buildings 2023, 13, 1436. [Google Scholar] [CrossRef]
- Sandt, R.; Le Bouar, Y.; Spatschek, R. Quantum annealing for microstructure equilibration with long-range elastic interactions. Sci. Rep. 2023, 13, 6036. [Google Scholar] [CrossRef]
- Tosti Balducci, G.; Chen, B.; Möller, M.; Gerritsma, M.; De Breuker, R. Review and perspectives in quantum computing for partial differential equations in structural mechanics. Front. Mech. Eng. 2022, 8, 75. [Google Scholar] [CrossRef]
- Bayerstadler, A.; Becquin, G.; Binder, J.; Botter, T.; Ehm, H.; Ehmer, T.; Erdmann, M.; Gaus, N.; Harbach, P.; Hess, M.; et al. Industry quantum computing applications. EPJ Quantum Technol. 2021, 8, 25. [Google Scholar]
- Bova, F.; Goldfarb, A.; Melko, R.G. Commercial applications of quantum computing. EPJ Quantum Technol. 2021, 8, 2. [Google Scholar] [CrossRef]
- Airbus. Airbus Quantum Computing Challenge: Bringing Flight Physics into the Quantum Era. 2019. Available online: https://www.airbus.com/en/innovation/disruptive-concepts/quantum-technologies/airbus-quantum-computing-challenge (accessed on 6 November 2019).
- Volkswagen. Volkswagen Optimizes Traffic Flow with Quantum Computers. 2019. Available online: https://www.volkswagen-newsroom.com/en/press-releases/volkswagen-optimizes-traffic-flow-with-quantum-computers-5507 (accessed on 4 September 2020).
- Glover, F.; Kochenberger, G.; Du, Y. A Tutorial on Formulating and Using QUBO Models. arXiv 2018, arXiv:1811.11538. [Google Scholar]
- Johnson, M.W.; Amin, M.H.S.; Gildert, S.; Lanting, T.; Hamze, F.; Dickson, N.; Harris, R.; Berkley, A.J.; Johansson, J.; Bunyk, P.; et al. Quantum annealing with manufactured spins. Nature 2011, 473, 194–198. [Google Scholar] [CrossRef]
- Boixo, S.; Albash, T.; Spedalieri, F.M.; Chancellor, N.; Lidar, D.A. Experimental signature of programmable quantum annealing. Nat. Commun. 2013, 4, 2067. [Google Scholar] [CrossRef] [Green Version]
- Borle, A.; Lomonaco, S.J. Analyzing the quantum annealing approach for solving linear least squares problems. In Proceedings of the International Workshop on Algorithms and Computation, Guwahati, India, 27 February–2 March 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 289–301. [Google Scholar]
- Shin, S.W.; Smith, G.; Smolin, J.A.; Vazirani, U. How “Quantum” is the D-Wave Machine? arXiv 2014, arXiv:1401.7087. [Google Scholar]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- Biswas, R.; Jiang, Z.; Kechezhi, K.; Knysh, S.; Mandrà, S.; O’Gorman, B.; Perdomo-Ortiz, A.; Petukhov, A.; Realpe-Gómez, J.; Rieffel, E.; et al. A NASA perspective on quantum computing: Opportunities and challenges. Parallel Comput. 2017, 64, 81–98. [Google Scholar] [CrossRef] [Green Version]
- McGeoch, C.C.; Harris, R.; Reinhardt, S.P.; Bunyk, P.I. Practical Annealing-Based Quantum Computing. Computer 2019, 52, 38–46. [Google Scholar] [CrossRef]
- McGeoch, C.C. Adiabatic Quantum Computation and Quantum Annealing: Theory and Practice; Morgan & Claypool Publishers LLC: San Rafael, CA, USA, 2014; Volume 5, pp. 1–93. [Google Scholar]
- Wils, K. Truss Sizing Optimization: Symbolic Finite Element Method QUBO Repository. DataverseNL. 2020. Available online: https://dataverse.nl/dataset.xhtml?persistentId=doi:10.34894/PYZGEX (accessed on 4 September 2020).
- Ajagekar, A.; Humble, T.; You, F. Quantum Computing based Hybrid Solution Strategies for Large-scale Discrete-Continuous Optimization Problems. arXiv 2019, arXiv:1910.13045. [Google Scholar] [CrossRef]
- D-Wave Systems Inc. Technical Description of the D-Wave Quantum Processing Unit: User Manual; D-Wave Systems Inc.: Burnaby, BC, Canada, 2020. [Google Scholar]
- D-Wave Systems Inc. QPU Properties: D-Wave 2000Q Online System (DW_2000Q_2_1): User Manual; D-Wave Systems Inc.: Burnaby, BC, Canada, 2019. [Google Scholar]
- Lucas, A. Hard combinatorial problems and minor embeddings on lattice graphs. Quantum Inf. Process. 2019, 18, 203. [Google Scholar] [CrossRef] [Green Version]
- Kochenberger, G.; Hao, J.K.; Glover, F.; Lewis, M.; Lü, Z.; Wang, H.; Wang, Y. The unconstrained binary quadratic programming problem: A survey. J. Comb. Optim. 2014, 28, 58–81. [Google Scholar] [CrossRef] [Green Version]
- Vyskočil, T.; Pakin, S.; Djidjev, H.N. Embedding Inequality Constraints for Quantum Annealing Optimization. In Quantum Technology and Optimization Problems; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 11–22. [Google Scholar]
- Dattani, N. Quadratization in discrete optimization and quantum mechanics. arXiv 2019, arXiv:1901.04405. [Google Scholar]
- D-Wave Systems Inc. dimod.make_quadratic. 2023. Available online: https://docs.ocean.dwavesys.com/en/stable/docs_dimod/reference/generated/dimod.make_quadratic.html (accessed on 8 August 2023).
- Fang, Y.L.; Warburton, P.A. Minimizing minor embedding energy: An application in quantum annealing. arXiv 2019, arXiv:1905.03291. [Google Scholar] [CrossRef]
- D-Wave Systems Inc. D-Wave Solver Properties and Parameters Reference: User Manual; D-Wave Systems Inc.: Burnaby, BC, Canada, 2020. [Google Scholar]
- Stolpe, M. Truss optimization with discrete design variables: A critical review. Struct. Multidiscip. Optim. 2016, 53, 349–374. [Google Scholar] [CrossRef]


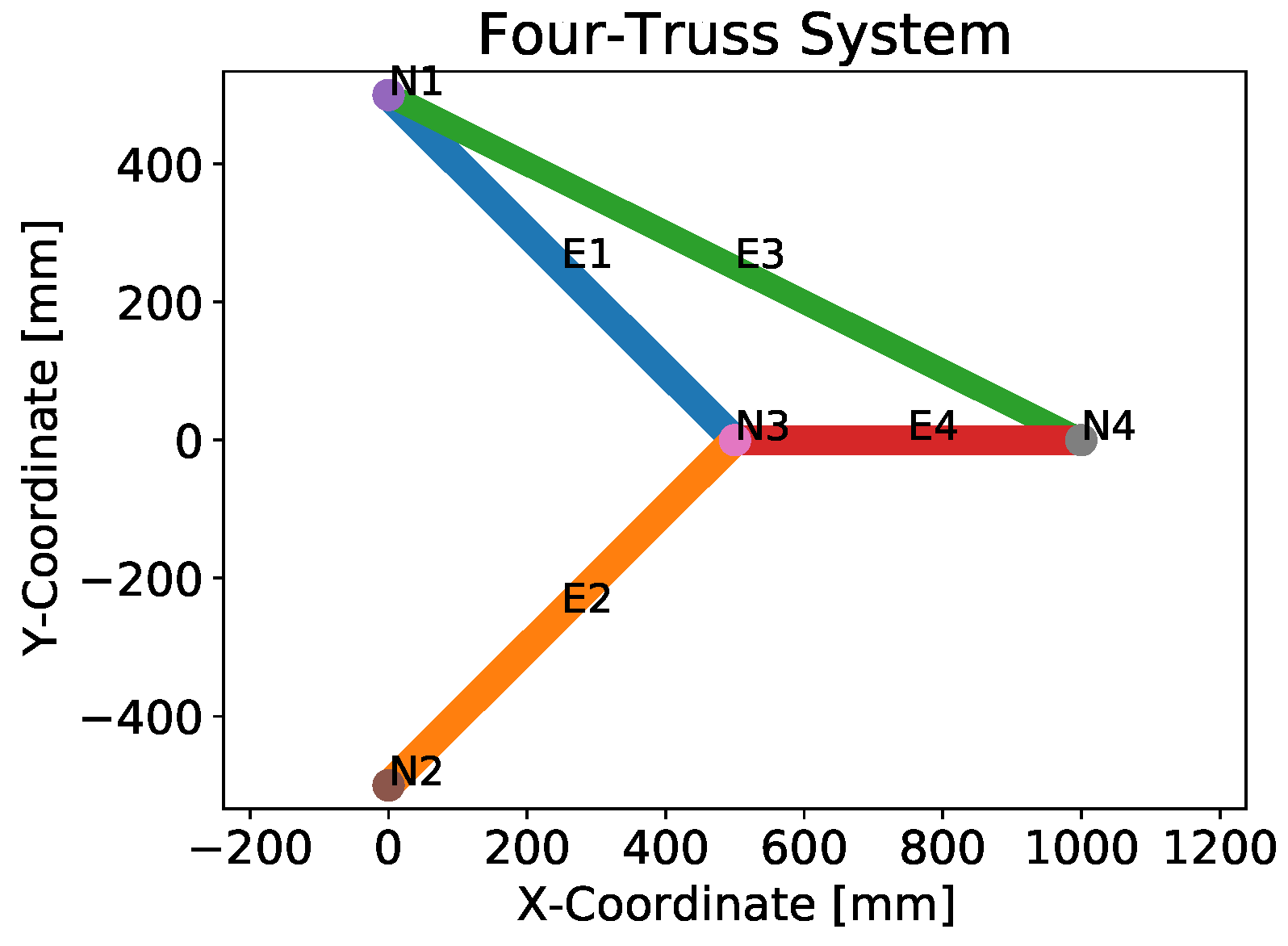




| Two-Truss | Three-Truss | Four-Truss | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Nodes | Node | X (mm) | Y (mm) | Node | X (mm) | Y (mm) | Node | X (mm) | Y (mm) |
| N1 | 0 | 0 | N1 | −500 | 500 | N1 | 0 | 500 | |
| N2 | 1000 | −1000 | N2 | −500 | −500 | N2 | 0 | −500 | |
| N3 | 0 | −1000 | N3 | 500 | 100 | N3 | 500 | 0 | |
| - | - | - | N4 | 0 | 0 | N4 | 1000 | 0 | |
| Elements | Element | Start Node | End Node | Element | Start Node | End Node | Element | Start Node | End Node |
| E1 | N1 | N2 | E1 | N1 | N4 | E1 | N1 | N3 | |
| E2 | N2 | N3 | E2 | N2 | N4 | E2 | N2 | N3 | |
| - | - | - | E3 | N3 | N4 | E3 | N1 | N4 | |
| - | - | - | - | - | - | E4 | N3 | N4 | |
| Load | Node | (kN) | (kN) | Node | (kN) | (kN) | Node | (kN) | (kN) |
| N2 | 0 | −70 | N4 | 0 | −100 | N4 | 0 | −100 | |
| BCs | Node | (mm) | (mm) | Node | (mm) | (mm) | Node | (mm) | (mm) |
| N1 | 0 | 0 | N1 | 0 | 0 | N1 | 0 | 0 | |
| N3 | 0 | 0 | N2 | 0 | 0 | N2 | 0 | 0 | |
| - | - | - | N3 | 0 | 0 | - | - | - | |
| Two-Truss Choices (mm2) | Three-Truss Choices (mm2) | Four-Truss Choices (mm2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Elements | Small | Mid | Large | Small | Mid | Large | Small | Mid | Large |
| E1 | 800 | 900 | 1000 | 400 | 500 | 600 | 2400 | 2500 | 2600 |
| E2 | 1400 | 1500 | 1600 | 950 | 1050 | 1150 | 2400 | 2500 | 2600 |
| E3 | - | - | - | 700 | 800 | 900 | 1900 | 2000 | 2100 |
| E4 | - | - | - | - | - | - | 2400 | 2500 | 2600 |
| Parameters | Brute Force | Quantum Annealing | ||||
|---|---|---|---|---|---|---|
| Truss system | 2-truss | 3-truss | 4-truss | 2-truss | 3-truss | 4-truss |
| Total number of times analyzed | 3 | 3 | 3 | 10 | 10 | 10 |
| Maximum number of iterations | NA | NA | NA | 15 | 15 | 15 |
| Iteration convergence threshold | NA | NA | NA | |||
| Number of reads per iteration | NA | NA | NA | |||
| Highest order terms allowed | NA | NA | NA | 2 | 3 | 4 |
| Linear scaling maximum magnitude | NA | NA | NA | 1 | 1 | 1 |
| Non-linear scaling strength | NA | NA | NA | 0.1 | 0.1 | 0.1 |
| Unary constraint strength | NA | NA | NA | 10 | 10 | 20 |
| Quadratization strength | NA | NA | NA | 10 | 10 | 20 |
| Precision truncation magnitude | NA | NA | NA | |||
| Chain strength | NA | NA | NA | 10 | 30 | 30 |
| Annealing time (μs) | NA | NA | NA | 20 | 20 | 20 |
| Item | Specifications |
|---|---|
| Device | Lenovo Legion Y540-15IRH |
| CPU | Intel Core i7-9750H 2.6 GHz |
| Memory | 16 GB DDR4 2667 MHz |
| GPU | Mobile NVIDIA RTX 2060 6 GB |
| Truss System | Variables | Setup Time (s) | Growth Factor |
|---|---|---|---|
| 2 | 6 | 13.504 | - |
| 3 | 9 | 81.390 | 6.0270 |
| 4 | 12 | 3430.542 | 42.1494 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wils, K.; Chen, B. A Symbolic Approach to Discrete Structural Optimization Using Quantum Annealing. Mathematics 2023, 11, 3451. https://doi.org/10.3390/math11163451
Wils K, Chen B. A Symbolic Approach to Discrete Structural Optimization Using Quantum Annealing. Mathematics. 2023; 11(16):3451. https://doi.org/10.3390/math11163451
Chicago/Turabian StyleWils, Kevin, and Boyang Chen. 2023. "A Symbolic Approach to Discrete Structural Optimization Using Quantum Annealing" Mathematics 11, no. 16: 3451. https://doi.org/10.3390/math11163451
APA StyleWils, K., & Chen, B. (2023). A Symbolic Approach to Discrete Structural Optimization Using Quantum Annealing. Mathematics, 11(16), 3451. https://doi.org/10.3390/math11163451







