Abstract
In this paper, the adaptive synchronization problem of quaternion-valued Cohen–Grossberg neural networks (QVCGNNs), with and without known parameters, is investigated. On the basis of constructing an appropriate Lyapunov function, and utilizing parameter identification theory and decomposition methods, two effective adaptive feedback schemes are proposed, to guarantee the realization of global synchronization of CGQVNNs. The control gain of the above schemes can be obtained using the Matlab LMI toolbox. The theoretical results presented in this work enrich the literature exploring the adaptive synchronization problem of quaternion-valued neural networks (QVNNs). Finally, the reliability of the theoretical schemes derived in this work is shown in two interesting numerical examples.
Keywords:
Cohen–Grossberg neural networks; quaternion; adaptive control; synchronization; linear matrix inequality (LMI) MSC:
34D06
1. Introduction
Over recent decades, Cohen–Grossberg neural networks (CGNNs), which were introduced and explored by Cohen and Grossberg [1], have aroused widespread interest for their potential applications in image processing, control problems, and optimizations, and a variety of outcomes utilizing CGNNs have been reported [2,3,4,5,6,7,8]. However, these results have mainly been concentrated in the real (complex) number field, and there are few reports on the exploration of CGNNs with quaternion parameters in the literature [9,10].
A quaternion, initially introduced and explored by Hamilton [11], consists of a real unit and three imaginary units. If we regard a quaternion as an extension of plural space into real space with higher dimensions, that is, treat a quaternion as four-dimensional real space, then problems that cannot be solved in three-dimensional space can be solved by mapping to four-dimensional space, such as gimbal lock, image compression, and so on. It is worth mentioning that, differently from the real number and plural, the multiplication exchange law no longer supports quaternions, which makes it more difficult to explore the dynamics of QVNNs. Therefore, studying the dynamic characteristics of QVNNs is a challenging topic. Recently, many results such as the -stability [12,13], stability [14,15,16,17,18], anti-synchronization [19,20], and synchronization [21,22,23,24,25,26] of QVNNs have been reported. However, to the best of our knowledge, there are few reports on the dynamic characteristics of QVCGNNs in the literature. Therefore, it is necessary to further explore QVCGNNs.
Synchronization involves coupled systems reaching identical dynamical behaviors at the same time. Since the synchronization of two chaotic systems was first achieved in 1990 by Pecora and Carrol [27] using the drive–response method, chaos synchronization began to enter the field of vision of researchers.To solve the synchronization problem, scholars have designed many control methods and obtained various outcomes [19,20,21,22,23,24,25,26,28,29,30,31,32]. Based on the Lyapunov stability theory and introducing a new definition for global quasi-synchronization, Refs. [21,29] explored the quasi-synchronization problem of chaotic systems with parameter mismatch. Based on parameter identification and utilizing adaptive control and Lyapunov functionals, Ref. [24] successfully explored exponential synchronization of CGNNs. For memristive neural networks (MNNs), refs. [22,26] designed different controllers to explore fixed-time synchronization in a quaternion field. Through dividing the model into equivalent real-valued systems, utilizing fixed-time theory, and constructing novel nonlinear feedback controllers, fixed-time synchronization of a neural network with delays was investigated in [23]. Based on the adaptive control theory and by designing a linear feedback controller with an update law, Ref. [32] achieved the synchronization of two coupled neural networks in the case of known or unknown parameters. However, reports about the synchronization of CGQVNNs are rare, let alone adaptive synchronization.
Motivated by the aforementioned factor, the goal of this work was to investigate the adaptive synchronization control of CGQVNNs, with and without known parameters. The main contributions of this work are outlined as follows:
- (1)
- Reports focusing on the adaptive synchronization of QVCGNNs are rare. This is the first exploration of the adaptive synchronization of QVCGNNs with known or unknown parameters;
- (2)
- Different easy to implement feedback control schemes are designed, to guarantee adaptive synchronization in the case of known and unknown parameters, utilizing parameter identification theory, decomposition methods, and Lyapunov theory;
- (3)
- QVNNs are an expansion of RVNNs and CVNNs; hence, the theoretical results presented in this paper can also be applied to RVNNs and CVNNs.
The remaining contents of this work are summarized as follows: In Section 2, we introduce the network model and preliminaries. The schemes of adaptive control are given in Section 3. In Section 4, simulation examples are presented, to demonstrate the correctness of the results.
Notations: denotes a quaternion-valued field. and denote the n-dimensional quaternion-valued vector space and the quaternion-valued matrix space with dimensions, respectively. and denote the n-dimensional real-valued vector space the real-valued matrix space with dimensions, respectively. means that C is a negative (positive) definite matrix. The smallest eigenvalue of matrix A is denoted by .
2. Model Description and Preliminaries
A quaternion , consisting of a real part and three imaginary parts, can be described as
where , ,, . , , are imaginary units. , , follow the Hamilton rules:
For any , means conjugate with , means modulus. means the norm, where .
For the two different quaternions q and p, where ; then, using the Hamilton rule, we can denote as
Remark 1.
According to the Hamilton rules, we can see that the commutative law does not hold for quaternion multiplication. For this reason, natures that hold for the real and complex fields may not be applicable to quaternions, which greatly increases the difficulty of calculation and analysis, and the previous methods dealing with RVNNS and CVNNs cannot be applied directly to QVNNs.Therefore, how to choose different methods for exploring the dynamic behaviors of QVNNs is a challenging problem.
Consider the following simplified QVCGNNs with time delays:
where represents the state vector. stands for the amplification gain. denotes the vector-valued behaved function. A, denote the connection weight matrix and the delayed connection weight matrix, respectively. and represent activation function without and with time delays, respectively. is the time delay with . stands for the external input vector.
Remark 2.
Compared with typical CGNNs, the amplification function in model (1) is constant. Thus, model (1) is a special case of the classical CGNNs.
For research purposes, the following assumptions are given:
Assumption 1.
Assume that for , there exist real diagonal matrices with , such that
Similarly, for , there exist real diagonal matrices with such that
Assumption 2.
Assume that, for , can be expressed as
Lemma 1 ([33]).
Assume that are real matrices with appropriate dimensions and satisfies , then for , one has
Then, the response system is designed as follows:
where is the response state vector, , is the external control input.
Define as the synchronization error signal between the drive and response system, then
where , , .
For reasons of simplicity, we show , , , . Let . Then, the error system can be divided into the following equivalent system:
where
To achieve global synchronization, we design a control scheme, as follows:
where . , are the coupling strength matrices that are updated on the basis of the following adaptive law:
where , , , are positive constants to be determined later, for . In addition, let .
3. Main Results
In this section, several criteria are proposed for achieving global synchronization of systems (1) and (4) with known and unknown parameters through designing effective controllers.
Theorem 1.
Assume that Assumption 1 holds if a positive matrix S and four positive diagonal matrices , , , exist, such that
where
Then, under the control function of the controller (6) and corresponding adaptive rule (7), systems (1) and (4) will be globally synchronized.
Proof.
First, we define the Lyapunov function through the following:
Combining with Lemma 2, the derivative of with respect to t through the solutions of system (5) is as follows:
where .
In the light of (2), for , we can obtain:
where , , , .
In the light of (3), the following inequality holds:
Based on (10)–(12), we obtain
where
According to (8), we know that is a negative definite matrix; thus, there exists a constant such that
where .
Therefore, the proof is completed and the global synchronization problem of QVCGNNs with known parameters is finally solved.
It is remarkable that certain parameter values of the system cannot be accurately known in practical applications, and such uncertain factors will disrupt synchronization. Therefore, it is of great significance to explore the adaptive synchronization of two QVCGNNs in the case of unknown parameters. Therefore, the drive system defined by us remains the same as (1), and the response system with unknown parameters is as follows:
where , are uncertain or unknown matrices that we need to estimate.
Here, the synchronization error signal between the response system (14) and drive system (1) remains denoted by . Then, the error dynamical system is as follows:
where
and , . □
Theorem 2.
If Assumption 1 holds, the positive matrix S and four positive diagonal matrices , , , exist, such that inequality (8) holds and the adaptive rules of parameter matrices , are designed as
where , any with , .
Then, using the control function of controller (6), as well as the corresponding adaptive rule (7), systems (1) and (14) will achieve global synchronization. Moreover, for
Proof.
First, the Lyapunov function is defined as
Calculating the derivative of and combining it with the inequalities (11) and (12), as well as Lemma 1 and the adaptive rules of the parameter matrices (16), we obtain
where parameters such as and are defined in exactly the same manner as those defined in inequality (13).
Therefore, global synchronization between system (1) and system (14) is realized. □
Remark 3.
According to theorems 1 and 2, constructing an appropriate Lyapunov function, and utilizing parameter identification theory, two effective adaptive feedback schemes are proposed, to guarantee the realization of global synchronization for quaternion-valued Cohen–Grossberg neural networks, with and without known parameters.
Remark 4.
It is worth mentioning that RVNNs and CVNNs are special cases of QVNNs, when and , respectively. Therefore, the adaptive synchronization criteria proposed in this paper could be applied to the problem of synchronization of other RVNNs and CVNNs.
4. Numerical Examples
In order to demonstrate the effectiveness and reliability of the synchronization schemes proposed in this paper, two interesting examples are given in this section.
Example 1.
Taking into account the following model as the drive system:
the response system is
where
and , . , , for and , , for is given as initial values.
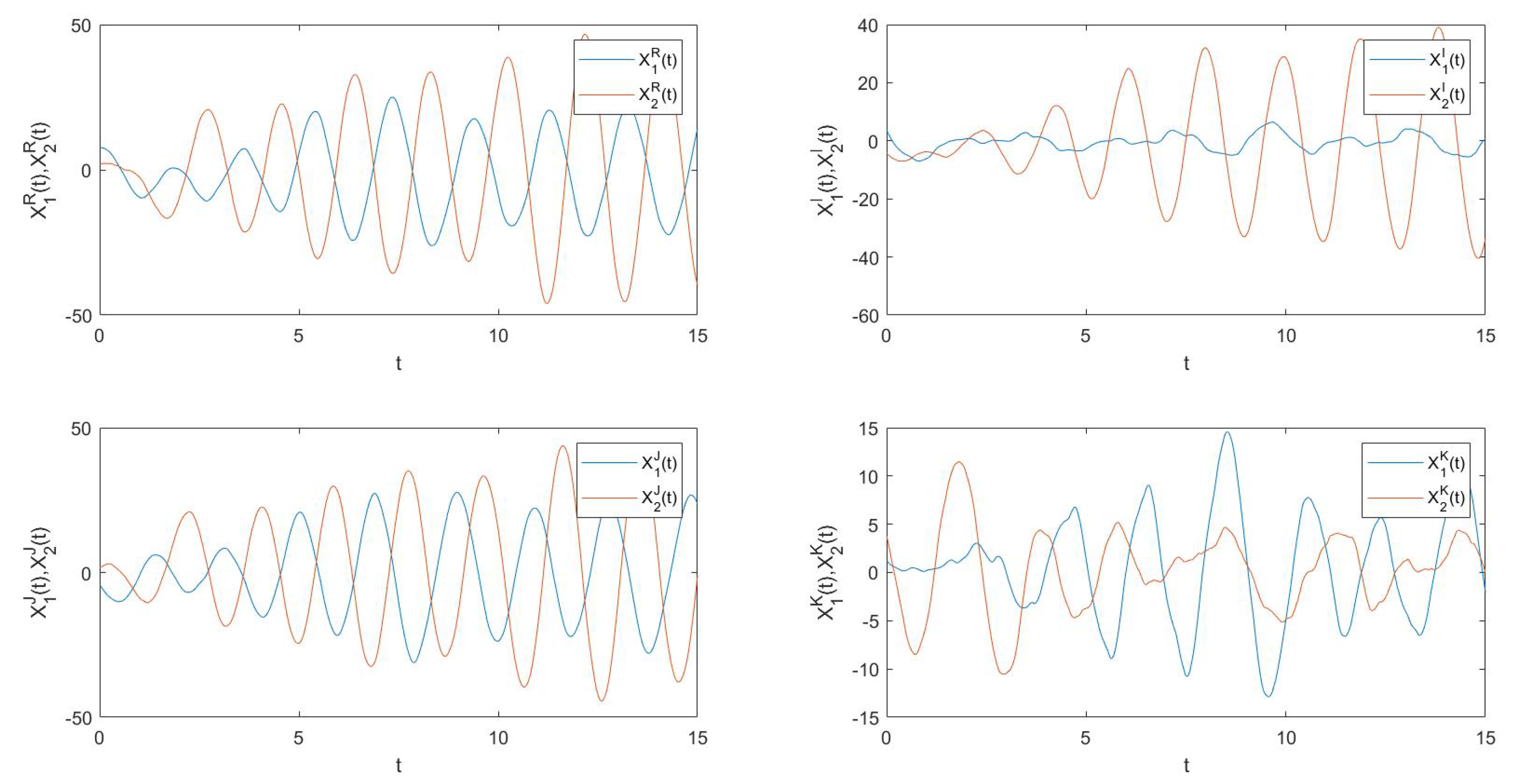
The error trajectories for the drive and response system without control are depicted in Figure 1, from which we can easily observe that the drive–response system has not achieved synchronization.
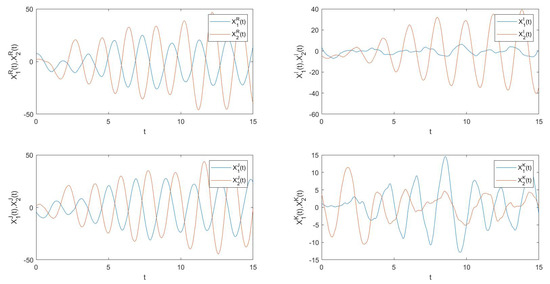
Figure 1.
The error trajectories for the drive–response system without control.
In light of Theorem 1, and by utilizing the Matlab LMI toolbox, a set of solutions is obtained, as follows: , , , , , , , . Thus, the conclusion that the drive and response system will achieve global synchronization under the adaptive controller (6) can be drawn.
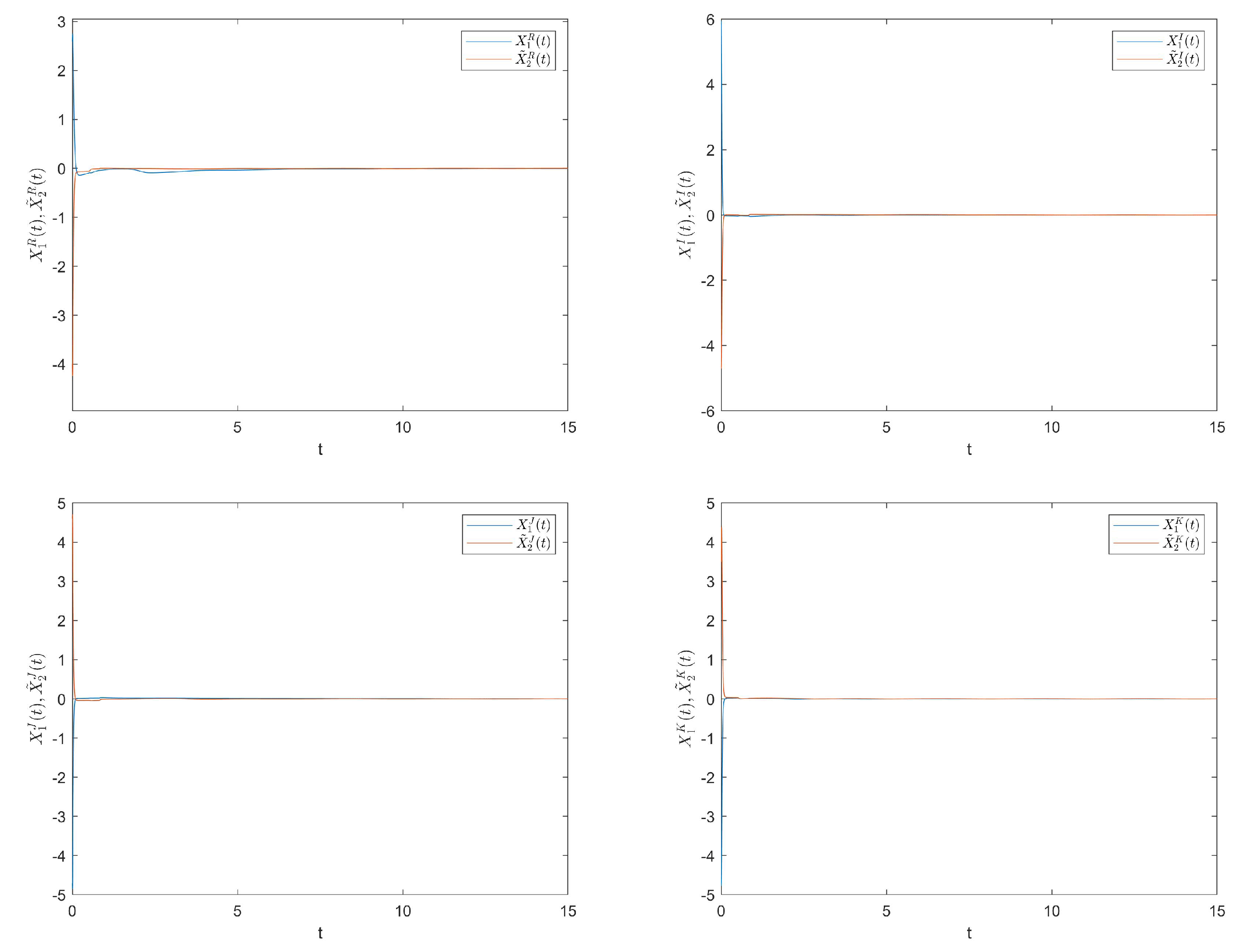
Choose initial values of control gains , , , , , , , . Figure 2 shows the trajectories of the synchronization errors between and . That is to say, system (1) and system (4) have evidently realized global synchronization.
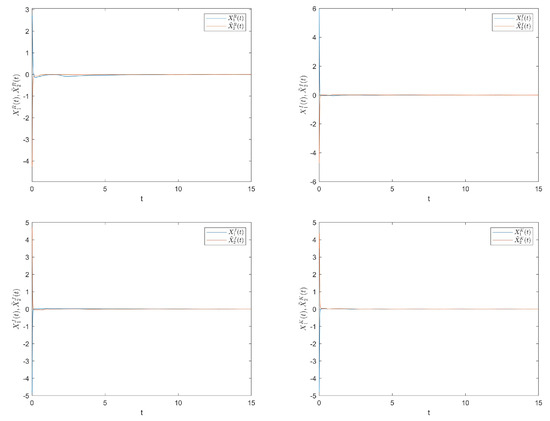
Figure 2.
The trajectories of synchronization errors between and .
Example 2.
Consider system (1) as the drive system, and give parameters as
and , .
Then, let us regard system (14) as the response system with unknown parameters. For reasons of simplicity, we will only identify four parameters: , , , . Hence, the connection weight matrices needed for identification are given in the following form as
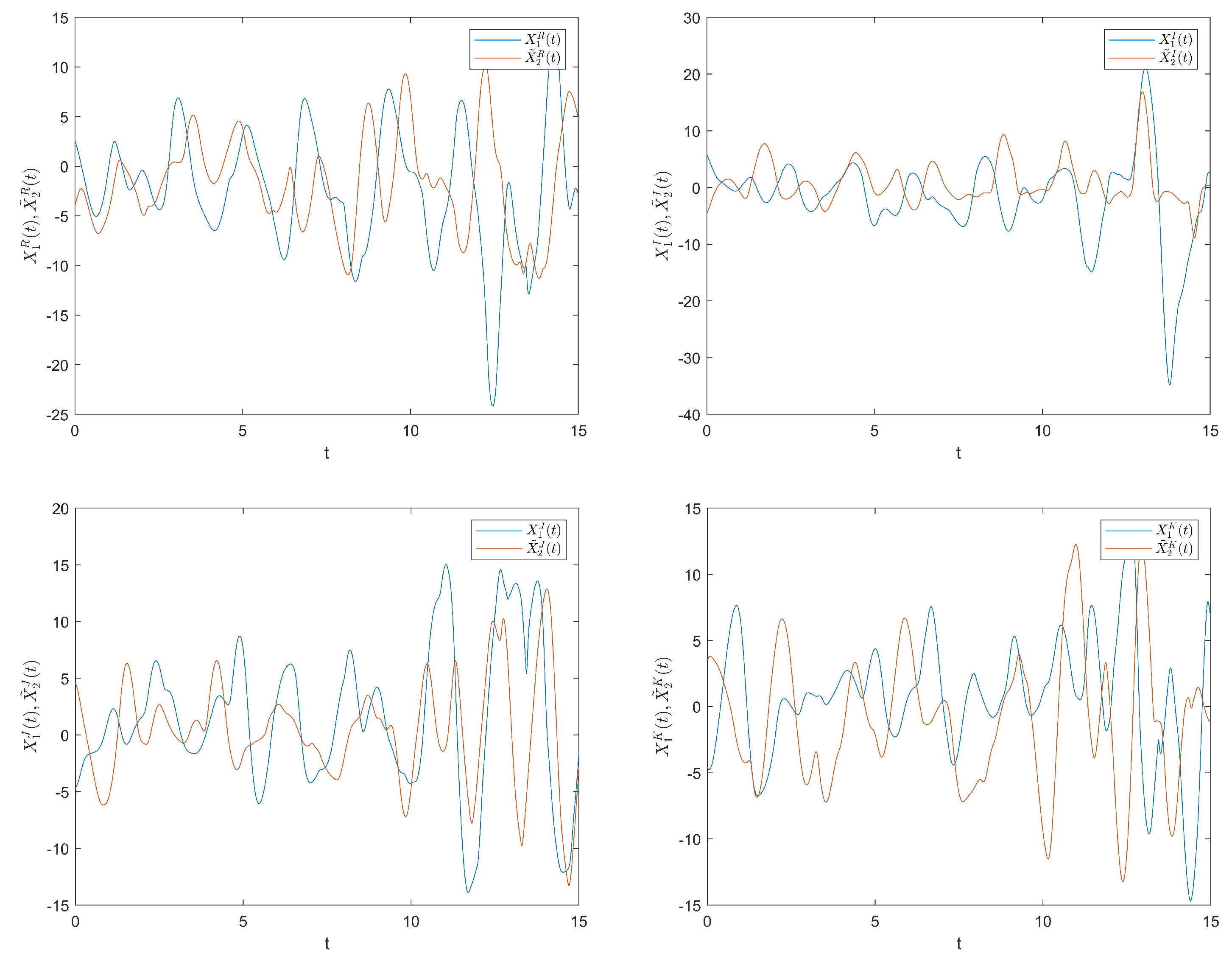
Choose initial values as , , for and , , for . Then, the error trajectories for the drive and response system without control are depicted in Figure 3, which shows that the drive and response system cannot achieve synchronization.
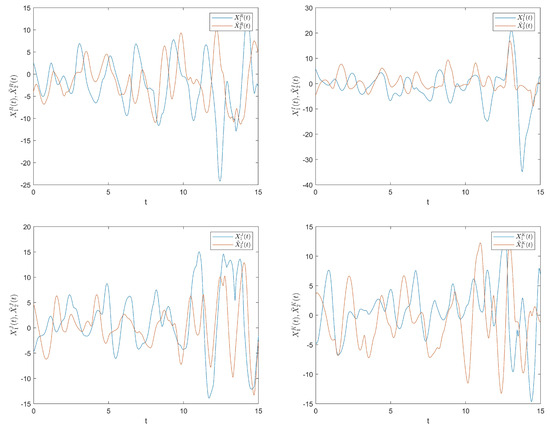
Figure 3.
The trajectories of synchronization errors between and without control .
In light of Theorem 2, and by utilizing the Matlab LMI toolbox, a set of solutions is obtained, as follows: , , , , , , , , which implies that system (1) and system (14) will be globally synchronized under the influence of the adaptive control scheme proposed in Theorem 2.
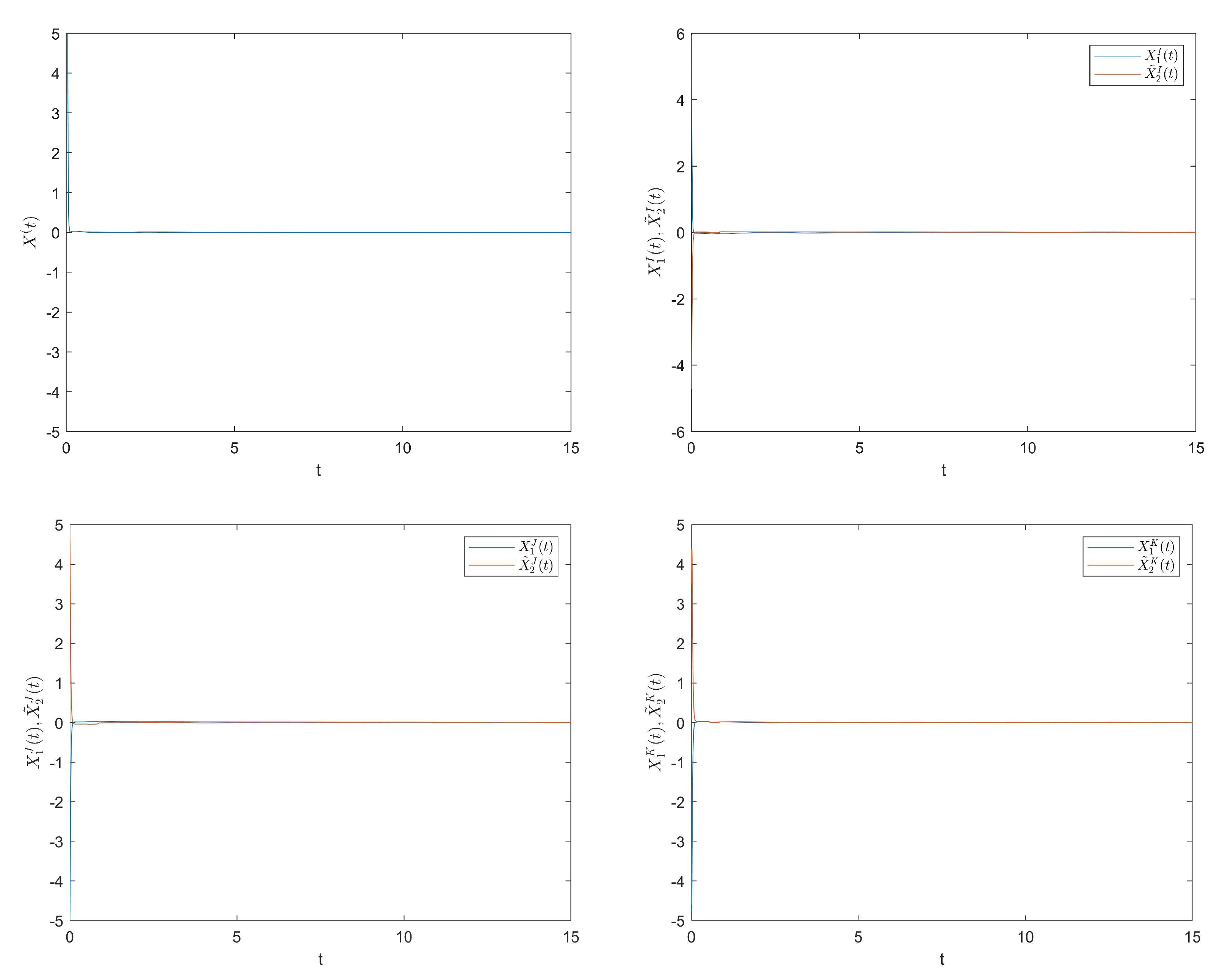
Choose initial values of control gains . Figure 4 shows the trajectories of the synchronization errors between and . Obviously, the drive system and response system have achieved global synchronization under the adaptive control scheme proposed in Theorem 2.
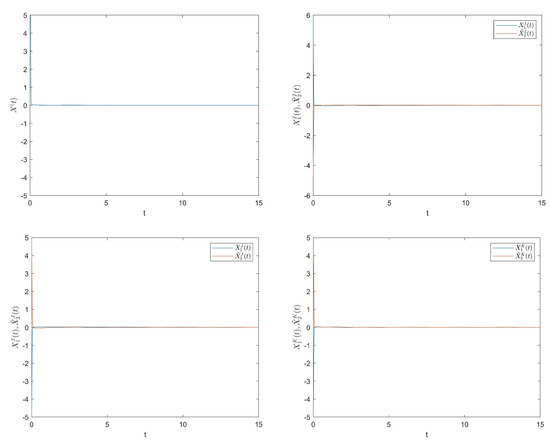
Figure 4.
The trajectories of synchronization errors between and .
5. Conclusions
In this paper, under the precondition of decomposing QVCGNNs into equivalent real-valued systems, the adaptive synchronization criteria of QVCGNNs with and without known parameters were explored. Using Lyapunov theory and the LMI technique, easy to implement controllers with simple adaptive rules were designed in the case of known parameters. Moreover, aiming at QVCGNNs with unknown parameters, an adaptive feedback control scheme combining adaptive control theory and parameter identification was proposed. Differently from the existing results, this paper discussed the adaptive synchronization of QVCGNNs with known or unknown parameters for the first time. Finally, the correctness of the schemes was demonstrated through two examples and corresponding simulations.
Author Contributions
Writing—original draft, Y.S. and W.L.; writing—review & editing, Y.C. and S.W.; project administration, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 61703354; the Sichuan National Applied Mathematics construction project 2022ZX004; the CUIT KYTD202243; the Scientific Research Foundation of Chengdu University of Information Technology KYTZ202184; Scientific Research Fund of Hunan Provincial Science and Technology Department 2022JJ30416.
Data Availability Statement
The datasets generated during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors extend their appreciation to the supported by the National Natural Science Foundation of China under Grant 61703354; the Sichuan National Applied Mathematics construction project 2022ZX004; the Scientific Research Foundation of Chengdu University of Information Technology KYTZ202184; the CUIT KYTD202243; Scientific Research Fund of Hunan Provincial Science and Technology Department 2022JJ30416; the Scientific Research Funds of Hunan Provincial Education Department 22A0483.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Cohen, M.; Grossberg, S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans. Syst. Cybern. 1983, 13, 815–826. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, J.; Zhou, D. Novel LMI-Based Condition on Global Asymptotic Stability for a Class of Cohen-Grossberg BAM Networks With Extended Activation Functions. IEEE Trans. Neural Netw. Learn. 2014, 25, 1161–1172. [Google Scholar]
- Yang, X.; Cao, J.; Yu, W. Exponential synchronization of memristive Cohen-Grossberg neural networks with mixed delays. Cogn. Neurodyn 2014, 8, 239–249. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Cao, J. Finite-time synchronization of memristive Cohen-Grossberg neural networks with time delays. Neurocomputing 2020, 377, 159–167. [Google Scholar] [CrossRef]
- Zhang, C.; Deng, F.; Peng, Y.; Zhang, B. Adaptive synchronization of Cohen-Grossberg neural network with mixed time-varying delays and stochastic perturbation. Appl. Math. Comput. 2015, 269, 792–801. [Google Scholar] [CrossRef]
- Zheng, M.; Li, L.; Peng, H. Finite-time stability and synchronization for memristor-based fractional-order Cohen-Grossberg neural network. Eur. Phys. J. B 2016, 89, 204. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, S. Global asymptotic stability for a class of complex-valued Cohen-Grossberg neural networks with time delays. Neurocomputing 2016, 171, 1158–1166. [Google Scholar] [CrossRef]
- Li, L. Discrete Analogue for a Class of Impulsive Cohen-Grossberg Neural Networks with Asynchronous Time-Varying Delays. Neural Process. Lett. 2019, 49, 331–345. [Google Scholar] [CrossRef]
- Cheng, Y.; Shi, Y. The Exponential Synchronization and Asymptotic Synchronization of Quaternion-Valued Memristor-Based Cohen-Grossberg Neural Networks with Time-Varying Delays. Neural Process. Lett. 2023, in press. [Google Scholar] [CrossRef]
- Wei, H.; Wu, B.; Tu, Z. Exponential synchronization and state estimation of inertial quaternion-valued Cohen-Grossberg neural networks: Lexicographical order method. Int. J. Robust Nonlinear Control. 2020, 30, 2171–2185. [Google Scholar] [CrossRef]
- Hamilton, W. Lectures on Quaternions; Hodges and Smith: Dublin, Ireland, 1853. [Google Scholar]
- You, X.; Song, Q.; Jing, L.; Liu, Y.; Alsaadi, F. Global μ-stability of quaternion-valued neural networks with mixed time-varying delays. Neurocomputing 2018, 290, 12–25. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.D.; Lu, J.; Cao, J. Global μ-stability criteria for quaternion-valued neural networks with unbounded time-varying delays. Inf. Sci. 2016, 360, 273–288. [Google Scholar] [CrossRef]
- Tu, Z.; Zhao, Y.; Ding, N.; Feng, Y.; Zhang, W. Stability analysis of quaternion-valued neural networks with both discrete and distributed delays. Appl. Math. Comput. 2019, 343, 342–353. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, X.; Yang, J.; Hu, J. Robust Exponential Stability for Discrete-Time Quaternion-Valued Neural Networks with Time Delays and Parameter Uncertainties. Neural Process. Lett. 2020, 51, 2317–2335. [Google Scholar] [CrossRef]
- Xu, X.; Xu, Q.; Yang, J.; Xue, H.; Xu, Y. Further research on exponential stability for quaternion-valued neural networks with mixed delays. Neurocomputing 2020, 400, 186–205. [Google Scholar] [CrossRef]
- Song, Q.; Long, L.; Zhao, Z.; Liu, Y.; Alsaadi, F. Stability criteria of quaternion-valued neutral-type delayed neural networks. Neurocomputing 2020, 412, 287–294. [Google Scholar] [CrossRef]
- Shu, J.; Xiong, L.; Wu, T.; Liu, Z. Stability Analysis of Quaternion-Valued Neutral-Type Neural Networks with Time-Varying Delay. Mathematics 2019, 7, 101. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, S.; Fang, X.; Wang, W. Adaptive anti-synchronization of memristor-based complex-valued neural networks with time delays. Phys. A Stat. Mech. Its Appl. 2019, 535, 122427. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Z.; Zhou, T.; Tan, S. Global Synchronization and Anti-Synchronization of Fractional-Order Complex-Valued Gene Regulatory Networks With Time-Varying Delays. IEEE Access 2020, 8, 150555–150572. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Liao, X.; Fan, Z. Chaos quasisynchronization induced by impulses with parameter mismatches. Chaos: Interdiscip. J. Nonlinear Sci. 2006, 16, 1–101. [Google Scholar] [CrossRef]
- Wei, R.; Cao, J. Fixed-time synchronization of quaternion-valued memristive neural networks with time delays. Neural Netw. 2019, 113, 1–10. [Google Scholar] [CrossRef]
- Deng, H.; Bao, H. Fixed-time synchronization of quaternion-valued neural networks. Phys. A Stat. Mech. 2019, 527, 1–16. [Google Scholar] [CrossRef]
- Hu, J.; Zeng, C. Adaptive exponential synchronization of complex-valued Cohen-Grossberg neural networks with known and unknown parameters. Neural Netw. 2017, 86, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhu, P. Finite-time synchronization of stochastic memristor-based delayed neural networks. Neural Comput. Appl. 2018, 29, 293–301. [Google Scholar] [CrossRef]
- Cheng, Y.; Shi, Y. Exponential synchronization of quaternion-valued memristor-based neural networks with time-varying delays. Int. J. Adapt. Control Signal Process. 2023, 37, 1762–1781. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Huang, J. Chaos synchronization between two novel different hyperchaotic systems with unknown parameters. Nonlinear Anal. 2008, 69, 4174–4181. [Google Scholar] [CrossRef]
- Huang, T.; Li, C.; Liao, X. Synchronization of a class of coupled chaotic delayed systems with parameter mismatch. Chaos 2007, 17, 033121. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Shi, K. Mixed-Delay-Dependent Augmented Functional for Synchronization of Uncertain Neutral-Type Neural Networks with Sampled-Data Control. Mathematics 2023, 11, 872. [Google Scholar] [CrossRef]
- Li, M.; Fan, Y. Aperiodic Sampled-Data Control for Anti-Synchronization of Chaotic Nonlinear Systems Subject to Input Saturation. Axioms 2023, 12, 403. [Google Scholar] [CrossRef]
- He, W.; Cao, J. Adaptive synchronization of a class of chaotic neural networks with known or unknown parameters. Phys. Lett. A 2008, 372, 408–416. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Global stability of complex-valued recurrent neural networks with time-delays. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 853–865. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).